ЭлективныЕ курсы по геометрии вусловиях профильного обучения математике в старших классах (на примере темы «Площадь. Равновеликие и равносоставленные многоугольники») >13. 00. 02 теория и методика обучения и воспитания (математика)

Вид материала

Автореферат

Содержание Утеева Роза Азербаевна Воробьёва Надежда Георгиевна Общая характеристика работы В.В. Прасолов Е.А. Ермак, И.А. Иванов, В.В. Орлов, Н.С. Подходова Объект исследования Цель исследования Гипотеза исследования Методологическую основу Теоретическими предпосылками На первом этапе Научная новизна Теоретическая значимость Практическую значимость На защиту На защиту Апробация результатов исследования Внедрение результатов исследования в практику Структура диссертации Основное содержание работы ... Полное содержание

Подобный материал:

• Элективные курсы (курсы по выбору) играют важную роль в системе профильного обучения, 138.92kb.
• План элективные курсы по физике и их роль в организации профильного и предпрофильного, 158.52kb.
• Вестник Калужского университета 200, 154.13kb.
• Программа вступительных экзаменов по математике и теории и методике обучения математике, 39.16kb.
• Методические особенности обучения школьников математике в классах естественно-научного, 9.62kb.
• Методика обучения решению математических задач учащихся основной школы в условиях дифференциации, 489.79kb.
• Вторая- организация профильного обучения в школе, 1770.94kb.
• Методика обучения геометрии в основной школе с использованием фузионистского подхода, 399.25kb.
• Программа курса повышения квалификации учителей математики, 15.17kb.
• Обучение чтению на английском языке в старших классах якутской школы (базовый уровень), 368.57kb.

На правах рукописи


Ермолаев Евгений Александрович


ЭлективныЕ курсы ПО ГЕОМЕТРИИ

В условиях профильного обучения

математике в старших классах

(на примере темы «Площадь. Равновеликие и

равносоставленные многоугольники»)


13.00.02 - теория и методика обучения и воспитания (математика)


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата педагогических наук


Саранск - 2010


Работа выполнена на кафедре алгебры и геометрии ГОУ ВПО
«Тольяттинский государственный университет»


Научный руководитель: доктор педагогических наук, профессор

Утеева Роза Азербаевна


Официальные оппоненты: доктор педагогических наук, доцент

Егорченко Игорь Викторович

кандидат педагогических наук, доцент

Воробьёва Надежда Георгиевна


Ведущая организация: ГОУ ВПО «Московский педагогический

государственный университет»


Защита состоится «___ » ___________2010 г. в ______часов на заседании диссертационного совета ДМ 212.118.01 по защите докторских и кандидатских диссертаций при ГОУ ВПО «Мордовский государственный педагогический институт им. М.Е. Евсевьева» по адресу: 430007, Республика Мордовия,
г. Саранск, ул. Студенческая, 11а, ауд. 320.


С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «Мордовский государственный педагогический институт им. М.Е. Евсевьева».


Автореферат разослан и размещен на сайте www.mordgpi.ru

«___»___________ 2010 г.


Ученый секретарь

диссертационного совета Л.С. Капкаева




ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность исследования. Концепция модернизации российского образования на старшей ступени общеобразовательной школы (2002 г.) предусматривает профильное обучение, которое обозначено как средство дифференциации и индивидуализации обучения. Оно позволяет за счет изменений в структуре, содержании и организации образовательного процесса более полно учитывать интересы, склонности и способности учащихся, создавать условия для обучения старшеклассников в соответствии с их профессиональными интересами и намерениями в отношении продолжения образования. Профильное обучение, целенаправленный переход к которому в Х-ХI классах общеобразовательных школ РФ начат с 2006/07 учебного года, подразумевает три типа учебных предметов. Базовые общеобразовательные предметы являются обязательными для всех учащихся во всех профилях обучения. Профильные общеобразовательные предметы – предметы повышенного уровня, определяющие направленность каждого конкретного профиля обучения. Элективные курсы – обязательные для посещения курсы по выбору учащихся, входящие в состав профиля обучения на старшей ступени школы. Примерное соотношение объемов данных типов учебных предметов соответственно 50:30:20.

Бесспорным является тот факт, что эффективность внедрения профильного обучения на старшей ступени общеобразовательной школы зависит от уровня разработанности содержательного и методического аспектов структурных компонентов профильного обучения. Как показывает практика, менее разработанным компонентом являются элективные курсы (ЭК).

В современном школьном математическом образовании старшеклассников геометрия находится «в тени» алгебры и начал математического анализа. Эта тенденция проявилась и по отношению к разработке элективных курсов по математике, большинство из которых, по алгебре. Одной из видимых причин сложившейся ситуации, по мнению ряда исследователей, явилось содержание ЕГЭ, в основном ориентированное на алгебраические задания. Исключением пока является демоверсия ЕГЭ 2010 г., в которой наметилась тенденция к увеличению числа заданий по геометрии: 3 в первой части В, 2 – во второй части С. Заслуженное увеличение доли геометрических заданий, в свою очередь, потребует от учителей математики усиления внимания к геометрической составляющей школьного образования.

Отметим, что в настоящее время учеными, авторами школьных и вузовских учебников геометрии, учителями-практиками разработаны некоторые элективные курсы по геометрии: «Алгебраические поверхности второго порядка»; «Геометрические построения на изображениях» (А.Ж. Жафяров); «Избранные задачи планиметрии»; «Геометрия окружностей»; «Треугольники и многоугольники»
( В.В. Прасолов); «Многогранники»; «Изображение пространственных фигур» (И.М. Смирнова, В.А. Смирнов); «Векторы и координаты как аппарат решения геометрических задач» (Е.В. Потоскуев); «Математика в архитектуре»
(Н.Л. Стефанова); «Геометрическое моделирование окружающего мира»
( Е.А. Ермак, И.А. Иванов, В.В. Орлов, Н.С. Подходова); «Инверсия и её приложение к решению задач» (А.В. Дмитриева); «Аналитическая геометрия для 10-11 классов» (О.Ю. Веслополова и В.Б. Поддельская).

Анализ ранее выполненных диссертационных работ, посвященных элективным курсам, показал, что они были рассмотрены в аспекте: формирования компетенций (А.В. Гетманская, 2003; А.А. Федорова, 2009); дифференциации обучения (С.В. Дорожкин, 2004); комплексов средств обучения (Н.С. Кудинова, 2005); методики реализации профильного обучения (Г.Э. Шахвеледов, 2005); конструирования и проектирования содержания (С.В. Студилин, 2004;
В.В. Бесценная, 2006; Ю.К. Нимировская, 2006; М.Г. Победоносцева, 2008); развития познавательной активности учащихся (Л.В. Федяева, 2008); преемственности между предпрофильной и профильной подготовкой по математике (О.И. Голованёва, 2006; Л.П. Коннова, 2009). Непосредственно элективным курсам по геометрии посвящены две работы: Н.Н. Зепновой (2005), в которой основное внимание уделено формированию пространственного мышления учащихся; А.С. Рвановой (2006) - реализации целевого и содержательного компонентов для классов математического профиля на основе локальной аксиоматизации.

Итак, можно констатировать, что элективные курсы по геометрии востребованы на практике; имеется опыт их проектирования и реализации в условиях профильного обучения математике, проведены ряд исследований. Однако в них методическая система проектирования элективных курсов по геометрии не являлась предметом специальных исследований. Констатирующий этап эксперимента, анализ научно-методической литературы по теме профильного обучения математике в общеобразовательной школе позволили выявить ряд малоисследованных проблем: какова роль, место, основные цели элективных курсов по геометрии; каким основным требованиям должно удовлетворять содержание элективных курсов по геометрии; каковы условия эффективной реализации элективных курсов по геометрии; каким должно быть соотношение между элективными и базовыми курсами, между элективными и профильными курсами?

Таким образом, актуальность темы исследования обусловлена сложившимися к настоящему времени противоречиями между необходимостью: 1) перехода к профильному обучению математике в общеобразовательной школе, предусматривающей также элективные курсы по геометрии, и не разработанностью теоретических основ их проектирования; 2) осуществления преемственности базового, профильного и элективного курсов по геометрии и отсутствием требований к отбору содержания последних; 3) предоставления права выбора учащимся, удовлетворения потребностей практики и отсутствием разнообразных по тематике элективных курсов по геометрии и их научно-методического обеспечения.

Указанные противоречия позволили сформулировать проблему диссертационного исследования: выявление особенностей проектирования элективных курсов по геометрии в старших классах общеобразовательной школы с учетом достижения основных целей и задач профильного обучения математике.

Объект исследования: математическое (в частности, геометрическое) образование в старших классах общеобразовательной школы.

Предмет исследования: методическая система проектирования и реализации элективных курсов по геометрии в условиях профильного обучения математике в старших классах (на примере темы «Площадь. Равновеликие и равносоставленные многоугольники»).

Цель исследования заключается в выявлении теоретических основ проектирования элективных курсов по геометрии и разработке методики их реализации в условиях профильного обучения математике учащихся старших классов общеобразовательной школы.

Гипотеза исследования основана на предположении о том, что если при проектировании элективных курсов по геометрии приоритетным компонентом методической системы будет определен содержательный, то элективные курсы по геометрии будут способствовать достижению целей профильного обучения математике и обеспечат преемственность с базовым и профильным курсами.

Для достижения поставленной цели и проверки сформулированной гипотезы необходимо было решить следующие задачи исследования:

1. Уточнить роль, место, цели и функции элективных курсов по геометрии как составной части профильного обучения математике в старших классах.

2. Обосновать и выделить принципы отбора содержания элективных курсов по геометрии в условиях профильного обучения математике учащихся старших классов.

3. Представить теоретическую модель проектирования элективных курсов по геометрии и выявить условия ее успешной реализации на практике.

4. Разработать элективный курс по теме «Площадь. Равновеликие и равносоставленные многоугольники» и его методическое обеспечение (авторскую программу курса, учебное пособие, хрестоматию и др.) с учетом выделенных принципов и построенной модели.

5. Проверить экспериментально эффективность разработанного элективного курса по теме «Площадь. Равновеликие и равносоставленные многоугольники» и методики его реализации.

6. Разработать и апробировать программу подготовки учителей математики к реализации элективных курсов по математике (геометрии).

Для решения поставленных задач применялись следующие методы исследования: анализ психолого-педагогической, научной и учебно-методической литературы; изучение, наблюдение и обобщение школьной практики; анализ собственного опыта работы в школе и в вузе; анкетирование школьников, студентов и учителей; различные виды эксперимента по проверке основных положений исследования; статистические методы обработки результатов; экспертиза разработанного элективного курса.

Методологическую основу исследования составили основные положения деятельностного подхода к обучению математике (В.И. Крупич, Г.И. Саранцев, А.А. Столяр, Т.А. Иванова и др.): процесс обучения математике при реализации элективных курсов проектируется адекватно структуре учебной деятельности учащихся и творческой математической деятельности, направленной на овладение способами этой деятельности и методами научного познания.

Теоретическими предпосылками исследования явились: концепции профильной и уровневой дифференциации обучения математике (В.А. Гусев, Г.В. Дорофеев, Ю.М. Колягин, Г.И. Луканкин, Г.И.Саранцев, И.М. Смирнова, Р.А. Утеева и др.); результаты современных исследований в теории и методике обучения
геометрии (Н.Г. Воробьева, В.А. Гусев, В.А. Далингер, А. Пардала, Н.С. Подходова, Г.И. Саранцев и др.).

Исследование проводилось поэтапно. На первом этапе (2005-2006 гг.) изучалась и анализировалась литература по теме исследования; проводился констатирующий эксперимент. На втором этапе (2006 -2007 гг.) разрабатывалось содержание основных компонентов модели проектирования элективных курсов по геометрии в профильном обучении; принципы и критерии отбора содержания элективных курсов по геометрии; содержание элективного курса «Площадь. Равновеликие и равносоставленные многоугольники»; проводился поисковый эксперимент. На третьем этапе (2007 -2010 гг.) был проведён обучающий эксперимент, проанализированы и обобщены результаты исследования, сформулированы выводы.

Научная новизна проведенного исследования состоит в том, что в нём впервые ставится проблема выявления особенностей проектирования элективных курсов по геометрии в старших классах общеобразовательной школы. Она решена на основе идеи приоритета содержательного компонента построенной методической системы. Такой подход позволил выявить определенные требования к вариативному содержанию школьного курса геометрии (идейно-значимый теоретический материал; возможность построения эвристик, богатство практического материала, разнообразия задач) с учетом основных целей и задач профильного обучения математике. Он обеспечивает преемственность между базовыми, элективными и профильными курсами за счет дальнейшего развития той или иной содержательной линии школьного курса геометрии. Новыми научными результатами исследований являются выявленные теоретические основы проектирования элективных курсов по геометрии и разработанная методика их реализации в условиях профильного обучения математике учащихся общеобразовательных школ.

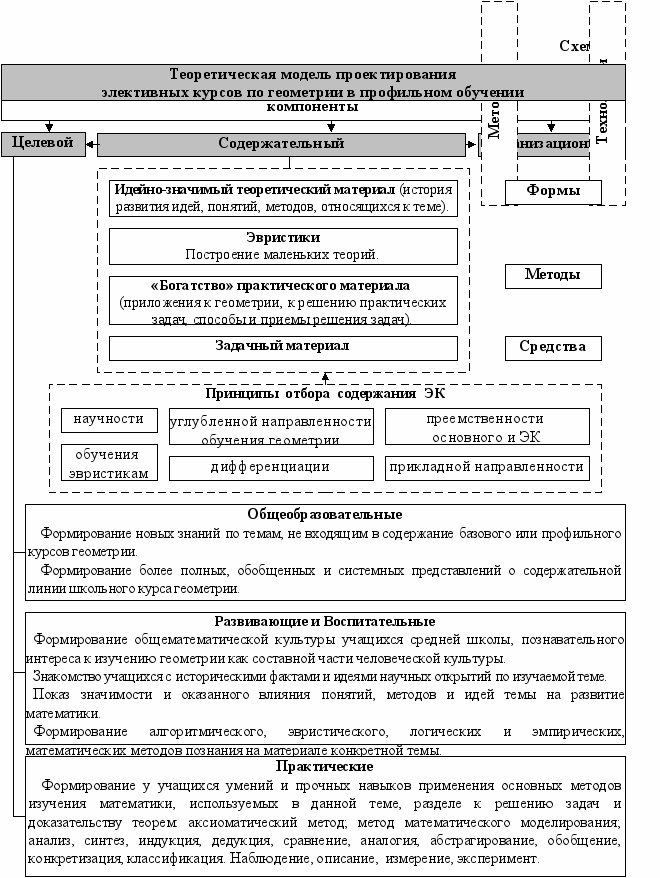
Теоретическая значимость результатов исследования, вносящих определенный вклад в теорию профильной дифференциации обучения математике учащихся старших классов, заключается в том, что в диссертации: проанализированы существующие подходы к проблеме проектирования элективных курсов; уточнены роль, место, цели и функции элективных курсов по геометрии в условиях профильного обучения математике (схема 1, таблица 1); обоснованы и выделены совокупность принципов отбора содержания элективных курсов по геометрии (научности, преемственности, углубленной направленности, обучения эвристикам, дифференциации, прикладной направленности), обеспечивающих достижение основных целей и задач профильного обучения и преемственность между базовым, профильным и элективным курсами; построена теоретическая модель проектирования элективных курсов по геометрии, приоритетным компонентом которой является содержательный (схема 2); разработан элективный курс по геометрии «Площадь. Равновеликие и равносоставленные многоугольники» для учащихся старших классов с учетом выделенных принципов и требований к содержательному компоненту модели (схема 3) и определена его значимость в существенном обогащении содержания математического образования старшеклассников в общеобразовательной школе; выявлены условия успешной реализации модели проектирования элективных курсов по геометрии в профильном обучении математике учащихся старших классов.

Практическую значимость результатов исследования составляют содержание элективного курса по теме «Площадь. Равновеликие и равносоставленные многоугольники» и его научно-методическое обеспечение, которые могут быть использованы в практике работы учителей при реализации профильного обучения в старших классах. Программа совершенствования методической подготовки учителей математики к разработке и реализации элективных курсов по математике может быть использована в практике обучения студентов-математиков и магистров в педвузе, на курсах повышения квалификации учителей математики. Результаты исследования могут быть положены в основу разработки новых элективных курсов как по геометрии, так и по другим предметам.

На защиту выносятся следующие положения:

1. Выявление особенностей проектирования элективных курсов по геометрии в условиях профильного обучения математике требует построения и исследования специальной методической системы. Представленная в диссертации такая методическая система характеризуется целостностью и взаимосвязью целевого, содержательного и организационного компонентов. Приоритетным компонентом системы, влияющим на определение содержания целевого и организационного, выбран содержательный компонент. Такой подход определяет механизм разработки элективных курсов по геометрии, обеспечивает достижение основных целей и задач профильного обучения математике и преемственность между базовым, профильным и элективным курсами.
   
2. Основными принципами отбора содержания элективных курсов по геометрии являются следующие: научности, преемственности, углубленной направленности, обучения эвристикам, дифференциации, прикладной направленности. Содержательно-методические линии школьного курса геометрии могут служить основой проектирования элективных курсов по геометрии при их соответствующем наполнении теоретическим (идеи, факты, понятия, свойства, методы, способы познания) и практическим материалом (задачи, методы и приемы), удовлетворяющим вышеуказанным принципам.
   
3. Целостность и взаимосвязь указанных компонентов методической системы проектирования элективных курсов по геометрии на практике обеспечивает реализацию их основных функций: направленность на углубленное и расширенное изучение геометрии; личностное развитие учащихся (культурная, духовная, интеллектуальная, творческая, эстетическая, нравственная, эмоциональная составляющие); профориентацию учащихся на выбор специальностей, связанных с высоким уровнем общеобразовательной математической подготовки учащихся, в том числе по геометрии.
   
4. Разработанный элективный курс по теме «Площадь. Равновеликие и равносоставленные многоугольники» является примером отбора содержания, основанного: на идейно-значимом теоретическом материале; с разнообразными историческими и практическими приложениями; учитывающего внутрипредметные связи и преемственность с базовым и профильным курсами геометрии; способствующего повышению качества знаний учащихся по геометрии в целом, формированию и развитию логической и эвристической составляющей математического мышления школьников.
   

На защиту также выносятся: методическое обеспечение (программа, содержание занятий, система задач с решениями и указаниями, методические рекомендации, хрестоматии, список тем проектов для учащихся по каждому блоку) разработанного элективного курса; программа подготовки учителей математики к реализации на практике элективных курсов.

Достоверность полученных результатов и обоснованность выводов и рекомендаций, сформулированных в работе, обеспечиваются: их опорой на результаты современных исследователей по теории и методике обучения математике; адекватностью используемого в исследовании методологического и методического инструментария его целям, предмету и задачам; положительными результатами педагогического эксперимента; разнообразием методов исследования.

Апробация результатов исследования осуществлялась путём выступлений на: Международных научных конференциях «Математика. Образование. Культура» (Тольятти, 2005, 2007, 2009), «Новые технологии в обучении математике и информатике в вузе и школе» (Орехово-Зуево, 2007), «Функциональные пространства. Дифференциальные операторы. Общая топология. Проблемы математического образования» (Москва, 2008); Всероссийских научных конференциях (Ульяновск, 2006), «Методическая подготовка студентов математических специальностей педвуза в условиях фундаментализации образования» (Саранск, 2009); выставке научно-технического творчества молодёжи (НТТМ-2006, Москва), семинаре «Геометрическое образование в современной средней и высшей школе» (Тольятти, 2009); научно-методических семинарах и заседаниях кафедры алгебры и геометрии Тольяттинского государственного университета (2005 – 2010), кафедры методики преподавания математики Мордовского государственного педагогического института им. М.Е. Евсевьева (Саранск, 2009).

Экспериментальная проверка разработанного ЭК «Площадь. Равновеликие и равносоставленные многоугольники» осуществлялась лично автором с учащимися 10 классов на занятиях в профильных центрах г.о. Тольятти: МОУ Лицей №19, СШ №41, Гимназия №39; со студентами 4 курса специальности «Математика» ТГУ в рамках спецкурса; в период руководства педагогической практикой студентов 3-5 курсов и при написании ими курсовых работ.

Внедрение результатов исследования в практику: разработанный ЭК «Площадь. Равновеликие и равносоставленные многоугольники» включен в перечень ЭК профильных центров г.о. Тольятти; методические рекомендации автора используются учителями школ; спецкурс «Проектирование и реализация элективных курсов по геометрии» включен в учебный план подготовки будущих учителей математики и в программу подготовки магистров по направлению «Физико-математическое образование» (профиль «Математическое образование») в ТГУ.

Основные результаты исследования отражены в 10 публикациях, одна из которых опубликована в журнале, рекомендованном ВАК.

Структура диссертации определена логикой и последовательностью решения задач исследования. Она состоит из введения, двух глав, заключения, списка литературы и приложений. В тексте диссертации имеются рисунки, таблицы, схемы.


ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность исследования, сформулирована проблема, цель и гипотеза, определены объект и предмет, поставлены задачи исследования, указаны методы, раскрыта новизна, теоретическая и практическая значимость работы, сформулированы основные положения, выносимые на защиту, охарактеризованы основные этапы исследования.

В первой главе раскрываются теоретические основы проектирования ЭК по геометрии в профильном обучении. Глава состоит из пяти параграфов.

В параграфе 1 рассматривается исторический аспект профильного обучения в отечественном и зарубежном образовании. В диссертации показано, что идея дифференциации не является новой, в этом направлении накоплен определенный опыт c начала XVIII века. Одной из первых форм реализации профильной дифференциации обучения в отечественной школе были факультативные курсы, введенные в практику обучения математике в 1967 г. В конце 90-х гг. прошлого века появились различные концепции профильной и уровневой дифференциации обучения математике. Например, по: содержанию для разных групп школьников (Г.В. Дорофеев, Л.В. Кузнецова, С.Б. Суворова, В.В. Фирсов); фуркации учебных планов и программ обучения для разных профилей (гуманитарный, технический, физико-математический, экономический - Ю.М. Колягин, Г.Л. Луканкин, М.В. Ткачева, Н.Е. Федорова); уровням «культуры и знаний» (общекультурный, прикладной и творческий - В.Г. Болтянский, Г.Д. Глейзер); уровням знаний и умений (базисный, основной, углубленный – М.И. Башмаков; базовый, продвинутый и высокий уровень - Р.А. Утеева); профилям (гуманитарный, прикладной и естественно-научный – И.М. Смирнова), структуре личности (мотивационный, операционально-действенный и эмоционально-волевой компоненты – Г.И. Саранцев) и др., которые подготовили почву для дальнейшей модернизации системы математического образования в современной школе. К 2000 г. дифференциация обучения становится ведущей тенденцией в математическом образовании, а элективные курсы – составной частью профильного обучения.

Параграф 2 посвящен определению роли и места элективных курсов в системе профильного обучения математике учащихся старших классов. Под элективными курсами понимаются – обязательные для посещения курсы по выбору учащихся, входящие в состав профиля обучения на старшей ступени школы (Концепция профильного обучения); дисциплины, целостно завершённые, которые выбираются учащимися и связаны с удовлетворением их индивидуальных образовательных интересов, способностей, жизненных планов в соответствии с избранным профилем (Ю.К. Нимировская); отдельные, не интегрированные курсы, которые предусматривают углублённое изучение предметов профиля (А.Ж. Жафяров).

По содержанию ЭК делятся на: предметные - направлены на углубление того или иного учебного предмета; межпредметные - интегрирующие знания учащихся из различных предметных областей. По целям и задачам ЭК делятся на: «пробные» (помогают определиться в правильности сделанного выбора учащимся в направлении дальнейшего обучения) и «ориентационные» (направлены на тщательное изучение выбранной образовательной области).

Т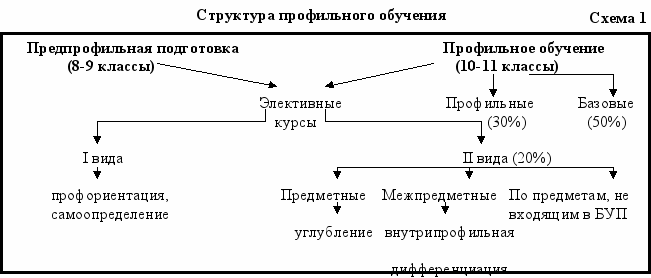аким образом, обобщая вышесказанное, структуру профильного обучения математике и место элективных курсов в нём представим в виде схемы 1.

В параграфе 3 уточнены цели, задачи и функции элективных курсов по геометрии в профильном обучении. Основные цели элективных курсов по геометрии в средней школе рассматривались в единстве с целями обучения математике в общем, и целями обучения геометрии, в частности. В диссертации подробно проанализированы различные подходы к постановке как общих целей обучения математике (В.А. Гусев, Ю.М. Колягин, Г.И. Саранцев), так и целей обучения геометрии (А.Д. Александров, Г.Д. Глейзер, Я.И. Перельман, А.В. Погорелов, А. Пардала, Е.В. Потоскуев, И.М. Смирнова, В.М. Тихомиров, И.Ф. Шарыгин и др.).

В научно-методической литературе выделены следующие основные цели и задачи элективных курсов: ориентация на индивидуализацию и социализацию обучения учащихся; углубление и расширение знаний; подготовка к вступительным экзаменам; развитие интереса к математике; профессиональная ориентация и самоопределение; удовлетворение познавательных потребностей и развитие творческих способностей учащихся. Значимость элективных курсов при реализации основных целей профильного обучения определяются их функциями (Таблица 1).


Таблица 1

Цели профильного обучения математике	Соответствующие им функции ЭК по геометрии
Обеспечить углубленное изучение программы полного общего образования.	Дополнение базового и профильного геометрического образования за счёт углубления и расширения.
Создать условия для дифференциации содержания обучения старшеклассников с широкими и гибкими возможностями построения школьниками индивидуальных образовательных программ.	Внутрипрофильная специализация обучения математике и построение индивидуальных образовательных траекторий; развитие интересов и профориентационных устремлений учащихся.
Расширить возможности социализации учащихся, обеспечить преемственность между общим и профессиональным образованием, подготовить выпускников школы к освоению программ ВПО.	Ориентация на выбор математических специальностей в будущем. Развитие общей культуры учащихся, способствующей формированию их творческой деятельности.

Итак, реализация базовых и профильных курсов (схема 1) позволяет достичь изучения математики лишь на общеобразовательном и профильном уровнях. Углубленное же изучение предмета программы полного общего образования осуществляется большей частью за счёт предметных элективных курсов. Кроме того, именно ЭК позволяют более полно учесть интересы и склонности учащихся, являясь главным средством построения их индивидуальных образовательных траекторий, которые реализуют личностно-ориентированный подход и более узкую внутрипрофильную дифференциацию. Преемственность между общим и профессиональным образованием обеспечивается посредством профильных курсов.

Определяя в параграфе 4 принципы отбора содержания ЭК по геометрии, мы исходили, прежде всего, из общих принципов дидактики (Ю.К. Бабанский, И.Я. Лернер, М.Н. Скаткин) и теории обучения математике (В.А. Гусев, Г.В. Дорофеев,
Ю.М. Колягин, Г.И. Саранцев, И.М. Смирнова, А.А. Столяр, Р.А. Утеева). Кроме того, были учтены результаты теоретических и практических исследований ряда авторов (В.В. Бесценной, А.В. Дмитриевой, Д.С. Ермакова, А.Ж. Жафярова, А.А. Зубрилина, Л.И. Звавича, А.Г. Каспржака, Ю.К. Нимировской, В.А. Орлова, А.С. Рвановой,
Я.В. Скибиной, Н.В. Чуйковой и др.), имеющих отношение к теме исследования.

Экспертиза авторской программы ЭК по теме «Площадь. Равновеликие и равносоставленные многоугольники» и его содержания, а также экспериментальная работа подтвердили обоснованность и достаточность выбора следующих принципов отбора содержания элективных курсов: научности, преемственности основного и ЭК, углубленной направленности обучения геометрии, обучения эвристикам, дифференциации, прикладной направленности.

В диссертации при реализации принципа научности за основу взята трактовка его содержания А.А. Столяром: содержание ЭК по геометрии должно отражать фундаментальные идеи и логику современной математики с учетом уровня мыслительной деятельности учащихся. Например, идея геометрических преобразований является одной из фундаментальных идей современной математики, которая сыграла огромную роль в развитии геометрии как науки. Существующие в настоящее время учебники по геометрии знакомят учащихся с этой идеей. Для более полной её реализации и знакомства с понятием группы преобразований целесообразно предложить учащимся старших классов элективный курс «Группы преобразований». Он дополнит базовый и профильный курсы геометрии и поможет сформировать у учащихся целостное представление о геометрии как науке, изучающей свойства фигур, инвариантных относительно преобразований некоторой группы.

Другим примером, знакомящим учащихся старших классов с идеей аксиоматических теорий и их интерпретаций, является идея измерения объектов различной природы. С измерениями различных объектов учащиеся сталкиваются уже в начальной школе и практически во всех курсах: математике, физике, биологии, астрономии, истории и т.д. В курсе геометрии учащиеся изучают три основные величины: длину, площадь и объем. В рамках ЭК по геометрии в 10-11 классах можно продолжить на более глубоком уровне изучение этих величин и знакомство учащихся с основами теории измерений и теории величин, которые должны стать частью математического образования.

Современные исследования по проблеме преемственности в обучении рассматривают ее в контексте непрерывного образования. Для ЭК на старшей ступени общеобразовательной школы характерны два типа преемственных связей: основной курс – ЭК; основной курс - ЭК – вузовский курс. Реализация первого типа связи предполагает как внутрипредметные связи содержательно-методических линий основного и элективного курсов, так и межпредметные связи элективного курса с другими предметами. В диссертации показано, что преемственность основного курса геометрии и элективного курса «Площадь. Равновеликие и равносоставленные многоугольники» достигается за счет последовательной трактовки основных понятий содержательно-методической линии «Измерение геометрических величин»: «площадь многоугольника - равновеликие многоугольники – равносоставленные многоугольники» и выхода на более высокий уровень их осмысления, а также определенной системы задач.

Суть принципа углублённой направленности обучения геометрии заключается в том, что содержание ЭК должно отражать идейно-значимый теоретический материал (история развития идей, понятий, методов, относящихся к теме) и быть направлено на формирование более полных, обобщенных и системных представлений о той или ной содержательной линии основного курса геометрии. Возможно также включение в ЭК материала, не входящего в содержание основного и профильного курсов.

В диссертации принцип обучения эвристикам при отборе содержания ЭК подразумевает, что оно включает такой теоретический и задачный материал, который направлен на формирование эвристик: базовые, специальные, эвристические приемы и методы научного познания (в соответствии с концепцией Г.И. Саранцева).

Принцип дифференциации предполагает наличие дифференцированных заданий в содержании ЭК, построенных с учетом особенностей типологических групп учащихся (в соответствии с концепцией Р.А. Утеевой).

Реализация принципа прикладной направленности предусматривает отбор такого содержания ЭК, который направлен на осуществление связи обучения геометрии с жизнью, другими науками, техникой, производством. Система прикладных задач должна мотивировать введение новых математических понятий и методов; иллюстрировать учебный материал; закреплять и углублять знания по предмету; развивать интуицию на доступном для учащихся уровне.

В параграфе 5 в соответствии с методологией Г.И. Саранцева описывается теоретическая модель проектирования ЭК по геометрии в профильном обучении, рассматриваемая как система определенной структуры, основными компонентами которой являются целевой, содержательный и организационный (схема 2). В диссертации подробно раскрыт каждый компонент модели.

Итак, методическая система проектирования ЭК по геометрии содержит компоненты: цели и задачи ЭК, принципы отбора содержания ЭК, содержание ЭК, методики и технологии обучения на ЭК. Внешняя среда, оказывающая существенное влияние на представленную систему, включает: цели обучения геометрии в общем, индивидуальные и типологические особенности учащихся.





Вторая глава «Содержание и методика реализации элективного курса по геометрии «Площадь. Равновеликие и равносоставленные многоугольники» в профильном обучении содержит шесть параграфов.

В параграфе 1 представлен анализ реализации в школьных и вузовских учебниках математики одной из основных содержательных линий «Измерение величин». В методике преподавания геометрии сложились два подхода к проблеме измерения. Первый подход – аксиоматический, основан на аксиоматике
А.Н. Колмогорова: Выбирается множество измеряемых объектов, в котором устанавливается порядок. Для этого в нем вводятся бинарные отношения «больше», «меньше», «равно» и тернарное отношение «быть суммой». Эти отношения должны удовлетворять 10 аксиомам. Тогда множество, в котором выполняется соответствующая аксиоматика, называется множеством величин, а сами элементы – величинами. Далее строится однозначное отображение множества величин в множество действительных чисел: равным величинам соответствуют равные числа; большей величине – большее число; сумме двух величин – сумма соответствующих чисел и т.д. Второй подход – подход А. Лебега осуществляется по схеме: Множество объектов измерения множество мер величин (множество неотрицательных чисел). Непосредственное измерение элементов методом наложения сеток.

В большинстве школьных учебников в основном реализуется второй подход. При этом многие авторы уже в 5 - 6 классах используют термин «величина», не раскрывая смысла этого понятия. Исключением является пособие
В.А. Гусева, в котором (в духе А.Н. Колмогорова), на доступном уровне представлено первичное знакомство учащихся с одним из основных математических понятий – величина. В курсе геометрии 7-9 классов большинство авторов современных школьных учебников определяют площадь как положительную величину (в частности, - положительное число), удовлетворяющую основным свойствам, необходимость введения которых поясняют тем, что они будут использованы при выводе формул площади прямоугольника.

Таким образом, в диссертации показано, что содержательная линия «Измерение величин»: недостаточно полно раскрыта в курсе геометрии средней школы; её изучение связано с определенными трудностями; в то же время знакомство с основами теории измерений должно стать частью математического образования (А. Лебег, И.А. Лурье, А.Н. Колмогоров, А.И. Фетисов, И.М. Яглом и др.). Поэтому она была положена в основу разработанного в диссертации ЭК по геометрии для учащихся старших классов.

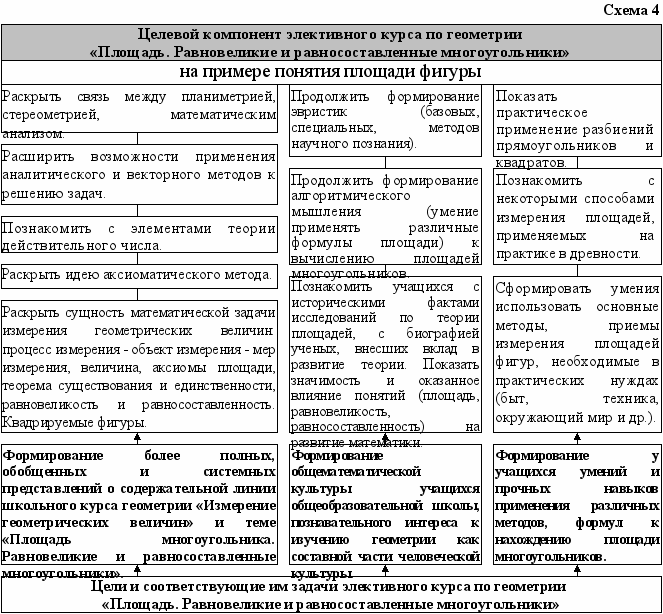
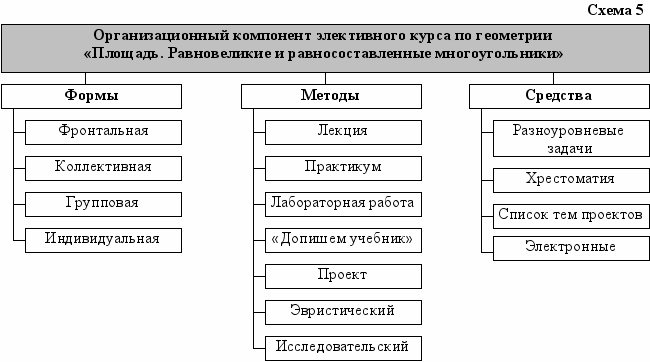
Структура разработанного в диссертации ЭК представлена тремя блоками (§2-4), позволяющая изучать также каждый из них отдельно в зависимости от определенных условий (наличие времени, выделяемого на курс, уровень подготовленности учащихся, профиль класса или школы) (схема 3). Конкретное содержание целевого и организационного компонентов методической системы спроектированного ЭК показано на схемах 4 и 5.

Первый блок «Площадь многоугольника» (24/12 часов). В нем предложен материал, обобщающий, систематизирующий и углубляющий знания по теме «Площадь многоугольника». Изучение учащимися аксиоматики скалярных величин А.Н. Колмогорова и её применение к понятию площади фигуры способствует формированию у них более высокого уровня знаний, расширяет и углубляет их представления об аксиоматическом методе. Далее рассматривается задача измерения геометрических величин: процесс измерения – объект измерения – мера измерения. Приводится доказательство теоремы о существовании и единственности площади и вводится понятие квадрируемой фигуры.











Доказательство теоремы о площади прямоугольника для любых действительных чисел устраняет ранее существовавшие пробелы в базовом курсе.

Изучение «новых» формул площади треугольника, не входящих в программу школьного курса геометрии расширяет возможности учащихся в решении задач по теме. В базовом курсе геометрии рассматривается в основном вычисление площадей двух видов выпуклых четырехугольников: параллелограмма и трапеции. Здесь учащиеся знакомятся с аналогом формулы Герона: 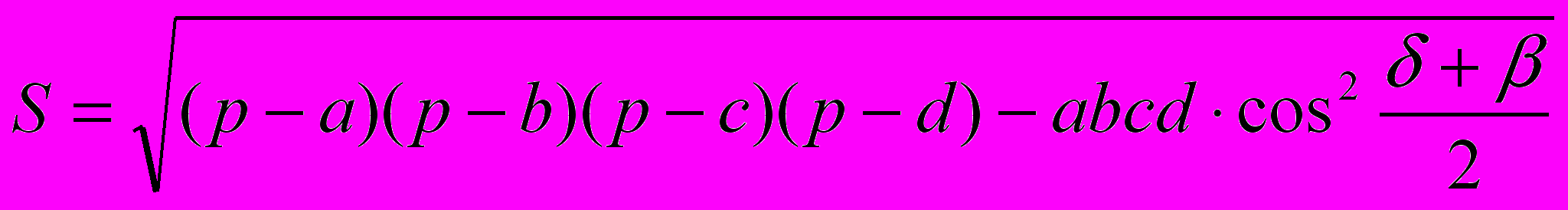, где a, b, c, d - длины сторон, р – полупериметр, δ и β – противолежащие углы четырехугольника. В случае если четырехугольник: 1) вписан в окружность (сумма противоположных углов вписанного в окружность четырехугольника равна 180⁰), формула приобретает вид: 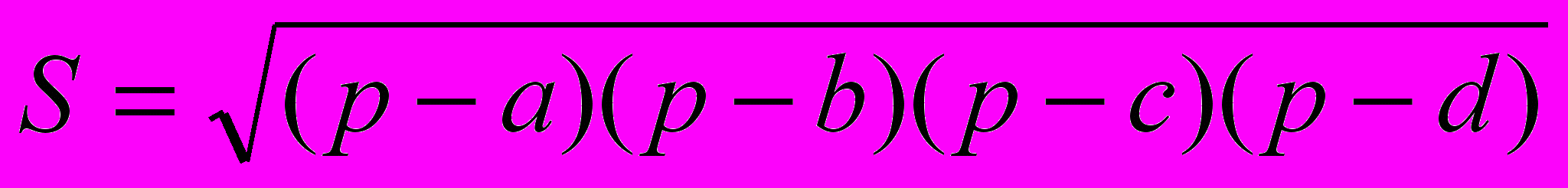; 2) описан около окружности (сумма противоположных сторон равна), то площадь такого четырехугольника равна: ;
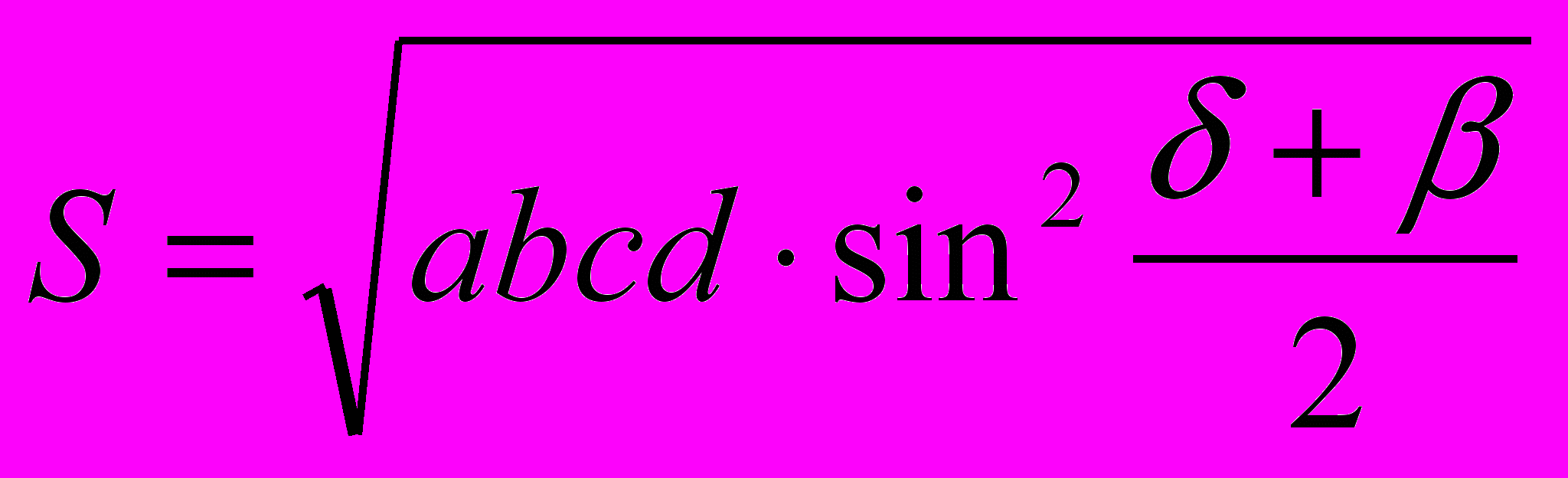3) вписан в окружность и описан около окружности одновременно:.

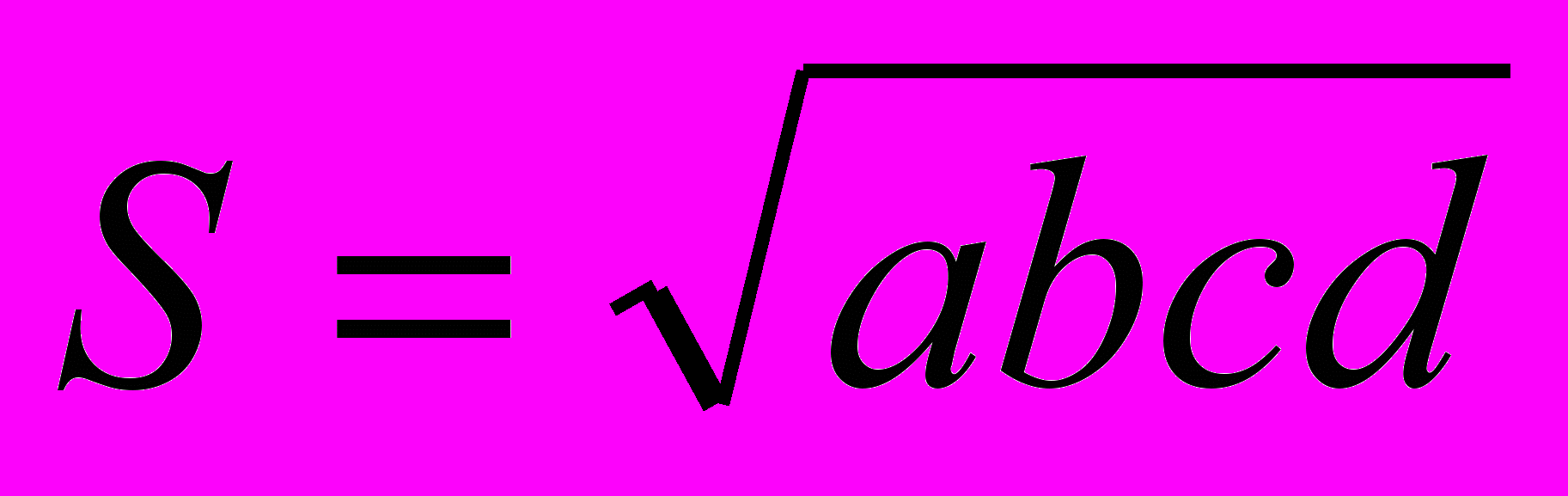Задачи, связанные с трапецией, занимают особое место в школьном курсе геометрии. В ЭК учащиеся знакомятся с формулами площади трапеции через её вторую среднюю линию: 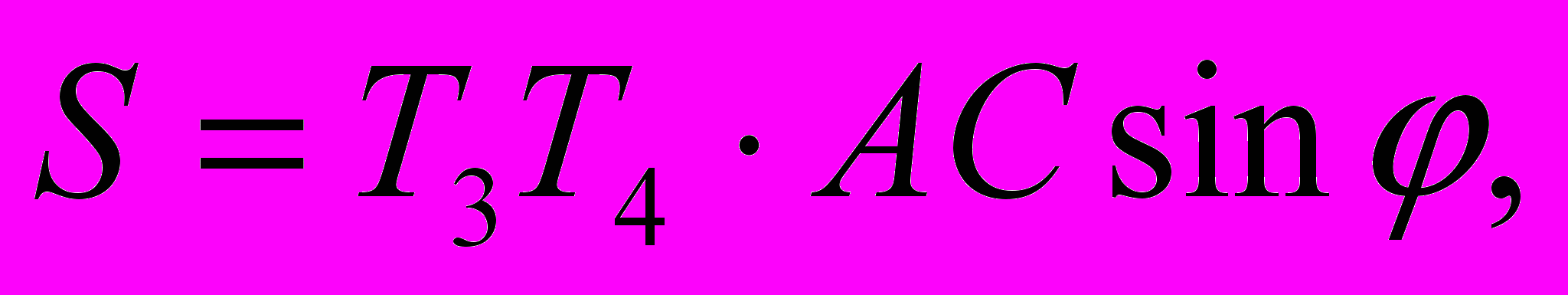где - угол между второй средней линией и диагональю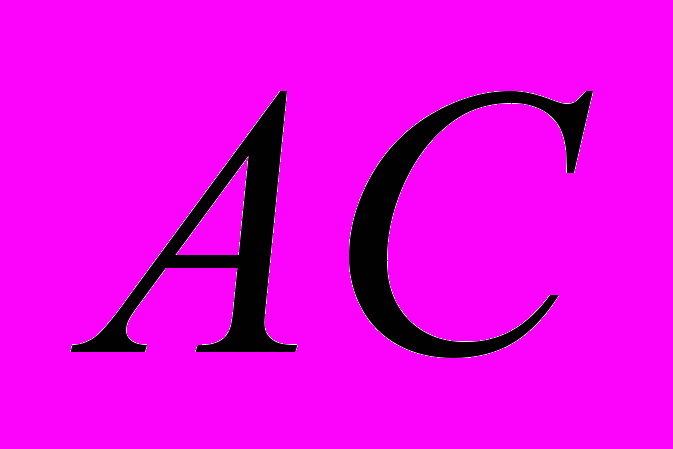трапеции ABCD; 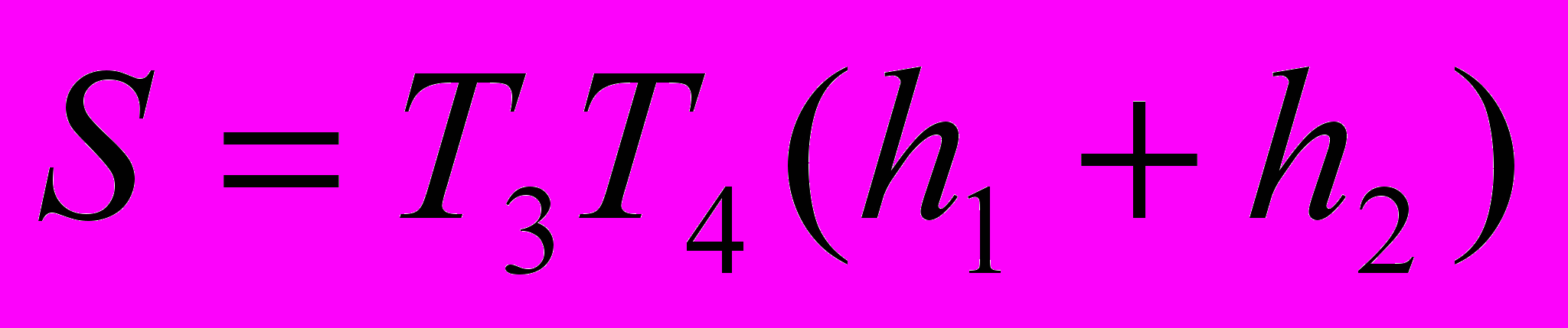, где Т₃Т₄ – вторая средняя линия трапеции, а h₁ и h₂ - перпендикуляры, проведенные к ней из двух противоположных вершин трапеции.

Большое внимание в ЭК уделено координатному и векторному методам при выводе формул площади треугольника, четырехугольника, n-угольника через координаты его вершин. Для вычисления площадей решётчатых многоугольников предлагается формула Пика - по имени математика, открывшего ее в 1899 году: 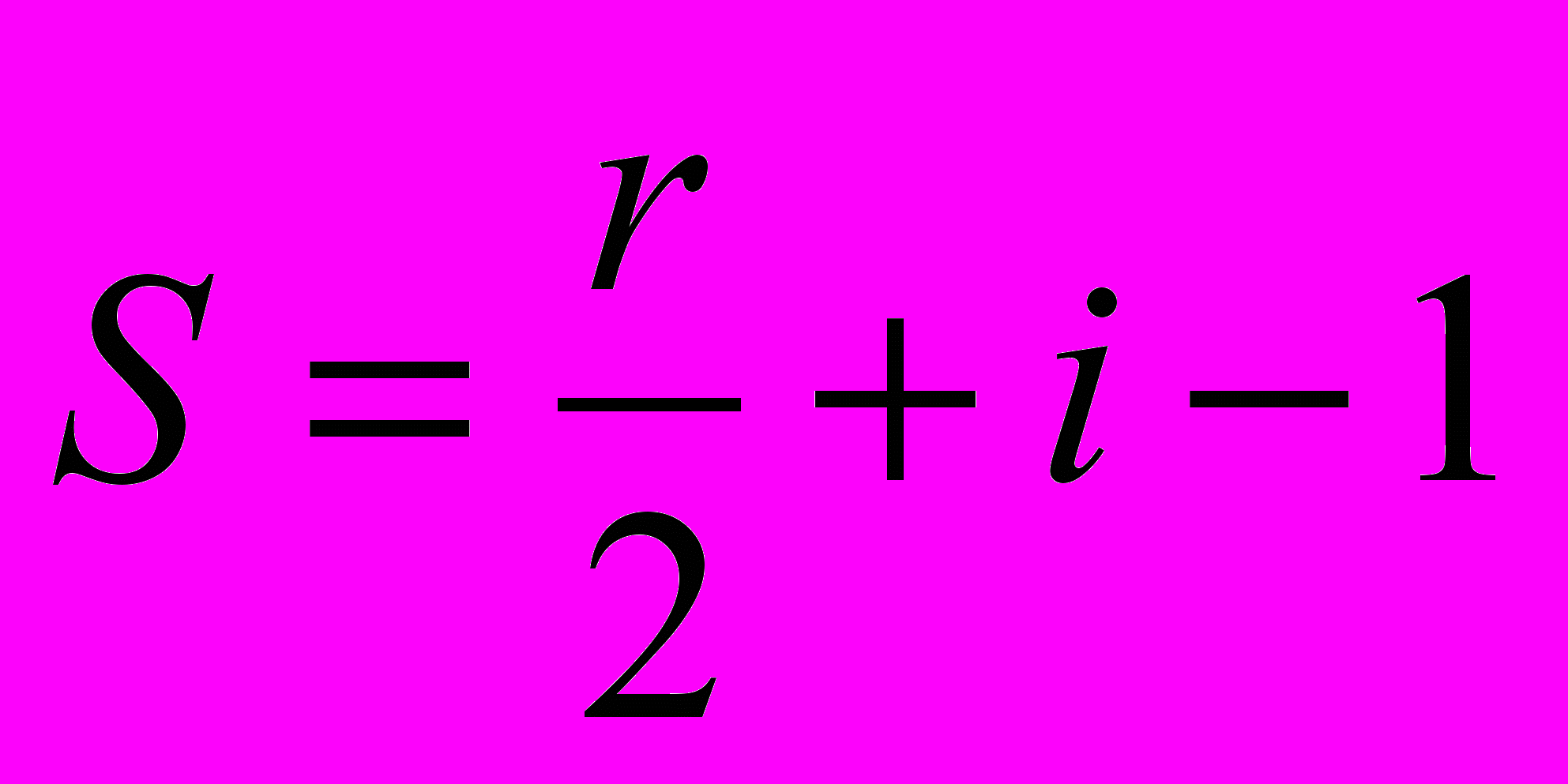, где S - площадь, r - число узлов, которые лежат на границе многоугольника (на сторонах и в вершинах), i - число узлов, которые лежат строго внутри многоугольника.

Изучение данного блока завершается лабораторной работой практического характера. В
А
результате изучения материала первого блока учащиеся должны знать: аксиоматическое и конструктивное определения площади многоугольника; основные свойства (теоремы) вычисления площадей многоугольников; изученные формулы вычисления площадей различных многоугольников и их комбинаций с окружностью; уметь: применять определение и формулы площади многоугольника при доказательстве теорем и решении задач; доказывать основные свойства вычисления площадей многоугольников.

Центральным элементом второго блока «Равновеликие и равносоставленные многоугольники» (20/14 часов) является теорема о равновеликости равносоставленных фигур Бояйи-Гервина (доказанная независимо друг от друга в 30-е гг. XIX в.). Она представляет для учащихся ценность в познавательном, историческом и развивающем планах. В основу теории положено важное свойство многоугольников, не имеющее аналога в трехмерном пространстве, - равносоставленность равновеликих многоугольников. Задачи, связанные с преобразованием фигур, интересовали ученых в разные времена. В настоящее время они широко могут быть использованы в вопросах рационального использования различных материалов, например, раскроя тканей, кожи и т.д. В связи с этим отдельное место уделено способам деления прямыми треугольников и четырехугольников на равновеликие части, составление квадрата из различных многоугольников. Многие из предложенных способов широко применимы при решении задач на нахождение площадей фигур, имеют прикладной характер.

Задачи о спрямлении окружности и квадратуре круга пользовались исключительной известностью с древнейших времён и тысячелетиями привлекали к себе внимание математиков. Они привели к изучению свойств числа π, в частности, установлению в XVIII веке математиками Ламбертом и Лежандром его иррациональности и доказанную в 1889 г. Линдеманом его трансцендентности. Изучение блока завершает лабораторная работа «Приемы приближенного спрямления окружности и квадратуры круга».

В результате изучения второго блока учащиеся должны знать: понятия равновеликих и равносоставленных многоугольников; теоремы о равносоставленности треугольника и параллелограмма; о равновеликости двух треугольников с одинаковыми основаниями и равными высотами; Бояйи-Гервина; способы деления треугольника на равновеликие части (медианой; прямой через произвольную точку стороны треугольника; прямой, параллельной или перпендикулярной данной стороне); деления треугольника на части в определённом отношении; деления выпуклого четырёхугольника на равновеликие части (прямой, проходящей через точку, лежащую на стороне; прямой, проходящей через вершину); понятие спрямления окружности и квадратуры круга, приёмы Л. Маскерони, А. Коханского, Г. Мюллера, Бинга. Учащиеся должны уметь: применять изученные понятия и теоремы при решении задач; доказывать основные свойства и теорему Бояйи-Гервина; использовать способы деления многоугольников на заданные части; составлять квадрат из различных многоугольников; применять формулы Л. Маскерони, А. Коханского, Г. Мюллера, Бинга для нахождения длины стороны квадрата, равновеликого данному кругу.

Третий блок «Задачи на разрезание» (20/10 часов) - заключительный.

Задачами на разрезание увлекались еще древние греки, китайцы, но первый систематический трактат на эту тему принадлежит перу Абу-л-Вафа, знаменитого персидского астронома X века, жившего в Багдаде.

Одними из основоположников этого увлекательного раздела геометрии были Генри Э. Дьюдени, Гарри Линдгрен. Отечественные ученые Л.В. Канторович и В.А. Залгаллер в первой половине прошлого века определили задачу рационального раскроя материалов, которая с успехом востребована и по сей день. Ее применение в промышленном производстве дает ощутимый экономический эффект.

Из задач на разрезание родилась теорема Бояйи-Гервина, а затем третья проблема Гильберта: верно ли аналогичное утверждение для многогранников?

Исследованию задач на разрезания посвящены работы многих авторов
(М. Гарднер, Ж.Г. Дедовец, М.А. Екимова, А.Т. Колотов, Б.А. Кордемский,
Г. Линдгрен, Ю.А. Шашкин, И.М. Яглом и др.). 

Анализ школьных учебников геометрии показывает, что можно выделить такие этапы обучения решению задач на разрезание. Первый этап (7 класс) - знакомство с операциями разрезания, достраивания, составления и перекраивания. Второй этап (8 класс) - обучение решению задач на перекраивание, использование которых позволяет комплексно реализовать дидактические возможности таких задач. Геометрическое содержание этих задач соответствует теме «Четырехугольники». Третий этап - учащиеся применяют метод разрезания фигур при самостоятельном выводе формул площадей многоугольников. В качестве четвертого этапа можно рассматривать изучение третьего блока ЭК.

Содержание этого блока построено по схеме «занимательный материал» - «математическая теория». В связи с этим, на первом занятии рассматриваются традиционные занимательные задачи на разрезание. Далее - задача о разрезании прямоугольника на попарно неравные квадраты; треугольников на n подобных треугольников. Проблема соответствия графов разбиениям прямоугольников наглядно демонстрирует межпредметные связи геометрии и физики. Содержание данного блока знакомит с одним из направлений развития геометрии в XX веке.

Завершается изучение данного блока и всего ЭК защитой проектных работ учащихся. В диссертации приведена тематика проектов по каждому блоку и указана соответствующая литература к ним.

В результате изучения третьего блока учащиеся должны уметь: использовать методы вспомогательной площади и перегруппировки; различные способы разрезания «греческого креста» на части и составления из них заданных многоугольников; применять ступенчатый и ошибочный разрезы при решении практических задач; выполнять разрезание треугольника на n подобных между собой треугольников; складывать прямоугольник из наименьшего числа попарно неравных квадратов.

В параграфе 5 описаны организация и результаты эксперимента, который осуществлялся в 3 этапа в течение 5 лет (2005-2010 гг.).

Целью констатирующего этапа эксперимента (2005/2006 учебный год) явилось исследование проблемы с точки зрения: 1) выяснения отношения учителей математики к постановке ЭК по геометрии для учащихся старших классов; 2) анализа реального состояния проблемы ЭК на практике; 3) определения уровня геометрической подготовки учащихся 10 классов и студентов первого курса по геометрии. Его результаты нашли отражение при корректировке задач исследования и подтвердили актуальность темы исследования.

Поисковый этап экспериментального исследования был проведен в 2006/2007 учебном году с целью определения содержания основных компонентов теоретической модели проектирования ЭК по геометрии, апробации содержания ЭК «Площадь. Равновеликие и равносоставленные многоугольники». Его результаты нашли отражение в диссертации в виде выводов или предположений.

Обучающий этап экспериментального исследования был проведен в 2007-2010 гг. в 10 классах профильных центров г.о. Тольятти и в рамках спецкурса со студентами 4 курса ТГУ – будущими учителями математиками. Его основной целью было определение: доступности содержания ЭК «Площадь. Равновеликие и равносоставленные многоугольники»; его влияния на качество знаний и умений учащихся по геометрии в целом; достижения основных целей и задач профильного обучения математике.

С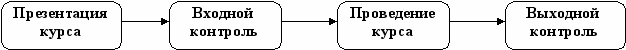хему обучающего этапа эксперимента можно представить так:


На входном контроле выявлялся исходный уровень обученности геометрии учащихся с помощью диагностической работы базового уровня по теме «Площадь многоугольников». Обработка результатов проводилась с помощью метода хи-квадрат, который показал отсутствие статистически значимых различий между исходными уровнями обученности у учащихся экспериментальных и контрольных групп. В качестве выходного контроля учащимся тех же групп была предложена контрольная работа. Ее содержание построено на основе материала базового курса геометрии, изучаемого в обоих классах по традиционной методике у одного и того же учителя указанных выше школ. Полученные статистические результаты свидетельствует о наличии существенных различий в уровнях обученности геометрии учащихся указанных групп. Также проверялось влияние изучения ЭК «Площадь. Равновеликие и равносоставленные многоугольники» на уровень успеваемости учащихся по геометрии. Для этого сравнивались итоговые оценки по геометрии учащихся, результаты контрольных работ до изучения ЭК (9 класс) и после него (10 класс).

Обработка результатов проводилась с помощью критерия знаков. Полученные результаты служат основанием для вывода о влиянии содержания и методики реализации ЭК «Площадь. Равновеликие и равносоставленные многоугольники» на повышение качества геометрического образования в целом.

Завершает главу параграф 6, посвященный совершенствованию методической подготовки будущих учителей математики. Разработанная авторская программа и содержание спецкурса «Проектирование и реализация элективных курсов по геометрии» (7 семестр, 28 часов, зачет) восполняют существующие пробелы в учебных планах подготовки будущих учителей математики в педвузах и университетах к работе на старшей ступени профильного обучения. Аналогичный курс включен также в учебный план подготовки магистров физико-математического образования (профиль «Математика», 11 семестр, 64 ч., экзамен).

В данной работе нашли решение задачи, выдвинутые в связи с проблемой, целью и гипотезой исследования.

Получены следующие основные результаты и выводы:

1. Элективные курсы по геометрии должны стать неотъемлемой частью математического образования старшеклассников в условиях профильного обучения математике в общеобразовательной школе, так как они не только востребованы на практике, но и обладают специфическими особенностями и возможностями, заложенными в природе геометрического знания, её методов и способов познания. Однако в настоящее время их возможности в достижении основных целей и задач профильного обучения остаются нереализованными.

2. Определено место элективных курсов по геометрии в условиях профильного обучения математике: они относятся к предметным и являются ориентационными, так как направлены на дальнейшее углубленное изучение предмета и продолжение образования в вузах, связанного с достаточно высоким уровнем математической подготовки школьников.

3. С учетом общих целей обучения геометрии, целей профильного обучения математике определены основные цели и задачи элективных курсов по геометрии. Показано, что значимость элективных курсов при реализации целей профильного обучения математике определяется их функциями. Конкретизация общих целей элективных курсов достаточно подробно описана на примере ЭК «Площадь. Равновеликие и равносоставленные многоугольники».

4. Представлена методическая система (цели, задачи, принципы, содержание, формы, методы, средства) проектирования элективных курсов по геометрии. Для её исследования построена теоретическая модель проектирования элективных курсов по геометрии, включающая три взаимосвязанных компонента: целевой, организационный и содержательный. Определена роль содержательного компонента, как приоритетного и обоснованы принципы отбора содержания элективных курсов по геометрии. Экспериментально подтверждено, что предложенная модель позволяет проектировать элективные курсы по геометрии, направленные на повышение качества знаний учащихся по геометрии и достижение целей профильного обучения математике.

5. Разработан элективный курс «Площадь. Равновеликие и равносоставленные многоугольники» для учащихся старших классов на основе модели проектирования элективных курсов по геометрии, удовлетворяющий выделенным принципам. Его апробация на практике показала, что он способствует повышению качества знаний учащихся по геометрии и достижению целей профильного обучения математике (учет интересов, потребностей и способностей учащихся, развитие творческих способностей, профориентация и самоопределение и др.).

6. Разработана и апробирована на курсах повышения квалификации учителей математики соответствующая программа их подготовки к проектированию и реализации элективных курсов по математике, сформулированы методические рекомендации. Авторский спецкурс «Проектирование и реализация элективных курсов по математике для профильной школы» включен в учебный план подготовки специалистов и магистров в ТГУ.

Полученные результаты являются новыми, они свидетельствуют о том, что поставленные задачи исследования решены; выдвинутая гипотеза подтверждена; положения, выносимые на защиту, обоснованы; цель исследования достигнута.

Перспективы исследования могут быть связаны с решением проблемы мотивации учащихся на выбор ЭК по геометрии; проектирования ЭК на основе других содержательно-методических линий школьного курса геометрии.

Основное содержание и результаты исследования отражены в следующих публикациях:

1. Публикации в научных журналах, рекомендованных ВАК РФ
   

1. Ермолаев, Е.А. Принципы отбора содержания элективных курсов по геометрии [Текст] / Е.А. Ермолаев // Интеграция образования. Научно-методический журнал. – 2008. - №3 (52). – С. 97 – 102.

II. Публикации в других изданиях

2. Ермолаев, Е.А. Элективный курс по геометрии «Площадь. Равновеликость и равносоставленность многоугольников» для 10 класса профильной школы [Текст] / Е.А. Ермолаев // Концепции математического образования: сборник трудов II Международной научной конференции «Математика. Образование. Культура»: в 3-х ч. – Часть 2. - Тольятти: ТГУ, 2005. – С. 112-113.

3. Ермолаев, Е.А. Элективные курсы по геометрии [Текст] / Е.А. Ермолаев // VI Всероссийская выставка научно-технического творчества молодежи НТТМ-2006: сборник материалов. – М.: ВВЦ, 2006. – С. 163 – 164.

4. Ермолаев, Е.А. Содержательные аспекты элективных курсов по геометрии для учащихся профильной школы [Текст] / Е.А. Ермолаев // Математическое образование: концепции, методики, технологии: сборник трудов III Международной научной конференции «Математика. Образование. Культура» (к 85-летию со дня рождения профессора В.И. Крупича): в 4-х ч. – Часть 3. - Тольятти: ТГУ, 2007. – С. 308-309.

5. Ермолаев, Е.А. Подготовка будущего учителя к реализации элективных курсов по математике [Текст] / Е.А. Ермолаев // Новые технологии в обучении математике и информатике в вузе и школе: материалы 2-ой Международной научно-практической конференции. - Орехово-Зуево: МГОПИ, 2007. – С. 227-228.

6. Ермолаев, Е.А. Элективные курсы в системе профильного обучения [Текст] / Е.А. Ермолаев // Функциональные пространства. Дифференциальные операторы. Общая топология. Проблемы математического образования: тезисы докладов 3-й Международной конференции, посв. 85-летию Л.Д. Кудрявцева. – М.: МФТИ, 2008. – С. 601-602.

7. Ермолаев, Е.А. О содержании элективных курсов по геометрии [Текст] / Е.А. Ермолаев // Воспитание, обучение, развитие в XXI веке: материалы Международной научно-практической конференции, посвященной 70-летию доктора педагогических наук, профессора К.Г. Кожабаева. - Казахстан, Кокшетау: КГУ им. Ш. Уалиханова, 2008. – 247-250.

8. Ермолаев, Е.А. Программа элективного курса по геометрии «Площадь. Равновеликие и равносоставленные многоугольники» [Текст] / Е.А. Ермолаев // Математическое образование: концепции, методики, технологии: сборник трудов IV Международной научной конференции «Математика. Образование. Культура»: в 3-х ч. - Часть 2. - Тольятти: ТГУ, 2009. – С. 124-128.

9. Ермолаев, Е.А. Цели и задачи элективных курсов по геометрии в профильном обучении [Текст] / Е.А. Ермолаев // Методическая подготовка студентов математических специальностей педвуза в условиях фундаментализации образования: материалы Всероссийской научной конференции: в 2-х ч. - Часть II. – Саранск: МГПИ им. М.Е. Евсевьева, 2009. – С. 69-73.

10. Ермолаев, Е.А. Содержательная линия «Измерения величин» в курсе геометрии средней школы [Текст] / Р.А. Утеева, Е.А. Ермолаев // Геометрическое образование: концепции, методики, технологии: сборник трудов Всероссийского научно-методического семинара «Геометрическое образование в современной средней и высшей школе» (к 70-летнему юбилею профессора
Е.В. Потоскуева). – Тольятти: ТГУ, 2009. – С. 219-228. (авт. -50%)