Нта (ЭМ) имеют особенности взаимодействия контурных релейных регуляторов выходной и промежуточных координат эп при совместной их работе в скользящем режиме (CP)
| Вид материала | Документы |
СодержаниеЦелью работы Материал и результаты исследований Таблица 1 – Значения коэффициентов в АУ (4) для различных вариантов ОКБ Выбранная ОКБ |
- Решение. Метод контурных токов, 63.32kb.
- Решение поставленных задач во многом зависит от скоординированности и заинтересованности, 497.14kb.
- Г. А. Федяева моделирование перспективного маневрового тепловоза, 111.66kb.
- Ії приймання навігаційної інформації, обчислювання координат супутників, обчислювання, 175.51kb.
- Н. И. Лобачевского факультет вычислительной математики и кибернетики лаборатория «информационные, 1555.24kb.
- Сказка о прыгуне и скользящем "Сказка о Прыгуне и Скользящем", 961.81kb.
- Лекция 4 аксонометрические проекции. Многогранные и кривые поверхности, 219.26kb.
- План проведения оперативных совещаний при начальнике уфмс россии по рсо-алания, 60.52kb.
- Нформаційні системи І моделювання, 103.77kb.
- Назначение программы для обучения работе в графическом режиме Роль ЭВМ в учебном процессе, 3479.23kb.
ЕЛЕКТРОМЕХАНІЧНІ СИСТЕМИ ТА АВТОМАТИЗАЦІЯ
УДк: 62-83:621.313
Асинхронные электроприводы с векторным
полеориентированным управлением и многомерными
скользящими режимами
Садовой А.В., Клименко Ю.Ю., Клименко Ю.М.
Днепродзержинский государственный технический университет
Введение. Перспективными направлениями развития теории и практики автоматизированного электропривода в настоящее время является создание глубокорегулируемого бесконтактного электропривода (ЭП) на основе короткозамкнутого асинхронного двигателя (КАД) и быстродействующих преобразователей на силовых транзисторных модулях (ПСТМ). В [1-4] изложены результаты работ авторов, выполненных на кафедре электрооборудования Днепродзержинского государственного технического университета по созданию глубоко регулируемых асинхронных электроприводов (АЭП) с векторным полеориентированным управлением (ВПУ), соответствующих требованиям механизмов точного воспроизведения сложных движений.
Традиционно выполняемые по принципам каскадно-подчиненного управления глубоко регулируемые АЭП с высоким качеством формирования электромагнитного момента (ЭМ) имеют особенности взаимодействия контурных релейных регуляторов выходной и промежуточных координат ЭП при совместной их работе в скользящем режиме (CP). При вхождении в СР регуляторов внешних контуров регулирования (КР) потокосцепления (КРП), скорости (КРС) или момента (КРМ) они подчиняют себе работу релейных регуляторов тока (РРТ) контура формирования фазных токов (КФФТ), размыкают контуры РРТ и фактически разрушают их режим скольжения. При этом КФФТ переходит в режим переключений с низкой частотой, представляющей собой сложную комбинацию частот регуляторов КРП и КРС, изменяющуюся при колебаниях в широких пределах скважности сигналов на их выходах.
В структурах СУ без форсирования СР во внешних КР с помощью ОС по производным реальные частоты СР регуляторов КРП и КРС значительно ниже потенциально возможных частот СР РРТ. В этом случае резко увеличиваются пульсации формируемых фазных токов и ЭМ, нарушаются, достигаемые при работе в СР, линейность свойств КФФТ, его инвариантность к возмущающим воздействиям, эффективность компенсации внутренних перекрестных связей (ВПС). По указанным причинам в СУ такой структуры отсутствует замкнутый КФФТ, а вместо него на входе ПСТМ используют блок компараторов. В АЭП, работающих в режимах частых пусков, реверсов или стопорений при размыканиях КРС, необходимым является использование пассивных средств ограничения тока в виде реакторов, включаемых последовательно с каждой из фаз КАД или в звено постоянного тока преобразователя для ограничения тока через транзисторы. Применение этих средств повышает порядок системы и предопределяет при организации СР использование производных в АУ. При косвенном парировании регуляторами контуров КРП и КРС возмущений в виде изменений напряжения питания или сопротивлений обмоток АД при колебаниях температуры АД в системе возникают дополнительные динамические ошибки. В системах без КФФТ нелинейность характеристик ПСТМ оказывает влияние на работу КРП и КРС. Перечисленное ограничивает практическое применение таких систем управления (СУ).
Целью работы - совершенствование систем ВПУ АЭП путем устранения перечисленных недостатков за счет организации в контурах СУ многомерных скользящих режимов (МСР), формируемых с применением принципа эквивалентного управления, обеспечивающего разделение разнотемповых движений внешних и внутренних КР.
Материал и результаты исследований. Многомерным принято называть СР [5,6], формируемый в системе произвольного порядка с целью обеспечения движения изображающей точки по многообразию S = 0 пересечений "m" плоскостей переключения SeT= 0 ( e = 1, ..., m).
При управлении многомерными, многосвязными структурами ЭП, осуществляемом без форсировок СР регуляторов внешних контуров за счет использования производных регулируемых координат, создание систем с МСР на основе прямых РУ затруднено. Решение этой проблемы возможно путем создания схемотехнических решений, обеспечивающих оптимальное взаимодействие КР и позволяющих организовать МСР в СУ. Сложность решения перечисленных проблем привела к тому, что результаты работ по созданию МСР для структур с прямыми РУ во внешних и внутренних КР, в серийно выпускаемых ЭП, не нашли своего практического применения.
Альтернативным является путь организации МСР при сочетании непрямых РУ во внешних КР с прямыми РУ во внутренних КР. Он может быть реализован на основе практического применения метода эквивалентного управления, широко применяемого в теории автоматического управления для формализации описания и анализа автоматических систем с РУ [5]. Этот метод фактически представляет собой формальную математическую процедуру, в соответствии с которой для систем общего вида
dχ /dt =A(χ,t) + Β(χ,t) U + f (χ,t), (1)
где Α(χ,t), B(χ,t) и f(χ,t) - матрицы размерностей (nxn), (nxm) и (nxn); f(χ,t) – матрица возмущающих воздействий; U = Uе - "е" - мерное векторное управление, компоненты которого на выбранных в процессе синтеза поверхностях переключения претерпевают разрывы
 .
. На траекториях скольжения вдоль S(χ) = 0 приравнивают нулю производную по времени функции переключения:
dS /dt = G(χ,t) f(χ,t) + G(χ,t) B(χ,t) U = 0, (2)
решают уравнение (2) относительно U = Ueq , называемого "эквивалентным" управлением
Ueq = - [G(χ,t) B(χ,t)] -1 G(χ,t) f(χ,t). (3)
Управление Ueq (t) не содержит высокочастотного разрывного сигнала и представляет собой аналог непрерывного управления в функции координат объекта управления (ОУ), обеспечивающий такой же характер движения ОУ по S(χ)= 0 и желаемые свойства СУ, как и исходный сигнал РУ, по которому вычисляется Ueq (t). В отличие от доопределений СР на границах разрывов, полученных в работах А.Ф. Филиппова [7], М.А. Айзермана и Е.С. Пят-ницкого [8], рассматриваемая концепция имеет не только теоретическое значение как одна из эффективных процедур анализа и синтеза систем с РУ, но и важное практическое значение при использовании ее в качестве средства организации МСР в АЭП с подчиненным принципом релейного управления.
Из всего множества вариантов построения многоконтурных систем подчиненного регулирования с непрямым РУ наиболее целесообразным является применение метода эквивалентного управления путем разделения разнотемповых движений во внешних и внутренних КР. При этом сигнал управления на выходе релейного регулятора внешнего контура при работе его в СР, с изменяющимися в широких пределах частотой и скважностью, может быть разделен на высокочастотную составляющую, имеющую частоту СР, и низкочастотную составляющую, являющуюся, для подчиненного ему внутреннего КР, основным задающим воздействием. Низкочастотная составляющая имеет темпы изменения, совпадающие с темпами изменения регулируемых координат внутреннего КР и их производных в статических и динамических режимах [6].
В теории и практике систем управления с СР наиболее перспективным является применение устройств выделения эквивалентного управления (ВЭУ) на основе моделей ОУ [6]. Для проведения исследований АЭП с ВПУ и МСР в качестве базы для сравнения используем структуру [1], полученную в процессе структурно-алгоритмического синтеза с применением вариационных методов путем решения задачи аналитического конструирования оптимальных регуляторов, обеспечивающих при работе в скользящем режиме (СР) минимум интегральных квадратичных отклонений траекторий движения от траекторий, заданных программно. При этом алгоритмы ВПУ АЭП в фазовом пространстве отклонений координат истинного и программного движений получены в виде уравнений:
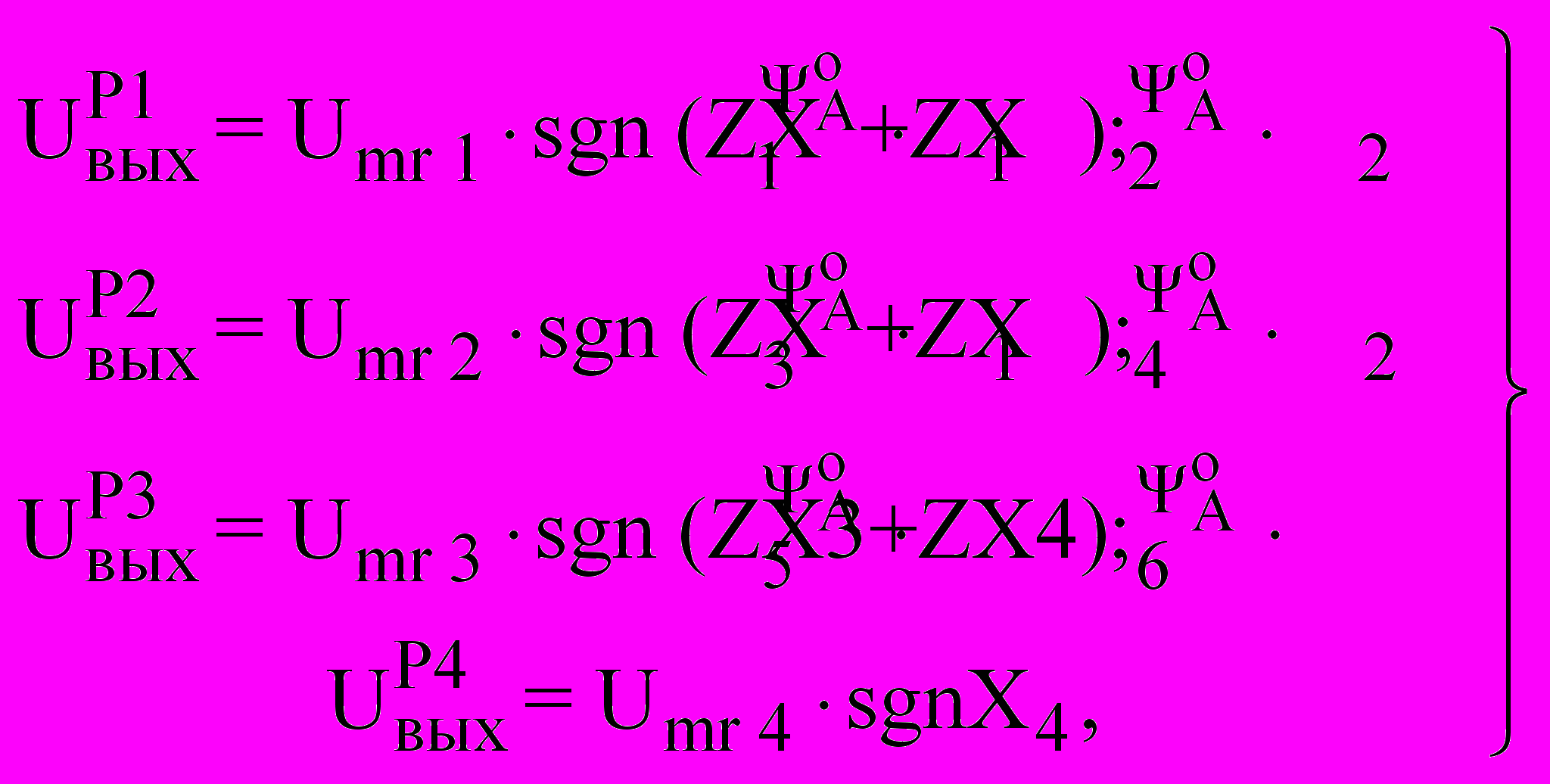 (4)
(4)где Х1, ..., Х4 - ошибки, определяемые как разности между задающими воздействиями (●)* и сигналами обратных связей по соответствующим регулируемым координатам:

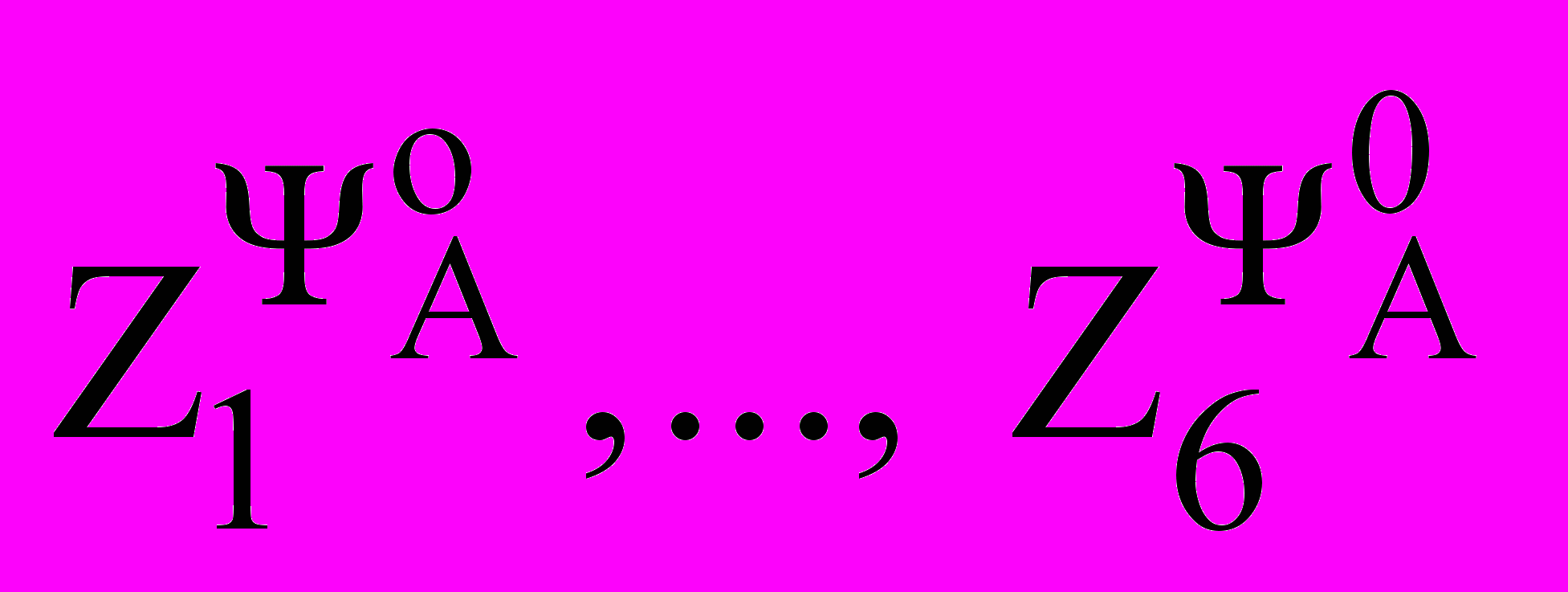 - коэффициенты из табл. 1 для выбранной ОКБ по одному из векторов
- коэффициенты из табл. 1 для выбранной ОКБ по одному из векторов 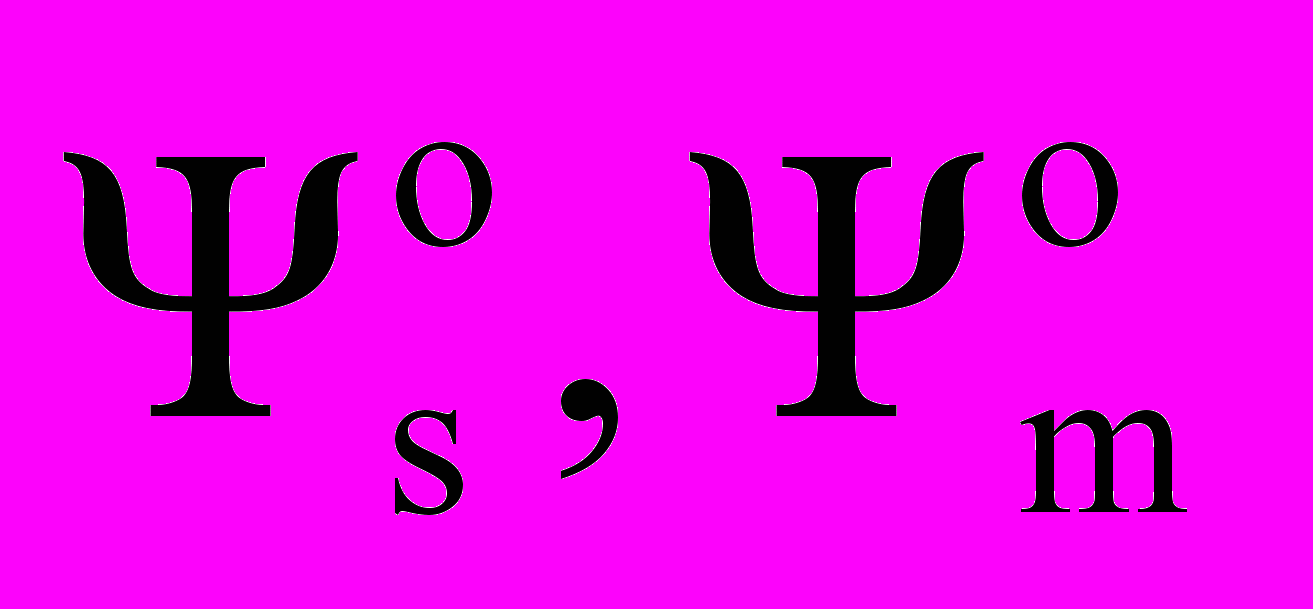 или
или  . В табл. 1 приведены параметры КАД: Ts, Tr – постоянные времени статора и ротора; ks, kr – коэффициенты связи статора и ротора; σ, σs, σr - коэффициенты рассеяния; L's, Lm, Ls, Lr – индуктивности КАД; Ψ*- заданный уровень потокосцепления; J – момент инерции; m – число фаз; zp – число пар полюсов.
. В табл. 1 приведены параметры КАД: Ts, Tr – постоянные времени статора и ротора; ks, kr – коэффициенты связи статора и ротора; σ, σs, σr - коэффициенты рассеяния; L's, Lm, Ls, Lr – индуктивности КАД; Ψ*- заданный уровень потокосцепления; J – момент инерции; m – число фаз; zp – число пар полюсов.Синтезированные АУ реализованы в виде унифицированной для вариантов ОКБ структуры управляющей части СУ, представленной на рис. 1 и содержащей релейные регуляторы потокосцепления (РП), скорости (РС), активной (РАТ) и реактивной (РРТ) составляющих тока статора.
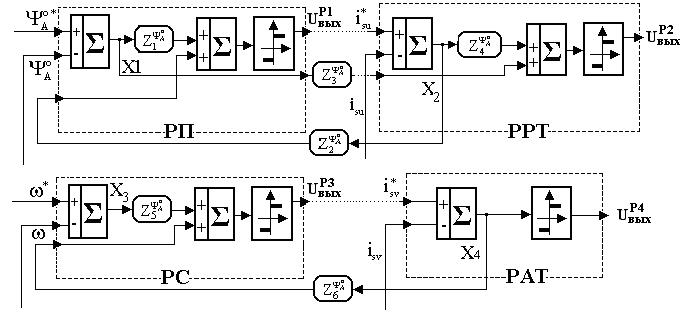
Рисунок 1 - Структурные схемы КР КРП и КРС с АУ (4)
Таблица 1 –
Значения коэффициентов в АУ (4) для различных вариантов ОКБ
| Коэффициеты в АУ (4) | Выбранная ОКБ | ||
ΨоА ≡ Ψs | ΨоА ≡ Ψm | ΨоА ≡ Ψr | |
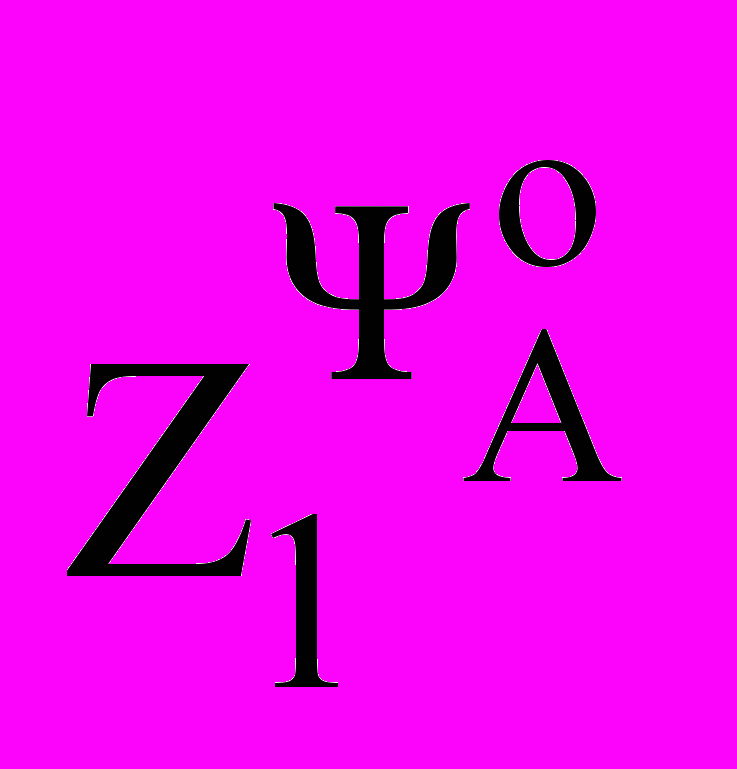 | 1-σTs(Ts+Tr)-1+ +(Ts+Tr) Tr-1 | 1+σrTs(Ts·σs-Tr·σr)-1[σs+ +(Tr+ksTs)Ts-1-σTs(Tr+ +ks·Ts)-1] | Tr+ks·kr·Ts - σTs |
 | L's[1-Tr(Ts+Tr)-1] | Lm(Ts·σs-Tr·σr)(Tr+ksTs)-1+ +Lm·σr | kr·Lm·σTs |
 | (L'sTr)-1 | L's-1σ | L's-1 |
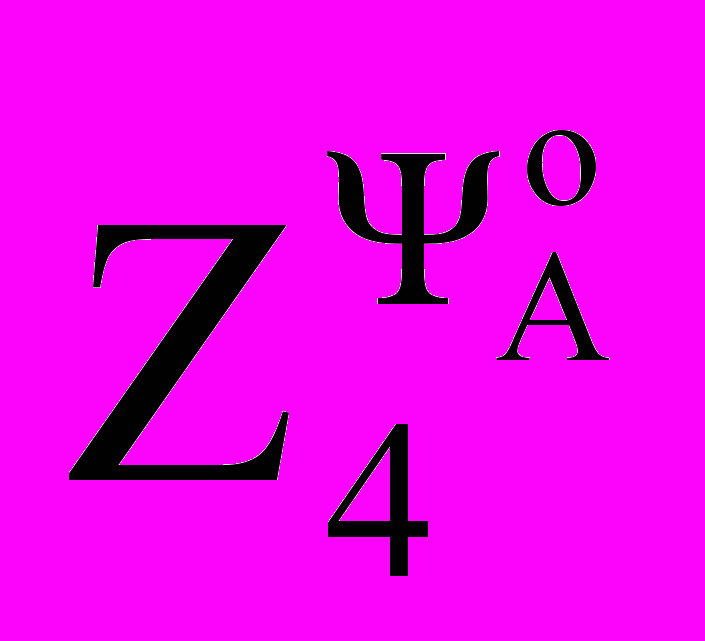 | Ts(LsTr)-1 | σs·σ-1(σs+(Tr+ksTs)Ts-1)- -Lm(Ts·σs-Tr·σr)(L'sTs)-1+ +Lmσr·σsL's-1 | 1+(Tr+ks·kr·Ts) (σTs)-1-kr·Lm·L's-1 |
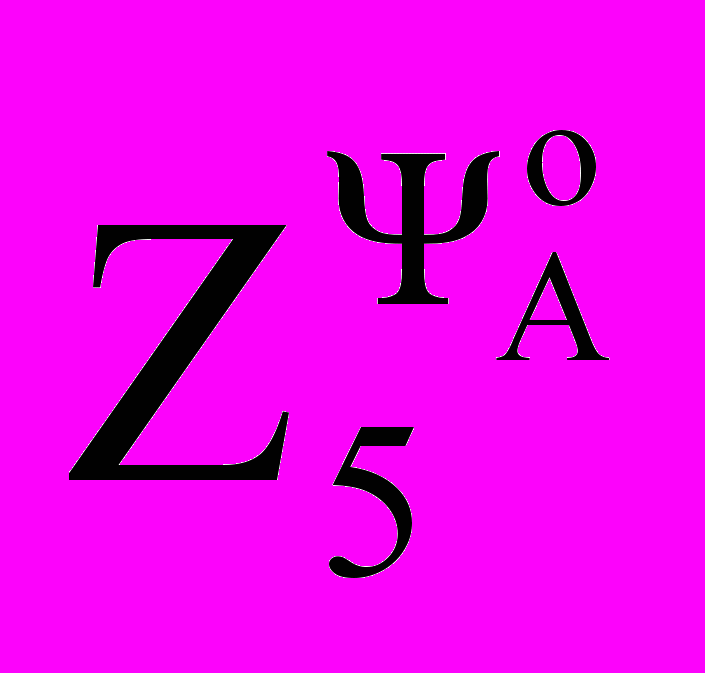 | (Tr+Ts) (σTsTr)-1 | (Tr+ks·Ts) (σTsTr)-1 | (Tr+ks·kr·Ts) (σTsTr)-1 |
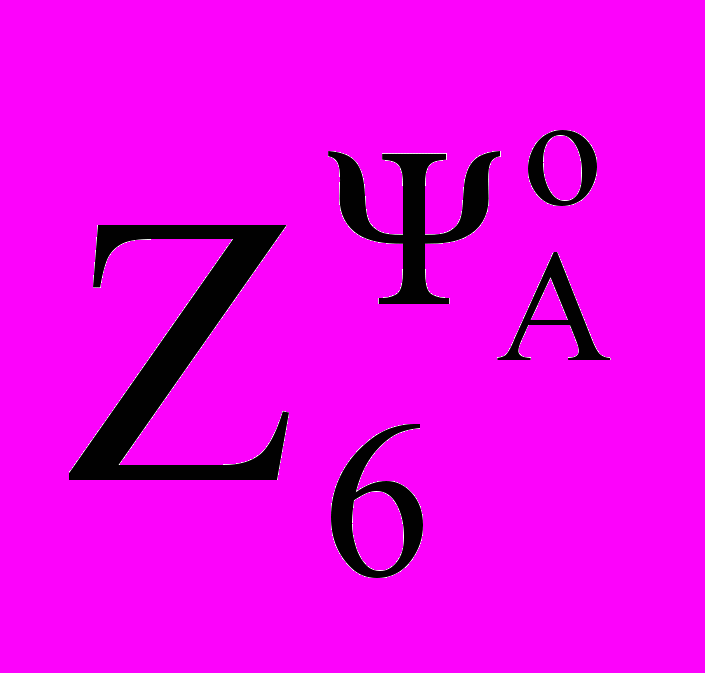 | 0.5·m·zp·Ψ*·J-1 | 0.5·m·zp·Ψ*·J-1 | 0.5·m·zp·kr·Ψ*·J-1 |
На рис. 2 представлены структурные схемы АЭП с ВПУ и прямыми разрывными управлениями в КР (рис. 2, а) и с МСР (рис. 2, б) [4]. Исследование АЭП с АУ (4) осуществлено путем цифрового моделирования системы для ОКБ ΨoA ≡ |Ψr| в программной среде пакета MATLAB7/ SIMULINK в соответствии со структурными схемами вариантов СУ с прямыми и непрямыми РУ в КРП и КРС, представленными на рис. 2, б.
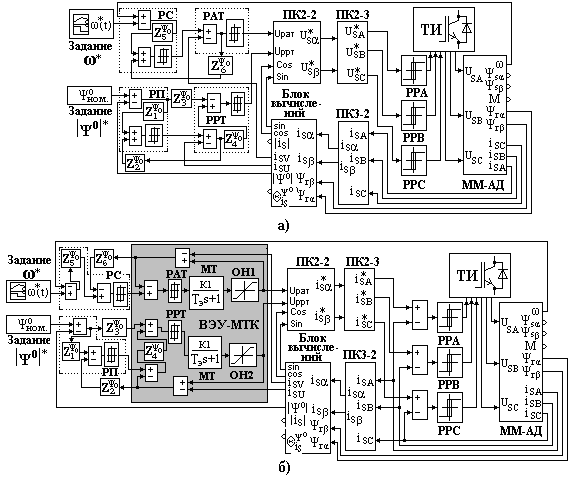
Рисунок 2 - Структурные схемы АЭП с ВПУ с прямыми РУ во внешних КР (а) и с МСР (б)
В процессе исследований применена математическая модель (ММ) КАД [2], учитывающая нелинейность цепи намагничивания машины и реализованная в СК АоВС; блок вычислений переменных состояния

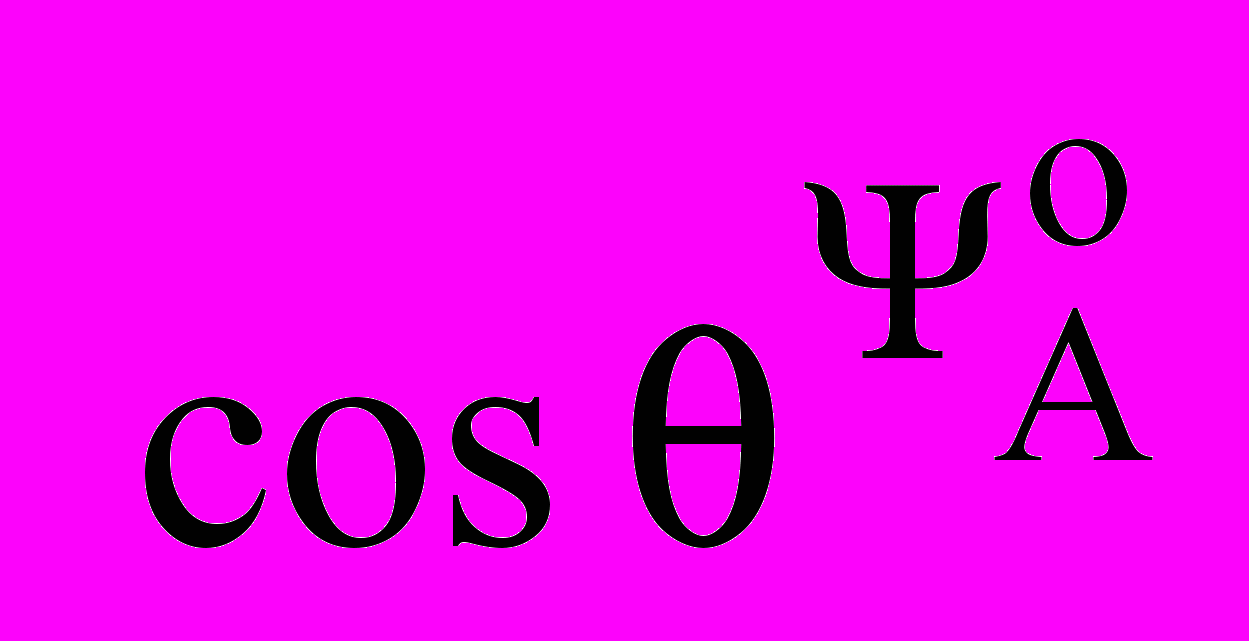 и преобразователи координат ПК3-2, ПК2-2, ПК2-3; регуляторы РП, РС, РРТ, РАТ с АУ (4).
и преобразователи координат ПК3-2, ПК2-2, ПК2-3; регуляторы РП, РС, РРТ, РАТ с АУ (4).Главными отличительными особенностями исследуемых структур является применение прямых РУ регуляторов РП, РС, РРТ, РАТ в структуре рис. 2, а и регуляторов РП, РС с ВЭУ в структуре рис. 2, б. Выделитель Ueq представляет собой замкнутую по сигналам UРАТ, UРРТ модель токового контура (МТК), содержащую регуляторы РРТ, РАТ, апериодическое звено МТ с параметрами статорной цепи АД и ограничители напряжений ОН1, 2. Выбор уровней ограничения каждого из них определяет требуемые динамические и энергетические характеристики АЭП, соответствующие цели управления. В структуре c ВЭУ (рис. 2, б) использован КФФТ, замкнутый по токам is А,В,С и функционирующий в непрерывных СР.
На рис. 3 представлены осциллограммы изменения координат ω(t), М(t), |Ψr|(t), isu(t), |is|(t), is А,В,С(t), Ψrα,β (t),
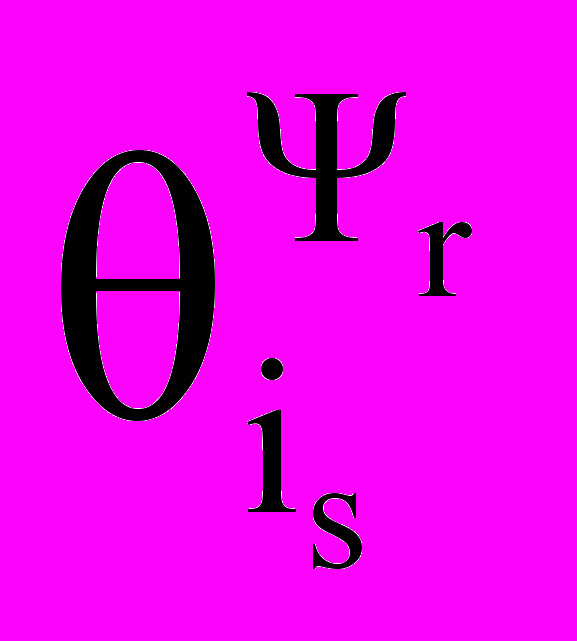 (t), полученные при моделировании структуры СУ с прямыми СР во внешних КР (рис.3, а) и с МСР (рис. 3, б).
(t), полученные при моделировании структуры СУ с прямыми СР во внешних КР (рис.3, а) и с МСР (рис. 3, б). 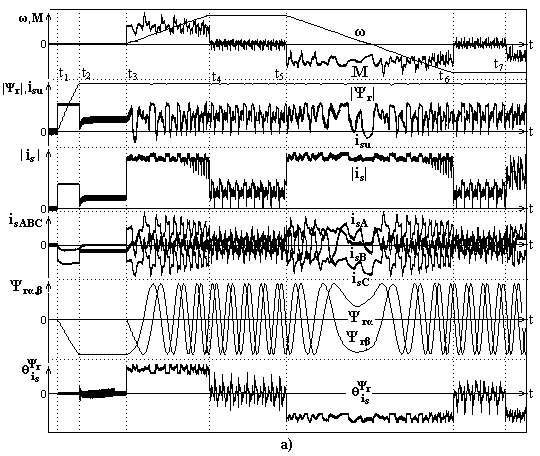
а)
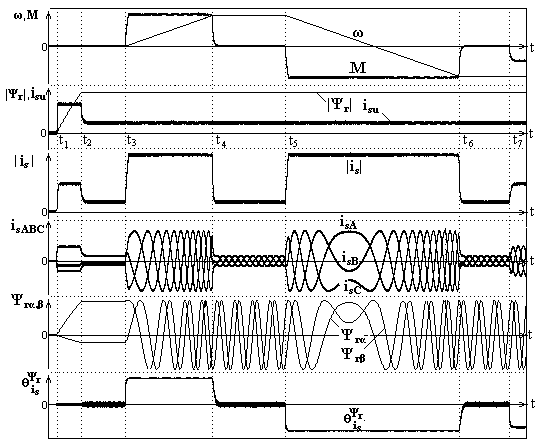
б)
Рисунок 3 - Результаты исследования сравниваемых вариантов структур АЭП с ВПУ
Осциллограммы получены в режимах работы Мс=0 (0 - t7) при: |Ψr|* = 0, ω* = 0 (0 - t1); возбуждении машины | Ψr |* = | Ψr |ном на интервале времени (t1 - t2) при ω*=0; работе АЭП при ω*=0 и | Ψr |ном (t2 – t3) разгоне машины до значения скорости ω = ω* = ωном (t3 - t4) и работе с ω = ωном. (t4 - t5); реверсе КАД до значений скорости ω = -ω* = - ωном (t5 - t6) и работе с ω = - ωном. (t6 - t7); приложении момента сопротивления Мс=Мном при ω = - ωном. (t7 - t). Анализ полученных результатов показывает неоспоримые преимущества СУ с МСР. Введение в структуру СУ МТК не приводит к необходимости повторного синтеза АУ с учетом динамики МТ, т.к. коэффициенты передачи МТК при работе их регуляторов в СР имеют фактически значения кМТК ≈ 1. В силу организации в МТК СР отклонения настроечных параметров МТ от параметров КАД, обусловленные нестационарностью его характеристик, существенного влияния на работу СУ не оказывают.
Выводы. Применение разработанной концепции построения и принципов практической реализации АЭП с ВПУ, организацией МСР, синтеза АУ и структуры системы, унифицированной для вариантов ОКБ по векторам Ψs, Ψr или Ψm, в отличие от известных структур с прямыми РУ во внешних контурах позволяет за счет разделения разнотемповых движений внешних и внутренних контуров регулирования путем применения принципа эквивалентного управления, организовать в системе многомерные, а в каждом контуре - устойчивые, автономные скользящие режимы. При этом в системе обеспечивается: высокое качество отработки задающих воздействий; малые пульсации ЭМ и высокие равномерность вращения вала КАД в зоне низких угловых скоростей и частоты скользящих режимов в контурах системы; формирование токов в фазах КАД с низким уровнем высших гармоник.
ЛИТЕРАТУРА
1. Клименко Ю.М., Садовой А.В., Клименко Ю.Ю. Асинхронный электропривод с векторным управлением и адаптивным задатчиком траекторий оптимальных движений // Вісник Кременчуцького політехнічного університету: Наукові праці КДПУ.- Кременчук: КДПУ, 2004. - Вип. 2(25). C. 16-20
2. Клименко Ю.М., Садовой А.В., Клименко Ю.Ю. Практическая реализация асинхронных электроприводов с векторным полеориентированным управлением (II) // Вісник Кременчуцького політехнічного університету: Наукові праці КДПУ. - Кременчук: КДПУ, 2003, Вип. 2(19), T.1. C. 43-48.
3. Клименко Ю.М., Садовой А.В. Техническая реализация транзисторных асинхронных электроприводов с векторным полеориентированным управлением / Проблемы создания новых машин и технологий. Сборник научных трудов Кременчугского государственного политехнического института: Выпуск 1/ 2000 (8).-Кременчуг: КГПИ, - 2000. -C. 75-80.
4. Патент 27886 Украина, МКИ Н02Р 7/42 Асинхронный электропривод с разрывным фазовектроным управлением // Клименко Ю.М., Садовой А.В. - №94117492; Заявл. 09.11.1994, Опубл. 16.10.2000, Бюл. №5.
5. Уткин В.И. Скользящие режимы в задачах оптимизации и управления. - М.: Наука, 1981. - 376с.
6. Борцов Ю.А., Юнгер И.Б. Автоматические системы с разрывным управлением. - Л.: Энергоатомиздат, 1986. - 167с.
7. Филиппов А.Ф. Диффернциальные уравнения с правой частью, разрывной на пересекающихся поверхностях. - Дифференциальные уравнения, 1979, т. ХV №10. C. 814 - 823.
8. Айзерман М.А., Пятницкий Е.С. Основы теории разрывных систем. // Автоматика и телемеханика-1974 № 7, №8.
Стаття надійшла 25.04.2006 р.
Рекомендована до друку
д.т.н., проф. Родькіним Д.Й.
Вісник КДПУ. Випуск 4/2006 (39). Частина 1
