Синтез, оптические спектры и стереоатомный анализ структуры сложных халькогенидов, активированных фторидов и оксидов 01. 04. 07 физика конденсированного состояния

Вид материала

Автореферат

Подобный материал:

• Взаимосвязь электрических и магнитных свойств в сильно коррелированных электронных, 1439.13kb.
• Учебно-методический комплекс по дисциплине Физика Конденсированного Состояния Для специальности, 322.8kb.
• Паспорт специальности 01. 04. 07 – физика конденсированного состояния, 1004.81kb.
• Ён Викторович Методы визуализации кинетики зарождения и роста углеродных наноструктур, 219.01kb.
• Рабочая программа учебной дисциплины «Физика конденсированного состояния, термодинамика,, 223.9kb.
• Министерство образования Российской Федерации международный университет природы, общества, 1374.95kb.
• Рентгенографические исследования и построение моделей структуры ряда углеродных материалов, 315.25kb.
• Дефекты структуры, механические, электрические и магнитные свойства монокристаллических, 445.28kb.
• Аннотация рабочей программы дисциплины «Дифракционный структурный анализ» Направление, 26.86kb.
• Кинетика старения медно-бериллиевых сплавов в постоянном магнитном поле 01. 04., 427.06kb.

третьей главы приведены основные положения стереоатомной модели структуры кристалла, базирующейся на анализе значений характеристик полиэдров Вороного-Дирихле. Полиэдром Вороного-Дирихле (или атомным доменом) некоторого атома А называется выпуклый многогранник, ограниченный плоскостями, которые проведены через середины отрезков, связывающих этот атом с его соседями, перпендикулярно этим отрезкам. Например, если атом А окружен в кристалле шестью атомами X, образующими координационный полиэдр в виде правильного октаэдра, то полиэдр Вороного-Дирихле этого атома имеет форму куба. Таким образом, общее число атомов, окружающих некоторый атом А в структуре кристалла, равно числу граней его полиэдра Вороного-Дирихле, так как каждая грань этого полиэдра отвечает одному соседнему атому. Полиэдр Вороного-Дирихле любого атома в структуре некоторого кристалла можно охарактеризовать следующими важнейшими параметрами: V_ПВД–объем полиэдра; R_СД–радиус сферы, объем которой равен объему полиэдра Вороного-Дирихле; N_f–число граней полиэдра; D_A–смещение ядра атома из геометрического центра тяжести его полиэдра Вороного-Дирихле; G₃–безразмерная величина второго момента полиэдра Вороного-Дирихле, характеризующая степень его сферичности. Использование полиэдров Вороного-Дирихле позволяет охарактеризовать каждое межатомное взаимодействие А - Х тремя новыми параметрами: величиной площади общей грани (S) полиэдров Вороного-Дирихле соседних атомов А и X; значением телесного угла (Ω), под которым общая грань полиэдров Вороного-Дирихле атомов видна из точки, отвечающей положению ядра любого из них, а также объемом бипирамиды, в основании которой лежит общая грань полиэдров Вороного-Дирихле атомов А и X, а ядра атомов находятся в апикальных позициях этой бипирамиды.

Далее приведены основные положения метода пересекающихся сфер, в рамках которого атому в кристалле приписывается два радиуса: фиксированный r_S (слейтеровский радиус), значение которого однозначно обусловлено химической природой этого атома, т.е. характеризует условно изолированные, т.е. химически не связанные, атомы; переменный R_СД, значение которого определяется химическим составом, структурой соединения, т.е. природой атомов окружения и их взаимным пространственным размещением.

С учетом постулированной двухсферной модели квазиизолированных атомов А и X возможны 18 вариантов парного межатомного взаимодействия (а именно: А-А, Х-Х и А-Х), с которыми в общем случае можно столкнуться в структурe любых кристаллов. Два атома, находящиеся на расстояниях, превышающих суммы радиусов их внешних сфер, считаются химически не связанными, так как в этом случае итоговое перекрывание их сфер (тип П₀) равно нулю. Химическое взаимодействие двух атомов начинаемся с момента пересечения внешних сфер этих атомов. Такое взаимодействие называется одинарным перекрыванием П₁. И так до тех пор, пока попарно перекрываются каждая из двух сфер одного атома с каждой из двух сфер соседнею атома (четверное перекрывание, тип П₄).

Анализируется применение методов стереоатомного анализа, которые можно разделить на анализ структурных особенностей кристаллических материалов и на исследование взаимосвязи этих особенностей с физическими свойствами кристаллов.

Во второй части третьей главы с помощью комплекса программ TOPOS [3] на основании сведений о параметрах элементарных ячеек, пространственных группах симметрии и координатах атомов [4] для всех соединений, содержащих в структуре атомы кадмия в окружении серы, были рассчитаны характеристики полиэдров Вороного-Дирихле (ВД) базисных атомов.

Как показывают полученные результаты, атомы Cd по отношению к атомам серы могут проявлять КЧ 3, 4, 5 или 6. Наиболее характерна для атомов Cd тетраэдрическая координация, соответствующая КЧ 4. Значительно реже атомы Cd проявляют КЧ 5 и 6. При КЧ 5 во всех случаях образуются координационные полиэдры в виде искаженной тригональной бипирамиды, в которой расстояние Cd-S до одного апикального атома серы значительно длиннее (3.0(2)Å), чем до четырех остальных атомов серы (в среднем 2.58(5)Å). При КЧ 6 координационные полиэдры имеют форму октаэдра или тригональной призмы.

Длина связей Cd-S в 318 координационных полиэдрах CdS_n изменяется в диапазоне от 2.39 до 3.29Å, а соответствующие им телесные углы () составляют от 9 до 24% полного телесного угла, равного 4 стерадиан. Несмотря на разнообразие формы полиэдров ВД атомов Cd, по данным регрессионного анализа, как валентные, так и невалентные взаимодействия независимо от КЧ атомов кадмия описываются единой линейной зависимостью

(Cd-S) = 42.1(2) - 9.30(5)r(Cd-S) (22)

с коэффициентом корреляции r = -0.970 для всех 2118 граней типа Cd-S или Cd/S. Именно наличие линейной зависимости типа (1) с  r  > 0.9 является в общем случае критерием существования ближнего порядка, обусловленного сильными химическими взаимодействиями в структуре кристаллов.

Согласно полученным данным, в зависимости от КЧ и формы координационных полиэдров атомов Cd объем (V_ПВД) их полиэдров ВД изменяется в пределах от 19 до 23 ų (табл. 4.2), а радиусы сферических доменов (R_СД), объем которых равен V_ПВД, лежат в области 1.66-1.77Å.

Интегральным параметром, количественно характеризующим нецентросимметричность окружения атома комплексообразователя в структуре кристалла, является величина смещения атома из центра тяжести собственного полиэдра ВД (D_A). По имеющимся данным, в большинстве случаев в пределах 2(D_A) для атомов кадмия D_A=0.

В структуре обсуждаемых соединений безразмерный параметр G₃, характеризующий степень сферичности полиэдров ВД атомов Cd (для сферы G₃=0.077), изменяется от 0.080 до 0.094. Наименьшее среднее значение G₃ имеют атомы Cd с октаэдрической координацией, для которых оно совпадает с теоретическим значением 0.083 для правильного октаэдра. Максимальные значения G₃ (в среднем 0.088(3)) соответствуют атомам Cd с тетраэдрической координацией. При этом для всех атомов Cd c КЧ 4 реальная величина G₃ меньше теоретического значения 0.104 для идеального тетраэдра, что можно считать следствием влияния невалентных взаимодействий Cd/Z.

Аналогичные расчеты для полиэдров ZnS_n показывают, что в зависимости от КЧ и формы координационных полиэдров атомов Zn объем их полиэдров ВД изменяется в пределах от 16 до 18.5ų, а радиусы сферических доменов лежат в области 1.57-1.64Å. Безразмерный параметр G₃, характеризующий степень сферичности полиэдров ВД атомов Zn, изменяется от 0.081 до 0.099. Наименьшее среднее значение G₃ имеют атомы Zn с октаэдрической координацией, для которых оно совпадает с теоретическим значением 0.083 для идеального октаэдра. Максимальные значения G₃ (в среднем 0.089) соответствуют атомам Zn с треугольной, тетраэдрической или тригонально-призматической координацией.

Согласно полученным результатам (для координационных полиэдров GaS_n в структуре кристаллов) в зависимости от КЧ и степени окисления атомов Ga объем их полиэдров ВД (V_ПВД) изменяется в широких пределах от 14.7 до 21.1ų, а радиусы сферических доменов (R_СД), объем которых равен V_ПВД, лежат в области 1.52-1.72Å. Отметим, что для атомов Ga(III) с КЧ 6 и 3 значения R_СД практически совпадают (соответственно 1.522 и 1.529Å), тогда как для Ga(III) с КЧ 4 R_СД увеличено в среднем до 1.64Å. Этот факт связан со сравнительно сильным искажением в структуре кристаллов как линейных, так и угловых параметров тетраэдров GaS₄.

В заключение заметим, что параметры полиэдров ВД являются важными интегральными характеристиками атомов в структуре кристаллов. Поэтому их существенное отклонение от среднего значения для атомов некоторого элемента с фиксированной природой атомов первой координационной сферы позволяет легко выявлять ошибки в кристаллоструктурной информации, содержащейся в базах данных [4]. Например, в процессе данного исследования было обнаружено, что в структуре MgGa₂S₄ {15350} [5], содержащей три разных атома Ga c КЧ 4, характеристики полиэдров ВД Ga(1) и Ga(3) аномально отличаются от


Табл. 1. Влияние ошибки в координате атома S(6) на некоторые параметры

полиэдров ВД атомов галлия в структуре MgGa₂S₄ {15350}.

Параметр полиэдра ВД	Ga(1)		Ga(2)		Ga(3)		Среднее значение для Ga(III) с КЧ 4
	с ошибкой	без ошибки	с ошибкой	без ошибки	с ошибкой	без ошибки
RСД, Å	1.617	1.652	1.643	1.643	1.732	1.648	1.638(29)
DA, Å	0.15	0.10	0.06	0.06	0.23	0.06	0.06(5)
G3 (104)	934	927	921	921	909	928	928(29)

таковых для Ga(2), так и от средних значений для остальных атомов Ga(III) с КЧ 4 (табл. 3). Проведенный с помощью комплекса TOPOS анализ позволил установить, что в статье [5] имеется опечатка для координаты z атома S(6) (вместо правильного значения 0.01223 опубликовано 0.1223), которая была повторена и в базе данных [4]. Как видно из данных табл. 1, после устранения указанной ошибки характеристики атомов Ga(1) и Ga(3) в пределах погрешности совпали со среднестатистическими значениями, тогда как для Ga(2) полиэдр ВД не изменился. Это и не удивительно, так как полиэдр ВД атома Ga(2), в отличие от Ga(1) или Ga(3), не имеет ни одной общей грани с полиэдром ВД атома S(6).

В четвертой главе на основе анализа литературных данных показано, что физической причиной взаимодействия мод является гиротропия кристаллов, причем под гиротропией понимают наблюдаемые в кристаллооптике оптические явления, связанные с проявлением эффектов пространственной дисперсии первого порядка. Помимо явления оптической активности, связанного со способностью вещества вращать плоскость поляризации света, к ним относятся: циркулярный дихроизм, эллиптическое двулучепреломление, возникновение продольной составляющей электрического поля, появление добавочных световых волн. Кристаллы, для которых псевдотензор гирации g_ik отличен от нуля, называют оптически активными. Оптической активностью могут обладать кристаллы всех сингоний. Необходимым условием является наличие в структуре кристалла винтовых осей симметрии. Исключив из 32 видов симметрии 11 центросимметричных и 10, имеющих инверсионные оси и плоскости симметрии, получим 11 видов симметрии, кристаллы которых обладают способностью вращать плоскость поляризации. Показано, что носителем гиротропии в халькопиритных кристаллах является фрагмент структуры – искаженный тетраэдр СА₂В₂. Однако соображения, основанные на анализе симметрии, лишь разрешают гиротропию, но не доказывают ее существование.

Поскольку изотропная точка в кристаллах со структурой дефектного халькопирита обнаружена только в тиогаллате кадмия, был проведен стереоатомный анализ его структуры с помощью программного комплекса TOPOS. Используя программы AutoCN и Dirichlet программного комплекса TOPOS, мы установили типы связи атома халькогена, входящего в структуру CdGa₂S₄ и других изоструктурных ему соединений. Показано, что сокращение межъядерных расстояний r(A-X) в общем случае неизбежно сопровождается увеличением объема соответствующих парных пересечений типа

r_SR_СД (23)

и/или

R_СДr_S. (24)

Ненулевые по величине пересечения типа (23) или (24) можно интерпретировать как наличие переноса электронной плотности с валентной оболочки атома радиуса r_S на вакантные валентные орбитали соседнего атома с радиусом R_СД. С указанной точки зрения пересечения типа П₂, при которых одно из двух произведений вида (23) или (24) непременно равно нулю, можно трактовать как донорно-акцепторные или ионные связи. Поэтому при образовании связи донором электронов (в рамках ковалентной модели химической связи) или образующимся катионом (с позиций ионной модели) будет являться тот атом, значение r_S которого входит в ненулевое по абсолютной величине произведение (23) или (24). Например, если для некоторой связи А-Х r_S(А)R_СД(Х) = 0, а R_СД(А)r_S(Х) > 0, то атом Х является донором электронов (катионом), а атом А - акцептором электронов (анионом).

В тех случаях, когда оба произведения (23) или (24) одновременно не равны нулю (пересечения типа П₄ или П₃), реально возможны две ситуации. Так, если взаимодействующие атомы идентичны как химически (при этом их значения r_S = const), так и кристаллографически (при этом их значения R_СД = const), то пересечения r_SR_СД  R_СДr_S > 0 и возникающая связь будет ковалентной неполярной, так как перенос электронной плотности от левого атома к правому (определяется пересечением (23)) будет полностью компенсироваться идентичным по величине переносом от правого атома к левому (определяется пересечением (24)). Если же при перекрывании типа П₃ или П₄ вследствие химической и (или) кристаллографической неэквивалентности взаимодействующих атомов значения произведений (23) и (24) отличаются, то соответствующую связь можно назвать ионно-ковалентной (или полярной ковалентной). При этом в некоторой связи А-Х атомом, приобретающим заряд ⁺, будет являться тот атом, значение r_S которого входит в большее по абсолютной величине произведение (23) или (24). Например, если для связи А-Х r_S(А)R_СД(Х) > R_СД(А)r_S(Х) > 0, то итогом химического взаимодействия изначально нейтральных атомов А и Х явится увеличение электронной плотности (возникнет некоторый заряд ^-) в области действия атома Х, тогда как у атома А, являющегося более сильным донором (или более слабым акцептором) электронов, возникнет равный по абсолютной величине заряд ⁺. Таким образом, согласно использованной модели при пересечениях типа П₂, П₃ или П₄ перенос электронной плотности между атомами А и Х при возникновении связи А-Х, в общем случае должен быть пропорционален разности

П(А-Х)=r_S(А)R_СД(Х) - R_СД(А)r_S(Х). (25)

Так как объем ПВД атомов халькогенов также зависит от состава соединения, то для сравнения степени переноса электронной плотности используем безразмерную величину =П_i/V_ПВД.

Для соединений I-V (ZnGa₂S₄ (I), CdGa₂S₄ (II), HgGa₂S₄ (III), CdGa₂Se₄ (IV) и CdGa₂Te₄ (V))  равно соответственно 0.137, 0.157, 0.146, 0.100 и 0.025. Таким образом, в изоструктурных I-V соединениях максимальная величина μ и, как следствие, максимальный отрицательный заряд ^- на атомах халькогена отвечает кристаллам CdGa₂S₄ (II), обладающим точкой изотропии. Поэтому указанные данные позволяют предположить, что особенности оптических свойств изоструктурных соединений I-V зависят от степени ионности связей металл – халькоген. Имеющиеся экспериментальные данные для I-V дают основание считать, что точкой изотропии обладают вещества только с относительно высокой степенью ионности связей М-Х (>0.15). У веществ же со сравнительно небольшой степенью ионности связей М-Х (<0.15) точка изотропии отсутствует.

Твердые растворы замещения кристаллических полупроводников представляют собой особый класс неупорядоченных систем, в котором беспорядок обусловлен случайным характером расположения атомов, образующих твердый раствор, по узлам кристаллической решетки. Беспорядок, таким образом, является внутренним свойством твердого раствора и может иметь различные формы. Однако некоторые свойства твердых растворов могут быть достаточно хорошо описаны в модели виртуального кристалла, в рамках которой реальный твердый раствор аппроксимируется идеальным псевдокристаллом, в узлах которого находятся псевдоатомы, свойства которых определяются линейной комбинацией соответствующих свойств реальных атомов, из которых построен раствор. В этой модели, не учитывающей вообще наличие беспорядка, удается, тем не менее, описать в первом приближении многие важные свойства, в частности, концентрационные зависимости ширин запрещенных зон, а также постоянных решетки твердого раствора.

Используя предложенную модель, рассматриваем структурные особенности кристаллов твердых растворов на основе тиогаллата кадмия, для которых известно о существовании изотропной точки. В системе CdGa₂S₄ – ZnGa₂S₄ существует непрерывный ряд твердых растворов, причем для кристаллов CdGa₂S₄ изотропная точка существует и наблюдается при λ₀ = 493 Å, тогда как для ZnGa₂S₄ она отсутствует. Однако для кристаллов твердых растворов состава Cd_1-хZn_xGa₂S₄, где х изменяется в пределах от 0 до 0,072, изотропная точка существует и изменяется от 493 до 661 Å. Полученные результаты показывают, что замещение атомов кадмия атомами цинка сопровождается закономерным понижением суммы П в твердых растворах Cd_1-хZn_хGa₂S₄. При этом с ростом концентрации цинка (х) безразмерный параметр  = П / V_ПВД практически линейно уменьшается, составляя при x = 0, 0.2, 0.4, 0.6, 0.8 и 1 соответственно 0.157, 0.153, 0.149, 0.145, 0.141 и 0.137. Существенно, что для всех твердых растворов Cd_1-хZn_хGa₂S₄ при х 0.2 параметр   0.15, и поэтому такие твердые растворы, как и CdGa₂S₄, должны обладать точкой изотропии, что нами экспериментально подтверждено данными для образцов с х<0.072.

Аналогичные расчеты для систем твердых растворов CdGa₂S₄ – HgGa₂S₄, CdGa₂S₄ – CdGa₂Se₄, и CdGa₂S₄ – CdGa₂Te₄ показывают, что предельные соединения Cd_0,68Hg_0,32Ga₂S₄, CdGa₂S_3,76Se_0,24, CdGa₂S_3,94Te_0,06 должны обладать изотропной точкой. Первое и последнее соединения на наличие ИТ не исследовались, а для системы CdGa₂S₄ – CdGa₂Se₄ нами установлено, что для состава CdGa₂S_3,92Se_0,08 длина волны изотропии λ_о равна 654 нм.

Таким образом, критерий >0.15, где величина  определяет степень ионности связей М-Х, указывает на вещества со структурой дефектного халькопирита, которые обладают точкой изотропии.

Анализ полученных данных об основных характеристиках полиэдров ПВД показывает, что такие характеристики, как объем полиэдров Вороного – Дирихле, объем координационного полиэдра и площадь поверхности ПВД всех атомов, входящих в структуру, уменьшаются линейно с увеличением концентрации Ga₂S₃ (рис. 7).

Вместе с тем, как показано в четвертой главе, для кристаллов твердых растворов на основе тиогаллата кадмия в системе CdS – Ga₂S₃ наблюдается линейный рост положения изотропной точки с увеличением концентрации Ga₂S₃. Таким образом, можно сделать вывод о том, что уменьшение объема полиэдра Вороного-Дирихле атома серы закономерно ведет к увеличению значений длины волны изотропии в кристаллах со структурой дефектного халькопирита.

Действительно, построенные по рассчитанным данным графики зависимости объема полиэдров Вороного – Дирихле от состава в системе CdGa₂S₄–ZnGa₂S₄ показывают, что они уменьшаются нелинейно с увеличением концентрации ZnGa₂S₄. Что сопровождается нелинейным ростом положения изотропной точки.

Аналогичные зависимости наблюдаются и в системе CdGa₂S₄ - MgGa₂S₄ (рис. 9).

Таким образом, в системах твердых растворов на основе тиогаллата кадмия наблюдается закономерный рост значений длины волны изотропии с уменьшением объема полиэдра Вороного-Дирихле, а ее существование ограничено величиной степени ионности химической связи μ халькогена с элементами, входящими в полиэдр С□АВ₂.




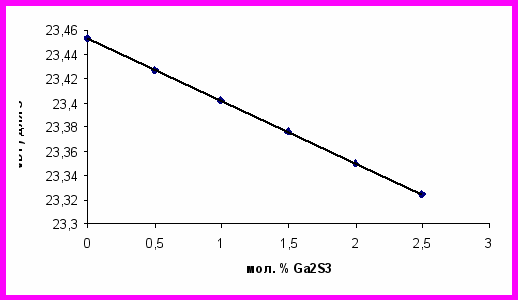
Рис. 7. Зависимость объема ПВД атома серы от концентрации Ga₂S₃ в системе CdS – Ga₂S₃.

С целью подтверждения возможности использования предложенного критерия существования изотропной точки и распространения области его применения во второй части