Программы. Проблемы организации вычислений на многопроцессорных вычислительных системах. Аппаратная реализация иса. Инвариантные свойства иса

Вид материала

Лекция

Содержание 3. Информационная архитектура программы. 4. Отображение ИСА и их совокупностей на 5. Проблема оптимизации памяти. Теорема А.П.Ершова Формулировка теоремы А.П.Ершова.

Подобный материал:

• Информатика, вычислительная техника и инженерное образование. − 2011, №4 (6) раздел, 247.88kb.
• Реализация алгоритмов решения задач газовой динамики на многопроцессорных вычислительных, 9.14kb.
• Решение задач глобальной оптимизации большой размерности на многопроцессорных комплексах, 143.77kb.
• Э. В. Прозорова «Вычислительные методы механики сплошной среды» СпбГУ, 1999, 119.9kb.
• Решение задач математического программирования на многопроцессорных вычислительных, 87.2kb.
• Планы и программы подготовки специалистов по параллельным компьютерным технологиям,, 24.65kb.
• Вопросы на экзамен по дисциплине «Архитектура вычислительных систем» (авс), 29kb.
• Домашнее задание по Теория информационных процессов, 227.65kb.
• Лекция 3 Тактика и стратегия туристского похода, 90.93kb.
• Архитектура Вычислительных Систем», Университет «Дубна» лекция, 193.82kb.

Лекция 5

Информационные структуры алгоритмов. Инвариантные свойства ИСА. Процессорная реализация алгоритмов.

Теорема А.П.Ершова о max разрезе ИСА и min памяти

программы. Проблемы организации вычислений на

многопроцессорных вычислительных системах. Аппаратная реализация ИСА.

1. Инвариантные свойства ИСА. ИСА по определению задаёт взаимные поставки информации между функциями, из которых она сконструирована. Взаимные поставки информации суть подстановки (суперпозиции) при помощи которых строится сложная функция из составляющих. Операция подстановки (суперпозиция) единственная операция для конструирования сложных функций. Составляющие функции, из которых собирается конструкция (архитектура) ИСА либо базовые (заданы от бога) либо сконструированы при помощи подстановок. Алгоритм, вычисляющий функцию, может быть уточнён в виде «вычислительной машины» (ВМ) самыми различными способами. Но любая ВМ должна уметь делать две операции: а) уметь вычислять составляющие ИСА функции; б) осуществлять поставки информации между составляющими согласно ИСА. Таким образом ИСА не зависит от ВМ и является в этом смысле инвариантом. Программа (последовательность вычисления составляющих функции ИСА) очень часто подвергается преобразованию, цель преобразований может быть различна (оптимизация кода и/или памяти). Две программы (П_i, П_j) называются функционально эквивалентными, если они реализуют одну и ту же ИСА.
   
2. Ярусно-параллельное представление (разложение) ИСА (ЯПФ).
   

ЯПФ очень удобная форма представления графа ИСА и часто используется для различных целей анализа. Пример ЯПФ приведен на рис. 1. На каждом ярусе расположены функции (операции), которые вычисляются независимо друг от друга, они не поставляют друг другу информацию. На каждой паре соседних ярусов на Я_i находятся поставщики информации и только для функций яруса Я_i+1. В ЯПФ вводится дополнительная функция «хранения информации» на ярусе (обозначена как «=» и имеет смысл операции тождества). Заметим, что ИСА может иметь несколько вариантов ЯПФ – разложения. Составляющие функции «+» и «» в ИСА на рис. 1 не нужно понимать как обычные «сложение» и «умножение», это обозначение разных и может быть очень сложных функций, которые в свою очередь имеют ИСА.

3. Информационная архитектура программы.

Программа, написанная для некоторой ВМ, по сути дела представляет собой систему (совокупность) функций, которые должны быть вычислены. В самом общем случае функции могут быть информационно связанными. Другими словами в ИСА функции связаны взаимными поставками информации (т.е. подстановками). Информационной архитектурой программы называется совокупность ИСА функций, вычислимых в программе. На рис. 2 показана архитектура системы функций, в виде ЯПФ. ИСА для функций могут иметь любой тип схемы подстановок – конечные, примитивно-рекурсивные, бесконечно изменяющиеся, итерационные. Важно, что архитектура описывает поставки информации от функции к функции.



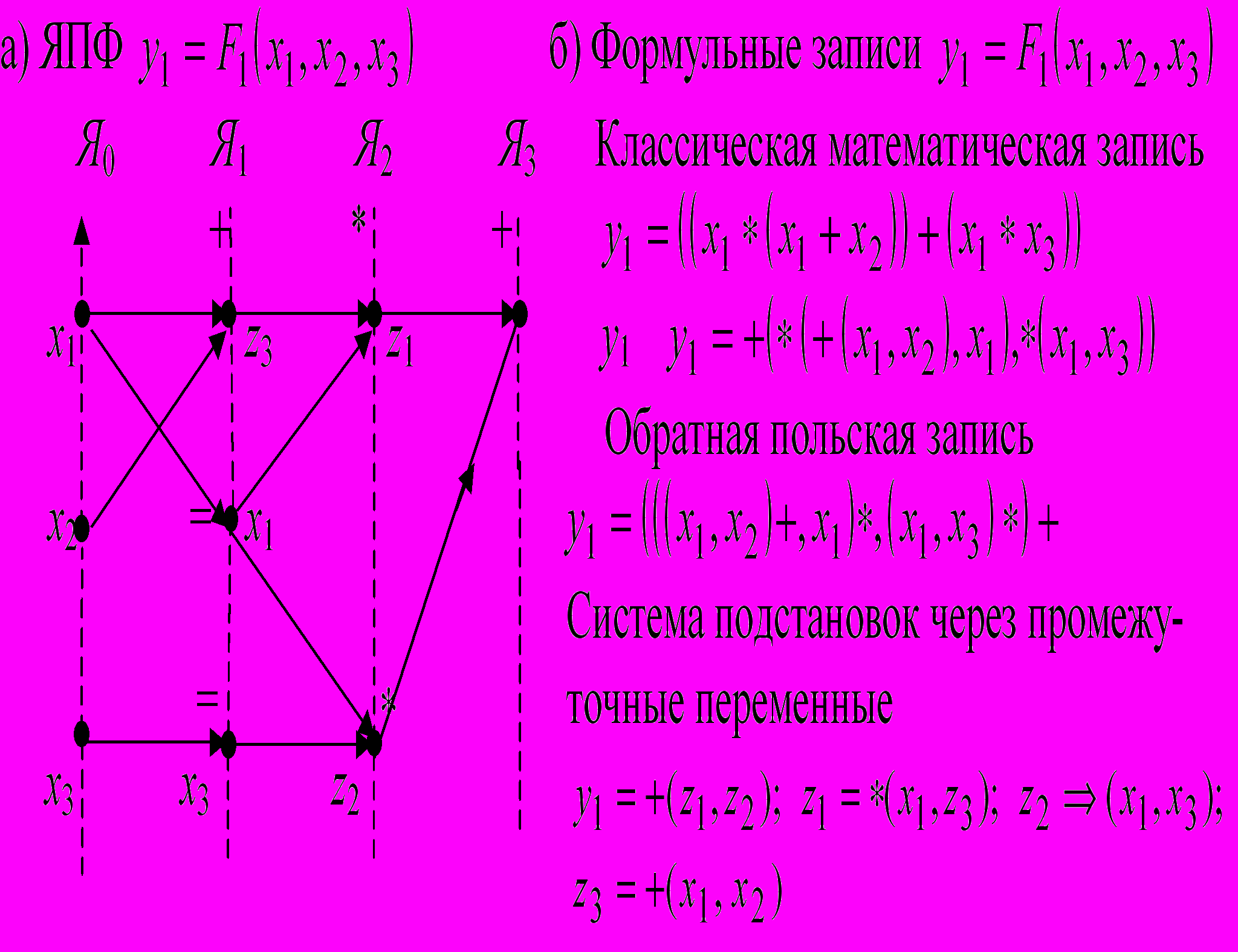
Рис. 1. Ярусно-параллельная форма ИСА функции




а)




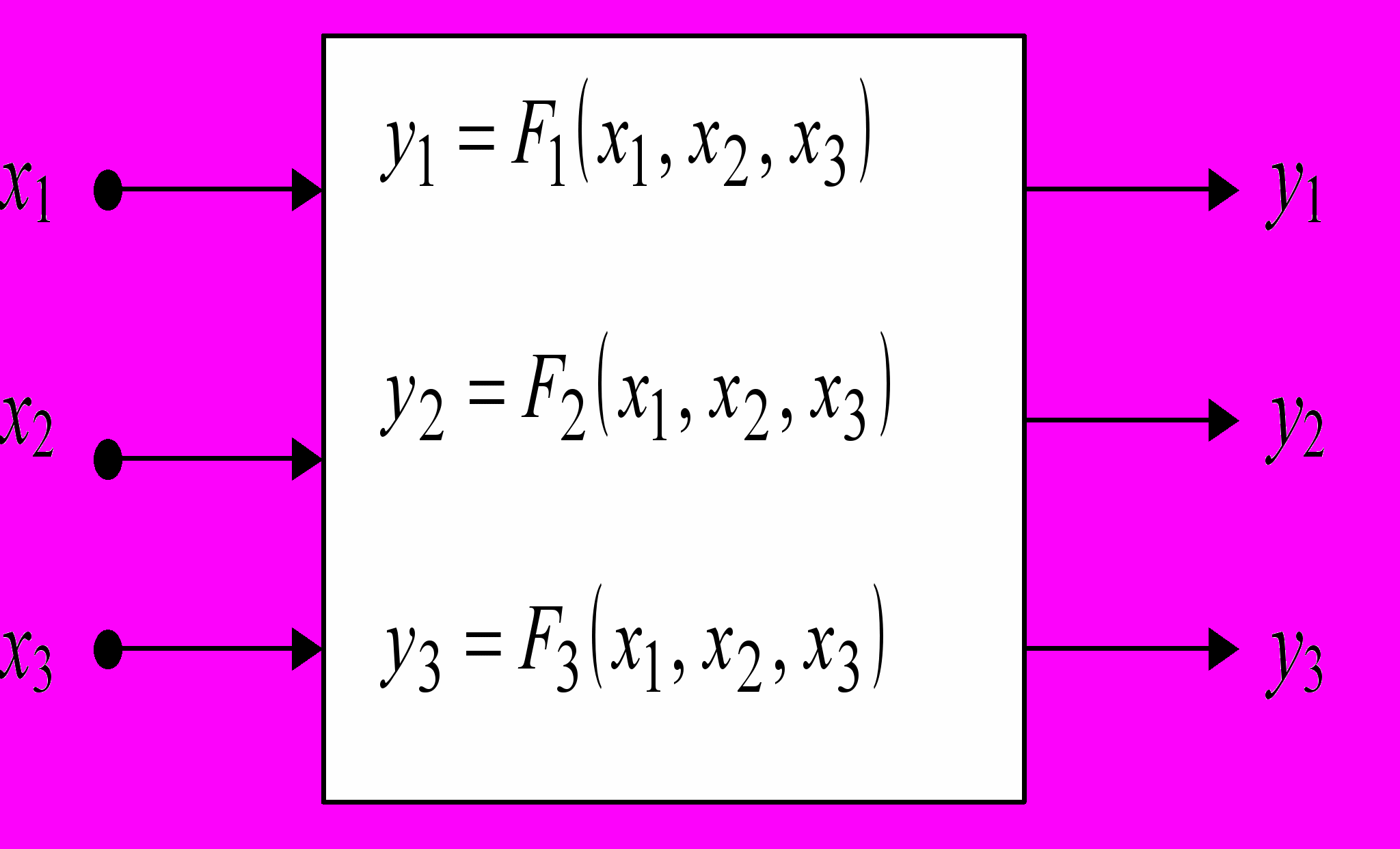
б) Система функций в виде формул







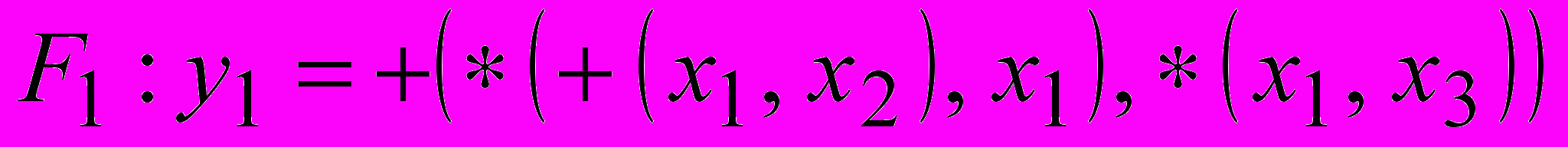
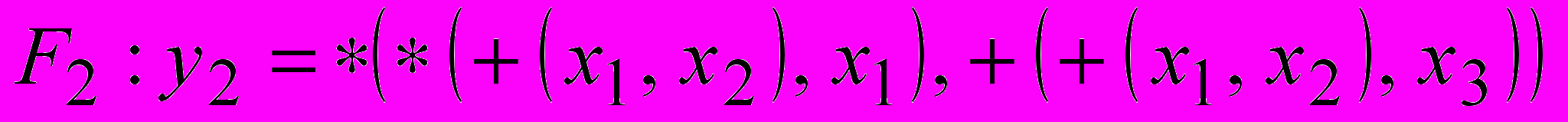
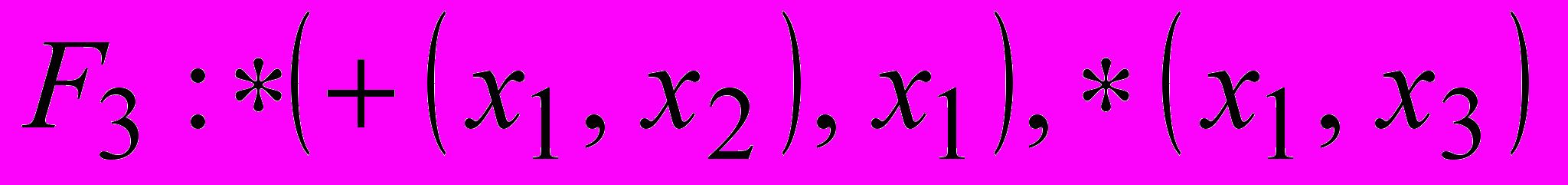
в)




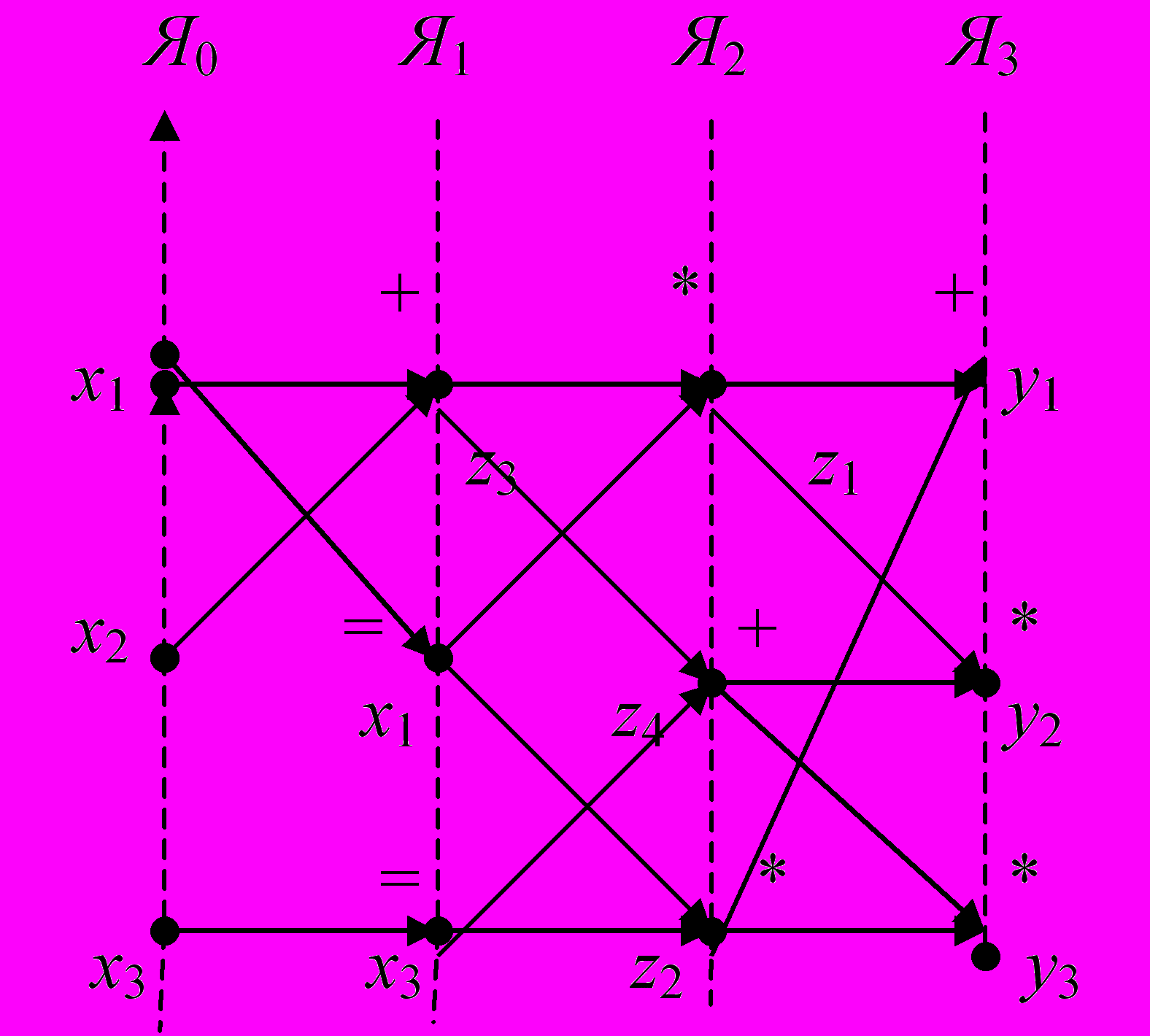
Рис. 2. Архитектура информационно – связанной системы функций.

а) «Чёрный ящик»: система функций F₁, F₂, F₃

б) Структура «чёрного ящика», заданная системой

формул

в) Архитектура «чёрного ящика», заданная в виде ЯПФ,

связанных между собой ИСА функций F₁, F₂, F₃.

4. Отображение ИСА и их совокупностей на

вычислительную систему (ВС).

Понятно, что архитектура ВС может быть достаточно сложной. Здесь рассматривается два типа ВС: однопроцессорная ВС, с общей памятью, где любой элемент памяти доступен процессору без ограничений; многопроцессорная ВС, состоящая из универсальных равноправных процессоров с общей памятью или памятью, распределённой между процессорами без ограничений обмена информацией.

1П-разложение суть отображение ИСА в языки процедурного программирования, которые предполагают выполнение, записанной на них программы, последовательно на одном процессоре. 1П-разложение, это ЯПФ, где каждый ярус содержит ровно одну элементарную функцию, вычислимую алгоритмом (процессором) и некоторую совокупность переменных, значения которых нужно хранить для обеспечения будущих вычислений. Понятно, что для одной и той же ИСА может быть несколько различных 1П- разложений (программ) (см.рис. 3.б,в для 1П-разложения отдельной ИСА и рис. 4а,б для архитектуры ИСА).

nП-разложение суть отображение ИСА на «n» процессоров в виде ЯПФ, где каждый ярус содержит не более «n» элементарных функций вычислимых алгоритмом (процессором). Пример 2П-разложения системы функций с архитектурой рис. 2в показан на рис. 5а.

5. Проблема оптимизации памяти.

Обычно эту проблему в самом простом случае (каждый элемент памяти равнодоступен для каждого процессора) связывают с минимизацией оперативной памяти. Заметим, что далее будут описаны другие более сложные способы организации памяти (например, стек), которые требуют других отображений, других разложений ИСА (например, для стека требуется древесное разложение).

Теорема А.П.Ершова «О максимальном разрезе информационного графа программы». Информационный граф программы суть ИСА, которая реализуется в программе. На рис. 3а показаны такие разрезы для 1П-разложения ИСА (программы). Каждый разрез характеризуется списком переменных, которые были вычислены в соответствующий такт выполнения программы и списком переменных, значения которых необходимы для будущих вычислений

Формулировка теоремы А.П.Ершова. Минимальное количество элементов памяти для выполнения программы равно максимальному разрезу (максимальному списку переменных, характеризующих разрез). Такой разрез называется max – разрезом.

На рис. 3а,в приведены разрезы ИСА для программы П₁ и программы П₂ (имеющей ту же самую ИСА). Программы П₁ и П₂ имеют одинаковые max разрезы и поэтому требуют одинаковое min количество элементов памяти, равное трём.

В оптимизирующих трансляторах строят специальные таблицы отображения переменных программы (1П-разложения ИСА) на элементы памяти т.н. информационные карты (рис. 3г) и операционные карты (рис. 3д), которые показывают какие элементы памяти использует процессор в каждый такт вычисления составляющей функции.

Оптимизация памяти на множестве эквивалентных программных реализаций, требует перебора всех возможных программ, построенных по инварианту ИСА. Во многих случаях такой перебор затруднителен. Считается, что максимальный разрез для случайно выбранной программной реализации незначительно отличается от min {max-разрезов} всех возможных программ (см. пример на рис. 4). Оценка разброса величин max-разрезов эквивалентных программ является нерешённой проблемой.

Планирование оптимального распределения информации в памяти может быть решено только для ИСА примитивно-рекурсивных функций, где выделяется всегда фрагмент с конечными подстановками (см. пример ИСА функции Фибоначчи на рис. 5). В случае, когда ИСА изменяется в процессе работы программы, такого оптимального планирования памяти провести невозможно. Обычно используют два способа обойти эту проблему: а) переход на более сложные структуры данных, в которых ИСА имеет примитивно-рекурсивную схему подстановок; б) в транслятор встраивают программу – интерпретатор, которая отслеживает потактное изменение ИСА в процессе вычисления.

а) 1П-разложение ИСА функции

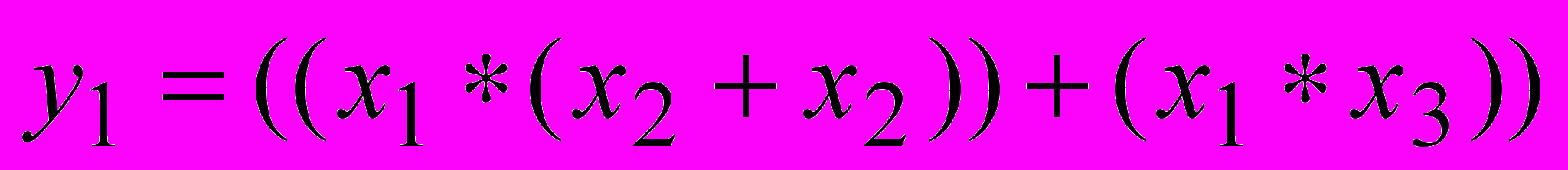
Максимальный разрез графа ИСА (max C)





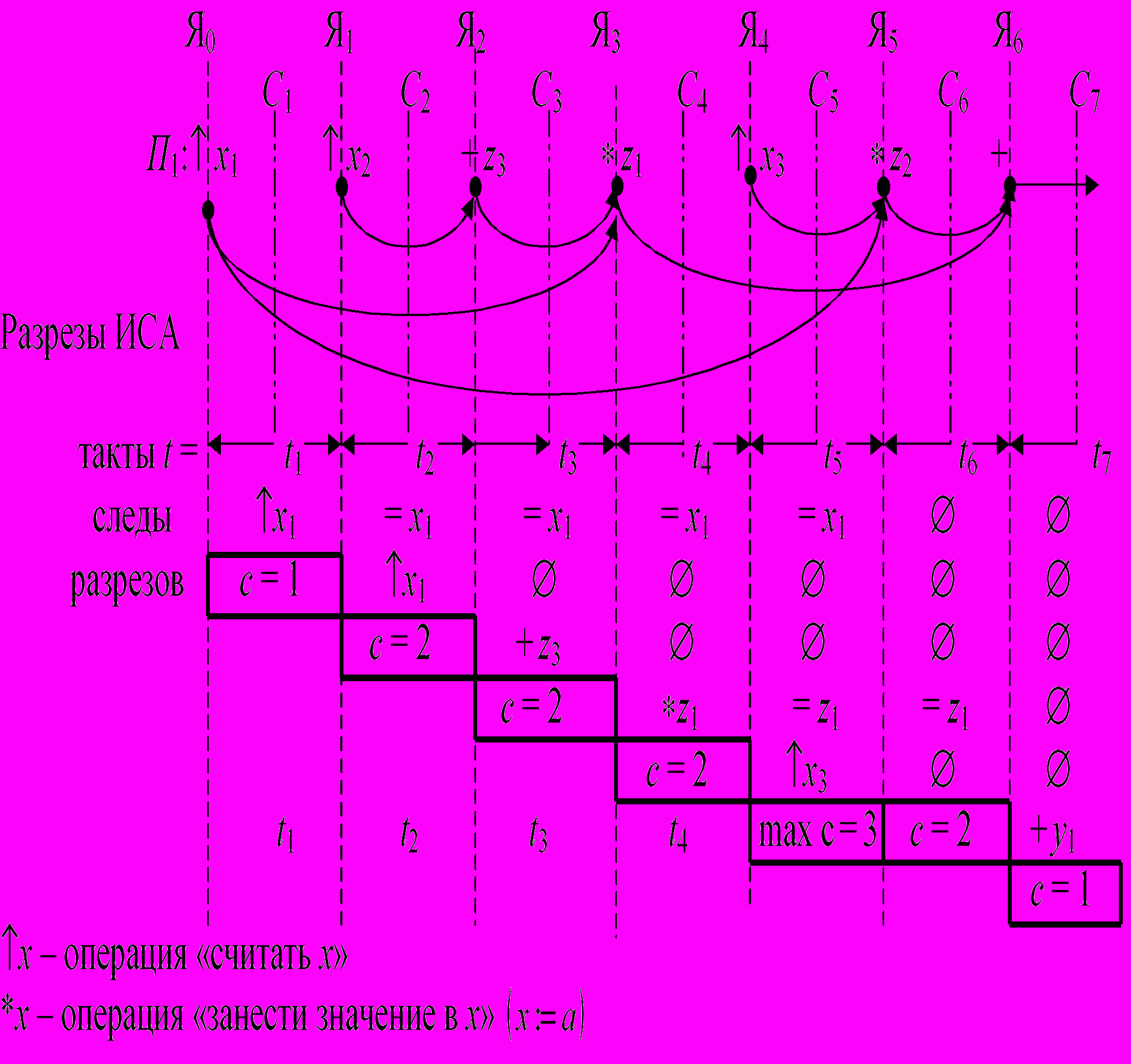
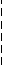
б) программа П₁ для 1П-разложения на рис а)






в) максимальный разрез графа ИСА для программы П₂






Рис. 3. 1П – отображение функции, заданной ИСА



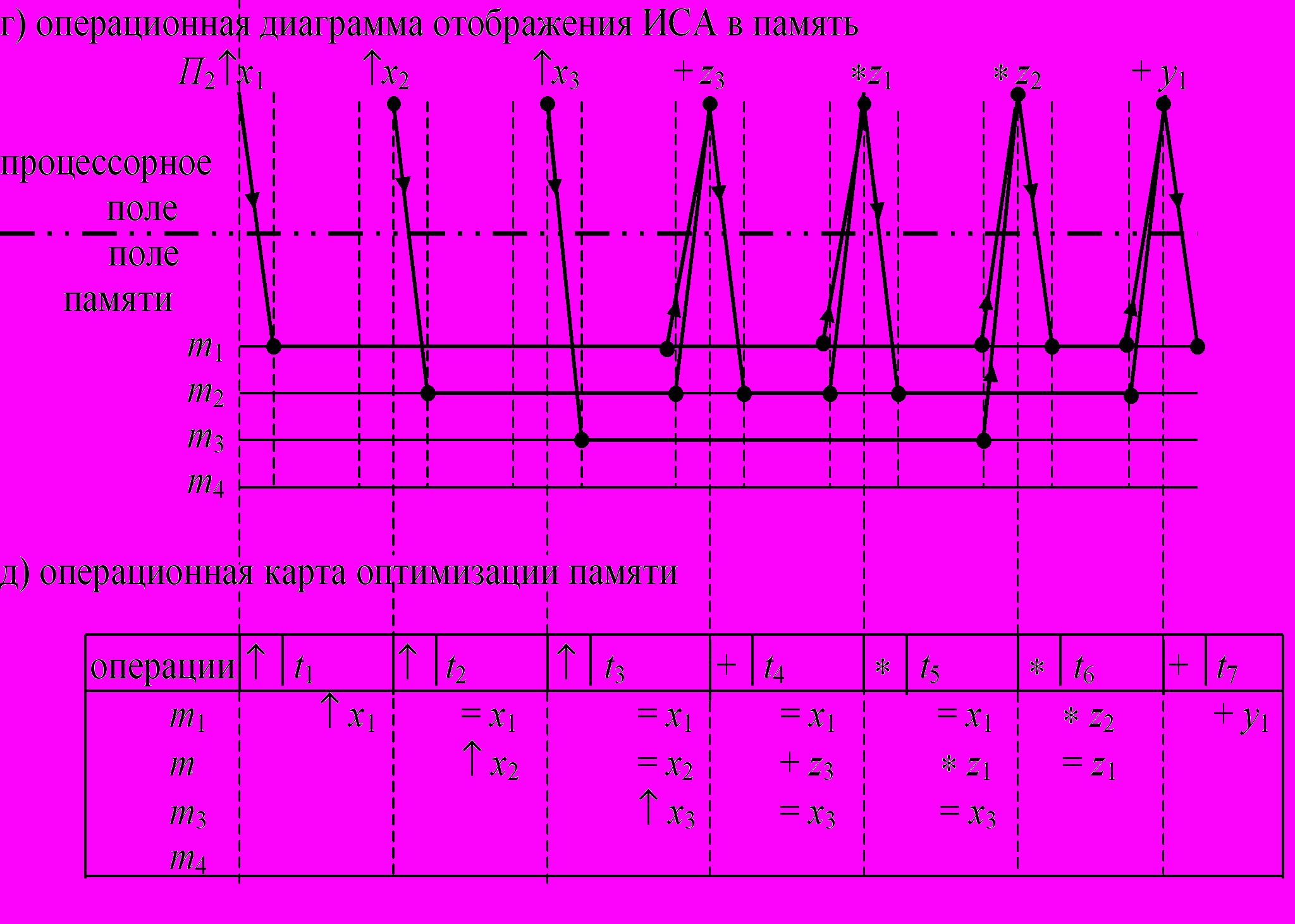
Рис. 3. Трансляторное отображение функции, заданной ИСА

а)

б)




Рис. 4. Информационные карты для различных 1П–разложений

системы функций с архитектурой (рис. 2в)

а) Информационная карта для программы П₁ (min размер памяти=4)

б) Информационная карта для программы П₂ (min размер памяти=5)





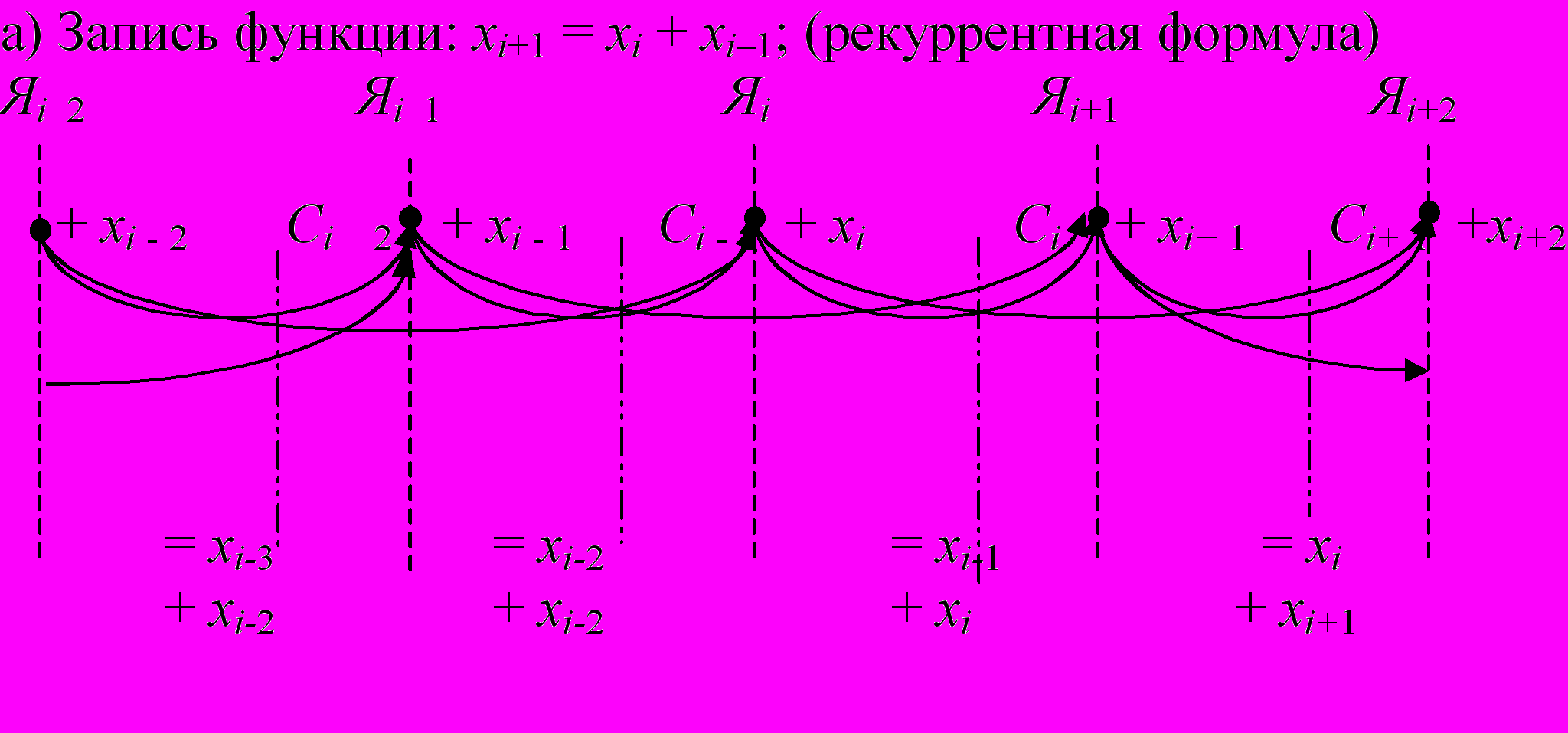
б)



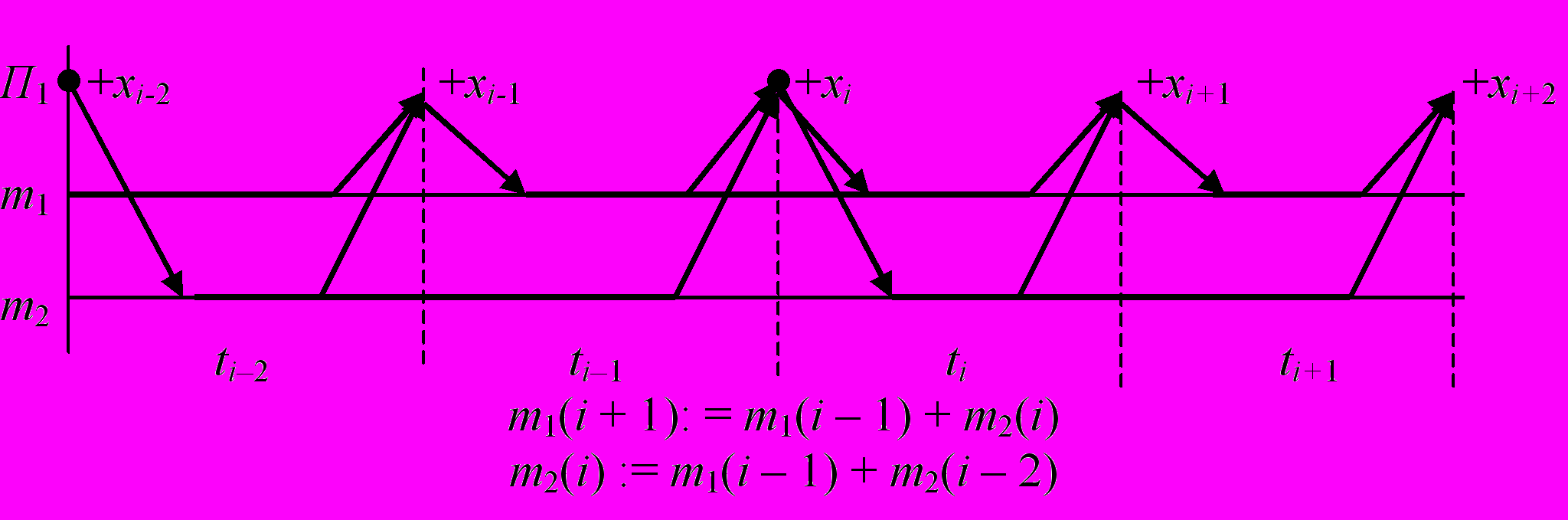
Рис. 5. Планирование памяти для вычисления функции

Фибоначчи

а) Разрезы ИСА для функции Фибоначчи

б) Динамика оптимальной загрузки памяти при вычислении

функции Фибоначчи

6. Планирование вычислений в многопроцессорных ВС.

В однородных ВС, состоящих из одинаковых процессоров с одинаковыми элементами памяти, основной проблемой является уменьшение пересылок информации между процессорами. Практика программирования показывает, что для различных эквивалентных (относительно системы ИСА) программных реализаций объём пересылок имеет значительный разброс. Оценок такого разброса до сих пор не имеется (пример см. на рис. 5).

7. Аппаратная реализация ИСА.
   

Выше было замечено, что дуга в графе ИСА (подстановка переменной) аналогична некоторому информационному каналу. А для аппаратной реализации обычному электрическому проводнику (проводу). ИСА в этом случае представляет т.н. функциональную схему устройства, вычисляющую значение функции за один такт без использования памяти. Такие схемы называются комбинационными. Для примитивно – рекурсивных ИСА приходится строить т.н. последовательную машину, в которой повторяющейся фрагмент вычисляется комбинационной схемой за один такт, а задействие следующего фрагмента происходит через специальную память «задержки на один такт». Пример такой аппаратной реализации показан на рис. 7. Аппаратная реализация ИСА с изменяющейся структурой требует подключения микропроцессоров.




Рис. 6. Отображение системы функций с информационной

архитектурой (рис. 2в) на двухпроцессорную

вычислительную систему

а) 2П-разложение системы связанных ИСА

б)



в)

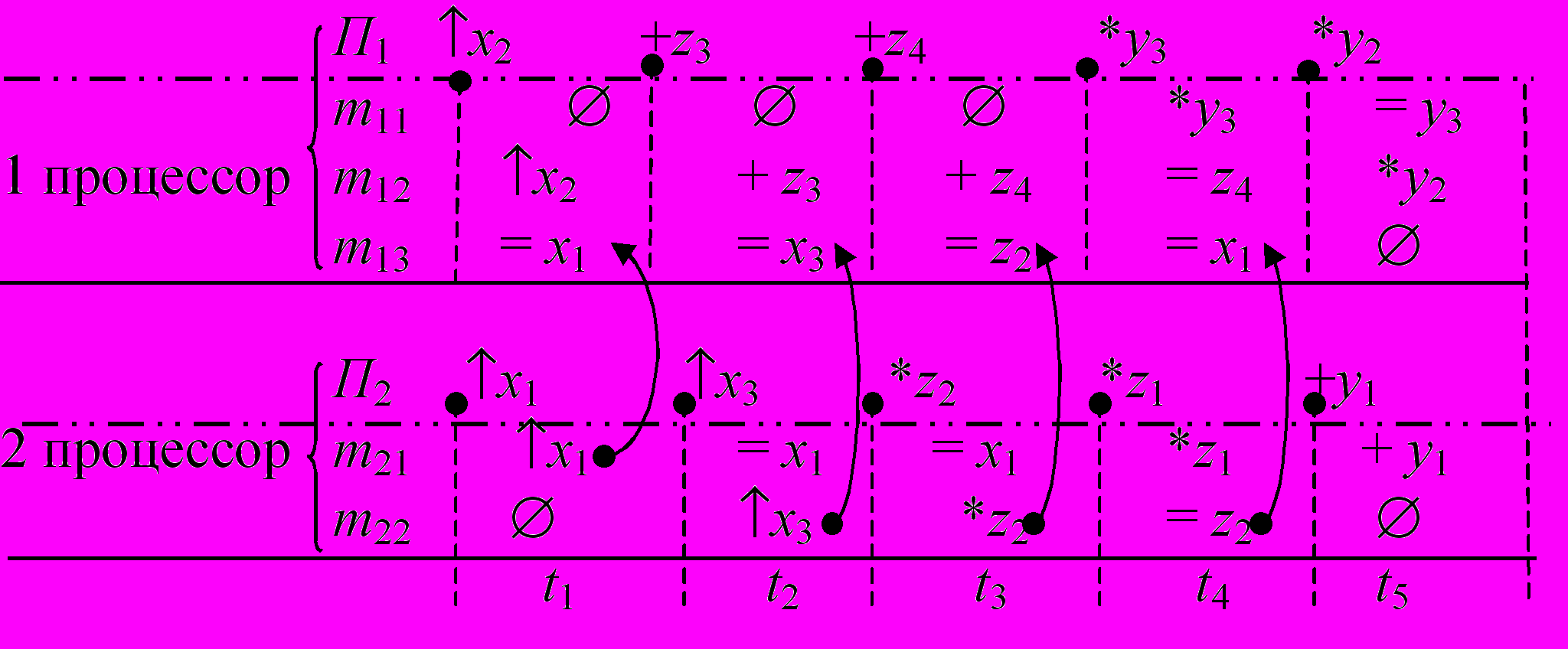Рис. 6. Отображение системы функций с архитектурой (рис. 2в) на двухпроцессорную вычислительную систему

б) информационная карта 2П-разложения с общей памятью

в) операционная карта 2П-разложения с пересылками

информации между процессорами







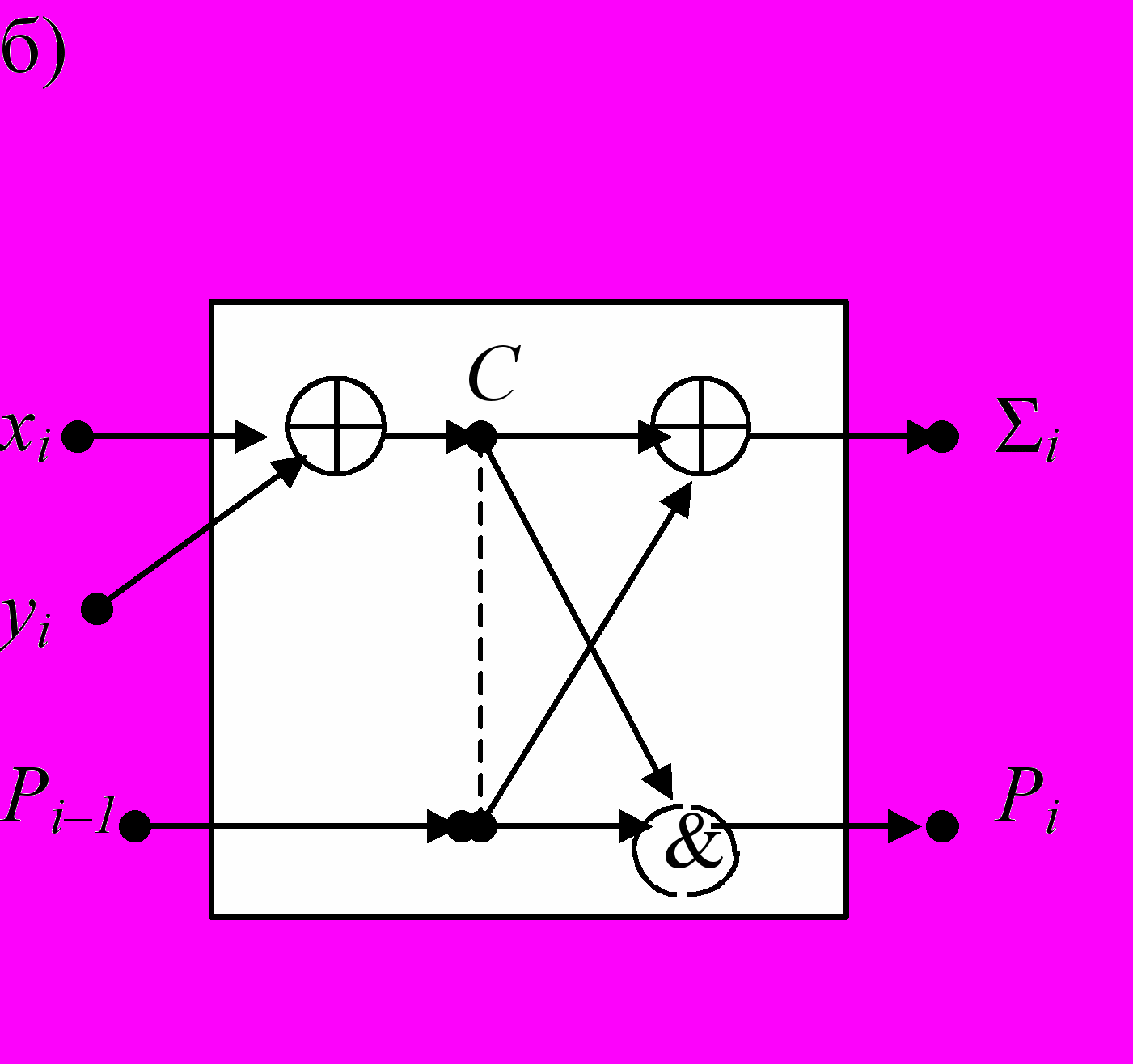
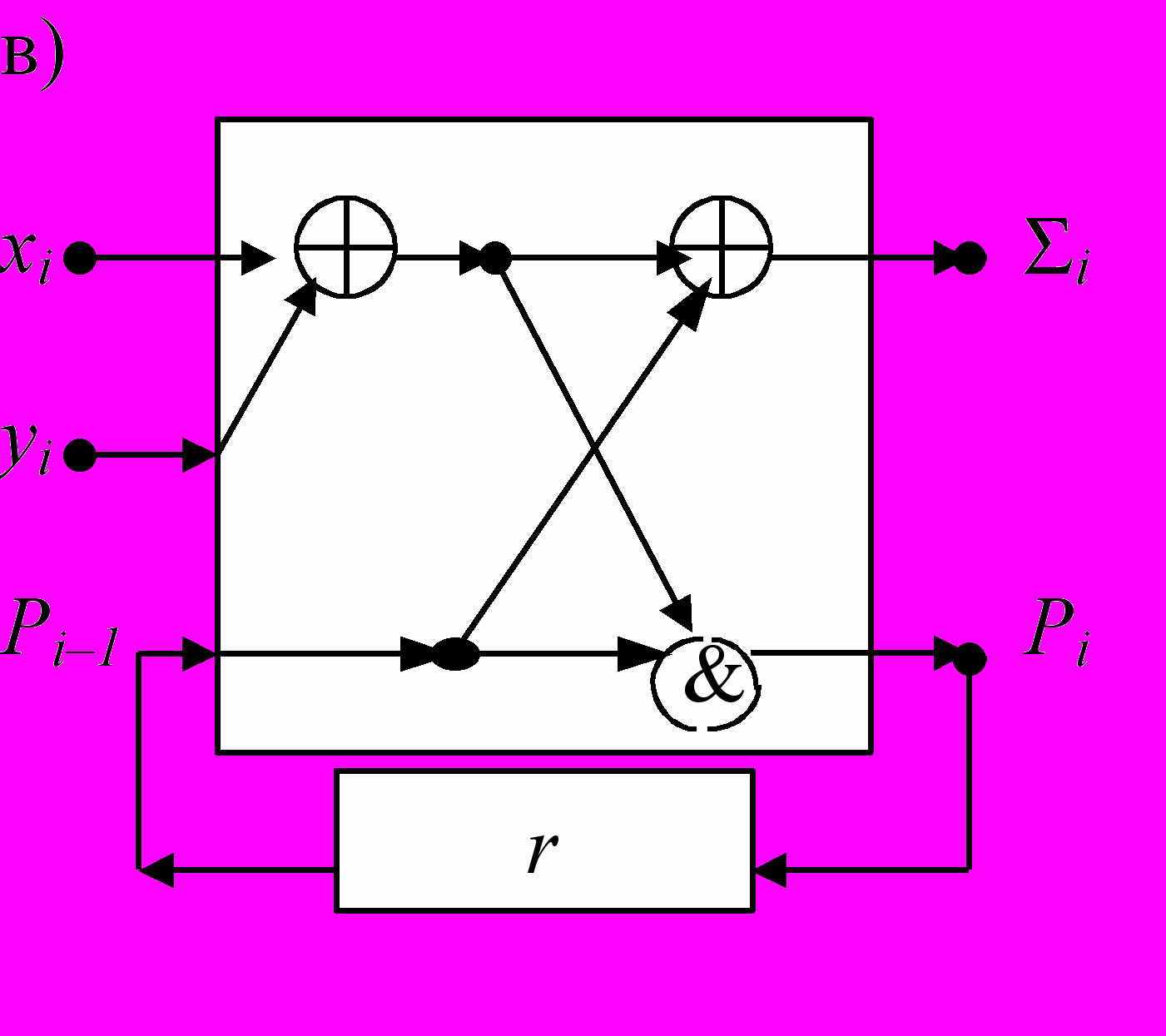
Рис. 7. Аппаратная реализация ИСА «сумматора»

а) Таблицы и рекуррентные формулы для «суммы» и «переноса»

б) ИСА сумматора

в) последовательный сумматор с задержкой на 1 такт

(запоминание P_i в регистре «r»)

г) комбинационный n – разрядный сумматор.