Решение задач математического программирования на многопроцессорных вычислительных системах

Вид материала

Решение

Содержание 2. Основные определения и обозначения 2. Метод неравномерных покрытий для задачи математического программирования 3. Параллельная реализация метода неравномерных покрытий 4. Результаты вычислительного эксперимента Таблица 1. Заключение Рис. 4. Зависимость времени расчетов от числа рабочих процессов. Литература

Подобный материал:

• Литература: [1,8-11,16,18], 419.3kb.
• Решение задач глобальной оптимизации большой размерности на многопроцессорных комплексах, 143.77kb.
• Реализация алгоритмов решения задач газовой динамики на многопроцессорных вычислительных, 9.14kb.
• Краткий обзор моделей стохастического программирования и методов решения экономических, 59.55kb.
• Вопросы на экзамен по дисциплине «Архитектура вычислительных систем» (авс), 29kb.
• Домашнее задание по Теория информационных процессов, 227.65kb.
• Вопросы к экзамену по курсу "Математическое программирование", 16.36kb.
• «решение оптимизационных экономических задач методами линейного программирования», 283.33kb.
• Под названием "транспортная задача" объединяется широкий круг задач с единой математической, 142.19kb.
• Программы. Проблемы организации вычислений на многопроцессорных вычислительных системах., 86.92kb.

Решение задач математического программирования на многопроцессорных вычислительных системах¹

М.А. Посыпкин
Центр Грид-технологий и распределенных вычислений, ИСА РАН
mposypkin@mail.ru

1. Введение

Задачи математического программирования, также называемые задачами условной оптимизации, распространены в технике, физике, экономике, управлении технологическими процессами и других облас­тях. Метод неравномерных покрытий[1], предложенный Ю.Г. Евтушенко, позволяет получать решения задачи непрерывной оптимизации с задан­ной гарантированной точностью. В данной работе предлагается обобщение метода неравномерных покрытий для задач математического программирования. В ряде случаев предложенный метод не только гарантирует оптимальность, но и позволяет получать существенно меньшие зна­чения целевой функции по сравнению с эвристическими подходами. Подтверждающий тестовый пример приводится в данной работе.

Зачастую решение таких задач за приемлемое время невозможно получить на однопроцессорных рабочих станциях. В этих случаях целе­сообразно переходить к вычислениям на параллельных системах. Вычислительная схема метода неравномерных покрытий в целом со­ответствует схеме метода ветвей и границ. Поэтому для реализации этого метода была выбрана библиотека BNB-Solver[2], предназначенная для решения задач оптимизации методами ветвей и границ на много­процессорных вычислительных системах. В работе приводится описание параллельной реализации и результаты вычислительного эксперимента, подтверждающие ее эффективность.

2. Основные определения и обозначения

В работе компоненты вектора нумеруются верхними индексами: 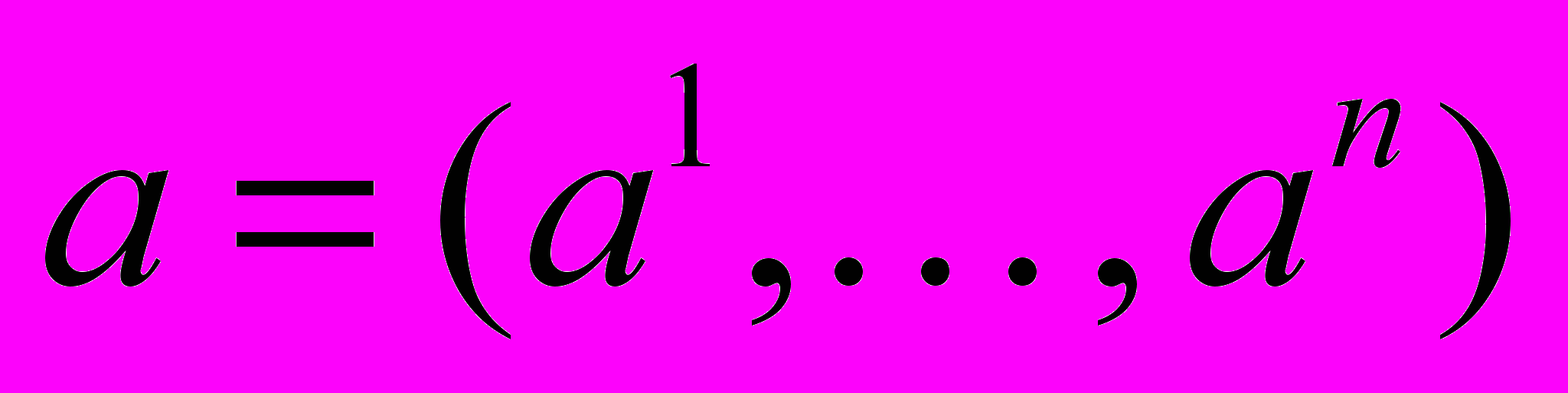. Также вводится сокращенная запись для векторных операций и неравенств: 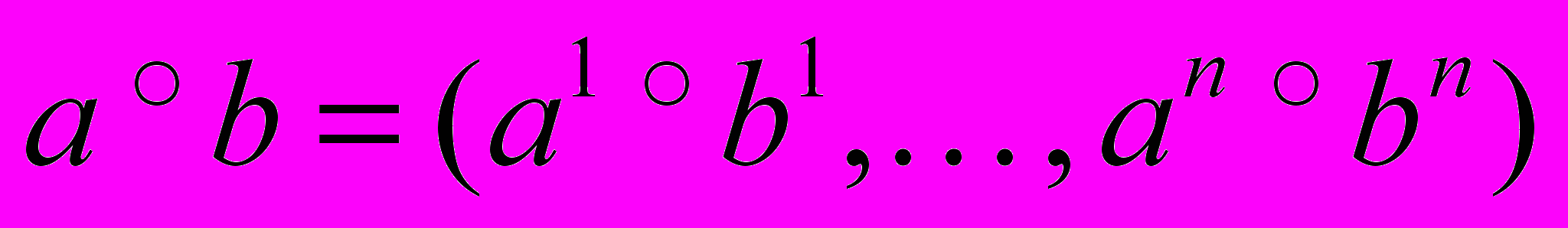, где 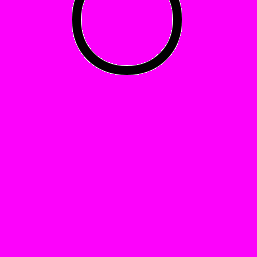- арифметиче­ская бинарная операция, знак равенства или неравенства. Векторное неравенство (равенство) считается выполненным, если выполнены все неравенства (равенства) для соответствующих компонент.

Минорантой функции 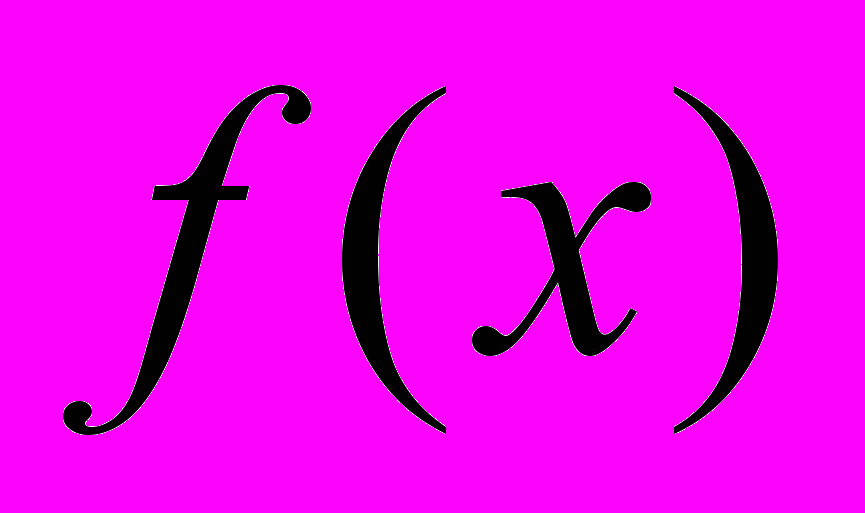на множестве 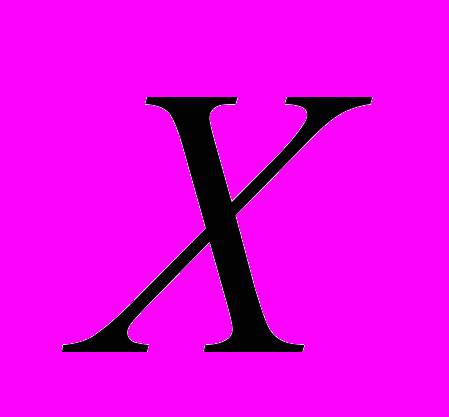называется такая функция 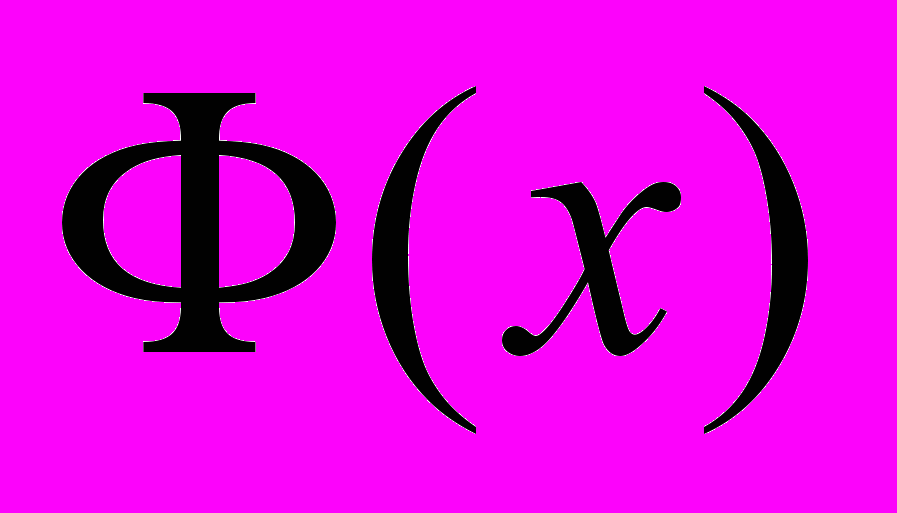, что 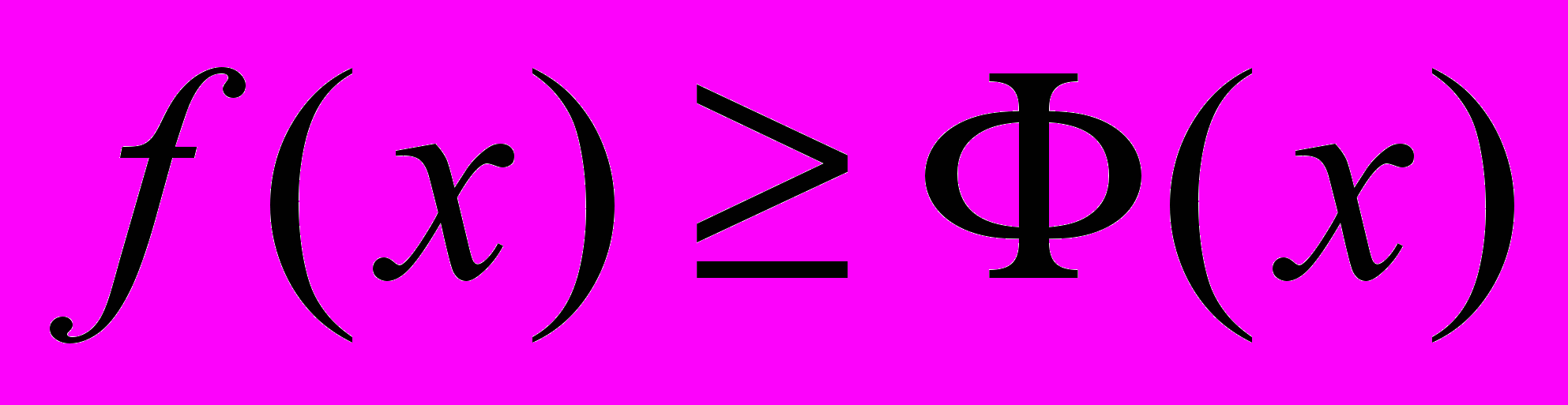для всех 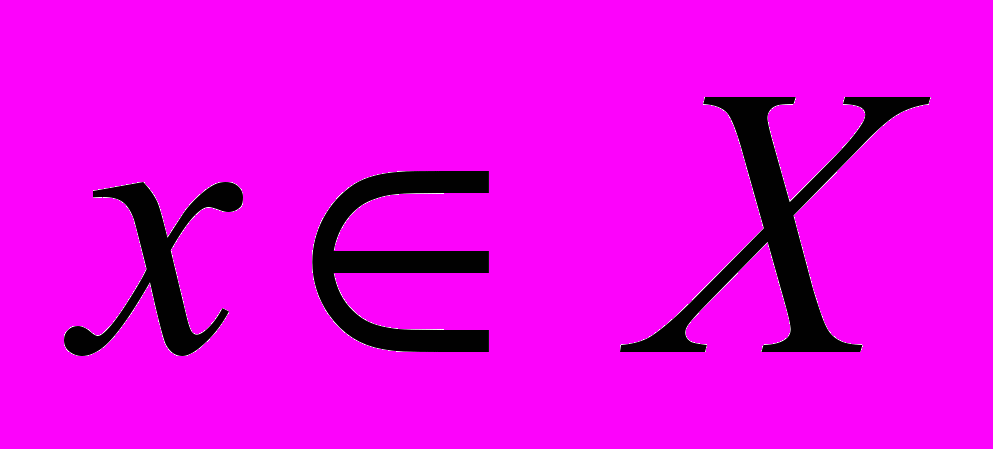. Рассмотрим две миноранты для функции 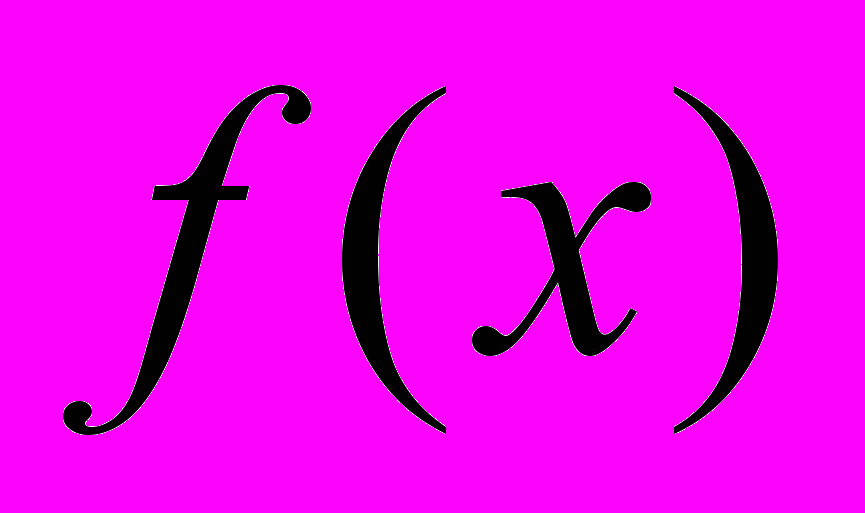, полученные при разных предположениях.

1. Пусть функция 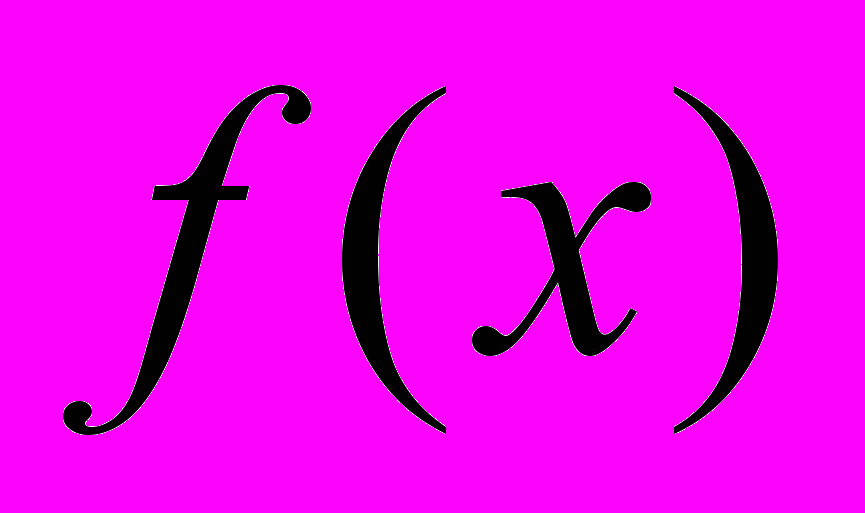удовлетворяет условию Липшица с константой 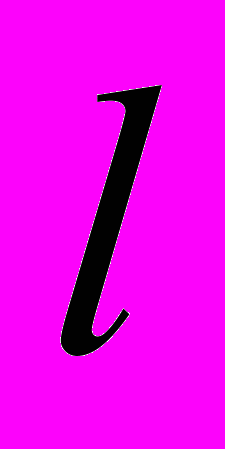на множестве 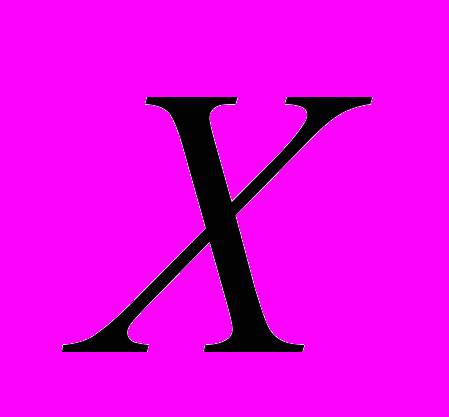: 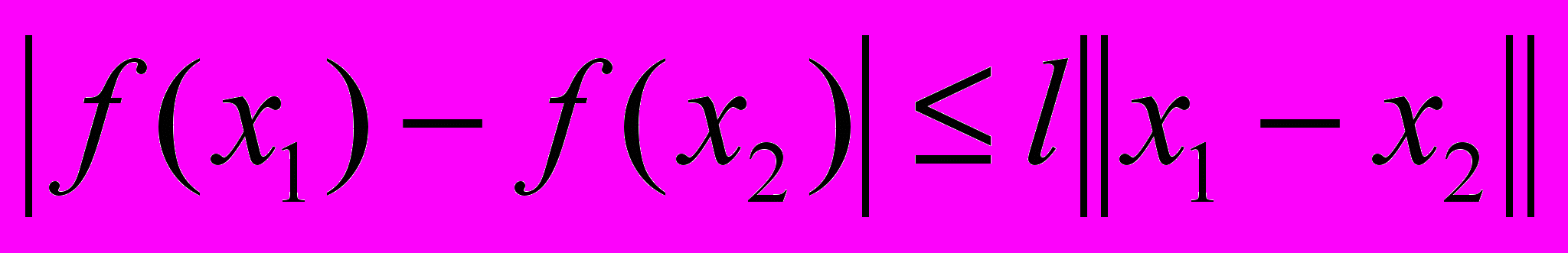для всех 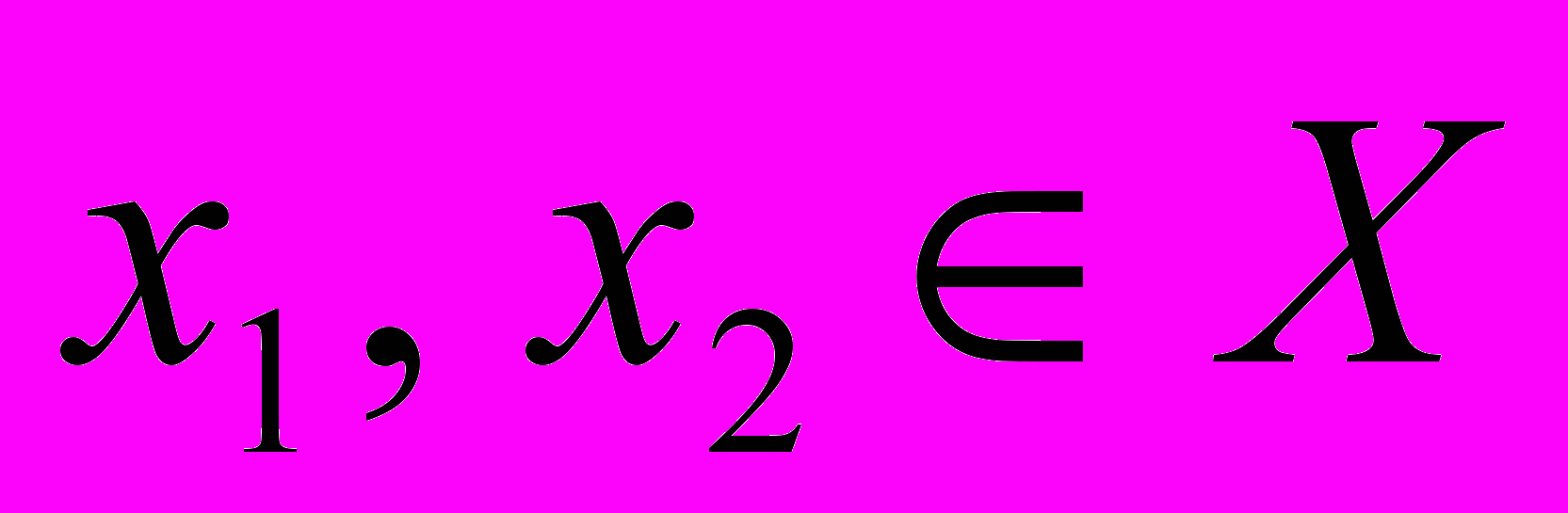. Тогда функция 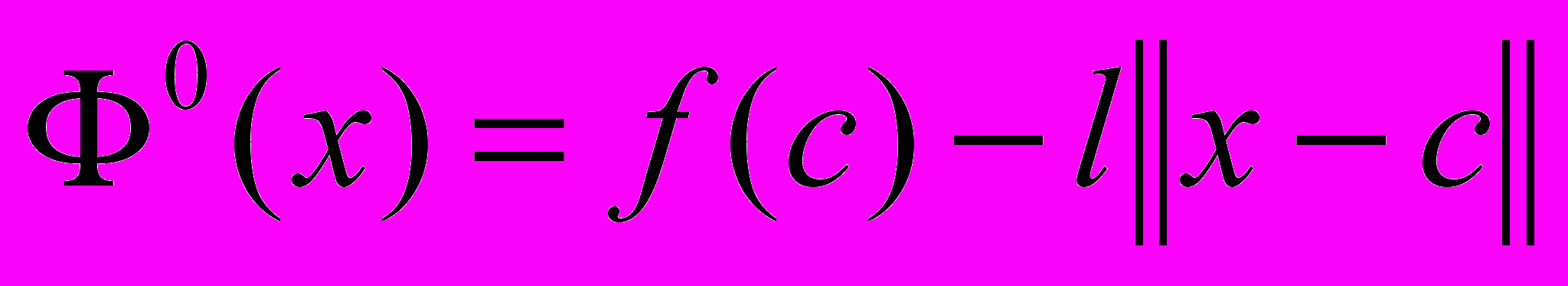, 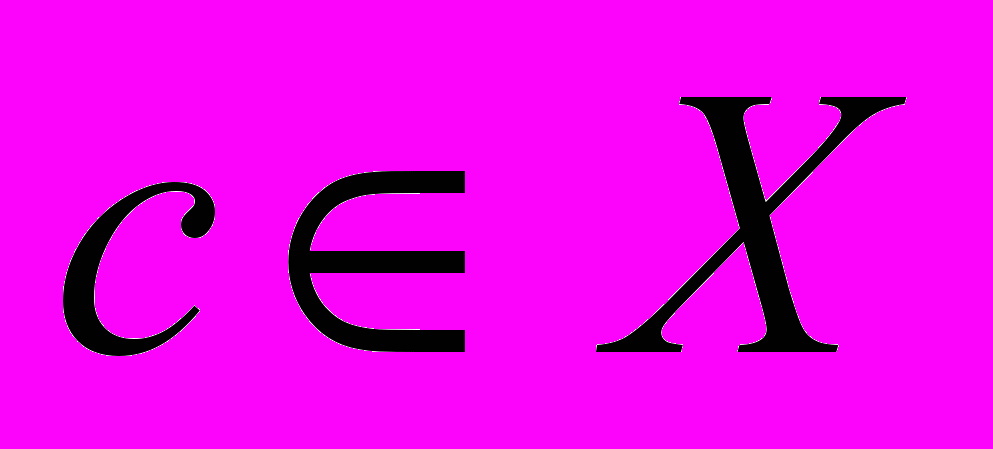является минорантой функции 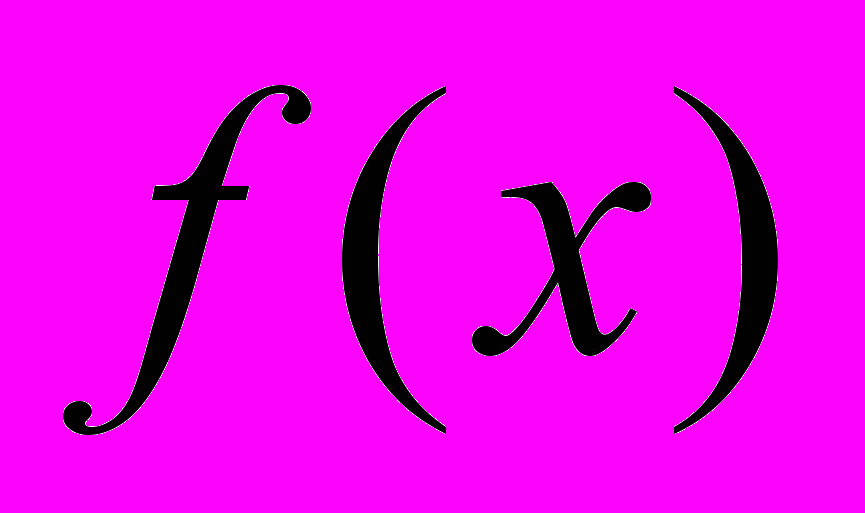на множестве 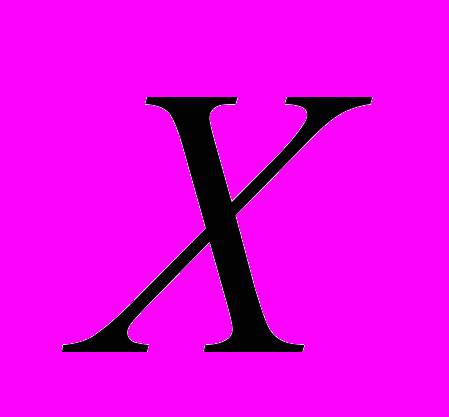. Будем называть функцию 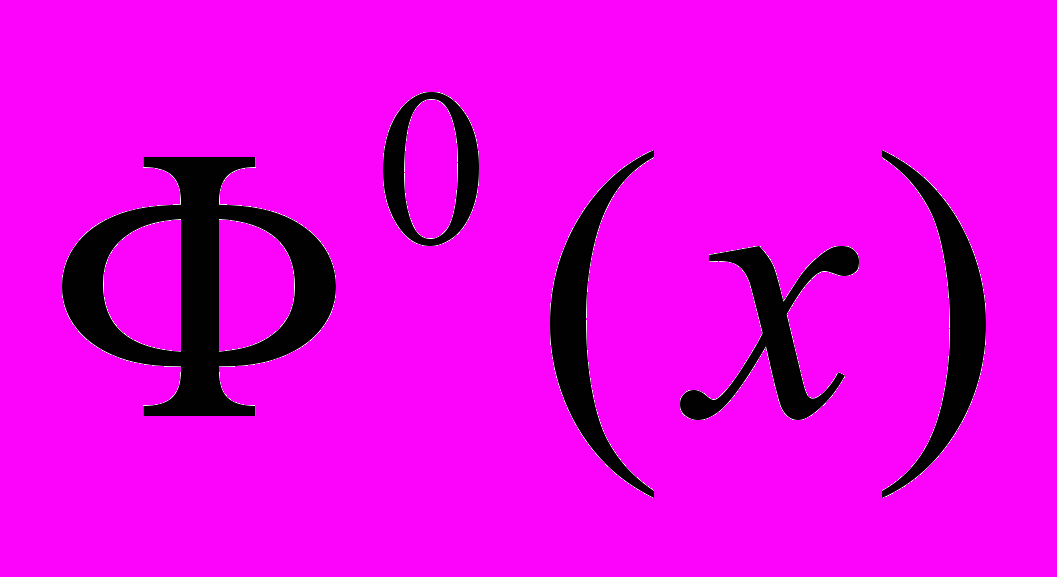минорантой 0 функции .

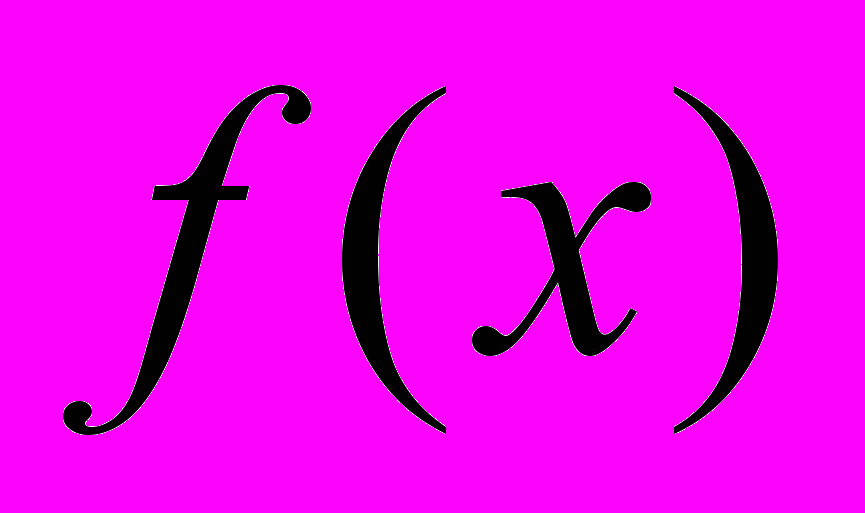2. Пусть градиент 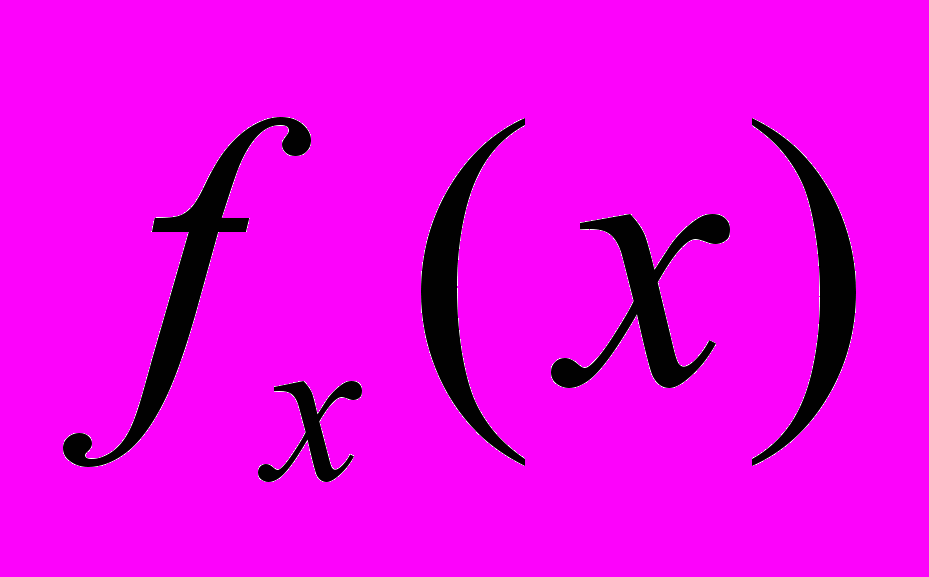функции 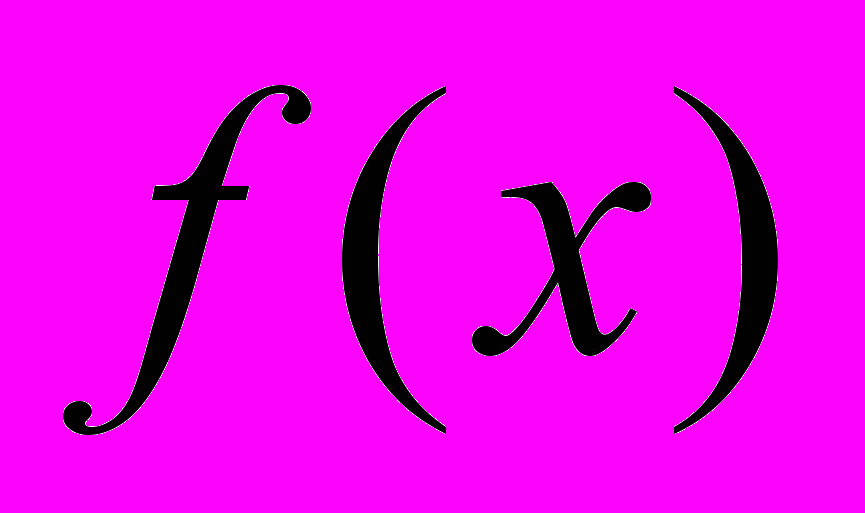удовлетворяет условию Липшица с константой 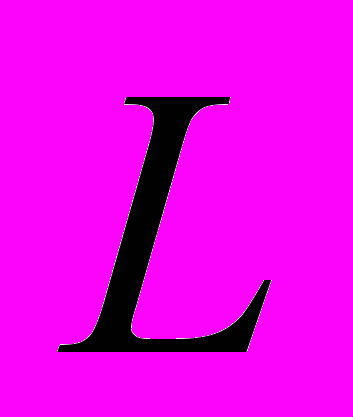на множестве 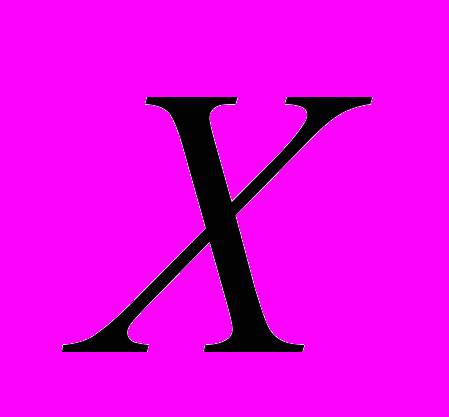: 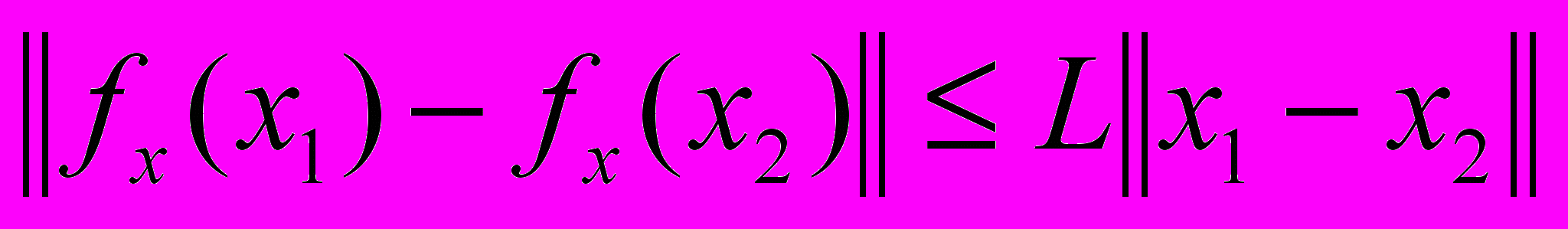для всех 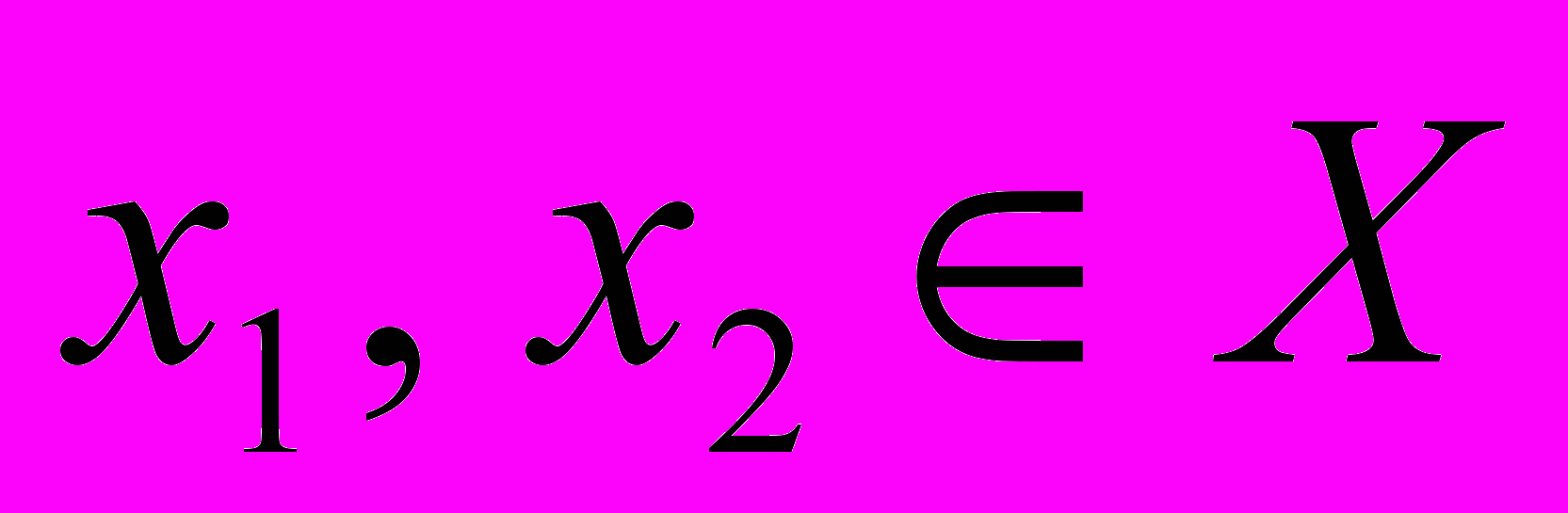. Тогда функция 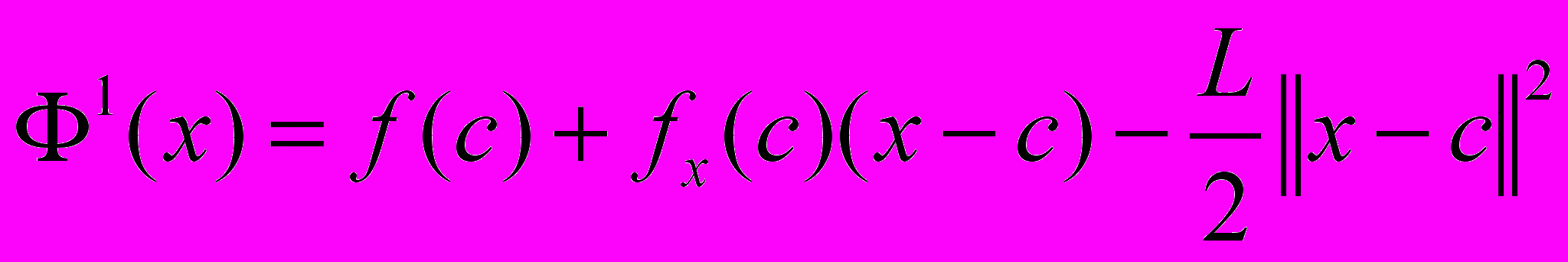, 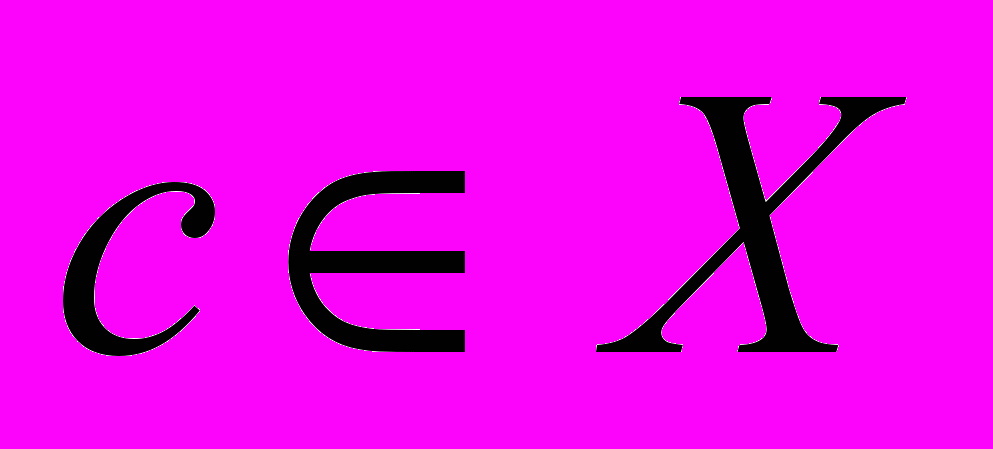является минорантой функции 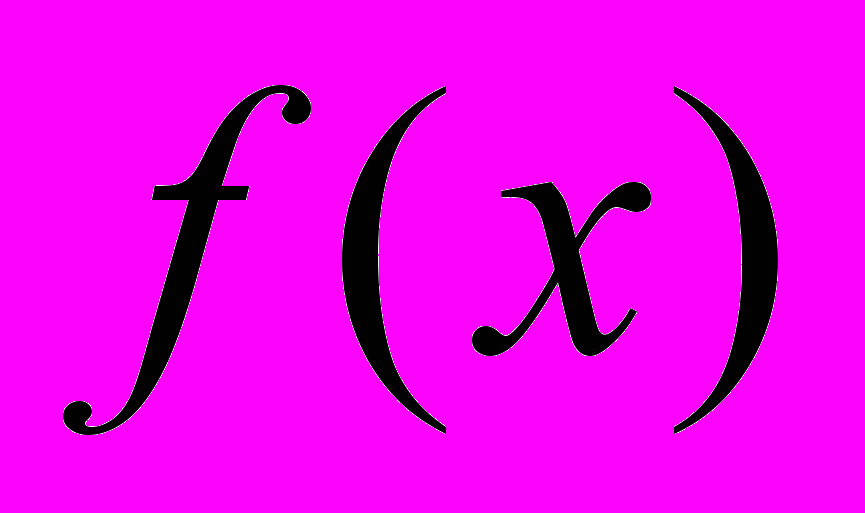на множестве 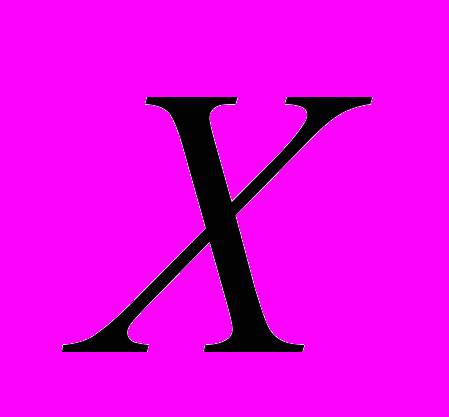. Будем называть функцию 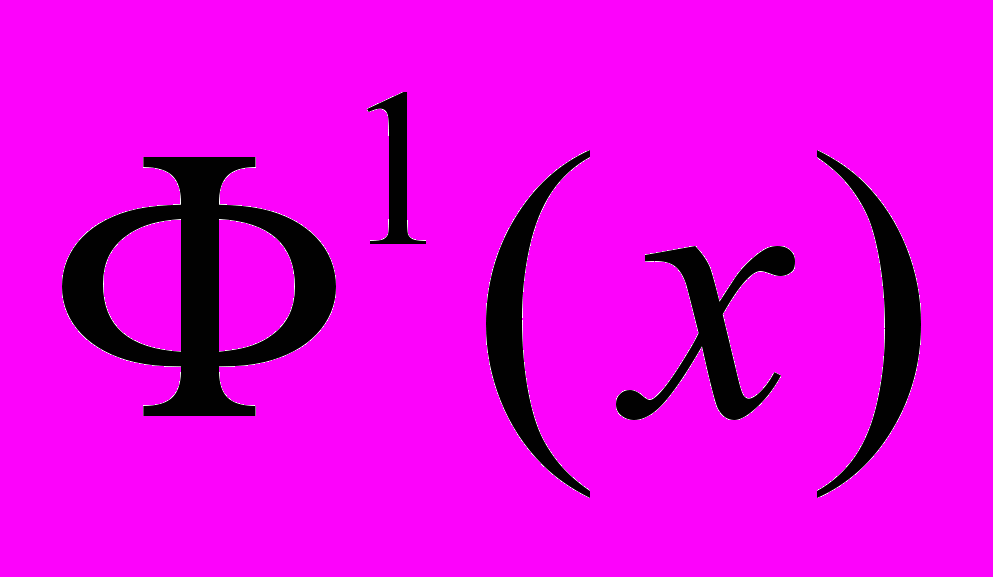минорантой 1 функции .

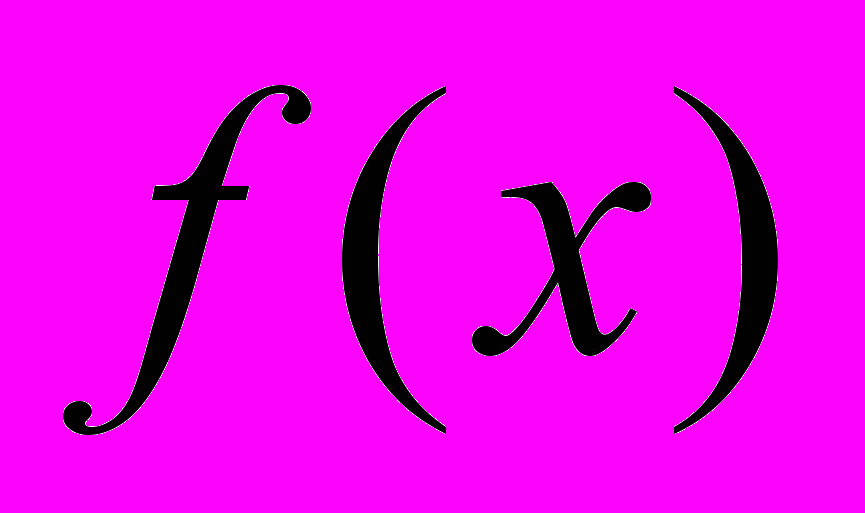Далее в статье рассматривается случай, когда 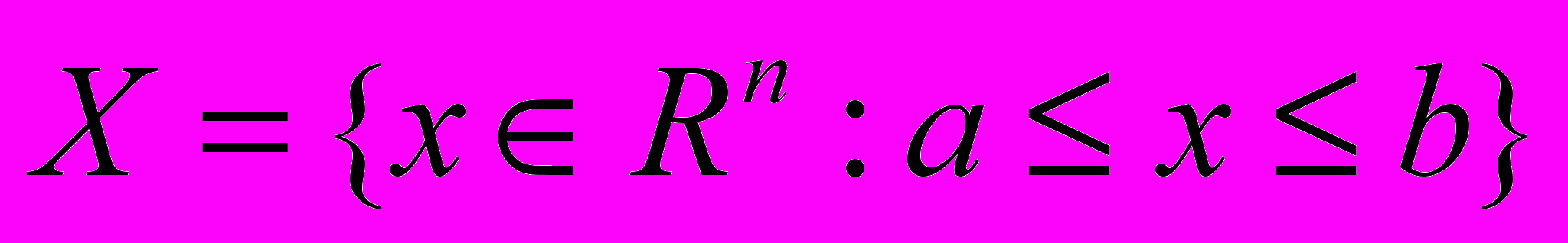- параллелепипед, 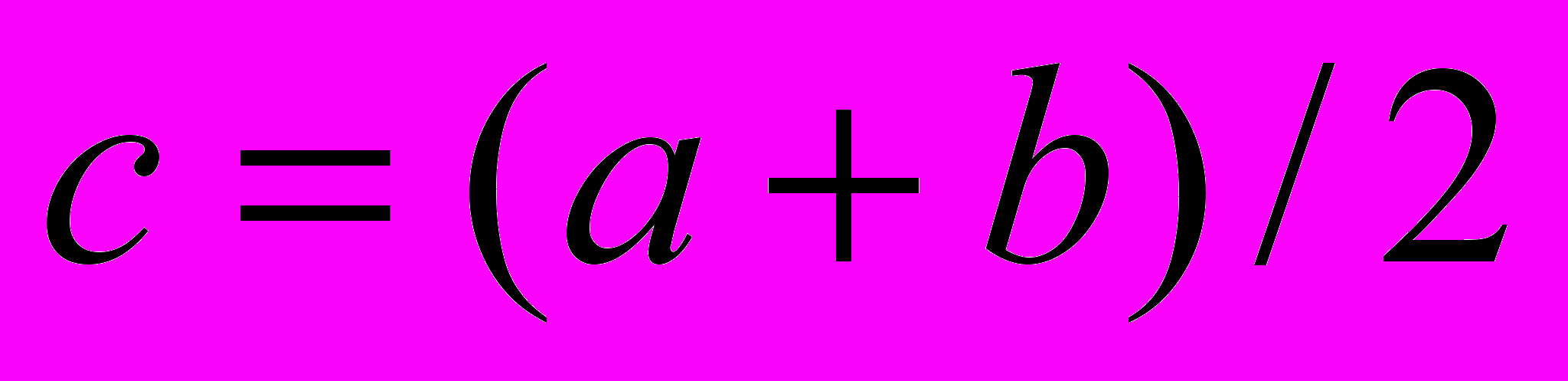- центр параллелепипеда. В этом случае можно получить (см. [3]) аналитические выражения для минимумов этих минорант на параллелепипеде .

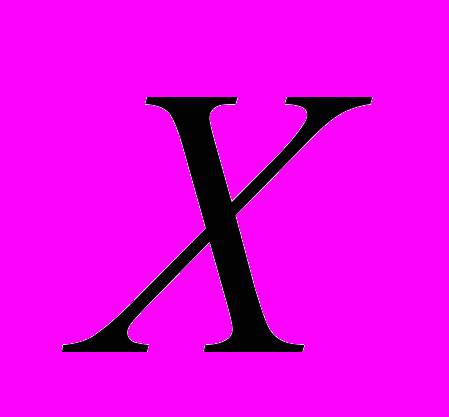2. Метод неравномерных покрытий для задачи математического программирования

Задача математического программирования формулируется следующим образом. Пусть заданы целевая функция 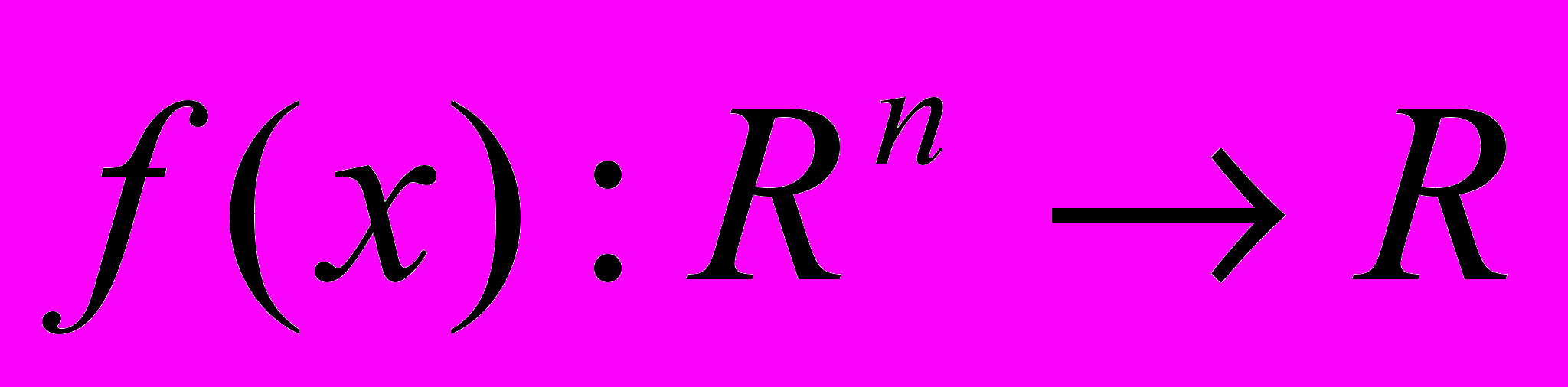, функции ограничений типа равенства 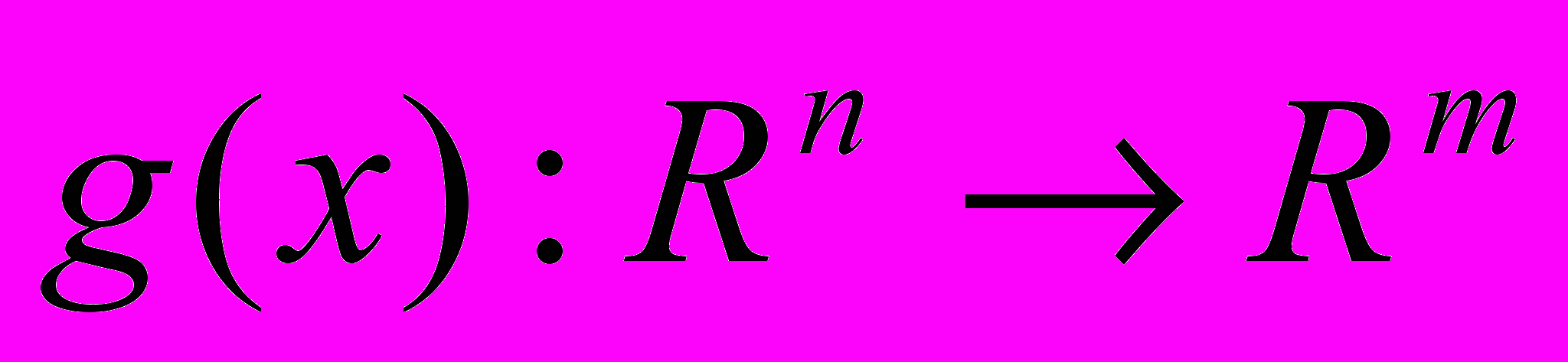и функция ограничений типа неравенства 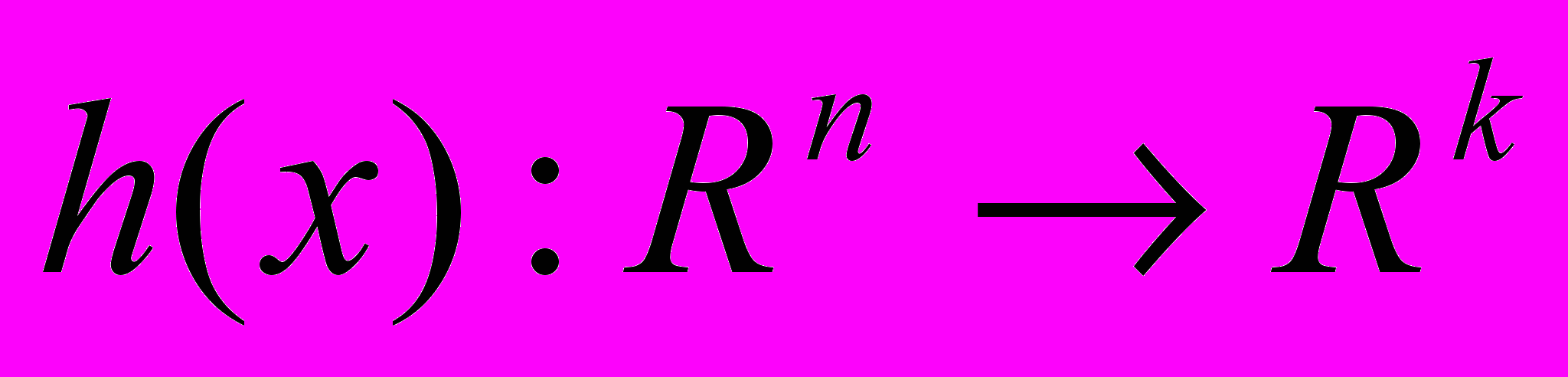. Требуется найти минимум функции при условии соблюдения ограничений 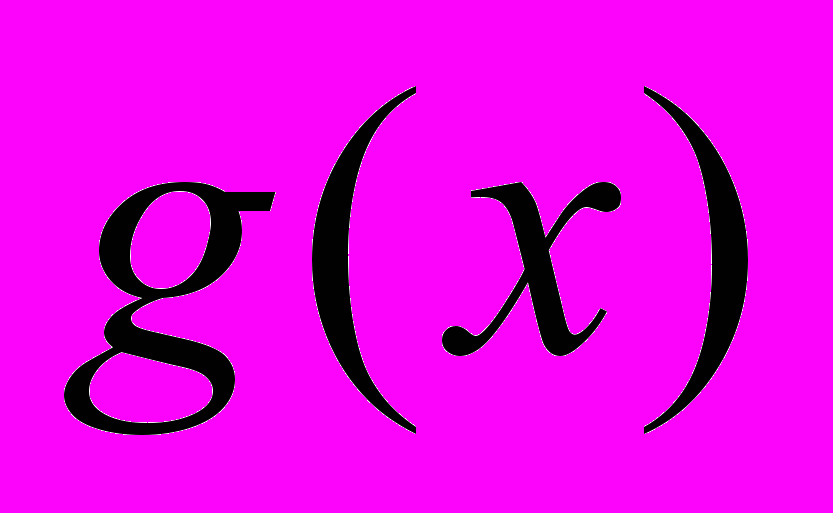и :

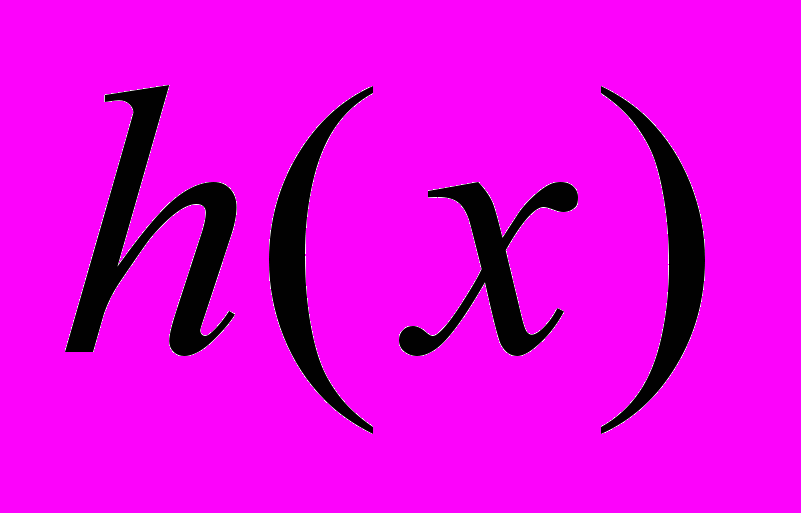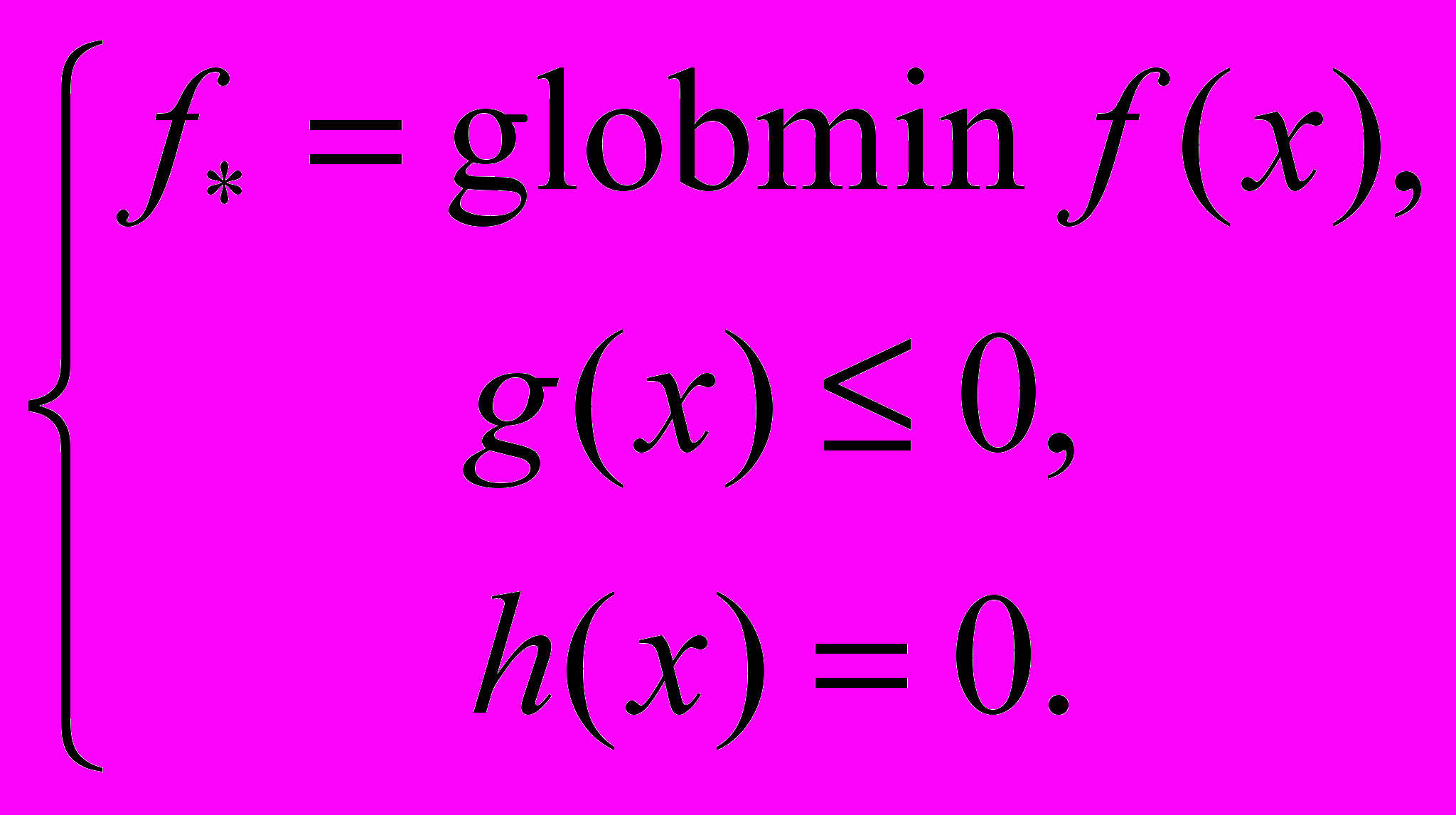(1)

Как правило, удается оценить заранее диапазон возможных изменений переменных и задать параллелепипед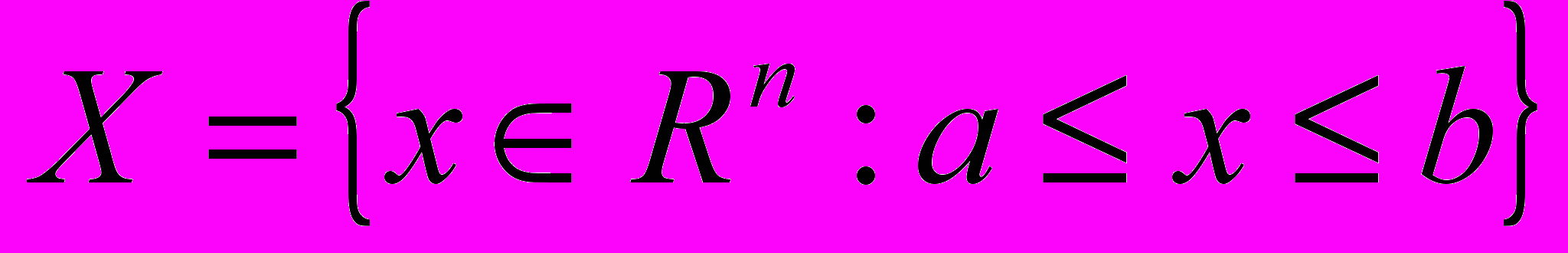, заведомо содержащий точку минимума. Тогда постановка задачи примет следующий вид:

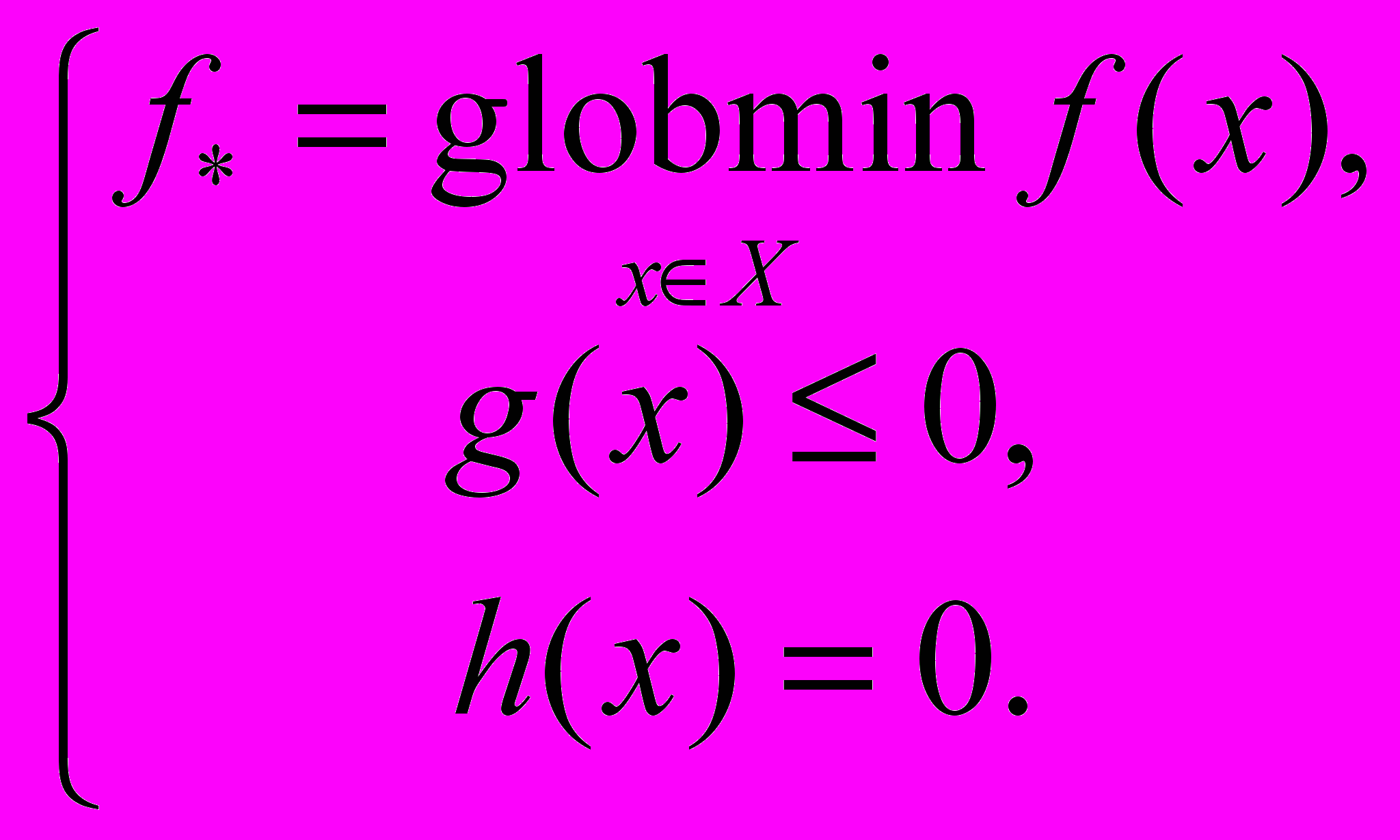(2)

Требуется найти хотя бы одну точку из множества оптимальных решений .

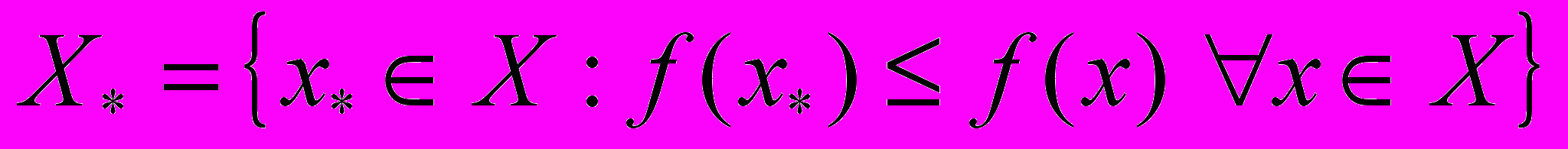Обычно рассматривают задачу поиска приближенного решения. Для любых 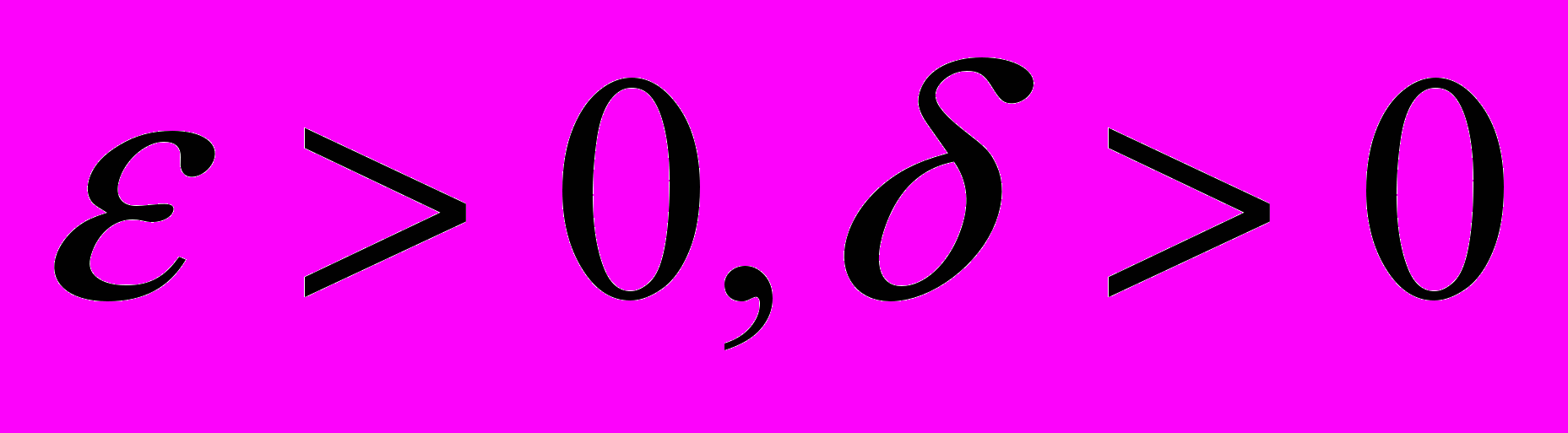определим множество 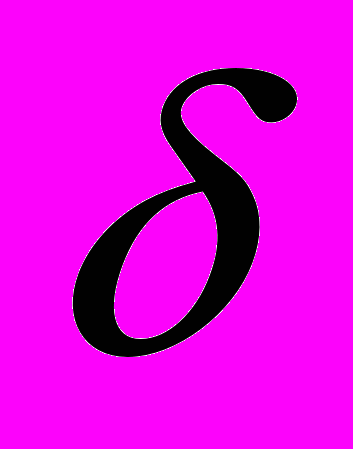-допустимых 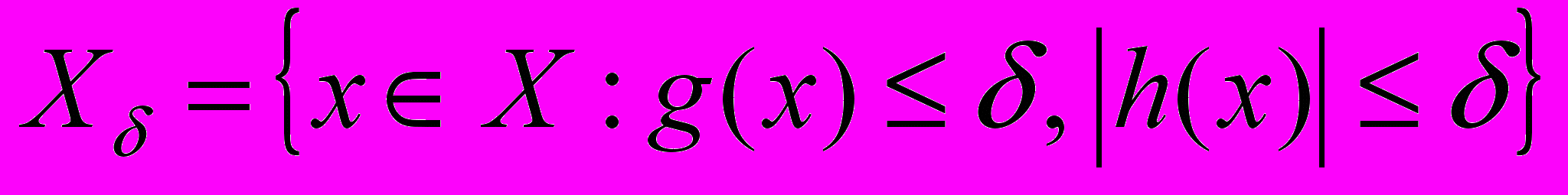и множество 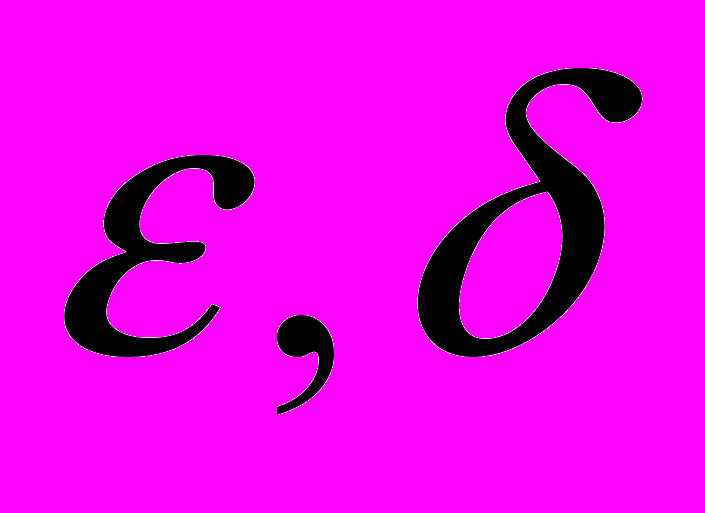-оптимальных решений: 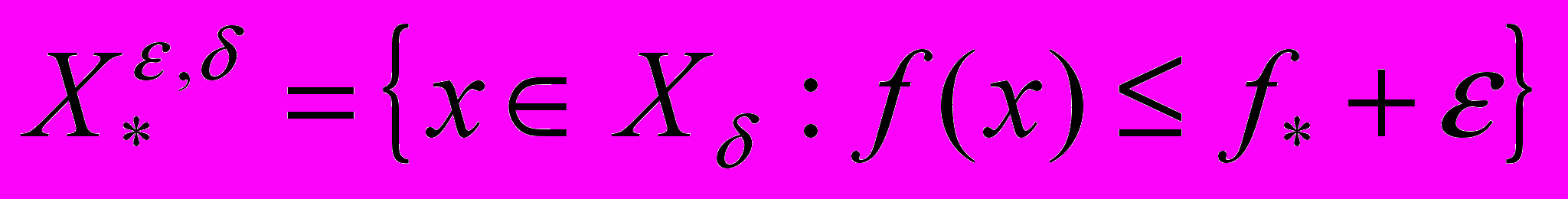. В приближенной постановке требуется найти хотя бы один из элементов множества .

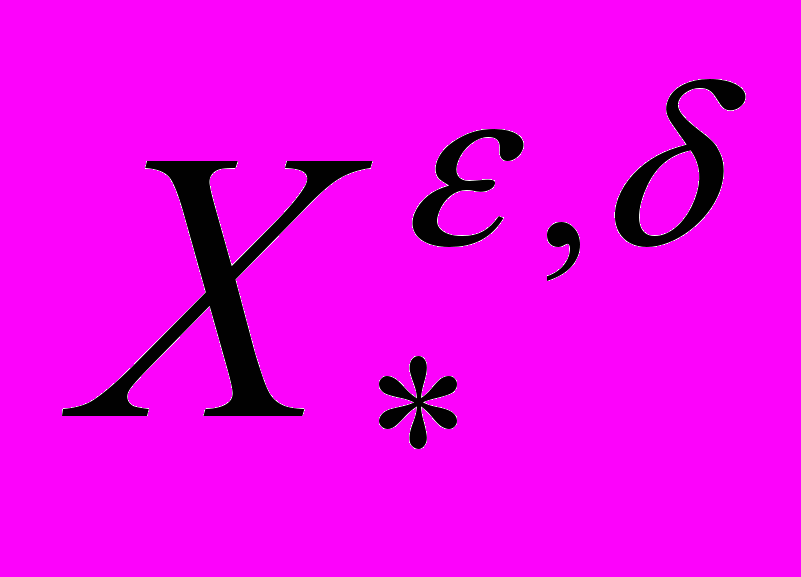В процессе вычислений методом неравномерных покрытий (МНП) хранится наименьшее найденное значение целевой функции 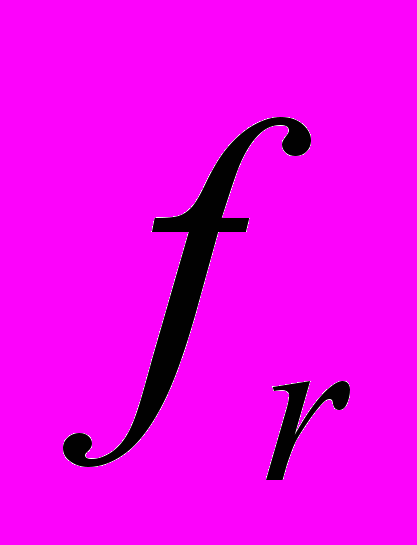и точка 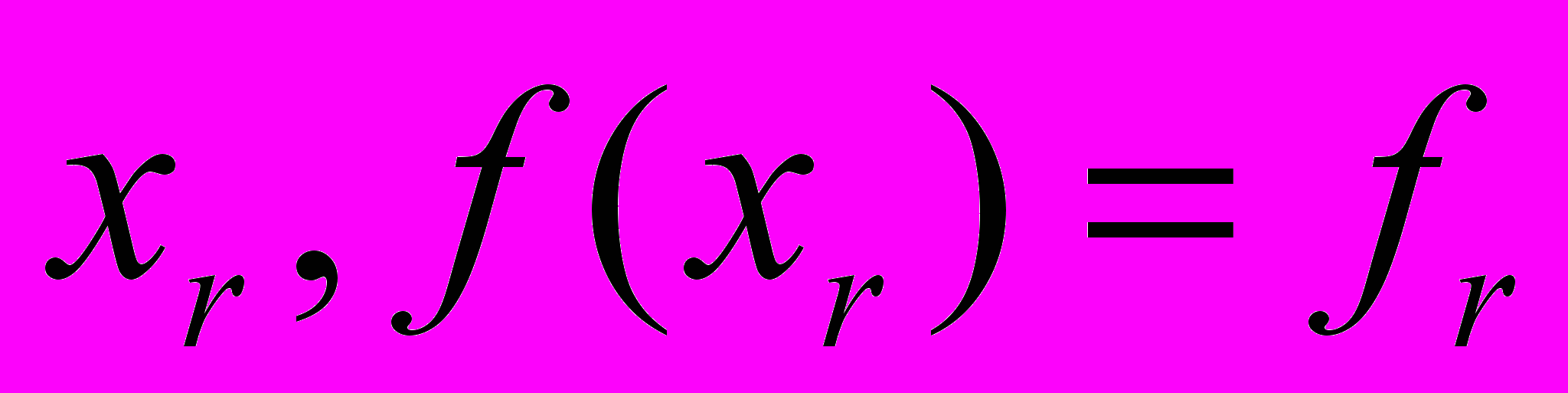, в которой оно достигается. Также поддерживается список параллелепипедов 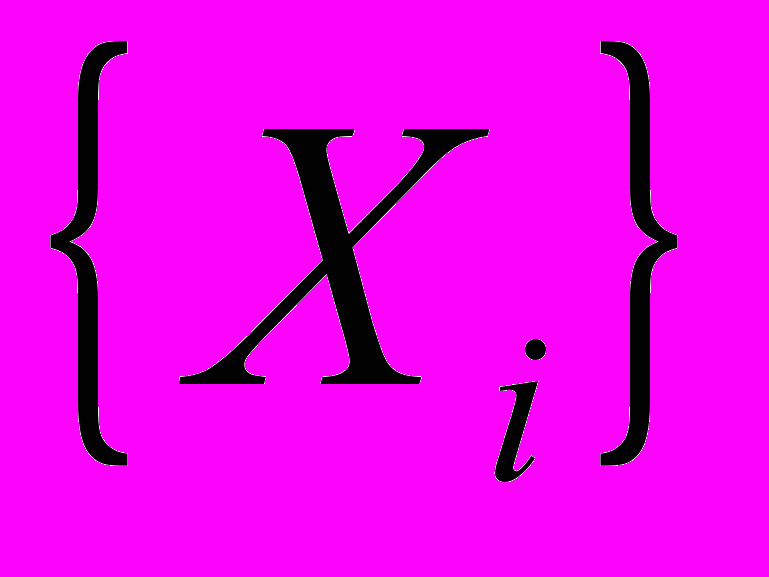, который на первом шаге содержит только исходный параллелепипед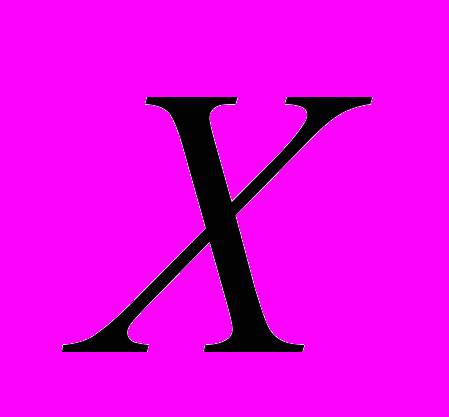. На каждой последующей итерации МНП из списка выбирается один параллелепипед и разбивается на два по наибольшему ребру. Для каждого из полученных параллелепипедов проверяется выполнение условия отсева. Выполнение условия отсева гарантирует, что параллелепипед не содержит точек допустимого множества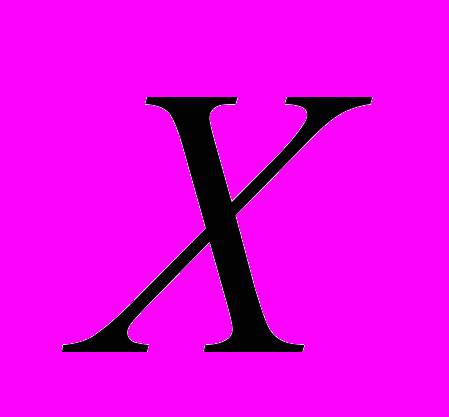, в которых значение функции меньше чем 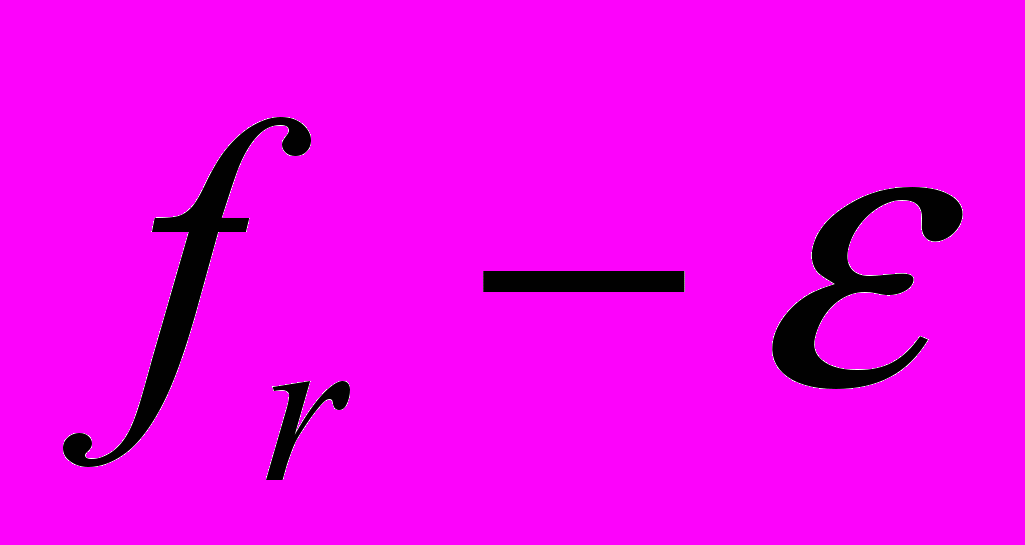. Параллелепипеды, удовлетворяющие условиям отсева, исключаются из дальнейшего рассмотрения. Также в процессе выполнения МНП происходит обновление рекорда по формул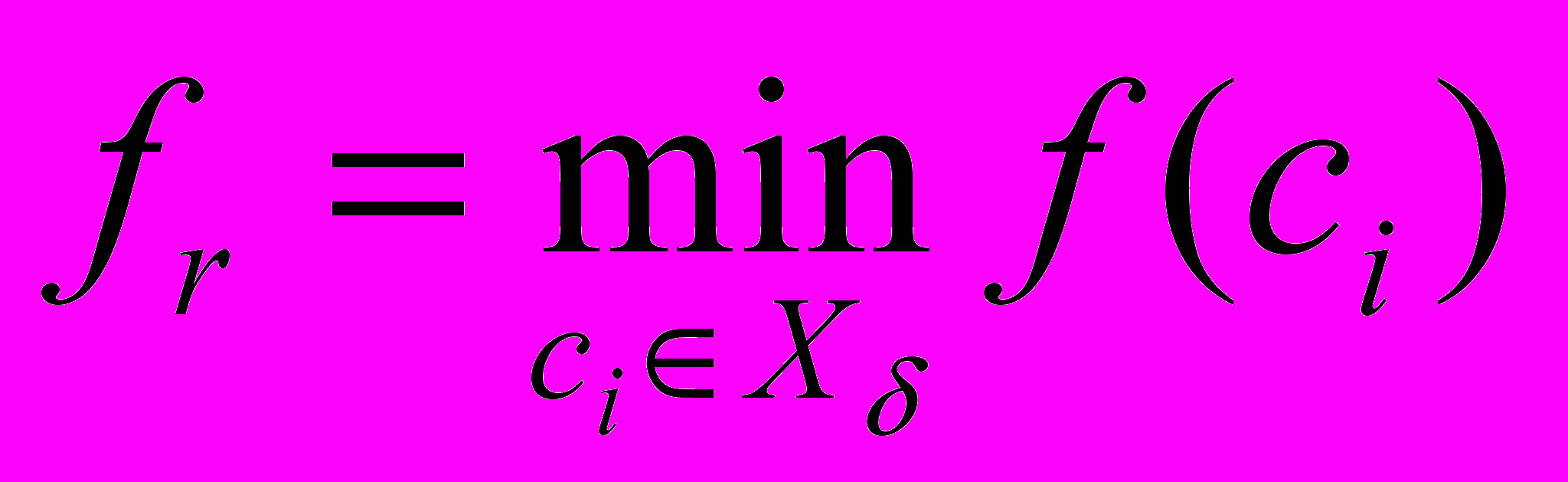е: , где 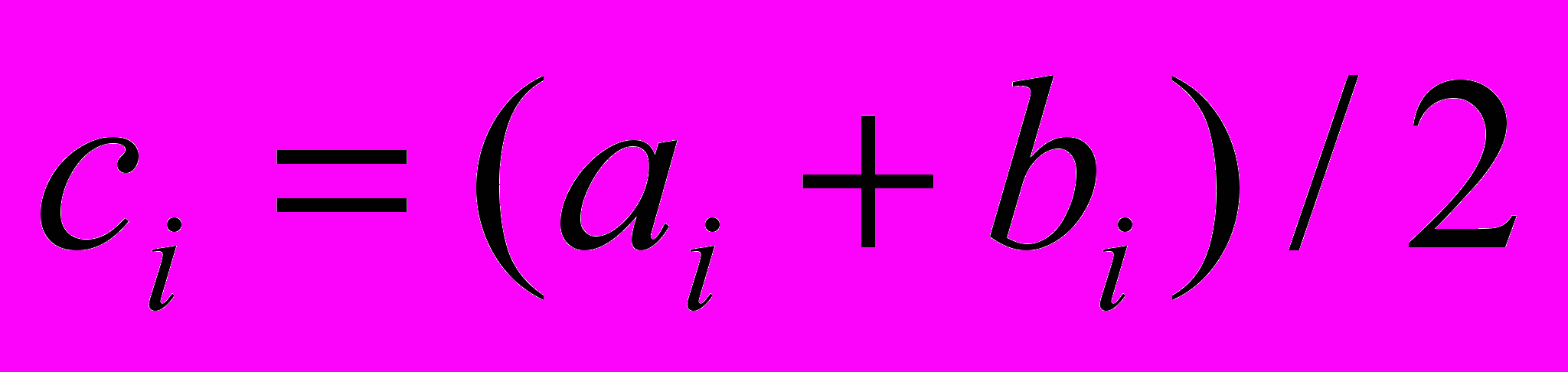– центры параллелепипедов .

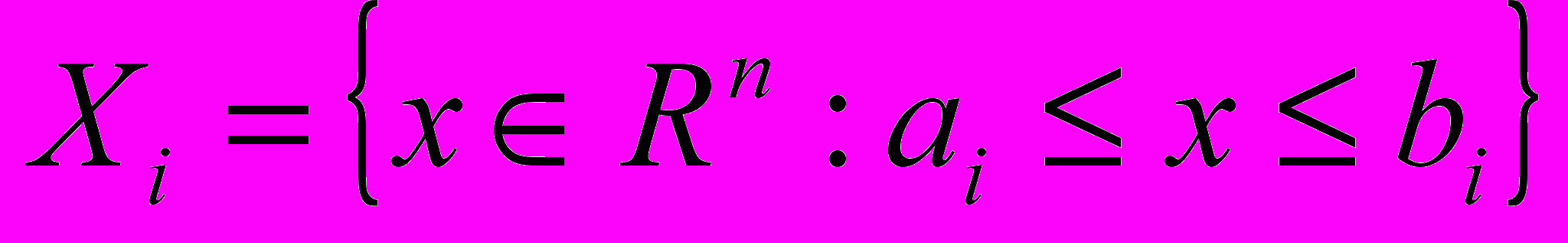Пусть 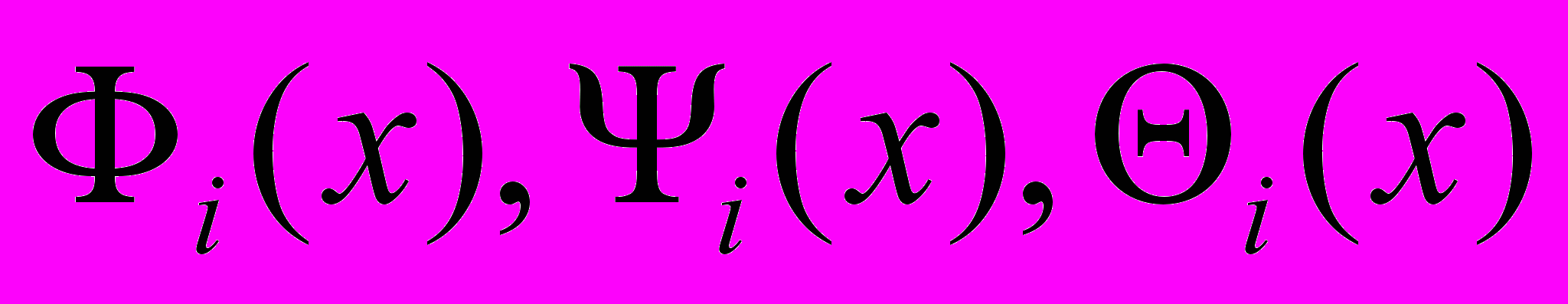- миноранты функций 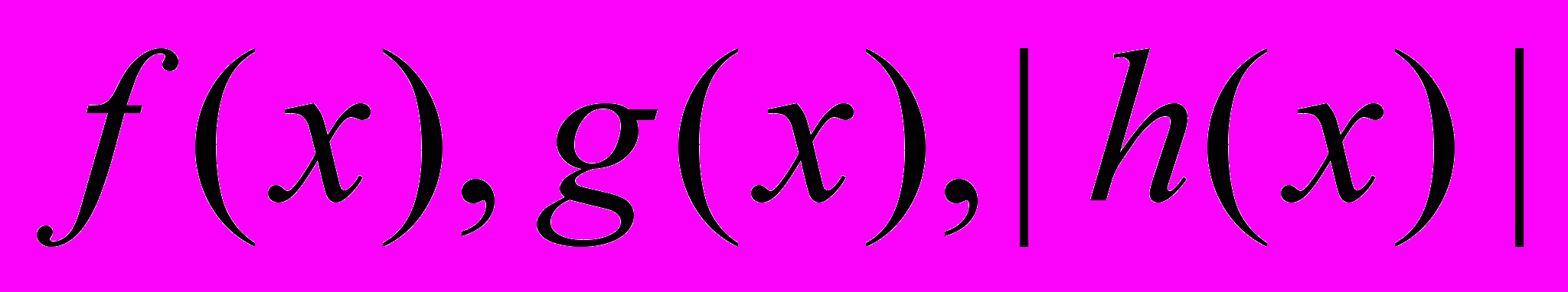на параллелепипеде 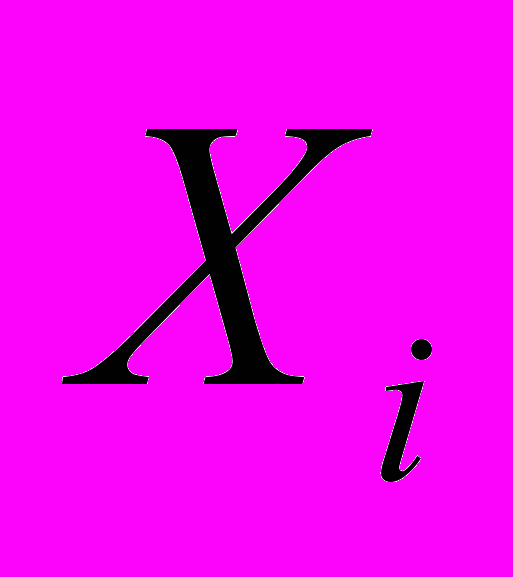: 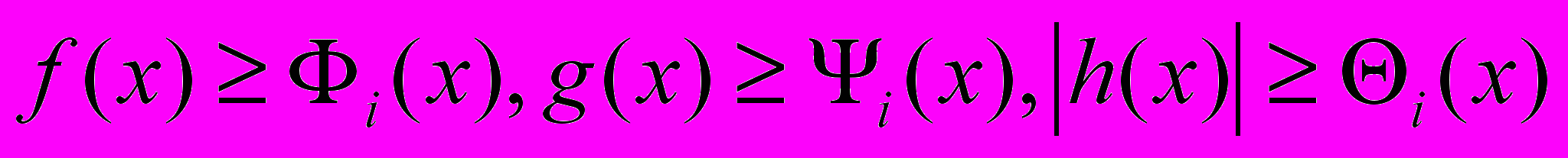при 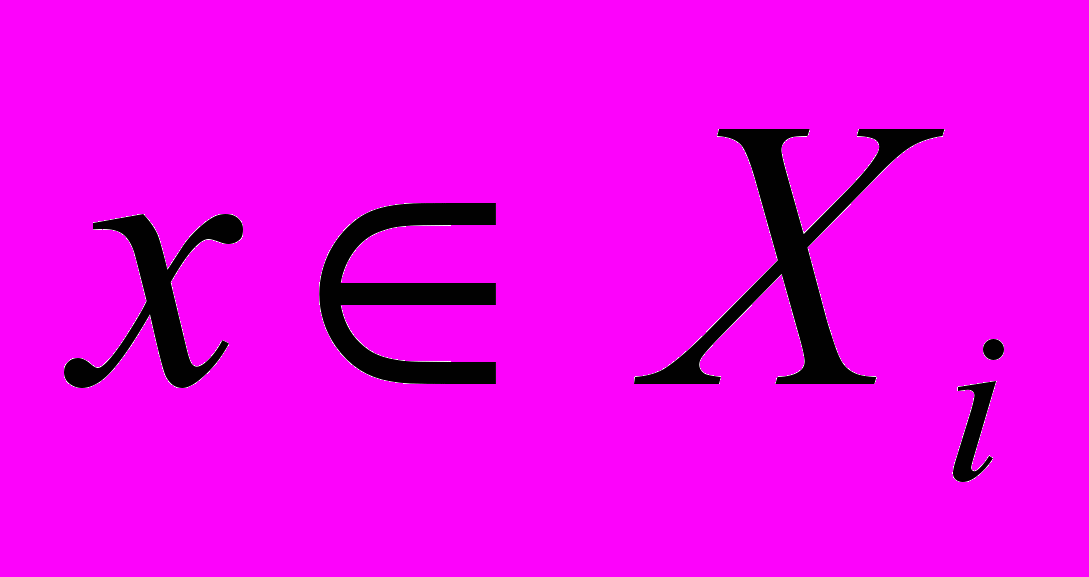. Введем обозначения для минимумов этих минорант на параллелепипеде :



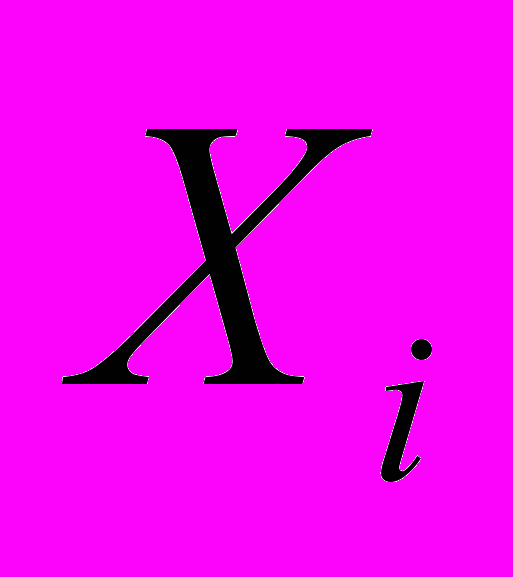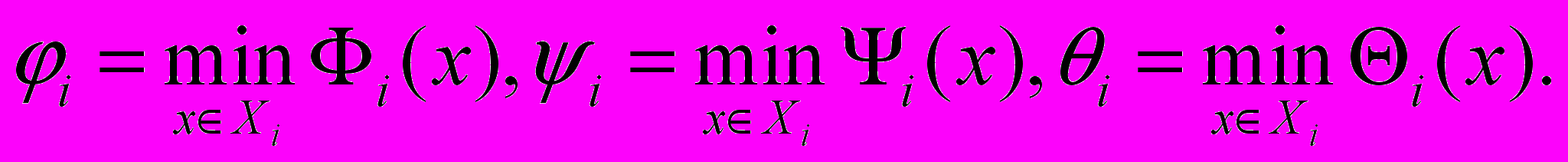
Сформулируем условие отсева. Если хотя бы одно из следующих трех неравенств выполнено:

,
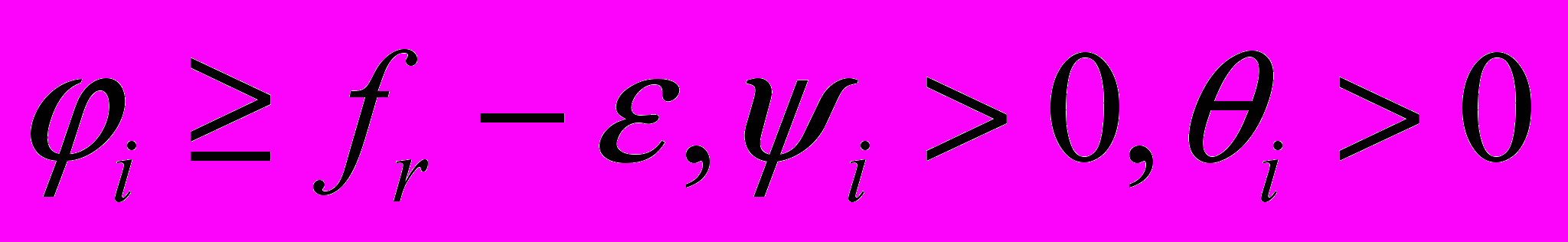то параллелепипед 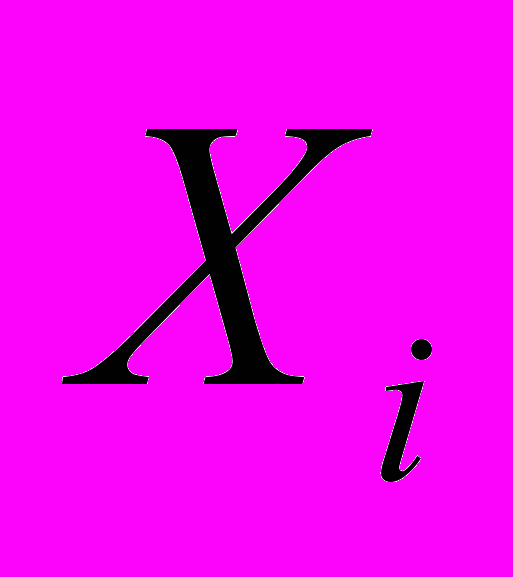может быть исключен из рассмотрения. Данное условие отсева позволяет исключать из рассмотрения параллелепипеды, которые либо не содержат точек, удовлетворяющих ограничению, либо значение функции в пределах этого прямоугольника не уменьшит ранее найденный рекорд более чем на .

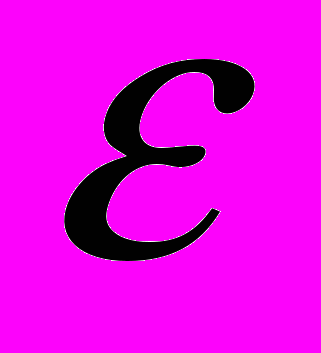3. Параллельная реализация метода неравномерных покрытий

Можно строго показать, что если целевая функция и ограничения удовлетворяют условиям Липшица, то при использовании минорант 0 или 1 метод неравномерных покрытий для задачи (2) завершится за конечное число шагов при любых 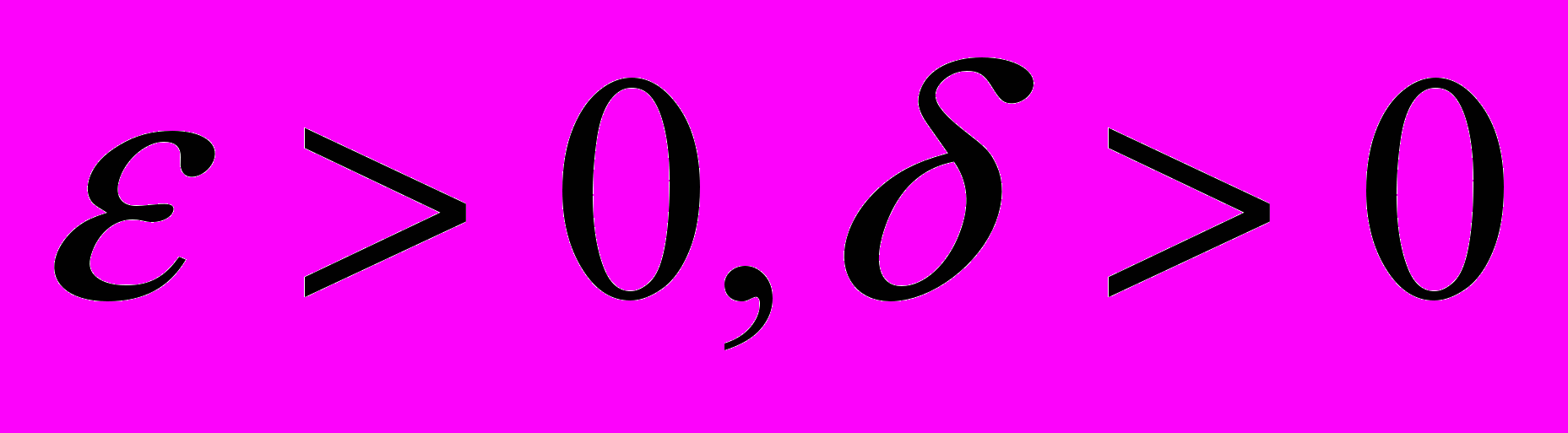. При этом, число шагов может быть достаточно большим. Верхняя оценка, приведенная в работе [3], экспоненциально растет с ростом размерности задачи. Эксперименты, проведенные для различных задач, показали целесообразность перехода к расчетам на многопроцессорных вычислительных системах (МВС).

Метод неравномерных покрытий работает в соответствии со стандартной схемой, принятой в методах ветвей и границ. Общая идея реализации МВГ на системах с распределенной памятью заключается в том, что каждый процессор работает со своим списком подмножеств, сохраняемым в локальной памяти. Если в результате выполнения разбиений локальный список становится пустым, то для предотвращения простоев дополнительные множества пересылаются с другого процессора. Задача считается решенной, когда на всех процессорах списки не содержат подмножеств. В данной работе рассматриваются централизованные схемы организации вычислений: выделенный управляющий процессор отправляет рабочим процессорам области поиска и последний рекорд. Эти процессоры выполняют разбиения полученного подмножества, при необходимости пересылая на управляющий процессор часть подмножеств.

Методы ветвей и границ (МВГ) применяются при решении различных задач дискретной и непрерывной оптимизации. Вычисления в различных вариантах МВГ проводятся по общей схеме, отличаясь в способах вычисления верхних и нижних оценок, способе разбиения допустимого множества, эвристических процедурах. Поэтому представ­ляется целесообразным разработать единую параметризованную реализацию общей схемы. Конкретные методы при этом получаются за счет подстановки в нее требуемых алгоритмов в качестве параметров. Такой подход особенно эффективен на многопроцессорных вычислительных комплексах, так как в этом случае параллельная реализация также выполняется на уровне общей схемы, и при добавлении очередного алгоритма или класса задач работу по распараллеливанию повторно проводить не требуется.

Нашим коллективом была разработана библиотека BNB-Solver, предназначенная для поиска глобального экстремума на МВС. Библиотека написана на языке Си++ с использованием механизма шаблонов (templates), которые позволяют эффективно реализовать параметрический подход. Для распараллеливания используется MPI.

Модульная структура библиотеки представлена на рис. 1. Библиотека имеет многослойную структуру. Базовый слой составляют различные часто используемые вычислительные подпрограммы: методы решения линейных систем, локальной оптимизации, сортировки, и набор коммуникационных примитивов. Набор коммуникационных примитивов изолирует детали системного ПО, используемого на МВК, от логики работы приложения, облегчая тем самым переход на другие системы. За счет использования шаблонов и перегрузки функций коммуникационные примитивы BNB-Solver более удобны для задач рассматриваемого класса по сравнению с общим интерфейсом MPI.

Применяется следующая централизованная схема балансировки нагрузки. Управляющий процесс BM координирует работу некоторого числа рабочих процессов B₁,...,B_n . На начальном этапе решения задачи управляющий процесс выполняет MT разбиений, в результате формируется начальное состояние списка подзадач на процессе BM. Полученные подзадачи рассылаются рабочим процессам: по одной на каждый процесс. Процесс B_i управляется двумя параметрами – T и S, посылаемыми ему управляющим процессом. Получив подмножество для обработки, рабочий процесс выполняет T разбиений, после чего пересылает не более S сгенерированных подмножеств на управляющий процесс. Процесс B_i, у которого список подзадач стал пустым, направляет запрос на управляющий процесс и получает в ответ новое подмножество.

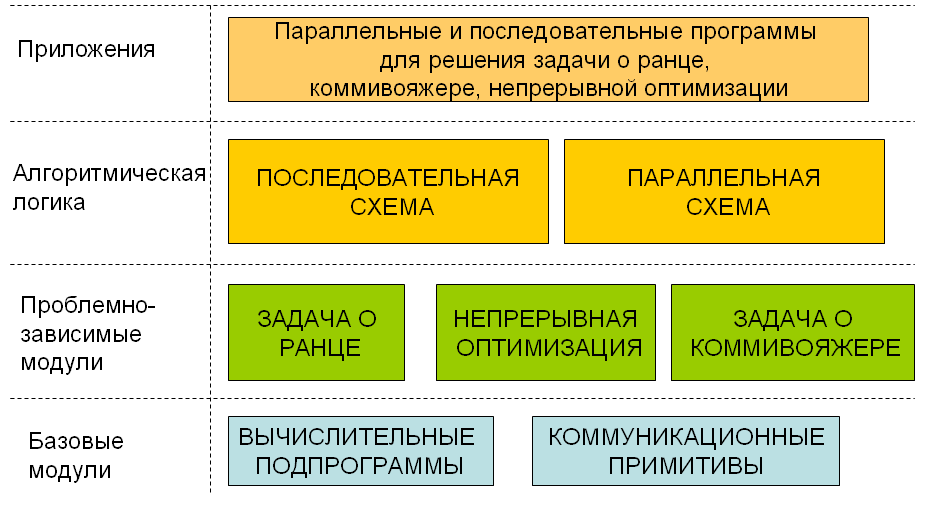Рис. 1. Модульная структура библиотеки BNB-Solver.

Для предотвращения переполнения памяти на управляющем процессе введено два пороговых параметра m₀ и M₀, m₀0. Если число подмножеств на управляющем процессе становится больше M₀, то управляющий процесс рассылает всем рабочим процесса новое значения S­, равное 0, и процессы B_i перестают пересылать подмножества управляющему процессу BM. Когда число подмножеств на управляющем процессе становится меньшим m₀, он рассылает рабочим процессам первоначальные значения T, M и передача подмножеств с рабочих процессов управляющему возобновляется. Параметры MT, T и S подбираются с учетом специфики решаемой задачи на основании решения сходных задач и предварительных экспериментов.

4. Результаты вычислительного эксперимента

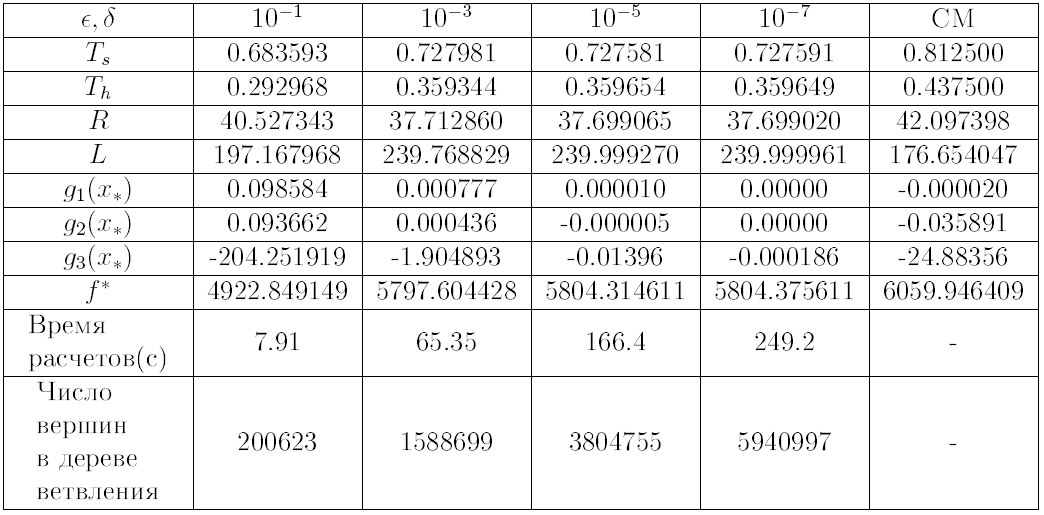
Для вычислительного эксперимента была выбрана тестовая задача из работы [4], состоящая в расчете формы котла, при которой достигается минимальная стоимость при условии соблюдения технологических ограничений. Математическая формулировка задачи и чертеж котла приведены на Рис 2. В таблице 1 приведены результаты расчетов для различных значений величин 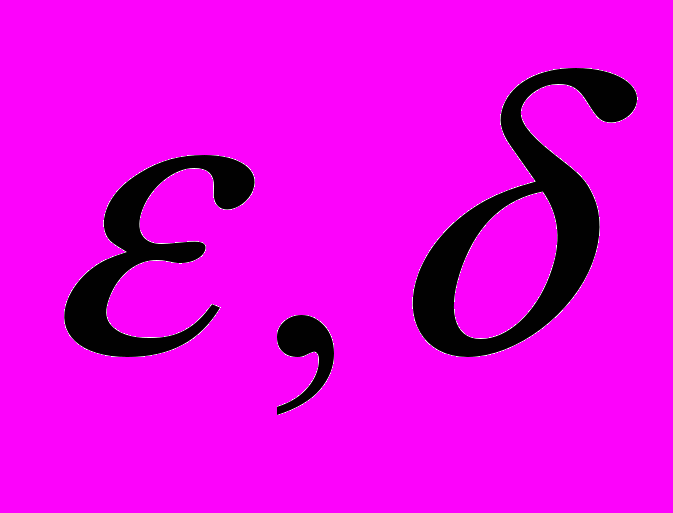, полученные на рабочей станции Pentium IV, 3 GHz. Для сравнения приведен лучший результат из работы[4]. На основании этих результатов можно сделать вывод о том, что метод неравномерных по­крытий позволяет получать решения с гарантией оптимальности и дос­таточно высокой точностью, превосходящей точность эвристических алгоритмов.


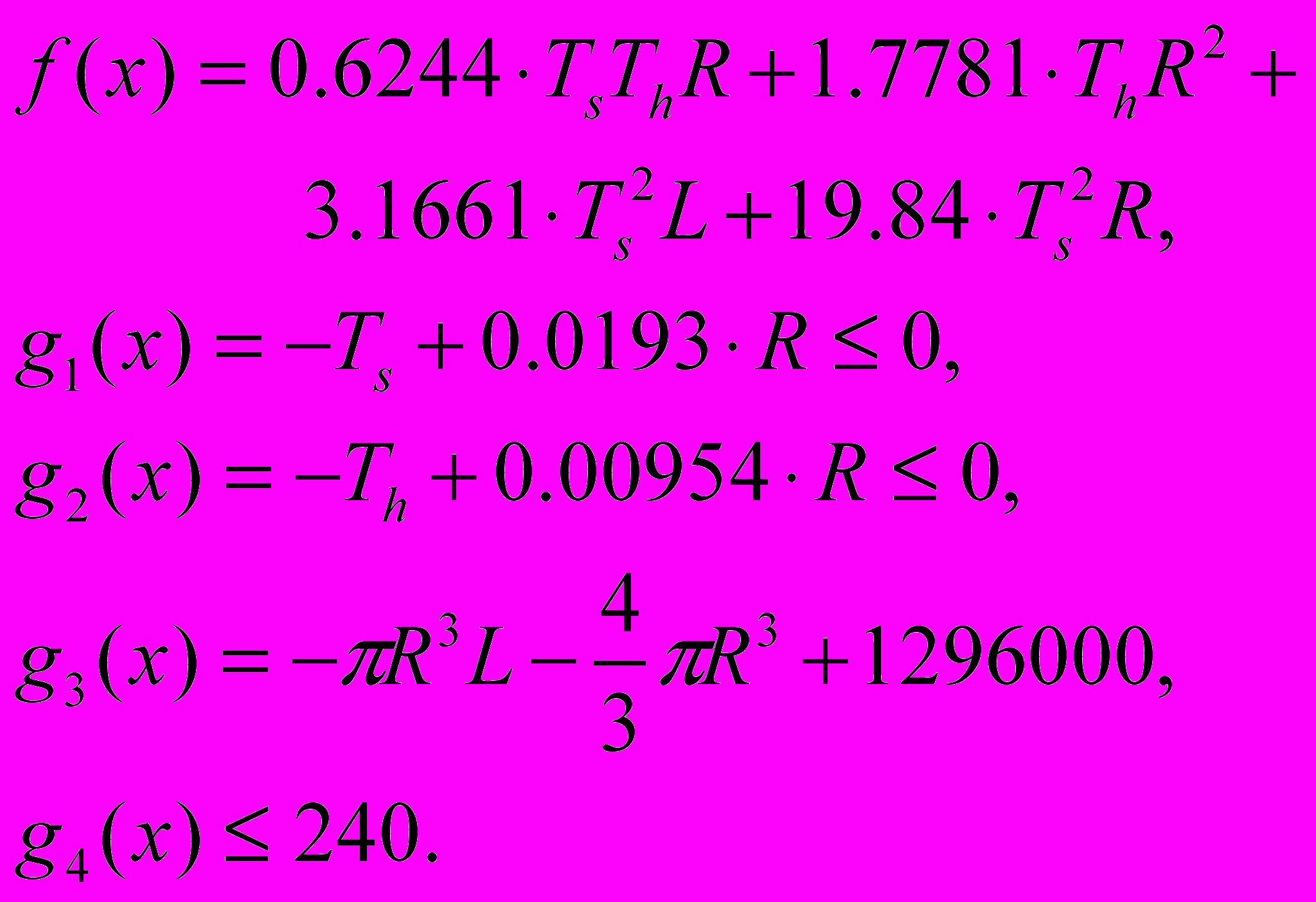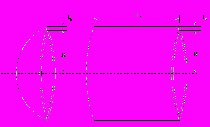Рис. 2. Параметры котла под давлением


На Рис. 4 приведена зависимость времени вычислений от числа рабочих процессов для рассматриваемой задачи на многопроцессорном комплексе МВС 6000IM, установленном в МСЦ РАН. Этот комплекс содержит 256 процессоров Intel Itanium 2, 2.2 GHz. Приведенные результаты показывают, что время существенно (с 89.9 до 6.69 секунд) снижается с увеличением количества процессоров, что говорит о хорошей масштабируемости алгоритма.


Таблица 1.

Заключение

В статье рассмотрена реализация метода неравномерных покрытий для задач математического программирования в последовательном и параллельном вариантах. Проведенные эксперименты подтвердили высокую эффективность метода по сравнению с известными эвристическими подходами. Метод был распараллелен с использованием библиотеки BNB-Solver, в результате чего получено существенное ускорение процесса вычислений.

В дальнейшем планируется исследование производительности предложенного метода на других тестовых и реальных задачах математического программирования, в том числе и с применением многопроцессорной вычислительной техники. Автор выражает глубокую благодарность академику РАН Ю.Г. Евтушенко за постановку задачи и руководство данными исследованиями.



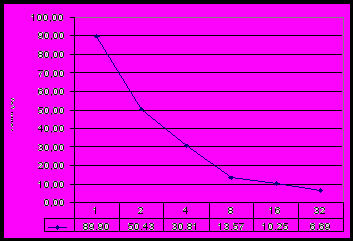
Рис. 4. Зависимость времени расчетов от числа рабочих процессов.

Литература

[1] Ю. Г. Евтушенко.Численный метод поиска глобального экстремума (перебор на неравномерной сетке).Журнал вычислительной математики и математической физики, Т. 11, N 6, С. 1390-1403.

[2] М.А.Посыпкин, Архитектура и программная организация библиотеки для решения задач дискретной оптимизации методом ветвей и границ на многопроцессорных вычислительных комплексах// Труды ИСА РАН, Т. 25, с. 18-25.

[3] Ю.Г. Евтушенко, М.А. Посыпкин, Параллельные методы решения задач глобальной оптимизации//Пленарные и избранные доклады Четвертой Международной конференции "Параллельные вычисления и задачи управления" PACO'2008. Москва, 27-29 октября 2008 г. М.: Учреждение российской академии наук Институт проблем управления им. В.А. Трапезникова РАН, 2008. С. 5-15.

[4] Carlos A. Coello Coello and Efre'n Mezura Montes,Constraint-handling in genetic algorithms through the use of dominance-based tournament selection // Advanced Engineering Informatics, Vol. 16, 2002.

1 Работа выполнена при поддержке гранта РФФИ № 08-01-00619, программы президиума РАН № 14-2, гранта президента РФ НШ-5073.2008.1