Информатика, вычислительная техника и инженерное образование. − 2011, №4 (6) раздел V. Вычислительные комплексы нового поколения и нейрокомпьютеры

Вид материала

Статья

Содержание Docking realization for molecular modeling on reconfigurable computer systems Описание математической модели и структуры решаемой задачи Рис. 1. Основные фрагменты задачи Оптимизация фрагментов задачи и адаптация архитектуры РВС под V0 – объем свободного аппаратного ресурса, V(n) Отображение вычислительной структуры задачи на структуру РВС Результаты вычислительных экспериментов Библиографический список Сорокин Дмитрий Анатольевич Бовкун Александр Викторович

Подобный материал:

• Информатика, вычислительная техника и инженерное образование. − 2011, №4 (6) раздел, 134.8kb.
• Программа сквозной практической подготовки для студентов направления 654600 специальности, 176.46kb.
• Рабочая программа дисциплины «Параллельные вычислительные процессы» по направлению, 108.72kb.
• Компьютерная графика, 205.26kb.
• Рабочая программа, 258.96kb.
• Рабочая программа по курсу «Высокопроизводительные вычислительные системы» по направлению, 95.97kb.
• Микропроцессорные системы, 177.83kb.
• Заместителя Председателя Госкомвуза России от 27. 03. 2000. Программу составил Хмелевский, 143.77kb.
• «Информатика и вычислительная техника», 723.11kb.
• Информатика, вычислительная техника и инженерное образование. 2011, 1595.3kb.

РАЗДЕЛ V. ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ НОВОГО ПОКОЛЕНИЯ И НЕЙРОКОМПЬЮТЕРЫ

УДК 004.382.2

А.И. Дордопуло, Д.А. Сорокин, А.В. Бовкун


АППАРАТНАЯ РЕАЛИЗАЦИЯ ДОКИНГА ЛИГАНДОВ НА РЕКОНФИГУРИРУЕМЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ


Статья посвящена описанию аппаратной реализации докинга – метода молекулярного моделирования. Отличительной особенностью описываемого решения по сравнению с известными реализациями является функционально завершенное решение полной задачи докинга на реконфигурируемой вычислительной системе, обеспечивающее согласованность функционирования всех фрагментов задачи в едином вычислительном контуре. Описано применение методов оптимизации фрагментов задачи и адаптации архитектуры реконфигурируемой вычислительной системы под структуру решаемой задачи.

Ключевые слова: аппаратная реализация, докинг, суперкомпьютерное молекулярное моделирование, реконфигурируемые вычислительные системы, лиганд.


A.I. Dordopulo, D.A.Sorokin, A.V. Bovkun


DOCKING REALIZATION FOR MOLECULAR MODELING ON RECONFIGURABLE COMPUTER SYSTEMS


The paper is devoted to description of docking (method of molecular modeling) hardware realization. In comparison with existing realizations, the distinctive feature of the viewed solution is all-in-one solution of complete problem of docking on reconfigurable computer system, providing coordinated functioning of all fragments of the task in a single computer system. Of methods of task fragments optimization and adaptation of architecture of reconfigurable computer system to the structure of the solving task use is described.

Hardware realization, docking, supercomputer molecular modeling, reconfigurable computer systems, ligand.


Введение


Создание новых лекарственных средств и повышение эффективности существующих препаратов является актуальной сферой применения высокопроизводительной вычислительной техники. Правильный выбор перспективных соединений-кандидатов для исследуемого препарата в значительной степени определяет материальные затраты, а также продолжительность и эффективность последующих этапов исследований нового лекарства, занимающих в среднем около 5 лет.

Для выбора соединений-кандидатов широко используются методы молекулярного моделирования, одним из которых является докинг молекулы-ингибитора (лиганда) в активный центр молекулы-мишени (белка). Процедура докинга [1,2] представляет собой перебор пространственных конфигураций молекулы-лиганда, для каждой из которых выполняется оценка энергии связывания молекулы-лиганда и молекулы-белка. Докинг обеспечивает достаточную точность получаемых решений, но характеризуется высокой вычислительной сложностью, которая обусловлена большим числом входных параметров для модели взаимодействующих молекул и принадлежностью задачи к классу NP [2]. Поэтому на практике при решении задачи докинга широко используют суперкомпьютерные технологии моделирования, эмпирические методы сокращения пространства перебора [3] и, в частности, генетический алгоритм [2,4]. Использование кластерных многопроцессорных вычислительных систем позволяет сократить время решения задачи докинга, но не приводит к росту производительности, пропорциональному числу задействованных вычислительных узлов.

Для более эффективного решения задачи докинга необходимы средства адаптации архитектуры вычислительной системы к структуре решаемой задачи, которыми обладают, в частности, реконфигурируемые вычислительные системы (РВС), построенные на основе программируемых логических интегральных схем (ПЛИС) [5], успешно применяемые для решения вычислительно-трудоемких задач. Известны [6-10] реализации отдельных фрагментов докинга на РВС [6-10], но качественно новое решение задачи докинга, удовлетворяющее требованиям по быстродействию, возможно при согласованной аппаратной реализации всех фрагментов задачи в едином вычислительном контуре.


Описание математической модели и структуры решаемой задачи


Настоящая статья описывает аппаратную реализацию метода докинга лигандов в активный центр белка-мишени, обоснование и подробное математическое описание которого представлено в работе [2]. Физическим смыслом докинга является поиск оптимального положения лиганда в поле белка, которое характеризуется минимумом энергии связывания комплекса «лиганд-белок», что в вычислительном плане представляет собой расчет значения энергии такого комплекса, зависящего от пространственной конфигурации и ориентации лиганда в многомерном пространстве.

Поиск оптимального положения лиганда в поле белка является итерационным процессом, в котором можно выделить следующие этапы: создание очередной пространственной конфигурации лиганда (с учетом его ориентации относительно центра белка), вычисление энергетических характеристик созданной конфигурации и оценку конфигурации лиганда по критериям задачи.

Наибольшая вычислительная трудоемкость характерна для первых двух этапов. Так, на этапе создания очередной пространственной конфигурации выполняются расчет конфигурации лиганда с учетом вращения фрагментов молекулы (гибкий докинг) и позиционирование лиганда в многомерном пространстве с учетом вращения молекулы как целого, что требует неоднократного пересчета координат каждого атома. На этапе вычисления энергетических характеристик созданной конфигурации выполняется расчет общей энергии связывания, состоящей из трех основных слагаемых, вычисление каждого из которых является вычислительно трудоемким и зависит от рассчитанных на предыдущем этапе координат и типа каждого атома лиганда.

На этапе оценки конфигурации лиганда по критериям задачи выполняется сравнение рассчитанных энергетических характеристик текущей конфигурации с допустимым по условию пороговым значением и с лучшим из рассчитанных значений для определения целесообразности хранения и дальнейшего использования полученной конфигурации.

Для решения задачи используются следующие параметры:

- число атомов лиганда не превышает 200, каждый атом характеризуется своими пространственными координатами x, y и z (32-разрядные вещественные числа);

- число точек внутреннего вращения (торсионные степени свободы) не превышает 20, каждая точка внутреннего вращения характеризуется углом в интервале [0,] и положением в молекуле (номера двух атомов, характеризующие неподвижную и подвижную части молекулы);

- угол вращения молекулы как единого целого в интервале [0,] задается с помощью системы кватернионов.

Таким образом, максимальное число параметров, характеризующих конфигурацию лиганда, составляет 27, что позволяет с большим запасом учитывать как существующие, так и большинство планируемых к созданию лекарственных препаратов и белков.

Структура вычислений в задаче докинга представлена на рис. 1. Для позиционирования лиганда в поле белка осуществляются расчет координат атомов лиганда с учетом поворота фрагментов молекулы в точках внутреннего вращения (блок R) и расчет координат всех атомов лиганда относительно центра молекулы белка с учетом поступательного и вращательного движения лиганда как целого (блок RT). Затем производится расчет суммарной энергии связывания Eall (блок E) для текущей конфигурации, значение которой поступает на блок оценки конфигурации лиганда (блок MPS). В зависимости от результатов оценки параметры текущей конфигурации либо сохраняются в списке лучших конфигураций и передаются на блок создания новых конфигураций (блок GEN), либо в случае неудовлетворительного значения суммарной энергии связывания не сохраняются и не учитываются.





Рис. 1. Основные фрагменты задачи


Вычислительно-трудоемкими фрагментами в структуре задачи являются фрагменты R, RT, E и Gen, оперирующие 32-разрядными значениями с плавающей запятой.

Аппаратной платформой для решения задачи докинга является плата вычислительного модуля (ПВМ) 16V5-75, содержащая 16 вычислительных ПЛИС XC5VLX110 по 11 млн. эквивалентных вентилей в каждой, 2 Гбайта распределенной памяти. Тактовая частота составляет 250 МГц, а производительность для 32-разрядной арифметики с плавающей запятой составляет 140 Гфлопс. Внешний вид ПВМ 16V5-75 представлен на рис. 2.




Рис. 2. ПВМ 16V5-75


Для эффективного решения задачи докинга на РВС необходимо реализовать этапы создания новых конфигураций лиганда, вычисления энергетических характеристик конфигурации и оценки конфигурации лиганда, обеспечив при этом как их согласованную работу, так и сбалансированную загрузку фиксированного аппаратного ресурса – одной ПВМ 16V5-75.


Оптимизация фрагментов задачи и адаптация архитектуры РВС под

структуру решаемой задачи


Для решения задачи докинга на ПВМ 16V5-75 необходимо в едином вычислительном контуре построить эффективный вычислительный конвейер, удовлетворяющий условиям задачи по критерию «производительность/объем аппаратного ресурса», для чего, как правило, используется структурный [5] метод организации вычислений на РВС.

Предварительный анализ структурной реализации задачи докинга показал, что требуемый вычислительный ресурс значительно превышает имеющийся на ПВМ 16V5-75, поэтому для успешного решения задачи необходимо выполнить оптимизацию организации вычислений для вычислительно-трудоемких фрагментов и адаптировать ресурсы РВС под структуру решаемой задачи.

Для удовлетворения заданным параметрам по занимаемому ресурсу и быстродействию к фрагментам задачи докинга были применены следующие разработанные методы оптимизации:

1) Редукция вычислительной структуры графа фрагмента задачи путем эквивалентных математических преобразований исходных формул, позволяющая сократить занимаемый аппаратный ресурс реконфигурируемой вычислительной системы;

2) Использование предвычисленных массивов для хранения результатов повторяющихся операций, значения которых не меняются для данного итерационного процесса, позволяющее рационально использовать ресурс внутренней памяти ПЛИС и сократить объем используемого вычислительного оборудования;

3) Согласованное распараллеливание подграфов графа задачи, обеспечивающее сбалансированную загрузку вычислительных устройств существенно для переменных по интенсивности информационно-значимых потоков данных, возрастающих на два десятичных порядка в процессе решения по сравнению с входным потоком данных;

4) Использование специальной структуры хранения данных с распределением по банкам динамической памяти, позволяющее в 9-10 раз ускорить доступ к памяти.

Рассмотрим применение разработанных методов на примере структурной реализации вычислительно-трудоемких фрагментов задачи.

Вычислительно-трудоемкий фрагмент R [2] выполняет расчет внутренней геометрии лиганда для текущей конфигурации путем преобразования координат каждого атома лиганда для каждой точки вращения. В вычислительной структуре задачи это соответствует циклическим вызовам этого фрагмента в последовательной программе, число которых определяется числом торсионных связей вращения, максимальное значение которых равно 20.

Преобразование декартовых координат атомов с учетом заданных торсионных углов поворота частей молекулы вокруг химических связей, выполняется по следующим формулам [2]:

, (1)

где – координаты неподвижного атома торсионной пары; – коэффициенты преобразования координат, которые рассчитываются по формулам:

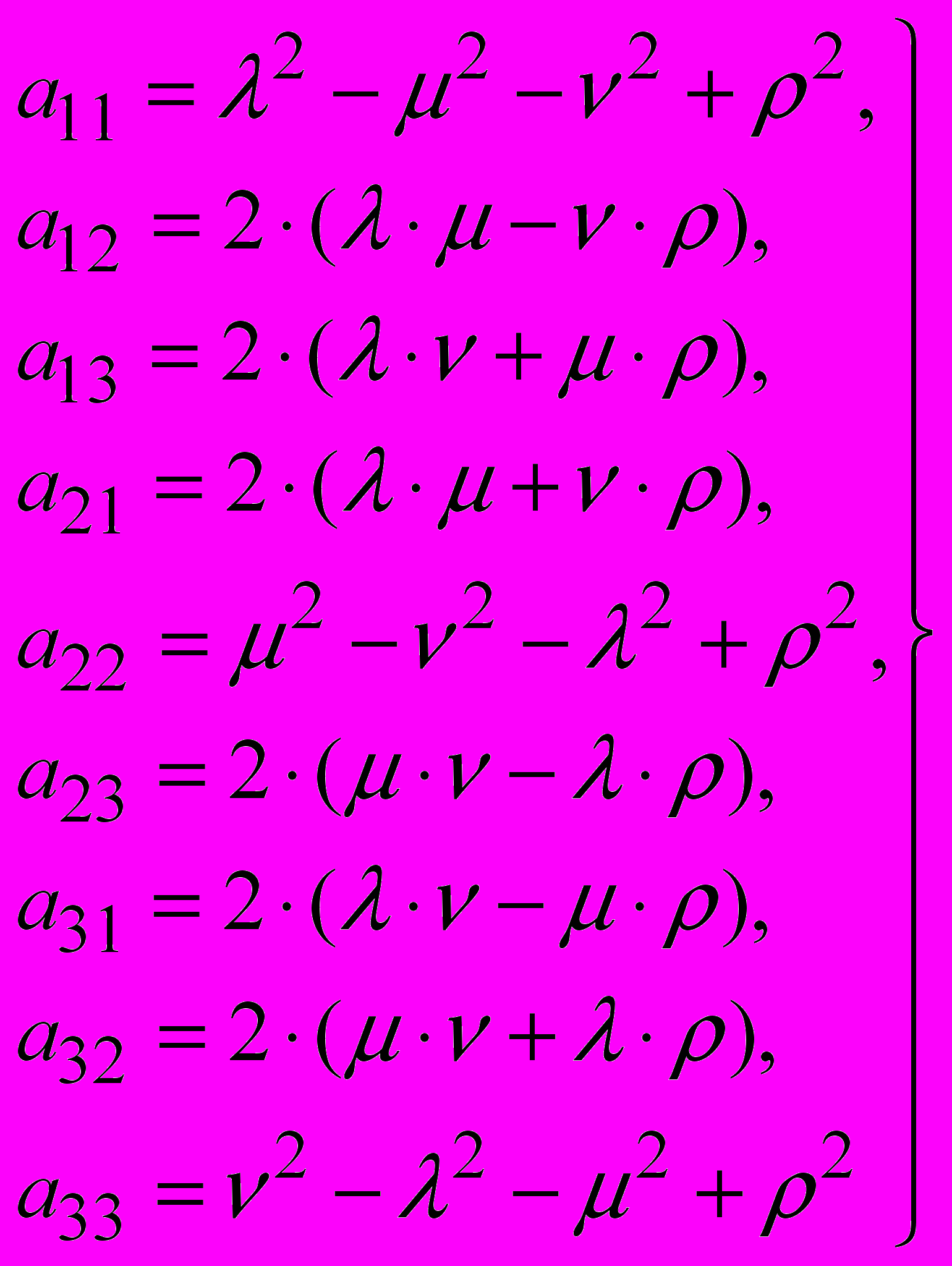(2)

где – параметры, вычисляемые следующим образом:

,

, (3)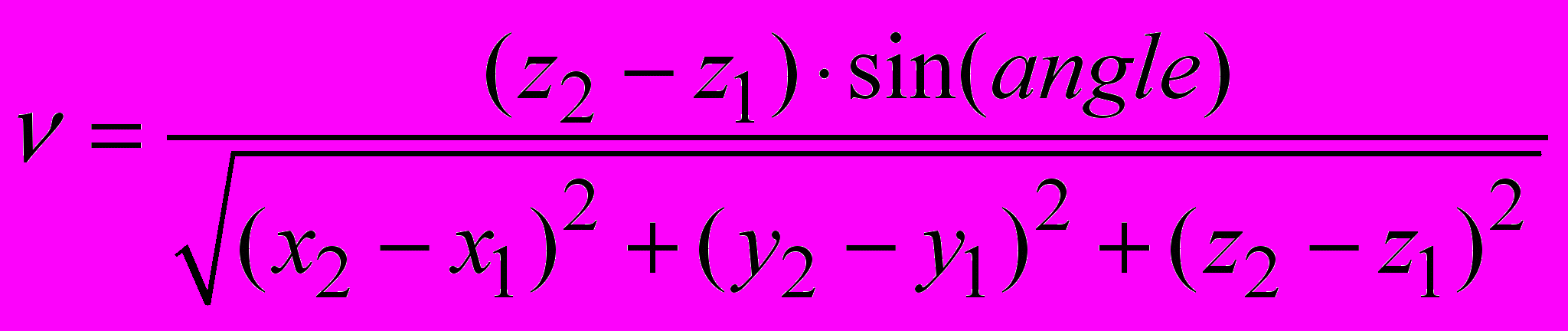

,

;

– координаты вращающегося атома торсионной пары;

– угол торсионного поворота.

Нетрудно подсчитать, что для прямой структурной реализации вычислений по формулам (1)-(3) необходимо задействовать 35 устройств, выполняющих операцию суммирования, 32 – умножения, 3 – деления, 3 – извлечения квадратного корня, 1 – косинус и 3 – синус, что в сумме составит 77 устройств, реализующих 32-разрядные математические операции в стандарте IEEE754.

Для сокращения времени вычисления преобразований R, согласно принципам структурной реализации вычислений [5], циклические вызовы фрагмента R можно распараллелить по числу точек вращения. Время вычисления преобразований R при структурной реализации можно вычислить по формуле:

, (4)

где N_atom – число атомов в лиганде; t_atom – время вычисления преобразований для одного атома лиганда.

При структурной реализации фрагмент R будет 20-кратно распараллелен, поэтому t_atom составит 1 такт ПВМ (один такт работы ПВМ 16V5-75 на частоте 250 МГц составляет 4 нс). При максимальном количестве атомов N_atom=200 время вычислений t_R составит 200 тактов.

Такое распараллеливание потребует задействовать 1540 устройств, что превышает доступный ресурс ПВМ 16V5-75 и приводит к необходимости оптимизации организации вычислений во фрагменте R для сокращения занимаемого ресурса. Применим метод (1) и перейдем от параллельной обработки координат атомов (x,y,z) к последовательной, что увеличит время обработки в 3 раза и сократит занимаемый аппаратный ресурс в 3 раза. Формула (1) в этом случае в матричной записи примет вид:

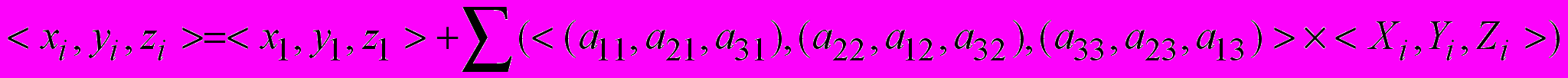, (5)

где форма записи означает последовательную обработку значений



Очевидно, что t_atom составит 3 такта. Следовательно, при максимальном значении N_atom=200 время вычисления преобразований t_R составит 600 тактов.

Следующими преобразованиями для сокращения занимаемого аппаратного ресурса, которые целесообразно использовать в данном случае, являются редукция графа (метод 1) и использование предвычисленных значений (метод 2) для вычислений по формулам (2) и (3). Используя для редукции основное тригонометрическое тождество и формулы тригонометрии, в результате получим:



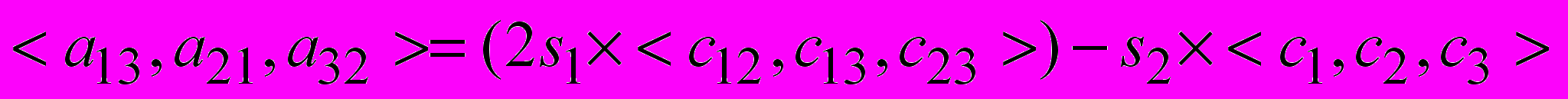(6)

,

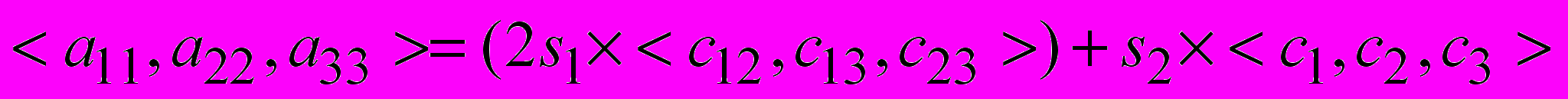где

,

,





При структурной реализации вычисление переменных s₁ и s₂ для всей процедуры R может выполняться независимо от вычисления ступеней преобразования R, поэтому их распараллеливать нет необходимости. Значение переменной определяется только неизменными для данного лиганда координатами точек вращения, являясь инвариантом относительно конфигураций лиганда, поэтому это значение можно предварительно рассчитать, сохранить во внутренней памяти ПЛИС и подать на обработку как константу.

Применение методов оптимизации 1 и 2 к формулам (2) и (3) позволяет сократить аппаратный ресурс для одной ступени преобразования R с 77 до 22 устройств, т.е. в 3,5 раза. При требуемом 20-кратном распараллеливании фрагмента R теперь понадобится 440 устройств, реализующих 32-разрядные математические операции в стандарте IEEE754. Редукция вычислительного графа фрагмента R приводит к построению конвейера с последовательной обработкой координат атома лиганда, что увеличивает время обработки в 3 раза (t_atom=3, а t_R для максимального числа атомов составит 600 тактов), но позволяет сократить необходимый ресурс на построение вычислительной структуры R в 3,5 раза при сохранении точности вычислений.

В вычислительно-трудоемком фрагменте RT, выполняющем пересчет декартовых координат атомов лиганда с учетом вращательных степеней свободы лиганда как целого, согласно описанию алгоритма, приведенного в [2], обработка координат выполняется по следующей формуле:

(7)

где – постоянные параметры, определяющие размеры области позиционирования; – смещения координат для текущей конфигурации лиганда;

– коэффициенты преобразования координат, которые рассчитываются с помощью кватернионов , задающих трехмерное вращение лиганда как целого, по формуле:

(8)

Структурная реализация фрагмента RT требует 51 устройство, реализующее 32-разрядные математические операции в стандарте IEEE754, и выполняет все операции параллельно. Для согласования фрагментов R и RT в фрагменте RT целесообразно также использовать конвейерную обработку координат, что сохранит время обработки фрагмента RT при N_atom=200, равным 600 тактов, и приведет к сокращению оборудования в 3 раза (17 устройств).

Одним из наиболее вычислительно-трудоемких фрагментов является блок E, реализующий расчет энергии связывания комплекса «лиганд-белок» и содержащий расчет нескольких компонентов суммарной энергии по формуле

, (9)

где – внутренняя энергия лиганда, – энергия лиганда в поле протеина.

Внутренняя энергия лиганда E_inner [2] учитывает энергию Ван-дер-Ваальса, электростатическую энергию, энергию лиганда в поле протеина и рассчитывается по формуле

, (10)

где 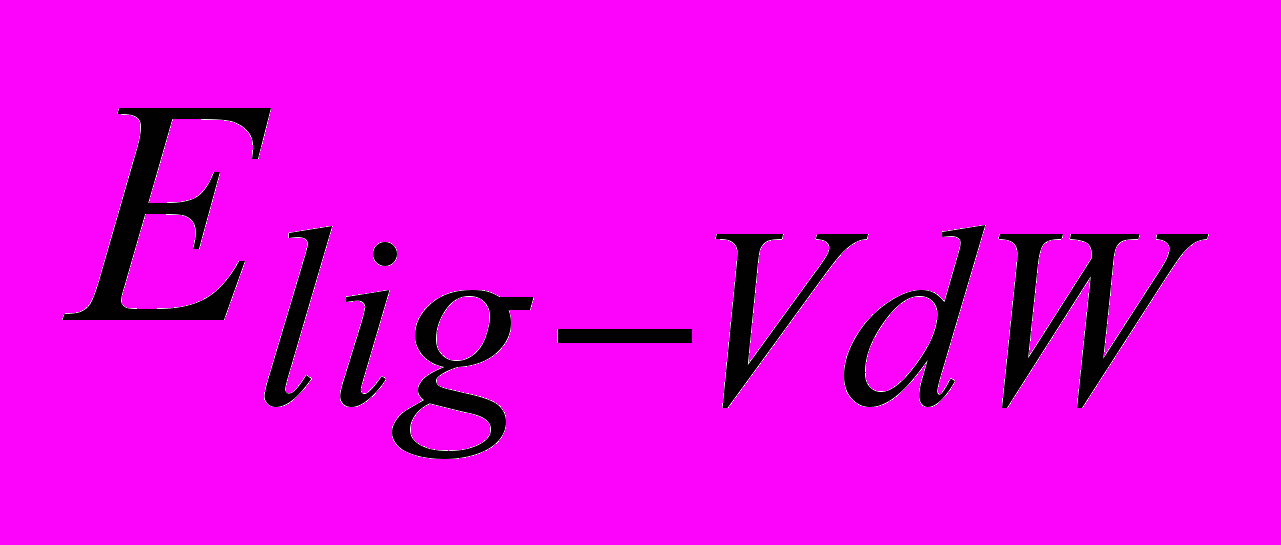– энергия Ван-дер-Ваальсовых взаимодействий между атомами;

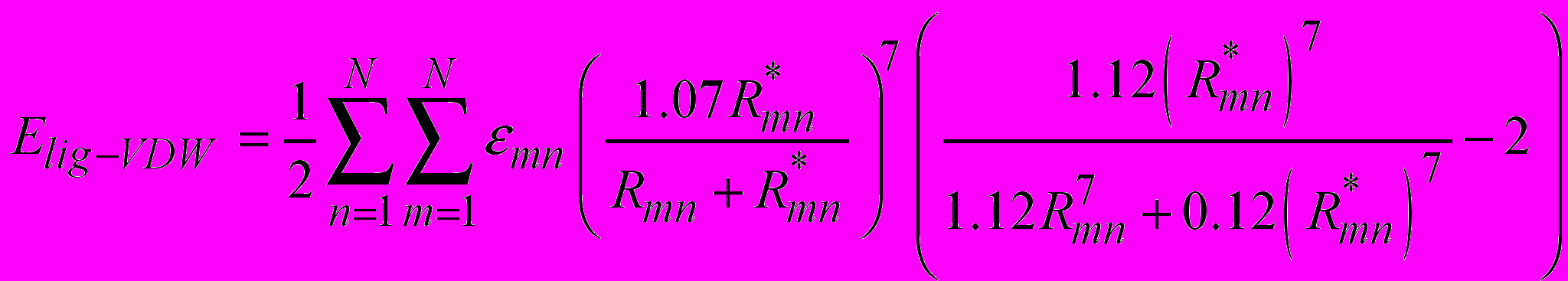, (11)

N – число атомов в лиганде;

– расстояние между точкой, в которой находится пробный атом m с координатами, соответствующими узлу сетки с нумерацией i,j,k, и атом протеина с номером n;

, (12)

R^*_mn, ε_mn – постоянные коэффициенты, соответствующие минимуму Ван-дер-Ваальсового потенциала, между атомами m и n.

Энергия электростатического взаимодействия между атомами E_lig-ES определяется как

, (13)

где q_m и q_n – парциальные заряды на атомах лиганда m и n; ε_m – коэффициент диэлектрической проницаемости для вычисления внутренней электростатической энергии лиганда; σ_mn – коэффициент, определяющий величину вклада электростатической энергии пары атомов m-n.

Энергия торсионного напряжения конформера рассчитывается как

, (14)

где

,






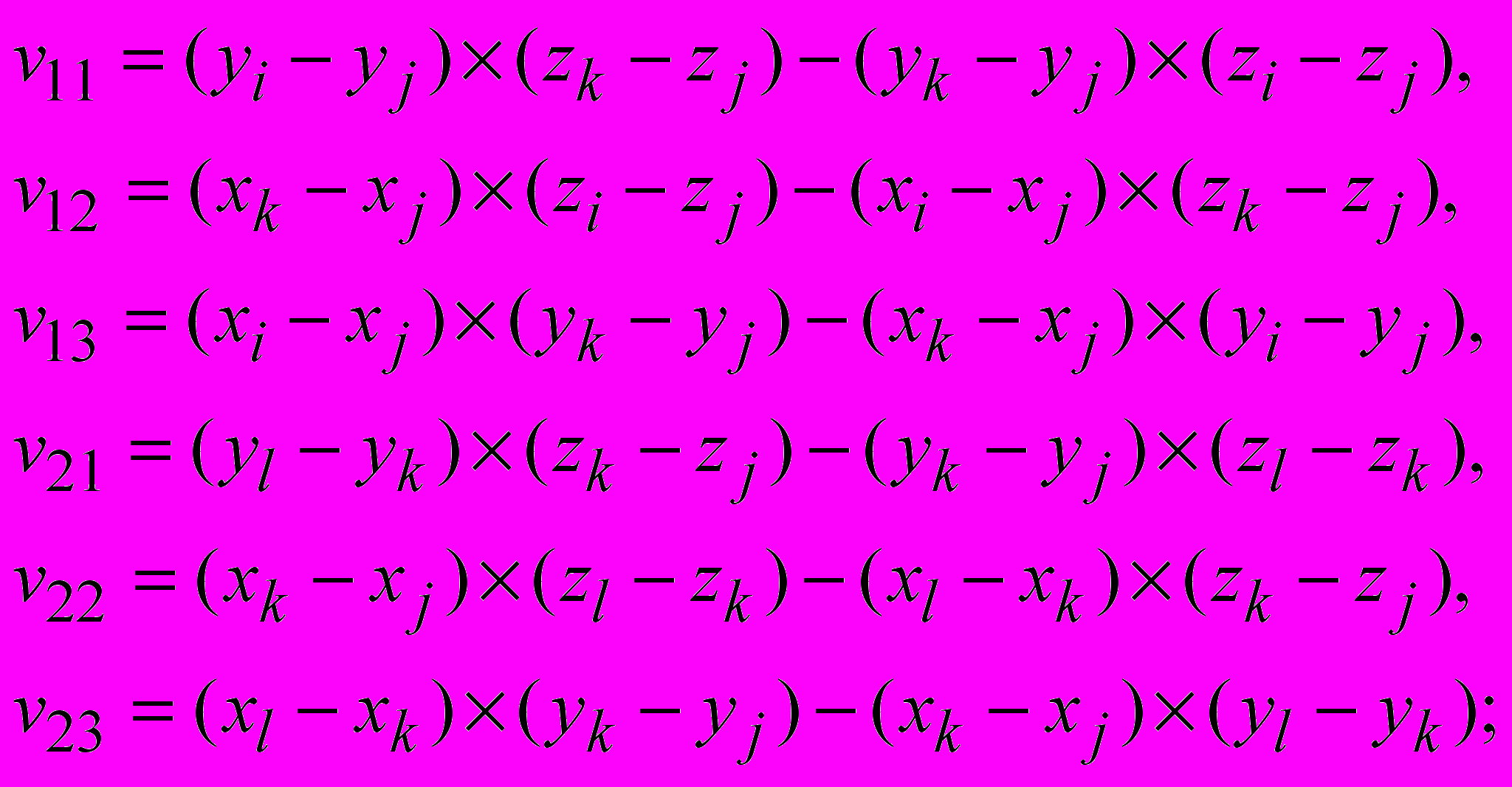
где (x_i,y_i,z_i), (x_j,y_j,z_j), (x_k,y_k,z_k), (x_l,y_l,z_l) – координаты атомов i-j-k-l, связанных цепочкой связей в приведенном порядке;

N_tors– количество возможных четверок атомов i-j-k-l;

Ф_n – двугранный угол, образуемый плоскостями i-j-k и j-k-l, образованными вышеупомянутой четверкой атомов;

V_1n, V_2n, V_3n, – энергетические параметры для торсионного вращения, определяемые типизацией четверки i-j-k-l согласно силовому полю MMFF.

Расчет внутренней энергии лиганда по формулам (11)-(14) состоит из разнородных по плотности потока обрабатываемых данных процедур.

Так, расчет E_lig-tors выполняется однократно, время обработки одного лиганда зависит от числа торсионных связей N_tors и времени на обработку одной связи t_tors и определяется по формуле:

,

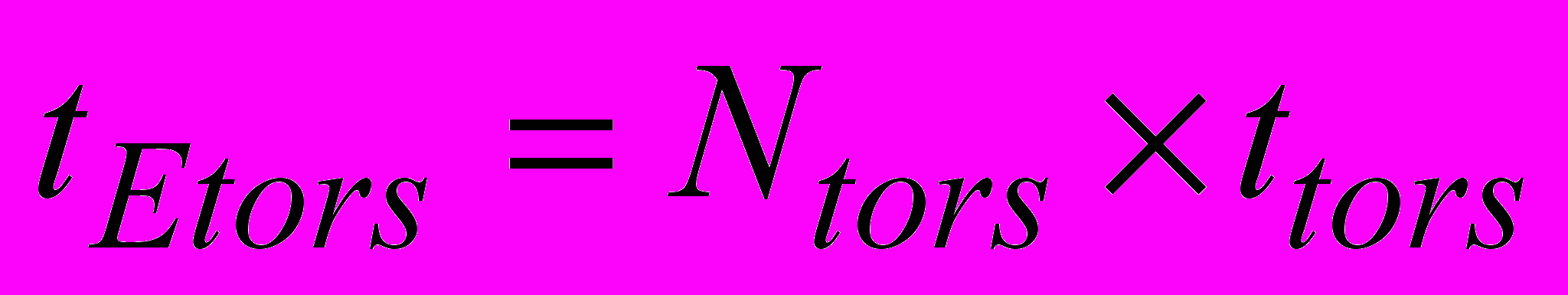где .

Согласно использованной математической модели [2] при количестве пар атомов jk=20, i_max=5 и l_max=5 максимальное число N_{tors max} не превышает 500. Тогда можно определить время обработки для расчета торсионной энергии при структурной реализации E_lig-tors, которое составляет t_Etors=500 тактов, поскольку время обработки одной связи t_tors=1 такт Полученное значение не превышает значения времени обработки для фрагментов R и RT, поэтому структурная реализация процедуры расчета E_lig-tors не требует распараллеливания для согласованной работы в едином вычислительном контуре.

При вычислении значений энергии Ван-дер-Ваальса E_lig-VDW и электростатического взаимодействия E_lig-ES используется принцип суперпозиции полей [2], когда для текущего атома необходимо учитывать влияние всех остальных атомов лиганда, в результате чего многократно (до двух десятичных порядков) возрастает поток промежуточных данных. Время расчета значений этих энергетических составляющих выполняется за время, определяемое по формуле:

, (15)

где t_vdw – время расчета одного прохода E_lig-VDW; t_es – время расчета одного прохода E_lig-ES.

Поскольку значения E_lig-VDW и E_lig-ES зависят только от переменной R_mn, то структурные реализации одного прохода расчета E_lig-VDW и E_lig-ES представляется целесообразным объединить в один блок, дабы сократить t_Evdw__es в два раза, а также не дублировать структурное вычисление значения R_mn. Тогда формула (11) примет вид:

,

где t_{vdw_es} – время расчета одного прохода E_{lig-VDW_ES}=E_lig-VDW+E_lig__ES, которое определяется по формуле:

,

где t_a – время обработки одной пары атомов лиганда.

При структурной реализации одного прохода E_{lig-VDW_ES} время обработки t_a=1 такт, а следовательно, для лиганда с числом атомов N=200 t_Evdw__es=19900 тактов. Далее, исходя из количества математических операций, блок, реализующий один проход расчета E_{lig-VDW_ES}, будет содержать 33 устройства, реализующих 32-разрядные математические операции в стандарте IEEE754.

Структурная реализация процедуры расчета E_{lig-VDW_ES} требует распараллеливания, поскольку t_Evdw__es>>t_Elig-prot. Степень распараллеливания n в данном случае определяется следующим соотношением:

, (16)

где t_П – пороговое значение времени выполнения процедуры, при котором загрузка вычислительных устройств оптимальна, то есть для данного случая при t_П=t_{Elig-prot t}.

Если t_Evdw__es =19900 и t_Elig-prot =950, то получим n ≈ 21.

При этом должно выполняться следующее условие:

, (17)

где V₀ – объем свободного аппаратного ресурса, V(n)– объем аппаратного ресурса, необходимого для построения всей вычислительной структуры E_{lig-VDW_ES}.

Минимальный объем аппаратного ресурса, необходимый для реализации сбалансированной вычислительной структуры E_{lig-1VDW_ES} , будет равен

,

где V_{vdw_es} – объем ресурса, затрачиваемого на структурную реализацию одного прохода E_{lig-VDW_ES}. При V_{Evdw_es} =33 и n=21 получим V_min(n)=693 32-разрядных устройства, стандарт IEEE754.

Исходя из анализа выбранной платформы ПВМ 16V5-75, после размещения на ней вычислительных структур R, RT и E_lig-prot аппаратный ресурс, доступный для построения вычислительной структуры E_{lig-VDW_ES}, будет определяться по формуле

,

где V_p – объем ресурса, эквивалентный всему доступному ресурсу платформы;

с – коэффициент, определяющий затраты на блоки, используемые для объединения и согласования потоков данных между вычислительными структурами и внутри них;

V_g – объем ресурса, затрачиваемый на построение блоков GEN и MPS; V_g=95;

V_R – объем ресурса, затрачиваемый на построение блока R; V_R=440;

V_RT – объем ресурса, затрачиваемый на построение блока RT; V_RT=17;

V_Etors – объем ресурса, затрачиваемый на построение блока E_lig-tors;

V_Etors=51;

V_Elig-prot – объем ресурса, затрачиваемый на построение блока E_lig-prot,

V_Elig-prot=55.

Как показали практические исследования при реализации задачи, с≈0,71. Таким образом, получим V₀ =438 устройств.

Очевидно, что условие (14) не выполняется, поэтому объем затрачиваемого аппаратного ресурса на реализацию вычислительной структуры E_{lig-VDW_ES} необходимо сокращать. Для этого к процедуре были применены методы оптимизации 2 и 3, после чего формулы (9) и (10) преобразовались к виду:

,

и

,

где



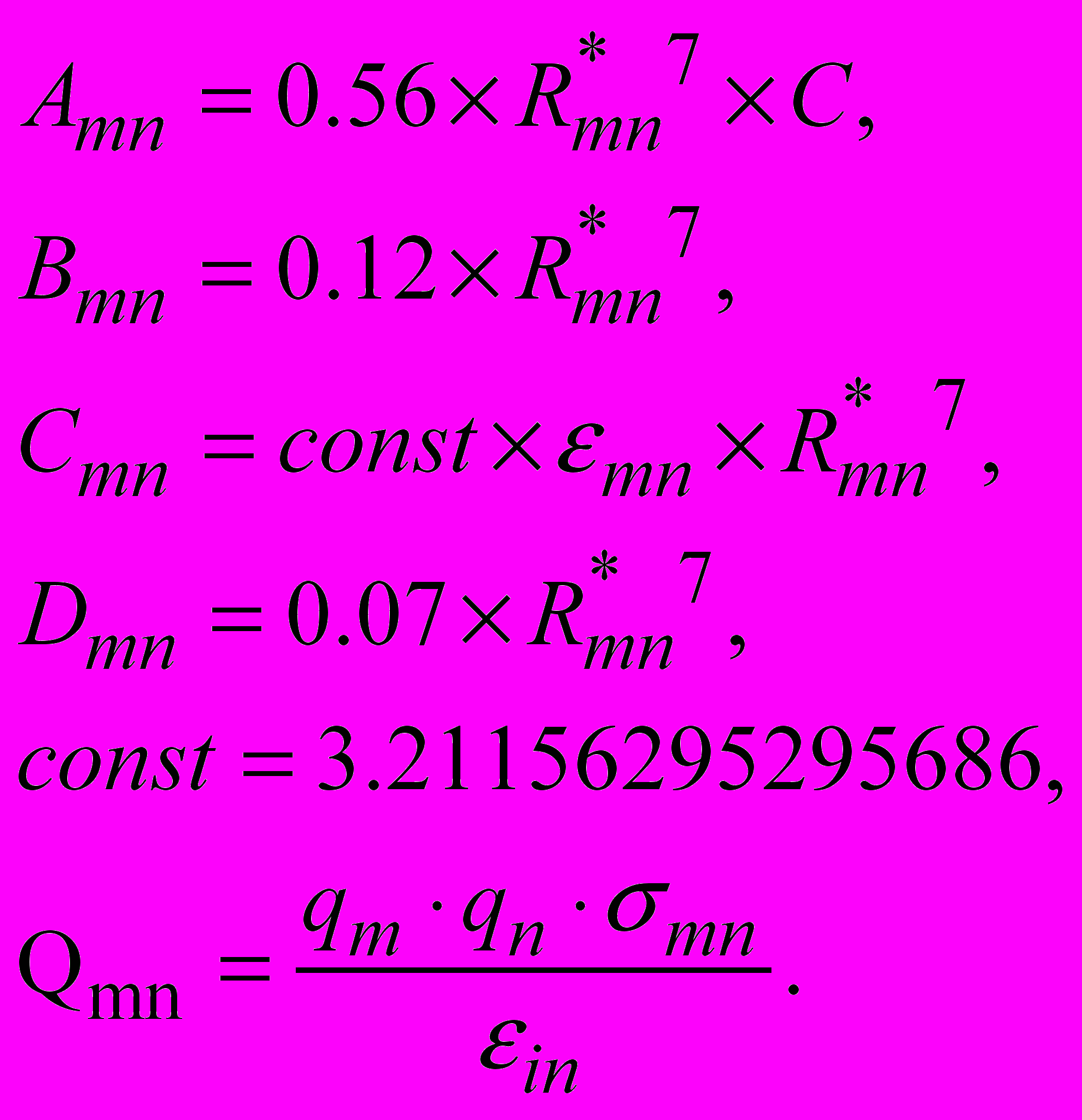
Следовательно,

.


Массивы A_mn, B_mn, C_mn, D_mn, Q_mn для каждого лиганда не меняются в процессе решения всей задачи, поэтому рассчитываются заранее и загружаются во внутреннюю память вычислительной структуры E_{lig-VDW_ES}. Каждый элемент этих массивов соответствует обрабатываемой паре атомом m-n лиганда.

Данные методы оптимизации позволили сократить объем затрачиваемого оборудования на реализацию одного прохода E_{lig-VDW_ES} в 1,5 раза, то есть V_{vdw_es}=21, и определить, что степень распараллеливания необходимо сократить до значения n=20, потому что условие (14) выполняется при V₀ =438 и V(n)=420.

Время обработки лиганда с числом атомов N=200 составит

(тактов).

Энергия лиганда в поле протеина рассчитывается по формуле

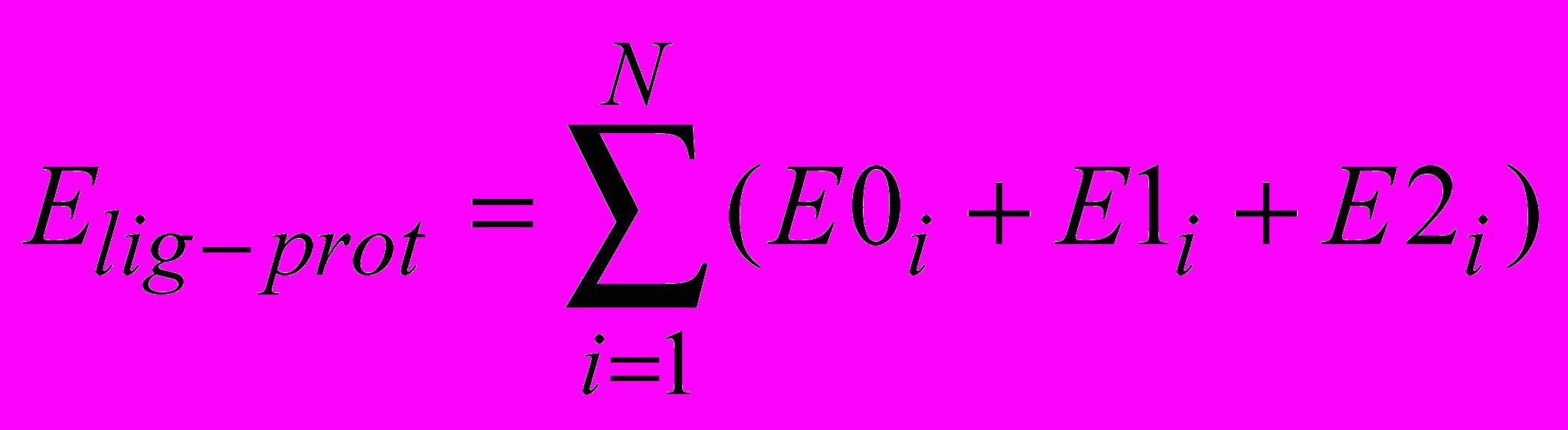, (18)

где E0_i, E1_i, E2_i - составляющие энергии атома, рассчитанные на трехмерных сетках потенциалов в соответствии с типизацией атома по MMFF94; N – количество атомов лиганда.

Вычисление E_lig-prot ведётся методом трилинейной интерполяции. Каждый атом лиганда условно помещается в куб c ребром единичной длины на сетке MMFF94. Структурная реализация вычислений E_lig-prot требует 55 устройств, реализующих 32-разрядные математические операции в стандарте IEEE754. Время обработки одного лиганда определяется по формуле

,

где t_atom – время чтения коэффициентов для одного атома лиганда из массивов трехмерных сеток потенциалов.

Для хранения массивов трехмерных сеток потенциалов необходимо около 200 Mб памяти, поэтому требуется задействовать распределенную память ПВМ 16V5-75, организованную на микросхемах типа SDRAM DDR2.

При вычислении энергии лиганда в поле протеина E_lig-prot для каждого атома выполняется чтение коэффициентов из массивов трехмерных сеток потенциалов, что приводит к чтению из памяти по произвольному адресу, время которого определяется технологическими задержками для памяти типа DDR2. Память типа DDR2 имеет максимальную пропускную способность при «линейном чтении» в пределах строки (содержащей 512 32-разрядных слов), а поскольку переключение между строками микросхемы памяти при произвольной адресации будет происходить постоянно, то время обработки запросов по чтению будет максимальным.

Время обработки запроса к одному из массивов составит, в среднем, 15 тактов, а обработка одного атома лиганда t_atom≈45 тактов соответственно, что составит примерно 72000 тактов работы фрагмента расчета энергии лиганда в поле протеина для лиганда с максимальным числом атомов N_atom=200.

Для решения задачи в едином вычислительном контуре возникает необходимость согласования темпа обработки в фрагментах R, RT и E_lig-prot. Для этого к фрагменту E_lig-prot применим методы оптимизации 3 и 4.

Первое преобразование состоит в сокращении объема используемых для данного лиганда данных в массивах трехмерных сеток потенциалов: в распределенную память ПВМ 16V5-75 загружаются только те коэффициенты, которые соответствуют типам атомов обрабатываемого лиганда, число сочетаний которых, как правило, для одного лиганда не превышает 8. Это позволяет уменьшить требования к объему памяти для массивов трехмерных сеток потенциалов до значения 32 Мб.

Второе преобразование состоит в объединении массивов трехмерных сеток потенциалов в единый массив, каждый элемент которого представляет собой кортеж из трех подряд идущих энергетических коэффициентов массивов трехмерных сеток потенциалов. Контроллер распределенной памяти, установленный на ПВМ 16V5-75, в случае нелинейного чтения позволяет организовать режим, при котором происходит чередование обращений к «строкам» между «банками» памяти, что позволяет сократить время обработки одного запроса при равномерном (или близком к нему) обращении к каждому банку памяти. При организации такого режима теоретическое время обработки одного атома лиганда t_atom составит 4 такта. На практике среднее реальное время обработки одного атома не превышает 4,75 такта, что связано с наличием в атомах лиганда повторяющихся групп атомов водорода, углерода, кислорода и др.

Третье преобразование заключается в согласованном распараллеливании вычислений E_lig-prot по восьми интерполяционным точкам для каждого атома лиганда. Это позволяет эффективно задействовать имеющуюся распределенную память ПВМ 16V5-75. Упорядоченный массив трехмерных сеток потенциалов дублируется для каждой из 8-ми точек и к нему организуется независимый канал доступа. Требуемый для такой организации вычислений объем памяти возрастает до 256 Мб, но, в тоже время, увеличивает скорость обработки E_lig-prot также в 8 раз.

Как показали практические исследования, при такой оптимизации время обработки лиганда N_atom=200 не превышает 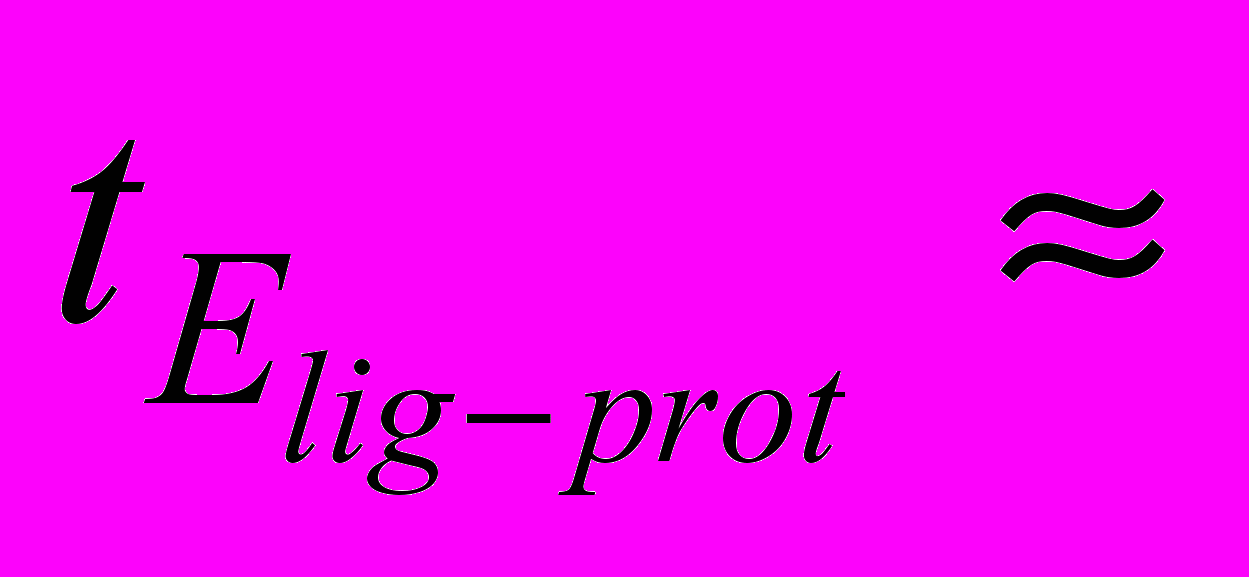950 тактов. Это значение времени обработки будем считать опорным для согласования скорости обработки фрагментов задачи докинга при объединении в единый вычислительный контур.

Исходя из всего вышеописанного, следует, что по скорости обработки данных структуру задачи можно разбить на две следующие группы процедур:

R, RT и E_lig-tors;

E_lig-VDW__ES, E_lig-prot.

Естественно, возникает необходимость согласования скорости обработки между этими группами. В ходе выполнения данной работы было принято простое решение – замедление скорости входного потока данных в 2 раза в соответствии со скоростями обработки на самом медленном участке задачи E_lig-VDW__ES и самом быстром участке E_lig-tors без оптимизации полученной вычислительной структуры. Несомненно, что вычислительная структура получилась избыточной, и фактически 50% времени вычислений половина задействованного оборудования простаивает, но подходящей альтернативы вычислительной платформе ПВМ 16V5-75 на тот момент не было, поэтому дальнейшие исследования были направлены на улучшение точности вычислений по сравнению с эталонной программой суперкомпьютерного молекулярного моделирования SOL [2].

Далее следует отметить, что методы оптимизации 1-3 в той или иной степени применялись и при реализации блоков MPS и GEN. Их особенности в данной статье мы рассматривать не будем в силу их малых вычислительной сложности и ресурсоемкости.


Отображение вычислительной структуры задачи на структуру РВС


Применение методов оптимизации 1-4, описанных в предыдущей главе при схемотехнической реализации алгоритма суперкомпьютерного молекулярного докинга в рамках выполнения НИР «Исследование и разработка методов и средств технологии суперкомпьютерного молекулярного моделирования на базе реконфигурируемых вычислительных систем», позволило до 4-х раз сократить объем затраченного оборудования при сохранении заданной скорости решения задачи.

На рис. 3 приведена синтезированная структура вычислительного конвейера, обеспечивающего полное решение задачи на РВС.

Было получено такое сочетание частоты, объема затраченного оборудования и степени распараллеливания фрагментов алгоритма, при котором построенная вычислительная структура на РВС решает задачу в 10-80 раз быстрее (в зависимости от параметров лиганда), чем системы с традиционной архитектурой. Общий объем задействованного оборудования на построение вычислительных блоков составил 1078 устройств, реализующих 32-разрядные математические операции в стандарте IEEE754.





Рис. 3. Структура вычислительного контура


На рис. 4 приведена структура конвейера задачи, отображенная на структуру платформы ПВМ 16V5-75.





Рис. 4. Расположение основных блоков задачи на платформе ПВМ 16V5-75


Общий объем задействованного оборудования на построение вычислительных блоков составил 1078 устройств, реализующих 32-разрядные математические операции в стандарте IEEE754.


Результаты вычислительных экспериментов


Для проверки, оценки и обобщения результатов реализации задачи докинга на РВС был проведен ряд вычислительных экспериментов для четырех тестовых выборок, две из которых содержат молекулы с одинаковым числом атомов (48 и 52), и разным количеством торсионных степеней свободы, третья выборка состоит из молекул с одинаковым количеством торсионных степеней свободы, равным 7, но разным числом атомов, а четвертая выборка состоит из молекул с большим количеством атомов (до 198) и большим числом торсионных степеней свободы (до 18).

Оценка проводилась сравнением времени выполнения задачи молекулярного докинга на нескольких вычислительных системах:

• на персональных компьютерах, оснащенных процессорами Intel Core2Duo 3 ГГц, оперативной памятью объемом 2 Гбайт;
  
• на одном стандартном вычислительном узле суперкомпьютера СКИФ МГУ «Чебышев» (2 четырехъядерных процессора Intel Xeon E5472 3.0 ГГц, имеющих общую оперативную память объемом 8 Гбайт), (НИВЦ МГУ имени М.В.Ломоносова);
  
• на нескольких (до 32-х процессоров) вычислительных узлах суперкомпьютера СКИФ МГУ «Чебышев» (НИВЦ МГУ имени М.В. Ломоносова);
  
• на ПВМ 16V5-75.
  

Для экспериментов по сравнению времени работы программы на РВС и кластерной системе стандартной архитектуры использовалась параллельная версия программы докинга SOL.

При докинге молекул тестовых выборок на РВС (ПВМ 16V5-75) была достигнута реальная производительность 125,7 Гфлопс, что составляет 89,8% от пиковой производительности.

В результате выигрыш ПВМ 16V5-75 во времени докинга для одного поколения из 30000 особей по сравнению с Intel Core2Duo 3 ГГц в зависимости от числа атомов и торсионных связей составил от 35 до 90 раз; выигрыш по сравнению со стандартным вычислительным узлом суперкомпьютера СКИФ МГУ «Чебышев» - от 6 до 15 раз; по сравнению с 32 процессорами суперкомпьютера СКИФ МГУ «Чебышев» − от 3 до 5 раз.


Заключение


Особенности организации вычислений в параллельной версии программы докинга SOL приводят к интенсивному обмену MPI-сообщениями, в результате чего на скорость решения задачи, в основном, начинает влиять латентность MPI-системы, а не скорость передачи данных. Для числа процессов, большего, чем 30, время, затрачиваемое на синхронизацию, оказывается сравнимым со временем, затрачиваемым на расчеты, поэтому оптимальное число процессоров для одного независимого запуска программы составляет 32, а максимальное значение ускорения, достигаемое на 32-х процессорах, – 5 раз. Дальнейшее увеличение количества процессоров не повлияет на ускорение одного независимого запуска, а с учетом дополнительной нагрузки на MPI-сеть в ходе обмена информацией между процессами будет наблюдаться даже замедление работы программы.

Значение ускорения выполнения программы на РВС существенно зависит от размера рассчитываемой молекулы: чем больше количество атомов и торсионных степеней свободы, тем значительнее выигрыш во времени решения задачи на РВС по сравнению с вычислительными системами традиционной архитектуры. Это связано, прежде всего, с гораздо более эффективным способом параллельной организации вычислений и меньшими накладными расходами на организацию вычислительного процесса на специализированных вычислительных системах, чем на кластерах стандартной архитектуры. ПВМ 16V5-75 обеспечивает многократный выигрыш в скорости докинга, доходящий до 70 раз для одного поколения популяции, который практически линейно увеличивается с увеличением числа атомов в лиганде и числа торсионных связей до их максимальных значений.

Полученные экспериментальные результаты позволяют сделать вывод о том, что использование РВС для докинга сложных органических молекул обеспечивает существенное ускорение: не менее чем на один десятичный порядок при пересчете на один процессор по сравнению с вычислительными системами традиционной архитектуры. Таким образом, применение РВС для суперкомпьютерного молекулярного моделирования позволяет существенно сократить время моделирования и материальные затраты на создание эффективных лекарственных средств нового поколения.


БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Молекулярная стыковка: dia.org/wiki/Докинг.
   
2. Романов А.Н., Кондакова О.А., Григорьев Ф.В. и др. Компьютерный дизайн лекарственных средств: программа докинга SOL // Вычислительные методы и программирование, 2008. − Т. 9. − С. 213-233.
   
3. Генетический алгоритм dia.org/wiki/Генетические_алгоритмы.
   
4. AutoDock. scripps.edu/.
   
5. Каляев И.А., Левин И.И., Семерников Е.А., Шмойлов В.И. Реконфигурируемые мультиконвейерные вычислительные структуры / Изд. 2-е, перераб., доп. / Под общ. ред. И.А. Каляева. − Ростов-на-Дону: Изд-во ЮНЦ РАН, 2009. – 344 с.
   
6. Van Court T. FPGA acceleration of rigid molecule interactions / T. Van Court, Y. Gu, M. Herbordt // Int. Conf. Field Programmable Logic and Applications (FPL 2004). – Antwerpen, Belgium, 2004, рр. 862-867.
   
7. Van Court T., Gu Y., Mundada M.C., Herdbordt M.C. Rigid molecular4 docking: FPGA recinfiguration for alternative force laws // J Appl. Signal Processing v.2006, 2006, рр. 1-10.
   
8. Herdbordt M.C., Gu Y., Van Court T., Model J., Sukhwani B., Chiu M. Computing models for FPGA-based accelerations with case studies in molecular modeling // Porcced. of the Reconfigurable systems summer institute (RSSI 2008), 2008.
   
9. Sukhwani B. Acceleration of a production rigid molecule docking code / B. Sukhwani, M. Herbordt // Int. Conf. Field Programmable Logic and Applications (FPL 2008). – Heidelberg, Germany, 2008, рр. 341-346.
   
10. Sukhwani B., Herdbordt M.C. FPGA accelaration of rigid-molecule docking codes // IET Computers & digital techniques (ACM-TRETS), 2009 (accepted for publication).
    
11. ссылка скрыта D., ссылка скрыта R., ссылка скрыта S.R., ссылка скрыта S. PIPER: an FFT-based protein docking program with pairwise potentials // Proteins: Structure, Function and Genetics, v.65, 2006, рр. 392-406.
    

Дордопуло Алексей Игоревич

Учреждение Российской академии наук «Южный научный центр РАН»

E-mail: scorpio@mvs.tsure.ru.

347900, г. Таганрог Ростовской области, 10-й переулок, 114/1, кв. 6.

Тел.: (8634) 368651.

Отдел ИТ и ПУ, к.т.н., с.н.с.


Сорокин Дмитрий Анатольевич

Научно-исследовательский институт многопроцессорных вычислительных систем имени академика А.В. Каляева федерального государственного автономного образовательного учреждения высшего профессионального образования «Южный федеральный университет»

E-mail: jotun@inbox.ru

347922, г. Таганрог Ростовской области, переулок Украинский, д.21, кв.30.

Тел.: (8634) 393820.

Научный сотрудник.


Бовкун Александр Викторович

Научно-исследовательский институт многопроцессорных вычислительных систем имени академика А.В. Каляева федерального государственного автономного образовательного учреждения высшего профессионального образования «Южный федеральный университет»

E-mail: simans2000@ mail.ru

347900, г. Таганрог Ростовской области, ул. 1-я Котельная, 77/3, кв .47.

Тел.: (8634) 321-401.

Программист.


Dordopulo Alexey Igorevich

Southern Scientific Centre of the Russian Academy of Sciences

E-mail: scorpio@mvs.tsure.ru.

347900, Taganrog, Rostov-on-Don region, 10^th lane, 114/1, apartment 6

Fone: (8634) 368-651.

Senior staff scientist, PhD


Sorokin Dmitry Anatolievich

Kalyaev Scientific Research Institute of Multiprocessor Computer Systems at Southern Federal University.

E-mail: jotun@inbox.ru.

347922, Taganrog, Rostov-on-Don region, Ukrainskiy lane, house 21, apartment 30.

Fone: (8634) 393-820.

Scientific associate.


Bovkun Alexandr Victorovich

Kalyaev Scientific Research Institute of Multiprocessor Computer Systems at Southern Federal University.

E-mail: jotun@inbox.ru

347900, Taganrog, Rostov-on-Don region, 1 Kotelnaya street, house 77/3, apartment 4.7.

Fone: (8634) 321-401.

Programmer.