Технологическое оборудование гап
| Вид материала | Задача |
- Рабочая программа по дисциплине дс. 02. 02 «Технологическое оборудование отрасли», 255.51kb.
- Рабочая программа по дисциплине сд 02. 02 «Технологическое оборудование», 267.47kb.
- Памятка для студентов групп мапп-31; мапп-32 по изучению дисциплины "Технологическое, 77.03kb.
- Технологические машины и оборудование, 7.35kb.
- Аннотация рабочей программы дисциплины «Основы расчета и конструирования машин и аппаратов, 40.28kb.
- Аннотация рабочей программы дисциплины «Монтаж, эксплуатация и ремонт технологического, 26.71kb.
- Аннотация рабочей программы дисциплины «Начертательная геометрия. Инженерная графика», 29.27kb.
- Аннотация рабочей программы дисциплины «Теория механизмов и машин» для направления, 28.8kb.
- Аннотация рабочей программы дисциплины «Экономика c/х и перерабатывающих предприятий», 127.54kb.
- Аннотация рабочей программы дисциплины «Технологические процессы переработки молока, 31.06kb.
6.3. Методы формализации и алгоритмизации задач синтеза структуры АСУ.
6.3.1. Задачи синтеза структуры АСУ.
Под структурой АСУ понимают организованную совокупность ее элементов.
В общем случае под элементом структуры АСУ понимается некоторый физический элемент (узел, техническое средство, исполнитель или коллектив исполнителей и т.д.), реализующий вполне определенным образом ту или иную функцию системы.
Под организованностью совокупности элементов структуры АСУ понимается их взаимосвязь, определяющая место элемента в системе (уровень управления, конкретное место размещения в КТС и технологической схеме обработки данных и принятия решений).
В общем случае задача синтеза структуры АСУ включает в себя:
- выбор принципов построения системы управления;
- распределение функций обработки информации и управления по узлам и уровням иерархии АСУ;
- рациональное размещение задач обработки информации и принятия решений по конкретным элементам с одновременным выбором методов их решения;
- согласование целей отдельных элементов, уровней и подсистем с общими целями для всей системы;
- распределение функций и задач между техническими средствами и коллективами специалистов по управлению;
- определение наиболее эффективных взаимосвязей между всеми составляющими структуры системы;
- выбор и назначение технических средств для решения задач и осуществления связи в АСУ.
Постановка и решение общей задачи синтеза структуры АСУ представляют вполне определенные трудности из-за большой размерности самой задачи и невозможности обеспечить полноту необходимой исходной информации. Поэтому формулируются и решаются более частные задачи, позволяющие оценить правильность принимаемых решений о структуре создаваемой АСУ.
Как правило, частные задачи отражают реальные аспекты процесса синтеза структуры АСУ, а результаты их решения позволяют специалистам по синтезу систем наметить наиболее перспективные пути решения общей задачи и выделить область наиболее целесообразных вариантов построения всей АСУ.
6.3.2. Методология решения задач синтеза структуры.
Различные постановки задач синтеза структуры систем приводят к весьма сложным задачам математического программирования, которые в графовой интерпретации сводятся к выделению оптимального подграфа на графе альтернативных вариантов (в частном случае этим подграфом может оказаться набор путей, контуров и т.д.).
Рассмотрим основные методы решения задач синтеза структуры. Эти методы могут быть классифицированы следующим образом:
- методы сведения произвольной задачи математического программирования к стандартной форме, для которой разработаны эффективные методы решения или имеется соответствующее программное обеспечение;
- методы сведения задачи синтеза структуры к графовой модели с последующим поиском допустимых и оптимального подграфа.
При сведении задачи синтеза структуры АСУ к некоторой стандартной форме может утрачиваться специфика решаемых задач. Кроме того, размерность решаемой задачи при этом подходе ограничена возможностями имеющегося программного обеспечения.
Задачи синтеза структуры часто допускают простую и наглядную интерпретацию в виде графовой модели. Эта модель может быть использована для построения эффективных алгоритмов их решения. Задача в этом случае сводится к поиску одного или нескольких кратчайших путей либо допустимого подграфа, удовлетворяющих заданным требованиям.
Общая схема решения такой задачи состоит из двух этапов:
1. выделение и исключение частей графа, заведомо не входящих в оптимальное
решение по заданным характеристикам;
2. перебор допустимых вариантов для нахождения оптимального решения.
Причем на этапе 2 при большом числе вариантов используются различные методы (типа "ветвей и границ"), позволяющие сократить перебор. Ветвление при этом может осуществляться по вершинам и дугам графовой модели, по выделенному набору путей, контуров и подграфов.
При решении задачи синтеза структуры АСУ следует учитывать непрерывное изменение внешних условий системы (система должна обладать способностью к адаптации -способностью перестраивать свою работу в соответствии с изменившимися требованиями).
Для решения задачи выбора рациональной структуры должны быть предварительно определены целевое назначение проектируемой АСУ, критерии эффективности, функции системы, перечень решаемых ею задач, основные звенья системы, предполагаемые технические средства и их характеристики.
Для каждой задачи Еі, I =1,п нужно определить алгоритм решения, юсодную и выходную информацию, а также провести оценку операций, необходимых для реализации алгоритма. Используя характеристики технических средств, оценивают длительность решения каждой задачи.
Далее определяют возможные варианты Mj, j = l,m распределения задач Ei по звеньям АСУ. При этом ограничиваются перебором только тех вариантов распределения, рассмотрение которых определяется заданными ограничениями и практическими соображениями. В выбранный вариант распределения можно вносить целенаправленные изменения для его улучшения.
В централизованных системах управления все задачи решают в высшем звене -центральном органе АСУ. Однако подавляющее большинство систем строятся либо как многоуровневые иерархические, либо распределенные системы управления. В распределенных системах управления функции центрального органа заключаются в определении стратегии системы и координации действий всей подсистем.
Таким образом, последовательное решение ряда самостоятельных задач приводит к определению рациональной структуры АСУ.
Процесс выбора рационального варианта структуры состоит из следующих основных этапов:
- выбор критериев для оценки различных вариантов структуры;
- определение перечня задач, возлагаемых на технические средства АСУ;
- перечисление априори наиболее рациональных вариантов распределения задач по звеньям системы с учетом ограничений.
- определение значения критериев для альтернативных вариантов структур;
- корректировка перечня задач, распределение их по звеньям и выбранным техническим средствам, т.е. повторение цикла 1)-4);
- определение наиболее рациональной структуры АСУ, при которой оценки критерия принимают экстремальные значения.
6.3.3. Математические модели и методы решения задач синтеза структуры АСУ.
В качестве примера рассмотрим математическую модель задачи оптимального распределения функций АСУ по заданным_уровням и звеньям системы. Критериями задач синтеза структуры АСУ могут использоваться: 1) затраты на реализацию задач в АСУ
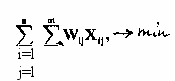
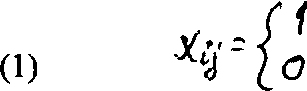
где Wij - затраты на реализацию i-задачи в j-звене, xij=1 - если i-задача выполняется в j-звене, хij=0 в противном случае;
2) общее время решения всех задач АСУ
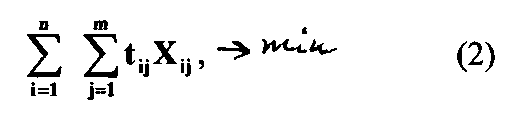
где tij - время решения i-задачи в j-звене;
3
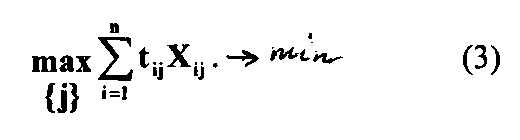 ) максимальное время решения задач АСУ в каждом звене
) максимальное время решения задач АСУ в каждом звенеПри решении задач все эти критерии минимизируются.
Возможна оптимизация по более сложным критериям, включающим в себя критерии (1)-(3), а также использование критериев более общего типа, таких, как прибыль, готовность системы и др.
При оптимизации могут накладываться ограничения на связи между задачами:
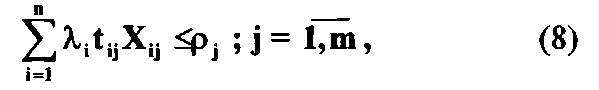
на затраты по реализации задач в каждом звене
на загрузку каждого звена
на связи между звеньями
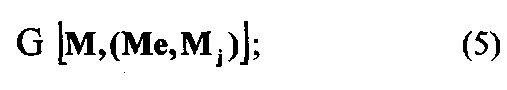
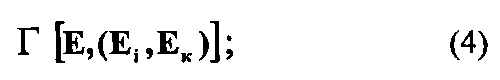
на общие затраты по реализации задач АСУ
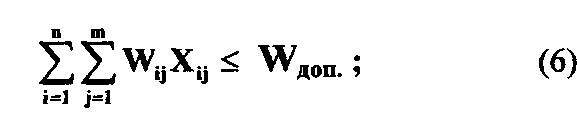
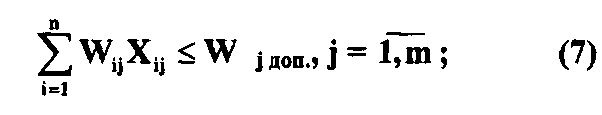
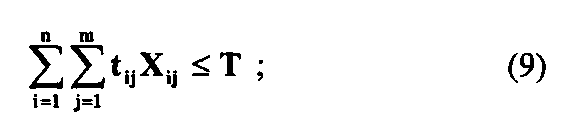
на время решения отдельных задач
где λі, - интенсивность поступления i-задачи на решение. Возможны дополнительные требования: на общее время решения всех задач
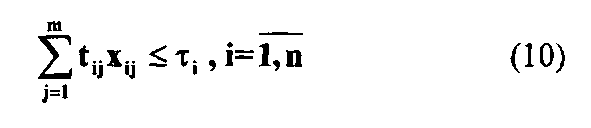
Довольно часто существует также условие, что каждая задача должна решаться только в одном звене системы
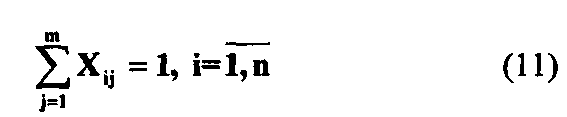
Большинство задач, связанных с синтезом структуры АСУ, являются задачами целочисленного линейного программирования.
Рассмотрим решение задачи распеделения задач по звеньям системы при минимизации общих затрат (1) либо общего времени решения (2) при ограничениях на загрузку каждого из звеньев (8) или на затраты в каждом j-звене (7), т.е. задачи вида:
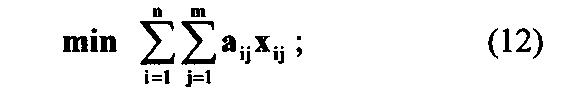
найти
п
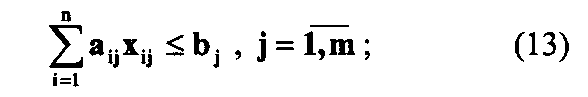 ри ограничениях
ри ограничениях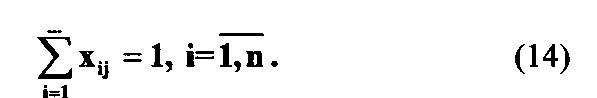
Такую задачу удобно решать известным в целочисленном программировании методом "ветвей и границ", который применительно к ней состоит в направленном движении по вершинам дерева, получаемого из матрицы системы (13) путем последовательного формирования переменной Xij, принимающей значение 0 или 1.
Сначала получают вершины первого уровня ветвления, полагая Xij=1 последовательно для всех i при j=l. Затем для каждой из вершин первого уровня выделяют вершины второго уровня ветвления, полагая Xij=1 последовательно для всех значений i при j=2 и т.д.
До ветвления исключают из матрицы коэффициентов аij все элементы, у которых аij>bj. При этом возможны случаи, когда в некотором столбце:
а) исключены все элементы аij- оптимального элемента нет;
б) остался лишь один элемент аij- он входит в оптимальное решение, если оно
существует. В этом случае значение bj заменяют на (bj - аij) и этот элемент в дальнейшем
поиске не участвует.
в) осталось несколько элементов аij - они участвуют в дальнейшем поиске
оптимального решения.
В процессе решения задачи, сопоставляя затраты при распределения задач по всем возможным ветвям дерева и выбирая ветви с минимальными затратами находят оптимальное распределение задач по звеньям системы.
Возможны и другие постановки задачи:
- минимизация затрат (1) или времени решения (2) при ограничениях на время (9) или затраты (6);
- минимизация затрат (1) или времени решения (2) при ограничениях на время (9) или затраты (6) с учетом дополнительного ограничения на загрузку звеньев (8);
- минимизация максимального суммарного времени выполнения задач в звеньях (3) при ограничении (10).
4. методы формализации и автоматизации проектирования информационного и
программного обеспечения.
6.4. Методы формализации и автоматизации проектирования информационного и программного обеспечения.
6.4.1. Задачи и этапы синтеза информационного обеспечения АСУ.
При проектировании систем ИО АСУ необходимо:
- разработать технологию сбора, преобразования, хранения, обновления, распределения и передачи данных от источников к потребителям информации;
- выбрать рациональную организацию входных, промежуточных, главных и выходных информационных массивов;
- определить процедуры преобразования и контроля информации и их рациональную организацию;
4) выбрать технические средства для хранения и преобразования информации.
Традиционно эти задачи решаются разработчиками на интуитивном уровне, а
рациональность решений в значительной степени зависит от квалификации и опыта разработчиков. Поэтому вопросы формализации, как объекта проектирования, так и процесса проектирования системы весьма актуальны.
Рассмотрим графовую модель для формализации синтеза системы информационного обеспечения АСУ.
Модель системы ИО представляется ориентированным мультиграфом G =(I, F, D),
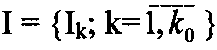
- множество массивов;
где
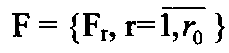
- множество процедур;
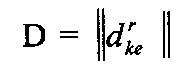
- матрица, отражающая структуру взаимосвязи массивов и процедур в
виде:
drke=1, если массив Jk необходим для формирования массива Je процедурой Fr (при этом
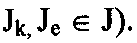
drke=0 - в противном случае. Массивы Je, Jk ставятся в соответствие вершинам графа, а процедуры Fr - его дугам. Массив и его характеристики определяются: смысловым содержанием массива;
• способами организации информационных полей, записей из информационных полей и массива из записей;
• типом носителя информации и ЗУ;
• стратегией обращения к массиву при поиске необходимой информации и записи вновь поступающей информации.
Процедура преобразования одних массивов в другие и ее характеристики определяются:
- набором операторов, достаточных для выполнения требуемого преобразования;
- порядком выполнения операторов в этом наборе.
Пример агрегированной графовой модели системы ИО приведен на рис. 6.1.
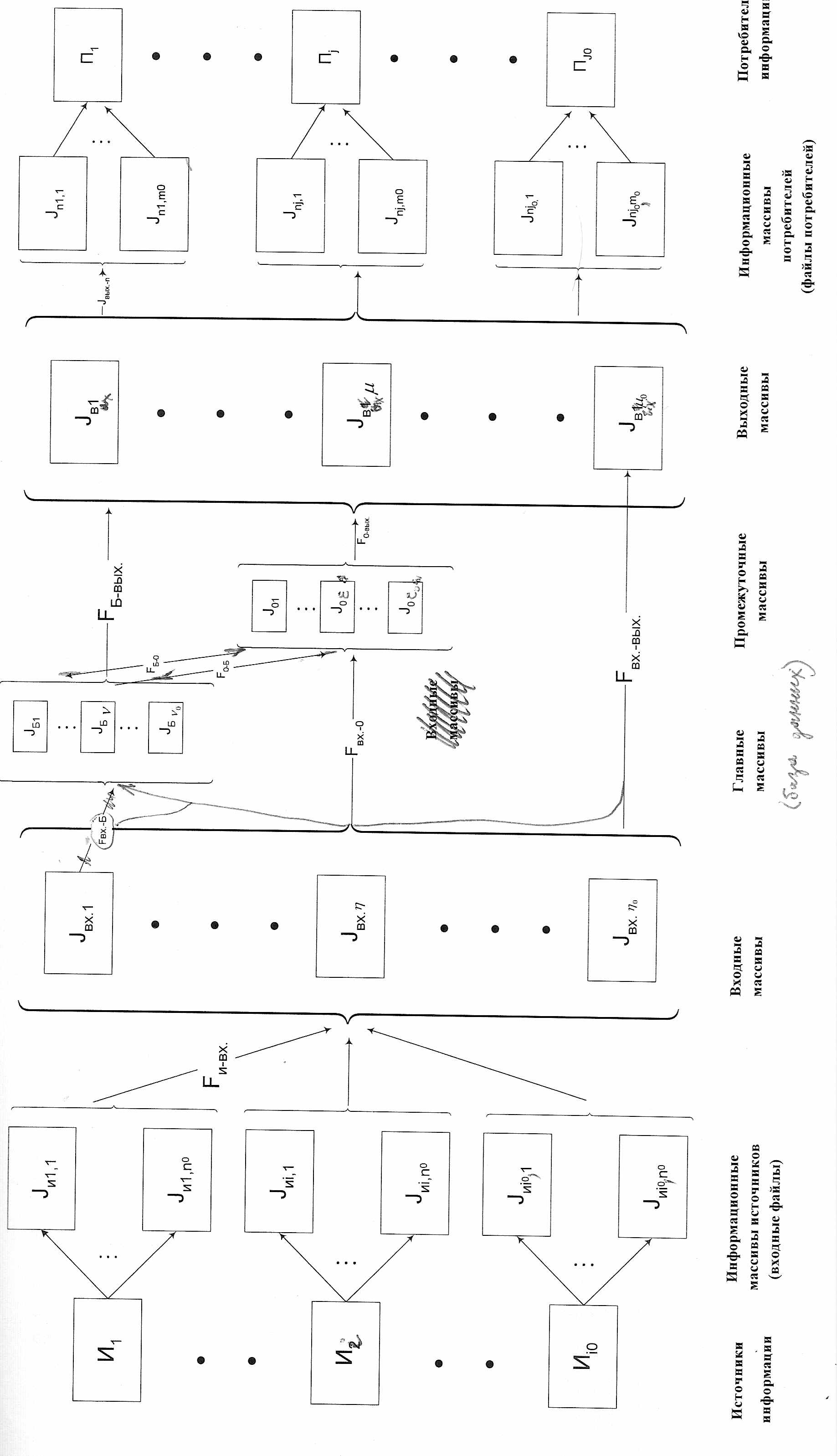
Рис. 6.1
Н
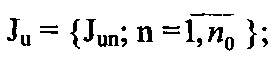 а схеме выделены:
а схеме выделены:- информационные массивы источников (входные файлы)
- информационные массивы (файлы) потребителей
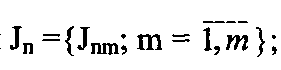
- главные массивы (база данных)
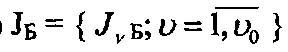 ;
;
- промежуточные массивы
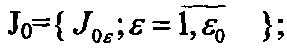
- входные массивы
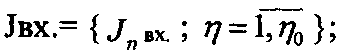
- выходные массивы

- подсистема формирования: входов
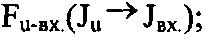
- подсистема формирования промежуточных массивов из входа
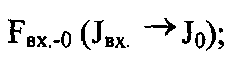
- подсистема формирования главных массивов (базы данных)
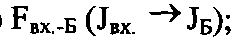
- подсистема формирования промежуточных массивов из главных
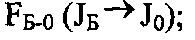
- подсистема формирования главных массивов из промежуточных
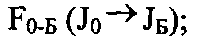
- подсистема формирования выходных массивов из главных
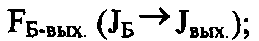
- подсистема формирования выходных из входных
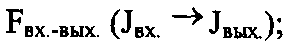
- подсистема формирования выходных массивов из промежуточных
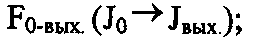
- подсистема формирования масивов потребителей из выходных
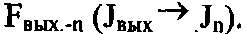 Граф возможных вариантов реализации системы
Граф возможных вариантов реализации системы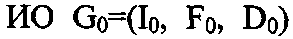 отличается от
отличается от
графовой модели G тем, что для каждого информационного массива
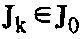 возможен выбор различных вариантов процедур
возможен выбор различных вариантов процедур При этом множество содержит
При этом множество содержит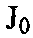 возможные
возможныеварианты организации информационных массивов, а каждому варианту процедуры Fr, как и на графовой модели G, соответствуют пучки дуг
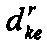
Таким образом, граф Go отображает возможные варианты преобразования входных массивов в выходные и может служить для выбора оптимального варианта по заданным критериям оптимальности с учетом ограничений.
Общая задача синтеза системы ИО может быть сформулирована следующим образом. Заданы потребители
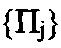 и источники
и источники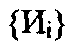 информации, а также соответствующие им множества информационных массивов Jn, Ju. Необходимо синтезировать граф Go и выбрать на нем оптимальный вариант реализации всей системы
информации, а также соответствующие им множества информационных массивов Jn, Ju. Необходимо синтезировать граф Go и выбрать на нем оптимальный вариант реализации всей системы с учетом
с учетомтребований к заданным характеристикам качества. Пример реализации графа Go приведен на рис. 6.2.
В такой постановке общая задача синтеза системы ИО разбивается на задачу синтеза графа возможных реализаций Go и задачи выбора на этом графе оптимального варианта.
Для синтеза графа Go возможен чисто комбинаторный подход: перебор всех возможных комбинаций из различных вариантов реализации основных элементов- информационных массивов и процедур их преобразования для получения требуемого выхода.
При таком подходе можно получить точное решение задачи синтеза системы. Однако даже при сравнительно небольшой размерности графов пришлось бы рассматривать огромное количество вариантов реализации, что практически невозможно. Более целесообразным является последовательный анализ возможных вариантов и частей системы с выделением на каждом этапе построения графа лучших по заданным показателям качества вариантов реализации системы из допустимых.
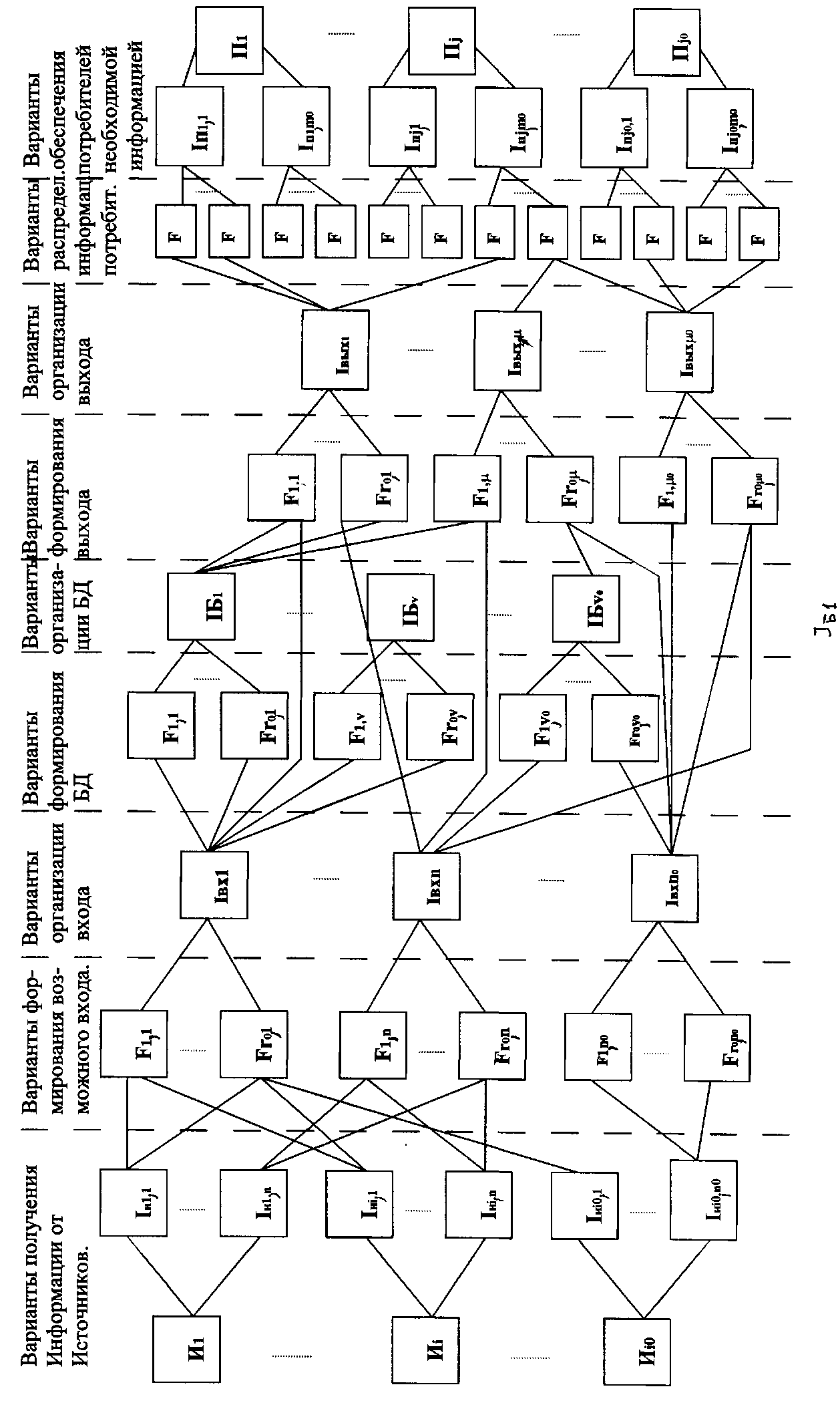
Рис.6.2. Пример реализации графа G0
При синтезе систем ИО основными характеристиками качества варианта системы являются:
- Затраты на создание и внедрение системы,
- Время разработки системы,
- Эксплуатационные расходы,
- Потери от несовершенного представления информации,
- Быстродействие системы,
- Необходимый объем памяти,
- Число различных ТС для выполнения отдельных процедур и алгоритмов.
Кроме того, при синтезе системы ИО необходимо учитывать как ограничения, так и другие характеристики системы: достоверность информации, надежность элементов системы и др.
В качестве критерия оптимальности при выборе варианта системы принимается та или иная основная характеристика, а остальные являются ограничениями. Можно также сформировать обобщенный критерий, в котором с соответствующими весовыми коэффициентами учитываются одновременно несколько основных характеристик качества.
При синтезе систем ИО возникает необходимость решения следующих типов задач:
- синтеза информационных массивов,
- синтеза процедур преобразования одних массивов в другие,
- определение оптимальных вариантов отдельных частей и всей системы ИО,
- выбора оптимального набора основных массивов (базы данных) и др.
В качестве примера рассмотрим математическую постановку одной из них.
