Инженерная логика против классической

Вид материала

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 20

Глава третья.

Триггеры

Триггером называется логическое устройство с двумя устойчивыми состояниями. Выходной сигнал на выходе такого устройства зависит не только от входных сигналов , действующих в данный момент , но и от сигналов , воздействовавших в предыдущий момент времени. Существует несколько видов триггеров.

Наиболее распространёнными из них являются SR- , D- , и JK- триггеры.

3.1 SR- триггеры.

SR- триггер имеет 2 управляющих входа S и R. Если S = 1 , то выход триггера Q = 1 , если R = 1 , то Q = 0. Комбинация S = 1 и R = 1 для SR - триггера является запрещённой. На рисунках представлены две реализации SR - триггера и его условное обозначение.

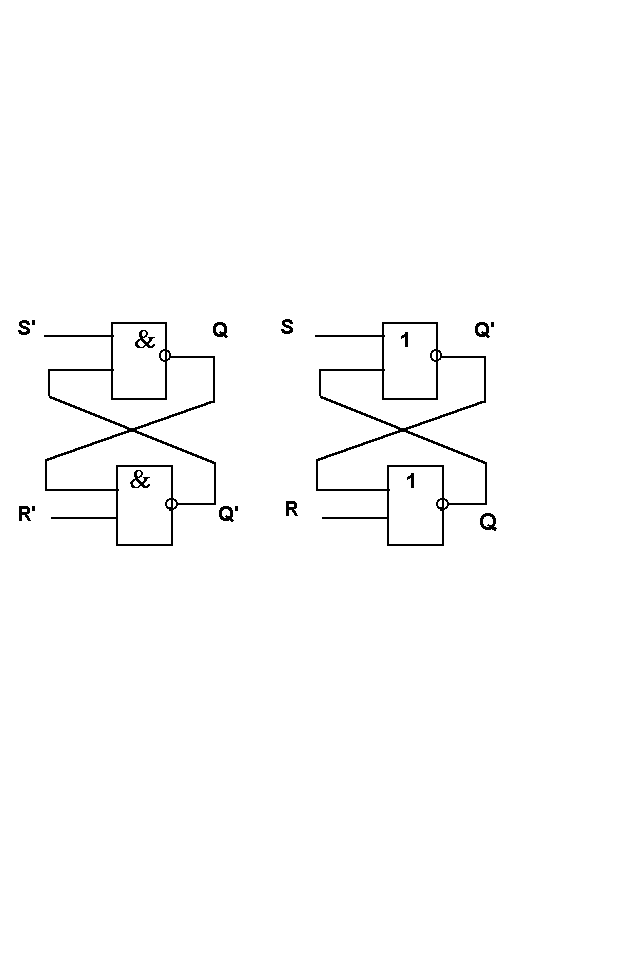
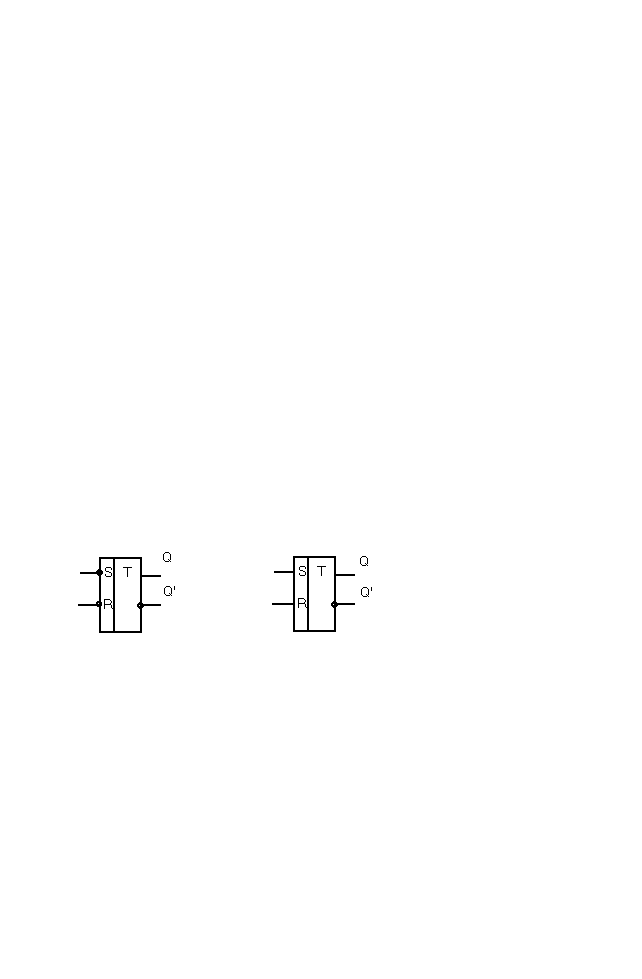
Схемы и обозначения SR-триггеров.

3.2 D- триггеры.

D- триггер при наличии разрешающего сигнала на тактовом входе устанавливается в состояние , соответствующее потенциалу на входе D.

Таким образом , D- триггер является тактируемым элементом памяти. Тактирование может осуществляться как потенциалом , так и фронтом (передним или задним).

Триггер, тактируемый потенциалом, может изменить своё состояние только при наличии определённого потенциала на тактовом входе C. Триггер , тактируемый фронтом, меняет своё состояние только с приходом определённого фронта сигнала на тактовый вход C.

На рисунках представлены тактируемые потенциалом и передним фронтом D- триггеры и их условные обозначения, а также временные диаграммы работы.

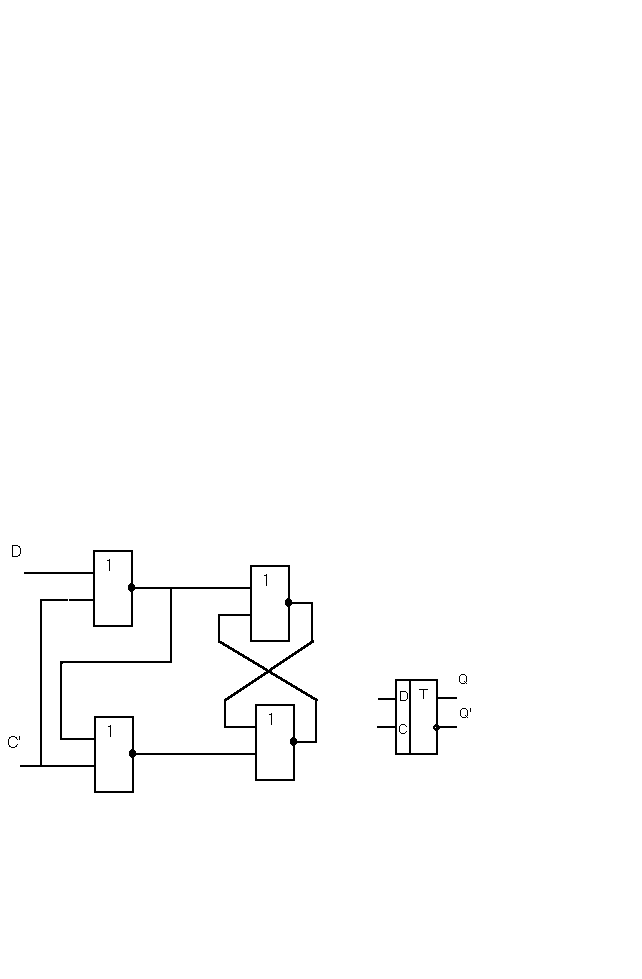
Схема и условное обозначение тактируемого потенциалом D-триггера.

Условное обозначение и диаграммы работы переднефронтового D-триггера

3.3 . JK- триггеры.

JK- триггеры являются самыми сложными из рассмотренных элементов памяти. Они обладают большими функциональными возможностями. JK- триггеры могут быть тактируемыми и нетактируемыми. Универсальный JK- триггер может работать во всех режимах. Например, для перевода универсального JK- триггера в нетактируемый режим достаточно на вход C подать потенциал C = 1. На рисунке изображён тактируемый задним фронтом JK- триггер серии134 (1ТК343) и временные диаграммы его работы.

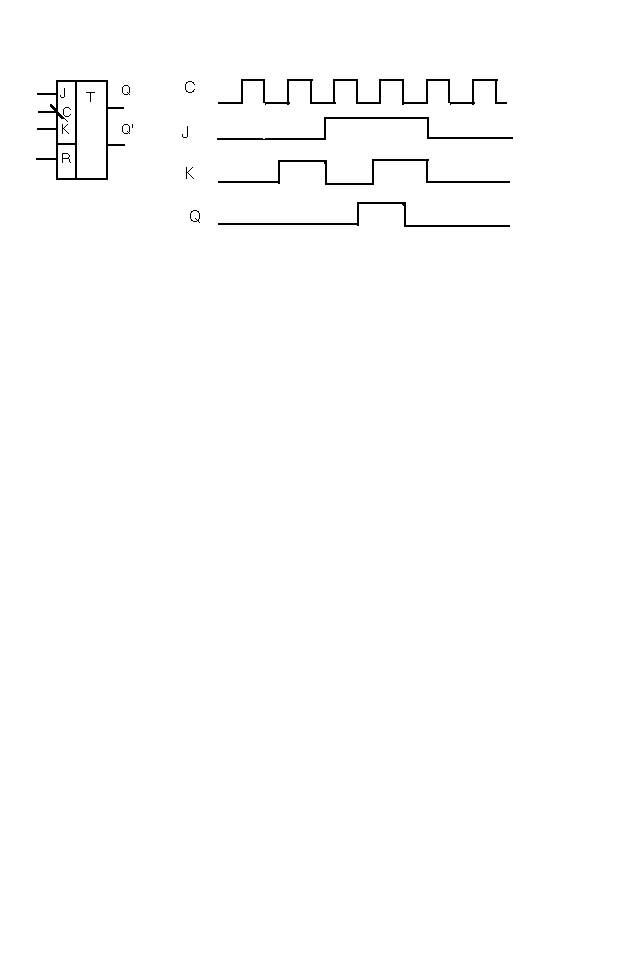
Условное обозначение и диаграммы работы заднефронтового JK-триггера.

Работает JK- триггер следующим образом. При J=1 и K= 1 тактовый импульс переводит триггер в противоположное состояние (Q_n = Q_n-1’) . При J = 0 и K = 0 триггер сохраняет предыдущее состояние (Q_n = Q_n-1). При J = 1 и K = 0 Q_n = 1 , при J = 0 и K = 1 Q_n= 0.

Работа любого триггера может быть однозначно описана с помощью таблицы переходов.

Таблица переходов для SR-, D- и JK- триггеров.

Вход 1	Вход 2	SR- триггер	JK- триггер	D- триггер
0 0 1 1	0 1 0 1	Q_n-1 0 1 -	Q_n-1 0 1 Q_n-1’	0 0 1 1

3.4 Анализ работы схем с памятью

Анализ работы схем с памятью может быть графическим или табличным. Наиболее удобным является табличный метод анализа, так как он позволяет оторваться от принципиальной схемы устройства. Этот способ основан на описании функций управляющих входов , или функций возбуждения.

Задача 12

Произвести анализ работы устройства, изображённого на рисунке, табличным способом.

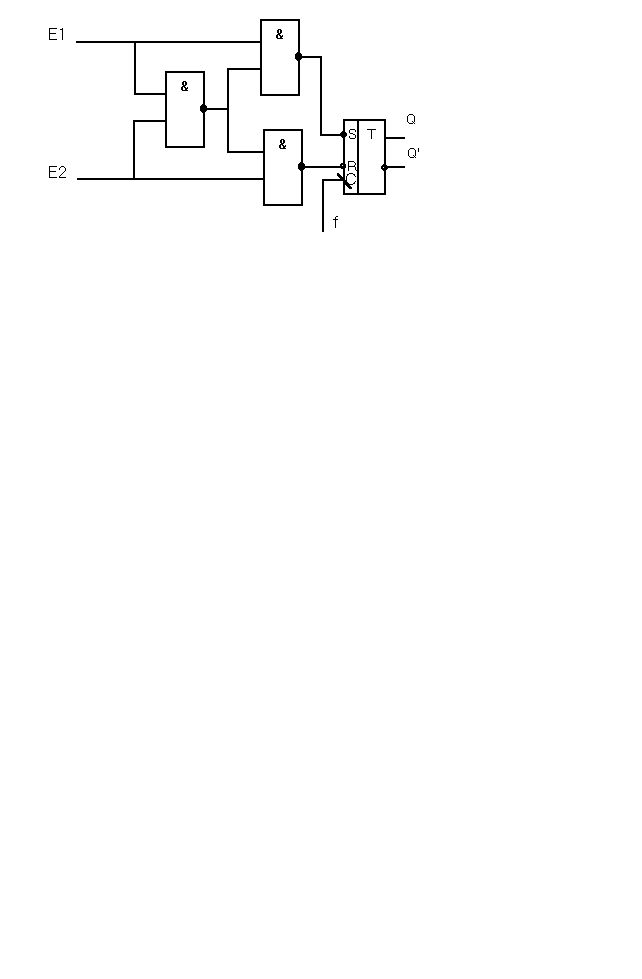
Схема устройства к задаче 12.

Решение.

Опишем функции возбуждения входов SR- триггера.

S = E₁(E₁E₂)’ = E₁(E₁’ + E₂’) = E₁E₂’

R = E₂(E₁’ + E₂’) = E₁’E₂

Зададим исходное состояние SR- триггера. Пусть Q₀ = 0. Далее будем изменять входные сигналы E₁ и E₂ , определять функции S и R , а по ним находить Q_n. Процесс анализа отражён в таблице.

E₁ E₂	S=E₁E₂’	R=E₁’E₂	Q_n	Примечание
0 0 0 1 1 0 1 1	0 0 1 0	0 1 0 0	0 0 1 1	Q₁=Q₀ , т.е Q_n=Q_n-1 Q₂=0 Q₃=1 Q₄=Q₃ , т.е. Q_n=Q_n-1

Даже простой пример показывает,насколько неудобен анализ работы схем с памятью.В главе «Конечные автоматы» мы познакомимся с более эффективным методом.