Инженерная логика против классической

Вид материала

Содержание

2.2. Алгоритм соседнего определения базы МОК.

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 20

2.2. Алгоритм соседнего определения базы МОК.

Алгоритм 1 требует раздельного размещения РОК и ЗОК. Приведение таблицы истинности к такому виду усложняет метод ОК.

Процесс минимизации методом ОК может быть существенно упрощен, если определение БМОК производить с использованием приводимого ниже алгоритма.

Алгоритм 2.

1. Присвоить индексу МОК значение 1, т.е. i := 1 .

2. Присвоить индексу РОК значение 1 , т.е. j := 1.

3. Взять РОК из исходной таблицы истинности и, сравнивая его со всеми ЗОК , определить переменные , по которым РОК может быть склеен с ЗОК. Эта совокупность переменных и будет базой МОК_i. Перейти к п.7.

4. Если РОК_j не имеет соседних ЗОК, то j := j + 1 и перейти к п.3. Если в таблице истинности нет ни одного РОК, соседнего хотя бы с одним ЗОК , то перейти к п.5.

5. Подсчитать по таблице истинности F₀ и F₁ для всех разрядов.

6. В качестве базы МОК_i(БМОК_i ) или дополнения к БМОК_i выбрать переменную с максимальной F₀ или F₁. Если F₀ = max, то переменная входит в БМОК_i нулём. Если F₁ = max , то переменная входит в БМОК_i единицей . Если несколько переменных имеют одинаковые оценочные (максимальные) функции , то выбрать в качестве БМОК_i ту переменную , у которой соответствующая запрещённая оценочная функция ( F₀^з или F₁^з ) имеет минимальное значение, в противном случае в качестве БМОК_i взять любую переменную с максимальной оценочной функцией F₀ или F₁ .

7. Выписать РОК и ЗОК , покрываемые базой МОК_i . Если БМОК_i не покрывает ни одного РОК или покрывает все ЗОК, то приравнять нулю оценочные функции F₀ и F₁ для данного разряда и перейти к п.6. Если покрываемых ЗОК нет , то перейти к п.9.

8. Подсчитать F₀ и F₁ для всех разрядов РОК и ЗОК , покрываемых данной базой, кроме разрядов (переменных) , образующих БМОК_i. Присоединить к БМОК_i переменную (дополнение к БМОК_i ) с максимальной оценочной функцией в соответствии с требованиями п.6. Считать полученный ОК новой базой МОК_i . Если новая БМОК_i покрывает столько же ЗОК, сколько и на предыдущем шаге, то приравнять нулю оценочные функции или дополнения к БМОК_i , отбросить присоединённую переменную и добавить к БМОК_i переменную с максимальной оценочной функцией в соответствии с положениями п.6, считать полученный ОК новой БМОК_i .Если БМОК_i покрывает хотя бы один ЗОК, перейти к п.7.

9. Принять в качестве МОК_i базу МОК_i .

10. Если все РОК из исходной таблицы истинности покрыты минимальными обобщёнными кодами, перейти к п.12.

11. Выписать из исходной таблицы истинности все ЗОК и те РОК , которые не покрыты минимальными обобщёнными кодами . Считать вновь полученную таблицу исходной таблицей истинности. Увеличить индекс МОК на единицу , т.е. i := i+1. Перейти к п.2.

12. Конец.

Задача 9.

Произвести минимизацию булевой функции , заданной таблицей.

№п/п	x₈x₇x₆x₅x₄x₃x₂x₁	y
1 2 3 4 5 6 7 8	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 1	1 1 1 1 1 1 1 1
1 2 3 4	0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 1 1 1 0 1 1 0 0 0 0 0 0 0 0 1 1 0	0 0 0 0

Решение.

1. По алгоритму 2 пп. 1-3 для РОК₂ находим соседний ЗОК, т.е. находим БМОК₁ = ---0----.

2. По алгоритму 2 пп. 7-9 находим

МОК₁ = ---0--0-

Так как МОК₁ покрывает все РОК , то в соответствии с п.10 алгоритма 2 получаем

y = x₅’x₂’

Сущность алгоритма 2 заключается в том , что отыскиваются в первую очередь « необходимые « МОК, т.е. МОК для тех РОК , развязывание которых с ЗОК максимально затруднено , так как они развязываются только по тем переменным , по которым возможно склеивание данного РОК со всеми ЗОК. Под развязыванием понимается процесс выявления тех переменных в РОК, которые не встречаются в ЗОК.

Задача 10.

Произвести минимизацию булевой функции , заданной таблицей.

№	x₆x₅x₄x₃x₂x₁	y
1 2 3 4 5 6	0 0 1 0 0 0 0 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 0 1 0 1 0 0 0 1 1 1 1 1 1	1 1 1 1 1 1
1 2 3 4 5 6	0 0 1 0 1 1 0 0 1 0 1 0 0 0 1 1 0 1 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 0 1	0 0 0 0 0 0

Решение .

1. По алгоритму 2 пп.1-3 для РОК₁ находим

БМОК₁ = ----0-

2. По алгоритму 2 пп.7, 8 строим таблицу.

1 2 5	0 0 1 0 0 0 0 0 1 0 0 1 1 0 1 0 0 0	1 1 1
	0 0 1 1 0 1 1 1 1 1 0 1	0 0

3. По алгоритму 2 п.8 из таблицы находим БМОК₁ = ---00-

4. По алгоритму 2 п.9

МОК₁ = БМОК₁ = ---00-

5. По алгоритму 2 для непокрытых РОК (для РОК₃) находим

БМОК₂ = -1----.

6. По алгоритму 2 пп.7, 8 , 11 строим таблицу.

3 4 6	0 1 1 0 1 1 0 1 1 1 1 0 1 1 1 1 1 1	1 1 1
	1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 0 1	0 0 0
	5 - 2 3 2 2 1 - 4 3 4 4	F₀ F₁

7. По алгоритму 2 п.9 находим МОК₂

МОК₂ = 01----

8. По алгоритму 2 пп.7, 8, 11 строим следующую таблицу .

1 1 1 1 1 1	1
0 0 1 0 1 1 0 0 1 0 1 0 0 0 1 1 0 1 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 0 1	0 0 0 0 0 0

9. По алгоритму 2 п.3 находим БМОК₃

БМОК₃ = ----1-

10. По алгоритму 2 пп. 7, 8, 11 строим таблицу.

1 1 1 1 1 1	1
0 0 1 0 1 1 0 0 1 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0	0 0 0 0
2 2 3 1 - 1 3 3 2 4 - 4	F₀ F₁

11. Из таблицы по алгоритму 2 п.8 находим

БМОК₃ = ----11

12. По алгоритму 2 пп. 7, 8 строим следующую таблицу.

1 1 1 1 1 1	1
0 0 1 0 1 1	0
0 0 1 0 - - 1 1 1 1 - -	F₀ F₁

13. По таблице 17 определяем

МОК₃ = -1--11

Таким образом ,

y = x₃’x₂’ + x₅x₂x₁ + x₆’x₅

На рисунке представлено решение задачи 10 с помощью карты Карно . Функция y представлена в виде МДНФ.

Из рисунка видно , что результаты минимизации по карте Карно и по методу обобщённых кодов совпадают.

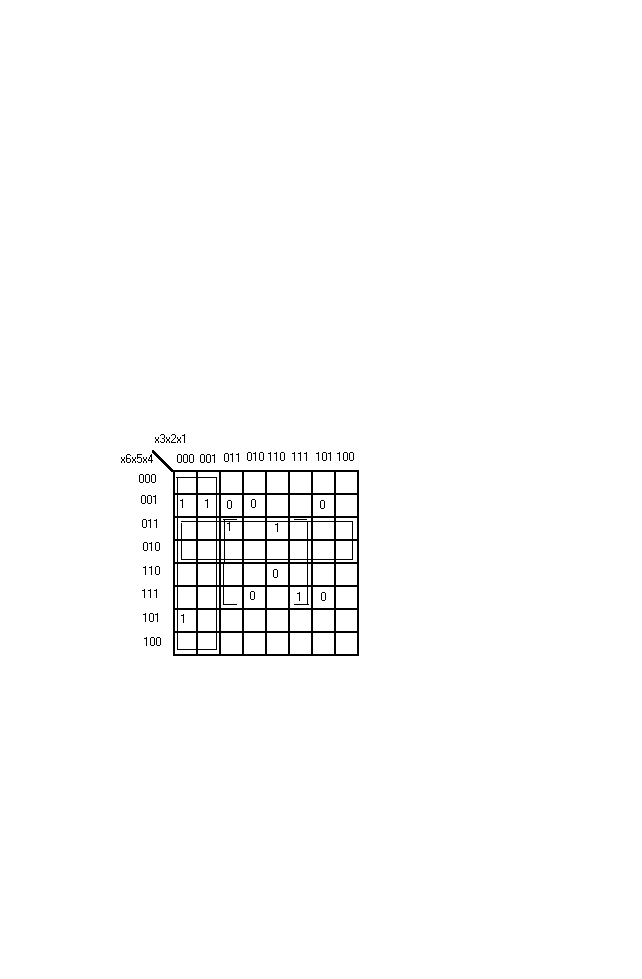
Карта Карно к задаче 10.

Задача 10а.

Произвести минимизацию логической функции, заданной таблицей истинности.

N%	x₈x₇x₆x₅x₄x₃x₂x₁	y
1 2 3 4 5 6 7	0 0 1 1 0 0 1 1 0 0 1 0 0 0 1 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 1 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 1 0	1 1 1 1 1 1 1
1 2 3 4 5	0 1 1 1 0 1 1 1 1 1 0 1 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 1 1 1 0	0 0 0 0 0
	9 8 3 7 7 8 5 5 3 4 9 5 5 4 7 7	F₀ F₁

Т.к. РОК₃ и ЗОК₁ являются соседними по x₇,то в качестве БМОК₁ выбираем х₇’,не обращая внимание на абсолютный максимум F₀ для х₈.БМОК₁ покрывает РОК₁ - РОК₅ и ЗОК₃,ЗОК₅.Подсчитаем оценочные функции для выбора дополнения к БМОК₁ и получения МОК₁.

N%	x₈x₇x₆x₅x₄x₃x₂x₁	y
1 2 3 4 5	0 0 1 1 0 0 1 1 0 0 1 0 0 0 1 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 1 0 1 1	1 1 1 1 1
3 5	0 0 0 1 1 1 1 0 1 0 1 0 1 1 1 0	0 0
	5 x 1 3 6 5 2 1 2 x 6 4 1 2 5 6	F₀ F₁

Дополнение х₄’ могло бы привести нас к МДНФ,поэтому мы выберем эквивалентное по оценочной функции дополнение х₁,чтобы убедиться в некоторых недостатках метода. В результате получим МОК₁ = x₇’x_1.Поскольку МОК₁ покрывает РОК с номерами 1,3 - 5,то стартовая таблица для синтеза БМОК₂ выглядит так:

N%	x₈x₇x₆x₅x₄x₃x₂x₁	y
2 6 7	0 0 1 0 0 0 1 0 0 1 1 0 1 1 0 1 0 1 1 1 1 1 1 0	1 1 1
1 2 3 4 5	0 1 1 1 0 1 1 1 1 1 0 1 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 1 1 1 0	0 0 0 0 0
	6 4 3 6 4 6 5 5 2 4 5 2 4 2 3 3	F₀ F₁

Исходя из этой таблицы получаем БМОК₂ = x₈’. Для нахождения МОК₂ строим следующую таблицу.

N%	x₈x₇x₆x₅x₄x₃x₂x₁	y
2 6 7	0 0 1 0 0 0 1 0 0 1 1 0 1 1 0 1 0 1 1 1 1 1 1 0	1 1 1
1 3	0 1 1 1 0 1 1 1 0 0 0 1 1 1 1 0	0 0
	х 2 1 4 2 3 3 3 х 3 4 1 3 2 2 2	F₀ F₁

Отсюда получаем МОК₂ = х₈’x₅’, который дополнительно покрывает РОК₂ и РОК₆. Найдём БМОК₃.

N%	x₈x₇x₆x₅x₄x₃x₂x₁	y
7	0 1 1 1 1 1 1 0	1
1 2 3 4 5	0 1 1 1 0 1 1 1 1 1 0 1 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 1 1 1 0	0 0 0 0 0
	4 3 3 4 3 5 4 4 2 3 3 2 3 1 2 2	F₀ F₁

F₀для х₃ имеет максимальное значение,но использовать x₃’ в качестве БМОК₃ нельзя,поскольку единственный РОК не имеет нуля в данном разряде. Принимаем БМОК₃ = x₈’. Строим очередную таблицу для синтеза последнего МОК.

N%	x₈x₇x₆x₅x₄x₃x₂x₁	y
7	0 1 1 1 1 1 1 0	1
1 3	0 1 1 1 0 1 1 1 0 0 0 1 1 1 1 0	0 0
	х 1 1 2 1 2 2 2 х 2 2 1 2 1 1 1	F₀ F₁

Blog

Инженерная логика против классической

Содержание

2.2. Алгоритм соседнего определения базы МОК.