Geum.ru

Геомеханическая оценка надежности оснований шахтных копров в системе «копер  фундамент  ствол (устье)  основание»

Вид материалаАвтореферат диссертации
3.3. Осадка основания башенного копра с фундаментом кольцевой формы
S устанавливается по формулам:S
Sм – осадка центра фундамента сооружения от моментных нагрузок; S
Рис. 5. Номограмма для определения безразмерных коэффициентов A, t
4. Оценка надежности оснований шахтных копров
Рис. 6. Расчетные схемы нагрузок на ствол (устье) в зоне влияния rc
Итоги детерминированного расчета для устья на глубине 20 м с толщиной крепи 0, 5 м
Таблица 7 Демонстрационные результаты моделирования крепи устья ствола
4.2. Оценка надежности несущей способности основания по фактору устойчивости
Первое отличие
Рис. 7. Схема построения поверхности скольжения
Второе отличие предлагаемого решения
H  глубина заложения фундамента; d
Третья отличительная особенность
Таблица 8 К оценке несущей способности системы «Копер  фундамент  ствол
Подобный материал:
1   2   3   4

3.3. Осадка основания башенного копра с фундаментом кольцевой формы


Оценка осадки является обязательным компонентом комплексного расчета оснований башенного копра. Осадка основания копра S устанавливается по формулам:


S = SG + Sм + Sи; SG(12)Wr(12)E1; Sмrt; Sиr2(12)(32R)1,

где SG – осадка центра фундамента сооружения от вертикальных нагрузок на основание; Sм – осадка центра фундамента сооружения от моментных нагрузок; Sи – осадка фундамента от искривления основания;  – коэффициент Пуассона грунта;  –давление на основание, равное частному от деления вертикальных нагрузок на площадь подошвы фундамента F; W – безразмерный коэффициент, определяемый в зависимости от ;  – отношения внутреннего радиуса кольца фундамента r1 к наружному r; Е – модуль общей деформации грунта; t – безразмерный коэффициент, определяемый по номограмме (см. рис. 5) в зависимости от выреза фундамента и отношения модуля упругости Еу к модулю общей деформации грунта Е, обозначенному К;  – крен копра; R  радиус искривления основания;  – расчетная осадка поверхности под центром фундамента от горных выработок.

Оценка надежности основания копра по осадке определяется по массиву случайных значений коэффициент запаса nз,iSн / Si, здесь Sн – предельно допустимая осадка башенного копра, составляющая 30 см согласно Руководству по расчету башенных копров угольных и рудных шахт, имеющему силу нормативного документа.

Особенности имитационного моделирования  генерация данных из номограммы, приведенной на рис. 5; распределение модулей деформации, упругости, крена по закону Грамма-Шарлье, коэффициента Пуассона по нормальному закону.



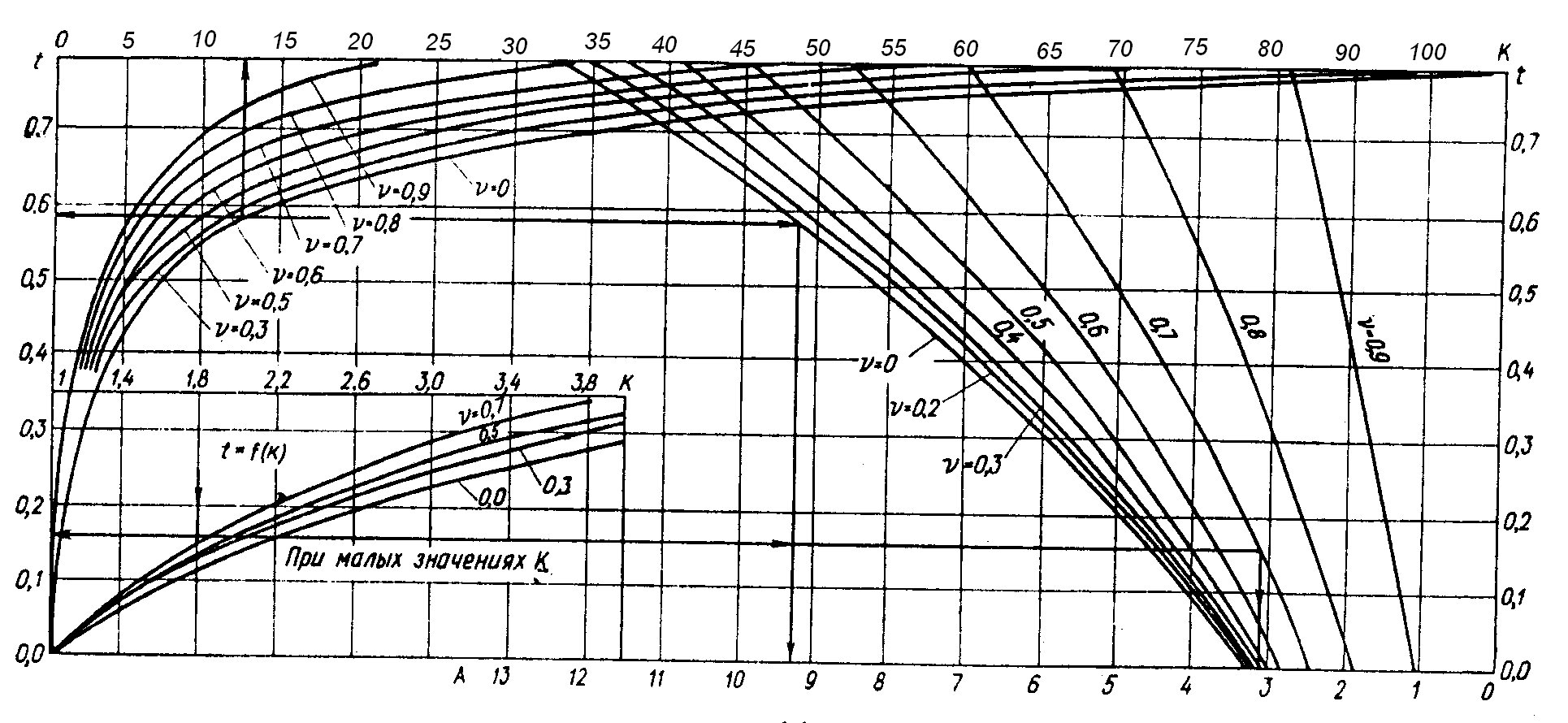
Рис. 5. Номограмма для определения безразмерных коэффициентов A, t


В условиях G  0,1 МН, r1  5, м r  9,5 м получены следующие детерминированные показатели: SG  0,2447763 м; Sм  6,031837E-03 м; Sи  0,1002604 м; S  0,3510685 м; nз  0,855. Поскольку осадка основания S превышает допустимую S > Sн, а nз < 1, следует увеличить размеры фундамента (радиус до 12,5 м) или произвести подготовку грунта (уплотнение грунта до модуля деформации Е  3000 т/м2). Детерминированные значения осадок и коэффициентов запаса в этих случаях составят S  0,2953661 м, nз  1,016 и S  0,2657927 м, nз 1,129. Соответственно, надежность вариантов, установленная имитационным методом, составит 0,97 и 1,00.


Реализация задач различного содержания в разнообразных геомеханических ситуациях по оценке надежности оснований в системе «Копер  фундамент  ствол (устье)  основание», в т. ч. задач, рассмотренных в автореферате, подтверждает широкие возможности, целесообразность и универсальность метода Монте-Карло. На основании выполненных исследований в совокупности с материалами, полученными во второй главе, сформулировано первое научное положение, фиксирующее отличительные особенности общего подхода к имитационному моделированию оснований шахтных копров.


4. Оценка надежности оснований шахтных копров

в сложных геомеханических ситуациях


4.1. Оценка асимметричного воздействия нагрузок на горную крепь от копра,

окружающих зданий и сооружений. Расчет крепи в условиях

неравнокомпонентного поля напряжений


Расчет крепи вертикальных стволов глубиной до 50 м или устьев стволов регламентируется действующим СНиП II-94-80 «Подземные горные выработки», предусматривающим определение нормативных и расчетных нагрузок на крепь с учетом пригрузки от зданий и сооружений, расположенных вблизи ствола, а также выбор материала и установление размеров крепи. Существующая методика дополняется имитационным анализом надежности системы «Копер  фундамент  ствол (устье)  основание» по фактору прочности крепи устья ствола.

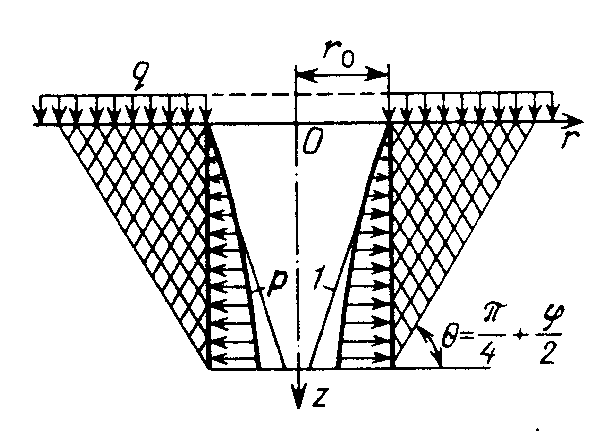
В результате имитационного моделирования по схемам рис. 6, а, б, в установлены границы зоны влияния от копра, сооружений и зданий, размещаемых вблизи ствола (устья) с заданной надежностью, определена надежность осесимметричных нагрузок на горную крепь от вмещающего массива и асимметричных нагрузок, передаваемых смежными фундаментами. Полученные результаты свидетельствуют об универсальности метода Монте-Карло, как средства полноценной оценки надежности системы «Копер  фундамент  ствол (устье)  основание». Вместе с тем действующая методика оценки воздействий на крепь, предусматривающая замену односторонней нагрузки (схема рис. 6, б) осесимметричной (схема рис. 6, в), нуждается в корректировке. Дело в том, что асимметричное нагружение ствола или устья ствола в зоне влияния шахтного копра, смежных зданий и сооружений сопровождается формированием неравнокомпонентного поля напряжений во вмещающем массиве.


а
б











2

3

в
г










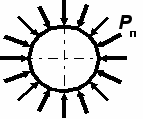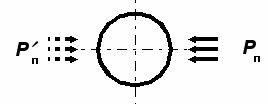Рис. 6. Расчетные схемы нагрузок на ствол (устье) в зоне влияния rc:

а  осесимметричное нагружение от вмещающего массива (В. Г. Березанцев); б  одностороннее нагружение PП от сооружений в зоне влияния (от фундаментов 1, 3 укосин копра и 2  здания подъемной машины); в  осесимметричное нагружение односторонней нагрузкой PП; г асимметричное нагружение


В этой ситуации для оценки надежности крепи стволов глубиной до 50 м и устьев вертикальных стволов целесообразно реализовать известную методику, разработанную проф. Н. С. Булычевым. Расчет выполняется следующим образом: 1  находятся компоненты напряженного состояния по направлению максимальной и минимальной нагрузки; 2  устанавливаются коэффициенты передачи внешних нагрузок от грунтового массива на горную крепь; 3  определяются напряжения на контактах крепи; 4  вычисляются нормальные тангенциальные напряжения на внутреннем и внешнем контурах сечения крепи; 5  находятся изгибающие моменты, возникающие в крепи; 6  определяются продольные силы; 7  устанавливаются предельные значения продольных сил; 8  вычисляются коэффициенты запаса.

Особенности имитационного моделирования: исходные компоненты поля напряжения устанавливаются по нагрузкам, воздействующим на горную на крепь, в соответствии с указаниями СНиП II-94-80; пять случайных характеристик  модули упругости и коэффициенты Пуассона грунта и крепи, удельный вес грунта генерируются по нормальному распределению, угол внутреннего трения  по распределению Грамма-Шарлье; вычисляются 20 массивов случайных чисел, 19-й и 20-й массивы коэффициентов запаса по направлениям максимальных и минимальных напряжений; надежность оценивается по массивам случайных значений коэффициентов запаса как вероятность P(nз < 1).


Итоги детерминированного расчета для устья на глубине 20 м с толщиной крепи 0, 5 м:


ДОПОЛНИТЕЛЬНАЯ НАГРУЗКА ОТ ЗДАНИЙ НА КРЕПЬ УСТЬЯ СТВОЛА, КПА, P = 10.47796; РАСЧЕТНАЯ ГОРИЗОНТАЛЬНАЯ НАГРУЗКА 1, MПА, N1= .228352; РАСЧЕТНАЯ ГОРИЗОНТАЛЬНАЯ НАГРУЗКА 2, MПА, N2= .2051957; КОЭФФИЦИЕНТЫ ПЕРЕДАЧИ НАГРУЗОК: KZ0= 1.331025 KZ11=-.6288911 KZ21=-2.346916; НАПРЯЖЕНИЯ НА КОНТАКТАХ КРЕПИ С МАССИВОМ: P0= .206094 P2=-4.680897E-03 Q2=-1.746832E-02; НОРМАЛЬНЫЕ ТАНГЕНЦИАЛЬНЫЕ НАПРЯЖЕНИЯ НА ВНУТРЕННЕМ И ВНЕШНЕМ КОНТУРЕ КРЕПИ: SGVN(I)= 2.060702 SGNA(I)= 2.564198 SGVN(I)= 3.045578 SGNA(I)= 2.006238; ИЗГИБАЮЩИЕ МОМЕНТЫ, ПРОДОЛЬНЫЕ СИЛЫ, ЭКСЦЕНТРИСИТЕТЫ, ПРЕДЕЛЬНЫЕ (ДОПУСТИМЫЕ) ПРОДОЛЬНЫЕ СИЛЫ: MM( 1 )=-1.363636E-02 NM( 1 )= 1.503093 E0( 1 )=-9.072202E-03 NU( 1 )= 3.51617 MM( 2 )= 2.814881E-02 NM( 2 )= 1.64184 E0( 2 )= 1.714467E-02 NU( 2 )= 3.160351; КОЭФФИЦИЕНТЫ ЗАПАСА: NZ1= 2.33929 NZ2= 1.924883.

В табл. 7 в качестве примера приведены завершающие результаты имитационного моделирования  массивы коэффициентов запаса в направлениях действия главных напряжений.

Таблица 7

Демонстрационные результаты моделирования крепи устья ствола



nз по направлению максимального напряжения
nз по направлению минимального напряжения

0,943 1,215 1,230 1,233 1,386 1,396 1,408 1,410 1,415

1,428 1,543 1,544 1,557 1,568 1,575 1,629 1,644 1,686

1,689 1,692 1,698 1,703 1,739 1,742 1,789 1,804 1,807

1,809 1,815 1,817 1,844 1,861 1,874 1,878 1,888 1,888

1,899 1,905 1,906 1,909 1,911 1,919 1,962 1,978 1,989

2,008 2,033 2,057 2,060 2,079 2,098 2,110 2,110 2,127

2,135 2,178 2,187 2,206 2,213 2,234 2,250 2,254 2,313

2,330 2,388 2,400 2,410 2,416 2,431 2,447 2,450 2,473

2,496 2,502 2,531 2,557 2,585 2,586 2,595 2,619 2,647

2,651 2,657 2,666 2,673 2,678 2,690 2,692 2,698 2,699

2,699 2,747 2,755 2,769 2,775 2,795 2,796 2,801 2,830

2,954 2,973 2,980 2,997 3,021 3,124 3,136 3,225 3,250

3,330 3,358 3,362 3,367 3,430 3,462 3,584 3,594 3,639

3,652 3,684 3,709 3,740 3,963 4,020 4,023 4,351 4,484

4,539 4,635 4,792 4,803 4,893 4,944 5,389 5,543 5,586
0,672 0,906 0,957 0,982 1,032 1,052 1,058 1,071 1,098

1,140 1,141 1,142 1,162 1,206 1,206 1,254 1,258 1,274

1,282 1,310 1,315 1,329 1,347 1,353 1,374 1,385 1,388

1,396 1,431 1,457 1,461 1,464 1,475 1,485 1,506 1,509

1,523 1,524 1,524 1,548 1,567 1,570 1,577 1,591 1,599

1,606 1,626 1,637 1,643 1,691 1,700 1,704 1,710 1,711

1,743 1,760 1,802 1,820 1,820 1,825 1,832 1,878 1,894

1,898 1,907 1,915 1,925 1,935 1,936 1,948 1,956 2,020

2,063 2,085 2,093 2,107 2,107 2,112 2,119 2,141 2,142

2,160 2,161 2,201 2,202 2,206 2,210 2,220 2,224 2,247

2,286 2,292 2,301 2,312 2,325 2,363 2,384 2,387 2,398

2,414 2,419 2,462 2,476 2,502 2,523 2,542 2,580 2,643

2,748 2,769 2,829 2,872 2,904 2,909 3,037 3,055 3,093

3,104 3,120 3,167 3,170 3,245 3,407 3,484 3,792 3,871

3,982 4,130 4,260 4,261 4,309 4,598 4,717 4,970 5,075

Надежность 0,9925926
Надежность 0,9703704


4.2. Оценка надежности несущей способности основания по фактору устойчивости


Методика оценки надежности несущей способности основания по фактору устойчивости, включая основания, расположенные вблизи откосов и неоднородные основания, в сравнении с известными графо-аналитическими методами, рекомендуемыми СНиП 2.02.01–83*, характеризуется тремя отличительными особенностями.

Первое отличие состоит в аналитическом задании поверхности скольжения двумя круглоцилиндрическими поверхностями  биарками, имеющими общую производную в точке касания (рис. 7). Такой прием позволяет аналитически задавать сколь угодно большое семейство поверхностей скольжения, обеспечив постоянство углов входа и выхода в точках A и D криволинейного участка поверхности, равных, по В. В. Соколовскому, 45  /2, здесь   угол внутреннего трения грунта.




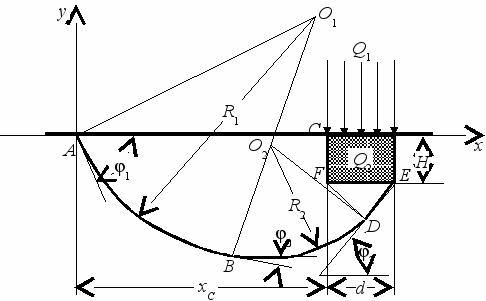
Рис. 7. Схема построения поверхности скольжения


Параметры «биарков» (радиусы сопряженных дуг R1 и R2, координаты центров вращения xO1, yO1, xO2, yO2, координаты xS, yS точки SB сопряжения двух дуг) в ситуациях, показанных на рис. 3.3, устанавливаются по формулам:


;

;
,

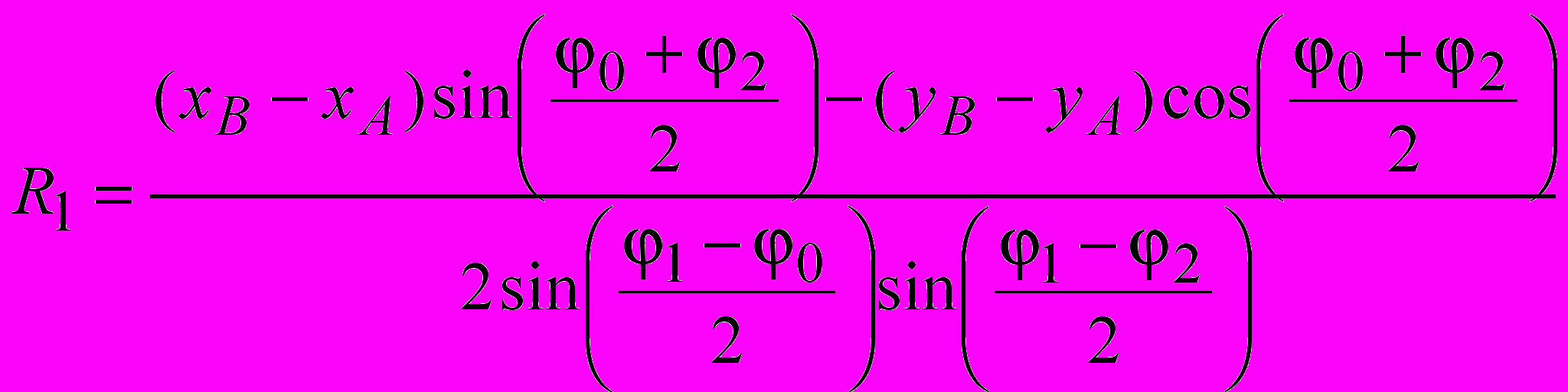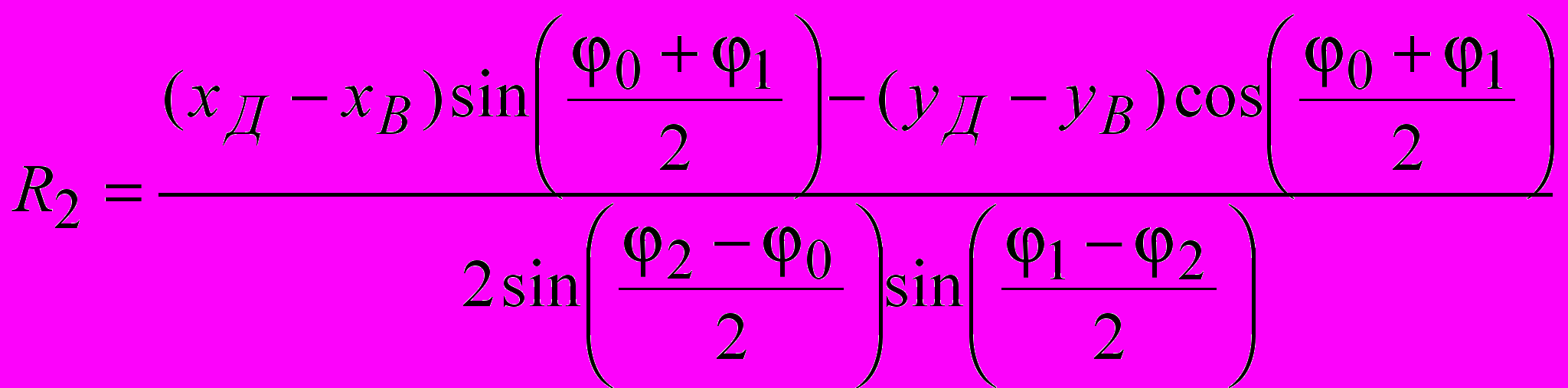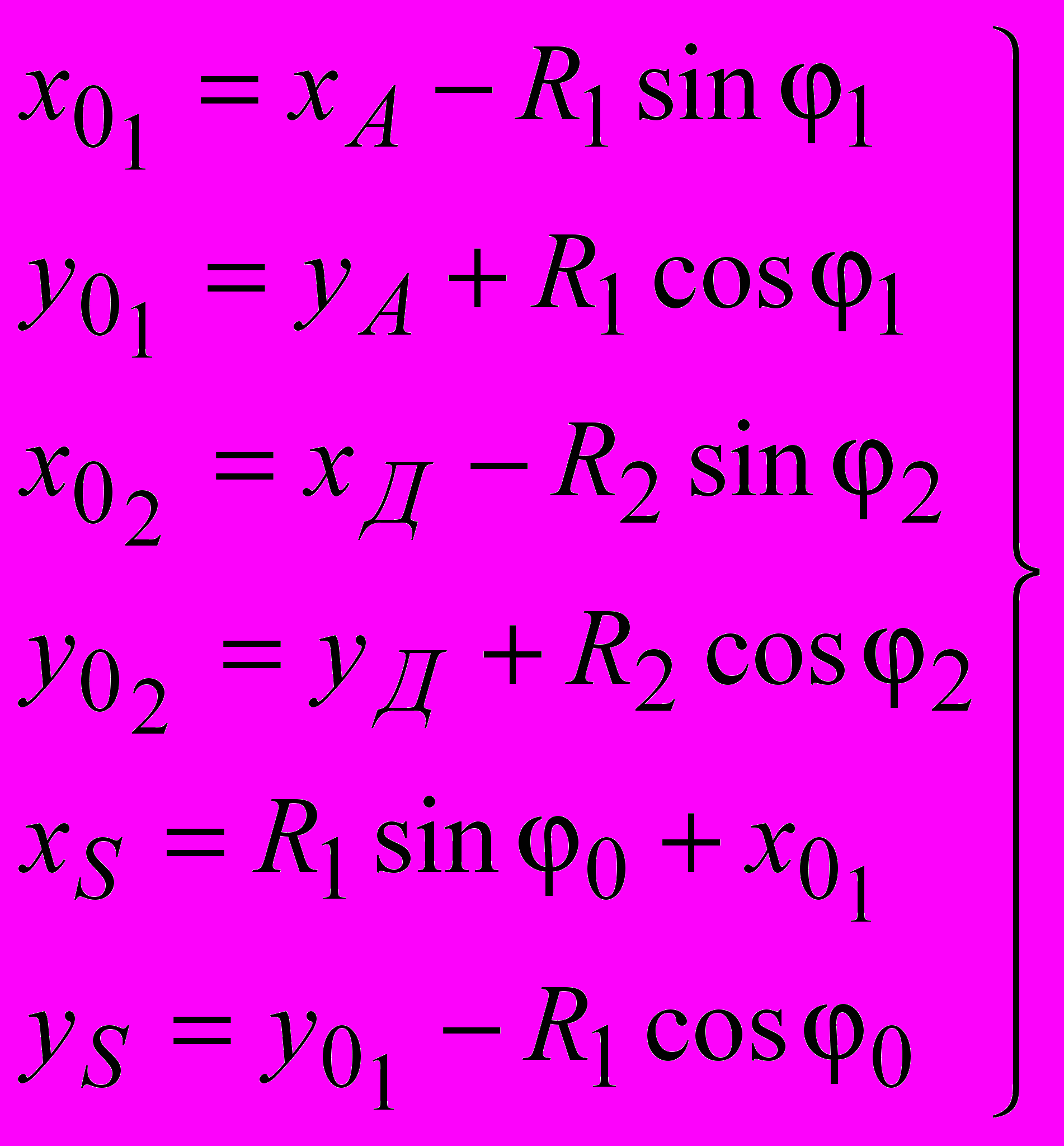где 1  A  – 45  /2; 2  D  45  /2; xA, yA, xD, yD – координаты начальной и конечной точек криволинейного участка поверхности скольжения;  – угол наклона откоса; 0 – угол наклона радиуса-сопряжения в точке касания двух дуг 0  (2 – 1) n–1; n – задаваемое число «биарков» в «пучке» поверхностей скольжения.

Второе отличие предлагаемого решения предусматривает замену традиционной графической процедуры разделения призмы выпирания (или скольжения) на отсеки вычислением определенных интегралов по характерным участкам поверхности скольжения. Коэффициенты запаса устойчивости основания в этом случае устанавливаются по формуле


m1 m2 m1

nз  ( tg i Ni   Cj LjG) ( TiK)–1,

i1 j1 i1


где nз – коэффициент запаса устойчивости; Ni – интеграл нормальной составляющей нагрузки по поверхности скольжения; Cj – сцепление; Lj – интеграл длины поверхности скольжения; Ti – интеграл касательной составляющей нагрузки по поверхности скольжения; m1, m2 – величины, характеризующие особенности расположения поверхностей скольжения и условия залегания грунтов; G  удерживающая составляющая нагрузки от копра и фундамента; K  сдвигающая составляющая нагрузки от копра и фундамента;




m1

 tg i Ni

i1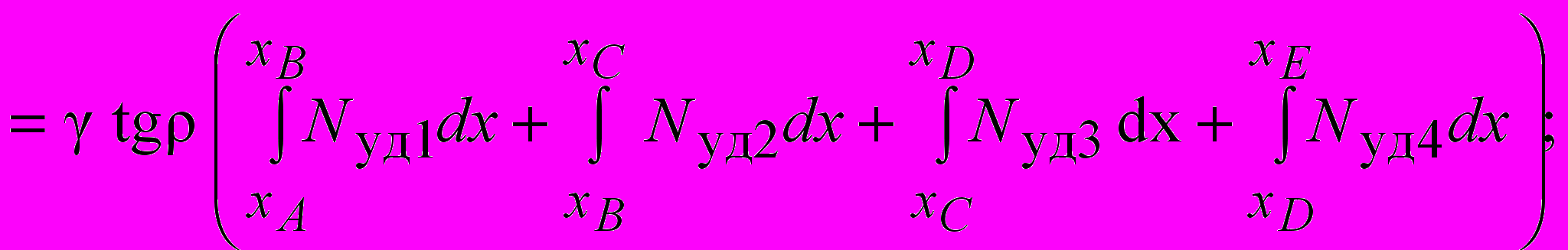












m2  cj Lj i1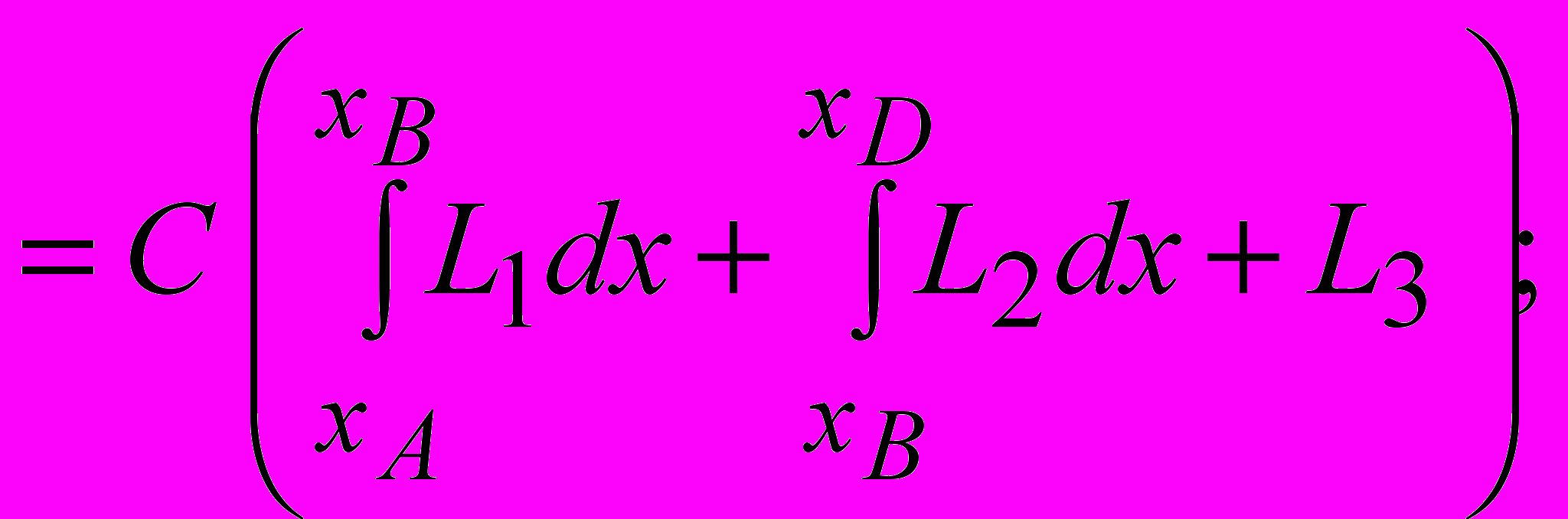
















m1Ti i1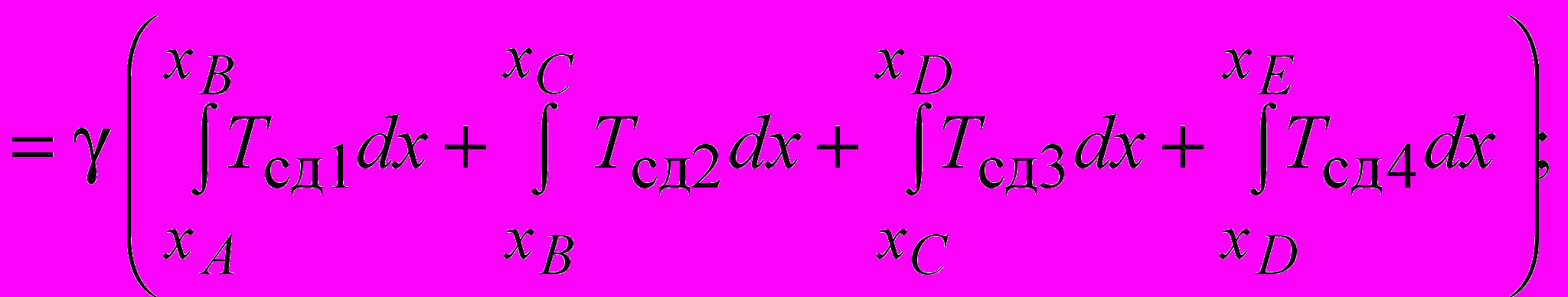




















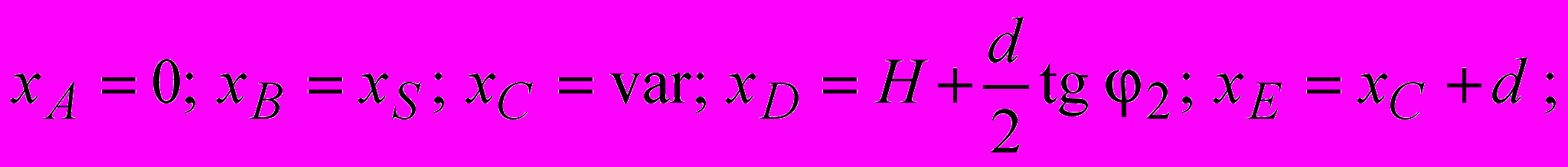
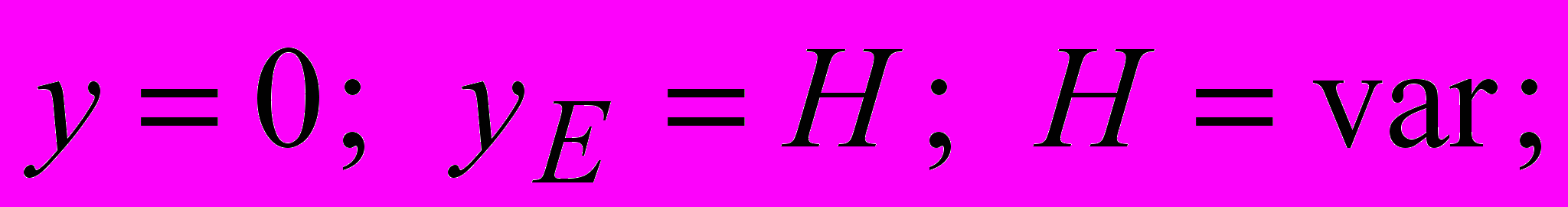
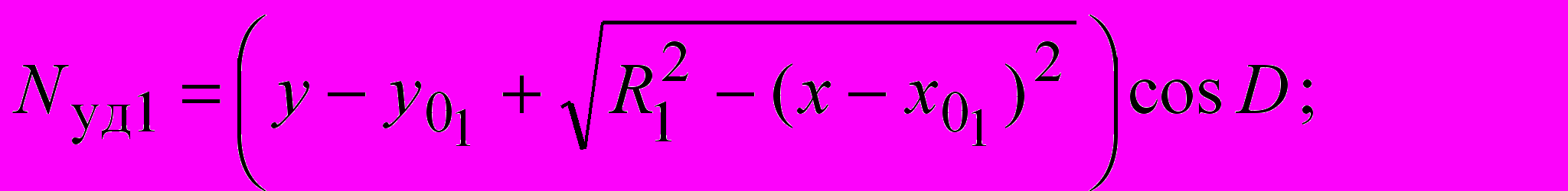
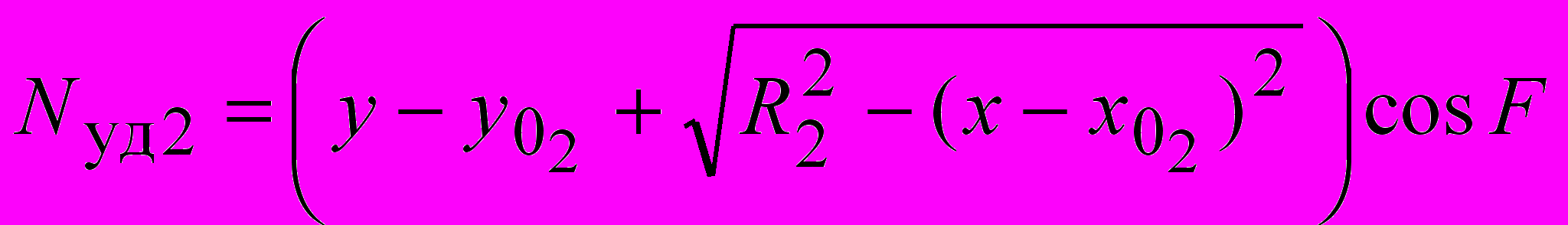
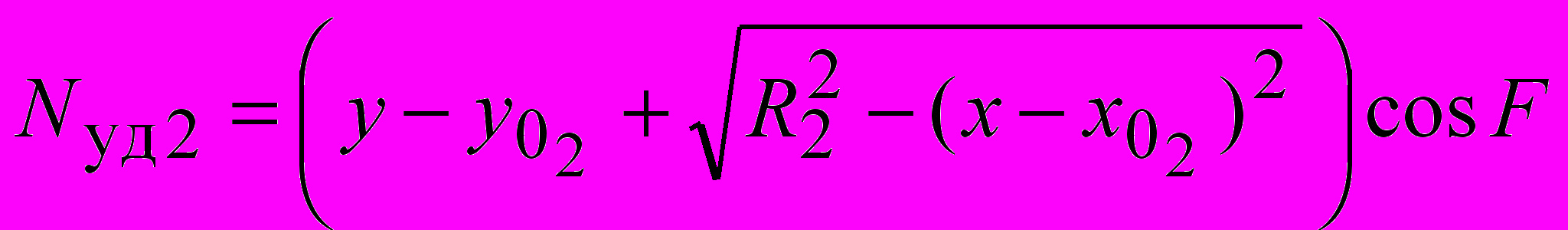
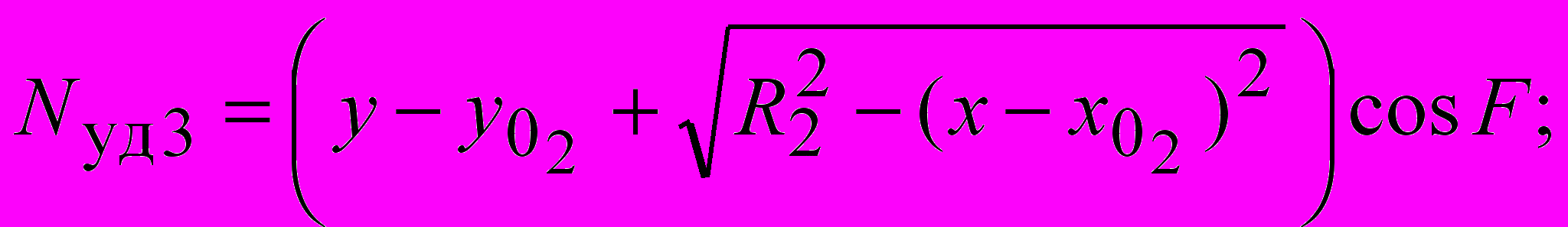
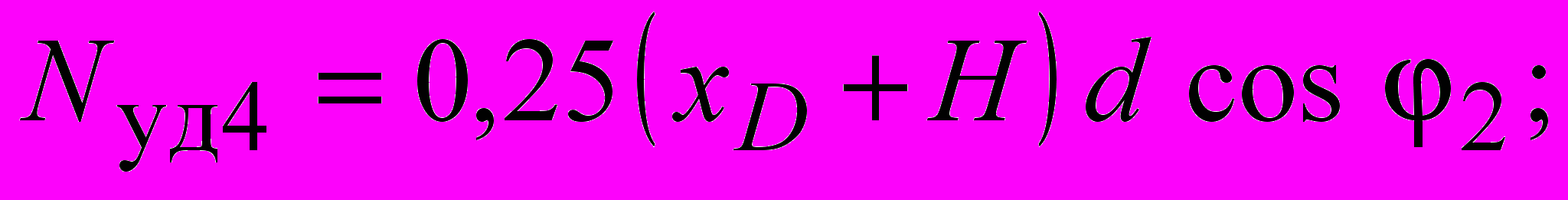
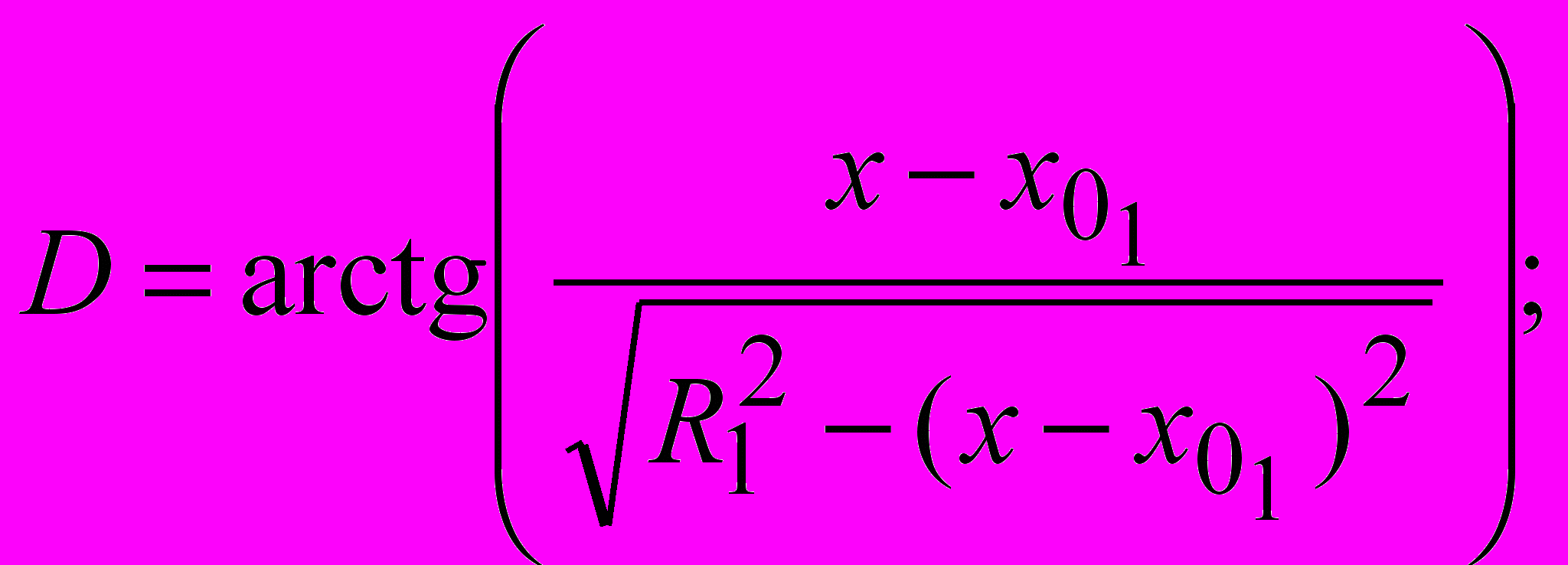
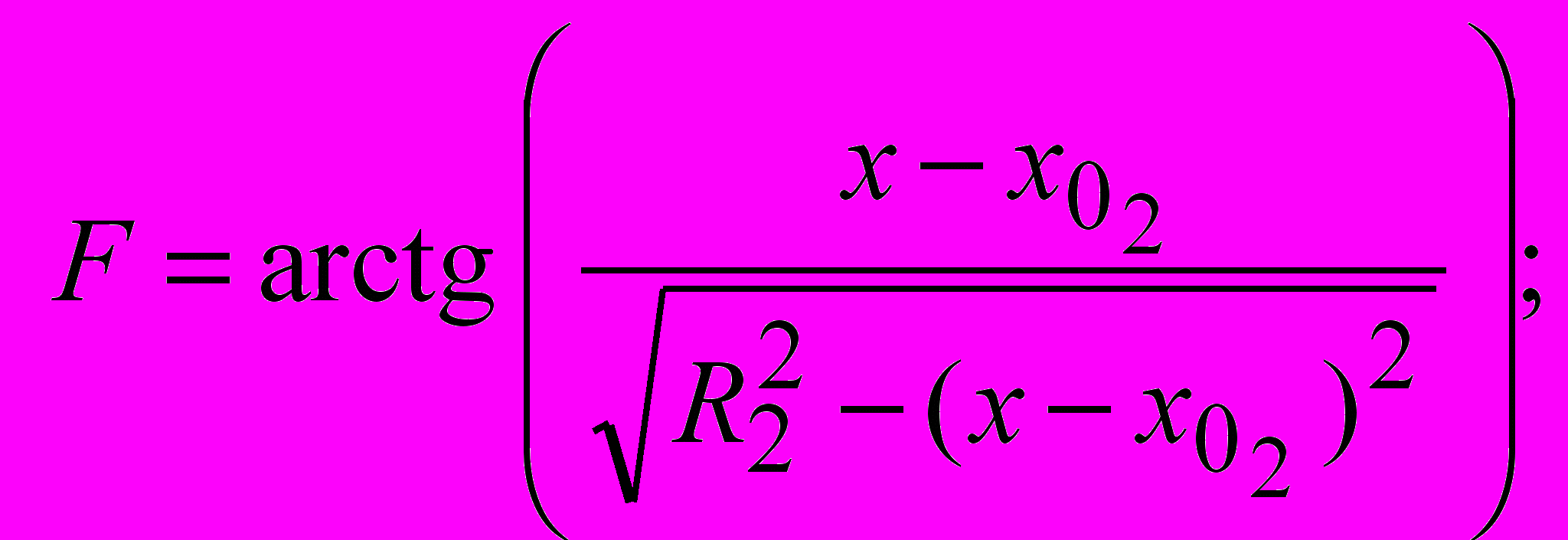
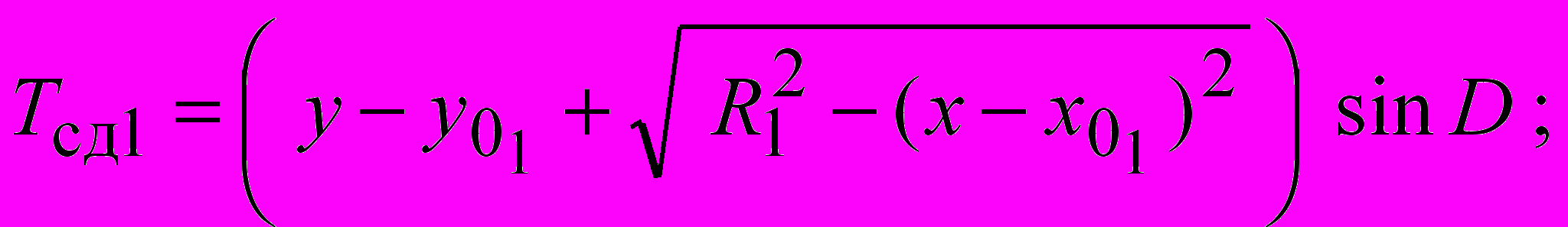
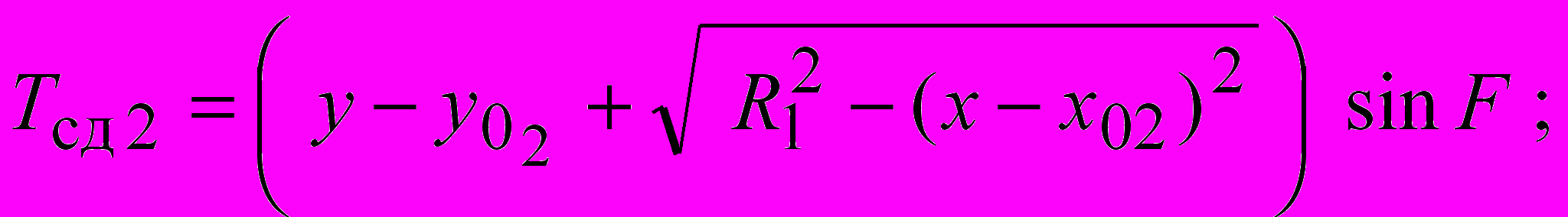
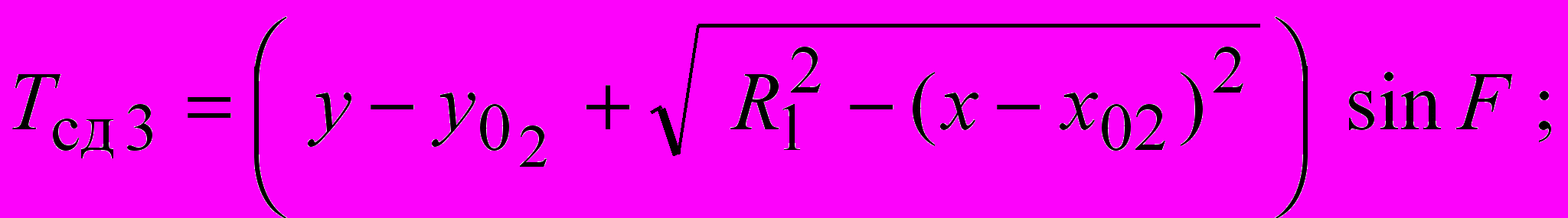
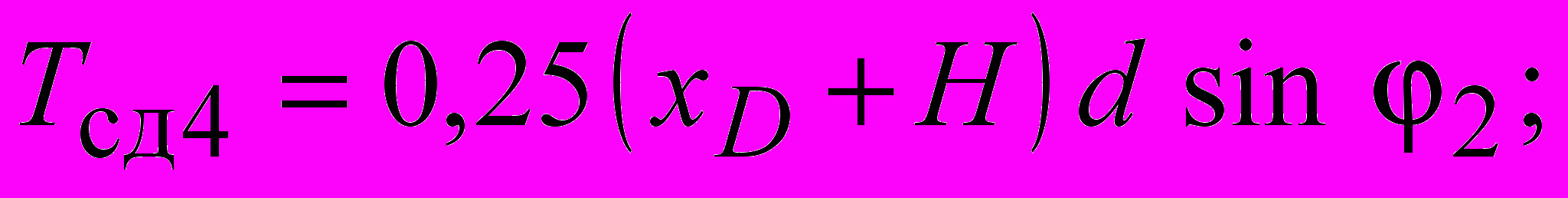
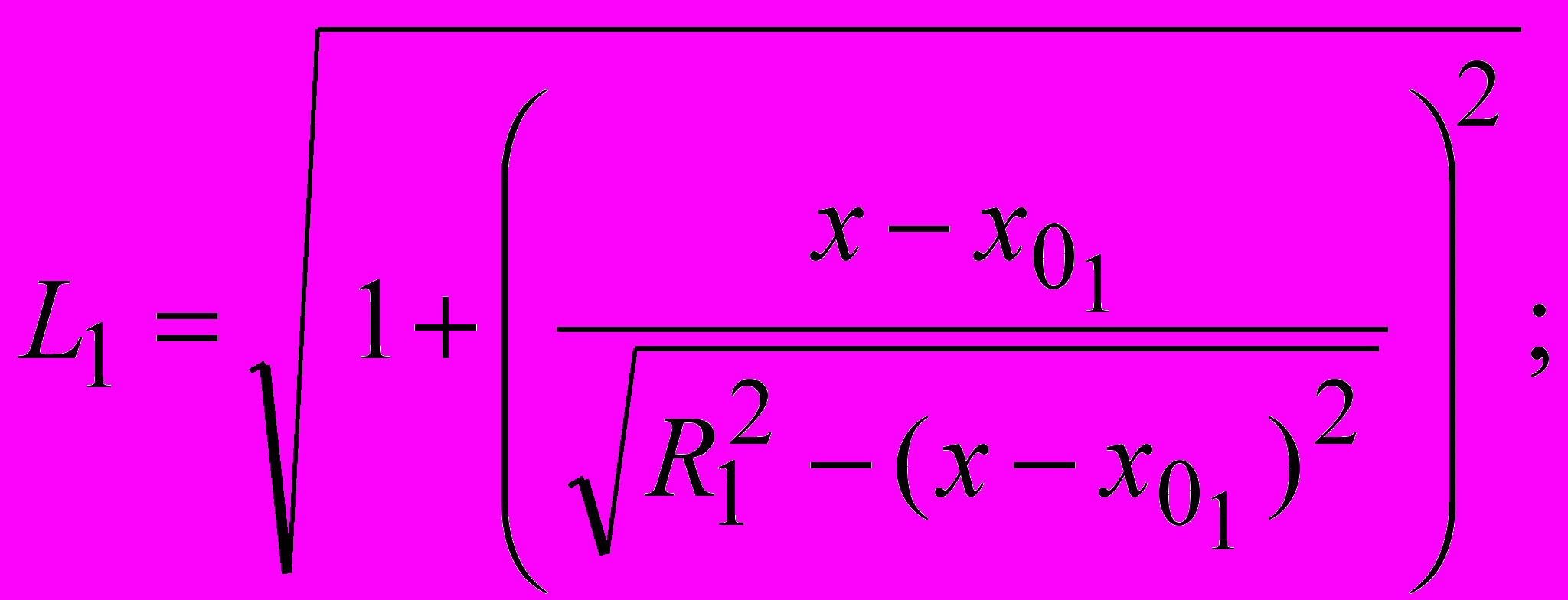
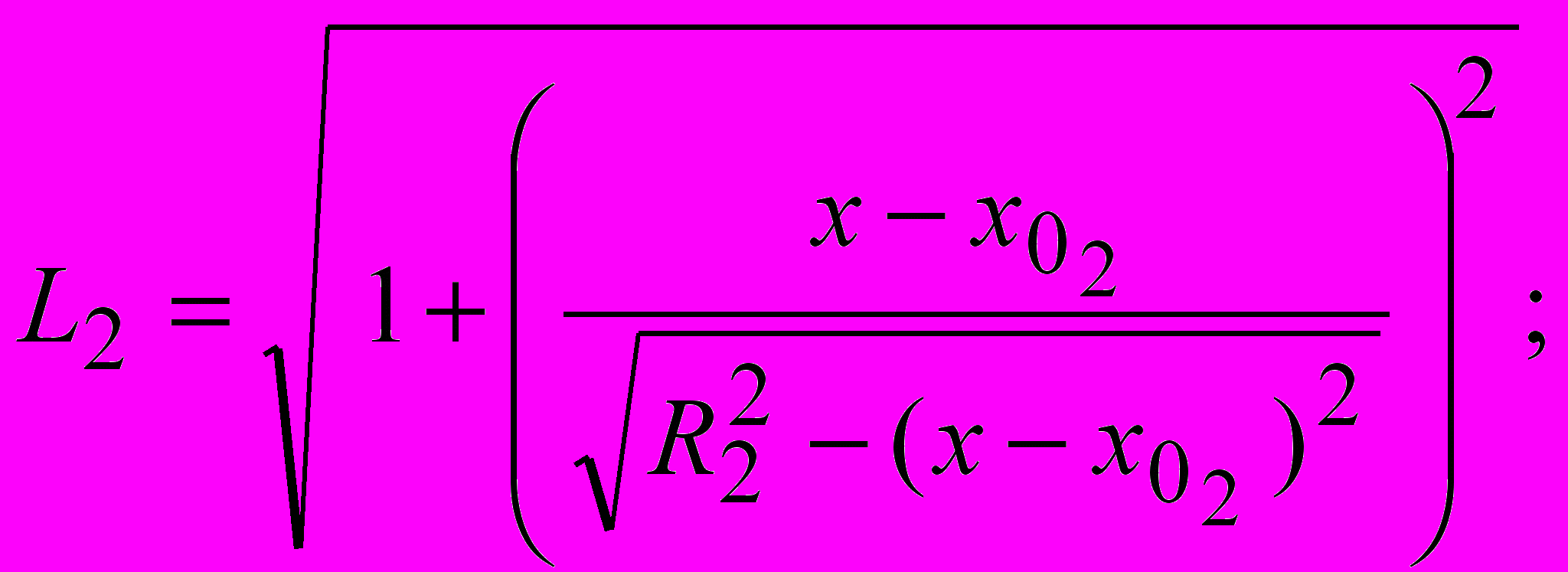
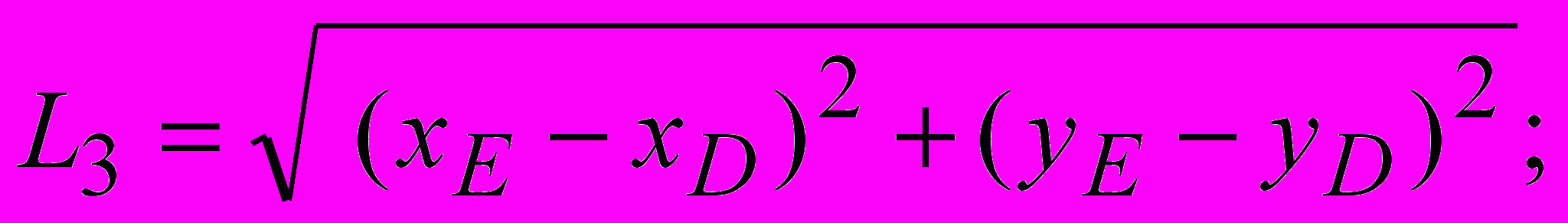
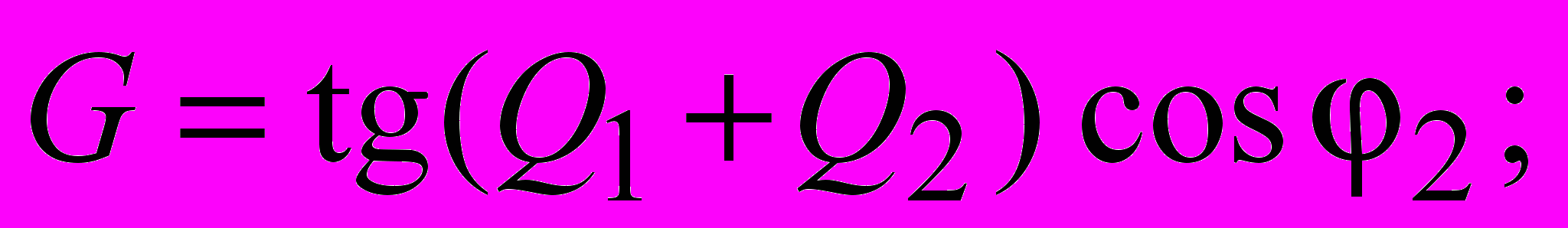
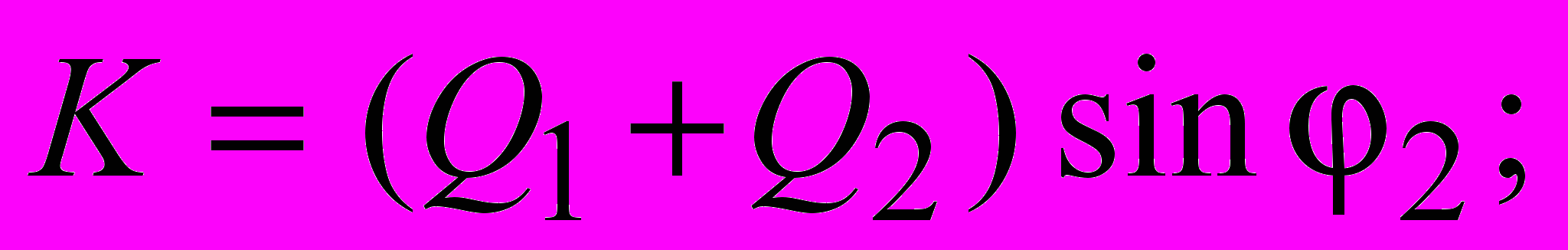
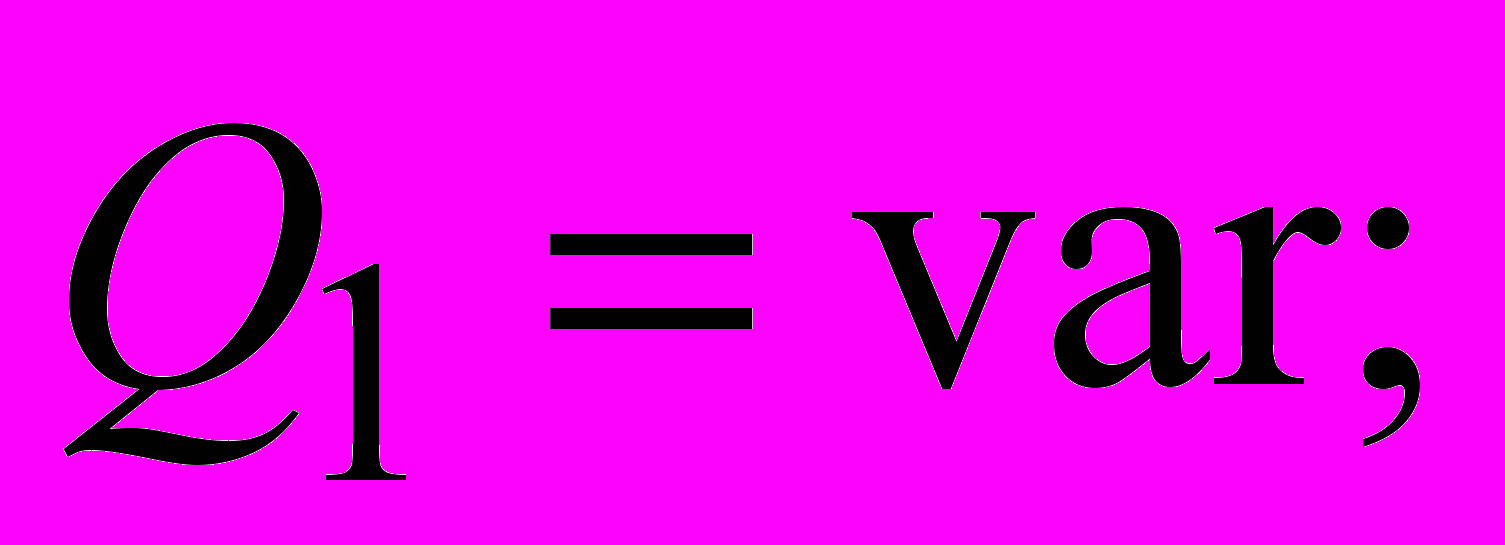
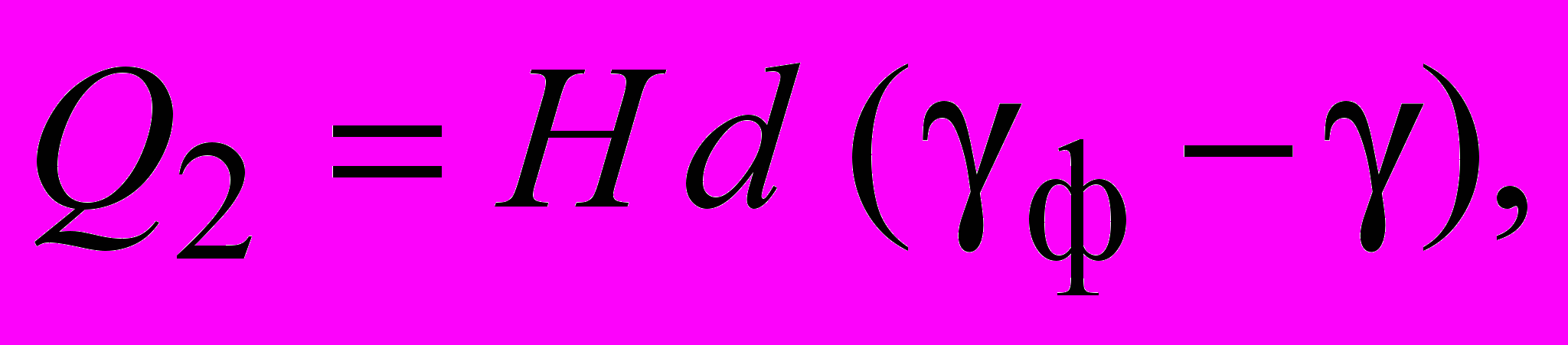
где   удельный вес грунта; H  глубина заложения фундамента; d  ширина фундамента; ф  удельный вес материала фундамента; Q1  нагрузка от шахтного копра и др., передаваемая через фундамент на основание; Q2  нагрузка от собственного веса фундамента, за вычетом веса грунта, замещенного фундаментом.

Третья отличительная особенность  собственно расчет надежности основания по фактору устойчивости, реализующий метод Монте-Карло: 1  положение пучка из пяти биарков задается варьируемой координатой xC; 2  для каждого биарка вычисляются коэффициент запаса устойчивости и записывается в память ЭВМ; 3  последовательно с принятым шагом  xC задаются положения других пучков семейства поверхностей скольжения с выполнением операций п. 2; 4  по завершении цикла операций пп. 1, 2, 3 находится минимальный коэффициент запаса устойчивости и фиксируются параметр xC min, определяющий положение наиболее опасной призмы выпирания; 5  при фиксированном значении xC min выполняется имитационное моделирование; 6  если полученные показатели не устраивают пользователя, изменяются глубина заложения или размеры фундамента и расчет надежности повторяется.

Особенность моделирования  многократное обращение к подпрограмме численного вычисления определенных интегралов. В табл. 8 приведены результаты детерминированных расчетов

Таблица 8

К оценке несущей способности системы «Копер  фундамент  ствол

(устье)  основание» по фактору устойчивости


xC, м
Номер биарка
Параметры биарка
nз

R1, м
x01, м
y01, м
R2, м
x02, м
y02, м

1
2
3
4
5
6
7
8
9

30
1
117,7
66,8
96,9
12,5
21,3
2,00
2,880

2
69,2
39,3
57,0
10,9
22,6
1,1
2,836

3
52,9
30,1
43,6
9,0
24,2
0,0
2,760

4
44,7
25,4
36,8
6,5
26,2
 1,4
2,658

5
39,7
22,5
32,7
3,0
29,0
 3,4
2,551

25
6
106,2
60,3
87,4
9,7
18,6
0,4
2,377

7
61,8
35,1
50,8
8,3
19,7
0,4
2,338

25
8
46,8
26,6
38,5
6,5
21,2
 1,4
2,279

9
39,3
22,3
32,3
4,2
23,1
2,7
2,206

10
34,7
19,7
28,5
1,1
25,6
 4,5
2,153

20
11
94,7
53,6
78,0
7,0
15,8
 1,2
1,929

12
54,3
30,8
44,7
5,7
16,9
 1,9
1,892

13
40,7
23,1
33,5
4,0
18,2
 2,8
1,851

14
30,8
19,2
27,8
2,0
19,9
 4,0
1,812

Окончание таблицы 8


1
2
3
4
5
6
7
8
9

15
15
83,2
47,2
68,5
4,2
13,1
 2,7
1,520

16
46,8
26,6
38,5
3,0
14,0
 3,4
1,499

17
34,6
19,6
28,5
1,6
15,2
 4,2
1,484

12,5
18
77,4
44,0
63,7
2,8
11,7
 3,5
1,338

19
43,1
24,5
35,5
1,7
12,6
 4,15
1,328

20
31,5
17,9
25,9
0,3
13,7
 4,9
1,333

10
21
71,7
40,7
10,3
1,4
59,0
4,3
1,177

22
39,3
22,5
11,2
0,4
32,4
 4,9
1,187

7,5
23
65,9
37,4
54,3
0,07
8,9
 5,1
1,049