Геомеханическая оценка надежности оснований шахтных копров в системе «копер  фундамент  ствол (устье)  основание»

Вид материала

Автореферат диссертации

Содержание Рис. 1. Гистограммы распределений характеристик грунтов  функций Rу  генерируемое случайное число; R 3. Оценка надежности оснований в системе 3.1. Несущая способность основания Таблица 5 Вертикальная составляющая силы предельного сопротивления основания 3.2. Предельное (критическое) давление на основание Таблица 6 Исходные данные. Отсортированные демонстрационные результаты

Подобный материал:

• Интервальный метод оценки надежности подстанций, 115.06kb.
• Секция краеведения и туризма Сочинского отдела Русского географического общества Сочинский, 471.56kb.
• Из опыта работы. Урок – практикум в системе модулього обучения, 103.87kb.
• Фактор надежности инженерно-технической службы, 41.32kb.
• Оптимизация надежности, 190.04kb.
• Программа дисциплины Оценка надежности информационных систем для направления 080500., 381.54kb.
• 4. Артериальный (боталлов) проток: а) функционирует в пренатальном онтогенезе; б) соединяет, 341.31kb.
• Вопросы для подготовки к экзамену по дисциплине «Теория надежности», 8-й семестр, 2011, 20.46kb.
• Использование корреляционных зависимостей при прогнозировании числа вторичных дефектов, 17.41kb.
• Фундаменты гражданских и промышленных зданий, 45.28kb.

Окончание таблицы 3

	1	2
	Формирование вариационного ряда H(i)	H(1) = 3 H(2) = 5 H(3) 6 H(4)  7 H(5) = 10 H(6) = 14 H(7)  17 H(8) = 18 H(9) = 20 H(10) = 22 H(11) = 36 H(12) = 39 H(13) = 40 H(14) = 48 H(15) = 49 H(16) = 52
	Ранжирование вариационного ряда	R(1) = 1 R(2) = 2 R(3) = 3 R(4) = 4 R(5) = 5 R(6) = 6 R(7) = 7 R(8) = 8 R(9) = 9 R(10) = 10 R(11) = 11 R(12) = 12 R(13) = 13 R(14) = 14 R(15) = 15 R(16) = 16
	Метка второй выборки	3,0001 5,0001 6,0001 10,0001 17,0001 18,0001 20,0001 39,0001
	Формирование вариационного ряда E(i) с метками второй выборки	E(1) = 3,0001 E(2) = 5,0001 E(3) = 6,0001 E(4) = 7 E(5) = 10,0001 E(6) = 14 E(7) = 17,0001 E(8) = 18,0001 E(9) = 20,0001 E(10) = 22 E(11) = 36 E(12) = 39,0001 E(13) = 40 E(14) = 48 E(15) = 49 E(16) = 52
	Определение суммы рангов первой выборки по условию: E(i) – H(i)  0	m R1(i1) = 89 i1=1
	Определение суммы рангов второй выборки по условию: E(i) – H(i) > 0	n R2(i2) = 43 i2=1
	U-cтатистики	U1mn0,5m(m1)–R1= 11, U 2=mn0,5n(n1)–R153
	U-крит.13 при   0,025 N, так как 11 < 13, гипотеза отвергается
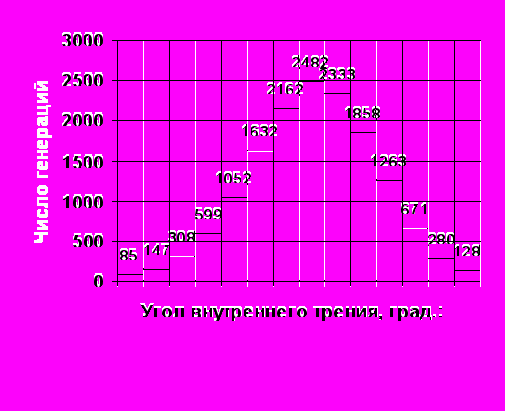Среднее выборочное 23,75; стандарт 3,20; асимметрия -0,137; эксцесс -0,039 Рис. 1. Гистограммы распределений характеристик грунтов  функций случайных аргументов, полученные методом Монте-Карло		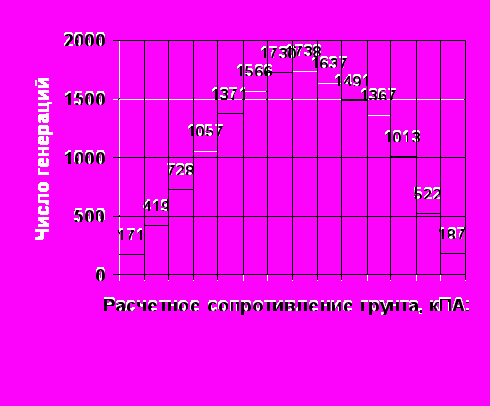	Среднее выборочное 470,4; стандарт 166,3; асимметрия -0,0794; эксцесс -0,7376

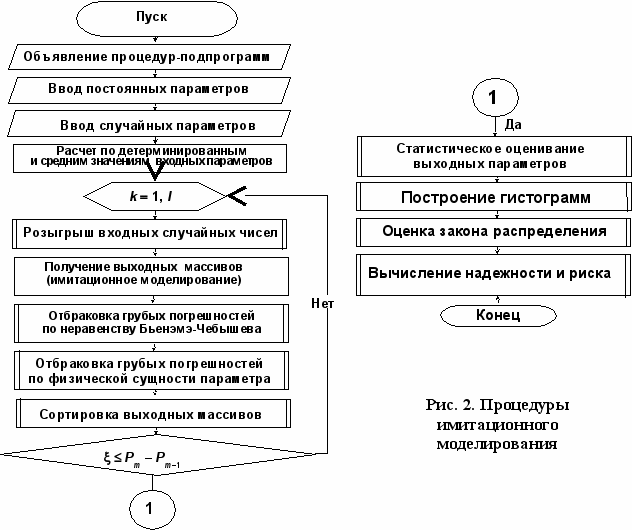
На рис. 2 представлена укрупненная блок-схема УГГУ, характеризующая порядок и процедуры имитационного моделирования. Три дополнительные процедуры  генерация табличной информации, генерация графической информации, генерация случайных чисел R_у, распределенных по законам Грамма-Шарлье и Эджворта, усовершенствованные в диссертации, существенно расширяют область применения метода Монте-Карло в плане оценки надежности оснований шахтных копров.

Генерация табличной и графической информации позволяет использовать таблицы и графики действующих нормативных документов, при этом «локальные» подпрограммы, обеспечивающие генерацию, вводятся в основную программу оценки надежности основания.





Генерация случайных чисел, распределенных по универсальным законам Грамма-Шарлье и Эджворта, выполняется численным методом по пяти и семи членам соответствующих рядов с учетом соотношения R_у  R_нs :


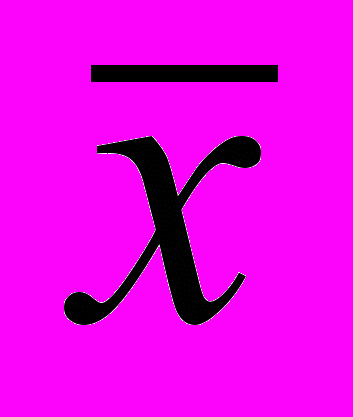1 1 ₃ 1 ₄ 1 ₅ ₃

r_i  –(1(R_н))– ––  –– ₀⁽²⁾(R_н)–– (–– – 3)₀⁽³⁾(R_н)– –– (–– –10 ––)₀⁽⁴⁾(R_н)

2 3!  ³ 4! ⁴ 5!  ⁵  ³

1 ₆ ₄

 ––(–– – 15 ––  30) ₀⁽⁶⁾(R_н)  … ;

6!  ⁶ ⁴


1 1 ₃ 1 ₄ 10 ₃²

r_i  –(1(R_н)) – ––  –– ₀⁽²⁾(R_н)  –– (–– –3)₀⁽³⁾(R_н)  –– –– ₀⁽⁵⁾(R_н) –

2 3! ³ 4! ⁴ 6! ⁶

1 ₅ ₃ 35 ₃ ₄ 280 ₃³

– – (–– – 10––)₀⁽⁴⁾(R_н) – –– ––(–– – 3)₀⁽⁶⁾(R_н) – –––(–––) ₀⁽⁸⁾(R_н)…,

5! ⁵ ³ 7! ³ ⁴ 9! ⁹


где R_у  генерируемое случайное число; R_н  значение, устанавливаемое численным методом; 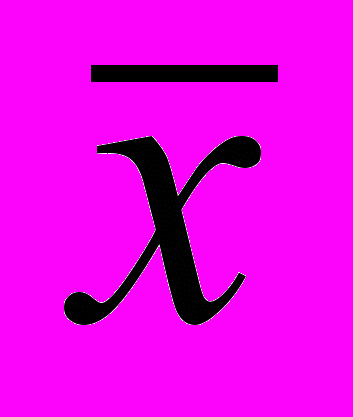 среднее выборочное; s  стандарт; r_i  равномерно распределенное число, задаваемое датчиком ЭВМ; (R_н)  интеграл вероятности; ₃, ₄, ₅, ₆  центральные моменты порядка с третьего по шестой; ₀(R_н)   (2 )^–0,5exp(– 0,5 R_н ²); ₀⁽²⁾(R_н)  (R_н² – 1) ₀(R_н); ₀⁽³⁾( R_н)  – (R_н³–3 R_н)₀(R_н); ₀⁽⁴⁾( R_н)   (R_н⁴–6 R_н²3)₀(R_н); ₀⁽⁵⁾( R_н)  – (R_н⁵–10 R_н³15 R_н)₀(R_н); ₀⁽⁶⁾( R_н)  (R_н⁶–15 R_н⁴45 R_н²–15)₀(R_н); ₀⁽⁷⁾( R_н)  –( R_н⁷–21 R_н⁵105R_н ³–105R_н)₀(R_н); ₀⁽⁸⁾(R_н)  (R_н⁸ – 28 R_н⁶  210R_н⁴  – 420 R_н² 105) ₀(R_н); ₀⁽⁹⁾( R_н)  – (R_н⁹–36 R_н⁷378 R_н⁵–1260 R_н³945 R_н)₀(R_н).

Скорость генерации составляет около 200 чисел R_у в секунду^.


3. Оценка надежности оснований в системе

«Копер  фундамент  ствол (устье)  основание»


В главе рассмотрены наиболее типичные задачи классического характера: оценка расчетного сопротивления грунта основания; определение несущей способности основания; оценка предельного давления на основание от фундамента глубокого заложения «колодец-оболочка»; расчет осадок оснований методами послойного суммирования и линейно деформируемого слоя; комплексная оценка надежности основания башенного копра. Проведенные исследования построены по единой логической схеме: «постановка задачи  особенности моделирования  детерминированное решение  собственно имитационное моделирование  фиксация уровней надежности  анализ результатов». В силу ограничений на объем автореферата в краткой форме рассматриваются три задачи, позволяющие получить достаточно полное представление о существе и универсальности разработанной методики оценки надежности оснований, а также об эффективности новых процедур имитационного моделирования.

3.1. Несущая способность основания


Несущая способность основания оценивается согласно СНиП 2.02.01–83* по формулам:


n_з  F_v (_c N_u / _n)^{ 1}; N_u  bl(N__b₁  N_q_q^₁d  N_c_cc₁);

b  b  2 e_b; l  l  2 e_l; _  1  0,25 / ; _q  1  1,5 / ; _c  1  0,3 / ,   l / b,

где F_v – расчетная нагрузка на основание; U_u – сила предельного сопротивления основания; _с – коэффициент условий работы; _n  коэффициент надежности по назначению сооружения; b и l  соответственно приведенные ширина и длина фундамента; e_b и e_l – соответственно эксцентриситеты приложения равнодействующей нагрузок в направлении поперечной и продольной осей фундамента; ₁ и ^₁  расчетные значения удельного веса грунтов, находящихся в пределах возможной призмы выпирания соответственно ниже и выше подошвы фундамента; d  глубина заложения фундамента; c₁  расчетное значение удельного сцепления грунта.

Особенности моделирования:

 в программу имитационного моделирования введена таблица «коэффициентов несущей способности N_, N_q, N_c», включенная в СНиП 2.02.01-83*;

 случайные величины: текучесть, плотность грунта, плотность материала фундамента  распределены по нормальному закону; пористость и равнодействующая всех вертикальных нагрузок  по закону Грамма-Шарлье; значения частных коэффициентов запаса вводятся в вероятностную модель двумя параметрами одностороннего нормального распределения (среднее значение приравнивается единице, стандарт составляет (k_з – 1)/3).


Результаты детерминированных расчетов:


  0,3277196 рад., с  18,67 кПа (с учетом коэффициента надежности по грунту); N_   0,448311, N_q  2,636337, N_c  4,823395; N_u  278,5719 кН (с учетом коэффициентов _с, _n); F_v  262,12 кН; Коэффициент запаса 1,062765.


Результаты имитационного моделирования приводятся в табл. 4, 5.


Таблица 4

Значения _i и c_i с учетом коэффициентов надежности по грунту, _{с1, i}

Угол внутреннего трения, град.

Удельное сцепление, кПа

21,85 20,71 19,25 19,37 20,87 22,15 18,19 21,25 18,73 20,21 21,50 21,01 18,77 21,16 21,04 21,03 21,40 20,03 20,07 20,69 22,62 18,54 21,18 20,10 21,77 20,46 22,50 20,33 21,12 20,92 21,17 19,18 21,62 22,92 21,06 21,92 20,74 20,32 19,43 20,74 20,63 21,02 21,04 20,54 21,49 21,46 20,18 19,69 19,83 20,20 19,77 21,86 19,49 20,40 22,14 21,08 20,48 19,77 20,75 19,32 21,50 20,44 21,08 21,51 19,72 20,57 21,31 19,94 20,31 20,57 21,61 22,34 21,24 18,44 20,35 21,01 22,59 21,46 21,01 22,78 20,83 20,05 21,21 19,71 20,81 21,15 21,56 21,29 21,83 20,74 20,73 21,30 21,74 19,82 21,06 21,85 20,96 20,72 20,42 21,29 19,92 19,89 20,73 21,42 20,95 18,33 18,13 20,16 22,26 20,78 21,94 20,18 22,07 20,41 20,19 19,67 20,67 21,27 20,39 21,05 22,17 20,13 20,62 19,10 20,77 19,44 21,78 20,21 19,60 18,13 19,24 21,48 21,89 21,57 22,11

22,20 28,59 28,11 17,07 28,50 27,67 20,75 25,69 23,56 25,88 28,46 25,13 16,66 22,36 17,06 26,26 19,60 26,37 21,34 24,66 24,22 21,92 21,01 24,95 28,83 18,17 28,40 21,99 20,72 21,39 24,96 28,25 27,88 31,64 29,94 28,41 20,47 18,63 21,61 18,82 29,59 20,87 21,06 25,43 23,31 28,41 20,75 19,33 19,84 25,82 22,38 24,28 22,27 18,27 29,99 18,02 25,33 21,04 23,19 21,49 21,57 23,58 32,90 26,59 18,33 20,40 30,01 22,74 22,33 22,97 28,87 29,73 23,30 25,55 26,99 28,13 32,96 21,97 22,53 29,87 18,22 23,74 28,83 20,76 22,77 18,79 28,40 22,04 23,39 20,86 25,39 23,92 25,71 26,85 28,42 18,43 24,27 24,04 21,82 21,63 22,71 31,61 25,37 27,56 16,70 22,89 17,44 22,39 33,63 21,68 27,88 21,03 25,82 20,70 17,71 25,25 24,54 26,30 21,65 19,16 21,51 20,12 21,50 21,38 20,37 20,63 32,83 28,24 21,96 19,23 17,26 24,57 18,74 21,13 22,96

Таблица 5

Вертикальная составляющая силы предельного сопротивления основания

и коэффициент запаса

Nu,i , кН

nз

536,64 483,85 467,00 322,88 428,30 709,21 316,70 491,87 333,30 462,94 555,56 502,29 309,66 524,31 392,10 469,98 463,71 453,51 411,68 448,53 566,70 279,71 477,65 431,21 554,06 431,56 609,21 372,79 475,11 480,07 514,50 347,33 541,02 663,22 547,69 628,07 441,52 426,12 391,63 431,56 548,04 476,34 481,75 435,19 536,55 532,32 466,03 353,33 374,00 485,02 405,05 595,87 424,58 374,63 691,54 417,80 493,52 383,18 499,58 362,16 563,40 496,10 635,32 601,07 337,57 495,38 601,34 384,21 454,04 484,44 593,55 661,31 561,12 313,89 497,86 595,67 678,02 472,19 487,56 786,70 394,53 419,78 599,19 371,40 494,27 521,77 560,71 499,83 572,23 451,52 508,84 554,10 564,60 401,82 567,42 441,87 540,96 507,57 459,54 504,71 409,45 486,62 488,29 580,44 366,42 317,88 241,68 427,60 625,67 475,09 654,23 486,58 549,35 440,19 347,67 407,22 484,48 578,39 408,23 473,01 510,99 432,75 444,96 364,23 420,80 391,91 705,64 509,77 359,53 302,12 333,01 544,47 480,58 478,74 559,20

0,92 1,07 1,15 1,18 1,20 1,21 1,21 1,23 1,27 1,27 1,29 1,32 1,33 1,35 1,37 1,38 1,39 1,40 1,42 1,42 1,43 1,43 1,46 1,46 1,49 1,49 1,49 1,50 1,53 1,54 1,55 1,56 1,56 1,57 1,59 1,60 1,60 1,62 1,62 1,63 1,63 1,64 1,65 1,65 1,65 1,66 1,68 1,68 1,68 1,70 1,71 1,72 1,73 1,73 1,75 1,76 1,77 1,78 1,78 1,79 1,80 1,80 1,81 1,81 1,82 1,82 1,82 1,83 1,83 1,84 1,84 1,85 1,85 1,85 1,85 1,85 1,86 1,86 1,87 1,88 1,88 1,89 1,89 1,90 1,90 1,91 1,91 1,92 1,93 1,94 1,94 1,95 1,96 1,99 2,00 2,03 2,05 2,05 2,06 2,06 2,08 2,09 2,09 2,09 2,11 2,11 2,12 2,13 2,14 2,14 2,15 2,15 2,16 2,16 2,18 2,20 2,21 2,26 2,27 2,27 2,28 2,29 2,29 2,32 2,38 2,39 2,42 2,49 2,52 2,53 2,58 2,64 2,69 2,70 3,00

Уровень надежности по условию P(n_з>1) составляет 0,992.

3.2. Предельное (критическое) давление на основание

фундамента глубокого заложения «колодец-оболочка»


На рис. 3, 4 приведены теоретическая эпюра распределения предельных напряжений по поверхности конического уплотненного ядра под фундаментом глубокого заложения «колодец-оболочка» (В. Г. Березанцев) и график для определения коэффициента B_к в формуле для расчета средней интенсивности критической нагрузки _к  B_к  d, здесь B_к  функция угла внутреннего трения  и относительного заглубления фундамента h / d;   удельный вес грунта; d  внешний диаметр «колодца-оболочки».

Кривые h/d аппроксимируются с запасом 1,03 ÷ 1,07 кубичными сплайнами:


B_{к, h/d=4}  40,85859  8,076771(  26)  0,208422(  26)²  0,041562(  26)³; B_{к, h/d=8}  89,44445  5,828514(  26)  0,452743(  26)²  0,0589225(  26)³; B_{к, h/d=12}  120,9594  15,67901(  26)  0,649832(  26)²  0,136269(  26)³; B_{к, h/d=16}  159,8483  18,36599(  26)  0,031084(  26)²  0,137312(  26)³; B_{к, h/d=20}  194,0406  41,53954(  26)  3,802266(  26)²  0,341959(  26)³; B_{к, h/d=24}  245,2526  31,35218(  26)  0,842346(  26)²  0,234638(  26)³;

B_{к, h/d=28}  276,2122  44,76545(  26)  2,729969(  26)²  0,3630048(  26)³; B_{к, h/d=32}  318,6865 32,41802(  26)  0,532496(  26)²  0,2467407(  26)³.

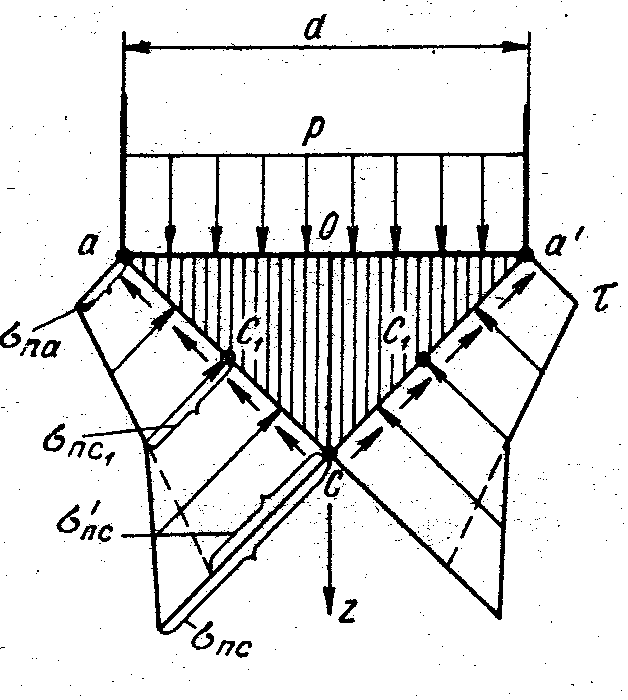
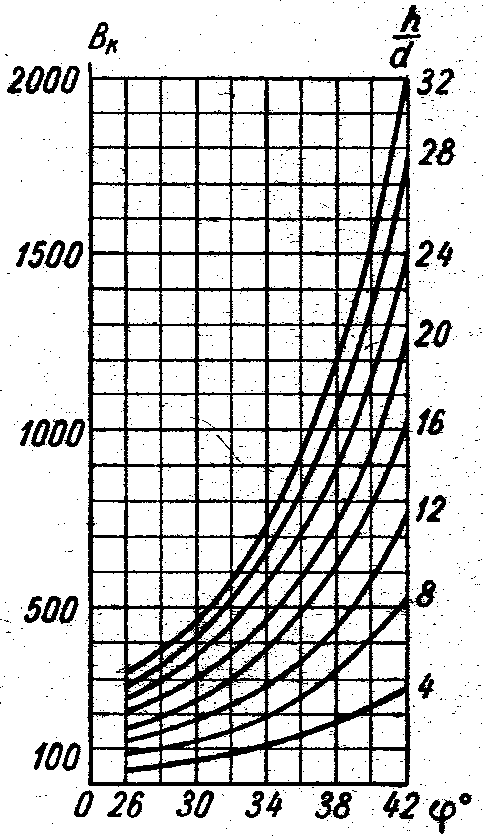
Рис. 3. Теоретическая эпюра распределения предельных напряжений по поверхности конического уплотненного ядра под фундаментом	Рис. 4. График для определения коэффициента Bк

В табл. 6 приведены исходные данные и результаты генерации коэффициентов B_к и выходной случайный массив предельных давлений на основание.

Таблица 6

Исходные данные. Отсортированные демонстрационные результаты

Исходные данные: h  7 м; d  3 м; ср  30; S  2; A  0,256; E  0,1; ср  25 кН/м3; S  3 кН/м3

Bкi

77,3 77,3 77,4 78,1 78,9 82,3 82,3 83,2 83,5 83,5 84,0 85,2 85,8 85,9 87,2 87,3 87,6 87,7 87,8 87,9 89,3 90,6 90,9 91,0 91,2 91,4 92,6 92,9 93,7 93,9 94,7 95,5 95,5 96,1 96,3 96,5 96,7 97,1 7,2 97,4 97,6 97,6 97,9 98,0 98,1 98,2 99,2 99,5 100,4 100,6 100,9 100,9 101,3 101,5 101,7 102,0 102,0 102,5 102,6 102,9 103,0 103,0 103,6 103,7 104,7 104,9 105,0 105,1 105,4 105,6 106,1 106,1 106,1 106,1 107,8 108,2 108,2 108,3 108,5 108,6 108,6 109,4 110,0 110,2 110,4 110,7 110,8 111,0 112,2 112,5 112,5 112,7 112,7 113,4 113,5 113,8 113,9 114,9 115,0 115,0 115,9 115,9 116,5 116,7 116,9 119,3 119,8 120,2 120,7 121,3 121,4 121,8 122,4 123,6 124,4 124,6 124,8 125,1 125,2 127,8 128,7 132,9 133,6 134,0 134,4 134,9 138,3 140,5 140,7 144,1 150,9 151,3 151,4 155,4 184,6

кi, кПа

4562,6 4666,1 4935,8 5014,4 5043,5 5149,0 5220,5 5303,4 5549,2 5566,6 5656,5 5677,7 5831,7 5977,1 5983,2 5988,5 5996,8 6001,6 6048,6 6086,8 6141,1 6152,3 6167,9 6185,2 6209,4 6285,4 6417,8 6449,5 6463,9 6525,3 6542,5 6641,5 6660,1 6674,8 6688,5 6695,0 6696,9 6733,7 6795,1 6835,5 6843,9 6875,6 6886,9 6897,2 6930,8 6951,9 6961,4 7004,7 7032,9 7081,8 7132,7 7167,9 7251,4 7262,5 7271,3 7291,2 7344,6 7347,4 7366,2 7433,9 7499,1 7505,6 7518,8 7524,8 7566,9 7576,6 7687,9 7705,6 7801,6 7856,6 7875,0 7909,9 7932,2 7958,7 7965,8 8014,0 8044,5 8045,1 8103,2 8115,9 8127,1 8127,5 8186,8 8230,2 8235,9 8285,5 8358,9 8389,0 8473,1 8485,6 8552,0 8594,8 8610,5 8632,8 8659,7 8769,7 8786,7 8872,3 8908,4 9090,1 9125,4 9171,4 9247,6 9281,9 9315,8 9341,2 9432,9 9448,7 9480,5 9509,4 9813,9 9817,3 9884,5 9980,0 10044,3 10086,7 10392,5 10663,1 10677,5 10699,9 10773,4 10855,4 10952,6 11348,4 11514,6 11653,4 11944,9 12128,3 12136,1 12169,5 12184,9 12186,3 13333,9 13593,1 13979,1

_{С надежностью 0,95 i-е значение критического давления i   INT(0,95135)  1  129, соответственно критическое давление к 129  12136,1 кПа (в табл. 6 выделено полужирным шрифтом).}