Оптимизация надежности

Вид материала

Документы

Содержание P0 (вероятности готовности объекта к работе) или вероятности аварийного отказа Q P1,3 оказывают интенсивность отказов l и периодичность контроля технического состояния t T0 - случайное время безотказной работы при стандартной нагрузке S S0 = 20С средняя наработка составила T K12 - корреляционный момент (ковариация) случайных величин S Оптимальная периодичность технического обслуживания

Подобный материал:

• Вопросы для подготовки к экзамену по дисциплине «Теория надежности», 8-й семестр, 2011, 20.46kb.
• Методы обеспечения надежности задачи обеспечения надежности, 302.01kb.
• Интервальный метод оценки надежности подстанций, 115.06kb.
• Повышение надежности программного обеспечения ядерных радиационно-опасных объектов, 223.97kb.
• Итоги работ по диагностике электрооборудования схемы выдачи мощности аэс, рекомендации, 7.77kb.
• Optimization Toolbox – Оптимизация, 780.37kb.
• Надежность систем. Общие понятия и определения основы расчета надежности систем. Общие, 54.06kb.
• Пресс-релиз 31 марта 2011, 97.4kb.
• Мониторинг сми РФ по пенсионной тематике 11 апреля 2011 года, 1171.12kb.
• Місця збереження документів, 153.78kb.

ОПТИМИЗАЦИЯ НАДЕЖНОСТИ


Е.Н.Окладникова, Е.В.Сугак

Красноярск (Сибирский государственный аэрокосмический университет)


Надежность техники всегда была одной из основных инженерных проблем, и ей всегда уделялось большое внимание. Основные условия обеспечения надежности состоят в строгом выполнении правила «триады надежности»: надежность закладывается при проектировании, обеспечивается при изготовлении и поддерживается при эксплуатации. В последнее время все большую актуальность приобретают вопросы моделирования и расчета показателей надежности и безопасности производственных объектов. В решении этих задач важное место занимают методы структурного анализа опасности и оценка риска сложных технических и организационных систем.

Требования достижения высокой надежности зачастую находятся в противоречии с другими необходимыми характеристиками, такими как уменьшение размеров, получение высокой точности, низкая стоимость и т.д. Поэтому возникает вопрос, как оптимально выбрать необходимые количественные характеристики для получения компромиссного решения.

Конкретная постановка задачи оптимизации надежности системы определяется видом и сложностью технической системы, характером и важностью выполняемых функций, числом и видом возможных состояний, тяжестью последствий отказов, а также стратегией её технического обслуживания. Решение задач оптимизации системы технического обслуживания включает, как правило, построение графа состояний, составление модели функционирования и определение параметров системы технического обслуживания.

Например, для простейшего случая непрерывно контролируемого в процессе эксплуатации объекта возможны только два состояния (работоспособное и состояние отказа) и при известной интенсивности отказов l модель включает только один управляющий параметр - среднее время T_в или интенсивность восстановления m (T_в = 1/m). Для установившегося режима эксплуатации (t®¥) система дифференциальных уравнений относительно вероятностей состояний объекта P₀ и P₁ вырождается в систему алгебраических уравнений относительно «финальных» вероятностей P₀ и P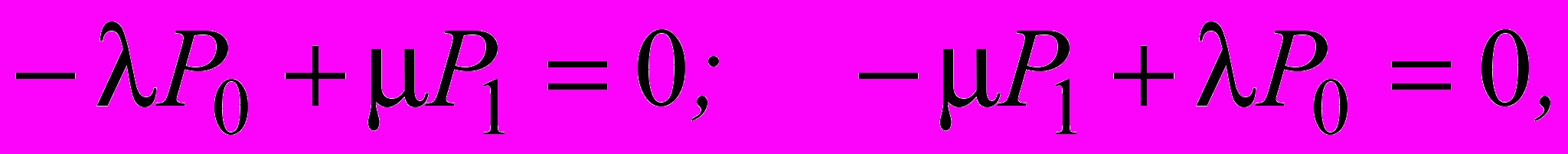₁:

(1)

из которой, с учетом нормирующего условия P₀ + P₁ = 1, можно получить [1]

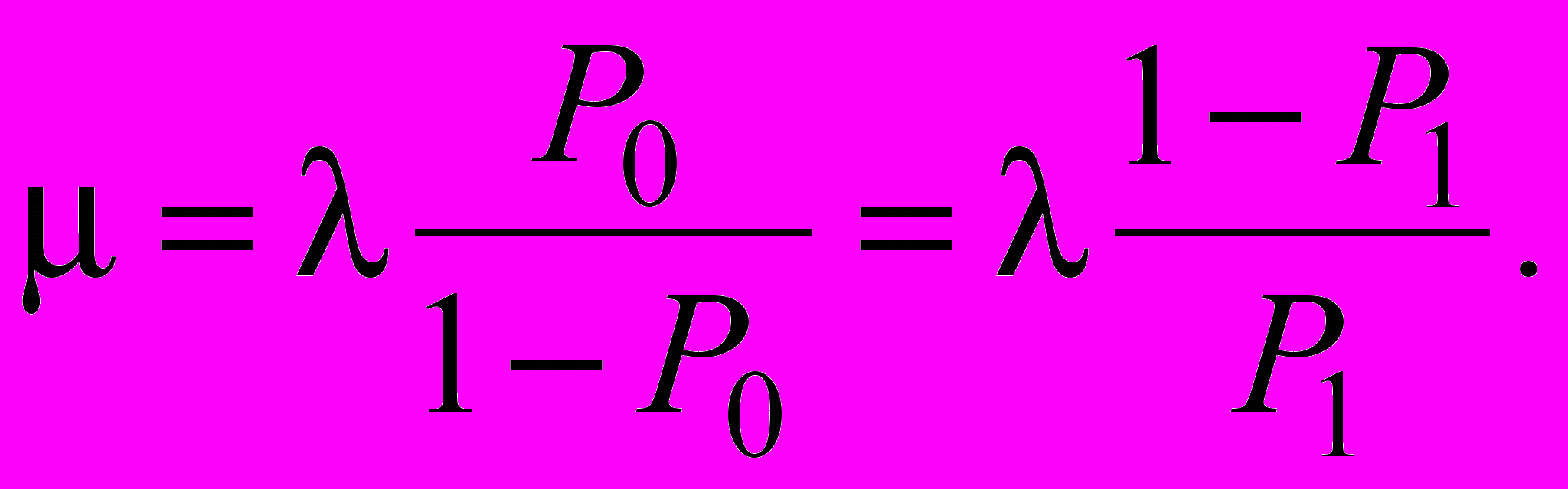(2)

При известной интенсивности отказов l и заданном уровне надежности P₀ (вероятности готовности объекта к работе) или вероятности аварийного отказа Q = P₁ = 1 – P₀ («технического риска») можно определить предельное значение среднего времени восстановления объекта и, соответственно, остальные параметры системы технического обслуживания.

В более сложных случаях для решения задач оптимизации необходимо определить некоторые дополнительные характеристики, которые не могут быть заданы исходя их экспериментальных исследований или практики эксплуатации объекта.



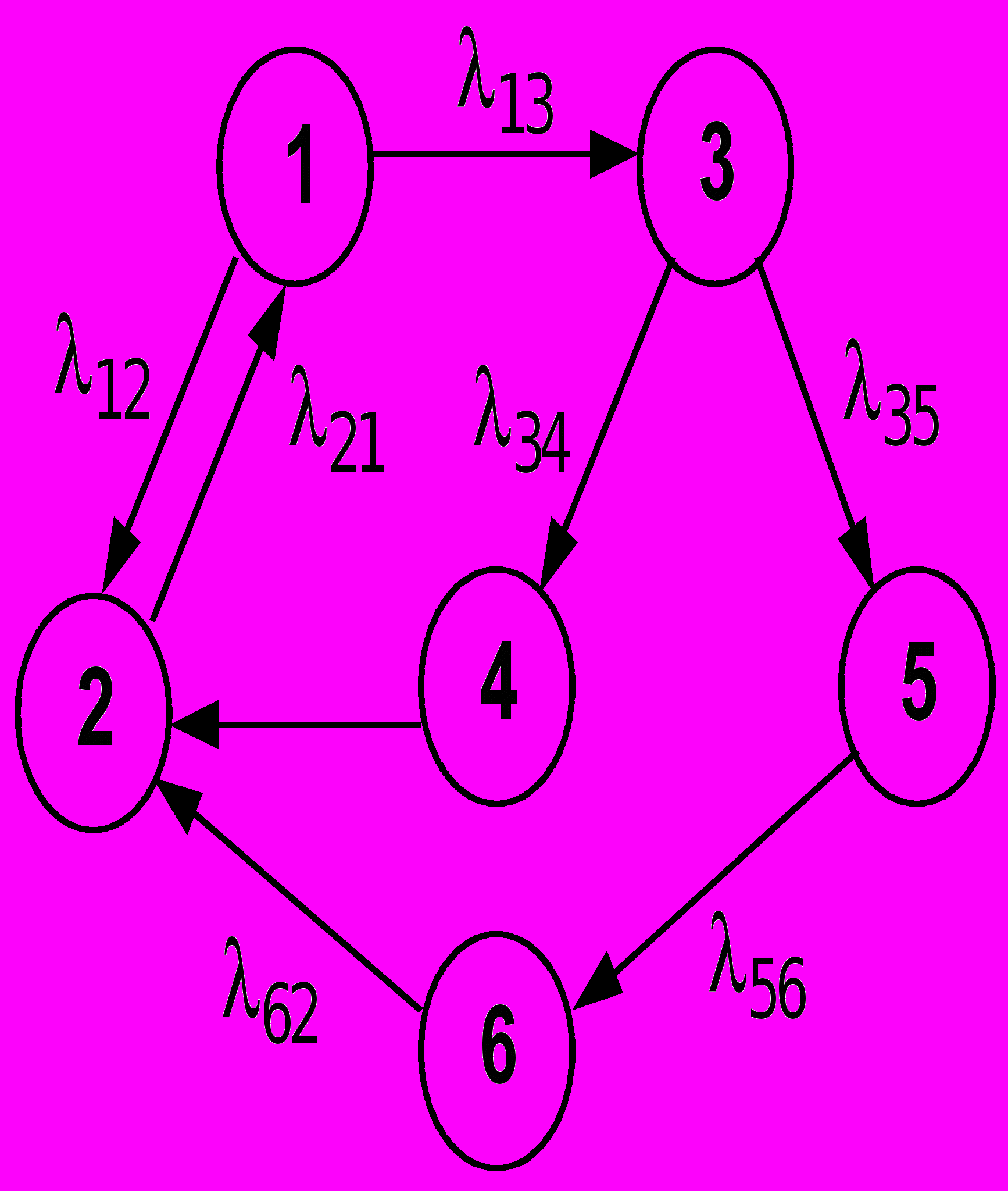
Рис.1. Граф состояний резервированного объекта с периодическим контролем технического состояния:

1 - работоспособное состояние (готовность к работе) основного и резервного объектов; 2 - периодический контроль при двух работоспособных объектах; 3 - работоспособное состояние (готовность к работе) одного из объектов; 4 - периодический контроль при одном работоспособным объектом; 5 - скрытый отказ второго объекта; 6 - периодический контроль при двух отказавших объектах


Например, в модели резервированного объекта с периодическим контролем технического состояния количество состояний составляет шесть и, соответственно, возможны переходы восьми видов (рис.1) [1].

Если для периодического контроля объекты выводятся из работоспособного состояния (состояния готовности), т.е. отключаются, то работоспособными являются только состояния 1 и 3 (готовности к работе двух и одного объекта, соответственно) и поэтому основным показателем надежности можно считать суммарную вероятность P_1,3=P₁+P₃. Если же контроль осуществляется без отключения, то работоспособными являются состояния 1, 2, 3 и 4 и основным показателем надежности является суммарная вероятность P_1-4=P₁+P₂+P₃+P₄.

Интенсивность отказов l, периодичность контроля t_к, среднее время контроля t_к и устранения отказов (ремонта) t_р и, соответственно, интенсивности переходов l₁₂=1/t_к, l₁₃=2l, l₂₁=1/t_к, l₃₅=l, l₄₂=l₆₂=1/(t_к+t_р) могут быть получены по результатам экспериментальных исследований или задаются регламентом. Для нахождения интенсивностей переходов l₃₄ и l₅₆ можно воспользоваться свойствами марковских процессов с непрерывным временем:

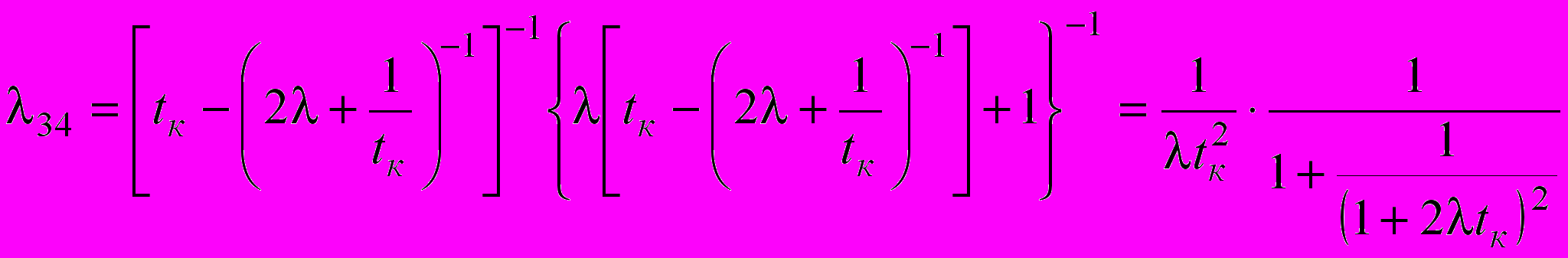. (3)

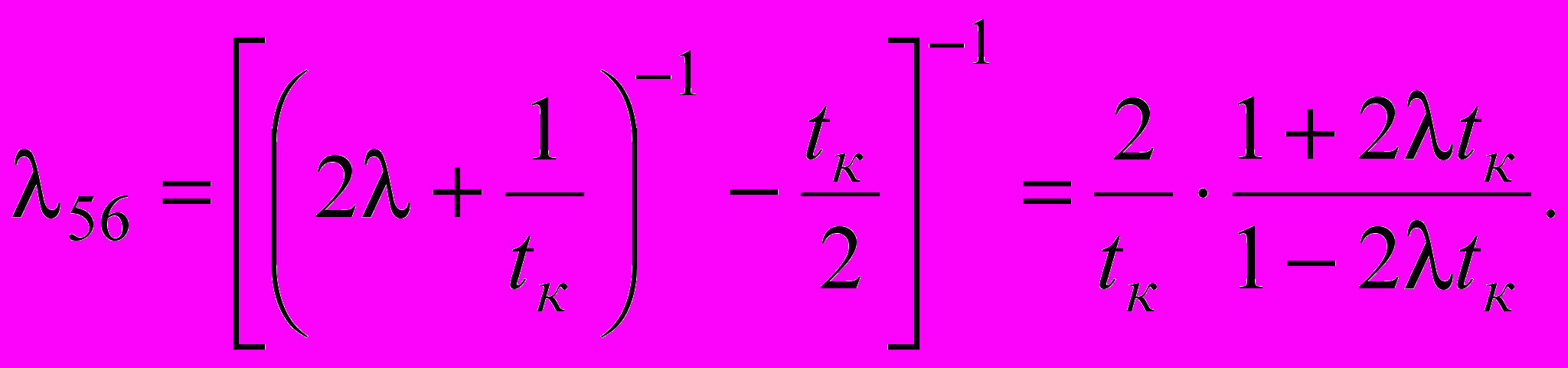(4)

Система дифференциальных уравнений имеет вид:

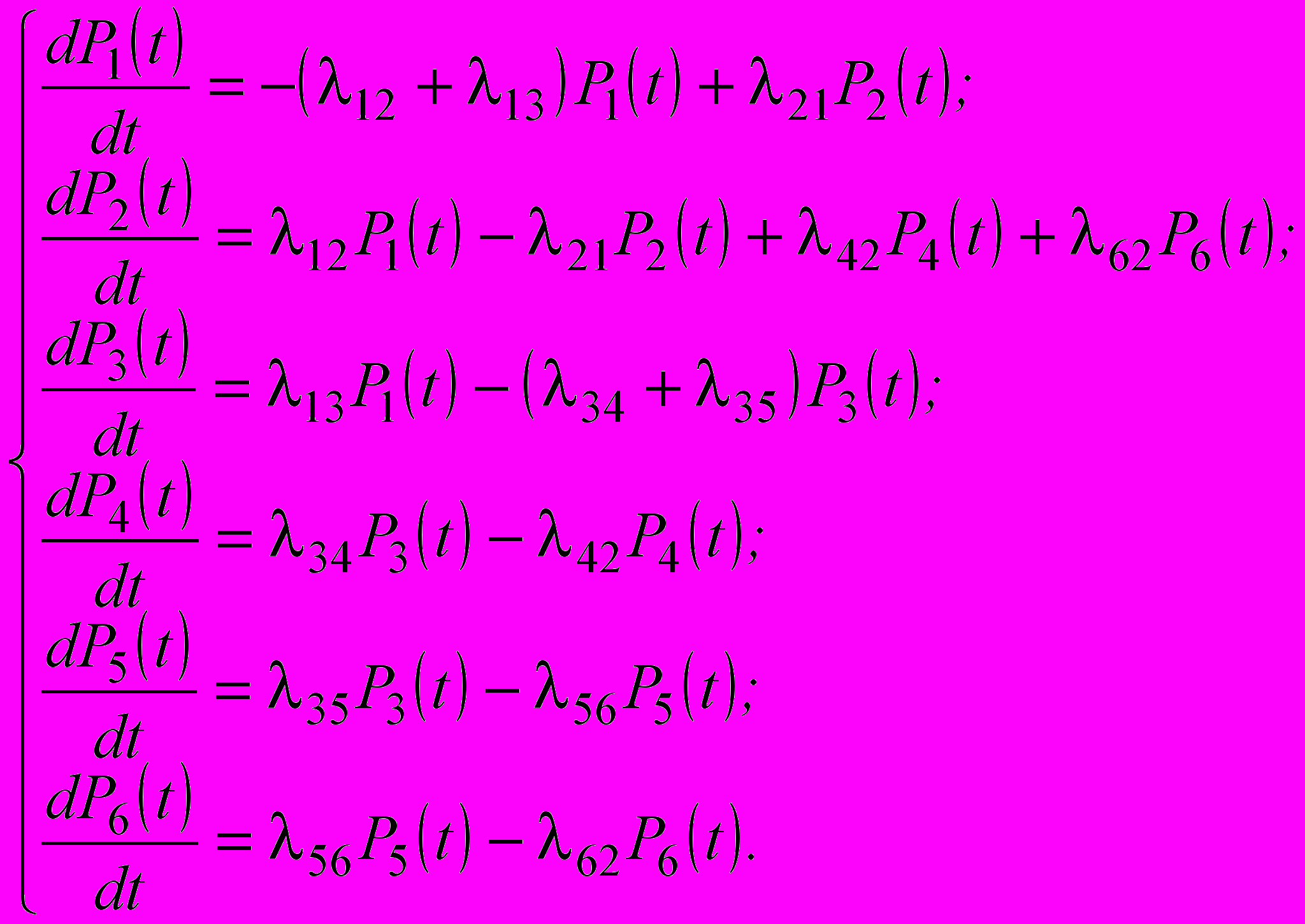(5)

Систему (5) необходимо дополнить нормирующим условием P₁(t)+P₂(t)+P₃(t)+P₄(t)+P₅(t)+P₆(t)=1 и начальными условиями. Численный анализ системы дифференциальных уравнений (5*) показывает, что при l£10^-5 ч^-1 переходные процессы в модели практически отсутствуют и при ее анализе можно перейти к системе алгебраических уравнений, составленных для установившегося режима:

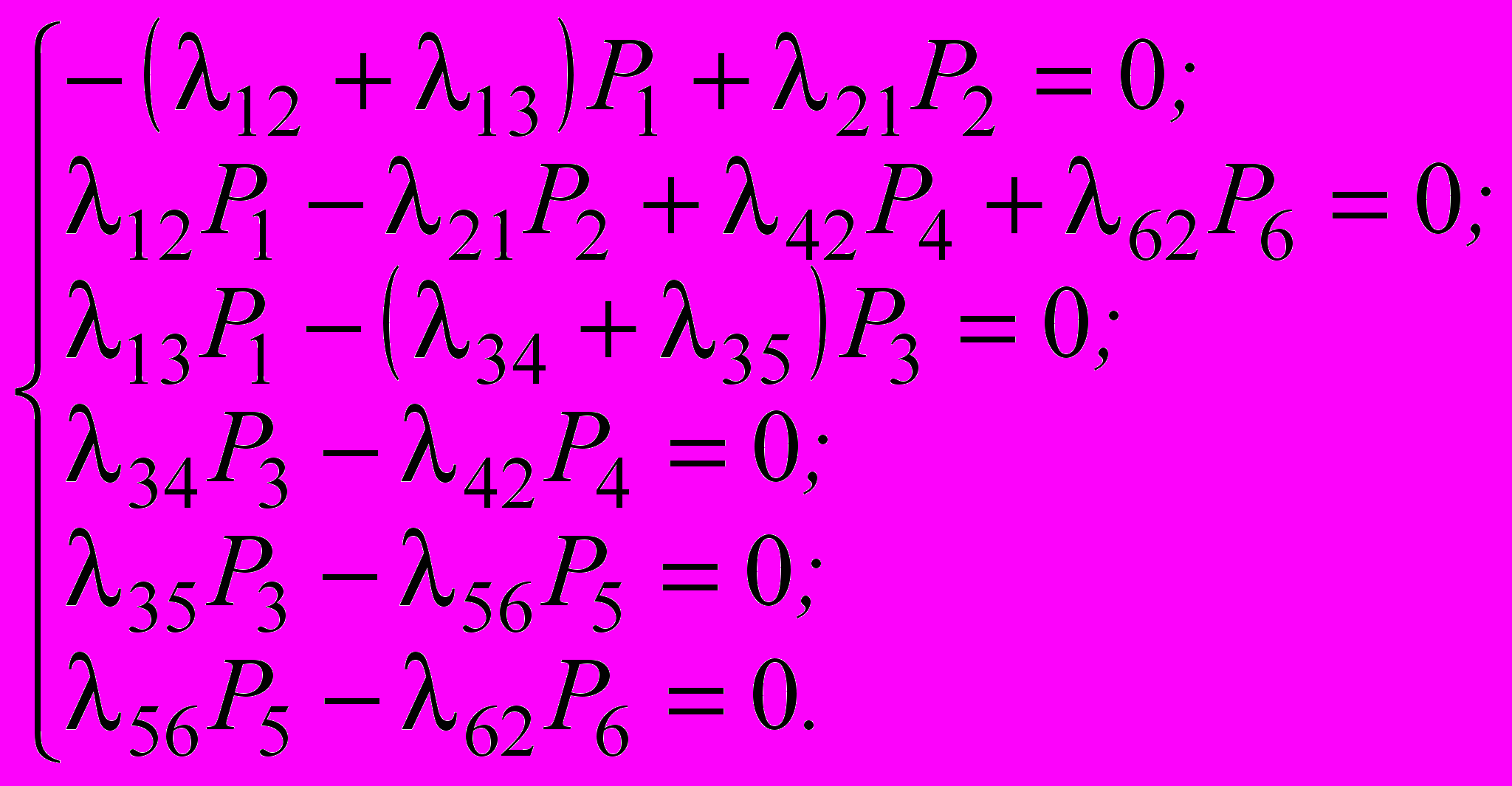(6)

Из решения системы уравнений (6) с учетом нормирующего условия P₁+P₂+P₃+P₄+P₅+P₆=1 можно получить выражения для вероятности работоспособных состояний для двух случаев - при контроле с отключением P_1,3=P₁+P₃ и контроле без отключения P_1-4=P₁+P₂+P₃+P₄:

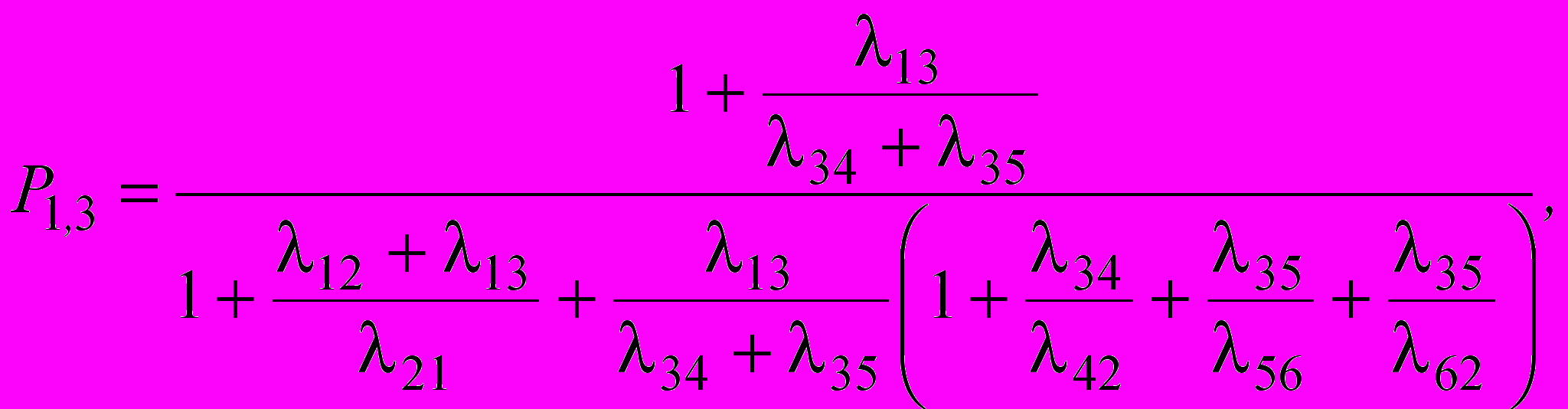(7)

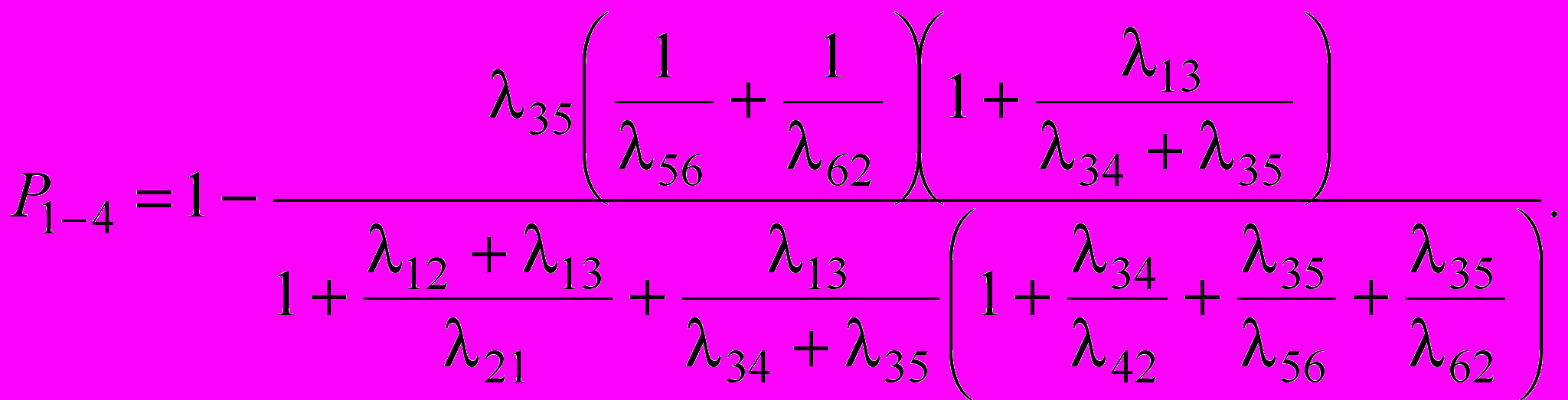(8)

Из анализа полученных зависимостей можно сделать следующие выводы:

- наибольшее влияние на вероятность P_1,3 оказывают интенсивность отказов l и периодичность контроля технического состояния t_к;

- максимум значения P_1,3 с уменьшением l смещается в сторону больших значений t_к (при l=10^-4 ч^-1 он соответствует значению t_к 1-2 месяца, при l=10^-5 ч^-1 - 9-10 месяцев), график P_1,3(t_к) при этом становится более пологим;

- оптимальная периодичность контроля пропорциональна увеличению его продолжительности t_к (например, для l=10^-4 ч^-1 увеличение t_к с 3 до 30 часов приводит к увеличению оптимальной периодичности с 1 до 2 месяцев, хотя максимальное значение вероятности P_1,3 при этом снижается на 2,5%);

- отклонения периодичности контроля от оптимального значения (особенно в сторону уменьшения) существенно снижают вероятность готовности объекта, особенно при больших значениях интенсивности отказов (например, для l=10^-4 ч^-1, t_к=3 ч и t_р=60 ч уменьшение t_к с 1 до 0,1 месяца снижает значение P_1,3 на 4% по сравнению с максимальным, а увеличение до 2 месяцев - на 1,5%).



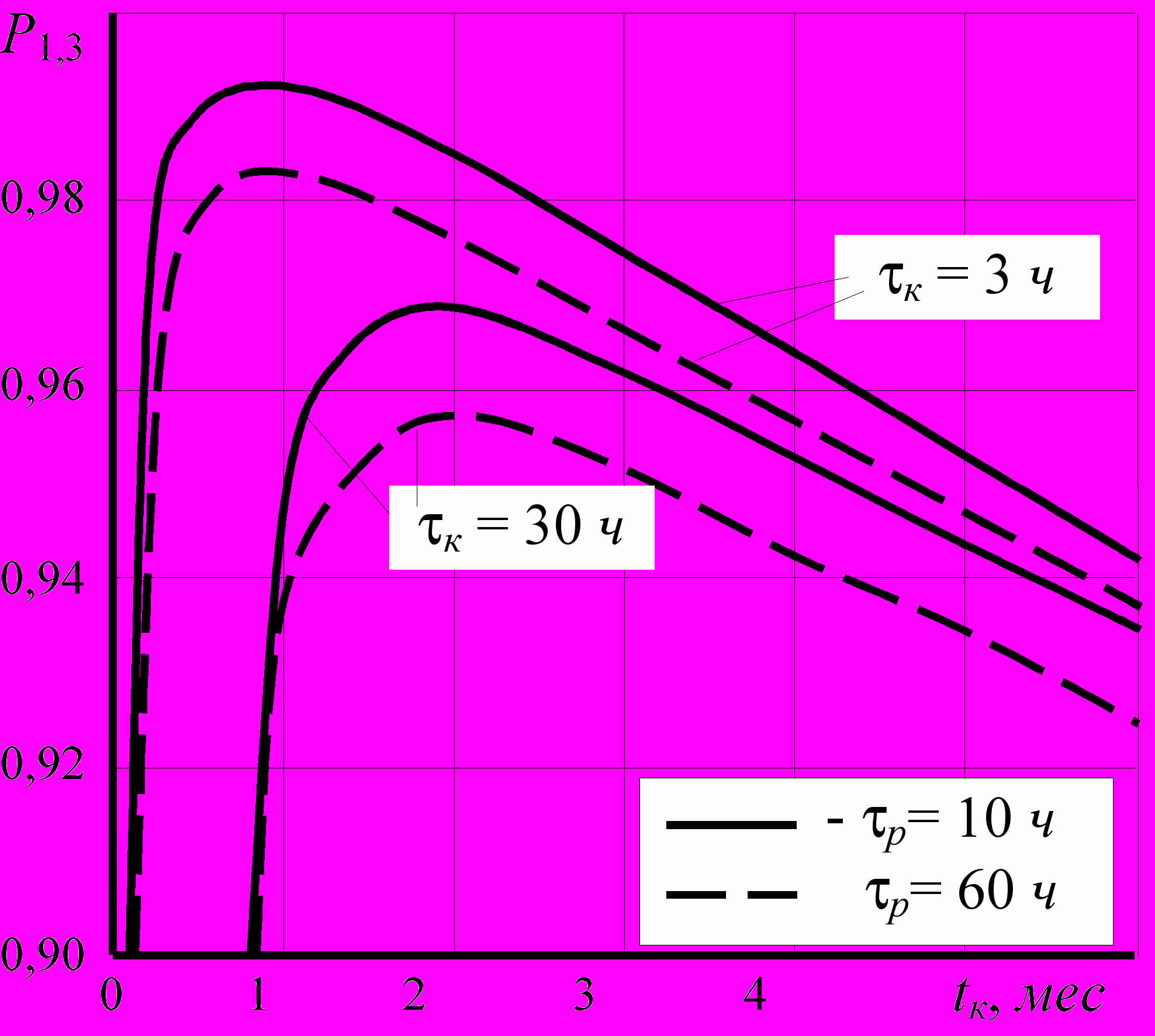
Рис.2 Зависимость вероятности готовности резервированного объекта от периодичности контроля (l = 10^-4 ч^-1)

В зависимости от постановки задачи оптимизации возможны различные варианты ее решения, в том числе предусматривающие изменение не только параметров, но и структуры самой системы технического обслуживания, в частности разработку и использование различных комбинированных и комплексных моделей с различными видами технического обслуживания, в том числе по фактическому техническому состоянию, что может быть связано с необходимостью его непрерывного или периодического контроля (диагностирования).

Для определения влияния изменения количественных характеристик различных факторов на изменение результирующих показателей с целью поддержки или обоснования принимаемых решений проводится анализ чувствительности по отношению к различным факторам: исходным событиям, функциям безопасности элементов, системам обеспечения безопасности и т.д.

Одной из разновидностей модели надежности можно считать зависимость ее характеристик (показателей) от условий применения или испытываемых нагрузок [2]. Например, наработка объекта до отказа (или между отказами) T конкретного технического объекта, очевидно, является случайной функцией случайной нагрузки S:

T = F(S) (9)

Для конкретного технического объекта наработка до отказа является неслучайной функцией случайной нагрузки F(S) - функциональной реализацией случайной функции случайной нагрузки (9). При неслучайной переменной нагрузке сечение S = S_i случайной функции T(S) - случайная аргументная реализация случайной функции случайного аргумента функции (9). Неслучайная величина T_ij = F_j(S_i) является полной (двойной) реализацией случайной функции случайного аргумента (9) [3]. Таким образом, при использовании зависимости (9) одновременно учитывается случайный характер нагрузки и случайные характеристики самого технического объекта.

Сравнивать различные технические объекты по наработке до отказа можно лишь в случае, если они находятся в одинаковых условиях. Для изделий определенного назначения при испытаниях целесообразно принять стандартные условия испытаний с нагрузкой, близкой к математическому ожиданию типичных нагрузок. Если стандартное значение нагрузки принять за начало отсчета, то случайную нагрузку можно представить в виде

S = S₀ +DS, (10)

где S₀ - стандартная неслучайная нагрузка; DS - случайное отклонение нагрузки от стандартного значения.

Разложив функцию (9) в ряд Тейлора в окрестностях точки S₀, ограничившись только тремя первыми членами, получим

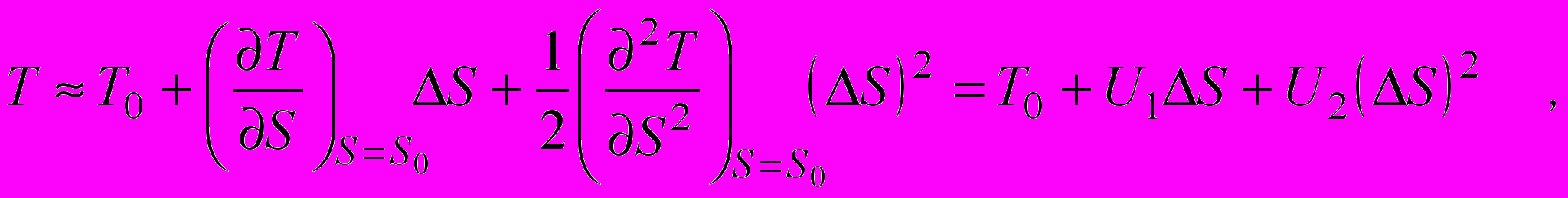(11)

где T₀ - случайное время безотказной работы при стандартной нагрузке S₀; DS = S–S₀; U₁ = ¶T/¶S и U₂ = ¶²T/¶S² - значения производных в окрестностях точки S = S₀.

В формуле (11) случайные величины T₀, U₁ и U₂ характеризуют технический объект, а случайная величина DS - отклонение случайной нагрузки от стандартной. Случайные величины U_n иногда называют чувствительностью n-го порядка к нагрузке.

Применив к зависимости теоремы о числовых характеристиках случайных величин, получим выражение для математического ожидания наработки (средней наработки) в виде [2]:

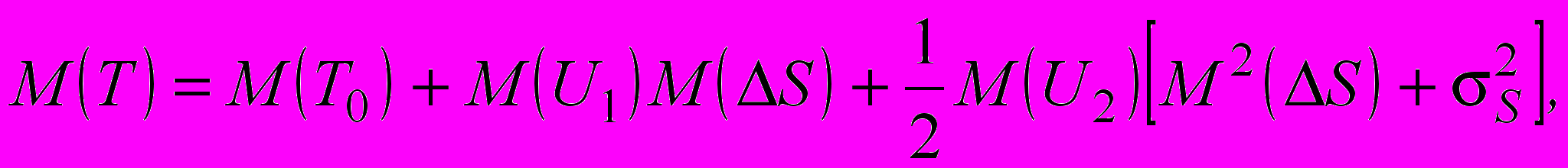(12)

где M(T₀) - средняя наработка при стандартной нагрузке (стандартная средняя наработка); M(U₁) = dM(T)/dS и M(U₂) = d²M(T)/dS² - значения производных средней наработки по нагрузке при S = S₀ (средние значения чувствительности к нагрузке); M(DS) и s_S - среднее значение (математическое ожидание) и среднее квадратическое отклонение отклонения нагрузки от стандартной.

Таким образом, надежность объекта можно приближенно характеризовать величинами, не зависящими от условий эксплуатации - стандартной средней наработкой M(T₀) = T_ср0 и средними чувствительностями к нагрузке первого и второго порядков M(U₁) = U_ср1 и M(U₂) = U_ср2. Пересчет средней наработки на другие (отличные от стандартных) условия эксплуатации можно производить по приближенной формуле (12)

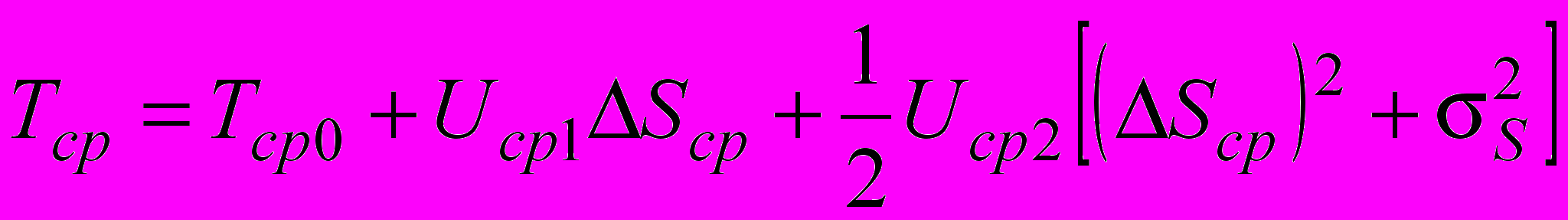. (13)

Если стандартная нагрузка совпадает со средним значением, т.е. DS = 0, то формула (13) принимает вид

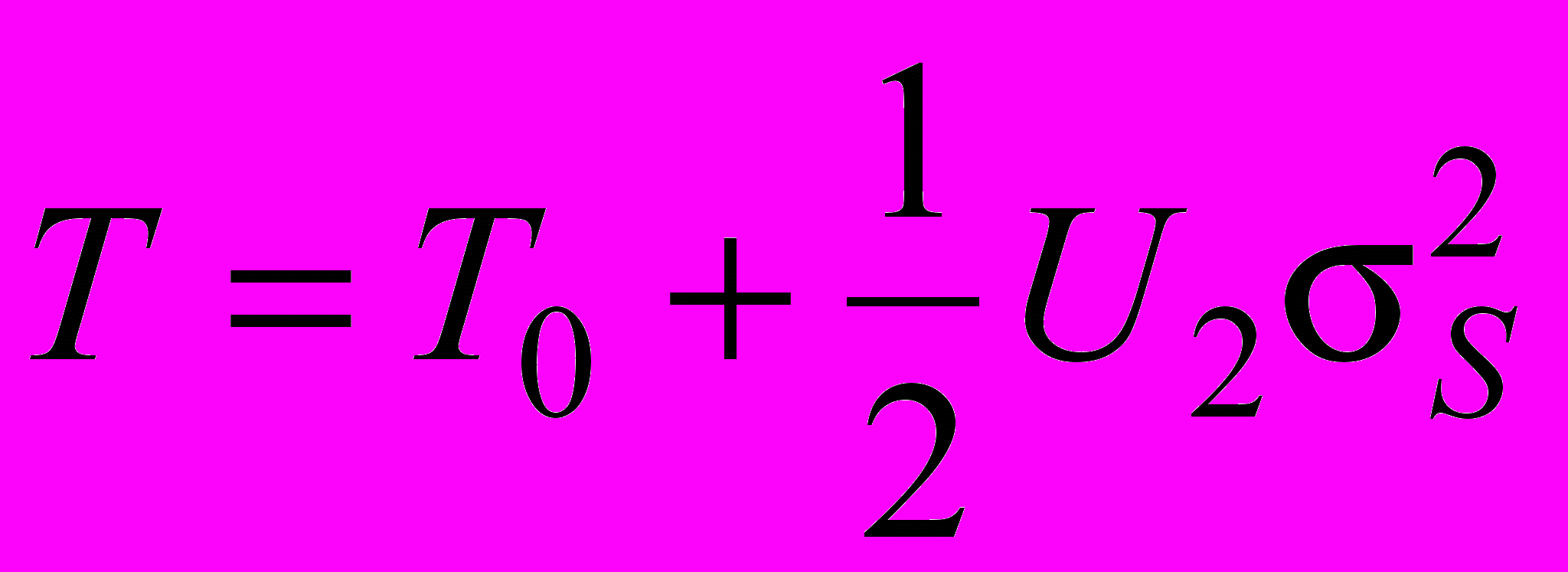. (14)

Для вычисления характеристик по результатам испытаний или данным эксплуатации должны быть известны значения средних наработок группы одинаковых объектов при трех или более режимах работы.

Параметры T₀, U₁ и U₂ находятся решением системы уравнений (14):

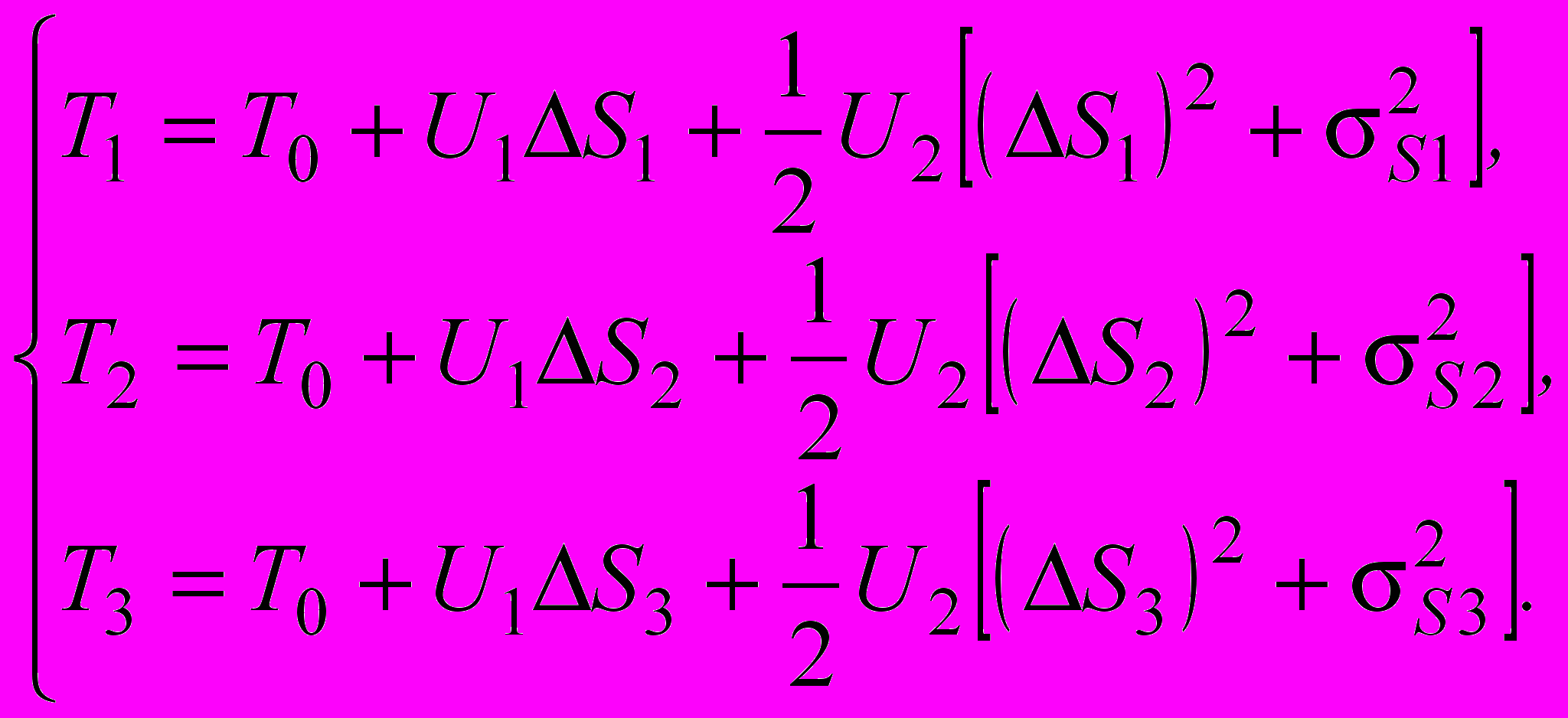(15)

Если в одном из режимов средняя нагрузка совпадает со стандартной (т.е. DS = 0), то система уравнений (15) превращается в систему из двух уравнений и вычисления упрощаются.

Пусть, например, при проведении лабораторных испытаний устройства при стандартной температуре S₀ = 20^оС средняя наработка составила T₀ = 256 ч, при температуре S₁ = 40^оС - T₁ = 112 ч . В процессе реальной эксплуатации при средней температуре S₂ = 30^оС и среднем квадратическом отклонении температуры s_S2 = 8^оС средняя наработка T₂ = 182 ч. Необходимо найти значение средней наработки T при средней температуре S = 10^оС и среднем квадратическом отклонении s_S = 10^оС.

Для рассматриваемого примера в системе уравнений (17) DS₁ = S₁ – S₀ = 20^оС, s_S1 = 0, DS₂ = 10^оС. После подстановки получим

112 = 256 + 20U₁ + 200U₂,

182 = 256 + 10U₁ + 82U₂ ,

откуда U₁ = –8,3, U₂ = 0,11. Тогда по формуле (16)

T = 256 + (–8,3)×(–10) + 0,11×[(–10)² + 10²]/2 = 256 + 83 + 11 = 350 ч.

Если известны значения средних наработок при более чем трех режимах нагружения, то для нахождения параметров T₀, U₁ и U₂ в уравнении (14) можно воспользоваться методом наименьших квадратов:

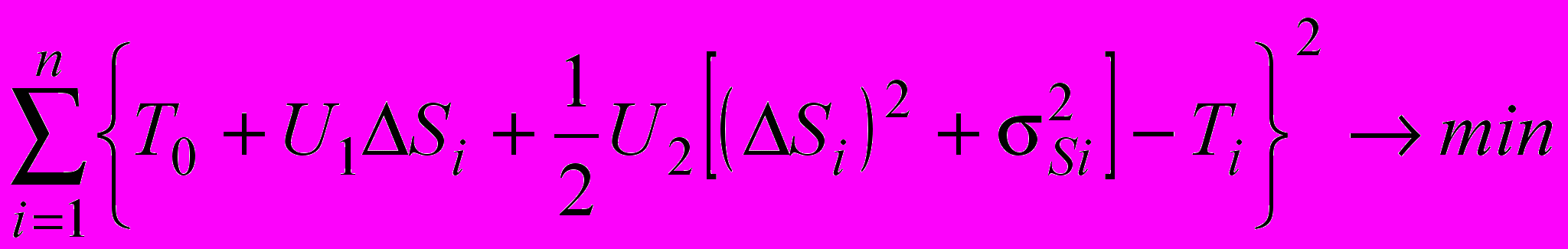, (16)

где i = 1¸n - номер режима работы.

Приравняв нулю частные производные суммы (16) по переменным T₀, U₁ и U₂, получим систему трех уравнений, решив которую можно определить искомые характеристики.

При двух или более видах нагрузки наработка до отказа рассматривается как случайная функция случайного вектора нагрузки. При этом аналогично одномерному случаю каждую из составляющих S_i вектора нагрузки можно считать состоящей из стандартной неслучайной нагрузки S_i0 и случайного отклонения DS_i, т.е. S_i = S_i0 + DS_i. Для двух случайных нагрузок S₁ и S₂ можно получить выражение для средней наработки:



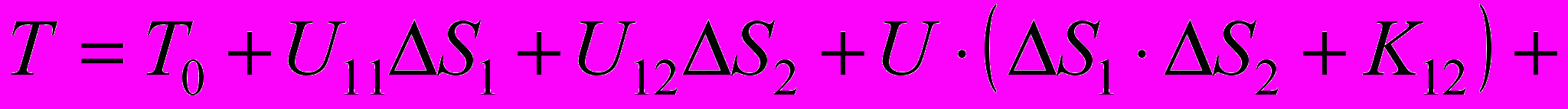
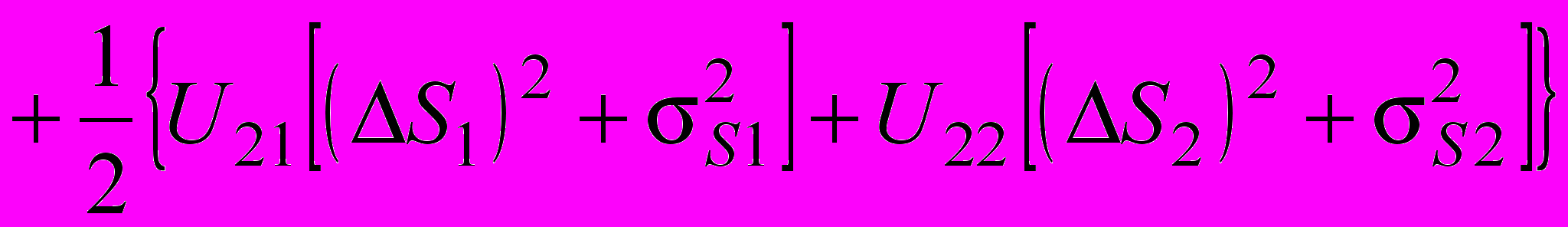, (17)

где U_ij - средние частные чувствительности к нагрузкам - значения частных производных средней наработки по соответствующим нагрузкам при S₁ = S₁₀ и S₂ = S₂₀:

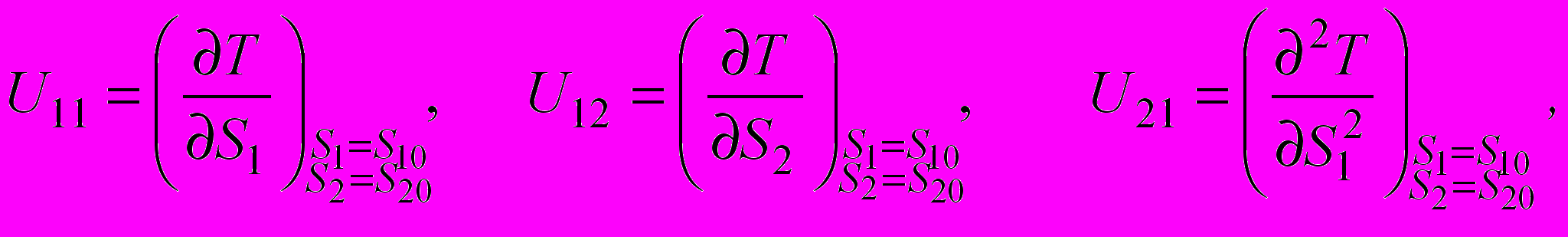(18)

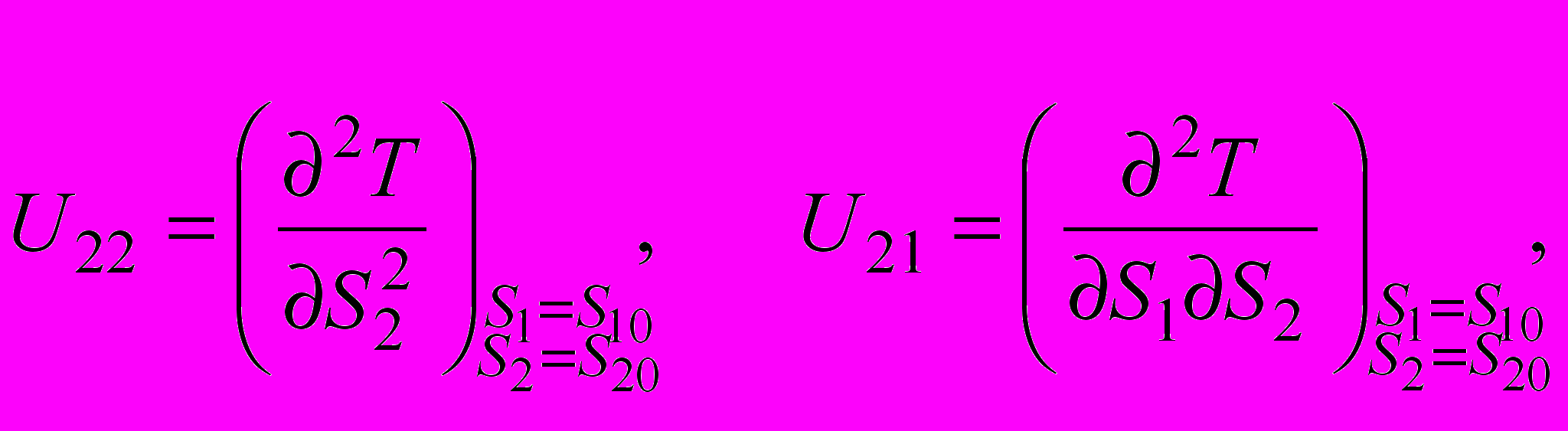(19)

K₁₂ - корреляционный момент (ковариация) случайных величин S₁ и S₂: для дискретных и непрерывных случайных величин, соответственно:

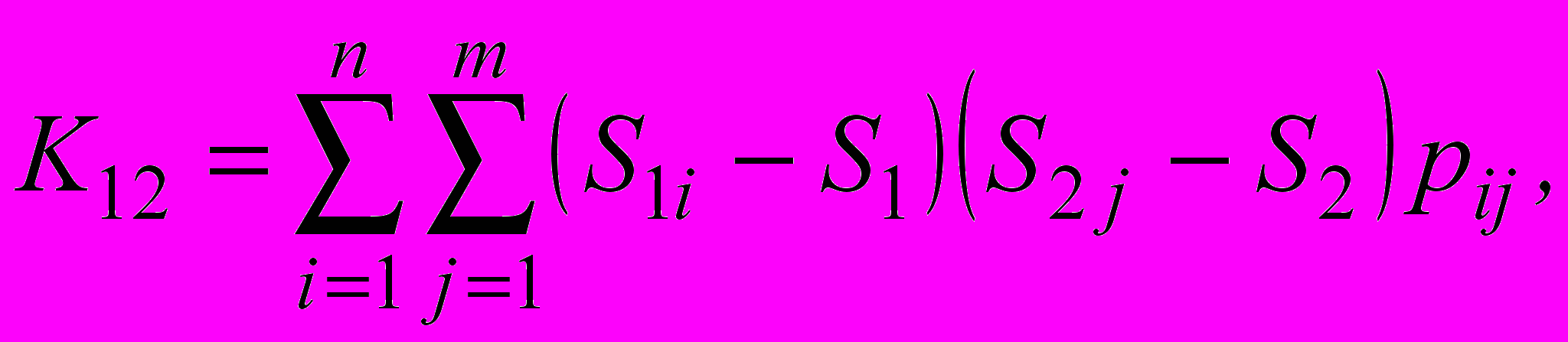(20)

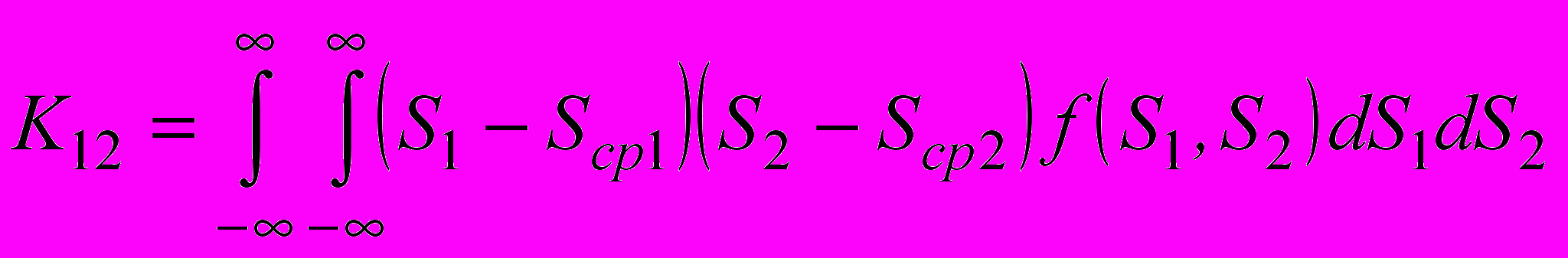, (21)

p_ij - вероятность отдельных значений S_1i и S_2j, f(S₁,S₂) - совместная плотность распределения случайных величин S_1i и S_2j [1].

Таким образом, при двух видах нагрузки технический объект характеризуется шестью величинами (T₀, U, U₁₁, U₁₂, U₂₁, U₂₂), а вектор нагрузки описывается пятью числовыми характеристиками - двумя средними значениями S₁ и S₂, двумя средними квадратическими отклонениями s_S1 и s_S2 и корреляционным моментом K₁₂.

Очевидно, для нахождения характеристик объекта необходимо в общем случае иметь значения средних наработок как минимум в шести различных режимах (при этом, соответственно, составляется и решается система шести уравнений).

Если в некоторых режимах одна или обе составляющие нагрузки равны стандартным (т.е. DS₁ = 0 и DS₂ = 0), то уравнение принимает вид

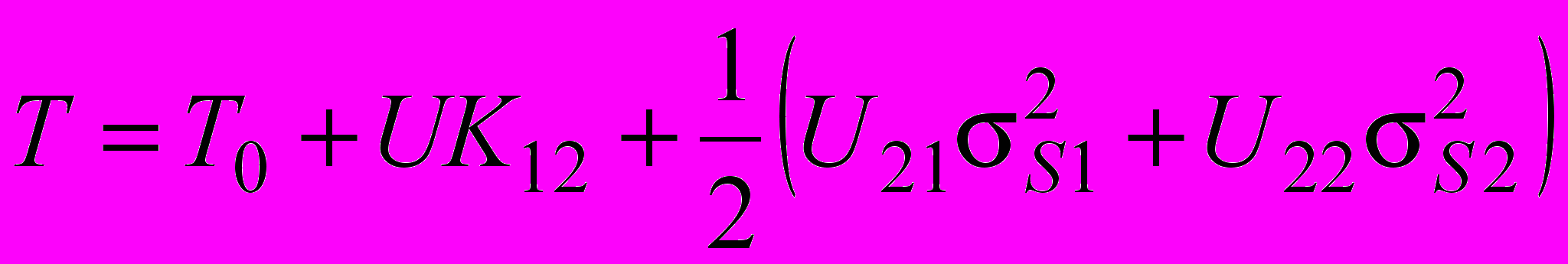, (22)

и система уравнений и ее решение упрощается. Если, кроме того, некоторые из режимов соответствуют принятым в лабораторных условиях и s_S1 = 0 или s_S2 = 0, то решение еще более упрощается.

Приведенным методом экспериментальные данные о надежности могут быть пересчитаны на новые условия эксплуатации при сопоставлении данных лабораторных испытаний с данными реальной эксплуатации, что значительно упрощает задачу обеспечения надежности технических объектов с учетом условий их эксплуатации.

Опыт применения концепции риска при проведении эксплуатационного контроля и вероятностного анализа надежности технических объектов также подтвердил её высокую эффективность, целесообразность и перспективность, как инструмента системного анализа безопасности технических объектов, который позволяет эффективно решать проблемы оптимизации техногенных рисков в условиях ограниченных ресурсов.

Задача управления техногенным риском и обеспечения надежности и промышленной безопасности на конкретном техническом объекте при проектировании и эксплуатации может быть формализована как минимизация функции, представляющей собой сумму рисков всех возможных событий в жизни технического объекта [4]:

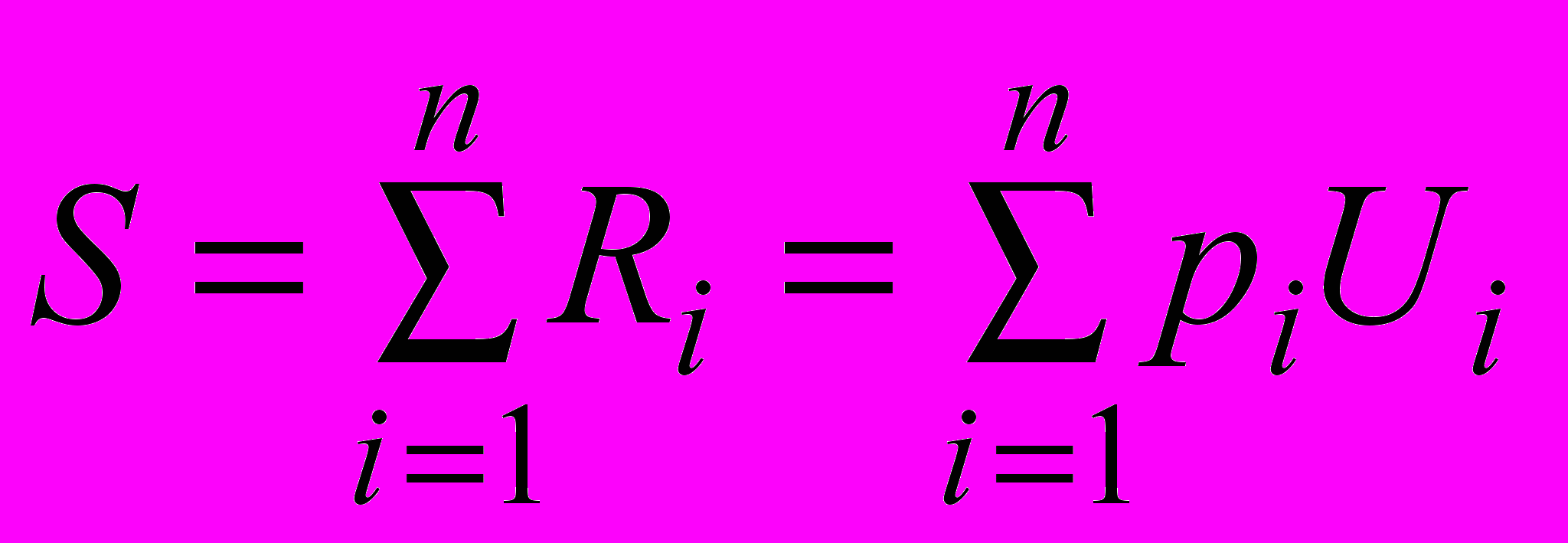, (23)

где p_i – вероятность i-го события, U_i – убытки при реализации i-го события.

Функция (23) может использоваться как для оценки надежности и безопасности, так и при выборе оптимальных проектных и управленческих решений и представляет собой простейший вариант модели «ожидаемой полезности» в теории принятия решений. При этом должны учитываться все возможные события – полный и частичные отказы, перевод объекта в состояния технического обслуживания разных видов, контроль, диагностика, профилактические работы и т.д. В качестве последствий аварийных отказов учитываются прямые и косвенные социальный, экономический и экологический ущербы [4]. При этом все виды ущерба должны выражаться количественно и в одних единицах измерения.

В простейшем случае в качестве критерия для расчета периодичности технического обслуживания (или проведения диагностики) может приниматься минимум средних удельных (на единицу времени) суммарных потерь от отказов и планового технического обслуживания в течение периода между восстановлениями:

S(t) = Up(tCp(t³t), (24)

где U – ущерб от отказа; C – затраты и потери, связанные с проведением технического обслуживания; t – время работы до отказа; t - период между техническими обслуживаниями.

Если известна функция вероятности безотказной работы P(t) или вероятности отказа Q(t) = 1 – P(t), то формулу (24) можно записать в виде

S(t) = UQ(t) + C[1 – Q(t)] = U[1 – P(t)] + CP(t). (25)

Очевидно время работы между восстановлениями t_p = min{t,t}.

Следовательно, математическое ожидание времени работы

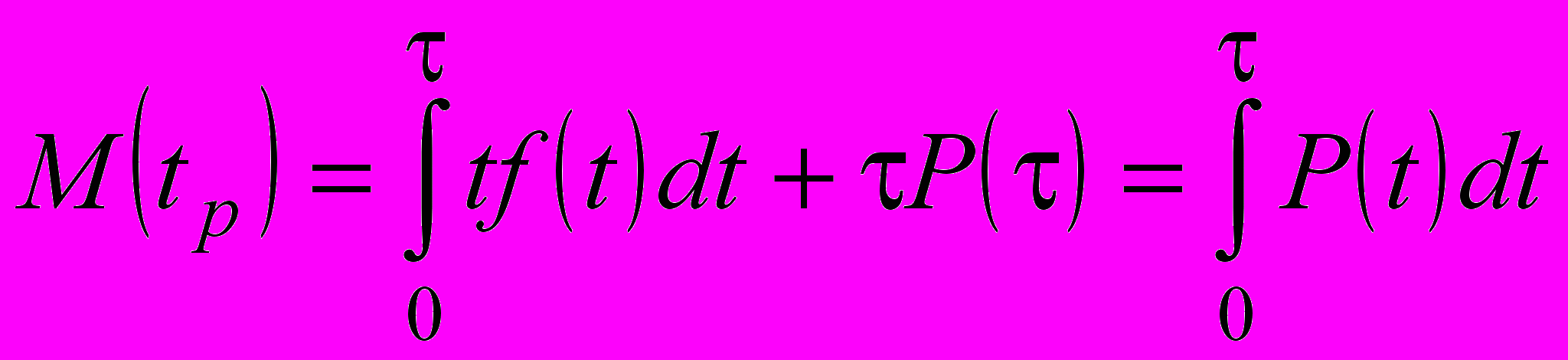. (26)

Тогда средние удельные затраты

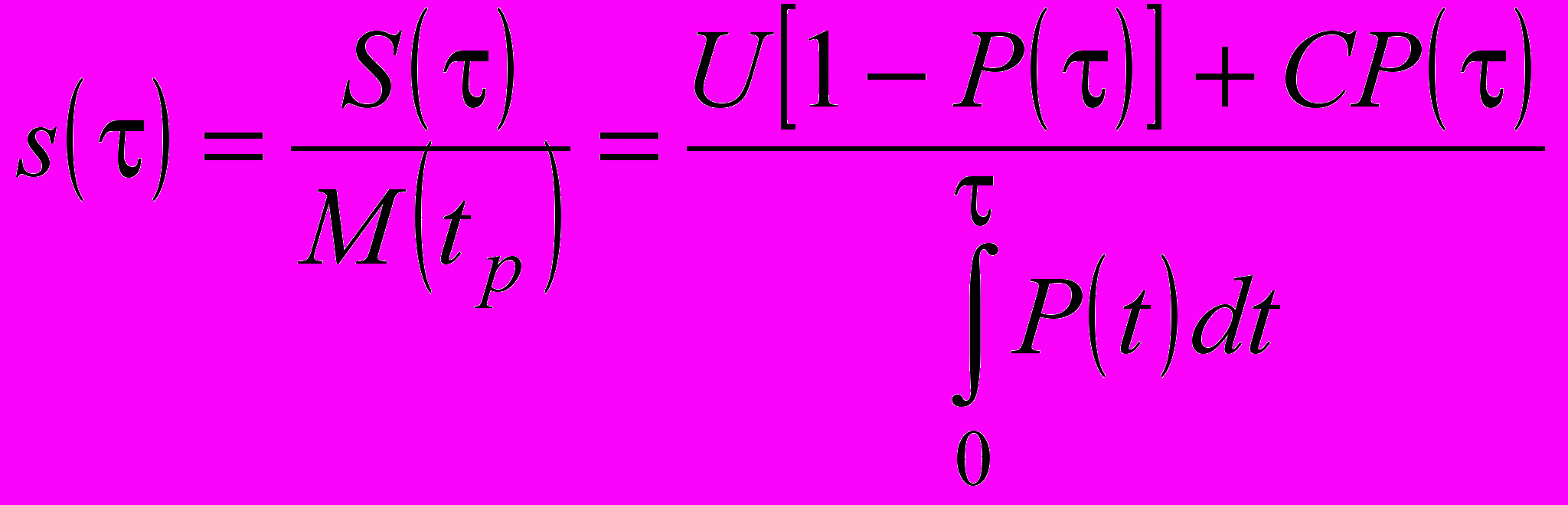. (27)

Для определения значения времени или наработки t, при которых средние удельные затраты s(t) будут минимальными, необходимо производную функции (27) приравнять нулю. После этого можно получить

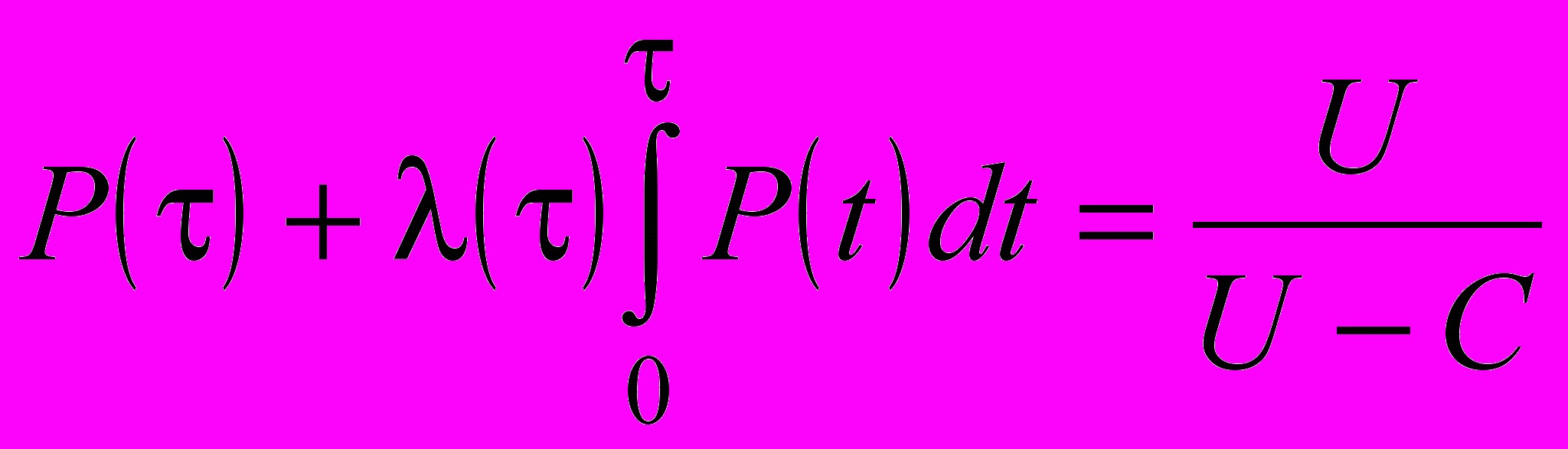. (28)

При известных функциях P(t) и l(t) уравнение (28) позволяет найти оптимальную продолжительность работы технического объекта между плановыми техническими обслуживаниями.

Если у объекта возможны только неявные отказы, то при прочих равных условиях в выражении (24) в суммарных затратах необходимо учесть дополнительные потери от скрытого отказа u:



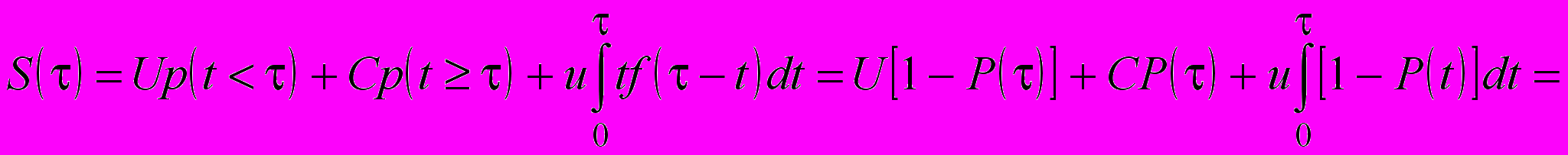
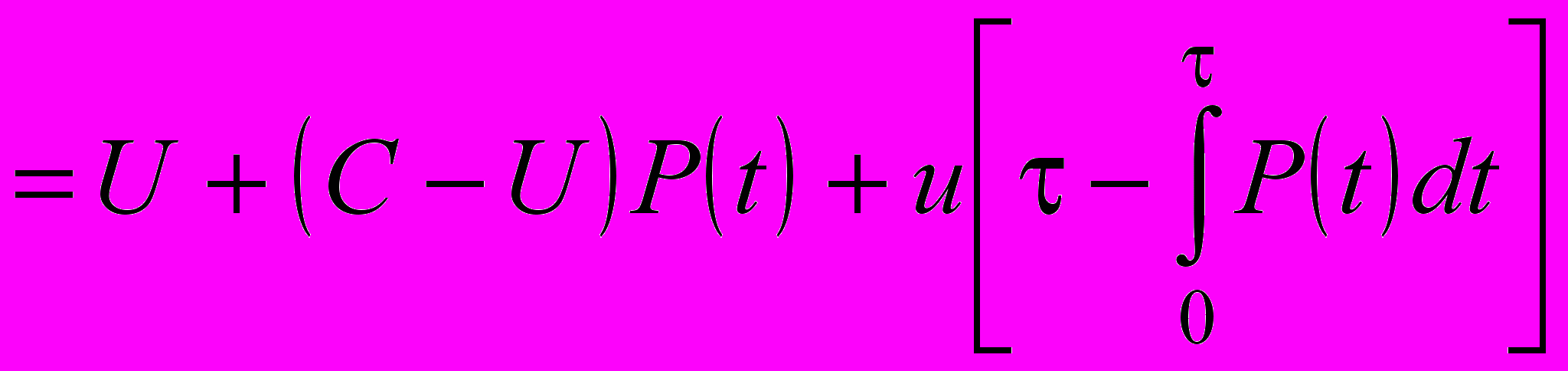. (29)

Средние удельные затраты за время t

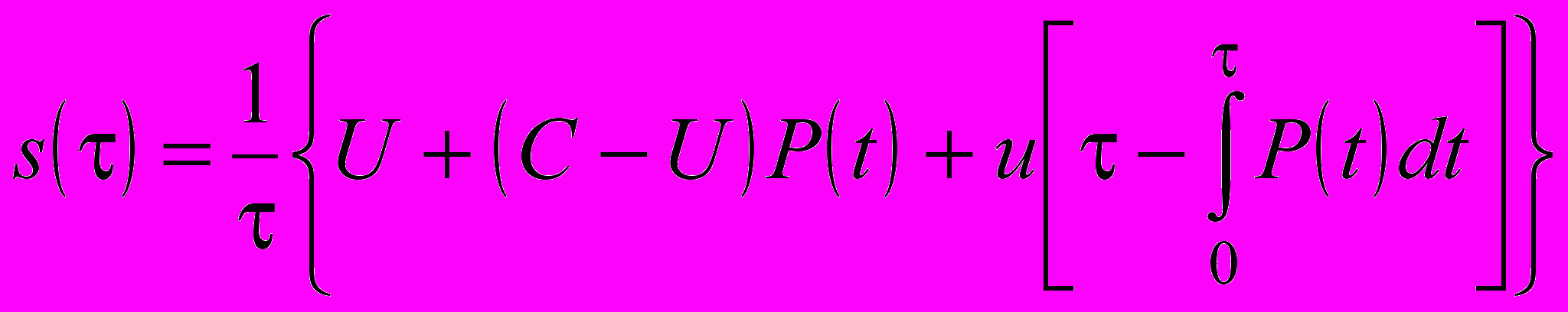. (30)

Приравняв нулю производную выражения (30) по t, получим уравнение:

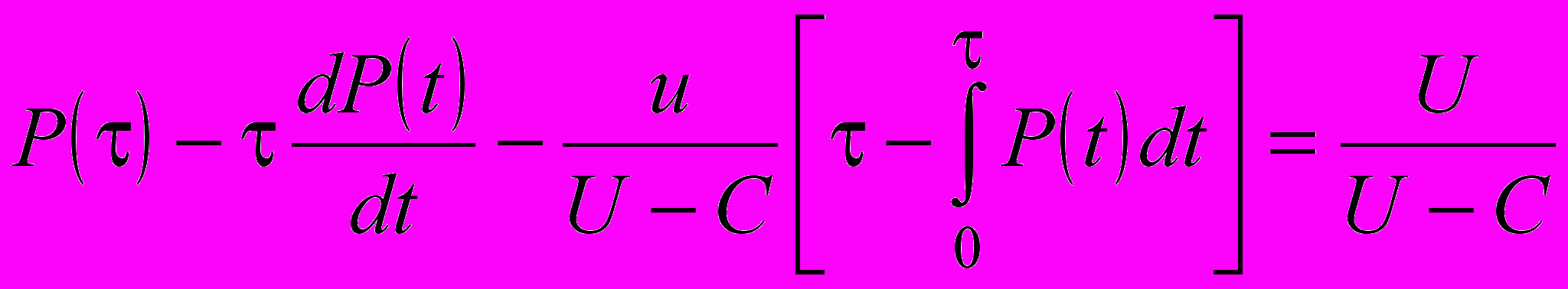, (31)

решением которого можно определить оптимальную периодичность технического обслуживания.

Для объекта с периодическим техническим обслуживанием функцию риска (23) можно представить в виде

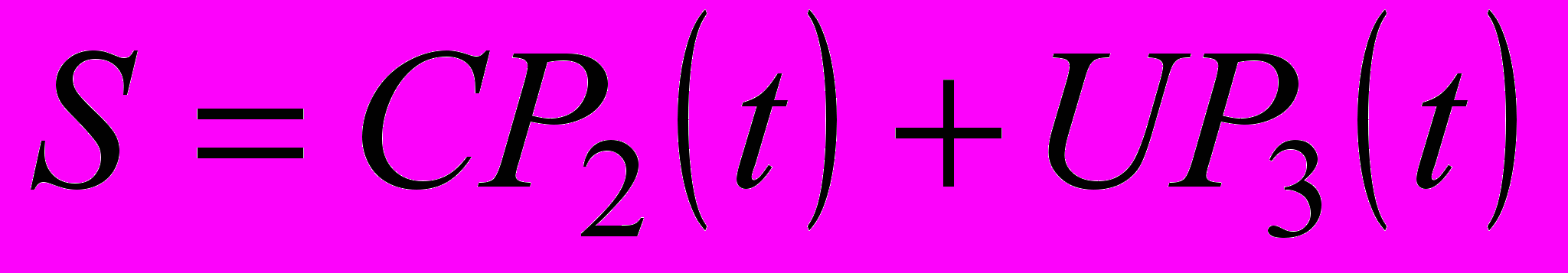. (32)

Для установившегося режима и финальных вероятностей состояний оптимальная периодичность технического обслуживания, обеспечивающая минимальное значение величины техногенного риска (32), определяется, в первую очередь, отношением ущерба от аварийного отказа U и затрат на техническое обслуживание C .

В табл.1 представлены результаты расчетов оптимальной периодичности технического обслуживания Т_opt, обеспечивающие минимальное значение величины техногенного риска S_min при заданных параметрах интенсивности отказов l, продолжительности технического обслуживания τ и отношения убытков (потерь) при аварийном отказе к затратам на техническое обслуживание U/C.

Например, при заданных l = 10^-7 ч^-1 и τ = 100 ч, отношении затрат U/C = 100 с учетом финальных вероятностей состояний величина минимального техногенного риска S_min = 0,0613 и оптимальная периодичность технического обслуживания Т_opt = 3066ч ≈ 5 мес.

Таблица 1
Оптимальная периодичность технического обслуживания
t, ч	U/C	Периодичность технического обслуживания Topt, ч
		l = 10-8 ч-1	l = 10-7 ч-1	l = 10-6 ч-1
10	10	9992	3154	992
	100	3152	990	307
	1000	990	306	91
	10000	306	91	23
20	10	14126	4456	1398
	100	4453	1395	428
	1000	1394	428	123
	10000	428	123	29
50	10	22321	7031	2196
	100	7022	2188	660
	1000	2187	659	179
	10000	659	179	37
100	10	31543	9920	3083
	100	9902	3066	907
	1000	3064	905	232
	10000	905	232	41

Приведенная методика и результаты расчетов оптимальной периодичности технического обслуживания, при заданных параметрах интенсивности отказов, продолжительности технического обслуживания и отношения убытков (потерь) при аварийном отказе к затратам на техническое обслуживание, позволяют минимизировать техногенный риск и обеспечить оптимальное управление надежностью потенциально опасных промышленных объектов.

До последнего времени процесс обеспечения надежности считался как бы сопутствующим процессу создания системы. В настоящее время серьезно возросли требования, предъявляемые к эффективности, а следовательно и к надежности технических систем. Разрабатываемые модели позволяют осуществлять эффективное управление контролируемыми системами, включать полученные результаты в полномасштабную систему менеджмента сложных технических объектов.

Литература

1. Сугак Е.В., Василенко Н.В., Назаров Г.Г. и др. Надежность технических систем.- Красноярск: МГП «Раско», 2001.- 608 с.

2. Сугак Е.В. Окладникова Е.Н. Чувствительность надежности технических систем к условиям эксплуатации. /Вестник университетского комплекса: Сб.научн.трудов / Под общей ред. профессора Н.В.Василенко; Красноярск: ВСФ РГУИТП, НИИ СУВПТ.- 2006.-Вып.7(21).С.36-40.

3. Дружинин Г.В. Надежность автоматизированных производственных систем.- М.: Энергоатомиздат, 1986.- 480 с.

4. Окладникова Е.Н., Сугак Е.В. Оптимизация техногенного риска и системы технического обслуживания потенциально-опасных объектов.- Тр. IV Всероссийской конференции по финансово-актуарной математике и смежным вопросам "ФАМ-2005". Ч.2.- Красноярск: ИВМ СО РАН, 2005, с.104-113.