Горбункова Галина Дмитриевна элективный курс
| Вид материала | Элективный курс |
- Элективный курс «глобальные проблемы человечества», 121.74kb.
- В. А. Ходаков моу воротынская средняя школа Перемышльского района Калужской области, 76.7kb.
- Элективный курс по астрономии, 93.86kb.
- Пояснительная записка Элективный курс «Природа тел Солнечной системы» предназначен, 50.52kb.
- Ф. В. Чижова методическая разработка элективный курс, 490.04kb.
- Элективный курс «Методы решения задач по физике» 10 11 классы 68 часов, 115.81kb.
- Багровникова Светлана Владимировна, к ф. н., доцент элективный курс, 110.32kb.
- Липецка Учитель Тарасова Светлана Васильевна. Предмет математика. Класс 9 элективный, 242.74kb.
- Джейранов Федор Елефтерович, к ф. н., доцент элективный курс, 116.47kb.
- Р. И. Горелова элективный курс «молекулярные основы наследственности», 116.13kb.
Занятие 24 Работа силы и мощность.
Появлению в физике понятия «работа» предшествовал долгий период накопления человеком знаний о природе, о мире, о законах, которым подчиняются все явления во Вселенной. Жизнь и производственная деятельность людей потребовали от ученых в 19 веке ответа на вопросы: Как получать из тепла механическую работу? Как рассчитывать паровые машины, шахтные насосы? Понятие о работе развивалось вначале в рамках технической науки и инженерного дела. В 1774году русский ученый Сергей Котельников в своем курсе механики использует для оценки действия силы произведение силы на расстояние. Он пишет: «Действие силы равно тягости, умноженной на перейденный ею путь. Действие машины состоит в произведенном количестве движения. А оное количество движения равно тягости, помноженной на путь, ею перейденный. Следовательно, и действие силы равно тягости, помноженной на перейденный ею путь». Само слово «работа» было введено в физику через 30 лет, французским механиком Жаном Понселе. Сейчас мы рассматриваем различные виды работ: работа силы тяжести; работа сил всемирного тяготения; работа силы трения.
Решение задач:
- Ведро с водой массой 10кг поднимают из колодца глубиной 8м равноускоренно за 3,2 с. Определить величину совершенной при этом работы.
Р
 ешение:
ешение:
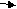 F
F
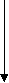
 mg
mgРабота постоянной силы при подъеме А=Fh, величину силы найдем из уравнения движения F-mg=mα. Ускорение α=2h/t2. Следовательно,
А=m(g+α)h=m(g+2h/t2)h.
А=910Дж.
- Чему равна работа по подъему цепи, взятой за один конец и лежащей на плоскости, на высоту, равную ее длине? Длина цепи 2м, масса 5кг.
- Определить работу, которую нужно произвести для того, чтобы сжать пружину на 10см. если для сжатия ее на 1см необходима сила 100н.
- Пуля ,летящая со скоростью 800м/с, пробивает несколько одинаковых досок, расположенных на некотором расстоянии друг от друга. В какой по счету доске застрянет пуля, если ее скорость после прохождения первой доски уменьшилась на 17%.
Мотор с полезной мощностью 25кВт, установленный на автомобиле. Может сообщить ему при движении по горизонтальному участку дороги скорость 90км/ч. Тот же мотор, установленный на моторной лодке, обеспечивает ей скорость не выше 15км/ч. Определить силу сопротивления движению автомобиля и моторной лодки при заданных скоростях.
Занятия 25 Динамика твердого тела. Момент инерции. Уравнение моментов.
В 1760 году вышла книга Леонардо Эйлера «Теория движения твердых и жестких тел». В этом труде Эйлер развил теорию моментов инерции и исследовал движение свободного твердого тела. Он пошел дальше исследования центрального движения, принятого со времен Ньютона, и рассмотрел в общем виде произвольное вращательное движение и движение под действием произвольных сил, подготовив, таким образом, почву для современной кинематики. В частности, вызывает восхищение в значительной части справедливое и сейчас аналитическое исследование движения волчка, в котором используются понятия момента и осей инерции.
Влияние собственных свойств тела на изменение вращательного движения оказывается значительно более сложным, чем в поступательном движении. Инертность тела по отношению к вращательному движению, ее влияние на угловое ускорение зависит не только от массы тела, но и от того, как она распределена относительно оси вращения. На инертность во вращательном движении влияют форма и геометрические размеры тела, его расположение относительно оси вращения, особенности распределения массы по объему тела. Момент инерции тела определяет инертность тела по отношению к вращательному движению. Инертность тела при вращении растет прямо пропорционально массе и квадрату расстояния от тела до оси вращения: J = mR2. Так находится момент инерции кольца при вращении вокруг выбранной оси. Момент инерции однородного диска такой же массы и такого же радиуса должен быть меньше, чем у кольца, так как значительная масса диска сосредоточена ближе к оси вращения: J =1/2 mR2. Момент силы М=βJ, где β – угловое ускорение. Это уравнение называется уравнением моментов.
Решение задач:
- Маховое колесо некоторой машины имеет радиус 2м и массу 1т. Маховик вращается, делая 120 оборотов в минуту. По окончанию работы маховик тормозится колодками, которые действуют на обод маховика с силой 100кгс. Определить, через какое время после начала торможения остановится маховик?
Решение:
Для простоты будем считать, что вся масса маховика сосредоточена на ободе и кроме колодок ничто не мешает его движению. Маховик совершает вращательное движение. Сила действия колодок создает момент силы М = FR, тормозящий движения этого маховика. Вращательное движения маховика будет замедляться. Нужно применить уравнение моментов, принимая направление вращения маховика положительным.
- FR = Jβ,
Так как по условию задачи, вся масса маховика сосредоточена на ободе, то его момент инерции равен: J = mR2.
Тогда: β = - F/mR.
По условию ускорение постоянно, тогда находим угловую скорость
ω = ω0 + βt, β меньше 0.
По условию задачи ω = 0, тогда
β = -- F/mR.
Отсюда
t = ω0mR/F, t=25с.
- Определить момент инерции диска радиусом 20см и массой 1кг относительно оси, перпендикулярной плоскости и проходящей через: а) центр диска; б) середину одного из радиусов диска
- Два маленьких шарика, массы которых 40г и 120г, соединены стержнем, длина которого 20см, а масса ничтожно мала. Определить момент инерции системы относительно оси, перпендикулярной стержню и проходящей: а) через середину стержня; б) сквозь центр массы системы.
- Найти момент инерции плоской однородной прямоугольной пластины массой 900г относительно оси, совпадающей с одной из сторон, если длина другой 20см.
- Маховик, момент инерции которого J=63,6кг·м2, вращается с постоянной угловой скоростью ω=31,4рад/с. Найти тормозящий момент, под действием которого маховик остановится через 20с.
Занятие 26 Закон сохранения момента импульса.
В механике имеется три закона сохранения: импульса, энергии и момента импульса. Все они являются следствиями законов движения. Если при вращении тела вокруг неподвижной оси момент внешних сил относительно этой оси равен нулю, то, равна нулю производная момента импульса, а это означает, что момент импульса остается постоянным:
Jω = соnst.
Из неизменности момента инерции J твердого тела, вращающегося вокруг определенной оси, следует постоянство угловой скорости вращения. Так, если бы не было силы трения, то не менялась бы угловая скорость вращающегося на оси колеса. В замкнутой системе тел полный момент импульса остается постоянным. Этот закон выполняется всегда, как и закон сохранения импульса.
Решение задач:
- Н
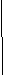 а краю горизонтальной платформы массой m и радиусом R , которая может свободно вращаться относительно оси ОА, закреплена небольшая пушка. Платформа сначала покоится. Затем из пушки производится выстрел. Снаряд летит по касательной к краю платформы со скоростью V. Масса снаряда mс, масса пушки mп. Определите угловую скорость платформы после выстрела. Пушку и снаряд можно рассматривать как материальные точки.
а краю горизонтальной платформы массой m и радиусом R , которая может свободно вращаться относительно оси ОА, закреплена небольшая пушка. Платформа сначала покоится. Затем из пушки производится выстрел. Снаряд летит по касательной к краю платформы со скоростью V. Масса снаряда mс, масса пушки mп. Определите угловую скорость платформы после выстрела. Пушку и снаряд можно рассматривать как материальные точки.
 О
О

А
Решение:
До выстрела момент внешних сил, действующих на пушку и платформу, равен нулю. Он равен нулю и после выстрела, так как при выстреле между пушкой и снарядом действуют лишь внутренние силы, суммарный момент которых равен нулю. Вследствие этого суммарный момент импульса снаряда, пушки и платформы остается неизменным. До выстрела он был равен нулю. Следовательно, он будет равняться нулю и после выстрела. Это означает, что момент импульса, которым обладает заряд, равен по модулю и противоположен по знаку моменту импульса платформы и пушки.
Момент импульса снаряда равен произведению импульса снаряда mсV на плечо, т.е. mсVR. Момент импульса платформы и пушки состоит из двух частей: момента импульса платформы 1/2· mR2ω. Учитывая, что момент импульса снаряда равен по модулю суммарному моменту импульса пушки и платформы, получим равенство:
mсVR. = mпR2ω + 1/2·mR2ω.
Отсюда находим угловую скорость вращения:
ω = mсVR/ (mп + 1/2m)R.
- На краю горизонтальной платформы, имеющий форму диска радиусом 2м и массой 4кг, стоит человек, масса которого 80кг. Платформа может свободно вращаться вокруг вертикальной оси, проходящей через ее центр. С какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью 2м/с относительно платформы?
- Однородный тонкий стержень массой 0,2кг и длиной 0,2м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О. В верхний конец стержня попадает пластилиновый шар массой 10г, движется со скоростью 10м/с и прилипает к стержню. Определить угловую скорость стержня.


 О
ОО
 mV
mV- Маховик, имеющий форму диска массой 48кг и радиусом 0,4м, может вращаться вокруг горизонтальной оси. К концу нити, намотанной на маховик, прикреплен груз массой 0,2кг, который удерживается на высоте 0,2м от пола. Какую максимальную угловую скорость приобретет маховик, если его отпустить?
- На барабан с горизонтальной осью вращения радиусом 0,5м намотан шнур, к концу которого привязан груз массой 10кг. Найдите момент инерции барабана, если известно, что угловое ускорение 2рад/с2. Трением пренебречь.
Занятие 27 Равновесие тел при отсутствии вращения.
Основателем статики заслужено считается Архимед. Первым научным трудом Архимеда было, по-видимому, исследование центров тяжести; в нем рассматриваются законы рычага и центры тяжести (барицентры) тел. Архимед выводит условие равновесие рычага, полученное из непосредственных опытов с рычагами:
« предположим, что равные тяжести, подвешенные на равных длинах, уравновешиваются. На неравных же длинах равные силы не уравновешиваются: опускается та часть (системы), где тяжесть подвешена на большем расстоянии»
« Соизмеримые величины уравновешиваются, если длины, на которых они подвешены, находятся в обратном отношении к тяжестям»
В работах Архимеда появляется фундаментальное понятие механики – понятие о центре тяжести.
С разработкой этого понятия связано и открытие другого фундаментального понятия механики – момента силы относительно прямой или плоскости:
«Две величины, подвешенные на плечах рычага, находятся в равновесии, если равны произведения их площадей или объемов на расстояние их центров тяжести от опоры»
Леонардо да Винчи также занимался исследованием центров тяжести плоских и объемных фигур. Как Архимед нашел центр тяжести треугольника, так и Леонардо находит центр тяжести и тетраэдра и пошел дальше, расширив понятие момента силы по отношению к точке, открыв для двух частных случаев теорему о разложении моментов и с удивительным искусством применив ее для решения задач о сложении и разложении сил.
Этими открытиями мы пользуемся при решении задач по статике.
Решение задач:
- Однородная балка лежит на платформе так, что один конец ее свешивается с платформы. Длина свешивающегося конца равна 0,25 длины всей балки. На конец балки в точке В действует сила 2.94 кН, под действием которой противоположный конец балки начинает подниматься. Найдите массу балки.
Решение:
 С О В
С О В
Сила тяжести, действующая на свешивающийся конец балки равна Р/4 и приложена к точке О. Уравнение моментов сил относительно точки С:
3Р/4 3l/8 =Fl/4 +Р/4 l/8, где l – длина балки; отсюда Р=F, или m =F/g =300кг.
2. Деревянный брусок лежит на наклонной плоскости. Масса бруска 2кг. Длина наклонной плоскости 1м, а высота 60см. Коэффициент трения бруска о наклонную плоскость 0,4. С какой силой нужно прижать брусок к наклонной плоскости, чтобы он оставался на ней в равновесии?
3. а) Два человека тянут канат за концы с силами равными по модулю, но противоположными по направлению; б)один конец каната прикреплен к неподвижной опоре, а другой тянет человек с силой 2F. В каком случае сила натяжения каната будет больше?
4. Какова должна быть приложенная сила, чтобы можно было равномерно двигать ящик массой 60 кг вдоль горизонтальной поверхности, если коэффициент трения между ящиком и площадкой 0,27, а сила действует под углом 30° к горизонту?
5. Груз массой 50кг прижат к вертикальной стене силой 118Н. Какую минимальную силу необходимо приложить к грузу, чтобы удержать его в покое; чтобы поднимать его равномерно вверх? Коэффициент трения скольжения 0.3.
Занятие 28 Центр тяжести.
Вопрос о центрах тяжести находится на стыке математики, прикладной и теоретической механики. Труды Аристотеля, Архимеда и Герона сохранены для всего средневековья. Леонардо да Винчи, несомненно, был знаком со многими трудами по механике. Помимо Аристотеля, Архимеда и Герона, он знал работы Евклида, Табита бен-Курра (826-901). Исследование центров тяжести плоских и объемных фигур, начатое великими мыслителями Архимедом и Героном, продолжил Леонардо да Винчи. Как Архимед нашел центр тяжести треугольника, так и Леонардо находит центр тяжести центр тяжести тетраэдра (а отсюда и произвольной пирамиды). К этому открытию он добавляет весьма изящную теорему о прямых, соединяющих вершины тетраэдра с центрами тяжести противоположных граней, пересекающихся в одной точке, являющейся центром тяжести тетраэдра и делящей каждую из прямых на две части, из которых та, что прилегает к вершине, втрое больше другой. Это первый результат, который наука добавила к исследованиям Архимеда о центрах тяжести.
Решение задач:
- И
 з квадратной стальной пластины со стороной 20см вырезан прямой круглый цилиндр, ось которого перпендикулярна основанию пластины и расположена на диагонали основания на расстоянии четвертой части этой диагонали от ближайшей вершины квадрата. Найти положение центра тяжести такой пластины. Радиус цилиндра 5см.
з квадратной стальной пластины со стороной 20см вырезан прямой круглый цилиндр, ось которого перпендикулярна основанию пластины и расположена на диагонали основания на расстоянии четвертой части этой диагонали от ближайшей вершины квадрата. Найти положение центра тяжести такой пластины. Радиус цилиндра 5см.
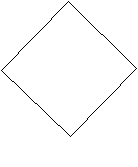


 СССОо·
СССОо·

 -Р1
-Р1

 h
h С О А Р1
С О А Р1 Р
РРешение: Центр тяжести цельной квадратной пластины расположен в точке О, а центр тяжести вырезанного цилиндра - в точке А. Центр тяжести фигуры, получившейся вычитанием цилиндра, расположен в точке приложения равнодействующей антипараллельных сил тяжести Р и –Р1.
Для сложения таких сил известно
СО/АС = Р1/Р.
Иначе СО/(АО +СО) = Р1/Р.
Значит, АО/СО +1+= Р1/Р.
А
 О – четверть диагонали основания пластины, а диагональ равна 2·ОВ = а√2 .
О – четверть диагонали основания пластины, а диагональ равна 2·ОВ = а√2 . АО =АВ = 1/4а √2 . Искомый отрезок СО =1,73·10-2м.
- Кусок какой длины нужно отрезать от однородного стержня, чтобы его центр тяжести сместился на 10см?
- Два шара одинакового объема, медный и цинковый, скреплены в точке касания. Найти положение центра тяжести системы шаров.
- Из однородного диска радиусом 105,6см вырезан квадрат так, как показано на рисунке. Определить положение центра тяжести диска с таким вырезом.


- В свинцовом шаре сделана сферическая полость, касающаяся поверхности шара и проходящая через его центр. Масса сплошного шара М, радиус шара R. Найти положение центра тяжести получившегося тела.
Занятие 29 Механические колебания.
Впервые о колебаниях маятника мы узнаем из работы Винченцо Вивиани, ученика Галилея « Исторические повествования о жизни синьора Галилея, члена академии деи Линчеи, благородного флорентийца». Винченцо Вивиани, ученик Галилея, который провел со своим учителем два последних года его жизни, рассказывает, что в 1583 году Галилей, наблюдая раскачивание лампады в Пизанском соборе, открыл закон постоянства периода качания маятника, причем, как советовал Кардан, время он измерял по биению собственного пульса. Это сообщение Вивиани многие считают легендой. Тем не менее Вивиани наверняка узнал об этом из собственных уст Галилея, и, если отбросить возможные приукрашивания, сущность рассказа Вивиани представляется истинной, потому что закон изохронизма рассматривается Галилеем и в «Диалоге о двух главнейших системах мира» и в «Беседах и математических доказательствах, касающихся двух новых наук». В последнем произведении один из участников диалога, Сальвиати, который представляет самого Галилея, действительно вспоминает о колебаниях лампады:
« Я тысячи раз наблюдал за колебаниями, в частности колебаниями подвешенной в церкви на длинном подвесе лампады, которую кто-нибудь нечаянно толкнул»
С этого началось изучение колебательных систем, а сейчас мы разбираем задачи о математических и пружинных маятниках, используя основные законы гармонических колебаний математической точки.
Решение задач:
- Математический маятник длиной Lсовершает колебания вблизи вертикальной стенки. Под точкой подвеса маятника, на расстоянии ½ от нее по вертикали, в стенке забит гвоздь. Найти период Т колебаний маятника.


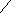
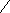
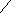
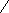
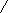
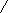
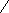
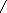



 А О В
А О ВРешение:
На участке АО маятник совершает колебания на нити длиной L.
П

 ериод таких колебаний Т = 2π√L/g , а время, затрачиваемое на прохождение дуги АО, t1=Т1/4. На участке ОВ маятник совершает колебания на нити длиной L/2 с периодом Т2 = 2π√(L/2)/g ,
ериод таких колебаний Т = 2π√L/g , а время, затрачиваемое на прохождение дуги АО, t1=Т1/4. На участке ОВ маятник совершает колебания на нити длиной L/2 с периодом Т2 = 2π√(L/2)/g ,причем время прохождения ОВ: t2 = Т2/4.
П
 усть Т – искомый период колебаний маятника, тогда Т/2 =Т1/4 + Т2/4, Т =(Т1 + Т2)/2 = π√L/g ( 1+1/√2 ).
усть Т – искомый период колебаний маятника, тогда Т/2 =Т1/4 + Т2/4, Т =(Т1 + Т2)/2 = π√L/g ( 1+1/√2 ).- На какую часть длины надо уменьшить длину математического маятника, чтобы период колебаний маятника на высоте 10км был равен периоду его колебаний на поверхности Земли? Радиус Земли 6400км.
- Определить период колебания тела массой 200г, подвешенного на пружине с коэффициентом жесткости 40Н/м.
- На вертикально расположенной пружине с коэффициентом жесткости 60 Н/м подвешен груз массой 300г. Грузу сообщают начальную скорость 10 м/с, направленную вертикально вниз. Определить период и амплитуду колебаний груза.
- Точка совершает гармонические колебания вдоль некоторой прямой с периодом 0, 6 с и с амплитудой 10 см. Найти среднюю скорость точки за время, в течении которого она проходит путь 5 см: 1) из положения равновесия; 2) из крайнего положения.
Занятие 30 Механические волны. Звук.
Теорию волнового распространения движения Ньютон начинает рассматривать с колебательного движения жидкости в U- образном сосуде и показывает, что колебания жидкости подобны колебаниям маятника. Затем он показывает, что возмущение, вызванное в точке А жидкости, распространяется волнообразно. Впервые применяется, по крайней мере как термин, общепринятое сейчас выражение «длина волны». Находится скорость распространения упругих волн, равная квадратному корню из отношения модуля упругости к плотности среды. В последнем «поучении» Ньютон заключает, что эти предложения применимы к распространению звука. Ньютон дал первый расчет длины волны звука и пришел к выводу, хорошо известному сейчас в физике. Что для любой открытой трубы длина волны испускаемого звука равна удвоенной длине трубы.
« И в этом состоят главнейшие звуковые явления».
На этом Ньютон заканчивает эту часть труда с чувством удовлетворения, ибо ему удалось превратить акустическую науку в раздел механики, чем она остается и поныне.
Решение:
- Определите скорость распространения продольной упругой волны малой амплитуды в стальном стержне.
Решение: Для того чтобы возбудить в стержне продольную волну, надо произвести удар по его торцу. В результате стержень деформируется на величину ΔL = uΔt, где u – скорость, приобретенная частицами стержня при ударе,Δt - время удара. За время Δt фронт возбужденной при деформации стержня продольной волны переместится на расстояние L = VΔt, где V – скорость распространения продольных волн. Следовательно, за время Δt в колебательное движение приходит часть стержня массой Δm =ρSL = ρSVΔt, где S – площадь поперечного сечения стержня. По второму закону Ньютона:
FΔt = Δ(mu) = Δmu = ρSVuΔt,
или F = ρSVu, где ρ – плотность стали.
Согласно закону Гука имеем:
F/S = ЕΔL/L, где Е – модуль Юнга.
Отсюда F =ЕS ΔL/L = ЕSuΔt/(VΔt) = ЕSu/V.
Получим ЕSu/V = ρSuV.
О
 тсюда V = √Е/ρ.
тсюда V = √Е/ρ.Е =2,1·1011Па, ρ = 7,8·103 кг/м3, определим V=5,2·103 м/с.
- Движущийся по реке теплоход дает свисток, частота которого 400Гц. Стоящий на берегу наблюдатель воспринимает звук свистка как колебания с частотой 395 Гц. С какой скоростью движется теплоход? Приближается или удаляется он от наблюдателя? Скорость звука принять равной 340 м/с.
- Определите собственные частоты колебаний воздушного столба в закрытой с обоих концов трубе длиной 3,4 м. Скорость звука принять 340 м/с.
- Скорость звука в стержне из дюралюминия 5100 м/с. Плотность дюралюминия 2700 кг/м3. Определите модуль Юнга.
- На расстоянии 1068 м от наблюдателя ударяют молотком по железнодорожному рельсу. Наблюдатель, приложив ухо к рельсу, услышал звук на 3 секунды раньше, чем он дошел до него по воздуху. Чему равна скорость звука в стали? Скорость звука в воздухе принять равной 333 м/с.
Занятие 31 Гидростатика.
Еще Леонардо да Винчи знал принцип сообщающихся сосудов для жидкостей различной плотности и основной закон гидростатики, известный теперь под названием «закона Паскаля. В эпоху Возрождения обострился старинный спор между сторонниками и противниками пустоты. Перипатетики продолжали объяснять различные физические явления, как, например, действие сифонов, медицинских банок, пипеток и др., тем, что природа боится пустоты. Сторонников пустоты (вакуистов) объединяла одна черта: они признавали что воздух обладает «абсолютным» весом, т.е. весом воздуха, «вынутого из атмосферы». Это может показаться странным сейчас, но для первых физиков воздух в воздухе ничего не весил, как и вода в воде. Но отрицать, что часть жидкости, находящаяся внутри жидкости, имеет вес, значит отрицать, что внутри массы жидкости уравновешиваются давления, приложенные к этому весу. Иными словами, наличие веса у воздуха не приводило к выводу об атмосферном давлении, а в некотором смысле даже исключало его. Некоторые идеи о внутреннем давлении были у Леонардо да Винчи, но их обобщение на воздух после определения его плотности Галилеем потребовало еще 30 лет работы до всем известного опыта Торричелли.
Решение задач:
- Сосуд, имеющий форму усеченного конуса с приставным днем, опущен в воду. Если в сосуд налить 200г воды, то дно оторвется. Отпадет ли дно, если на него поставить гирю 200г? Налить 200г масла? Налить 200г ртути?
Решение: Если сосуд сужается кверху, то гиря и ртуть не оторвут дно, а масло – оторвет. Если же сосуд сужается книзу, то наоборот.
На дно изнутри действует сила давления ghS
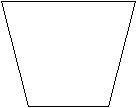















Если сосуд сужается кверху, то эта сила больше веса жидкости, налитой в конус, на величину веса жидкости, занимающей заштрихованный объем. Поэтому ртуть и гиря не оторвут дна. Масло оторвет дно, так как в случае конуса, сужающегося кверху, произведение h для масла больше, чем для воды (масло займет больший объем, чем такое же количество воды). Связанное с этим относительное увеличение высоты уровня h больше относительного уменьшения плотности .
Если сосуд сужается книзу, то сила давления жидкости, налитой в сосуд, на дно меньше ее веса на величину веса жидкости в заштрихованном объеме. Поэтому в этом случае масло не оторвет дна, а гиря и ртуть оторвут.
- В сосуд с водой вставлена трубка сечением 2см2 . В трубку налили 72г масла плотностью 900кг/м3. Найдите разность уровней масла и воды.
- Льдина площадью поперечного сечения 1м2 и высотой 0,4м плавает в воде. Какую работу нужно совершить, чтобы погрузить полностью льдину в воду?
- Прямоугольная коробочка из жести массой 76г и площадью дна 38см2и высотой 6см плавает в воде. Определите высоту надводной части коробочки.
- Вес тела в воде в три раза меньше, чем в воздухе. Какова плотность материала тела?
Занятие32 Гидродинамика. Течение идеальной жидкости.
Вся первая книга «Начал» написана в предположении, что тела движутся в среде без сопротивления, под действием одних лишь приложенных сил. Для завершения учения о движении нужно исследовать, как это и делает Ньютон во второй книге, какие изменения испытывают найденные законы движения, когда тела движутся в жидкости, как это имеет место в земных условиях. В этой работе Ньютон рассматривает истечение жидкостей из сосудов. Многие экспериментаторы, начиная с Торричелли, занимались этим, но мало что добавили нового. Уже во втором издании книги Ньютон дал точный вывод скорости истечения. Он заметил сжатие струи жидкости у отверстия и приближенно измерил его, но дал ему неудовлетворительное объяснение, основываясь на представление о сходимости нитей потока жидкости. Идеальной жидкостью условились называть жидкость, если бы она была лишена трения. Однако во всех реальных жидкостях существует внутреннее трение.
Решение задач:
- Из брандспойта бьет струя воды. Расход воды Q=60л/мин. Какова площадь поперечного сечения струи S1 на высоте h =2м над концом брандспойта, если вблизи него сечение равно S0 = 1.5см2.
Решение:
Скорость воды у конца брандспойта V0=Q/S0.
Вылетая из брандспойта, вода движется равнозамедленно с ускорением g, и поэтому на высоте h скорость воды
 V=√V02 - 2gh.
V=√V02 - 2gh. Из уравнения непрерывности струи V0S0 =VS , выражающего собой то, что масса жидкости, протекающей через любое поперечное сечение струи в единицу времени, одна и также, получим:
Из уравнения непрерывности струи V0S0 =VS , выражающего собой то, что масса жидкости, протекающей через любое поперечное сечение струи в единицу времени, одна и также, получим:S = V0/V·S0 =Q/ √(Q/S0)2 - 2gh
S = 4,37 см2.
- Вода течет по горизонтальной трубе переменного сечения. Скорость течения в широкой части трубы 20 см/с. Определите скорость течения воды в узкой части тубы, диаметр которой в 1,5 раза меньше диаметра широкой части.
- В широкой части горизонтально расположенной трубы нефть течет со скоростью 2м/с. Определите скорость течения нефти в узкой части трубы, если разность давлений в широкой и узкой частях трубы составляет 50мм.рт.ст.
- На какой высоте площадь поперечного сечения струи фонтана будет в n раз больше площади выходного отверстия трубки? Скорость воды на выходном отверстии трубки V.
- Бак, заполненный водой до высоты 1м, пробивается пулей на высоте 0,1м. На какое расстояние от бака будет бить струя воды?
Литература:
- Баканина Л.П. Сборник задач по физике. М.: Наука, 1990.
- Балаш В.А. Задачи по физике. М.: Просвещение, 1983.
- Блудов М.И. Беседы по физике. М.: Просвещение, 1984.
- Бутиков Е.И. Физика в примерах и задачах. М.: Наука, 1989.
- Воробьев И.И. Задачи по физике. М.: Наука, 1988.
- Гольдфарб Н.И. Сборник вопросов и задач по физике. М.: Высшая школа, 1982.
- Евграфова Н.Н., Каган В.Л. Курс физики. М.: Высшая школа, 1973.
- Зубов В.Г. Задачи по физике. Задачи по физике. М.: Наука, 1985.
- Зубов В.Г. Начала физики. М.: наука, 1978.
- Марио Льоцци, История физики. М.: Мир, 1970.
- Мощанский В.Н. История физики в средней школе. М.: Просвещение, 1981.
- Роджерс Э. Физика для любознательных. М.: Мир, 1972.
