Горбункова Галина Дмитриевна элективный курс

Вид материала

Элективный курс

Содержание Занятие 1 История развития механики. Средние века Восемнадцатый век Занятие 2 Прямолинейное равномерное движение. Занятие 3 Относительность движения. Занятие 4 Прямолинейное равнопеременное движение. Занятие 5 Движение тела, брошенного вертикально. Занятие 6 Движение тела, брошенного под углом к горизонту. Занятие 7 Вращательное движение тел Занятие 8 О законе всемирного тяготения. Занятие 9 Законы Кеплера. Занятие 10 Закон Гука. Занятие 12 О силе трения Занятие 14 Динамика тела, движущегося прямолинейно (если тело движется по наклонной плоскости или под действием силы, приложенно Занятие 15 Динамика движения тела в вязкой среде. Занятие 16 Динамика движения системы тел. Занятие 19 Столкновения. Занятие 21 О потенциальной энергии Занятие 23 Применение законов физики в ядерной физике Занятия 25 Динамика твердого тела. Момент инерции. Уравнение моментов. ... Полное содержание

Подобный материал:

• Элективный курс «глобальные проблемы человечества», 121.74kb.
• В. А. Ходаков моу воротынская средняя школа Перемышльского района Калужской области, 76.7kb.
• Элективный курс по астрономии, 93.86kb.
• Пояснительная записка Элективный курс «Природа тел Солнечной системы» предназначен, 50.52kb.
• Ф. В. Чижова методическая разработка элективный курс, 490.04kb.
• Элективный курс «Методы решения задач по физике» 10 11 классы 68 часов, 115.81kb.
• Багровникова Светлана Владимировна, к ф. н., доцент элективный курс, 110.32kb.
• Липецка Учитель Тарасова Светлана Васильевна. Предмет математика. Класс 9 элективный, 242.74kb.
• Джейранов Федор Елефтерович, к ф. н., доцент элективный курс, 116.47kb.
• Р. И. Горелова элективный курс «молекулярные основы наследственности», 116.13kb.

Элективный курс по физике

«Многообразный мир движения»

Учитель МОУ «СОШ №50» Горбункова Галина Дмитриевна


Элективный курс «Многообразный мир движения» предназначен для учащихся 10 и 11 классов общеобразовательных школ. Основное направление современной физики – изучение наиболее общих форм движения материи, лежащих в основе всех природных явлений; установление законов этих движений и их всеобщей взаимосвязи между собой. Эти законы таковы, что им подчиняются все без исключения тела, где бы они не находились, когда бы не наблюдались и каким бы изменениям ни подвергались. Формы движения материи, изучаемые физикой, называют физическими процессами или физическими явлениями.

Простейшее, что мы видим повседневно, это непрерывно происходящие изменения положений тел друг относительно друга с течением времени. Это физическое явление служит предметом изучения раздела физики, называемого механикой. Законам механических явлений подчиняются не только тела, окружающие нас на Земле. Им подчиняются в своих движениях и звезды, и галактики, и самые маленькие, невидимые частицы вещества - атомы и их составные части. Механические процессы принадлежат к числу наиболее общих форм движения материи, и они присутствуют как обязательные участники во всех других явлениях природы.

Логика школьного курса физики требует, чтобы его изучение начиналось с механики. Так как из всех форм движения материи механическое движение наиболее наглядно; в классической физике моделирование физических явлений связано с созданием преимущественно механических образов структуры физических систем и происходящих в нем процессов.

Выбор данной темы для элективного курса обоснован тем, что при изучении механики имеется возможность показать, как с помощью минимального числа физических законов едиными методами решается большое число задач на движение и равновесие тел. Целесообразно на занятиях элективного курса уделить внимание истории изучения механического движения, показать его значимость.

«…от явлений движения к исследованию природы сил и затем от этих сил - к демонстрации других явлений: … движения планет, комет, Луны и моря…»

Исаак Ньютон (1686 г.)

Курс рассчитан на 34 часа. Занятия включают в себя и исторические сведения, и описание известных задач физики, но основную часть занимает решение задач. Основная цель курса в том, чтобы учащиеся овладели такими общими научными методами, как анализ и синтез, индукция и дедукция, пополнили свой банк решенных задач, так как решение задач по механике способствует развитию научно- технического мышления, политехнического обучения.

Планируется, что после завершения изучения данного курса учащиеся будут лучше разбираться в вопросах механики твердого тела, самостоятельно применять основные принципы и законы в практической деятельности, видеть действие этих принципов в новых открытиях и достижениях техники.


Содержание курса:

Тема занятия:	Кол-во занятий
Введение. История развития механики.	1
Кинематика	6
О прямолинейном равномерном движении	1
Относительность движения	1
Прямолинейное равнопеременное движение	1
Движение тела, брошенного вертикально	1
Движение тела, брошенного под углом к горизонту	1
Вращательное движение тела	1
Силы в механике	5
Всемирное тяготение	1
Законы Кеплера	1
Закон Гука	1
Вес тела	1
Сила трения	1
Динамика	5
Динамика тела, движущегося прямолинейно	2
Динамика движения системы тел	1
Динамика движения тела в вязкой среде	1
Динамика вращательного движения тела	1
Закон сохранения импульса	1
Столкновения	1
Энергия и закон сохранения энергии	5
О кинетической энергии	1
О потенциальной энергии тела	1
Закон сохранения энергии	1
Применение законов механики в ядерной физике	1
Работа и мощность	1
Динамика твердого тела	2
Вращение тела. Момент инерции. Уравнение моментов	1
Закон сохранения момента импульса	1
Статика	2
Равновесие тел при отсутствии вращения	1
Центр тяжести	1
Механические колебания	1
Механические волны. Звук	1
Гидростатика	1
Гидродинамика. Течение идеальной жидкости.	1
Подведение итогов. Конкурс на самую красивую задачу по механике	2

Занятие 1 История развития механики.


Античность. Эллинский период.

Наличие обширного комплекса практических знаний и технических навыков, высокий общий культурный уровень, а также язык, уже отточенный на тонких философских и математических исследованиях, - все это создало почву в Греции в IV веке до н.э. для начала работы по описанию, упорядочению и объяснению явлений природы. Вокруг этого ядра в течение веков сформировалась физика.

Практические знания и технический опыт, как и некоторые начатки научных исследований, пришли к грекам от народов еще более древней культуры, в первую очередь из Вавилона и Египта; самые древние научные достижения Китая, начало которых можно отнести к XIII веку до нашей эры. Так в Вавилоне и Древнем Египте был предпринят ряд попыток упорядочения данных опыта и наблюдения: введение уже к 2500 году до н.э. фиксированных единиц измерения длины, веса и емкости.

Общий уровень греческой культуры, несомненно, способствовал тому, что техника переросла в науку, связывающую воедино и объясняющую совокупность накопленных сведений и позволяющую таким образом предвидеть явления и влиять на них.

Особую роль в развитии физики сыграл Аристотель со своим трудом о природе. Организаторский гений Аристотеля позволил свести обширный материал в единую систему, которая в течение почти двух тысяч лет служила каркасом науки. Аристотелевская физика уделяет огромное значение механике. Он изучает свободное падение тел вниз. Большой заслугой аристотелевской кинематики была формулировка точного правила сложения перемещений, формулировку принципа инерции, формулировку правила равновесия рычага, описывает действие весов и блоков.

Данная эпоха ознаменована успехами Архимеда, который сконструировал мосты и дамбы, подъемный винт, различные боевые машины многое другое. Архимед считается основателем статики и гидростатики. Первым научным трудом Архимеда считается исследование центров тяжести.

Средние века

В общей механике арабы следовали Аристотелю и не внесли в нее сколько-нибудь значительных изменений, лишь внесли некоторый вклад в гидростатику. Аль – Наиризи написал трактат об атмосферных явлениях. Аль-Рази ввел в употребление гидростатические весы для определения удельного веса.

Возрождение

Эпоха возрождения связана с именем Леонардо да Винчи – великого изобретателя. Историки техники насчитывает сотни изобретений, среди которых приспособления для преобразования и передачи движения; простые и переплетенные ременные передачи; различного вида сцепления; роликовые опоры для уменьшения трения; «кардановое» соединение; различные станки и многое другое. В старинной науке гидравлике Леонардо был большим мастером и спроектировал землечерпалки, использовал принцип сообщающихся сосудов, нашел центр тяжести плоских и объемных фигур.

Пизанский период отмечен деятельностью Галилея, который открыл закон постоянства периода качания маятника, исследовал свободное падение тел, доказывает теорему моментов. Галилей закладывает два краеугольных камня современной динамики: принцип инерции и классический принцип относительности.

Современным своим видом классическая механика обязана Ньютону, который сформулировал основные законы движения.

Восемнадцатый век

Задачей восемнадцатого века было связать отдельные достижения ученых прошлого столетия в одну связную картину с помощью систематического применения методов математического анализа к исследованию физических явлений. В этом – главный вклад этого века в дальнейшее развитие науки.


Занятие 2 Прямолинейное равномерное движение. Движению, родившийся в 384 г. до н. э., Аристотель придавал значительно более широкий смысл, чем принято в физике со времен Галилея. Аристотель понимает под движением любое количественное или качественное изменение, благодаря которому явление реализуется. Такое широкое понимание движения позволяет ему утверждать, что в природе все есть движение. Частному понятию изменения положения тела с течением времени он дал наименование локального движения, а локальные движения он разделял на естественные и насильственные. К естественным он относил и прямолинейное равномерное движение.

Хотя этот вид движения является самым простым из всех видов движения, необходимо решение задачи разбить на несколько этапов:

Качественный анализ всех возможных движений каждого тела, данного в задаче.

Определение порядка отсчета времени и длин путей.

Указание начальных состояний движения для каждого тела.

Написание законов движения для каждого тела.*

Отыскание недостающих уравнений.

Алгебраическое решение полученной системы уравнений и отыскание расчетных формул для определения неизвестных величин.

Согласование единиц всех величин и арифметический расчет числовых значений неизвестных.

Решение задач:

1. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч. Далее половину пути он ехал со скоростью 6 км/ч, а затем до конца пути шел пешком со скоростью 4 км/ч. Определите среднюю скорость велосипедиста на всем пути.
   

Решение: Установив, что задача на прямолинейное равномерное движение одного тела, и представив себе весь процесс движения, делаем схематичный чертеж:


V₁ V₂ V₃

Ѕ ­­­­­­­­­­­­­­­­­­­­­­­­­­₁ Ѕ₂ Ѕ₃




t₁ t₂ t₃

Составляем уравнения движения для отрезка пути:

Ѕ₁=Ѕ₂+Ѕ₃; t₂=t₃; V(ср)= (Ѕ₁+Ѕ₂+Ѕ₃)/ (t₁+t₂+t₃)

Читаем еще раз условие задачи, выписываем числовые значения известных величин и, определив число неизвестных в полученной системе уравнений, решаем ее относительно искомой величины. Если при решении задачи учтены все условия, то решение системы относительно средней скорости дает:

V(ср)=2V₁(V₂+V₃) / (2V₁+V₂+V₃)

Подставив числовые значения в расчетную формулу, получим:

V(ср) ≈7 км/ч.

2. Материальная точка движется так, что координата изменяется со временем по закону: х=5t. Чему равна скорость материальной точки? Какой путь пройдет точка за 2с

3. Материальная точка движется вдоль оси Х так, что в момент времени t₁ ее координата 5м, а к моменту времени t₂ ее координата -3м. Найти скорость движения точки. Записать закон движения точки х(t). Найти перемещение и путь, пройденные точкой за любые Δt=2с движения.

4. По оси Х движутся две точки: первая по закону х₁=10+2t, вторая по закону х₂=4+5t. В какой момент они встретятся? Решить задачу аналитически и графически.

5. Материальная точка движется равномерно вдоль оси Х так, что в момент времени t₁=0 его координата х₁=10м, а через Δt=2мин координата 250м. С какой скоростью движется точка? Записать закон движения х(t).

Занятие 3 Относительность движения.

Все механические движения относительны. Относительность механического движения означает, что говорить о движении можно только тогда, когда указано не только тело движущееся, но и тело отсчета.

Из относительности движения вытекает первое, очень важное, требование к порядку действий при рассмотрении любого вопроса о движении:

При решении любой задачи о движении прежде всего должна быть указана та система отсчета, в которой будет рассматриваться движение.

Решение задач:

1. От буксира, идущего против течения реки, оторвалась лодка. В тот момент, когда на буксире заметили лодку, она находилась от него на достаточно большом расстоянии Ѕ₀. С буксира спустили катер, который доплыл до лодки и вернулся с ней назад. Сколько времени заняла поездка катера и какое расстояние он проплыл в одну и другую сторону, если скорости катера и буксира относительно воды равны соответственно V₁ и V₂?
   

Решение: В задаче рассматривается равномерное движение тел относительно друг друга, причем каждое тело участвует в сложном движении - оно движется относительно воды и вместе с водой, которая сама течет относительно берега. Изучая движение тел в системах отсчета, движущихся равномерно и прямолинейно относительно неподвижной системы отсчета, все расчеты можно производить так, как если бы переносного движения не было.

Изучая относительное движение двух или нескольких тел, систему отсчета удобно связывать с одним из этих тел, принимая его за тело отсчета, и рассматривать перемещения, скорости и ускорения относительно этого тела. Свяжем систему отсчета с буксиром. В этой системе буксир покоится, лодка удаляется от него со скоростью V₁+V₂, катер вместе с лодкой приближается к нему со скоростью V₁ - V₂

Допустим, что за время t₁, спустя которое катер догонит лодку, буксир удалился от лодки на расстояние Ѕ₁, тогда уравнение движения для катера и лодки за это время дает:

Ѕ₀+Ѕ₁=( V₁+V₂) t₁ и

Ѕ₁= V₂ t₁

Если для возвращения на буксир катеру потребовалось время t₂, то уравнение его движения имеет вид:

Ѕ₀+Ѕ₁+(V₁ - V₂) t₂.

Исковое время движения будет равно:

t= t₁ + t₂,

и за это время катер проплывет расстояние

Ѕ= 2(Ѕ₀+ Ѕ₁)

Решая уравнения совместно, находим:

t=2Ѕ₀/( V₁ - V₂); Ѕ = 2Ѕ₀ ( 1+ V₂/V₁).

2. Два поезда идут навстречу друг другу со скоростями 36км/ч и 54км/ч. Пассажир в первом поезде замечает, что второй поезд прошел мимо него за 6 секунд. Какова длина поезда?

3. Пассажир поднимается по неподвижному эскалатору метрополитена за 3мин, а по движущемуся вверх эскалатору за 2мин. Сможет ли он подняться по эскалатору, движущемуся с той же скоростью вниз? Если сможет, то за какое время?

4. Теплоход длиной 300м движется прямолинейно по озеру со скоростью V₁ . Катер, имеющий скорость 90км/ч, проходит расстояние от кормы до носа движущегося теплохода и обратно за 37,5с. Найти скорость теплохода.

5. Пролетая над пунктом А, пилот догнал воздушный шар, который сносило ветром по курсу вертолета. Через полчаса пилот повернул обратно и встретил шар в 30км от пункта А. Чему равна скорость ветра, если мощность двигателя вертолета осталась постоянной?

Занятие 4 Прямолинейное равнопеременное движение.

Наибольший вклад в изучение равно - переменного движения внес в период средневековья Никола Орезм (ок. 1328-1388). Применив впервые в истории науки графическое представление движения, соответствующее современному методу координат, он установил закон, используемый и сейчас и связывающий для равно - переменного движения пройденный движущимся телом путь со временем, затраченным на его прохождение.

Решение задач:

1. По наклонной доске пустили катиться снизу вверх шарик. На расстоянии 30см от начала пути шарик побывал дважды: через 1 секунду и через 2 секунды после начала движения. Определить начальную скорость и ускорение движения шарика, считая его постоянным.
   

Решение: Зависимость координаты тела вдоль наклонной плоскости от времени выражается формулой:

Х=V₀t - αt²/2. Отсюда t² - 2V₀t/α +2х/α=0. Так как t₁ и t₂ - корни этого уравнения при х = t, то, по теореме Виета, t₁ + t₂= 2V₀/α и t₁t₂= 2t/α. Из полученной системы получим V₀= 0,45м/с и α=0,3м/с².

2. В момент, когда тронулся поезд, провожающий начал равномерно бежать по ходу поезда со скоростью3,5м/с. Принимая движение поезда равноускоренным, определить скорость поезда в тот момент, когда провожатый поравнялся с провожающим.
   
3. За какую секунду от начала движения путь, пройденный телом в равноускоренном движении, втрое больше пути, пройденного в предыдущую секунду, если движение происходит без начальной скорости?
   
4. Реактивный самолет летит со скоростью 720км/ч. С некоторого момента самолет летит с ускорением в течение 10 секунд и в последнюю секунду проходит путь 295м. Определить ускорение и конечную скорость самолета.
   
5. Пуля, летящая со скоростью 400м/с, ударяет в земляной вал и проникает в него на глубину 36см. Сколько времени двигалась она внутри вала? С каким ускорением? На какой глубине скорость пули уменьшится в три раза?
   

Занятие 5 Движение тела, брошенного вертикально.

При изучении движения тел, движущихся под действием силы тяжести, нельзя не вспомнить о Галилео Галилее, который предположил, что скорость падающих тел одна и та же для всех тел независимо от их веса. Это свойство в 1590 году было подтверждено Галилеем в опытах на Пизанской башне, проведенным им с большой торжественностью в присутствии его коллег – последователей Аристотеля – и учеников.

Решение задач:

1. Тело брошено вертикально вверх с начальной скоростью V₀. Когда оно достигло высшей точки пути, из того же начального пункта с той же скоростью брошено второе тело. На какой высоте они встретятся?
   

Решение: Момент встречи делит время подъема, так же и время падения тел, на две равные части. Пути же, проходимые телом, падающим без начальной скорости, в последовательные равные промежутки времени относятся как 1:3. Следовательно, встреча произойдет на ¾ высоты.

2. Аэростат поднимается с земли вертикально вверх с ускорением 2м/с². Через 5с от начала его движения из него выпал предмет. Через сколько времени этот предмет упадет на Землю?
   
3. С какой начальной скоростью надо бросить вниз мяч с высоты 20м, чтобы он подпрыгнул на высоту 40м?
   
4. Свободно падающее тело за последнюю секунду падения прошло 1/3 своего пути. Найти время падения и высоту, с которой упало тело.
   
5. Из точек А и В, расположенных по вертикали (А выше) на расстоянии 100м друг от друга, бросают одновременно два тела с одинаковой скоростью 10м/с: из точки А вниз, а из точки В вверх. Через сколько времени и в каком месте они встретятся?
   

Занятие 6 Движение тела, брошенного под углом к горизонту.

При движении тела, брошенного под углом к горизонту, когда на тело действует сила тяжести, задачи решаются аналогично задачам на движение тела, брошенного вертикально.

Решение задач:

1. Начальная скорость брошенного камня 10м/с, а спустя 0,5с скорость камня 7м/с. На какую максимальную высоту поднимется камень?
   

Решение:

Очевидно, что камень брошен вверх под углом к горизонту, так как если бы он был брошен вертикально, то его скорость через 0,5с составляла бы V₀ -gt =5.1м/с.

Высота, на которую поднимется камень, Н=V₀t²/(2g), где V₀t -вертикальная составляющая начальной скорости, ее можно определить из следующей системы уравнений:

V₀² =Vt² +Vt²

V² =Vt² +(V₀t - gt²), где Vt-горизонтальная проекция начальной скорости.

Вычитая из второго уравнения первое, получим

V₀t = (V₀² - V² + g²t²)/(2gt).

Подставляя это уравнение в уравнение для максимальной высоты, получим

Н=(V₀² -V² +g²t²)²/(8gt²)

Н=2,8м

2. Под углом 60° к горизонту брошено тело с начальной скоростью 20м/с. Через сколько времени оно будет двигаться под углом 45° к горизонту?
   
3. На некоторой высоте одновременно из одной точки брошены два тела под углом 45° к вертикали со скоростью 20м/с: одно вниз, другое вверх. Определите разность высот, на которых будут тела через 2с.
   
4. Тело брошено под углом 60° к горизонту со скоростью 40м/с с поверхности Земли. Определить скорость тела на высоте 5м.
   
5. Артиллерийское орудие расположено на горе высотой 20м. Снаряд вылетает из ствола со скоростью 100м/с, направленной под углом 30° к горизонту. Определите дальность полета снаряда.
   

Занятие 7 Вращательное движение тел:

Впервые о вращательном движении можно было узнать из работы Ньютона «Математические начала натуральной философии» в первой книге, где центростремительное движение носит геометрический характер. Леонард Эйлер пошел дальше исследования центрального движения, принятого со времен Ньютона, и рассмотрел в общем виде произвольное вращательное движение, подготовив, таким образом, почву для современной кинематики.

Решение задач:

1. Через блок, радиусом R перекинута нить, на концах которой находятся два груза, установленные на одном уровне. Предоставленные самим себе, грузы приходят в равноускоренное движение и, спустя время t один находится под другим на высоте h. Определите угол поворота блока, его угловую скорость и полное ускорение точки А в конце интервала времени t. Нить не проскальзывает.
   

А




Решение: Так как по условию задачи нить по блоку не проскальзывает, то касательное ускорение всех точек, лежащих на ободе равно ускорению грузов.

Поскольку движение грузов равноускоренное и за время t они смещаются друг относительно друга на расстояние h, то уравнение движения для каждого груза будет иметь вид: h/2=α₀t²/2, так как ускорение у них одинаковое и каждый груз проходит расстояние h/2.

Запишем кинематические уравнения движения для блока, учитывая, что он вращается равноускоренно:

v=αt и x=αt²/2.

Угловая скорость и угловое ускорение блока связаны с нормальным и касательным ускорениями точки А формулами:

α(норм)=w²R и α=α(кас)/R.

Полное ускорение точки α=√α(кас)²+α(норм)².

Решая совместно уравнения, получим:

ϕ=h/(2 R); w= h/( Rᵼ); α=(h√h²+ R² ) /( Rᵼ²).

2. Поезд движется по закруглению радиусом 200м со скоростью 54км/ч. Найдите модуль нормального ускорения.
   
3. Точка начинает двигаться равноускоренно по окружности радиусом 1м и за 10 с проходит путь 50м. Чему равно нормальное ускорение точки через 5с после начала движения?
   
4. Поезд въезжает на закругленный участок пути с начальной скоростью 54км/ч и проходит путь 600м за 30с. Радиус закругления равен 1км. Определите модуль скорости и полное ускорение поезда в конце пути, считая тангенциальное ускорение постоянным по модулю.
   
5. Тело брошено с поверхности Земли под углом 60° к горизонту. Модуль начальной скорости равен 20м/с. Чему равен радиус кривизны траектории в точке максимального подъема?
   

Занятие 8 О законе всемирного тяготения.

Впервые о земном тяготении можно прочитать в работах Аристотеля. Регулярность и вечность круговращения звезд должны иметь какую – то причину, которую Аристотель усматривал в неподвижном перводвигателе, сообщающим движение всем сферам, к которым прикреплены звезды. А центр этих сфер совпадает с центром Земли. Помещение Земли в центре мироздания соответствовало данным повседневного опыта, который показывал, что звезды обращаются вокруг Земли. Из повседневного опыта известно, что есть тела, которые падают вниз. Отсюда следует заключение, что тяжелые тела стремятся к «своему месту», находящемуся в центре Земли. Но Галилей устами Сальвиати показал несоответствие учения Аристотеля данным астрономических наблюдений, с другой показал возможность гелиоцентрической системы мира.

Стремление подобного соединиться с подобным постулировалось еще первыми греческими школами (Эмпедокл, Анаксагор, Демокрит). Эта идея продолжала жить в течение всего средневековья и в эпоху Возрождения, поддерживаемая явлением магнитного притяжения, которое в известном смысле служило ее иллюстрацией. В 1674 году Гук публикует этюд о движении Земли. Там говорится: « все небесные тела испытывают притяжение и действие сил притяжения настолько больше, насколько ближе к центру притяжения тела, на которые они действуют». Ньютон признавал, что одно из писем Гука послужило ему поводом для расчета движения планет. Кеплер, еще до открытия своих законов, задавался вопросом о причине движения планет вокруг Солнца, а Луны вокруг Земли. В случае движения планет механическая причина заключена в Солнце; она убывает обратно пропорционально расстоянию.

Похоже, что Ньютон не знал об этой работе Кеплера, когда сформулировал свой закон всемирного тяготения. Ньютон сначала излагает установленные наблюдениями законы движения планет, Луны, спутников Юпитера и Сатурна. Ньютон дает динамическую интерпретацию этих законов по существу в том виде, как это делается теперь, и приходит к выводу, что во всех случаях центральная звезда действует на планету или планета действует на спутник с силой, обратно пропорциональной квадрату расстояния. Основным можно считать предложение, в котором Ньютон производил расчет, доказывающий, что сила, удерживающая Луну на ее орбите,- это та же сила, которая заставляет падать тела на Землю, лишь ослабленная за счет расстояния.

Приведя упомянутый расчет, Ньютон приходит к выводу:

« Тяготение существует ко всем телам вообще и пропорционально массе каждого из них»

Решение задач:

1. Свинцовый шар радиусом 50 см имеет внутри сферическую плоскость радиусом 5 см, центр которой находится на расстоянии 40 см от центра шара. С какой силой притягивается к шару материальная точка массой 10г, находящаяся на расстоянии 80 см от центра шара, если линия, соединяющая центры шара и полости, составляет угол 60°с линией, соединяющей центр шара с материальной точкой? Плотность свинца 11,3 г/см³.
   

Решение:



α А F F₁ 

F₂ ᵦ


Мысленно поместим в полость шарик таких же размеров, что и полость, тогда свинцовый шар будет сплошным. Его масса М =4/3πR³, и сила тяготения между материальной точкой и сплошным шаром будет:

F₁ = GМm/r²,

Сила тяготения точки и маленького шарика в полости, равна:

F₁ = Gm₁m/s ²,

Где m₁ - масса маленького шарика, а s –расстояние между центром полости и материальной точкой.

Из рисунка видно F =F₁ - F₂, и по теореме косинусов F = √ F₁² + F₂² -2F₁F₂cоs.

Расстояние s и косинус β можно найти по теоремам косинусов и синусов.

F = 5,7 мН.

2. На каком расстоянии от поверхности Земли ускорение силы тяжести равно 1 м/с²?
   
3. Определить ускорение силы тяжести на высоте 20 км над Землей, принимая ускорение силы тяжести на поверхности Земли 9,81 м/с², а радиус Земли 6400км.
   
4. На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность вещества 3000 кг/м ᶾ. Определите период обращения планеты вокруг собственной оси.
   
5. Каково ускорение свободного падения на высоте, равной радиусу Земли?
   

Занятие 9 Законы Кеплера.

Физика XVII века фактически состояла из двух разделов – механики и оптики, для которых общей областью применения была астрономия. Чтобы удовлетворить нужды астрономии, Иоганн Кеплер написал фундаментальный труд, состоящий из 11 глав, шесть из которых посвящены оптике и пять – астрономии. После принятия гелиоцентрической системы, Кеплер опубликовал первые два эмпирических закона движения планет, а в 1618г. – третий. В школьном курсе физики законам Кеплера отводится мало времени, но они заслуживают внимания.

Решение задач:

1. Спутник движется вокруг Земли по круговой орбите радиуса R= 3R_з, где R_з - радиус Земли, равный 6400км. В результате кратковременного действия тормозного устройства скорость спутника уменьшилась так, что он начинает двигаться по эллиптической орбите, касающейся поверхности Земли. Через какое время после этого спутник приземлится?
   

Решение: После торможения спутник движется по эллиптической орбите, большая полуось которой α =(R +R_З)/2. Если применить законы Кеплера к движению спутника по круговой и эллиптической орбитам, получим (Т/Т₀)² = (α/R)³. Период обращения спутника по круговой орбите находим из условия 4π²R/Т₀² = GМ_З/R². Но GМ_З =gR_З². Используя эти соотношения, находим период обращения спутника по эллиптической орбите:

Т = 2π/R_з(R³/g)^1/2((R +R_З)/2R)^3/2.

С момента торможения до посадки спутник пройдет половину эллиптической орбиты. Поэтому t=Т/2 =7150с. Около двух часов.

2. На какое максимальное расстояние от Солнца удаляется комета Галлея? Период обращения ее вокруг Солнца 76 лет, минимальное расстояние, на котором она проходит от Солнца 0,9 10⁸ км. Радиус орбиты Земли 1,5 10⁸ км.
   
3. Спутник, запущенный на круговую орбиту высотой 500 км над поверхностью Земли, тормозится в верхних слоях атмосферы. На какой высоте окажется спутник через месяц, если угловое ускорение спутника 3 10^-13рад/с².
   
4. Известно, что в настоящее время Луна удаляется от земли со скоростью 3,3 см/год. Найти угловое ускорение Луны. Среднее расстояние Луны от Земли 3,84 10⁵км, угловая скорость вращения Луны вокруг Земли 2,56 10^-6рад/сек.
   
5. Ракета запущена с поверхности Земли вертикально вверх с первой космической скоростью и возвращается на Землю недалеко от места старта. Сколько времени она находилась в полете?
   

Занятие 10 Закон Гука.

По мнению современников, характер у английского ученого, современника Ньютона, Роберта Гука был непростой, но у него был редкий изобретательский талант (ему предписывают около ста изобретений) и гениальная интуиция, которая позволила ему установить основные динамические законы, управляющие солнечной системой. Однако он не мог их систематически изложить из-за непостоянства характера и недостаточных математических знаний. Зависимость силы упругости от деформации Роберт Гук установил экспериментально. Закон Гука справедлив для упругой деформации растяжения и сжатия.

Решение задач:

1. К пружине, коэффициент жесткости которой равен 0.3 кН/м, подвешена гиря массой 0,6 кг. Найти удлинение пружины в случае подъема гири с постоянным ускорением 0,2 м/с². Как изменится деформация пружины в случае опускания гири с тем же по модулю ускорением?
   

Решение: Тело движется вверх с ускорением. На гирю действуют сила тяжести mg и сила упругости F_упр, возникающая вследствие удлинения пружины.

Х

F_упр


mg


Для проекций сил на ось Х по второму закону Ньютона F_упр –mg =mα. По закону Гука F_{упр =} k∆x, где∆x– удлинение пружины. Тогда k∆x - mg =mα и ∆x=m (g+α)/k, ∆x =0,02 м. При движении гири вниз с ускорением пружина сжата на ∆x₁ большее нуля, и получаем уравнение

mg - k∆x₁ = mα; ∆x_{1 =} m(g-α)/k; ∆x_{1 =} 0,192 м.

2. Найти удлинение буксирного троса с жесткостью 100кН/м при буксировке автомобиля массой 2т с ускорением 0,5м/с². Трением пренебречь.
   
3. На подставке лежит тело, подвешенное к потолку с помощью пружины. В начальный момент пружина не растянута. Подставку начинают опускать вниз с ускорением 0,5м/с². Через какое время тело оторвется от подставки? Жесткость пружины 40Н/м, масса тела 500г.
   
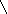
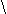
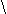
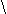4. На сколько переместится конец нити (точка А), перекинутой через неподвижный невесомый блок, если к концу нити приложить силу 20Н? Жесткости пружин равны 30Н/м и 40Н/м. Нить нерастяжима.
   

k₁



А

K₂

F

5. При помощи пружинного динамометра груз массой 10кг движется с ускорением 5м/с² по горизонтальной поверхности стола. Коэффициент трения груза о стол равен 0,1. Найдите удлинение пружины, если ее жесткость 2000Н. Занятие 11 Вес и невесомость.
   

Вес – очень знакомое слово. Однако очень часто, к сожалению, смешивают понятия «сила тяжести» и «вес тела», а в быту вес отождествляют с массой. Непосредственные предшественники Ньютона (Декарт и Гюйгенс) путали понятия массы и веса. Первое четкое различие между весом и массой мы находим в предисловии к работе Джована Баттисты Бальяни «О естественном движении тел»:

«…в то время как вес ведет себя как действующее начало, вещество ведет себя как пассивное начало, и поэтому тяжелые тела движутся в зависимости от отношения их веса к их веществу. Природа тяжелых тел такова, что их вес связан с веществом: каков вес, а значит, и его способность к действию, таково количество и вещества». Отсюда видно, что Бальяни было ясно не только понятие массы, но и ее пропорциональность весу.

Вес – это сила. Он ничем не отличается от любой другой силы, если не считать двух особенностей: вес направлен вертикально и действует постоянно, его невозможно устранить. Вес – это не что иное, как одно из проявлений силы упругости. Если тело лежит на опоре, то вследствие притяжения к Земле оно давит на опору. По этой же причине подвешенное тело растягивает подвес. Вес тела обладает особенностями, существенно отличающими его от силы тяжести. Во-первых, вес тела определяется всей совокупностью действующих на тело сил, а не только силой тяжести (так, вес тела в жидкости или воздухе меньше, чем в вакууме, из-за появления выталкивающей силы) Во- вторых, вес тела, как мы увидим при решении задач, существенно зависит от ускорения, с которым движется опора (подвес). А при свободном падении наступает невесомость.

Решение задач:

1. Найти вес автомобиля, движущегося в верхней точке выпуклого моста, радиус кривизны которого 800м, если автомобиль движется со скоростью 72км/ч. А его масса 1200кг.
   

Решение:

F





У α

F_т

Вес движущегося автомобиля равен по модулю силе упругости моста, действующей на транспорт. В уравнение второго закона Ньютона войдет именно эта сила упругости. В проекции на ось ОУ это уравнение имеет вид:

- F + mg = mα,

Или F = m(g – α).

Так как α = V²/R, то Р=F, Р=m(g-V²/R). Видно, что в верхней точке моста вес тела меньше силы тяжести.

Р=1200кг(9,8Н/кг – 400м²/с²/800м)=11160Н=11,16кН.

2. Космический корабль совершает мягкую посадку на Луну (g_л=1,6м/с²), двигаясь замедленно в вертикальном направлении (относительно Луны) с постоянным ускорением 8,4м/с². Сколько весит космонавт массой 70кг, находящийся в этом корабле?
   
3. С какой скоростью должен автомобиль проходить середину выпуклого моста радиусом 40м, чтобы пассажир на мгновение оказался в состоянии невесомости?
   
4. На экваторе некоторой планеты тела весят в два раза меньше, чем на полюсе. Плотность вещества планеты 3000кг/мᶾ. Определите период обращения планеты вокруг собственной оси.
   

5 . Найти среднюю плотность планеты, у которой на экваторе пружинные весы показывают вес тела на 10% меньше, чем на полюсе. Сутки на планете составляют 24 часа.

Занятие 12 О силе трения

Силы трения, как и силы упругости, имеют электромагнитную природу. Главная же особенность сил трения, отличающая их от гравитационных сил и сил упругости, состоит в том, что они зависят от скорости движения тел относительно друг друга. При малых относительных скоростях движения тел сила трения скольжения мало отличается от максимальной силы трения покоя. Силы трения действуют между всеми без исключения телами, и с ними приходится считаться. Очень часто в трении видят только помеху, не позволяющую создавать и сохранять неизменными движения тел. Но в тоже время без существования трения невозможно было бы движение тел по поверхности земли. Используя трение колес о землю или о рельсы, автомобили и поезда приходят в движение. Поэтому в технике решают задачу не только о том, как уменьшить трение там, где оно мешает движению, но и как его увеличить там, где оно помогает создать или передать движение. Например, тепловозы и электровозы делают возможно более тяжелыми. Сцепления в автомобиле передают движения от двигателя к колесам с помощью сил трения, которые должны быть большими. Чтобы добиться этого, диски сцепления прижимают друг к другу сильными пружинами. Этим создают большую силу нормального давления и добиваются значительного увеличения сил трения покоя, передающих движение от одной части машины к другой. Также поступают, когда силы трения используют для соединения деталей в различных механизмах. Для этого детали впрессовывают друг в друга. При этом возникают упругие силы, создающие большое нормальное давление на поверхность впрессованной детали. За счет этого в месте соединения развиваются необходимые большие силы трения. Такие же силы трения удерживают на месте любую туго завинченную гайку. При решении задач используют уравнение F_тр = µN как дополнительное, выражающее особые свойства сил трения скольжения.

Решение задач:

1. Автомобиль массой 1200 кг движется по горизонтальной дороге и совершает поворот по закруглению дороги радиусом 50 м. Какая скорость должна быть у автомобиля, чтобы его не занесло, если коэффициент трения между поверхностями колес и дороги равен 0,2?
   

Решение:

По второму закону Ньютона mα = ∑F. На автомобиль действует лишь сила трения.

mV²/R = µN; V² = µNR/m, а так как тело движется по горизонтальной дороге, то сила реакции опоры равна силе тяжести: N = mg.

V² = µmgR/m; V² = µgR; V= √ µgR.

V = √0.2 10 50 ; V = 10 м/с.

2. Упряжка собак при движении саней по снегу может действовать с максимальной силой 0,5 кН. Какой массы сани с грузом может перемещать упряжка, двигаясь равномерно, если коэффициент трения равен 0,1?
   
3. На соревнованиях лошадей тяжелоупряжных пород одна из них перевезла груз массой 20 т, двигаясь равномерно при коэффициенте трения 0,02. Найти силу тяги лошади. Движение считать равномерным.
   
4. Деревянный брусок массой 5 кг тянут равномерно по деревянной доске, расположенной горизонтально, с помощью пружины с жесткостью 100 Н/м. Коэффициент трения равен 0,3. Найти удлинение пружины.
   
5. Два деревянных бруска массой по 0,5 кг каждый лежат на деревянной доске.
   

А


Какую силу нужно приложить в точке А к нижнему бруску, чтобы вытащить его из под верхнего? Коэффициент трения на обеих поверхностях нижнего бруска равен 0,3. Занятие 13 Динамика тела, движущегося прямолинейно.

В динамике Аристотеля движущееся тело непрерывно находится под действием некоторой силы и скорость его прямо пропорциональна приложенной силе и обратно пропорциональна сопротивлению среды. Понятие силы как причины движения ввел еще Кеплер, но он измерял ее скоростью. У Галилея сила была эквивалентна весу, зато в отличие от Кеплера он измерял силу вызванным ускорением. У Ньютона, пожалуй, не было столь ясного представления, как у Галилея. Его определение гласит:

«…приложенная сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения».

Ньютон сформулировал основные законы движения, которые являются основой динамики.

Решение задач:

1. Груз массой 20кг поднимают вверх с помощью веревки так, что в течении первого промежутка времени 2с его скорость меняется от 2м/с до 6м/с. В последующий промежуток времени 1с скорость уменьшается до значения 2м/с. Найдите модуль сил, с которыми веревка действовала на груз в эти промежутки времени, считая эти силы постоянными.
   

Решение

F α

Х

В течение первого промежутка времени на тело действуют две силы: сила тяжести и сила натяжения нити. Согласно 2 закона Ньютона

mα=Т₁+F в проекции на ось оу, Т₁=Т₁, F= -mg.

Отсюда Т₁=m(g+α₁).

Для нахождения силы определить проекцию ускорения с помощью формулы скорости: α₁=(V₁ - V₀)/Δt₁

α₁= 2м/с².

Определим модуль силы Т

Т₁=m(g + (V₁ - V₀)/Δt₁)

Т₁=236 Н

Аналогично Т₂=116 Н

2. Какую массу балласта надо сбросить с равномерно опускающегося аэростата, чтобы он начал равномерно подниматься с той же скоростью? Масса аэростата с балластом 1200кг, подъемная сила аэростата постоянна и равна 8000 Н. Силу сопротивления воздуха считать одинаковой при подъеме и спуске.
   
3. Через сколько секунд тело, брошенное вертикально вверх со скоростью 44,8м/с, упало на землю, если сила сопротивления воздуха не зависела от скорости и составляла в среднем 1/7 силы тяжести,
   
4. Санки массой 5кг тянули в течение 5с горизонтально с силой 20Н. Коэффициент трения 0,3. Какое расстояние пройдут сани до полной остановки?
   
5. Динамометр вместе с прикрепленным к нему грузом сначала поднимают вертикально вверх, затем опускают. В обоих случаях движение происходит с ускорением, равным 6м/с². Чему равна масса груза, если разность показаний динамометра оказалась равной 29,4 Н?
   

Занятие 14 Динамика тела, движущегося прямолинейно (если тело движется по наклонной плоскости или под действием силы, приложенной под углом к горизонту)

Решение задач:

1. По канатной железной дороге с уклоном α=30⁰ к горизонту спускается вагонетка массой 500 кг. Найти силу натяжения каната при торможении вагонетки в конце спуска, если скорость вагонетки перед торможением 2 м/с, а время торможения 5 с. Коэффициент трения колес вагонетки о дорогу 0,01.
   

Решение: Ускорение вагонетки во время торможения α = V₀/t и направлено вверх вдоль уклона дороги. В этом направлении на вагонетку действуют сила натяжения каната Т и сила трения F_тр =kN =kmg cosα. Составляющая силы тяжести mg sinα направлена вдоль уклона дороги вниз. Уравнение второго закона Ньютона для вагонетки:

Т + F_тр - mg sinα = mα;

отсюда Т = m(α + g sinα) - kmg cosα;

Т = 2,6 кН

2. Какую силу нужно приложить для подъема вагонетки массой 500 кг по эстакаде с углом наклона 40⁰, если коэффициент сопротивления движению равен 0,05?
   
3. На наклонную плоскость с углом α помещена плоская плита массой m₂, а на нее брусок массой m₁. Коэффициент трения между бруском и плитой k₁. Определить при каких значениях коэффициента тренияk₂ между плитой и плоскостью плита не будет двигаться, если известно, что брусок скользит по плите.
   
4. За какое время первоначально покоившееся тело соскользнет с наклонной плоскости высотой 3 м, наклоненной под углом 30⁰ к горизонту, если при угле наклона плоскости к горизонту 10⁰ оно движется равномерно.
   
5. Бруски А и В массами m₁ и m₂ находятся на столе. К бруску В приложена сила F, направленная под углом α к горизонту. Найти ускорения движения брусков, если коэффициенты трения брусков друг о друга и бруска о стол равны соответственно k₁ и k₂. Сила трения между поверхностями максимальна.
   

F

α

В

А ААаАА