Geum.ru

Вестник Брянского государственного технического университета. 2006

Вид материалаДокументы

Содержание


Fn − нормальная нагрузка; HB()
Аа − номинальная площадь контакта; Fn
Management of process of interaction of a wheel with a rail by
Подобный материал:

Вестник Брянского государственного технического университета. 2006. № 1 (9)

удк 621.791.011


Д.В. Воробьев, В.П. Тихомиров, Г.В. Багров, В.С. Мицкович


Управление процессом сцепления колеса с рельсом путем

воздействия на контакт электрического тока и магнитного поля


Приведены результаты стендовых испытаний по схеме диск – плоскость для определения трибологических характеристик. Показано влияние электрического тока и магнитного поля на коэффициент сцепления. Установлена возможность управления сцеплением с помощью внешних физических полей.


Характер фрикционного взаимодействия колеса с рельсом изучался Н.П. Петровым, А.М. Бабичковым, Д.К. Миновым и другими исследователями. Количественной оценкой этого взаимодействия является коэффициент сцепления, который представляет собой отношение максимально реализуемого в момент трогания тягового усилия Fсц к нормальной нагрузке Fп, приложенной от колеса к опорной поверхности рельса.



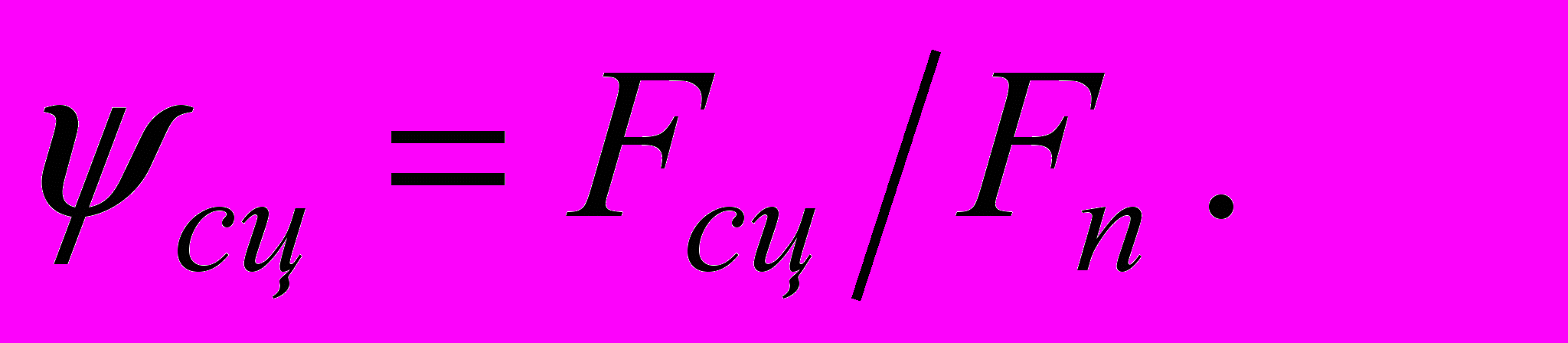
Ввиду того, что транспортные средства имеют колеса с отклонениями геометрических параметров, следует учитывать сцепление лимитирующей оси, выражаемое коэффициентом 0, и величину сцепного веса, определяемую коэффициентом , который отражает влияние конструктивных несовершенств, приводящих к расхождению значений тяговых нагрузок между осями.

Таким образом, коэффициент сцепления равен



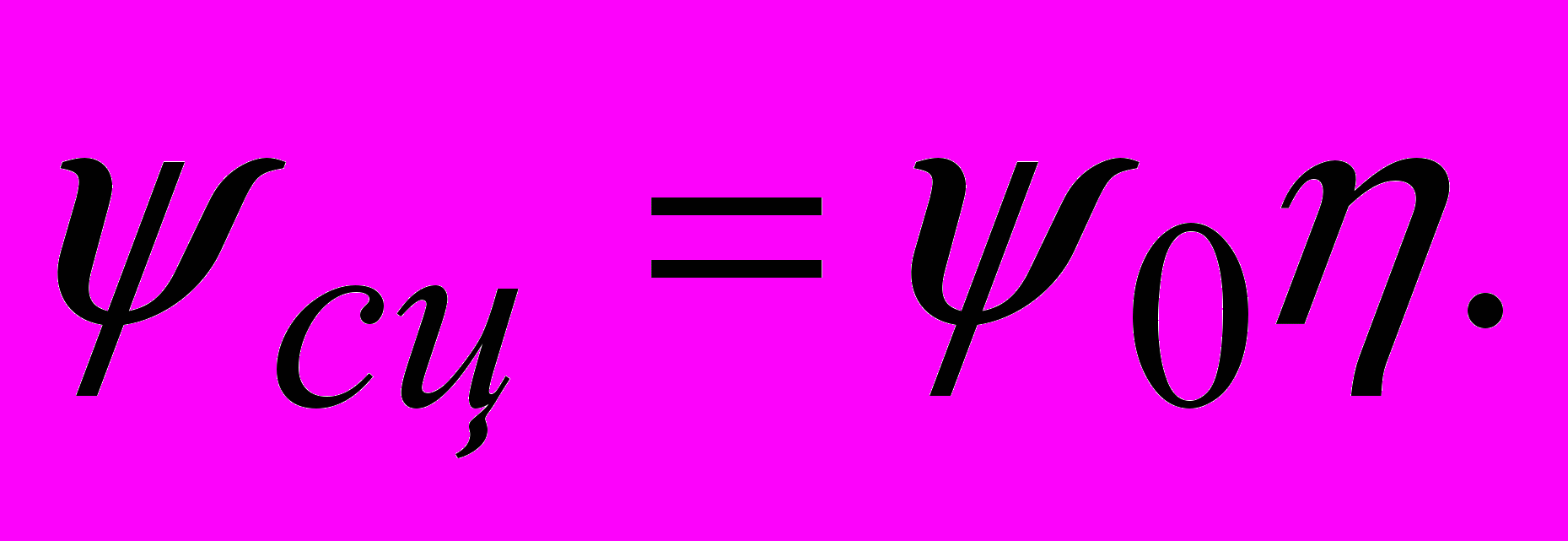
По данным ЦНИИ МПС и ряда авторов, величина коэффициента   0,98 в момент начала движения локомотива.

Можно считать, что коэффициент сцепления сц равен коэффициенту трения покоя f.

Анализ результатов исследований процесса сцепления колес с рельсами, выполненных в разных странах, позволил выявить 20 факторов, оказывающих влияние на сцепление. Среди важных факторов отметим нагрузку на контакт, трибологические свойства промежуточной среды (состояние поверхностных слоев при наличии загрязнений) и поверхностную твердость взаимодействующих металлических поверхностей.

Известно, что с ростом температуры твердость металла существенно уменьшается. При этом фактическая площадь контакта увеличивается в соответствии с выражением (для преимущественно пластического контакта)



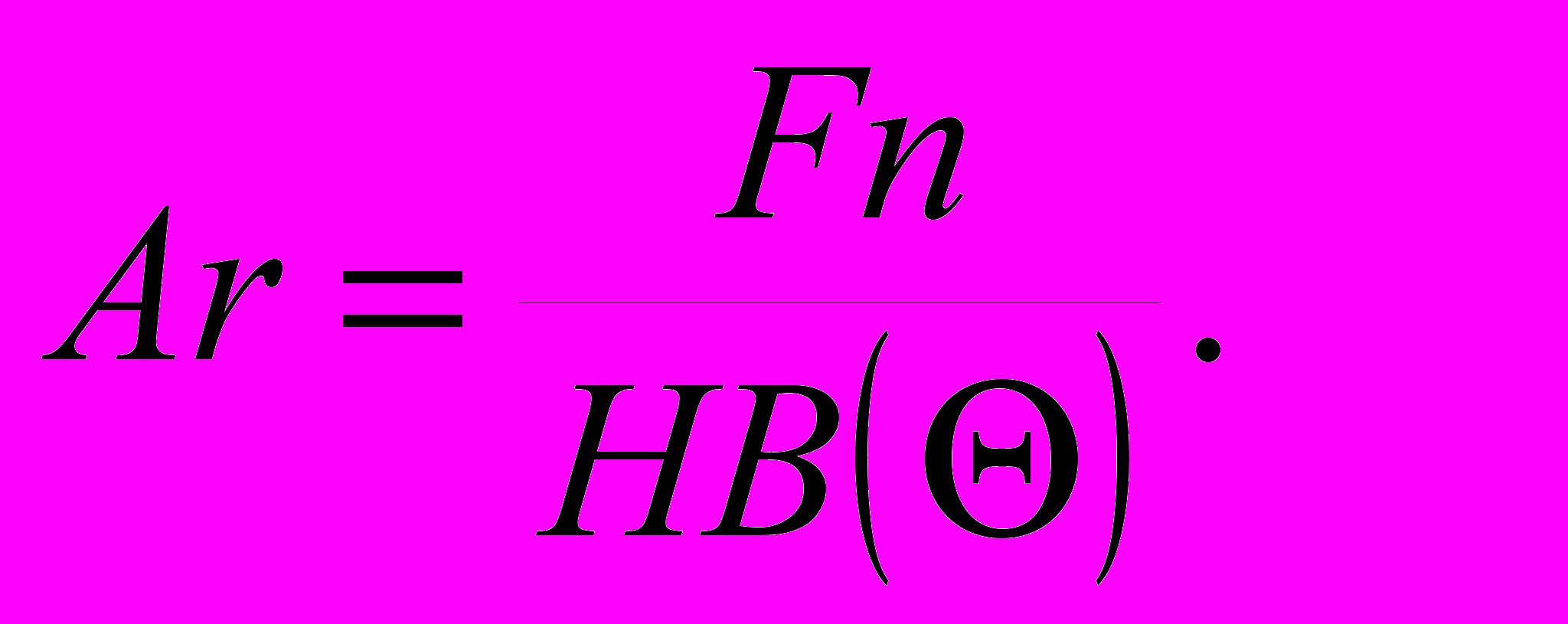
Здесь Fn − нормальная нагрузка; HB() − твердость по Бринеллю, зависящая от температуры.

Сила трения при примерно одинаковой исходной твердости контактирующих тел без учета механической составляющей коэффициента трения, определяемой взаимным внедрением неровностей, рассчитывается по формуле

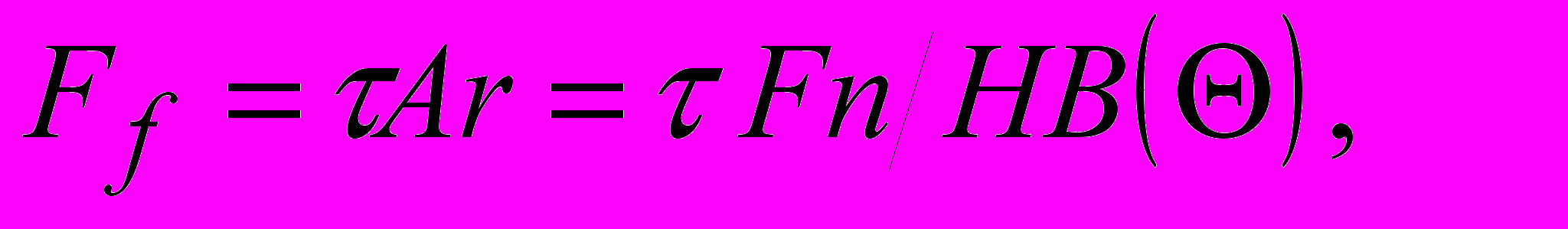(1)

где  − удельное сопротивление сдвигу сопряженных поверхностей в плоскости скольжения, равное

.

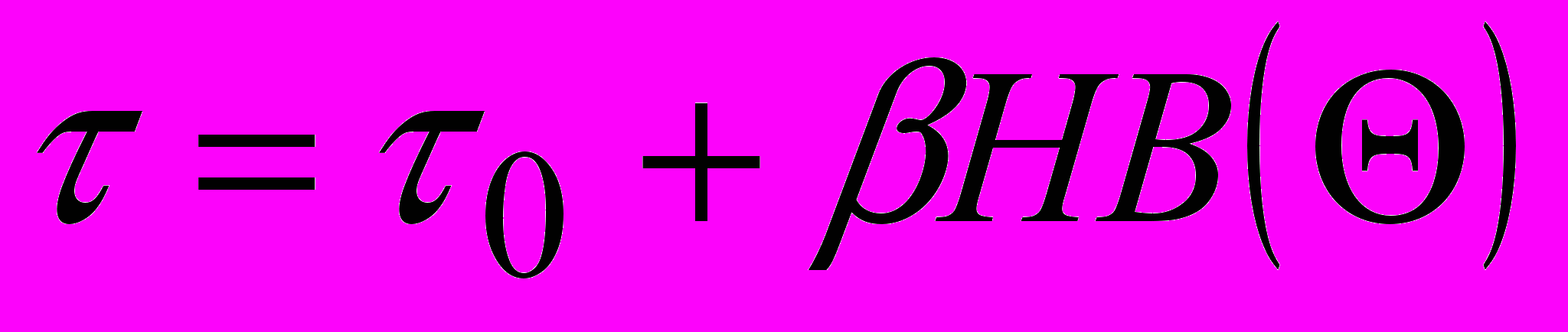Здесь 0 − удельное сдвиговое сопротивление при отсутствии нагрузки на контакт;  − упрочнение фрикционных связей.

Анализ выражения (1) показывает, что сила трения зависит от соотношения сдвигового сопротивления и твердости.

Значение коэффициента трения получим из выражения



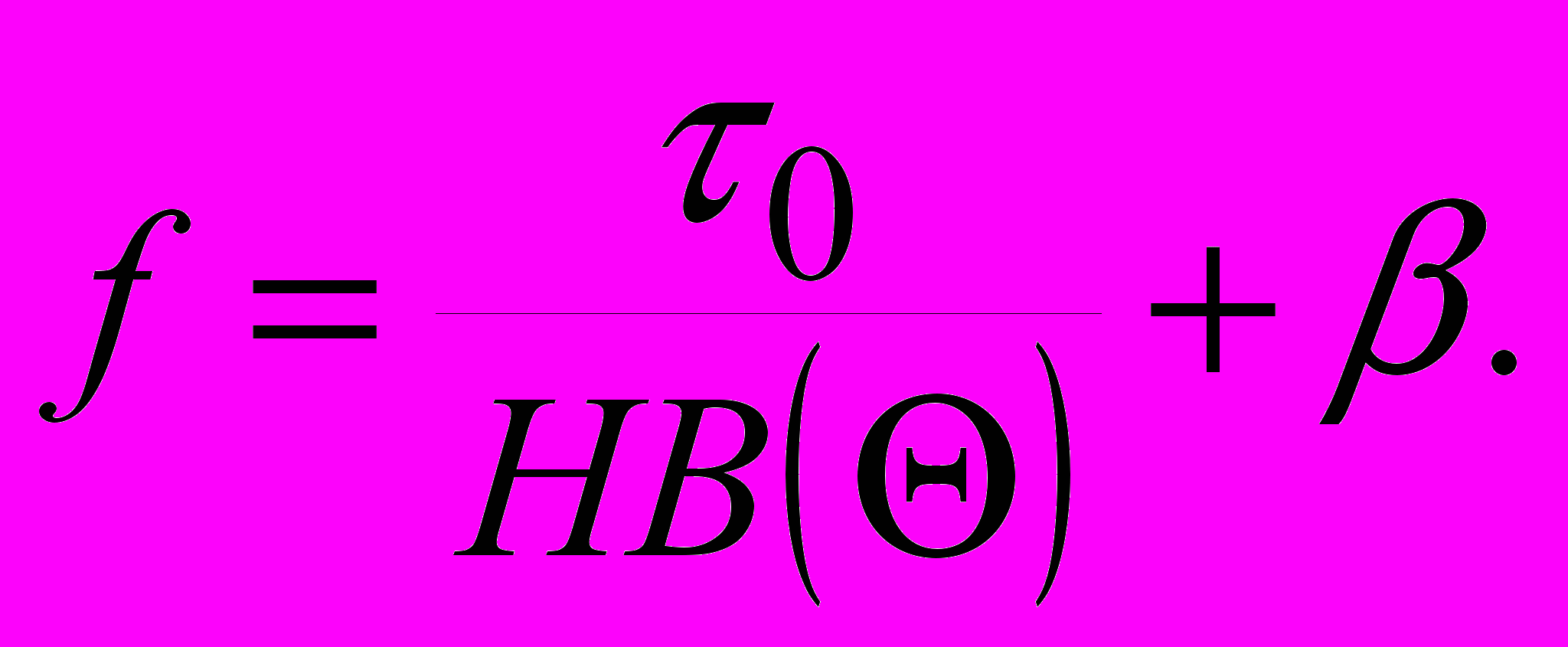
По данным А.В. Чичинадзе, для используемых в инженерной практике материалов коэффициент трения уменьшается с ростом температуры и увеличивается с ростом градиента температуры.

Важным фактором, влияющим на коэффициент трения, является градиент температуры по нормали к поверхности трения. Как впервые показал А.В. Чичинадзе, температурный градиент влияет на градиент механических свойств и коэффициент трения. При трогании локомотива с места температурный градиент можно создать путем воздействия на контакт электрического и магнитного полей. Таким образом реализуется возможность управления состоянием промежуточной среды (по И.В. Крагельскому – «третьего тела»).

Рассматривая фрикционный контакт как вязкопластическое «третье тело», И.В. Крагельский и Г.И. Трояновская [1] получили фундаментальную зависимость для коэффициента трения



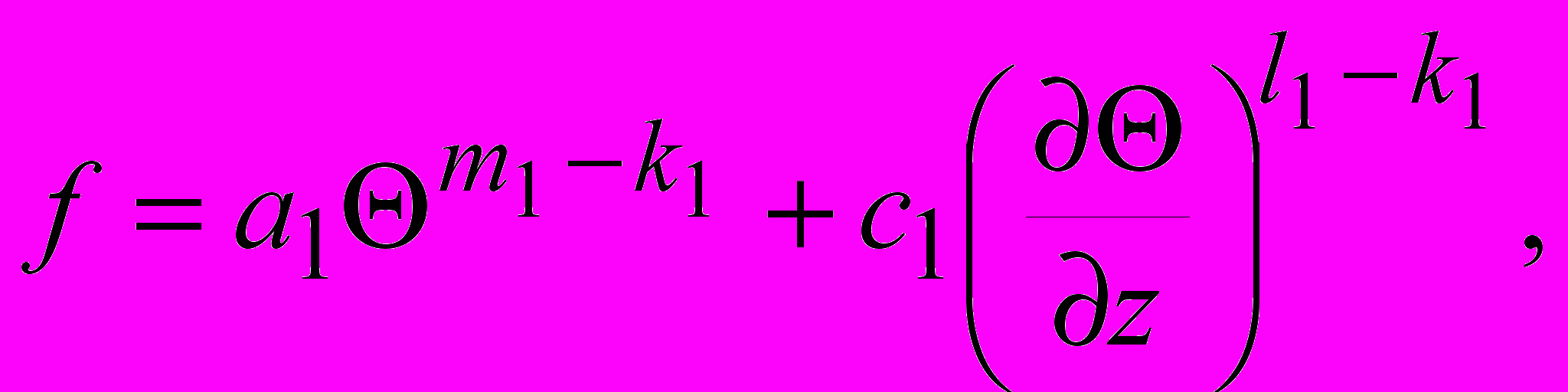
где c1, a1, m1, k1, l1 − коэффициенты.

Анализ этого выражения показывает, что в общем случае с ростом температуры в зависимости от значений коэффициентов c1, a1, m1, k1, l1 возможны как падение, так и рост коэффициента трения.

Объемные механические свойства материалов колеса и рельса и температура играют роль поправки к происходящим в зоне контакта процессам. Можно считать, что коэффициент трения зависит преимущественно от градиента температуры, влияющего на свойства тонкого приповерхностного слоя (промежуточной среды), находящегося между трущимися поверхностями и обладающего характеристиками, значительно отличающимися от объемных свойств контактирующих материалов.

Известно (по А.В. Чичинадзе), что общая температура равна сумме объемной, поверхностной и температуры вспышки. При пропускании через контакт электрического тока объемная и поверхностная температуры определяются джоулевым теплом и контактным сопротивлением.

При оценке влияния температуры и ее градиента на коэффициент трения учтем следующие соотношения.

Сопротивление стягивания (по Р. Хольму) неподвижного контакта при пятнах одинакового диаметра и одинаковых материалах равно



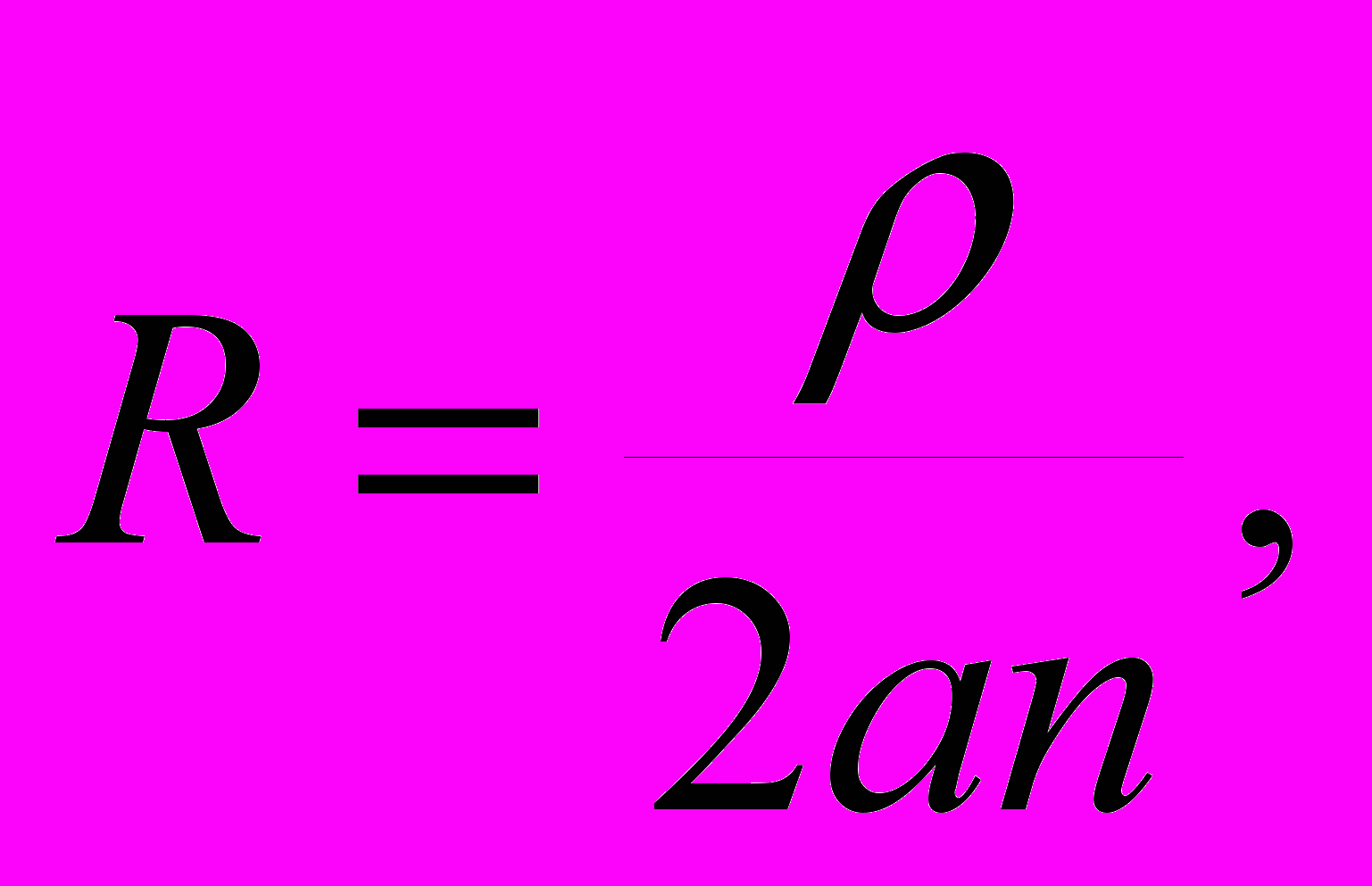
где − удельное сопротивление, Оммм2/м; 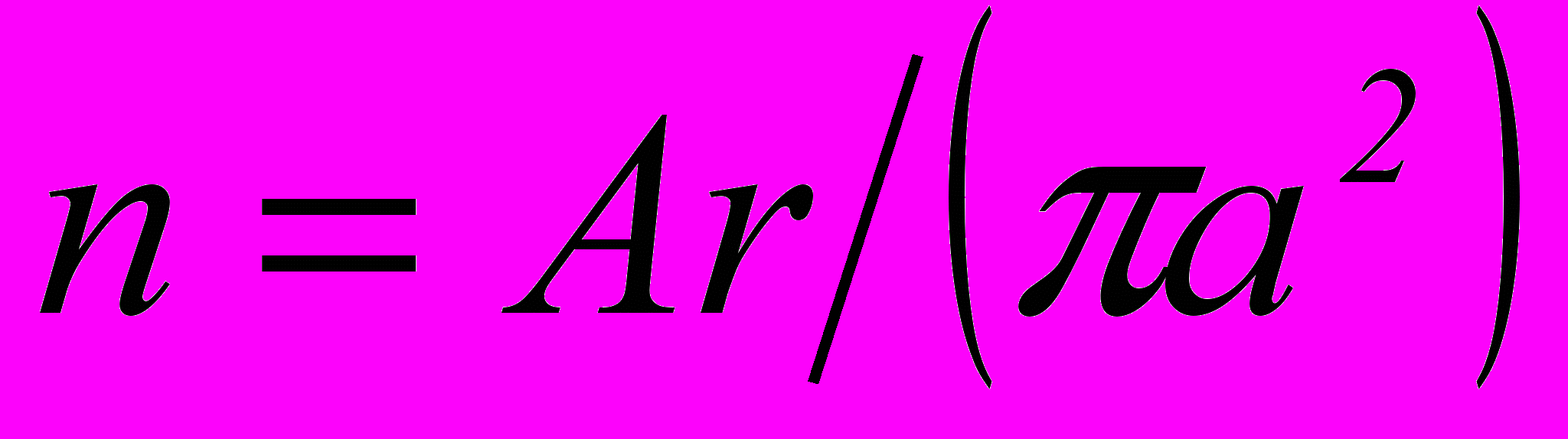− число пятен контакта радиусом а.

Удельный тепловой поток определяется по формуле



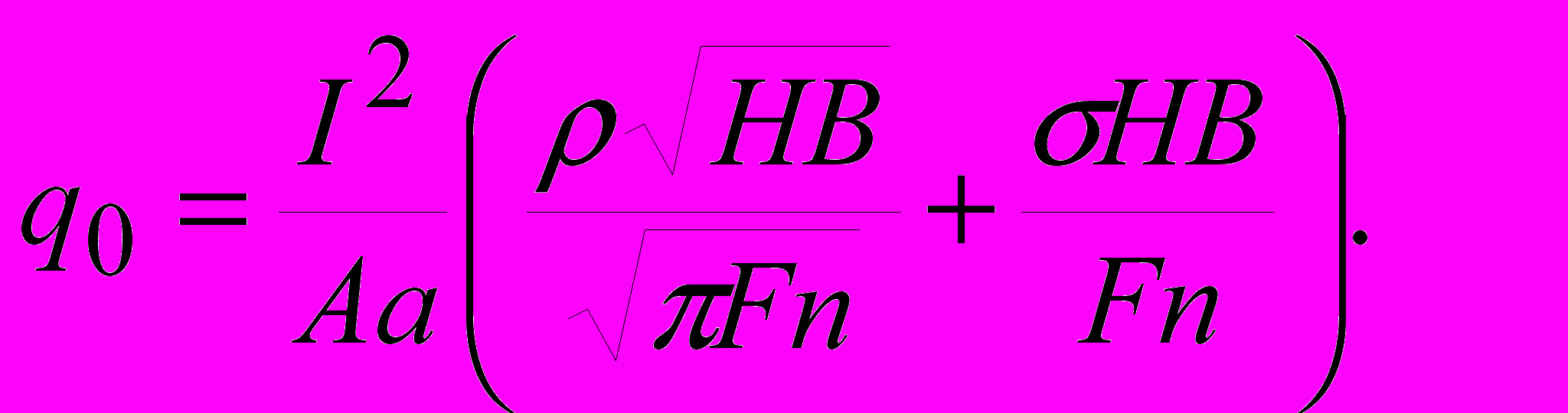
Здесь Аа − номинальная площадь контакта; Fn − нормальная нагрузка; HB − твердость по Бринеллю; I − сила тока, А; − удельное сопротивление пленок на контакте.

Дадим количественную оценку теплового потока при следующих исходных данных:

Аа =0,2 мм2; Fn =250 Н; HB =3000 МПа; I =100 А; =1110-5 Оммм.

Тогда

.

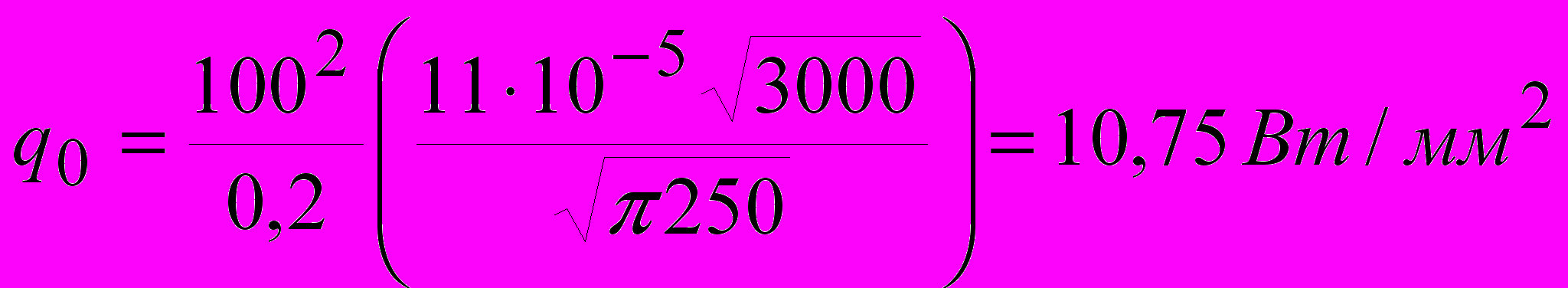В данном случае для приближенной оценки пренебрегаем сопротивлением пленок на поверхностях контакта.

Градиент температуры определяется из выражения

.

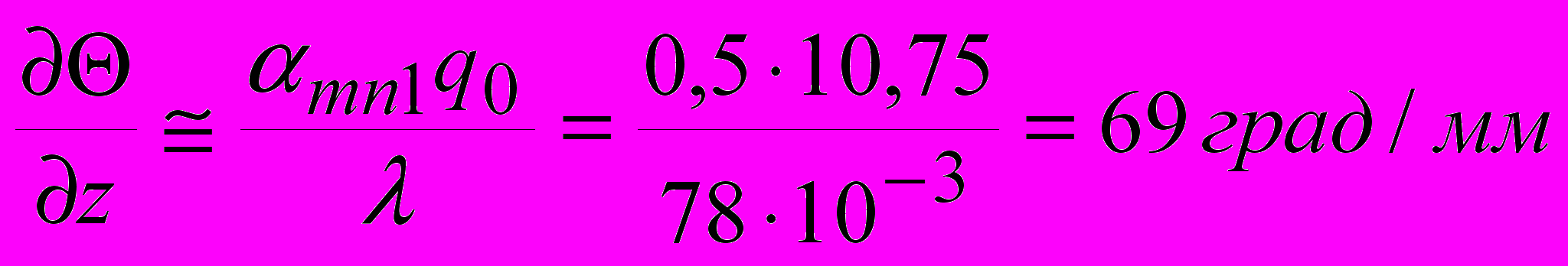При росте силы тока градиент температуры, как видно из предыдущих соотношений, увеличивается и следует ожидать роста коэффициента трения. Ф.Боуден и Д. Тейбор [2] отмечали, что электрическое сопротивление на контакте металлов, которое и определяет тепловыделение, возрастает при повышении температуры. Таким образом, с учетом этого эффекта, градиент температуры и, следовательно, коэффициент трения будут иметь большие значения, чем приближенно подсчитанная ранее величина .

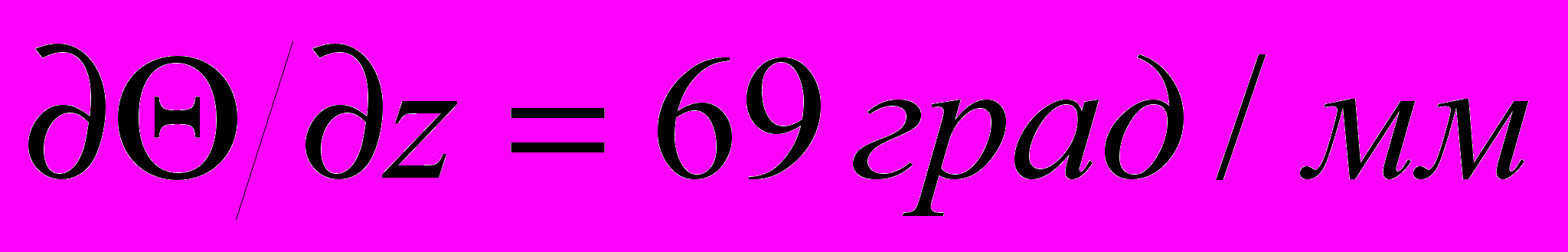Для количественной оценки эффекта влияния внешних физических полей были проведены экспериментальные исследования на стенде (рис. 1).


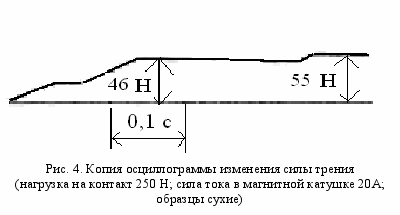
Целью экспериментальных исследований было выявить эффект влияния электрического и магнитного полей на величину коэффициента трения. Рассматривались две типичные ситуации: сухие образцы, имитирующие взаимодействие колеса и рельса, и образцы, смоченные водой. Методика проведения исследований предполагала оценивать коэффициент трения при дискретном изменении силы тока, проходящего через изолированный контакт, а также при воздействии магнитного потока. На рис. 2, 3, 4 представлены копии соответствующих осциллограмм. Стендовые триботехнические испытания проводились по схеме диск − плоскость, имитирующей взаимодействие колеса с рельсом. При этом учитывалось состояние промежуточной среды («сухой» контакт и наличие воды в зоне касания), характерное для рельсовых экипажей. На первом этапе оценивался коэффициент трения для «сухого» контакта, затем пропускался ток через контакт и оценивалось изменение коэффициента трения. Дополнительно измерялась сила трения для случая воздействия на контакт магнитного потока. Аналогичные испытания проводились при наличии в зоне касания воды.


Давление (по Г. Герцу) было принято во всех опытах постоянным и равным 217 МПа, сила тока изменялась от 100 до 200 А, сила тока в магнитной катушке, имеющей 560 витков, равнялась 10, 15, 20 А.




В табл. 1, 2 приведены средние (по пяти опытам) значения коэффициента трения (сцепления) при наличии тока и воздействии магнитного поля.

Таблица 1

Значения коэффициента трения (сцепления) для «сухого»
контакта при наличии тока

Коэффициент трения (сцепления) без тока
0,15 – 0,17
0,15 – 0,17
0,15 – 0,17

Сила тока I, А
100
150
200

Плотность тока J, А/мм2
68
102
136

Коэффициент трения (сцепления) при наличии тока
0,325
0,371
0,452


Таблица 2

Значения коэффициента трения (сцепления) для «сухого» контакта
при воздействии магнитного потока

Сила тока в магнитной катушке Ф, А
10
15
20

Коэффициент трения (сцепления) при воздействии магнитного потока
0,174
0,174
0,220


При наличии воды в зоне контакта среднее значение коэффициента трения без тока оказалось равным 0,165. Пропускание тока (сила тока I = 200 А) через нагруженный контакт с учетом наличия воды привело к росту коэффициента трения до величины
f = 0,371, т.е. более чем в два раза. При отсутствии воды (для «сухого» контакта) коэффициент трения (сцепления) при той же силе тока равнялся 0,452 (табл. 2).

Таким образом, на основании стендовых экспериментальных данных показано увеличение коэффициента сцепления при пропускании тока через контактную зону. Наличие магнитного поля приводит к некоторому повышению коэффициента сцепления в заданном диапазоне изменения тока в магнитной катушке.


список литературы

  1. Лужнов, Ю.М. К вопросу о причинах катастрофического изнашивания колес подвижного состава/Ю.М. Лужнов, А.В. Чичинадзе//Трение и износ. – 1998.−Т.19. – №3. − С.344−349.
  2. Боуден, Ф. Трение и смазка твердых тел: [пер. с англ.] / Ф. Боуден, Д. Тейбор.- М.: Машиностроение, 1968. – Ч. 2. – 542 c.


Материал поступил в редколлегию 16.01.06.


Д.В. Воробьев, В.П. Тихомиров,

Управление процессом сцепления колеса с рельсом путем

воздействия на контакт электрического тока и магнитного поля


Проведены стендовые испытания по схеме диск-плоскость для определения трибологических характеристик. Показано влияние электрического тока и магнитного поля на коэффициент сцепления. Установлена возможность управления сцеплением за счет внешних физических полей.


D.V.Vorob'ev, V.P.Tikhomirov, G.V. Bagrov, V.S. Mitscovich

Management of process of interaction of a wheel with a rail by

Influences on contact of an electric current and a magnetic field


Bench tests under the circuit a disk - plane for definition tribological characteristics are carried out. Influence of an electric current and a magnetic field on coefficient of friction is shown. The opportunity of management is established by adhesion of a wheel with a rail due to external physical fields.


Сведения об авторах

Воробьев Дмитрий Владимирович, инж. каф. "Локомотивы"

Тихомиров Виктор Петрович, д.т.н., проф., зав. кафедрой "Детали машин"

Багров Геннадий Владимирович, начальник завода №192 ЦЗЖТ

Мицкович Владимир Степанович, главный инженер завода №192 ЦЗЖТ