План. Механіка. Система відліку. Матеріальна точка Прискорення. Швидкість

Вид материала

Лекція

Содержание Поступальний рух 3. Прискорення. Прискорення при криволінійному русі 4. Рух точки по колу 5. Одиниці фізичних величин Динаміка матеріальної точки Маса — це властивість матерії, що характеризує її інертність і гравітацію.2. Перший закон Ньютона 3. Інерціальні системи відліку 4. Принцип відносності Галілея 5. Другий закон Ньютона 6. Детермінізм Лапласа 7. Третій закон Ньютона

Подобный материал:

• Програма вступного випробування та співбесіди з фізики для вступу на перший курс навчання, 85.23kb.
• План учебных занятий по курсу «Физика». 9 класс (4 часа в неделю), 72.35kb.
• Календарно-тематический план (балльно-рейтинговая система, 1 семестр), 58.92kb.
• Тема. Матеріальна відповідальність сторін трудового договору, 90.15kb.
• Урок на тему «Штучні супутники Землі», 21.17kb.
• Реферат на тему: Швидкість обігу грошей та чинники, що її визначають, 58.43kb.
• Организационный план 31 6 План производства 32 7 Финансовый план 38 План по рискам, 841.71kb.
• І. вступ сучасна система освіти зіткнулася з проблемою прискорення І непередбачуваності, 80.21kb.
• План Матеріальна культура Римської імперії Соціальний устрій, 294.96kb.
• Реферат на тему на тему Розпад СРСР та заснування снд, 97.55kb.

Лекція 1. Вступ. Кінематика матеріальної точки. Динаміка матеріальної точки. Робота і енергія.

План.

1. Механіка. Система відліку. Матеріальна точка Прискорення.
   
2. Швидкість
   
3. Прискорення при криволінійному русі.
   
4. Рух точки по колу
   
5. Одиниці фізичних величин
   

Рекомендована література.

Основна: 1. Чолпан П.П. Фізика: підручник. – К.: Вища школа, 2003. – С.39-49.

2. Воловник П.М. Фізики. Для ун-тів. – К:Ірпінь: Перун, 2005. – С.27-40..

Додаткова: Лаврова И.В. курс физики. Учебнре пособие для студентов биол-хим. Фак. Пед.инст. – М.: Просвещение. 1981. – С.6-9.


Теоретичні відомості.

КІНЕМАТИКА

1. Механіка. Система відліку. Матеріальна точка

Механіка — наука про найпростішу форму руху тіл (механічний рух, або переміщення). Рух у широкому філософському розумінні є зміна взагалі, будь-яка зміна чи процес: фізичний, хімічний, біологіч­ний тощо.

Під механічним рухом розуміють зміну положення тіла з часом відносно іншого тіла або системи тіл, що умовно вважають нерухоми­ми. Таку систему тіл разом з годинником називають системою відліку. Годинником може бути будь-який періодичний процес: коливання маят­ника, обертання Землі, електромагнітні коливання тощо.

Для строгого математичного описання руху з системою відліку пов'язують систему координат, наприклад декартову. Між системою відліку й системою координат є істотна відмінність. Систему відліку утворюють реальні тіла, а система координат є математичною абстрак­цією. Практично для того щоб описати рух, необхідно умовитись, від­носно якого іншого тіла (або групи нерухомих один від одного тіл) відраховуватиметься переміщення даного тіла. Обране для цього тіло (або група тіл) утворює разом з годинником систему відліку.

Координати тіла визначають його положення в просторі. Оскільки рух відбувається як в просторі, так і в часі, для описання руху необ­хідно також відлічувати час.

Маючи координатну систему, що пов'язана з обраним тілом відліку та годинником, можна приступати до описання руху тіла.

Тіло, деформаціями якого в умовах розглядуваної задачі можна знехтувати, називають абсолютно твердим.

Тіло, розмірами якого в умовах даної задачі можна знехтувати, на­зивають матеріальною точкою. Чи можна певне конкретне тіло вважати матеріальною точкою, чи ні — це залежить не від розмірів самого тіла, а від умови задачі. Те саме тіло можна вважати матеріальною точкою в одних умовах, в інших — його треба розглядати як таке, що має протяжність.

Будь-який рух твердого тіла можна розкласти на два головних види руху — поступальний та обертальний.

Поступальний рух — це такий рух, при якому будь-яка пряма, проведена в тілі, що рухається, залишається паралельною сама собі.

При обертальному русі всі точки тіла рухаються по колах, центри яких лежать на одній прямій, яку називають віссю обертання. Вісь обертання може знаходитись поза тілом. Далі під рухом розумітимемо механічний рух, а під тілом — матеріальну точку. Лінію, що її опи­сує під час руху матеріальна точка, називають траєкторією. За фор­мою траєкторії рухи поділяють на прямолінійні й криволінійні. Від­стань, яку відраховано вздовж траєкторії, називають пройденим шляхом.

Механіку поділяють на три розділи: кінематику; статику та динамі­ку. Кінематика вивчає рух тіл без врахування причин, що виклика­ють цей рух. Статика вивчає умови рівноваги тіл. Динаміка ви­вчає рух тіл у зв'язку з тими причинами (взаємодією між тілами), які породжують той або інший характер руху. Оскільки рівновага — окре­мий випадок руху, закони статики випливають із законів динаміки.


2. Швидкість


Положення матеріальної точки в просторі можна задати за допомогою радіуса-вектора 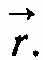Зафіксуємо певний момент часу t. Йому відповідає значення 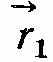радіуса-вектора (рис. 1.1). Протягом наступного (після моменту t) невеликого проміжку часу ∆t (називатимемо його елементарним) точка проходить елементарний шлях і дістає елементарне переміщення, яке збігається з приростом радіуса-вектора за час ∆t.

Відношення



є векторною величиною, що залежить від проміжку часу ∆t. При досить малих значеннях ∆t вектор (1.1) практично припиняє змінюватись як за величиною, так і за напрямом. Отже, при ∆t → 0 відношення (1.1) прямує до певної границі, яку називають швидкістю 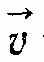точки, що рухається, в момент часу t:



Таким чином, швидкістю називають границю, до якої прямує відношення при необмеженому зменшенні ∆t. Отже, швидкість можна ви­значити як похідну від радіуса-вектора точки, що рухається, за часом:



Як випливає з означення, швидкість — величина векторна. Вектор швидкості має напрям, що збігається з напрямом дотичної до траєкторії в певній точці.

У відповідності з формулою (1.2) модуль вектора швидкості запишемо так:

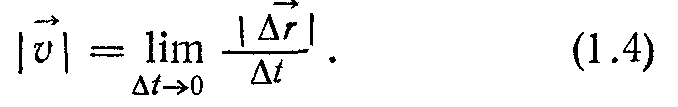
Тут замість 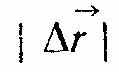не можна писати ∆r. Символ 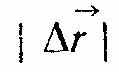означає модуль приросту вектора 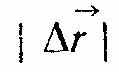, тоді як ∆r є приріст модуля цього вектора .

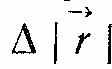Ці величини не дорівнюють одна одній: .

Елементарний шлях ∆s в загальному випадку відрізняється за величиною від модуля елементарного переміщення ∆ 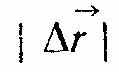(рис. 1.1). Проте для невеликих проміжків часу ∆t різниця між ∆s і буде невеликою, до того ж із зменшенням ∆t шлях ∆s із зростаючою точністю збігатиметься з . На цій підставі запишемо, що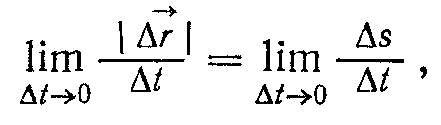



звідки у відповідності з (1.4) для модуля швидкості дістанемо



Формула (1.3) визначає вектор миттєвої швидкості, тобто швидкості для певного моменту часу. Середня швидкість визначається відношен­ням пройденого шляху s до часу t, за який цей шлях подолано:



Швидкість вимірюється в метрах на секунду (СІ) та сантиметрах на секунду (СГС).


3. Прискорення. Прискорення при криволінійному русі


Градієнт швидкості матеріальної точки з часом t характеризують прискоренням



Прискорення вимірюється в метрах на секунду в квадраті (СІ) та сантиметрах на секунду в квадраті (СГС).

П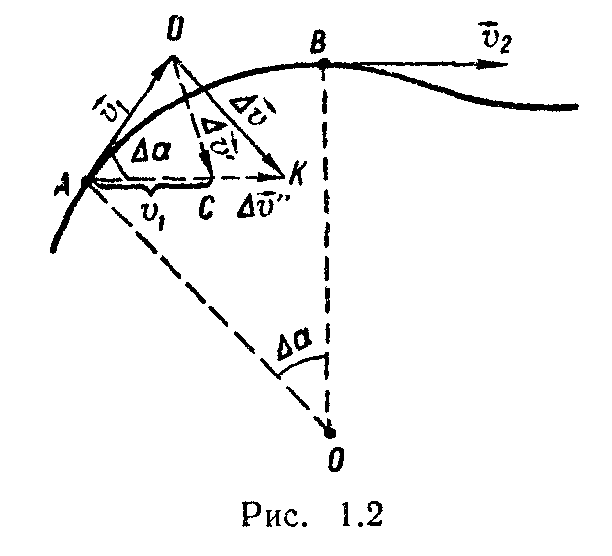ри прямолінійному русі вектор швидкості напрямлений вздовж однієї й тієї самої прямої — траєкторії, внаслідок чого напрям вектора а збігається з напрямом вектора або протилежний до нього. Якщо а збігається за напрямом з о, то швидкість збільшується, і рух буде прискореним. Якщо а протилежне за напрямом до v, то швид­кість зменшується, і рух буде сповільненим.

Прямолінійний рух із сталим при­скоренням називають рівнозмінним. В залежності від зміни швидкості в часі розрізняють рівномірно прискорений та рівномірно сповільнений рухи. При рівнозмінному прямолінійному русі справедлива формула



де 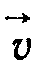— швидкість у момент часу t; — швидкість в початковий момент часу (при t = 0); 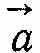— прискорення. При цьому вектори 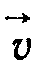,, 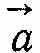напрямлені вздовж однієї прямої.

Визначимо прискорення точки у випадку її руху по криволінійній траєкторії (рис. 1.2). Нехай в момент часу t точка знаходилась в положенні А, а в момент часу t + ∆t — в положенні В. Швидкості та 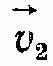в точках А і В напрямлені по дотичних до траєкторії в цих точках. Перенесемо вектор 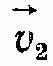в точку А. Зміна швидкості за проміжок часу ∆t визначиться вектором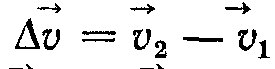. З рис. 1.2 бачимо, щ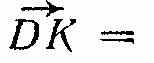о або . Тоді прискорення в точці А запишемо так: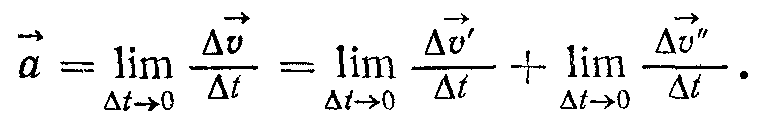



Вектор 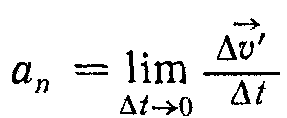- називають нормальним прискоренням, а вектор 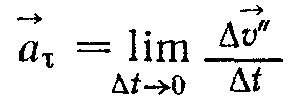- тангенціальним. Прискорення _п перпендикулярне до вектора швидкості і завжди напрямлене до центра кривизни. Звідси й назва цього вектора — нормальний (тобто перпендикулярний).

Визначимо модуль нормального прискорення. Як видно з рис. 1.2, для малого кута ∆α можна записати



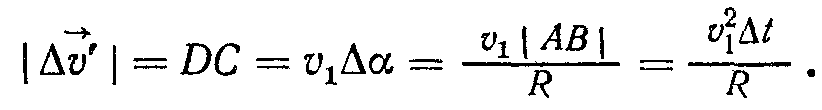
Тоді



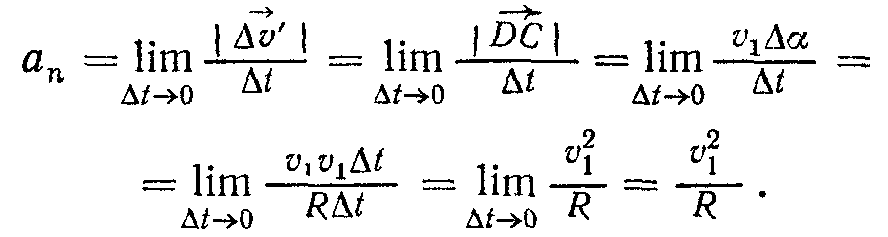
Отже, модуль _п в деякій точці траєкторії дорівнює відношенню квад­рата швидкості до радіуса кривизни траєкторії в цій самій точці: а_п = = v²/R.

Якщо на нормалі до траєкторії відкласти в точці А одиничний вектор , що напрямлений до центра кривизни, то вектор нормального прискорення можна записати так:



Розглянемо тепер вектор тангенціального прискорення



Зазначимо, що модуль вектора дорівнює за абсолютною величиною різниці модулів та (рис. 1.2). Тоді



Відповідно тангенціальне прискорення 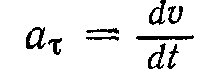або .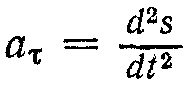

Отже, значення тангенціального прискорення дорівнює першій похідній від швидкості за часом або другій похідній від шляху. Напрям вектора 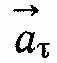визначається напрямом вектора , якого він набуває в граничному випадку, коли ∆t→0. Неважко побачити, що в граничному випадку вектор 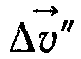напрямлений по дотичній до траєкторії в точці А. Звідси і назва цього вектора — тангенціальний (дотичний). Якщо ввес­ти одиничний вектор т, дотичний до траєкторії і напрямлений в бік ру­ху точки, можна вектор тангенціального прискорення записати так:



Вектор 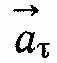вказує на те, як змінюється швидкість за величиною, а вектор _п характеризує зміну швидкості за напрямом. Отже, для повного при­скорення запишемо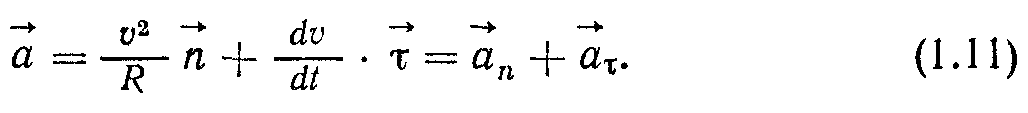



Модуль вектора загального прискорення знайдемо із співвідношення



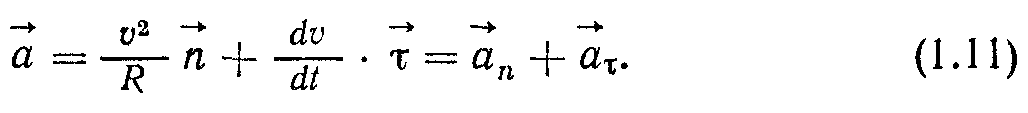
4. Рух точки по колу

Рух матеріальної точки по колу є окремим випадком криволіній­ного руху. Розглядаючи такі величини, як швидкість 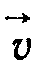, прискорення , радіус-вектор , питання про вибір їхнього напряму не виникало, оскільки воно витікало з їхньої природи. Подібні вектори називають полярними. Вектори типу dφ, напрям яких пов'язаний з напрямом обертання, називають аксіальними. У цьому разі кут можна розгляда­ти як вектор. Для дуже малих кутів повороту∆φ, оскільки шлях, що проходить матеріальна точка при такому малому повороті, можна роз­глядати як прямолінійний. Величину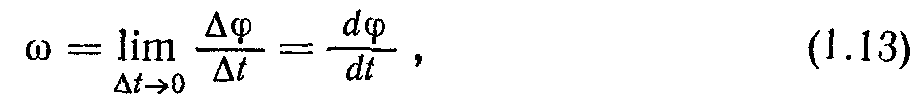



де ∆t — час, за який здійснюється поворот на кут ∆φ, називають кутовою швидкістю точки. Вектор со напрямлений вздовж осі, навколо якої обертається тіло. Напрям обертання визначається за правилом правого гвинта. Кутова швидкість — це аксіальний вектор. Модуль вектора кутової швидкості дорівнює 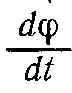. Обертання зі сталою куто­вою швидкістю називають рівномірним, при цьому . Отже, при рівномірному обертанні со показує, на який кут повертається ті­ло за одиницю часу.

Рівномірний рух можна характеризувати періодом Т. Це час, про­тягом якого тіло робить один оберт, тобто повертається на кут 2π. Оскільки проміжку часу ∆t = Т відповідає кут φ= 2π то



Частота періодичного процесу



Тоді



Вектор 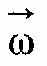може змінюватись як внаслідок зміни швидкості обертання тіла навколо осі (у цьому разі він змінюється за величиною), так і за рахунок повороту осі обертання в просторі (у цьому разі 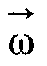змінюється за напрямом). Нехай за час ∆t вектор 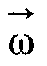дістав приріст ∆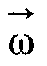. Зміну век­тора кутової швидкості з часом характеризують кутовим прискоренням



Вектор 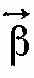, як і 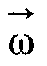, е аксіальним.

Якщо напрям осі обертання в просторі залишається сталим, то кутова швидкість змінюється лише за величиною, і 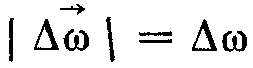. У цьому разі з формули (1.17) дістаємо



Вираз (1.18) запишемо у векторній формі



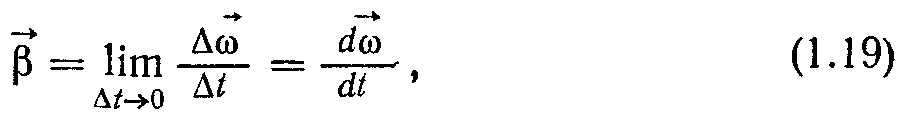
де — алгебраїчна величина, яка додатна, якщо со з часом збільшується (у цьому разі вектори та 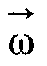мають однаковий напрям), і від'ємна, якщо со зменшується (у цьому разі напрями (5 та со протилежні). Лінійна швидкість v визначається кутовою швидкістю обертання тіла 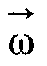та відстанню г матеріальної точки від осі обертання. Нехай за малий проміжок часу ∆t тіло повертається на кут ∆φ. Точка, яка знаходиться на відстані г від осі, проходить при цьому шлях



Лінійна швидкість точки



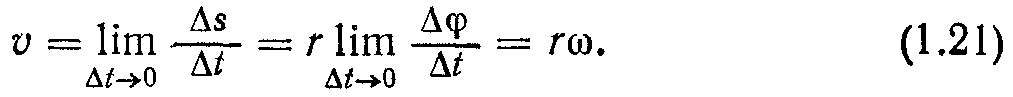
У векторній формі . Отже, чим далі знаходиться точка від осі обертання, тим з більшою лінійною швидкістю вона рухається.

Знайдемо зв'язок модулів лінійного та кутового прискорення, покладаючи, що r=const. Тоді, виходячи з (1.19), запишемо



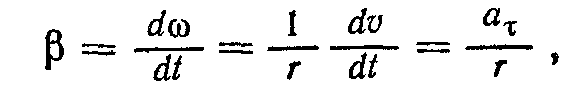
отже



При рівномірному русі точки по колу модуль швидкості залишається сталим, але напрям її безперервно змінюється. Розглянемо два 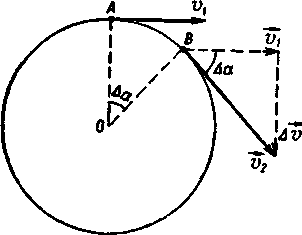вектори швидкості тіла через невели­кий проміжок часу ∆t. Віднімаючи перше значення швидкості , від наступного , дістанемо приріст




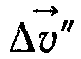
(рис. 1.3). За загальним правилом дії над векторами можна пере­нести початок векторів швидкості в одну точку (паралельний перенос). Напрям цих векторів збігається з напрямом дотичної до кола в тій точці, де лежить точка в даний момент. Вектор 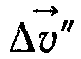не буде перпендикулярним ні до , ні до . Проте при ∆t→0 і 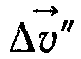→0 напрям вектора 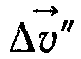стає перпендикулярним до вектора швидкості .

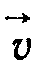Отже, нескінченно малий приріст вектора 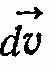перпендикулярнийдо вектора 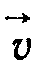, тому прискорення 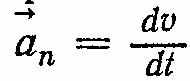- перпендикулярне до швидкості і напрямлене до центра кола. Значення прискорення можна пов'язати із значенням швидкості 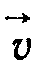руху тіла по колу й значенням радіуса . При малому ∆φ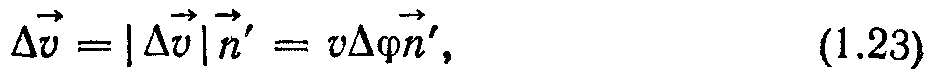



де 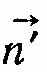— одиничний вектор, напрям якого збігається з напрямом вектора 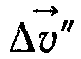. Підставляючи в (1.23) ∆φ з (1.20), дістанемо



Розділивши 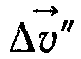на ∆t і зробивши відповідні перетворення, дістанемо



У цьому виразі v та r — сталі, відношення — 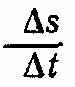в граничному випадку дає модуль швидкості у; одиничний вектор 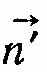в граничному випадку збігається з одиничним вектором 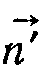, який перпендикулярний до кола в точці А і напрямлений до центра. Отже,



Знайдене прискорення напрямлене вздовж нормалі до траєкторії, тобто воно є нормальним.

Якщо матеріальна точка рухається по колу нерівномірно, то крім нормального (його у випадку руху по колу називають ще доцентровим) вона матиме тангенціальне прискорення



яке характеризує зміну швидкості за величиною. Враховуючи вираз (1.21), для тангенціального прискорення дістанемо



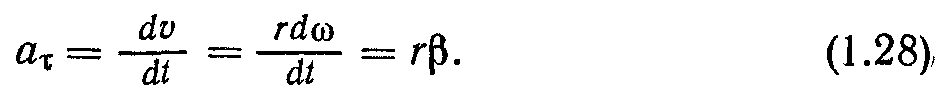
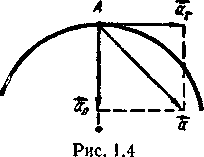
Отже, тангенціальне прискорення зростає лінійно із збільшенням відстані від осі обертання. Остаточно для вектора прискорення (рис. 1.4) запишемо

Завдання для самостійної роботи. Зробіть конспектування наступного матеріалу.

5. Одиниці фізичних величин

Існує кілька систем, що відрізняються вибором основних одиниць. Системи, в основу яких покладено одиниці довжини, маси і часу, називають абсолютними.

Основними одиницями в СІ є: одиниця довжини — метр (м), ма­си — кілограм (кг), часу — секунда (с), сили струму — ампер (А), термодинамічної температури — кельвін (К), кількості речовини — моль, сили світла — кандела (кд). Про ці одиниці йтиметься у відпо­відних розділах книги.

Метр — це довжина шляху, який проходить світло у вакуумі за інтервал часу 1/299 792 458 с. Застосовуються також кратні та часткові одиниці метра: кілометр (10³ м), сантиметр (10 м), міліметр (10 м), мікрометр (10 м) тощо.

Кілограм — це одиниця маси, яка дорівнює масі міжнародного прототипу кілограма.

Секунда — це час, що дорівнює 9192631770 періодам випромінюван­ня, що відповідає переходу між двома надтонкими рівнями основно­го стану атома цезію-133.

Ампер— це сила незмінюваного струму, який, проходячи по двох паралельних прямолінійних провідниках нескінченної довжини та дуже малої площі кругового перерізу, розміщених у вакуумі на від­стані 1 м один від одного, зумовлює на кожній ділянці провідника довжиною 1 м силу взаємодії, що дорівнює 2 • 10^-7 Н.

Одиницю температури і різниці температур за шкалою Кельвіна називають кельвіном (К). Кельвін дорівнює 1/273,16 частині термоди­намічної температури потрійної точки води.

За одиницю кількості речовини прийнято моль — кількість речо­вини системи, що містить стільки структурних елементів, скільки міститься атомів у вуглеці-12 масою 0,012 кг.

За одиницю сили світла прийнята кандела (кд) — сила світла в заданому напрямі джерела, що випромінює монохроматичне випромі­нювання з частотою 540 • 10¹² Гц, енергетична сила світла якого в цьому напрямі становить 1/683 Вт/ср (ср — стерадіан, див. розд. 8).

Для позначення розмірності довільної фізичної величини викори­стовують її символьне позначення, яке береться в квадратні дужки. Так, наприклад, символ [v] означає розмірність швидкості. Для розмірностей основних величин використовують спеціальні позначення: для довжини — L, для маси — М, для часу — Т. Отже, позначивши довжину літерою 1, масу — т, а час — t, запишемо [l] = L, [m] = = М, [t] = Т.

Нехай, наприклад, нас цікавить розмірність швидкості



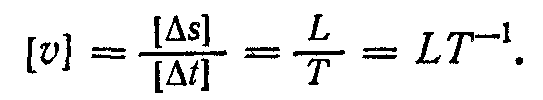
Записане співвідношення називають формулою розмірності, а його праву частину — розмірністю відповідної величини (у цьому разі швидкості).

Враховуючи співвідношення 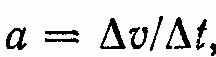, можна встановити розмірність прискорення:



Аналогічно можна дістати розмірності всіх інших величин.


Завдання для самоконтролю.

1.Що називається матеріальною точкою? 2. Назвіть основні види руху матеріальної точки. 3. Дайте визначення миттєвої швидкості і миттєвого прискорення. 4. Як напрямлений вектор миттєвої швидкості відносно траєкторії? 5. Як напрямлені тангенціальне і доцентрове прискорення відносно радіуса кривизни траєкторії? (і. При якому русі доцентрове прискорення дорівнює нулю, а тангенціальне приско­рення стале? 7. При якому русі тангенціальне прискорення дорівнює нулю, а нор­мальне прискорення стале? 8. Чому дорівнює відношення лінійної швидкості до куто­вої швидкості, якщо матеріальна точка рівномірно рухається по колу? 9. В яких одиницях вимірюється кутова швидкість і кутове прискорення? 10. Що являє собою похідна кутової швидкості за часом? 11. Накресліть графіки залежності шляху s, швидкості v і прискорення а від часу t при рівноприскореному русі без початкової швидкості. 12. Скільки основних одиниць фізичних величин має Міжнародна система? Дайте визначення їм. 13. Назвіть основні одиниці механіки та вкажіть їхні роз­мірності. 14. Чому дорівнює відношення розмірності фізичної величини до розмір­ності градієнта цієї самої фізичної величини?

План.

1. Класична механіка. Простір і час у механіці Ньютона. Сила.
   
2. Перший закон Ньютона
   
3. Інерціальні системи відліку
   
4. Принцип відносності Галілея
   
5. Другий закон Ньютона.
   
6. Детермінізм Лапласа.
   
7. Третій закон Ньютона
   
8. Закон всесвітнього тяжіння.
   
9. Інертна і гравітаційна маси
   

Рекомендована література.

Основна: 1.С.50-71; 2.С.43-51

Додаткова: 3. С.9-14.


Теоретичні відомості.