План. Механіка. Система відліку. Матеріальна точка Прискорення. Швидкість

Вид материала

Лекція

Содержание Динаміка матеріальної точки Маса — це властивість матерії, що характеризує її інертність і гравітацію.2. Перший закон Ньютона 3. Інерціальні системи відліку 4. Принцип відносності Галілея 5. Другий закон Ньютона 6. Детермінізм Лапласа 7. Третій закон Ньютона

Подобный материал:

• Програма вступного випробування та співбесіди з фізики для вступу на перший курс навчання, 85.23kb.
• План учебных занятий по курсу «Физика». 9 класс (4 часа в неделю), 72.35kb.
• Календарно-тематический план (балльно-рейтинговая система, 1 семестр), 58.92kb.
• Тема. Матеріальна відповідальність сторін трудового договору, 90.15kb.
• Урок на тему «Штучні супутники Землі», 21.17kb.
• Реферат на тему: Швидкість обігу грошей та чинники, що її визначають, 58.43kb.
• Организационный план 31 6 План производства 32 7 Финансовый план 38 План по рискам, 841.71kb.
• І. вступ сучасна система освіти зіткнулася з проблемою прискорення І непередбачуваності, 80.21kb.
• План Матеріальна культура Римської імперії Соціальний устрій, 294.96kb.
• Реферат на тему на тему Розпад СРСР та заснування снд, 97.55kb.

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ

1. Класична механіка. Простір і час у механіці Ньютона. Простір і час — форми існу­вання матерії. Простір у Ньютона абсолютний за самою своєю суттю, безвідносно до будь-чого зовнішнього, залишається завжди сталим і нерухомим. Простір однорідний в усіх своїх частинах і ізотропний (властивості його не залежать від напряму). Тобто, фізичний простір збігається з простором у геометрії Евкліда. Поняття простору, його геометричних елементів (точка, лінія, поверхня, об'єм) виникли як абстракції властивостей матеріальних тіл. Евклідів простір лише наближено відбиває властивості фізичного простору. Проте для меха­нічних явищ, які розглядатимуться далі, з великою точністю простір можна вважати евклідовим. Припущення про однорідність і ізотроп­ність простору в класичній механіці, яка розглядає рух макротіл з відносно малими швидкостями, також справедливе.

Інколи стверджують: механічний рух — це переміщення тіла в просторі з часом. Таке визначення потребує істотного уточнення. Адже при механічному русі відбувається переміщення одних тіл відносно інших. Якби існувало тільки одне тіло, то говорити про його перемі­щення було б безглуздо. Завжди відбувається переміщення одних тіл відносно інших. Фактично завжди система пов'язана з якимось тілом або тілами. Без матеріальних тіл не можна уявити простору, а точніше — він тоді б не існував.

Час за Ньютоном — абсолютна плинність, що існує незалежно від тіл. При відносно повільних рухах, коли швидкість дуже мала порів­няно з швидкістю світла, залежність часу від відносного руху системи відліку дуже мала і нею можна нехтувати. Тому вважатимемо спра­ведливим вибір однієї незмінної одиниці часу для всіх явищ у механіці. Отже, простір і час у механіці Ньютона об'єктивно реальні, але орга­нічно не зв'язані з матерією.

З поняттям абсолютних простору й часу Ньютона пов'язані прин­ципові труднощі у фізиці, глибока внутрішня суперечність між теорією і дослідом: теорія побудована на поняттях, які експериментальне не можна виявити. З часів Ньютона ця суперечність рухала фізику. Праг­нення розв'язати її привело до важливих експериментів і теоретичних досліджень. Історія фізики не раз підтверджувала основне положення діалектики про внутрішні суперечності як джерело розвитку. Супереч­ності, введені Ньютоном, розв'язав Ейнштейн.

Основними фізичними величинами в механіці Ньютона є сила і маса.

Сила. Фізичні тіла взаємодіють між собою. Але взаємодія взагалі дуже широке поняття, що означає взаємозв'язок, взаємовплив тіл.

Різні науки вивчають окремі види взаємодії. Механіка вивчає механічну взаємодію тіл, що характеризується силою. Під силою в ме­ханіці розуміють фізичну причину зміни стану руху тіла або його фор­ми і розмірів, які виникають у результаті взаємодії даного тіла з іншими тілами. Сила — кількісна характеристика механічної взаємо­дії тіл. Дія сили на тіло виявляється двояко: динамічно, коли тіло під впливом прикладеної до нього сили набуває прискорення, і ста­тично, коли тіло деформується. Сила характеризується точкою при­кладання, напрямом та абсолютною величиною (модулем).

Сила оцінюється за результатом дії одного тіла на інше: за при­скоренням, що його набуває тіло, або за деформацією. Отже, силу мож­на вимірювати за прискоренням і за деформацією еталонного тіла. Для вимірювання сил використовують пружинні терези, динамометри. Основним елементом цих приладів є стандартна пружина, яка під дією прикладеної сили деформується. В межах малих деформацій сила про­порційна величині деформації (закон Гука).

Маса — це властивість матерії, що характеризує її інертність і гравітацію.


2. Перший закон Ньютона


Кінематика не розкриває причин руху. Вона лише описує сам рух. Розкрити причини руху справа не така вже й проста.

До Галілея протягом майже двох тисяч років існувала динаміка Арістотеля (384—322 до н. е.). За Арістотелем, небесні тіла за своєю' природою відмінні від земних і рухаються лише по досконалих кри­вих— колах, першоджерело їхнього руху — дух (бог). Земні тіла самі по собі, без дії сил перебувають у стані спокою, причина їхнього руху — сила. Основне характерне положення динаміки Арістотеля: без сили немає руху. Тобто, для підтримання руху тіла потрібна дія на нього інших тіл. Ця точка зору відповідає безпосередньому, ін­туїтивному уявленню про рух.

Так, візок рухається лише тоді, коли його підштовхують. Якщо штовхнути візок сильніше, то він рухатиметься швидше і, нарешті, якщо зовсім припинити дію сили на нього, візок зупиниться.

Наявність у тіла швидкості пов'язувалась з дією на нього інших тіл, а величина і напрям швидкості — з характером та інтенсивністю цієї дії.

Уявлення Аристотеля про рух були спростовані Г. Галілеєм (1564— 1642), який вперше застосував метод наукового міркування в тлума­ченні поставлених ним експериментів.

Вивчаючи скочування гладенької кулі з похилої площини, Галілей помітив, що при русі вниз куля рухається прискорено, поступово збільшуючи швидкість, а при русі вгору — сповільнено. Звідси він зробив висновок, що, скотившись на горизонтальну площину, куля вічно рухатиметься з тією самою швидкістю на нескінченній площині, якщо ніщо не заважатиме її руху. Це саме можна спостерігати з віз­ком, що рухається по гладенькій поверхні. Зазнавши поштовху, ві­зок починає рухатись і через деякий час зупиниться. Але зменшуючи опір повітря й тертя між візком і площиною, можна необмежене збіль­шувати його шлях. У граничному наближенні (без тертя й опору повіт­ря) візок рухатиметься безмежно довго з сталою за величиною і напря­мом швидкістю. Це твердження називається законом інерції. Чітке визначення його вперше дав І. Ньютон: будь-яке тіло зберігає стан спокою або рівномірного прямолінійного руху доти, поки дія сил не при­мусить його змінити цей стан.

Властивість тіл зберігати стан спокою або рівномірного прямо­лінійного руху називають інерцією. Тому перший закон Ньютона на­зивають ще законом інерції.

Нескінченну площину реалізувати не можна, не можна поставити тіло і в такі умови, щоб на нього не діяли інші тіла. Але можна пере­вірити протилежне: у всіх випадках, коли тіло змінює свою швидкість за величиною і напрямом, тобто дістає прискорення, завжди¹ можна вказати тіла, дія яких викликає це прискорення. Наприклад, викрив­лення траєкторії тіла, яке кинули під кутом до горизонту, відбуваєть­ся під дією притягання з боку Землі; куля, зіткнувшись зі стіною, змі­нює свою швидкість під дією сили, яка діє з боку деформованої стіни.

Отже, причиною прискорення тіла є діюча на нього сила. Дослід показує, що напрями векторів сили й прискорення збігаються і що прискорення пропорційне діючій силі. Такого висновку дійшли Галілей і Ньютон. Вони також ототожнювали фізично стан спокою і рівномірного прямолінійного руху тіла, бо ці стани реалізуються за однакових умов — коли діюча на тіло сила (рівнодійна сил) дорівнює нулю. Із закону інерції можна зробити висновок, що тіло рухатиметься й тоді, коли на нього не діє сила. Все це суперечить динаміці Аристотеля, який вважав, що тіла рухаються лише тоді, коли на них діє сила, яка пропорційна швидкості (не прискоренню!) тіла. У динаміці Аристотеля явища розглядалися поверхово, а також неправильно тлумачилися.

Динаміка Галілея — Ньютона глибше проникає в суть явищ і правильно тлумачить їх. Проте вона не наочна, її закони ще слід до­вести. Історично це стало можливим на більш високому рівні розвит­ку науки (експерименту й теорії).

Ми переконались, що стан тіла змінюється під дією інших тіл. А як впливають на зміну стану властивості самого тіла? Нехай на якесь тіло, що перебуває в стані спокою, подіяла сила. Оскільки під дією сили тіло набуває не швидкості, а прискорення, то потрібний час для досягнення кінцевої швидкості. Цей час для різних тіл буде неодна­ковим.

Скалярна величина, що характеризує інерцію тіла, називається його інертною масою. Чим повільніше тіло змінює свій стан під дією сили, тим більша його маса. З визначення зрозуміло, що маса будь-якого тіла більша від нуля. Маса — величина адитивна. Вона не зале­жить ні від умов, в яких перебуває тіло, ні від взаємодії його з іншими тілами. Перший закон Ньютона справедливий не в будь-якій системі відліку, а лише в інерціальній.


3. Інерціальні системи відліку


Тіло або сукупність тіл, які умовно вважаються нерухомими і від­носно яких розглядається рух інших тіл, називають у фізиці тілами відліку. Систему відліку можна вибрати довільно. При цьому рух будь-якого тіла в різних системах відліку матиме неоднаковий вигляд, тобто тіло рухатиметься, наприклад, по різних траєкторіях. Якщо взяти довільну систему, то може трапитись, що навіть закони зовсім простих явищ будуть складними.

Природно вибрати систему відліку так, щоб явища природи опису­вались у ній найбільш просто. Для цього розглянемо тіло, що знахо­диться настільки далеко від інших тіл, що останні не діють на нього. Рух такого тіла називається вільним. Умови вільного руху можна реалізувати з більшою чи з меншою точністю.

Якщо система відліку пов'язана з якимось вільно рухомим тілом, то в ній вільний рух інших тіл має досить простий вигляд: він відбува­ється прямолінійно і рівномірно, тобто з сталою за величиною й на­прямом швидкістю. У цьому полягає зміст закону інерції. Тому систе­ма відліку, пов'язана з тілом, що вільно рухається, називається інер-иіальною. Якщо деяка система рухається відносно інерціальної систе­ми із сталою (за величиною й напрямом) швидкістю, то вона також буде інерціальною. Дослід показує, що інерціальні системи нічим не відрізняються між собою, фізичні явища в них відбуваються однаково, закони механіки мають однаковий вигляд. Отже, неможливо виділити одну із систем як особливу, бо такої системи не існує. Якби можна було виділити якусь систему, то це означало б, що існує абсолютний простір і абсолютний спокій відносно цієї виняткової системи відліку.

Системи відліку, які зв'язані з Сонцем і зірками, практично можна вважати інерціальними. Систему, початок якої поміщено в центр Сонця, точніше в центр мас Сонячної системи, а осі напрямлені до будь-яких трьох «нерухомих» зірок (що не беруть участь в обертанні Сон­ця навколо його осі), назвемо «сонячною», або геліоцентричною. Са­ме нею скористався Кеплер, вивчаючи кінематику небесних тіл, і відкрив закони руху планет. Перехід до сонячної системи відліку був нелегким, але він мав велике значення в боротьбі з геоцент­ризмом.

Якщо стверджують, що закони Ньютона справедливі в «світовому просторі», в «нерухомій системі», практично мають на увазі реальну Сонячну систему, а не ілюзорний абсолютний простір. Проте й це не є принциповим розв'язанням питання про систему відліку. Адже Сон­це у Всесвіті — звичайна зірка, тому в певному розумінні безглуздо віддавати перевагу як геліоцентризму, так і геоцентризму.

Практично системи відліку, що використовуються в фізичних екс­периментах, є інерціальними з більшою чи меншою точністю. Найбільш поширеною є система відліку, зв'язана з земною кулею. Але вона не є інерціальною, тому що Земля обертається навколо своєї осі і руха­ється по еліптичній орбіті навколо Сонця. Ці рухи здійснюються різ­ними точками земної кулі не з однаковими і не з сталими швидко­стями.

Враховуючи повільну зміну напряму швидкості обох рухів Землі, для багатьох фізичних експериментів з невеликою похибкою можна вважати «земну» систему відліку інерціальною. Зокрема, Земля за 30 хв. руху по орбіті із швидкістю 30 км/с описує дугу величиною лише Г. Сонячна система також обертається навколо центра Галактики, щоправда з періодом близько 200 млн. років і з швидкістю 250 км/с.

Завдання для самостійної роботи. Зробіть конспектування наступного матеріалу.

4. Принцип відносності Галілея

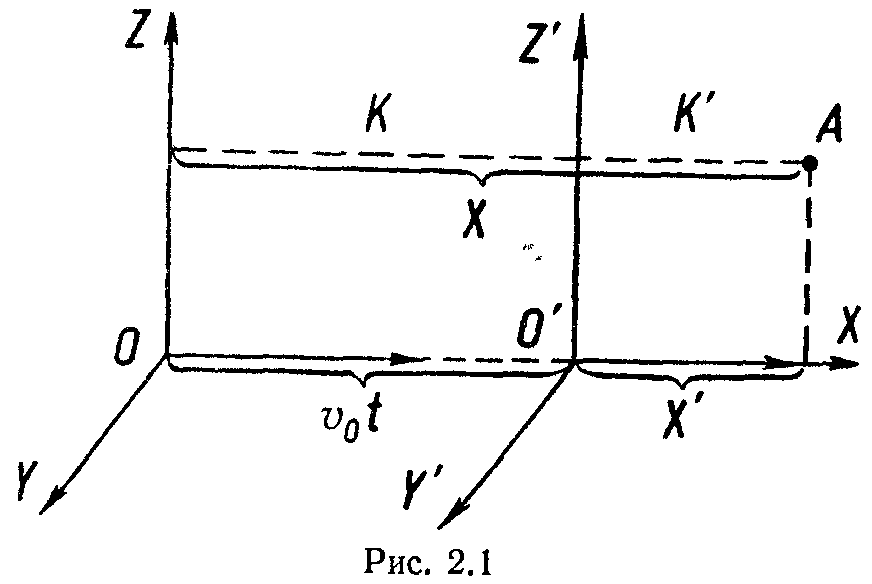
Розглянемо дві системи відліку К і К′ (рис. 2.1). Нехай система К′ рухається відносно системи К вздовж осі х з швидкістю v₀. Тоді можна записати зв'язок між координатами матеріальної точки А для цих систем:



Перші дві координати точки збігаються тому, що обмежено рух системи К' лише вздовж осі х. Тому з часом змінюється тільки ця координата. А в загальному випадку будуть змінюватися всі координати. Плинність часу в обох системах однакова.

Формули (2.1) називають перетвореннями Галілея. Якщо від перших трьох рівнянь (2.1) візьмемо похідні за часом, то дістанемо відповідні проекції швидкостей v'_z = v_z; v'_y — v_y; v'_x = v_x — v₀. Ці співвідношення можна записати у векторній формі:



Швидкість 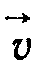відносно нерухомої системи відліку К складається із швидкості v' відносно рухомої системи К' і швидкості 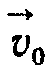системи К' відносно системи К. Формулу (2.2) називають за­коном додавання швид­костей.

Візьмемо похідну за часом від лівої та правої частин рівності (2.2).

Враховуючи, що 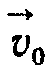є величина стала, дістанемо



тобто у всіх інерціальних системах прискорення залишається сталим.

Взагалі абсолютної системи відліку не існує, а поняття абсолютного спокою позбавлене сенсу. Якщо тіло перебуває в стані спокою в одній із інерціальних систем відліку, то відносно всіх інших воно рухатиметься з різними сталими швидкостями, тому немає підстав віддавати перевагу одній системі перед іншими. В класичній механіці немає поняття абсолютної швидкості, тільки відносна швидкість тіл має фізичний зміст. Разом з тим поняття абсолютного прискорення справедливе, оскільки воно в різних інерціальних системах відліку однакове.

Як видно з співвідношення (2.3), рівняння динаміки не змінюються, якщо перейти від однієї інерціальної системи відліку до іншої, тобто вони інваріантні щодо перетворень Галілея. З точки зору механіки всі інерціальні системи відліку абсолютно еквівалентні: жодній з них не можна віддавати перевагу перед іншими. Практично це виявляється в тому, що ніякими механічними дослідами, проведеними в да­ній системі відліку, не можна встановити, чи знаходиться вона в стані спокою, чи в стані рівномірного і прямолінійного руху.

Вказані властивості інерціальних систем були вперше з'ясовані Галілеєм. Принцип відносності Галілея можна сформулювати так: всі механічні явища в різних інерціальних системах відліку відбуваються однаково, внаслідок чого ніякими механічними дослідами неможливо встановити, нерухома дана система чи рухається рівномірно і прямолінійно.


5. Другий закон Ньютона


У 1687 р. І. Ньютон у своїх «Началах» сформулював всі основні за­кони механіки. Узагальнюючи численні досліди, Ньютон встановив зв'язок між масою і прискоренням тіла та діючою на нього силою



де F — векторна сума всіх сил, що діють на тіло; т — маса тіла; 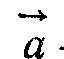— прискорення. Співвідношення (2.4) називають другим законом Ньюто­на, який можна сформулювати так: сила, що діє на тіло, дорівнює до­бутку маси тіла на прискорення, якого надає ця сила.

Слід зазначити, що закон інерції є наслідком другого закону Нью­тона. Справді, нехай на тіло не діє сила, тоді ліва частина рівності (2.4) дорівнює нулю. Оскільки т≠0, то нулю дорівнює прискорення.

А звідси випливає, що 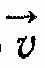= const, або 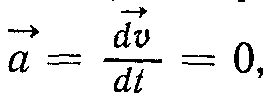, що є математичним виразом закону інерції. Істотним є в цьому випадку сталість вектора швидкості, що забезпечує прямолінійність руху. Вираз (2.4) ще нази­вають рівнянням руху тіла.

Основне завдання механіки полягає в тому, щоб за заданим станом тіла (координати і швидкість у даний момент) визначити в будь-який момент часу всі наступні його стани без додаткових вимірювань. При цьому припускається, що сили, які діють на тіло, відомі.

Другому закону Ньютона можна дати більш загальне визначення. Виконаємо деякі перетворення з рівнянням (2.4):



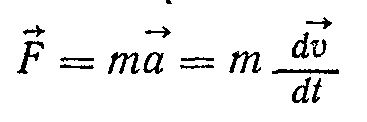
або



тут т = const.

Якщо маса тіла змінюється, то



де Fdt — елементарний імпульс сили, що відповідає досить малому проміжку часу dt; 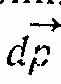— елементарна зміна імпульсу тіла; mv — імпульс або кількість руху. Отже, другий закон Ньютона можна сфор­мулювати так: імпульс сили, що діє на тіло протягом малого проміжку часу, дорівнює зміні імпульсу тіла за цей самий проміжок часу. Запишемо рівняння (2.6) у такому вигляді:



Це дає змогу дати другому закону Ньютона більш загальне формулювання: зміна імпульсу тіла за секунду в даний момент часу дорівнює прикладеній силі і відбувається в тому самому напрямі, в якому діє ця сила. Або: перша похідна за часом від імпульсу тіла дорівнює прикла­деній силі.

У другому законі Ньютона фігурують дві фізичні величини: сила та маса. Сила кількісно характеризує величину і напрям дії на дане тіло інших тіл. Маса є кількісною характеристикою інертності.

Одиницю сили в СІ називають ньютоном (Н). Згідно з рівністю (2.4) ньютон дорівнює силі, під дією якої тіло масою 1 кг дістає приско­рення 1 м/с³. Одиницю сили в системі СГС називають диною (дин). Одна дина дорівнює силі, під дією якої тіло масою 1 г дістає приско­рення 1 см/с². Між ньютоном та диною існує таке співвідношення: 1 Н = 1 кг • 1 м/с² = 10⁵ г • см/с² = 10⁵ дин.

У другому законі Ньютона йдеться про сили, що діють на дане (одне) тіло, але не відображено ролі другого тіла, з боку якого діє сила. Сила характеризує взаємодію принаймні двох тіл; роль другого тіла в динамічних явищах визначена третім законом Ньютона.


6. Детермінізм Лапласа


Другий закон Ньютона дає змогу виразити зв'язок станів механіч­ної системи у вигляді закону динамічного типу. В ньютонівському розумінні причиною зміни стану руху тіла виступає зовнішня дія на нього, при цьому початковий стан тіла є умовою його руху. В лапласївському розумінні початковий стан тіла розглядається як причина його кінцевого стану, а зовнішня дія на нього є умовою руху тіла.

При всіх відмінностях ньютонівське тлумачення причини як сили, що обумовлює механічний рух, і лапласівське тлумачення причинності як зв'язку станів механічної системи пов'язані одне з одним. Визначен­ня причинної обумовленості механічного об'єкта веде до визнання де­термінованості його станів і, навпаки, визнання детермінованого ста­ну пов'язане з визнанням обумовленості руху об'єкта певною силою.

Лапласівський детермінізм (твердження про можливість точного передбачення руху механічних об'єктів) являє собою визнання пізнаваності законів, що відображають зв'язок станів механічного об'єкта, а отже, пізнання причинних зв'язків, що обумовлюють його рух.

Лапласівський детермінізм в класичній механіці збігається з мате­матичним детермінізмом. Диференціальні рівняння, які описують рух механічної системи, при заданих початкових умовах мають тільки один розв'язок, за допомогою якого можна визначити поведінку цієї системи в майбутньому.

Другий закон Ньютона виражає в опосередкованій формі необхід­ний зв'язок між початковим станом системи та її станом в наступний момент часу при заданих зовнішніх діях на систему. Він виражає те, що даний початковий стан при заданих умовах неодмінно детермінує наступні стани, які, в свою чергу, детермінують свій наступний стан і т. д. Тому поняття необхідного зв'язку станів, так званий класичний детермінізм, може бути сформульоване так: з одного і того самого по­чаткового стану при однакових зовнішніх умовах виникає один і той самий ряд станів системи.

Необхідний зв'язок станів системи Лаплас ототожнював з причин­ним зв'язком, вважаючи, що сучасний стан Всесвіту е наслідком його попередніх станів та причиною наступних. Стан світу в даний момент, на його думку, визначає стан світу в будь-який інший наступний момент часу. Він вважає, що поняття необхідного зв'язку станів можна застосовувати не лише до Всесвіту в цілому, а і до скінченних систем. Кожне явище в природі — необхідний наслідок її законів. Випадкові причини, за Лапласом, це уявні, що насправді не існують, вони відкидаються в процесі розширення границі людського знання. Визнання об'єктивного зв'язку станів природних процесів є великою заслугою лапласівського детермінізму. Проте не можна погодитися з його погля­дом на випадкове, .як на таке, причину чого ми не знаємо. Категорія випадковості у Лапласа перетворюється в чисто суб'єктивну категорію

Лаплас визнає, що причинні зв'язки пізнаванні, і підкреслює, що на­ше знання цих зв'язків все більше розширюється і поглиблюється, наближаючись до повного і вичерпного знання. «Розум,— писав він,— який для якогось даного моменту часу знав би всі сили, що діють в природі, та відносне розташування її складових частин, якби він до того ж був достатньо великий, щоб піддати ці дані аналізу, охопив би в одній формулі рух найбільших тіл Всесвіту і найменшого атома, для нього не було б нічого неясного, і майбутнє, так само як і минуле, стало б перед його поглядом».

Іншими словами: якби демон Лапласа (прообраз всеосяжного розу­му) був у змозі фіксувати в будь-який момент положення і швидкості всіх атомів Всесвіту, всі сили, що діють на них, якби для нього не іс­нувало ніяких математичних труднощів, та щоб він міг миттєво ро­бити найскладніші розрахунки, то він міг би, за Лапласом, дати відомості про всю минулу та майбутню долю світу, передбачити всі події. У цьому полягає суть лапласівського детермінізму.

Механізм лапласівського детермінізму виходить з того, що зв'язок станів будь-яких об'єктів може бути описаний за допомогою понять і законів класичної механіки. Світ, за Лапласом, є сукупністю матеріальних точок, що змінюють свій стан під дією механічних сил, описуючи при цьому певні траєкторії. Корені обмеженості лапласівської концепції причинності полягають в універсалізації механічної картини світу.

Динамічна закономірність, що формулюється в механіці", відобра­жає об'єктивні, причинні зв'язки фізичних процесів. Проте причин­ність у динамічній закономірності однобічна. В законах класичної механіки причинність виступає як однозначна неминучість.

Причинність, яка є однією з форм зв'язку, однобічно відображає загальний зв'язок та взаємообумовленість об'єктів. Але вона відобра­жає також внутрішньо притаманну властивість матерії, що рухається в просторі й часі, спричиняти всю різноманітність явищ оточуючого нас світу, бути активним началом всіх його змін.

Отже, лапласівський детермінізм виражає одне з розумінь зако­номірностей зміни фізичних процесів в часі, яке виросло на грунті класичної механіки. Раціональним у цьому детермінізмі є визнання об'єктивності і пізнаванності зв'язку станів. Обмеженість його поля­гає в запереченні об'єктивного характеру випадковості та в абсолюти­зації механічної картини світу.

7. Третій закон Ньютона

Третій закон Ньютона відображає той факт, що сила є наслідком взаємодії двох або більше тіл. У другому законі розглядався лише один бік цієї взаємодії, насправді, завжди існує взаємодія і немає сил без протидіючої сили. Назви «дія» і «протидія» — чисто умовні, кожна з них може вважатись тим і іншим.

Третій закон Ньютона є узагальненням дослідних фактів. Його формулюють так: будь-яка дія тіл одне на одне носить характер взаємодії; сили, з якими діють одне на одне взаємодіючі тіла, завжди рівні між собою за величиною і протилежні за напрямом.

Звідси випливає, що сили завжди виникають парами: будь-якій силі, прикладеній до якогось тіла, можна ставити у відповідність та­ку саму за величиною та протилежну за напрямом силу, яку прикладено до іншого тіла, що взаємодіє з даним.

Слід зауважити також, що в третьому законі йдеться про сили, прикладені до різних тіл. Сили, що діють між тілами системи, нази­вають внутрішніми. Сили, що діють на систему з боку тіл, які не вхо­дять до складу її, називають зовнішніми. Якщо взаємодією між тілами системи і зовнішніми тілами можна нехтувати, то таку систему називають замкненою. В замкненій системі діють лише внутрішні сили. Розглянемо саме таку систему, що складається з трьох взаємодіючих між собою тіл (рис. 2.2).

На кожне тіло діють сили лише з боку двох інших тіл, тобто внутрішні сили. Позначимо їх буквою F з відповідними індексами, що вказують, до якого тіла прикладена сила і з боку якого тіла вона діє.

Користуючись формулою (2.7), запишемо для кожного з цих тіл другий закон Ньютона:



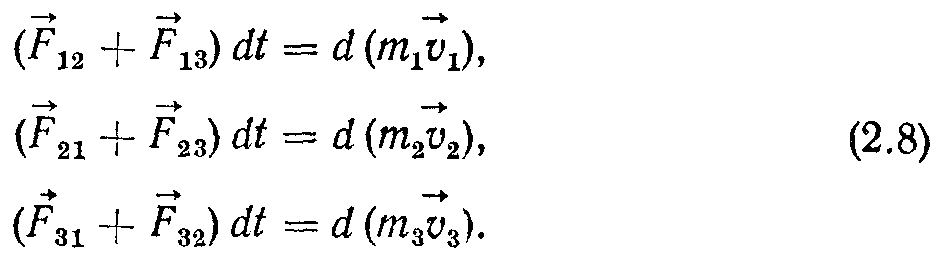
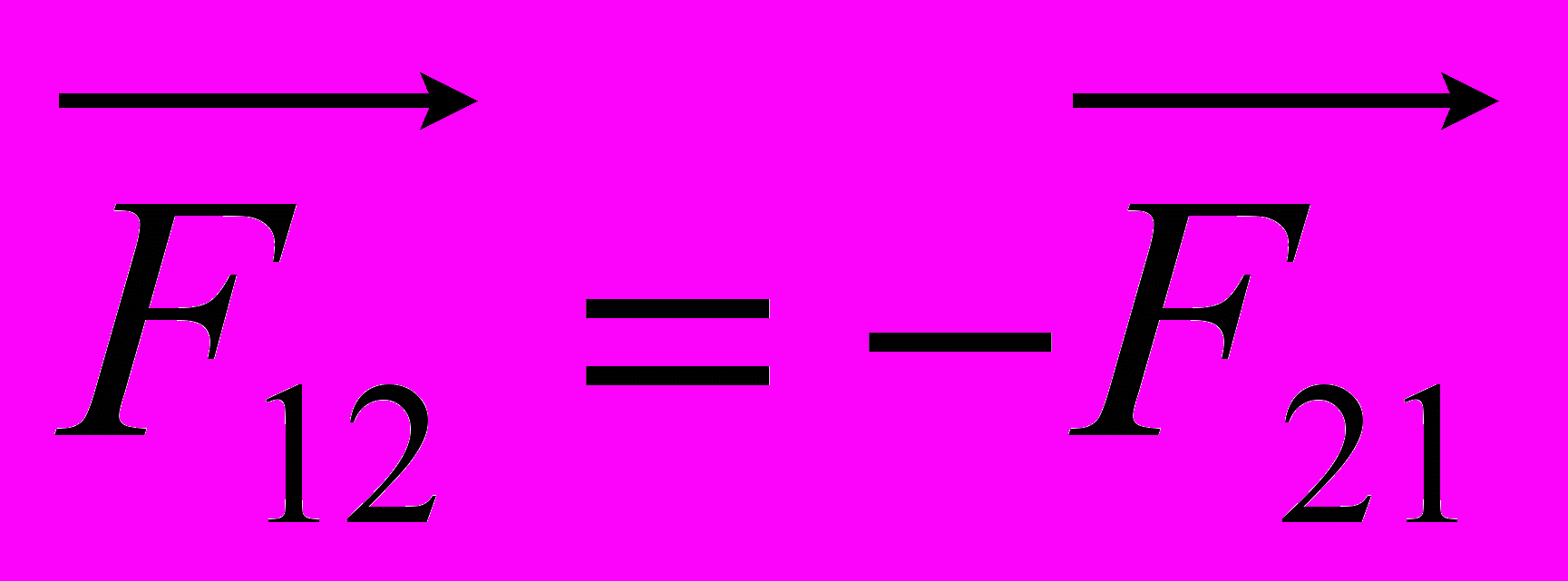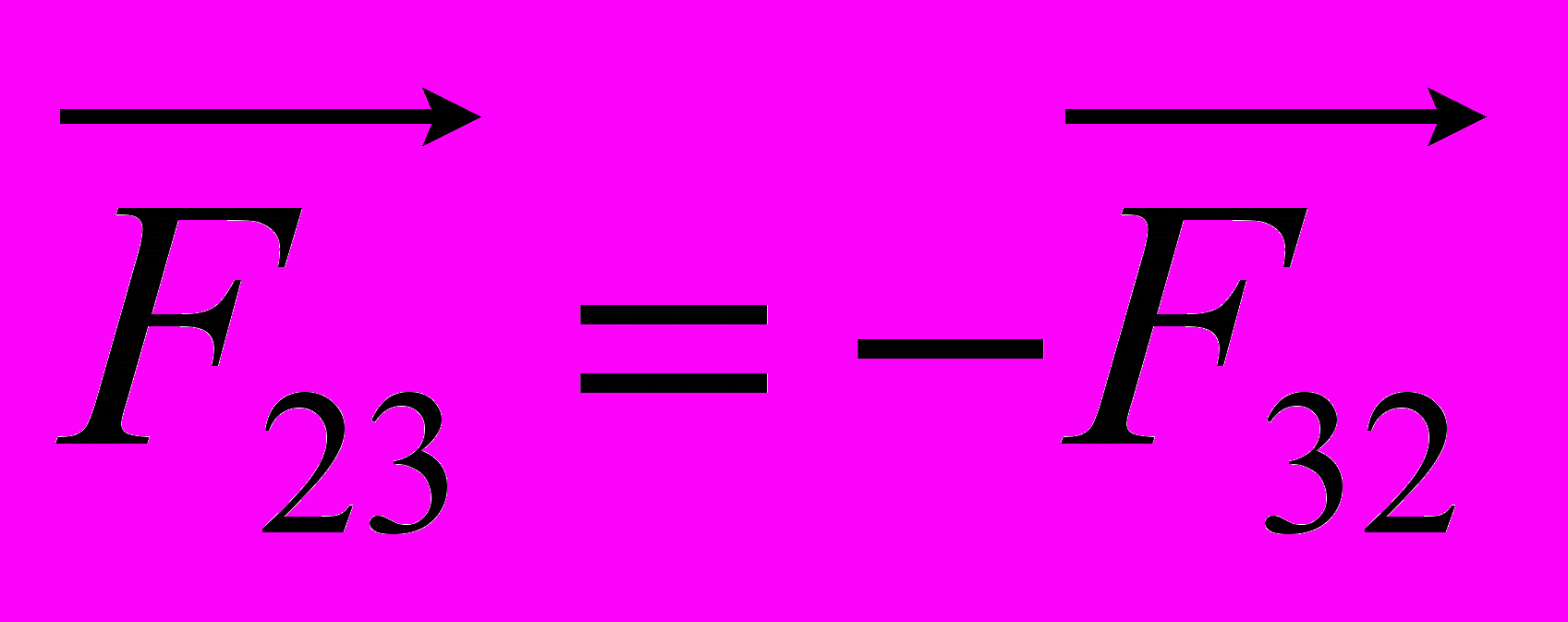Додаючи в рівняннях (2.8) відповідно ліві і праві частини та враховуючи, що за третім законом Ньютона , і 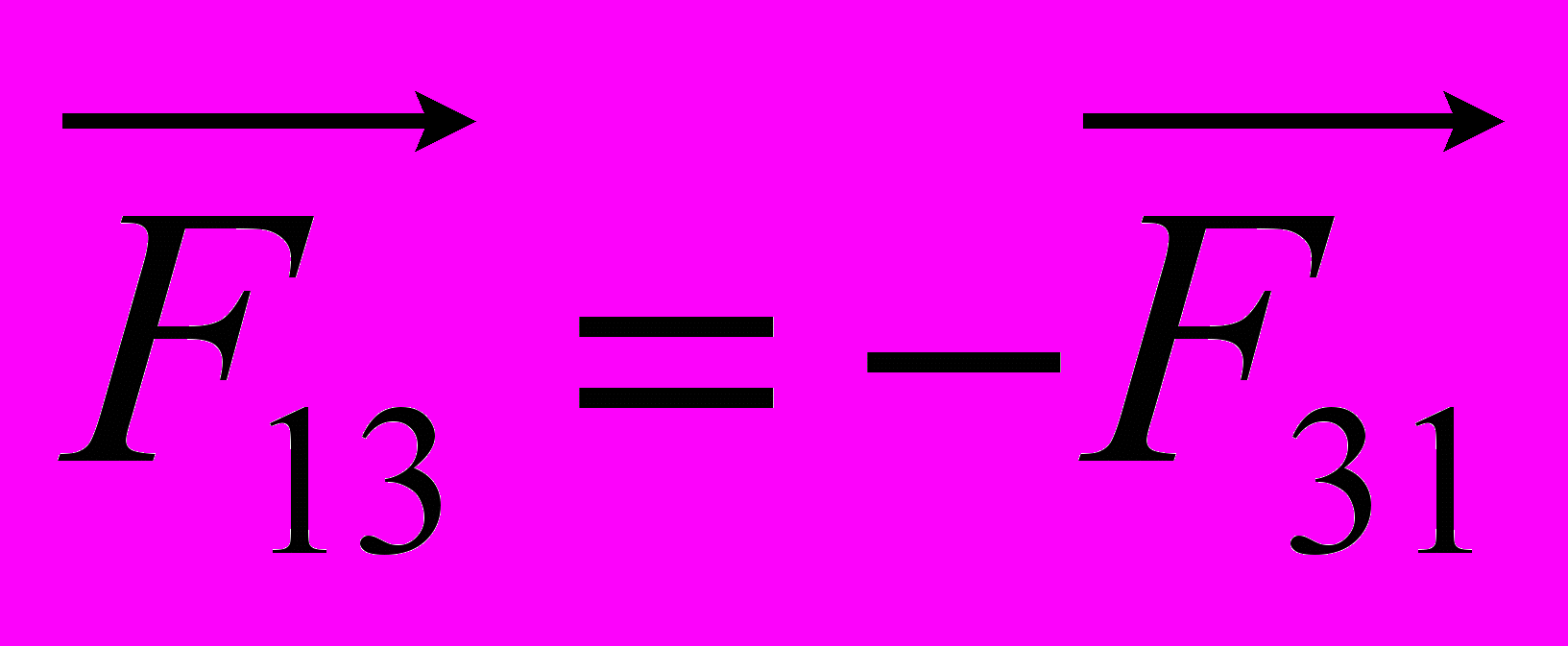, дістанемо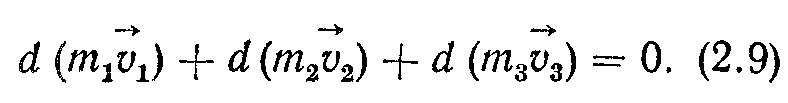



Отже, внутрішні сили компенсують одна одну, тому їх можна не враховувати. Тоді



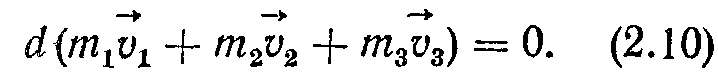
Оскільки зміна з часом імпульсу системи дорівнює нулю, то сам ім­пульс залишається сталим, тобто



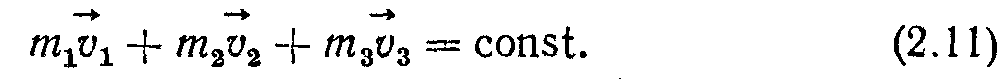
Такий самий результат матимемо для замкненої системи, що складається з п тіл:



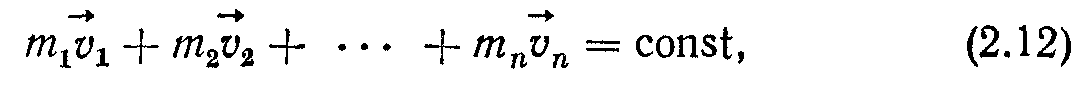
або



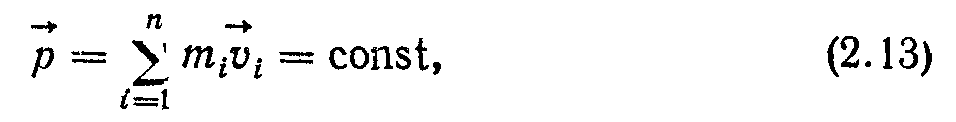
де 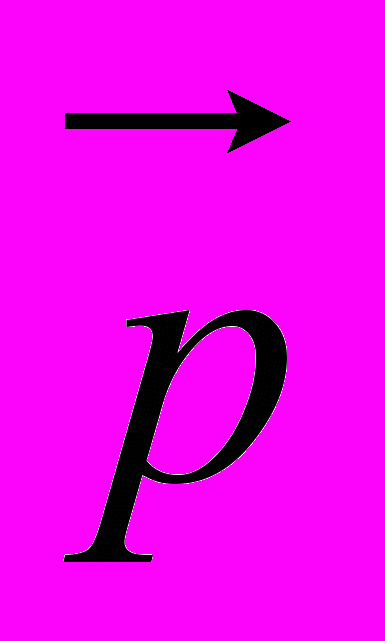— повний вектор імпульсу системи. Векторна рівність (2.13) еквівалентна трьом скалярним рівностям для трьох проекцій вектора на осі координат: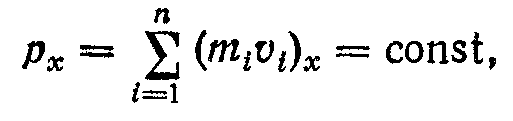



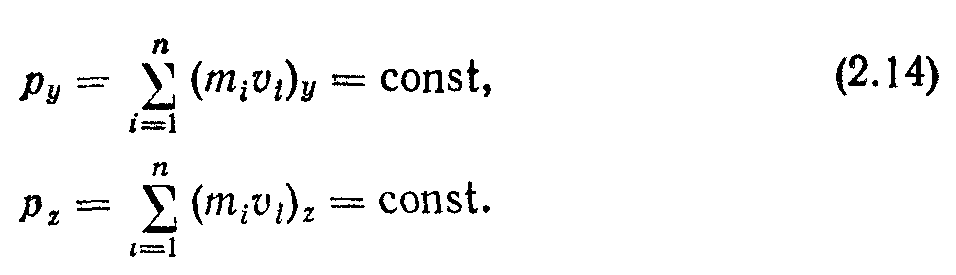
Тоді закон збереження імпульсу можна сформулювати так: повний вектор імпульсу замкненої системи, що е векторною сумою імпульсів всіх тіл системи, залишається незмінним.

Тривалий час вважали, що закони Ньютона цілком вичерпують об'єктивно існуючі зв'язки між механічними явищами природи.

Проте на початку XX ст. виявилось, що закони Ньютона не можуть пояснити особливостей руху тіл при великих швидкостях, які наближаються до швидкості світла. А це означає, що для законів Ньютона, як і для всіх законів природи, існують певні границі застосовності. З розкриттям нових зв'язків фізичні закони, природно, уточнюються та змінюються. В цьому полягає діалектика пізнання природи.