План. Механіка. Система відліку. Матеріальна точка Прискорення. Швидкість

Вид материала

Лекція

Подобный материал:

• Програма вступного випробування та співбесіди з фізики для вступу на перший курс навчання, 85.23kb.
• План учебных занятий по курсу «Физика». 9 класс (4 часа в неделю), 72.35kb.
• Календарно-тематический план (балльно-рейтинговая система, 1 семестр), 58.92kb.
• Тема. Матеріальна відповідальність сторін трудового договору, 90.15kb.
• Урок на тему «Штучні супутники Землі», 21.17kb.
• Реферат на тему: Швидкість обігу грошей та чинники, що її визначають, 58.43kb.
• Организационный план 31 6 План производства 32 7 Финансовый план 38 План по рискам, 841.71kb.
• І. вступ сучасна система освіти зіткнулася з проблемою прискорення І непередбачуваності, 80.21kb.
• План Матеріальна культура Римської імперії Соціальний устрій, 294.96kb.
• Реферат на тему на тему Розпад СРСР та заснування снд, 97.55kb.

8. Закон всесвітнього тяжіння


Всі тіла в природі взаємно притягуються. Закон, що описує це притягання, встановлений Ньютоном. Його називають законом все­світнього тяжіння. За цим законом будь-які дві матеріальні точки притягуються одна до одної з силами, що прямо пропорційні добутку їхніх мас і обернено пропорційні квадрату відстані між ними:



де G — коефіцієнт пропорційності, який називають гравітаційною сталою. Для визначення сили взаємодії тіл, які не можуть розгляда­тись як матеріальні точки, їх треба розділити на точкові елементарні маси Am, знайти значення сили взаємодії кожної елементарної маси одного тіла з елементарними масами іншого, а потім додати ці сили.

У випадку довільних тіл, тобто тіл різної густини та форми, роз­в'язання такої задачі досить складне. Ця задача спрощується для однорідних куль і таких тіл, в яких масу умовно можна зосередити в одній точці. Для таких тіл можна застосувати закон всесвітнього тяжіння у вигляді (2.23).

Гравітаційні сили порівняно слабкі. Наприклад, вони значно слаб­ші за електричні. Тому процеси всередині атома визначаються практич­но тільки електричними силами (якщо не враховувати внутрішньо­ядерні процеси).

Гравітаційні сили стають відчутними для тіл великих мас і косміч­них тіл — планет, зірок тощо. Маса Сонця в 750 раз більша від су­марної маси всіх планет Сонячної системи. Тому планети значно біль­ше притягуються Сонцем, ніж одна одною. Наприклад, Місяць є природним супутником Землі і на нього найбільше впливає поле її тяжіння. Центр мас Сонячної системи зміщений від центра Сонця всього на 2,15R Сонця (радіус Сонця 695989 км, відстань центра Сонця від центра мас Сонячної системи близько 1 486 000 км).

Для визначення сили гравітаційної взаємодії між тілами за зако­ном Ньютона (2.23) треба знати гравітаційну сталу G. Вперше її екс­периментальне визначив у 1798 р. Кавендіш. Він виміряв силу тяжін­ня між свинцевими кулями за допомогою крутильних терезів. Схема­тично основну частину приладу зображено на рис. 2.5. На одному стержні підвішено дві масивні свинцеві кулі, на другому — дві неве­ликі свинцеві кульки. Всю установку вміщували в спеціальну камеру



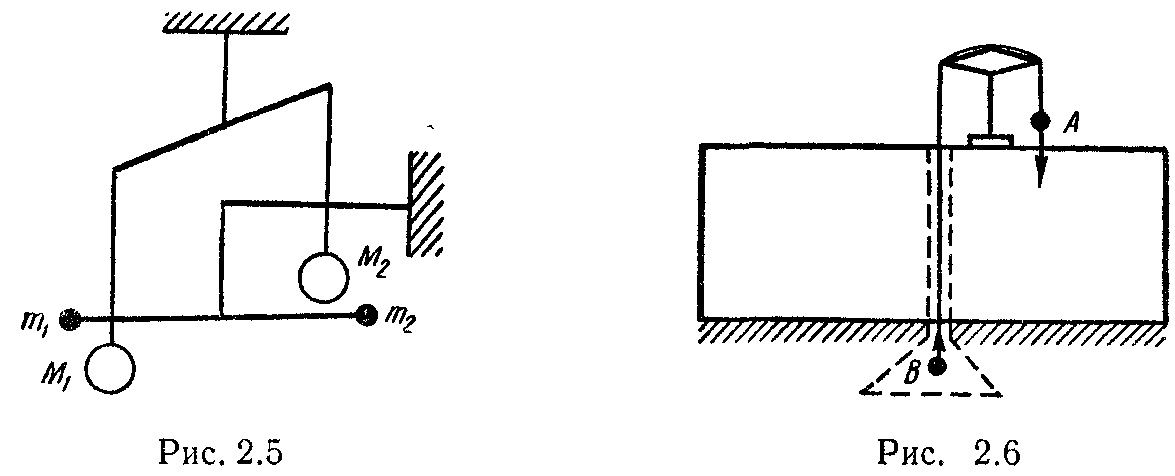
і захищали від коливань температури. Повертаючи стержень з вели­кими кулями, можна було спостерігати, що стержень з малими куль­ками, який підвішено на нитці з відомими пружними властивостями, повертається на деякий кут назустріч важким кулям. За кутом закру­чування підвісу Кавендіш підраховував сумарну силу притягання 2F між кулями M₁ і т₁ та M₂ і т₂. Відстань між центрами куль точно вимірювалась. Визначена Кавендішем величина G відрізнялась лише на 1% від тієї, яку дістали в наступних дослідах.

У 1898 р. Ріхарц до 100-річчя досліду Кавендіша за ідеєю Жоллі визначив гравітаційну сталу іншим способом. Схему досліду Ріхарца подано на рис. 2.6. До кінця коромисла терезів підвішено дві кульки А і В, що мають однакові маси (з урахуванням підвісу). Свинцева плита масою 100 т своїм тяжінням збільшує вагу кульки А і зменшує вагу кульки В. Тому терези відхиляються від положення рівнова­ги. За величиною відхилення коромисла терезів можна судити про силу тяжіння між кулями й свинцевою плитою. Цей спосіб визна­чення G вважається найбільш точним. Встановлено, що G =6,67259 – 10^-11 м³ · кг-¹ • с-².

Використовуючи закон всесвітнього тяжіння (2.23), можна знайти залежність прискорення вільного падіння від висоти над поверхнею Землі. Дійсно, вага тіла зв'язана з його масою співвідношенням

Р = mg. (2.24)

Якщо нехтувати впливом добового обертання Землі, то за законом тяжіння вага тіла визначається за формулою



де М_з — маса Землі; т — маса тіла; r — віддаль тіла від центра Землі, яка дорівнює радіусу Землі (R₃ = 6378164м), якщо тіло лежить на її поверхні. З формули (2.25) видно, що вага тіла зменшується з від­даленням тіла від земної поверхні. Оскільки маса тіла залишається сталою, то ця закономірність обумовлена характером поведінки при­скорення вільного падіння від висоти. Якщо прирівняти співвідношен­ня (2.24) і (2.25), то дістанемо аналітичний вираз цієї залежності



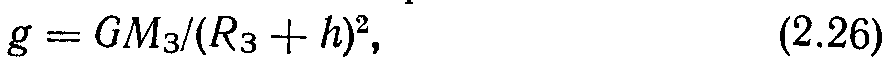
де R₃ — радіус Землі.


9. Інертна і гравітаційна маси


Маса фігурує у двох різних законах: у другому законі Ньютона і в законі всесвітнього тяжіння. В першому випадку вона характери­зує інертні властивості тіла, у другому — гравітаційні властивості, тобто властивість тіл притягувати одне одного. У зв'язку з цим вини­кає запитання, чи відрізняються між собою за величиною інертна і гра­вітаційна маси тіл. Ньютон вважав, що ці дві фізичні характеристики тіла збігаються, тому він користувався одним терміном — «кількість матерії», що рівнозначний тепер слову «маса». Справедливість твер­дження про рівність інертної і гравітаційної мас випливає з того, що прискорення вільного падіння в даній точці Землі для різних тіл є сталим. Справедливість цього твердження перевіряли спочатку І. Нью­тон, потім Бессель та Р. Етвеш. За Бесселем, різниця між інертною і гравітаційною масами не перевищує 1/20000; за Етвешом, вона не мо­же перебільшувати 1/10 000 000.

Принцип еквівалентності інертної і гравітаційної мас належить до таких положень наукового знання, для яких остаточне дослідне доведення неможливе: можна лише підтверджувати цей принцип з дея­ким ступенем точності, який можливий для даного етапу розвитку на­уки. Проте на відміну від більшості інших відносних істин цей принцип в своєму абсолютному виразі не викликає ніяких сумнівів через свою фундаментальність. В наш час еквівалентність інертної і гравітацій­ної мас встановив на досліді В. Б. Брагинський та інші з відносною точністю 10^-12.

Отже, сукупність дослідних фактів вказує на те, що інертна і гра­вітаційна маси всіх тіл пропорційні одна одній. Це означає, що при певному виборі одиниць вимірювання інертна і гравітаційна маси стають тотожними, тому в фізиці прийнято говорити просто про масу. Тотожність інертної і гравітаційної мас покладено Ейнштейном в ос­нову загальної теорії відносності.


Завдання для самоконтролю.

1. Що називається масою тіла? 2. Який фізичний зміст поняття сили? 3. Сформулюйте закони Ньютона. В яких системах відліку вони виконуються? Який взаємозв'язок між цими законами? 4. Як можуть рухатись одна відносно одної інерціальні системи відліку? Запишіть перетворення Галілея. 5. Сформулюйте принцип відносності Галілея. 6. Розкрийте суть детермінізму Лапласа. В чому його обмеженість? 7. Дайте визначення закону збереження імпульсу. Для яких систем він справедливий? Виведіть цей закон і наведіть приклади, що ілюструють його. 8. В яких системах відліку діють сили інерції? 9. Чи можна застосовувати третій закон Ньютона для сил інерції?