При обработке информации, связанной с изображением на мониторе, принято выделять три основных направления: распознавание образов, обработку изображений и машинную графику

Вид материала

Задача

Содержание Если к одной вершине присоединены несколько треугольников, то квадрик этой Заключает в себе триангуляции всех уровней разрешения. Но выигрыш в её

Подобный материал:

• Конспект Лекций Лекция 1 Введение в компьютерную геометрию и графику Основные направления, 1002.69kb.
• Задачи обработки изображения : Устранение дефектов изображения (напр., устранение снега, 98.28kb.
• Белорусский государственный университет применение информационных технологий при анализе, 187.23kb.
• Лабораторная работа № Нейросетевое распознавание печатных символов. Дисциплина: «Распознавание, 74.04kb.
• Распознавание и преобразование образов указатель документов описания первоисточников., 52.79kb.
• 7. западноевропейский тип культуры, 587.09kb.
• Нелинейная цифровая фильтрация лазерных изображений при регистрации и обработке, 242.95kb.
• Алгоритмы восстановления изображений при томографической обработке проекций, 48.43kb.
• Доклад посвящен методам сопоставления образов с шаблоном в системе автоматической обработки, 31.12kb.
• Программа по дисциплине "Распознавание образов/(по выбору)" для подготовки студентов, 89.53kb.

Если к одной вершине присоединены несколько треугольников, то квадрик этой

вершины будет равен сумме всех квадриков прилегающих к этой вершине треугольников:

   

Н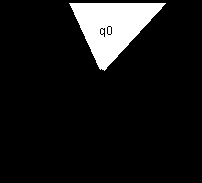апример:

В данном случае:

 

А так же важно записать следующее выражение:

 

Рассмотрим ещё один пример:

 

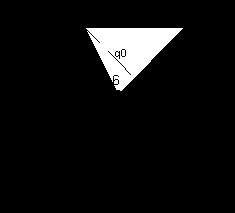
Допустим, мы хотим переместить точку 6 в точку 7.

Тогда:

 

А для точки 7 мы можем посчитать следующее:



Эта величина показывает на сколько вершина 7 отклоняется от окружающих плоскостей вершины 6.

Следовательно, квадрики позволяют оценить ошибки перемещения вершин, которые находятся в тренгуляции.

14.2.1. Механизм колабса ребра.

Цель: выбор ребра, от которого можно избавмться, но это избавление должно принести наименьшую ошибку. Рассмотрим пример:




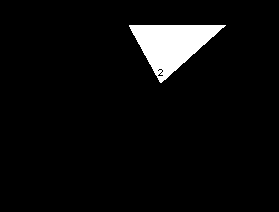
Во-первых, нам нужно найти квадрики всех вершин, а затем и рёбер.

Для примера возьмём ребро {1-2}:

 Квадрик этого ребра:

 

Во-вторых, для каждого ребра считаем критерий, выбирая лучший переброс:

 

 Критерий для ребра {1-2}:

 ,

  так как

 

Затем выбираем ребро с наименьшим значением  , которое и будет удалено.

Замыкание будет зависеть от следующего критерия:

  - удаляется

   - удаляется 

Результат:

  Мы выбрали такое перемещение, которое приносит наименьшую ошибку.

Примечание:

При перебросе квадрики вершин изменяются, следовательно, их нужно пересчи-

тать, а значит стоимость рёбер так же поменяется.

С помощью квадрика мы можем порождать новую вершину:

 Допустим, мы хотим перекинуть все связи в

  точку О. Координаты этой точки нам не изве-

 стны, но мы можем их найти следующим об-

 разом:

 

  Получается, что

  Минимальный критерий для точки  :

 

Т.е. квадрик несёт в себе информацию об оптимальной точке, в которую можно свести все связи.

Существует механизм, работающий на квадриках и записи информации предыдущего шага. Т.е., допустим, мы стягиваем все связи, принадлежащие точкам 1 и 2, в точку О. При этом мы можем запомнить эту информацию и при обратном шаге уже будем знать как разложить точку О(т.е. на точку 1 и точку 2).

14.2.2. Гипертриангуляция

Заключает в себе триангуляции всех уровней разрешения. Но выигрыш в её

применении, по сравнению с динамической триангуляцией, невелик.

Резюме:

1)      Существуют:

  а) Рельеф:

 представляется с разным уровнем разрешения (мультиразрешение)

 и наиболее удачна для этого триангуляция Делоне.

 б) Объект:

 представляется с постоянным уровнем разрешения, триангуляция

 Делоне не применяется, но используется математическое упроще-

 ние с помощью квадриков.

2)      Механизм квадриков можно перекинуть на работу с рельефом, а работу с

нормалью перекинуть на объекты.