При обработке информации, связанной с изображением на мониторе, принято выделять три основных направления: распознавание образов, обработку изображений и машинную графику

Вид материала

Задача

Содержание Обратное преобразование Частные случаи линейных преобразований Самое главное Сравним SS  и S

Подобный материал:

• Конспект Лекций Лекция 1 Введение в компьютерную геометрию и графику Основные направления, 1002.69kb.
• Задачи обработки изображения : Устранение дефектов изображения (напр., устранение снега, 98.28kb.
• Белорусский государственный университет применение информационных технологий при анализе, 187.23kb.
• Лабораторная работа № Нейросетевое распознавание печатных символов. Дисциплина: «Распознавание, 74.04kb.
• Распознавание и преобразование образов указатель документов описания первоисточников., 52.79kb.
• 7. западноевропейский тип культуры, 587.09kb.
• Нелинейная цифровая фильтрация лазерных изображений при регистрации и обработке, 242.95kb.
• Алгоритмы восстановления изображений при томографической обработке проекций, 48.43kb.
• Доклад посвящен методам сопоставления образов с шаблоном в системе автоматической обработки, 31.12kb.
• Программа по дисциплине "Распознавание образов/(по выбору)" для подготовки студентов, 89.53kb.

Пример

Q – (2m +1) *(2n+1)

Q’ – N*N.



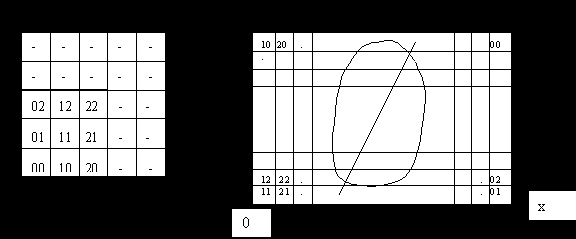
Операция свертки – частный случай линейного преобразования.

16.6. Линейные преобразования

F (n₁, n₂) – двумерная функция.

Тогда F – её линейное преобразование.

n₁, n₂, m₁, m₂ = 0 ……….. N-1.

 (m₁, m₂)= F(n₁, n₂) ∙A(n₁, n₂, m₁, m₂)

 

Назовём это преобразование  прямым.

Обратное преобразование

  F(n₁, n₂) =  (m₁, m₂) ∙B(n₁, n₂, m₁, m₂)

 

Матричная форма.

  F f  

 

[N2*N2]

[1*N2]

[1*N2]

 = f ∙  A - прямое преобразование в матричной форме.

f =  ∙ B  ; B = A^-1 – обратное преобразование.

Частные случаи линейных преобразований

1.)    Разделимые линейные преобразования

A(n₁, n₂, m₁, m₂) = A_c(n₁, m₁) ∙ A_s(n₂, m₂)

B(n₁, n₂, m₁, m₂) = B_c(n₁, m₁) ∙ B_s(n₂, m₂)

F  = A_c  ∙ F ∙ A_s^T

 


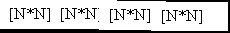
F = B_c ∙    ∙ B_s^T ; B_c = A_c^-1;  B_s = A_s^-1.

2.)    Свёртка

V_R(x, y) =  V_S(i, j) ∙ Q’(x-i, y-j)

Самое главное

L = (2m +1) (2n +1) – для каждой точки  сложность вычисления пространственной области.  S1 = L ∙ N2

	A

 

V_s  F_s 

B

[N*N]

[N*N]

 

	A

 

поэлементное умножение

[N*N]

[N*N]

Q’  F_Q 

V_R(r₁, r₂) =  V_S(i, j) ∙ Q’(r₁-i, r₂-j) (1)

F_s(m₁, m₂) =  V_S(n₁, n₂) ∙ A(n₁, n₂, m₁, m₂)   (2)

F_Q(q₁, q₂) =  Q’(l₁, l₂) ∙ A(l₁, l₂, q₁, q₂)   (3)

V_R(r₁, r₂) =  F_R(p₁, p₂) ∙ B(p₁, p₂ , r₁, r₂)  (4)

F_R(i ,j) = F_S(i ,j) ∙ F_Q(i ,j)  (5)

i , j = 0……………N-1.

Подставим величины из формул (2), (3), (5) в формулу (4).

В результата этого мы получим :

V_R(r₁, r₂) =  (V_S(n₁, n₂) ∙ A(n₁, n₂, p₁, p₂) ∙ Q’(l₁, l₂) ∙

A(l₁, l₂, p₁, p₂)) ∙ B(p₁, p₂ , r₁, r₂) =  V_S(n₁, n₂) ∙ Q’(l₁, l₂) ∙   A(n₁, n₂, p₁, p₂) ∙ A(l₁, l₂, p₁, p₂) ∙ B(p₁, p₂ , r₁, r₂)

Выделенная в формуле подчёркиванием часть зависит только от ядер.

Она равна 1 при  n₁= r₁ – l₁ или n₂= r₂ – l₂

 

 0 , иначе

d(n₁+l₁– r₁) ∙ d(n₂+l₂– r₂) (дельта – функция.)

 

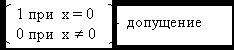d(x)  

A(n₁, n₂, p₁, p₂) = A_S(n₁, p₁) ∙ A_C(n₂, p₂)

  A_S = A_C = A

 B_S = B_C = B

B(p₁, p₂, r₁, r₂) = B_S(p₁, r₁) ∙ B_C(p₂, r₂)

(**)

 A(n₁, n₂, p₁, p₂) ∙ A(l₁, l₂, p₁, p₂) ∙ B(p₁, p₂ , r₁, r₂) = d(n₁+l₁– r₁) ∙ d(n₂+l₂– r₂)

 

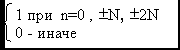d(x)  

A(n₁, n₂, p₁, p₂) = A_S(n₁, p₁) ∙ A_C(n₂, p₂) (1)

A_S = A_C  A’

B(p₁, p₂, r₁, r₂) = B’(p₁, r₁) ∙ B’(p₂, r₂)  (2)

Воспользовавшись формулами (1) и (2) преобразуем выражение (**) :

A’(n₁, p₁) ∙A’(l₁, p₁) ∙ B’(p₁, r₁) ∙ A’(n₂, p₂) ∙A’(l₂, p₂) ∙ B’(p₂, r₂) =

= d(n₁+l₁– r₁) ∙ d(n₂+l₂– r₂)

A’(n, p) = a^np ; A’(l, p) = a^lp ; B’(p, r) = a^-pr

 a^p(n+l-r) = d (n+l– r)

n+l– r  n

	apn =N∙d(n)
		(*)						(***)

 

 

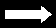Пусть n = 0, N.

Эквивалентность выражения (*) докажем , домножив обе части уравнения на

(1 - aⁿ).

1

(1 - aⁿ)  a^pn =   a^pn -  a^n(p+1) = 1+   a^pn - a^pN – a^nN =1 – (a^N)ⁿ = 0 

1 = N∙ d(0) ; аналогично для n=N,-N.

Теперь уравнение (***) будет основным

Решим его :

a^N =1 = e^i∙2p - комплексное преобразование 1.

a = e^i∙2p/N – решение в области комплексных чисел.

Re + i∙Im

 ) =a^nm ∙F(n) =  e^{i∙(2p/N) ∙n∙m} ∙F(n) =

 =F(n) ∙cos (∙n ∙m ) + i ∙ F(n) ∙sin(∙n ∙m ) =

	Re		Im

 

F(n) = ∙ a^-nm ∙ ) =  e^{i∙(2p/N) ∙n∙m} ∙ ) =   ) ∙cos (∙n ∙m ) –

- i∙   ) ∙ sin(∙n ∙m )

Связь между спектральными коэффициентами и корреляционной функцией

Пусть имеется входной сигнал, описываемый функцией F(n). Тогда квадрат коэффициента корреляции k равен:

k² =   F(n) ∙ sin(∙n ∙m +y) =  F(n) ∙ sin(∙n ∙m) ∙ cos(y) +  F(n) ∙ cos(∙n ∙m) ∙ sin(y)

Так как

Принимая   , и , получим:



 ;  ; 

Оценка сложности:

1. Вычисляются спектральные коэффициенты строк

2. Вычисляются спектральные коэффициенты столбцов

Для каждого отсчета надо сделать N операций

,

где N — сложность вычисления одного коэффициента, k — коэффициент сложности работы с комплексными числами

Сложность прямого преобразования:

 — это только по строкам

Аналогично получается сложность по столбцам

Тогда общая сложность:

— суммарная сложность прямого преобразования





S_S = S_пр + S_обр = 2N³∙k

k – коэффицент , отражающий специфику работы с комплексными числами.

 

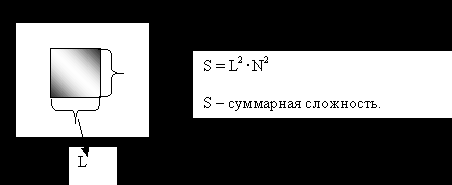
Сравним S_S  и S :

Проверка

Пусть N=512 ; k=2.

Ответ : L > 45. – выгодно использовать пространственное преобразование при больших фильтрах.