Нелинейная цифровая фильтрация лазерных изображений при регистрации и обработке
| Вид материала | Документы |
- Белорусский государственный университет применение информационных технологий при анализе, 187.23kb.
- Цифровая фильтрация, 139.58kb.
- Мультимедийный 24'' монитор Benq g2400WD, 292.01kb.
- Алгоритмы восстановления изображений при томографической обработке проекций, 48.43kb.
- Экспресс-контроль цветовых характеристик мясного сырья и мясопродуктов, основанный, 316.99kb.
- Цифровая обработка многомерных сигналов, 307.08kb.
- Цифровая фильтрация, 50.52kb.
- При обработке информации, связанной с изображением на мониторе, принято выделять три, 1091.99kb.
- «Применение ит в обработке медицинских изображений», 399.46kb.
- Математическое моделирование процессов взаимодействия водорода с металлами при анодной, 53.75kb.
Нелинейная цифровая фильтрация лазерных изображений
при регистрации и обработке
Малов А.Н., Онацкий А.Н.
Иркутский государственный университет, г. Иркутск, Россия
В случае применения ПЗС-матриц для анализа спекл-изображений, являющихся по своей природе разновидностью шума, использование компьютерных структурных методов распознавания не всегда эффективно. Если для первичной обработки лазерных спекл-изображений шероховатых объектов использовать нелинейные свойства цветной ПЗС-матрицы [1], то при компьютерном анализе по синим и зеленым RGB- компонентам можно построить пространство признаков - рассчитать центральные статистические моменты гистограмм распределения яркости в цветовых плоскостях. Для распознавания спекл-изображений с наименьшей вероятностью ошибки, необходимо анализировать не только статистические характеристики, но и спектральные - наилучший результат достигается при анализе как всех трех RGB-компонент, так и основного изображения.
На первом этапе выполняется пространственная фильтрация цветных изображений, которая заключается в повышении резкости с помощью линейного пространственного Лапласиан-фильтра. Затем выполняется цветовая сегментация - выделение объектов на изображении RGB, цвет которых лежит в определенном диапазоне. Обладая некоторой репрезентативной выборкой векторов, имеющих интересующий цвет, определяется оценка «среднего» цвета, который необходимо выделить. Задача сегментации состоит в том, чтобы классифицировать каждый RGB пиксель изображения и определить, принадлежит он выделенному «среднему» цветовому классу или нет. В результате сегментации получим бинарное изображение, характеризующее распределение «среднего» цвета. На рис. 1 представлены спекл-изображения и их сегментированные представления двух различных классов. Из рисунков видно, что визуальная похожесть исходных изображений достаточно велика, однако их сегментированные аналоги имеют текстуру различного характера. Подобный результат можно достичь только в случае наличия RGB компонентов. Данный метод обладает адаптивными возможностями.
 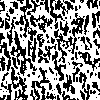 а) |   б) |
| Рис. 1. Спекл-изображения (слева) двух различных классов (а, б) и их сегментированные представления (справа) | |
Эта особенность позволяет применить корреляционные методы распознавания спекл-изображений по их сегментированным представлениям. Расчет двумерных коэффициентов корреляции для исходных изображений, принадлежащих различным классам, дает 0,84-0,93, а для соответствующих сегментированных – 0,32-0,46, что говорит о возможности выбора более широкой разделяющей границы между классами. Применяя корреляционный метод распознавания к цветовым плоскостям изображений различных классов (рис. 1) получим вектор
 , а между изображениями одного класса
, а между изображениями одного класса 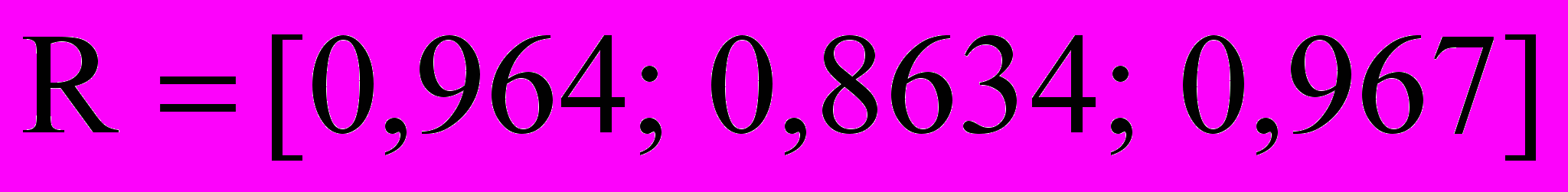 .
.Дальнейший анализ спекл-изображений основан на анализе характеристик внутренней текстуры. Первый метод основан на статистических свойствах гистограмм яркости. Вектор признаков выглядит следующим образом
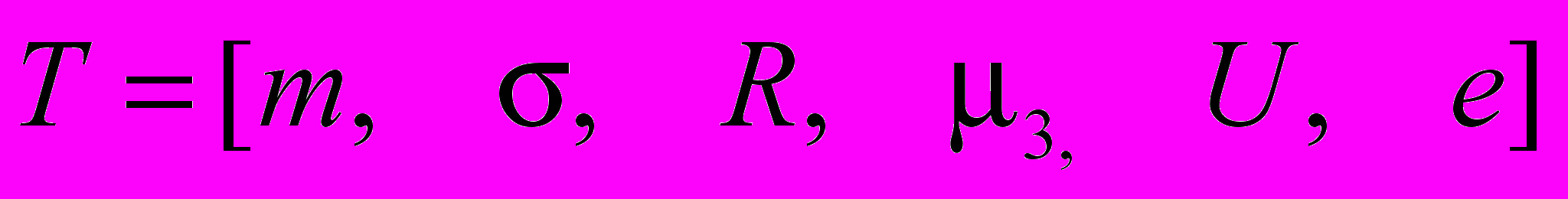 ,
,где
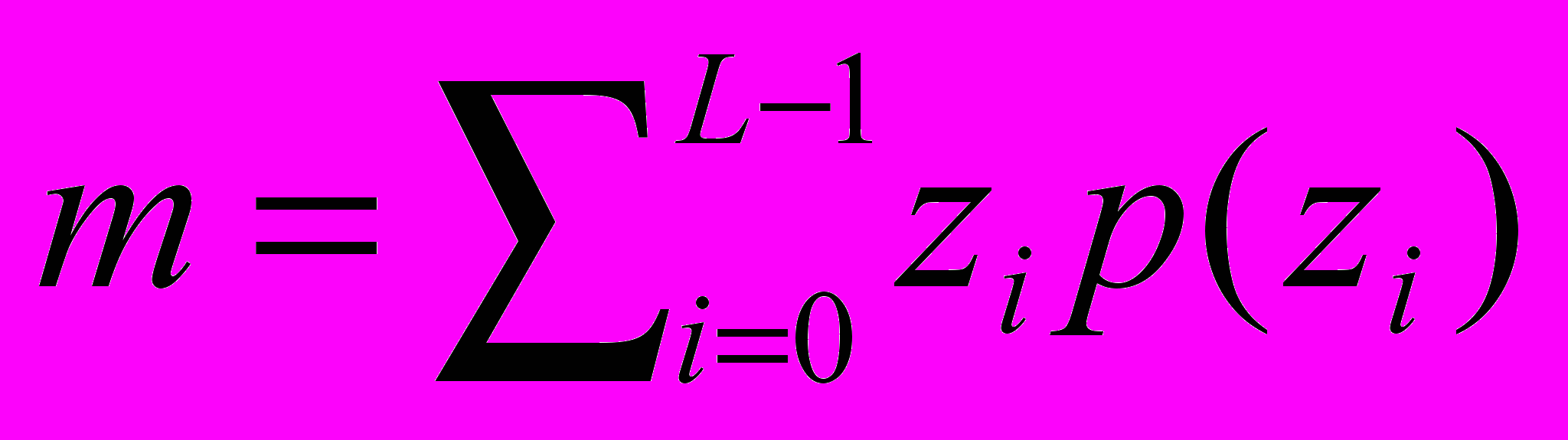 – среднее значение;
– среднее значение;  – стандартное отклонение;
– стандартное отклонение; 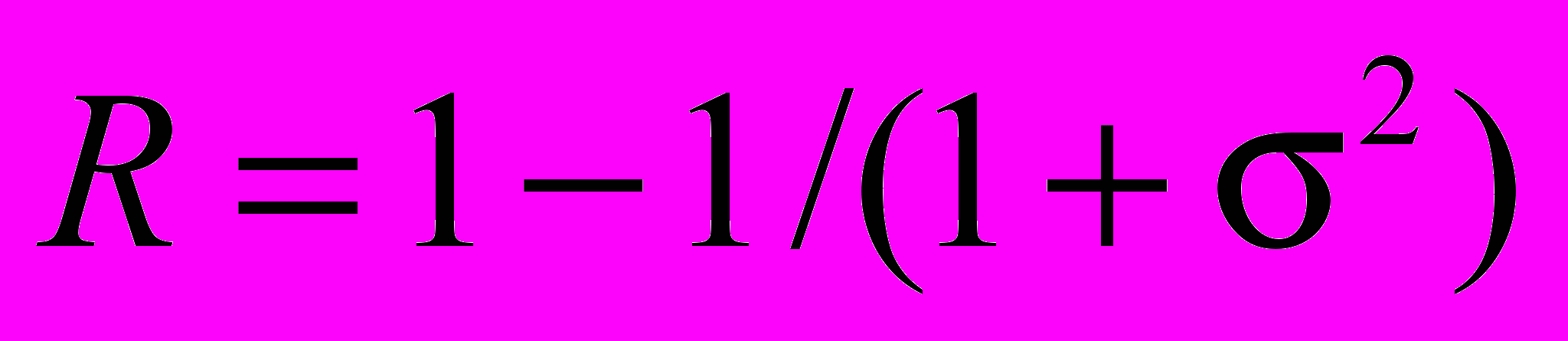 – гладкости;
– гладкости;  – третий момент;
– третий момент; 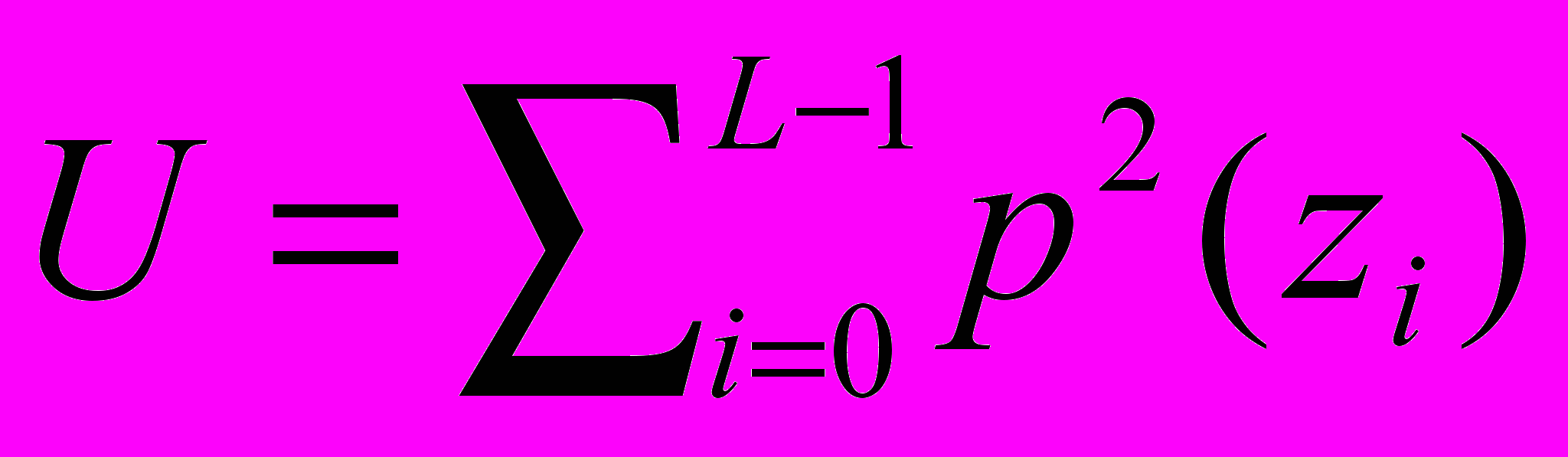 – однородность;
– однородность; 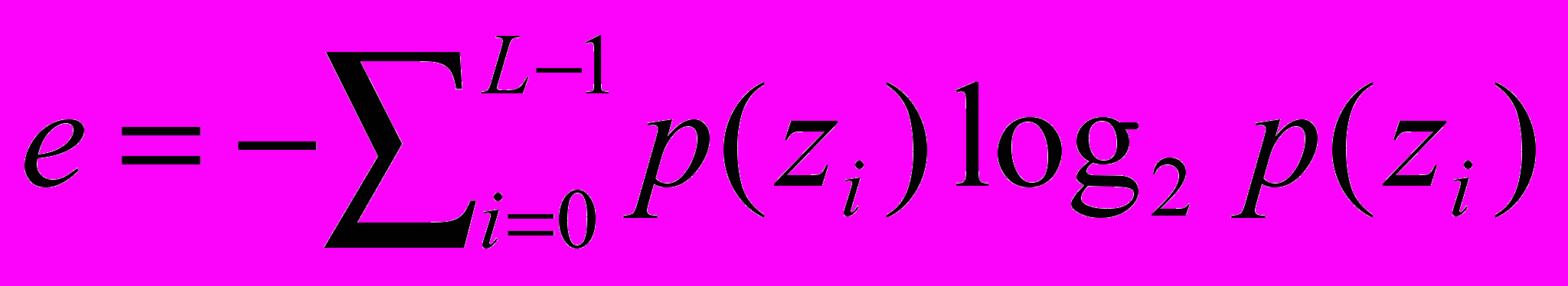 – энтропия. Спектральная мера текстуры основана на спектре Фурье, который идеально подходит для описания направленности присутствующих в изображении периодических или квазипериодических двумерных текстур, которые присущи спекл-изображениям. Для обнаружения спектральных признаков перейдем к полярным координатам, в которых спектральная функция выражается в виде
– энтропия. Спектральная мера текстуры основана на спектре Фурье, который идеально подходит для описания направленности присутствующих в изображении периодических или квазипериодических двумерных текстур, которые присущи спекл-изображениям. Для обнаружения спектральных признаков перейдем к полярным координатам, в которых спектральная функция выражается в виде 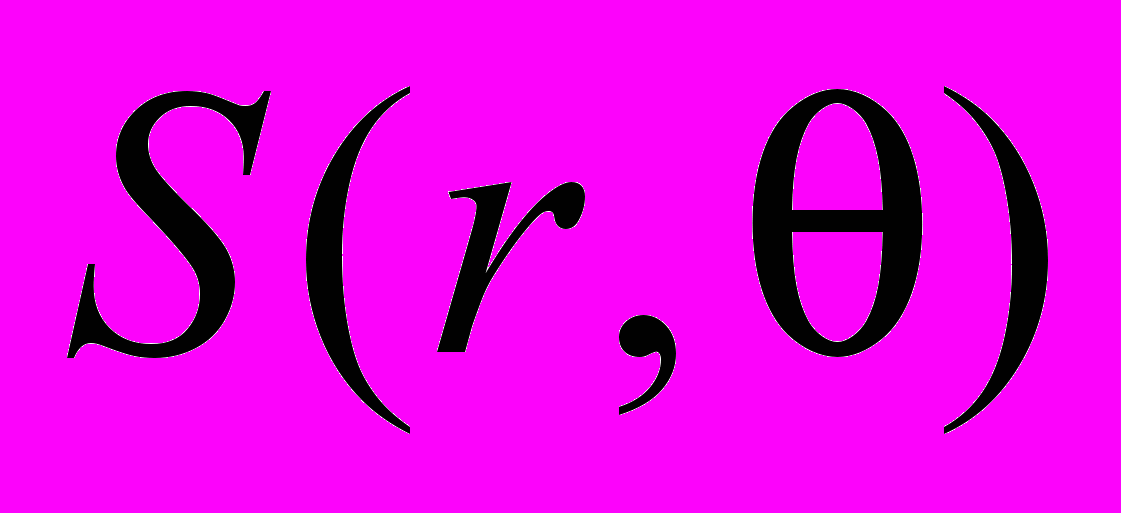 , где
, где 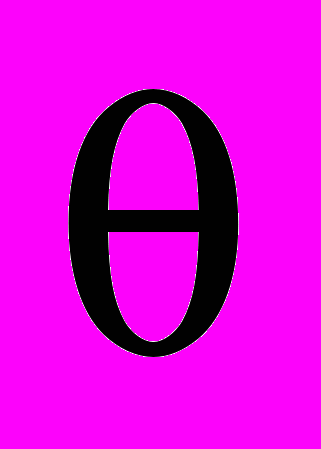 и
и 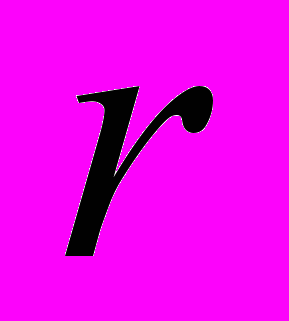 переменные в этой системе координат. Анализ функции
переменные в этой системе координат. Анализ функции 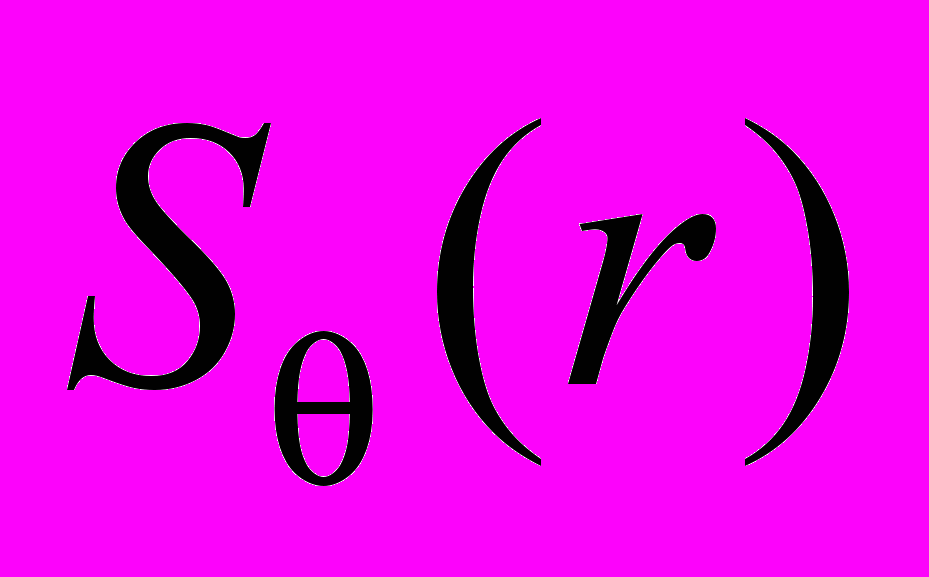 при фиксированном
при фиксированном 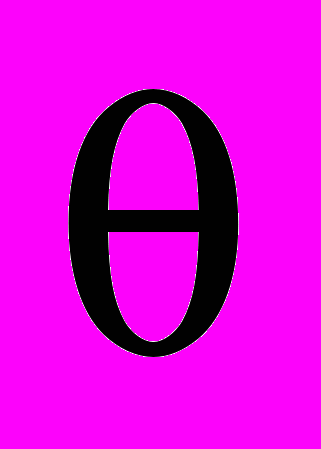 дает представление о поведении спектра по направлению радиуса из начала координат, а исследуя
дает представление о поведении спектра по направлению радиуса из начала координат, а исследуя 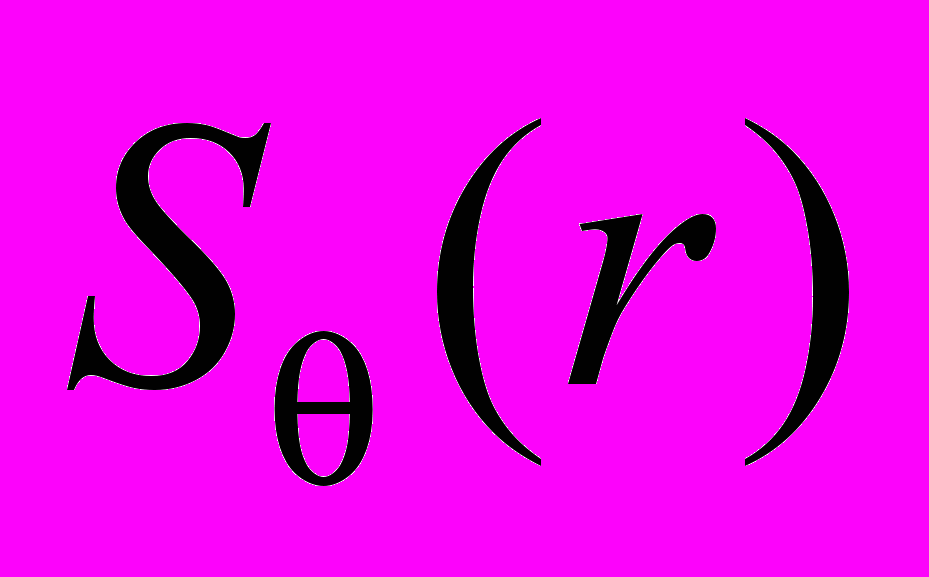 при фиксированном
при фиксированном 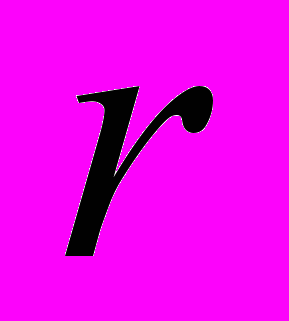 , получаем поведение спектральной функции по окружности с центром в начале координат. Общее описание получается при интегрировании этих функций:
, получаем поведение спектральной функции по окружности с центром в начале координат. Общее описание получается при интегрировании этих функций: ,
, 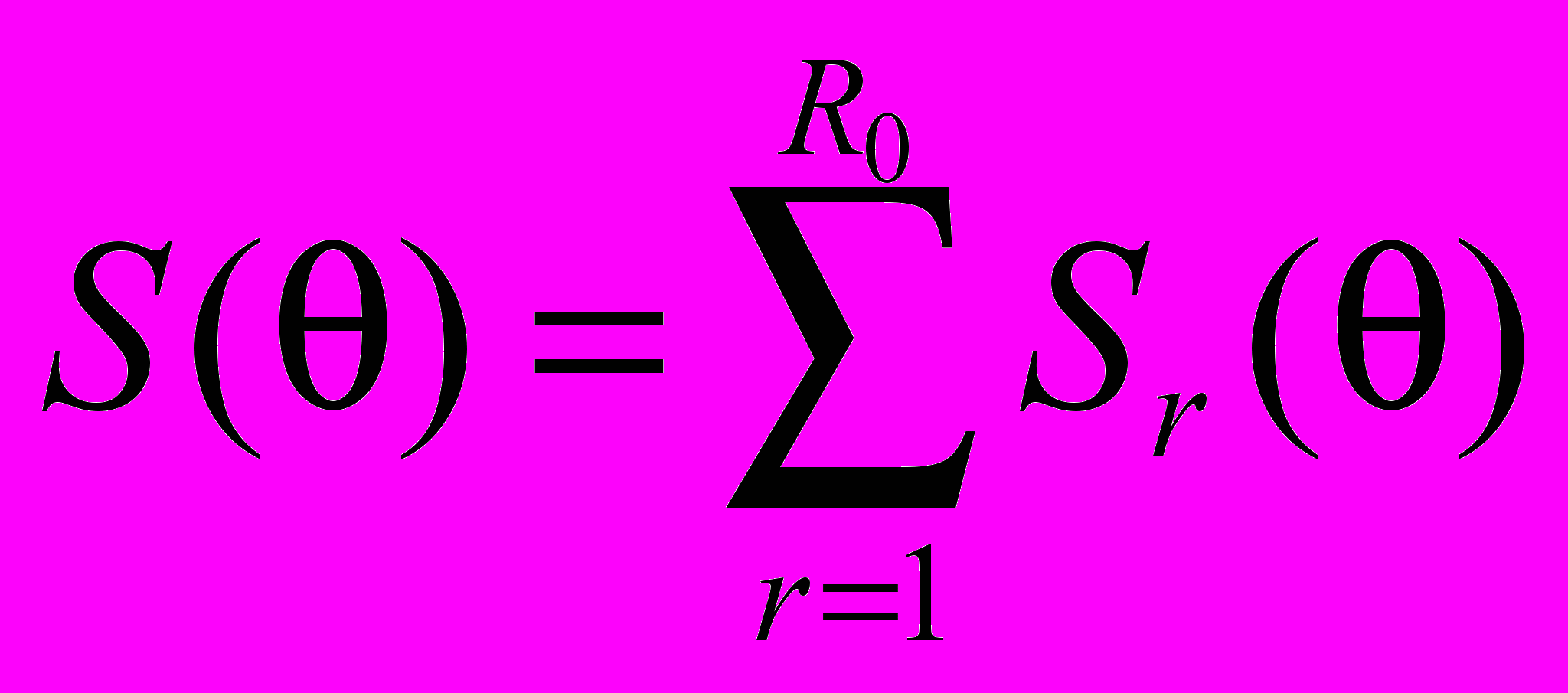 ,
,где
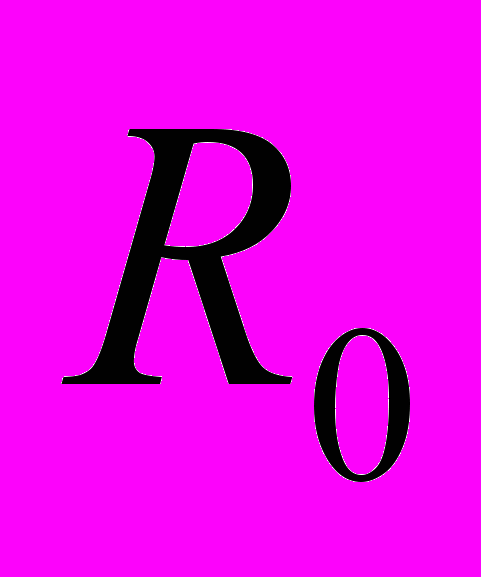 – радиус круга с центром в начале координат. Результатом вычислений является пара значений
– радиус круга с центром в начале координат. Результатом вычислений является пара значений  , для каждой точки спектра с координатами
, для каждой точки спектра с координатами 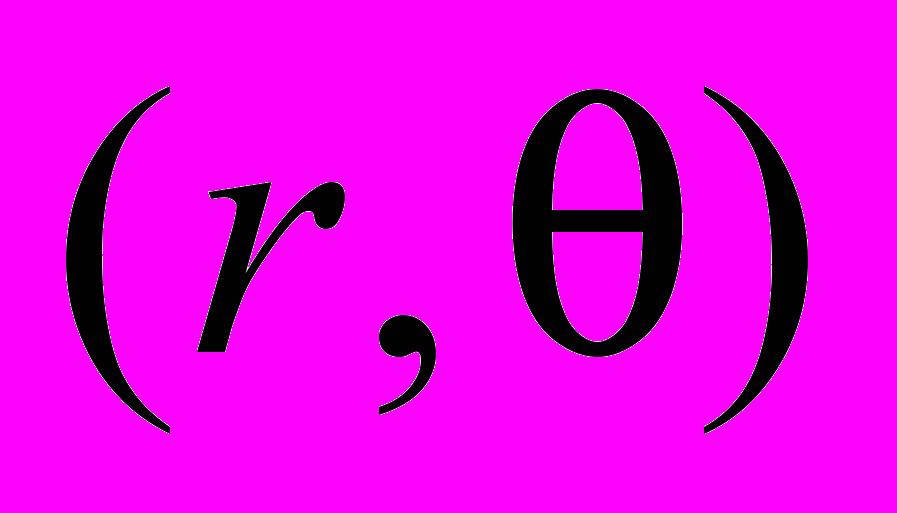 . Варьируя эти координаты, можно построить две одномерные функции
. Варьируя эти координаты, можно построить две одномерные функции 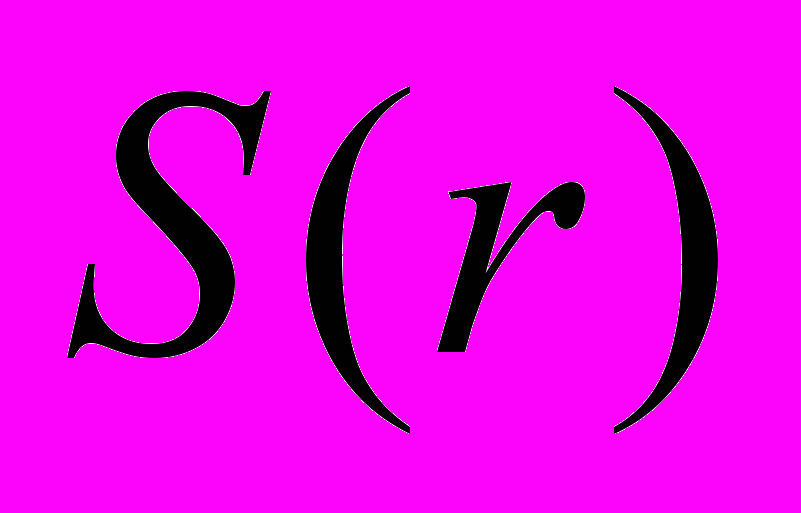 и
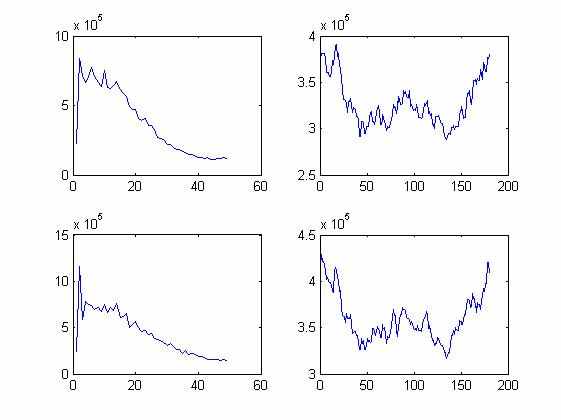
и  , описывающие текстуру всего изображения в терминах энергии спектра (рис. 2). Из рис. 2 видно, что спектральные характеристики RGB текстуры спекл-изображений различаются по расположению максимумов, форме и др. параметрам. Таким образом, формируется комплексный вектор признаков для дальнейшего распознавания спекл-изображений:
, описывающие текстуру всего изображения в терминах энергии спектра (рис. 2). Из рис. 2 видно, что спектральные характеристики RGB текстуры спекл-изображений различаются по расположению максимумов, форме и др. параметрам. Таким образом, формируется комплексный вектор признаков для дальнейшего распознавания спекл-изображений: .
.  |  | |
 | ||
| а) | б) | в) |
| Рис. 2. Исходные изображения первого и второго классов – а); графики функций 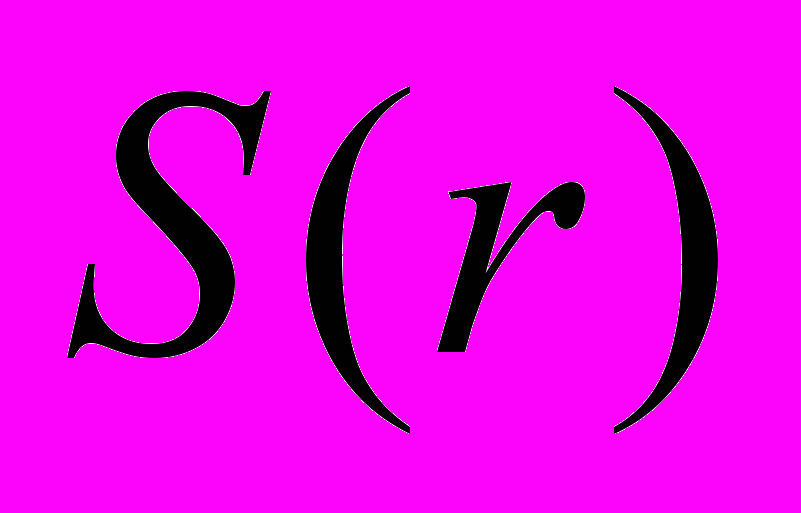 – б); графики функций – б); графики функций  – в) соответственно для первого и второго классов – в) соответственно для первого и второго классов | ||
Преобразование Гильберта
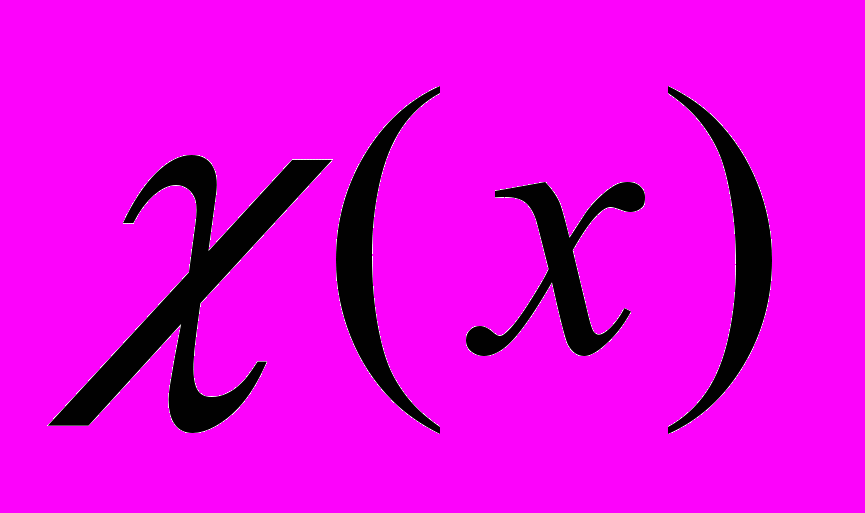
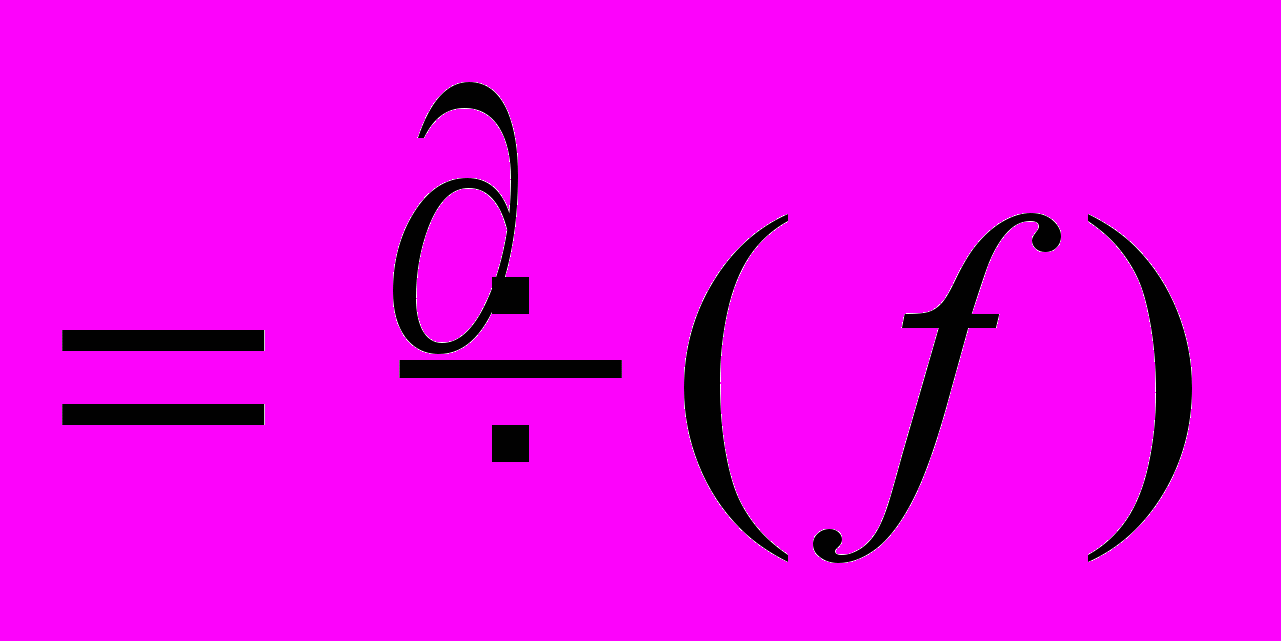 функции
функции 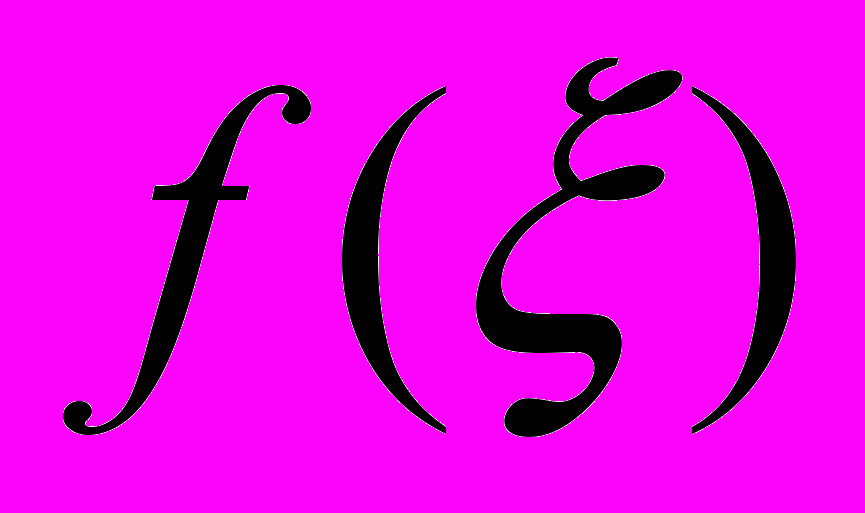
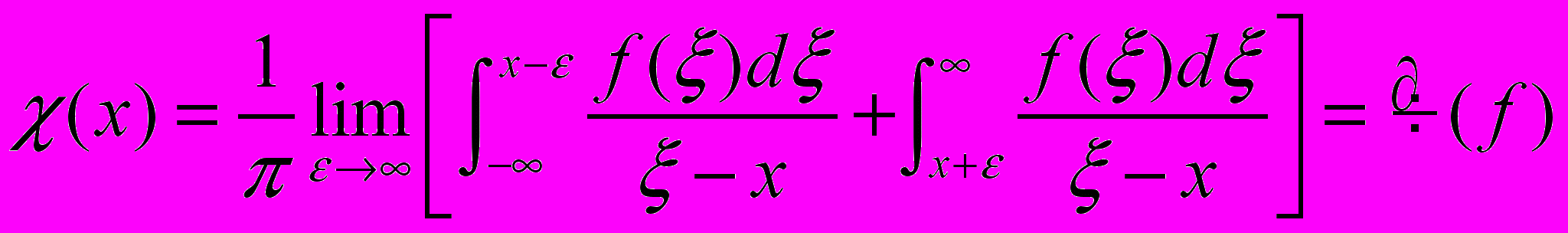 (1)
(1)позволяет визуализировать фазовое распределение электромагнитного поля и широко используется в теневых приборах и при оптической обработке информации как аналог операции дифференцирования [3]. Преобразование Гильберта можно рассматривать как вариант линейной фильтрации, а в терминах Фурье-анализа оно может быть описано как манипуляция с фазами Фурье-компонент сигнала. Фазовая манипуляция оказывается возможной в оптике при условии наличия пространственной когерентности светового поля, которое выполняется в изображающих и когерентных (лазерных) оптических системах. При ненулевой степени пространственной когерентности оптического поля сохраняются разности фаз между различными выделенными спектральными компонентами изображения, а изменение этой разности приводит к перераспределению интенсивности (квадрата модуля комплексной амплитуды поля) в плоскости изображения и позволяет, при определенных условиях, визуализировать фазовую структуру объекта.
Наиболее известной оптической реализацией
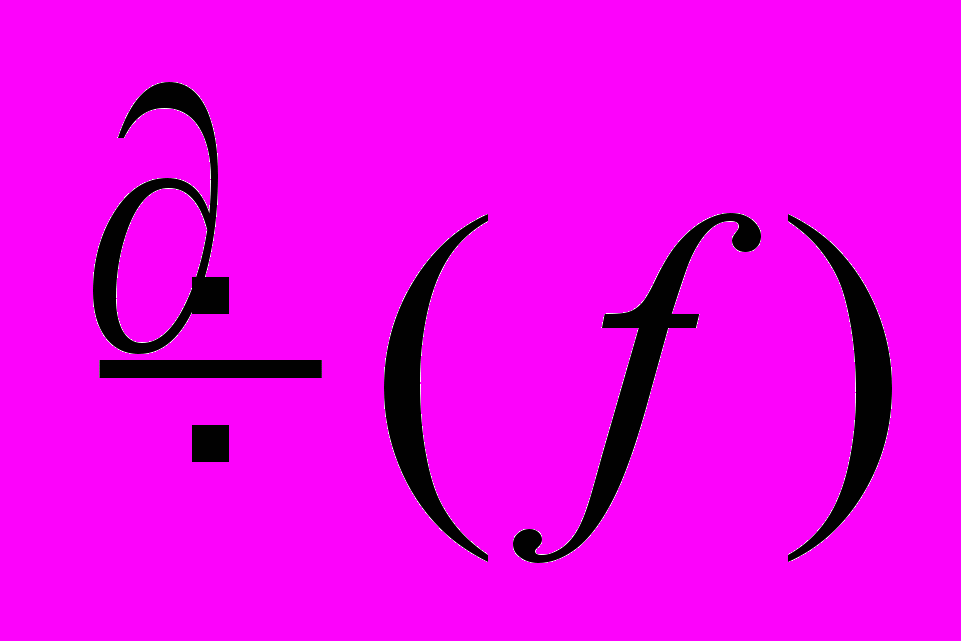 является нож Фуко, когда вырезаются диагональные квадранты в плоскости пространственных частот [3]. Подобные теневые приборы позволяют наблюдать и количественно исследовать оптические неоднородности в различных средах. Вместо непрозрачной маски может использоваться фазовая маска, меняющая в соответствующих областях пространственно-частотной плоскости (Фурье-плоскости) фазу Фурье-компонент сигнала. В оптике действие ножа Фуко на изображение описывается математическим аппаратом, основанным на использовании комплексных функций.
является нож Фуко, когда вырезаются диагональные квадранты в плоскости пространственных частот [3]. Подобные теневые приборы позволяют наблюдать и количественно исследовать оптические неоднородности в различных средах. Вместо непрозрачной маски может использоваться фазовая маска, меняющая в соответствующих областях пространственно-частотной плоскости (Фурье-плоскости) фазу Фурье-компонент сигнала. В оптике действие ножа Фуко на изображение описывается математическим аппаратом, основанным на использовании комплексных функций. Цифровое изображение, состоящее из двумерного массива дискретных отсчетных значений (пикселей), подвергнутое какому-либо интегральному преобразованию
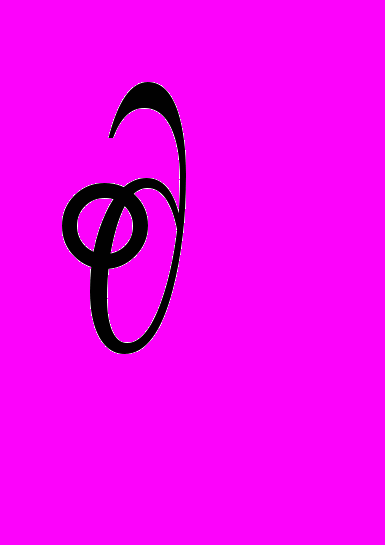 , может быть представлено в виде:
, может быть представлено в виде: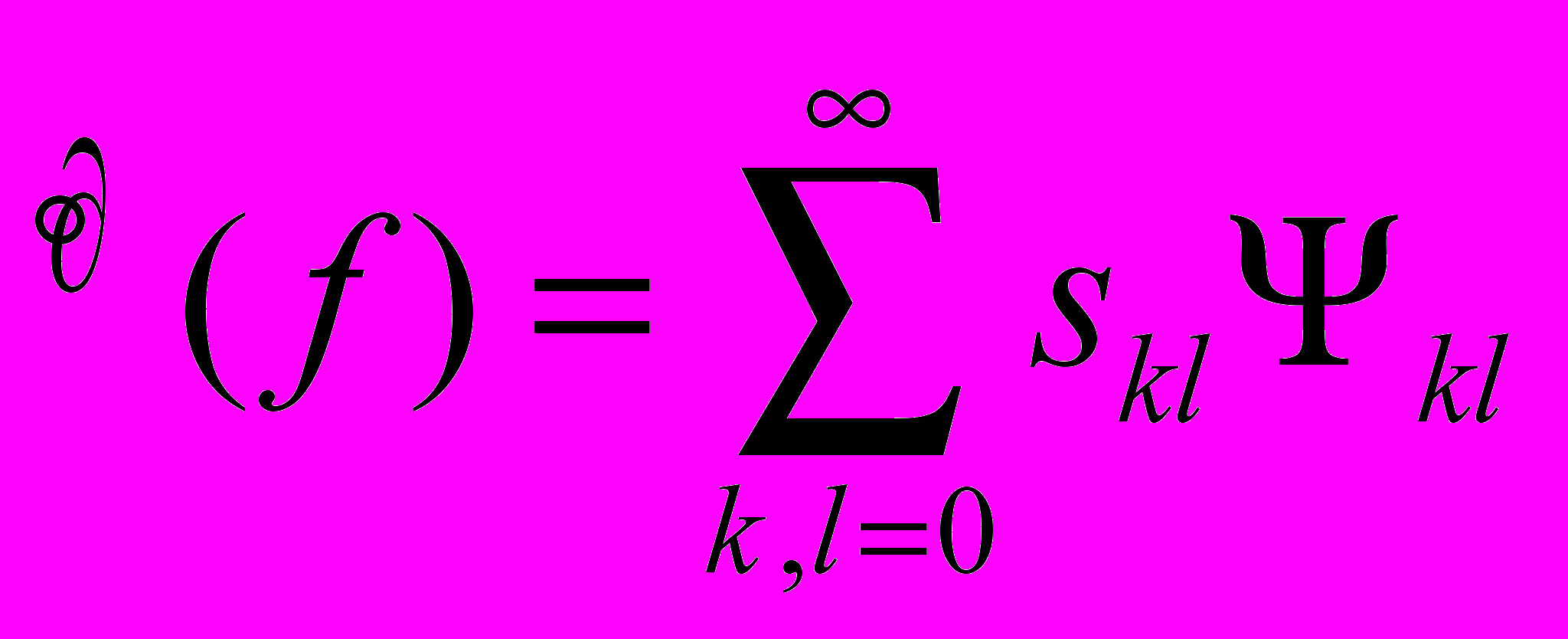 (2)
(2)где
 - весовой коэффициент,
- весовой коэффициент, 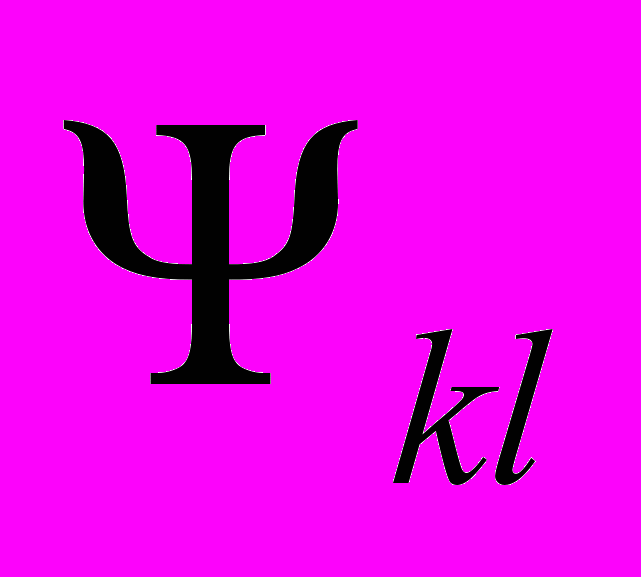 - функции базиса интегрального преобразования [4]. В случае цифровых изображений, описываемых действительными числами, оптическая фаза в явном виде отсутствует, а ее аналогом следует считать номера k, l и знак весового коэффициента в выражении (2). Поэтому фазовое манипулирование при цифровой обработке сводится к обнулению упорядоченных подмножеств весовых компонентов или изменению их знаков.
- функции базиса интегрального преобразования [4]. В случае цифровых изображений, описываемых действительными числами, оптическая фаза в явном виде отсутствует, а ее аналогом следует считать номера k, l и знак весового коэффициента в выражении (2). Поэтому фазовое манипулирование при цифровой обработке сводится к обнулению упорядоченных подмножеств весовых компонентов или изменению их знаков. В настоящей работе методом компьютерного моделирования рассматривается «цифровое фазовое манипулирование» для обработки изображений по алгоритму, аналогичному ножу Фуко, а именно исследовался вопрос о сохранении качества изображений при изменении значений его высоких частот при разложении в спектр Уолша-Адамара и Хаара. Данные преобразования достаточно хорошо изучены и описаны, например, в [4, 5].
Эксперимент выполнялся следующим образом:
 Рис. 3. Деление спектра изображения на четверти |
2. Полученный спектр изображения делится на четыре равные части (четверти), как показано на рис. 3.
3. Выбирается одна или несколько таких четвертей спектра и спектральным коэффициентам в них присваиваются нулевые значения, причем коэффициент с индексом (0,0), являющийся средним значением яркости изображения специально сохраняется прежним без изменений. Следует учитывать, что обнуление спектральных коэффициентов избранных четвертей приводит к уменьшению яркости изображения после обратного преобразования, но мы не будем рассматривать этот вопрос, поскольку пересчет значений спектральных коэффициентов является тривиальной задачей.
4. Выполняется обратное преобразование усеченного спектра.
Результат применения такой схемы обработки для полутоновых изображений абсолютного контраста представлен на рис. 4. Для зануления коэффициентов были выбраны четверти I и III (рис. 3). Из рис. 4 видно, что в случае преобразований Уолша-Адамара и Хаара полученные изображения (рис. 4, з, и), содержат контур исходного изображения (рис. 4, а). Отметим, что в случае преобразования Фурье преобразованное изображение отличается от преобразований Уолша-Адамара и Хаара и выделение контура не происходит (см. рис. 4, к), но выделяется перепад яркости в направлении, зависящем от выбора обнуляемых четвертей спектра. В данном случае обнуление четвертей I и III приводит к выделению перепада яркости в направлении, параллельном линии соединяющей квадранты 2 – 4 и наоборот.
Применение данного метода для полутоновых изображений также выделяет контур, который затем можно дополнительно визуально «подчеркнуть» каким-либо из алгоритмов определения контура, например фильтром Робертса [5] (рис. 4) или коррекцией контраста изображения.
Рис. 4. Выделение контура на изображении (зануление I и III квадрантов): а) – исходное изображение; б, д, з – спектры Уолша-Адамара, Хаара, Фурье изображения «треугольник» в, е, и – усеченные спектры Уолша-Адамара, Хаара, Фурье соответственно; г, ж, к – Результат обратного преобразования Уолша-Адамара, Хаара Фурье соответственно; | ||||||||||||||||||||||||
Рис. 5. Применение алгоритма цифрового ножа Фуко к полутоновым изображениям: а) – исходное изображение; б) – обратное преобразование Хаара с вырезанием I и III квадрантов; в) – применение фильтра Робертса к преобразованному изображению |
В преобразовании Гильберта (1) имеется особая (сингулярная) точка -
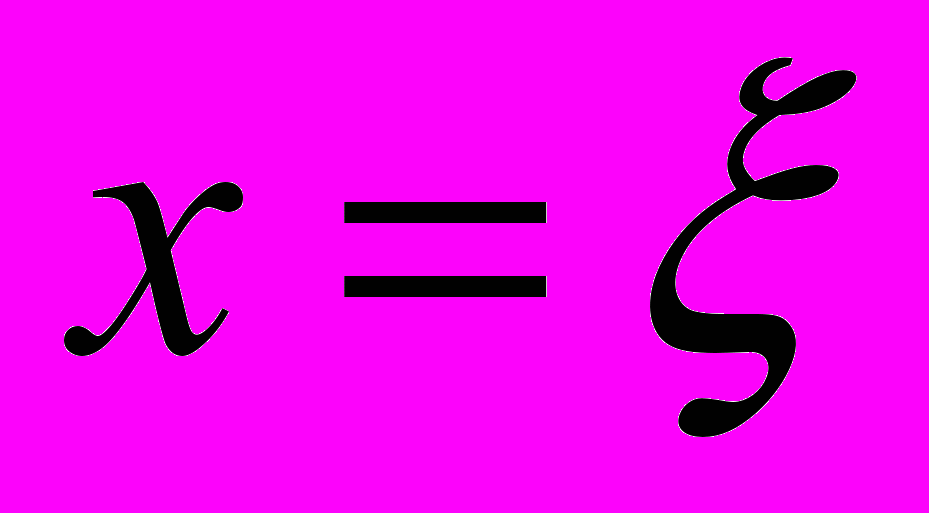 , соответствующая оптической оси системы. Смещение ножа Фуко от этой точки существенно влияет на структуру выходного изображения и, как правило, приводит к разъюстировке. Рассмотрим поэтому поведение подобной точки в цифровом варианте ножа Фуко. Для этого последовательно в спектрах Уолша-Адамара и Хаара исходного изображения (рис. 6, а) обнулим коэффициенты с координатами
, соответствующая оптической оси системы. Смещение ножа Фуко от этой точки существенно влияет на структуру выходного изображения и, как правило, приводит к разъюстировке. Рассмотрим поэтому поведение подобной точки в цифровом варианте ножа Фуко. Для этого последовательно в спектрах Уолша-Адамара и Хаара исходного изображения (рис. 6, а) обнулим коэффициенты с координатами  ,
,  и
и 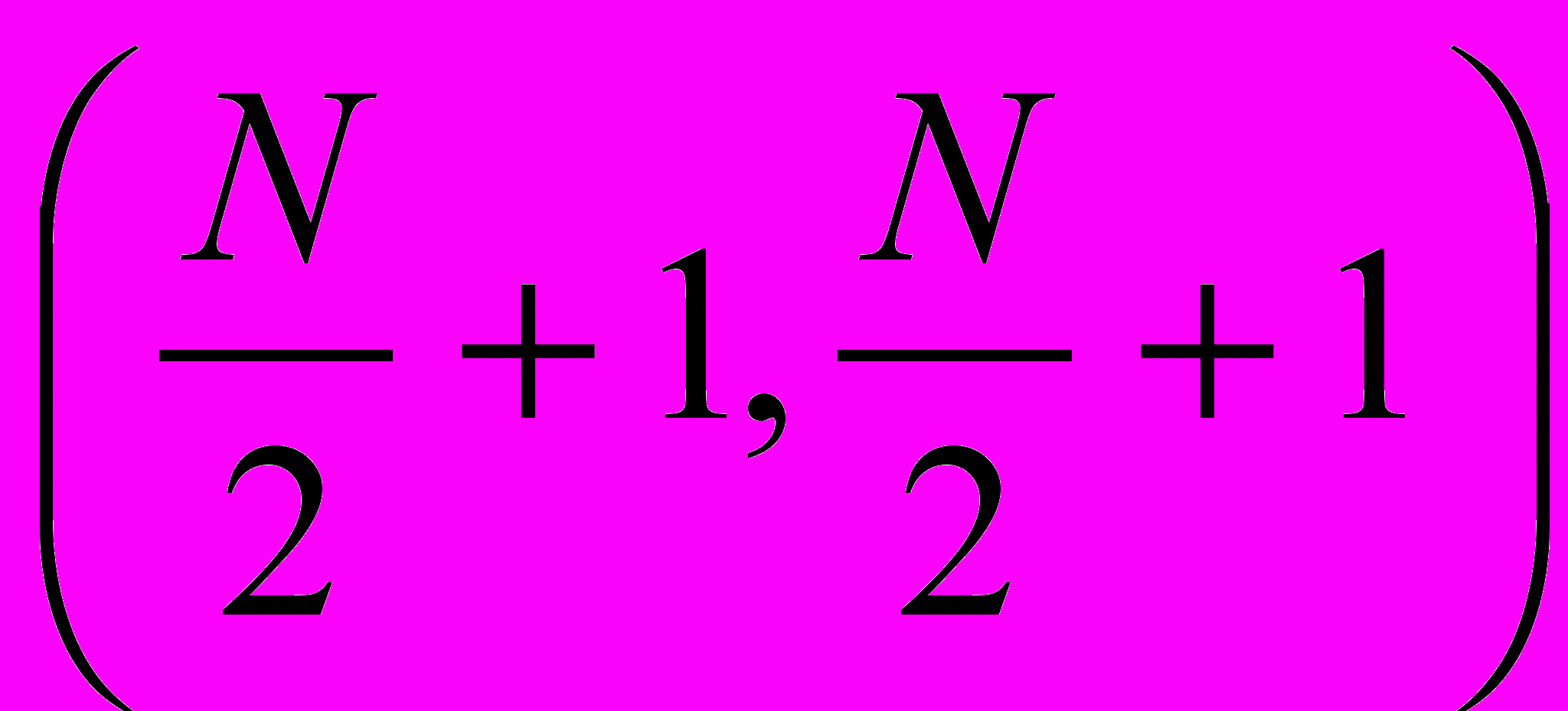 , где
, где  – размерность строки или столбца изображения, как показано на рис. 3 для изображения
– размерность строки или столбца изображения, как показано на рис. 3 для изображения 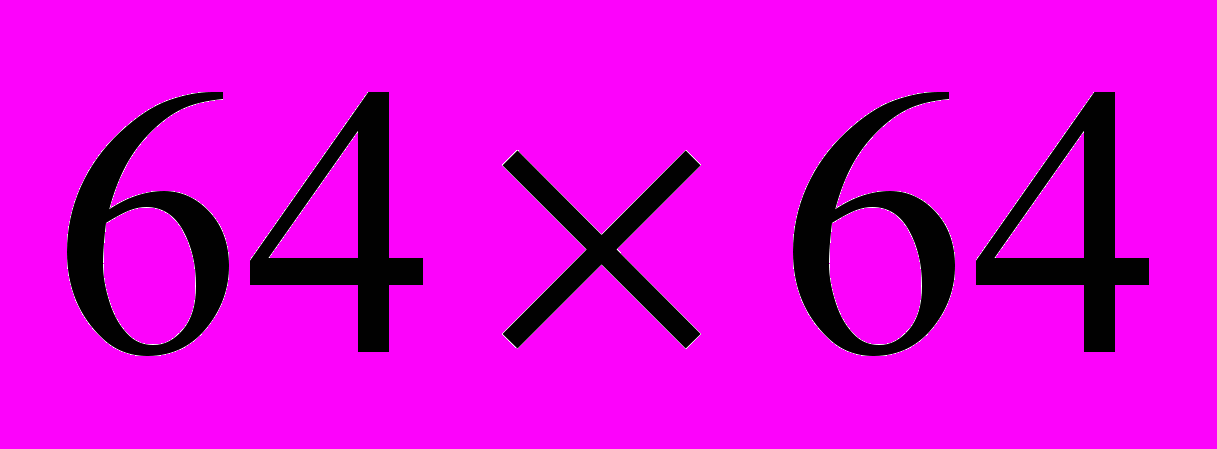 пикселя, и, затем для каждого случая выполним обратное преобразование.
пикселя, и, затем для каждого случая выполним обратное преобразование.
Рис. 6. Исследование «средней точки»: а) – восстановленное изображение преобразования Уолша-Адамара с обнуленным квадратом 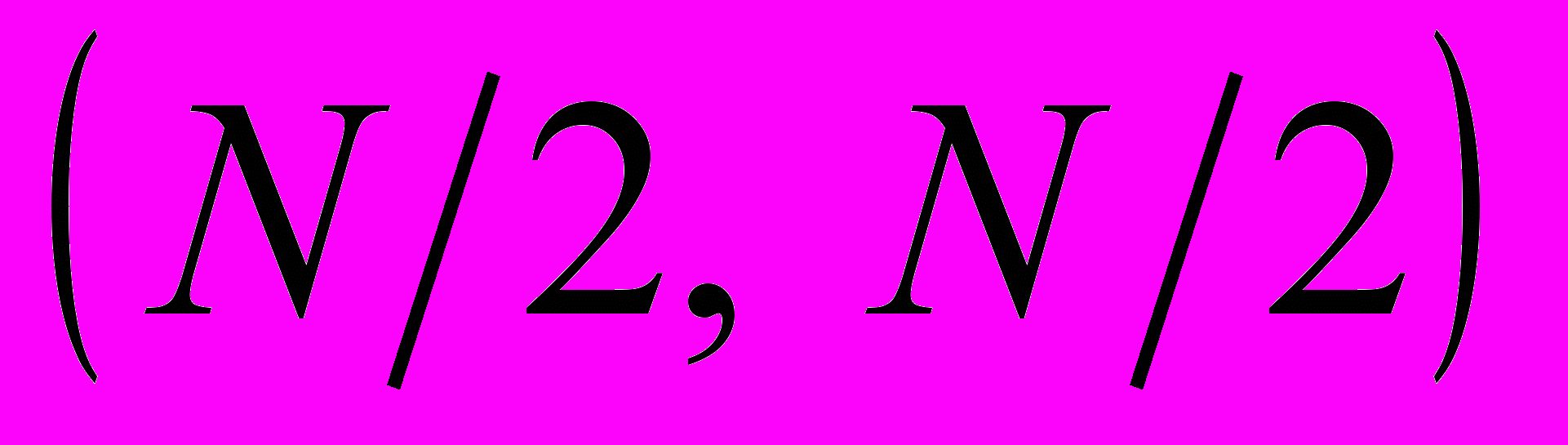 ; ; б) – восстановленное изображение преобразования Уолша-Адамара с обнуленным квадрантом 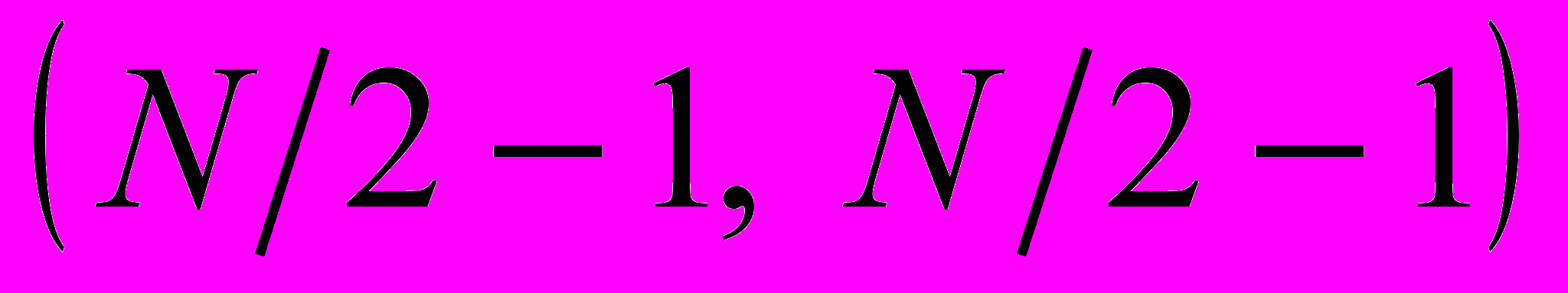 ; в) – восстановленное изображение преобразования Уолша-Адамара с обнуленным квадрантом ; в) – восстановленное изображение преобразования Уолша-Адамара с обнуленным квадрантом 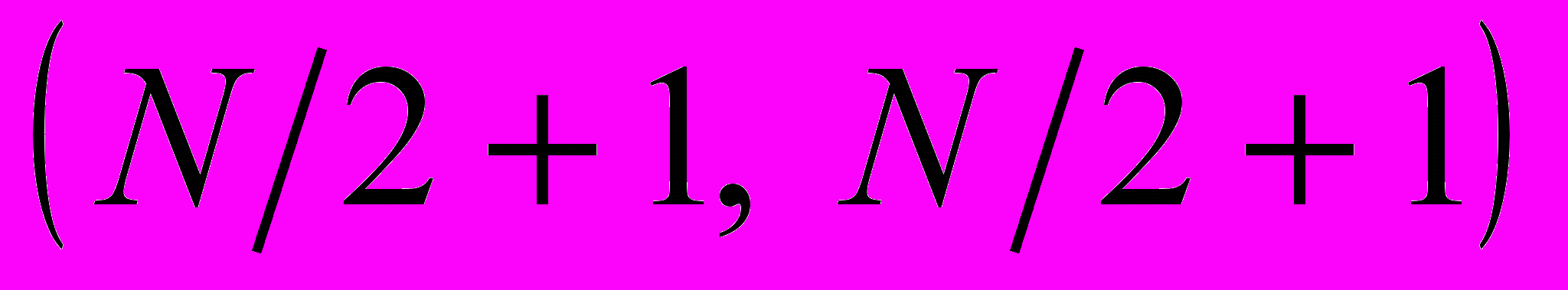 ; г) – восстановленное изображение преобразования Хаара с обнуленным квадрантом ; г) – восстановленное изображение преобразования Хаара с обнуленным квадрантом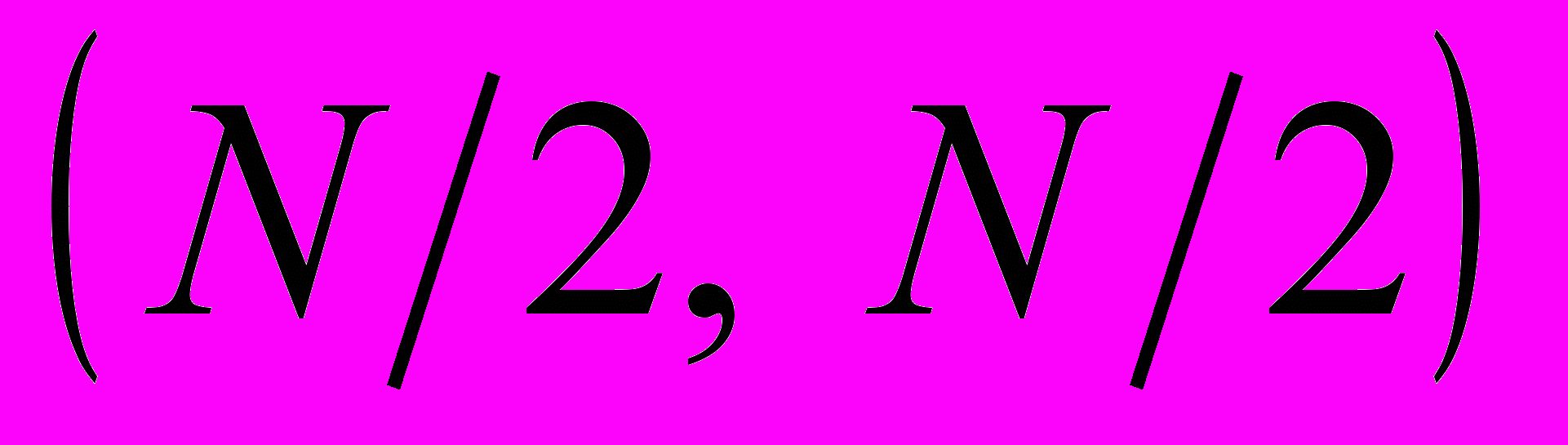 ; д) – восстановленное изображение преобразования Хаара с обнуленным квадрантом ; д) – восстановленное изображение преобразования Хаара с обнуленным квадрантом 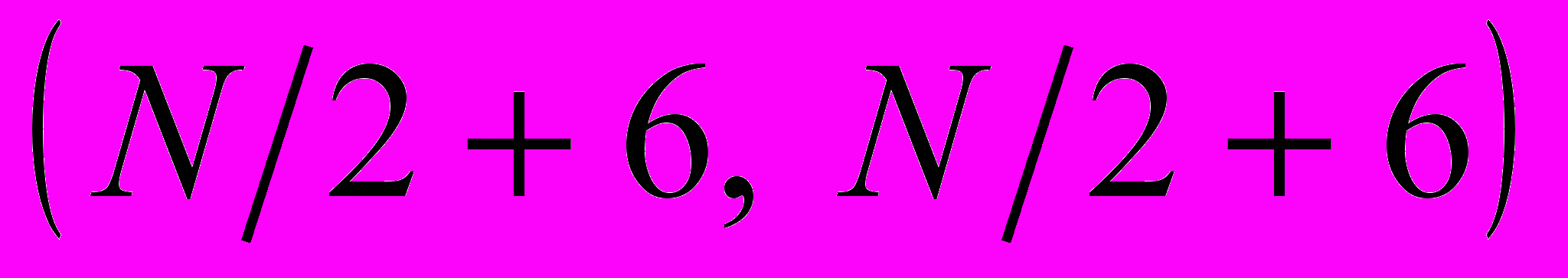 ; е) – восстановленное изображение преобразования Хаара с обнуленным квадрантом ; е) – восстановленное изображение преобразования Хаара с обнуленным квадрантом 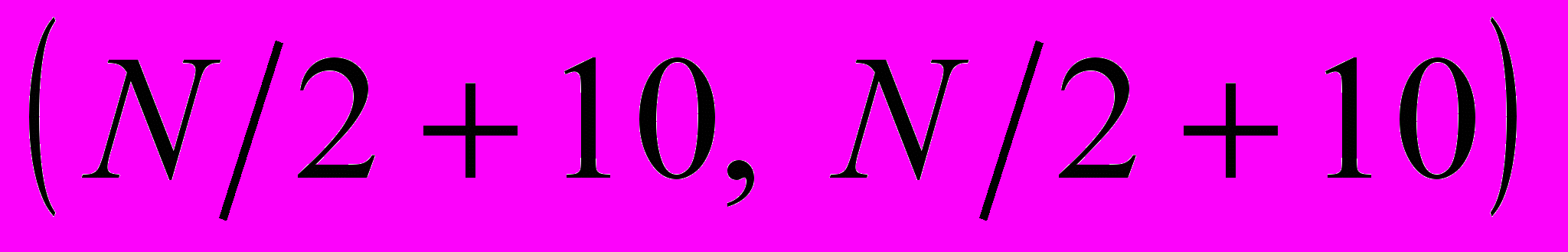 . . |
Для преобразования Уолша-Адамара качественное изображение возникает только в «средней точке» с координатами
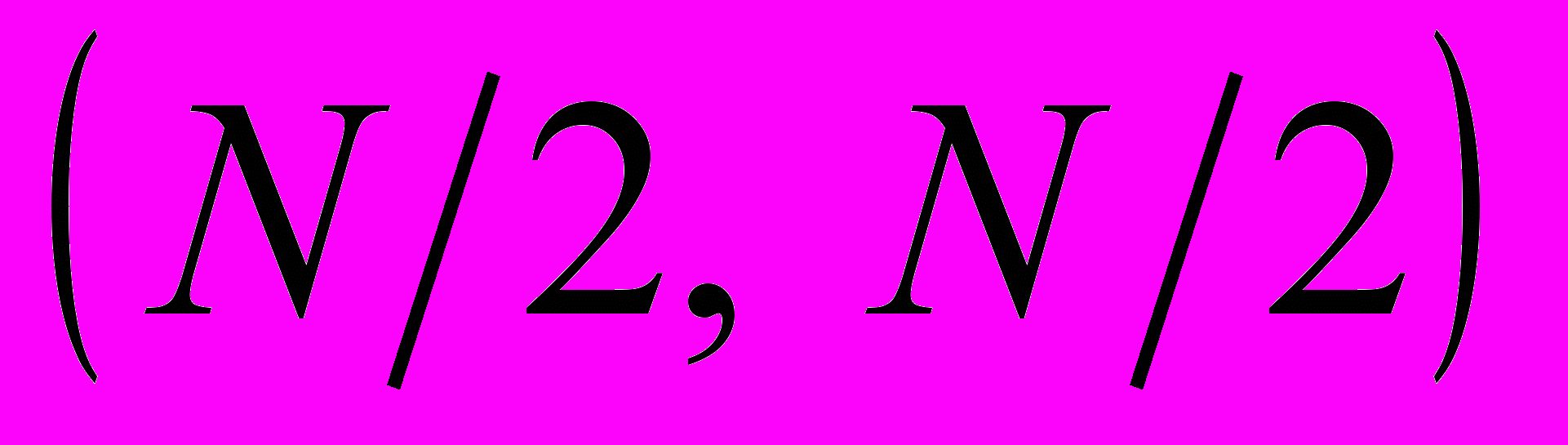 , в остальных случаях изображение имеет шумоподобный вид. Преобразование Хаара оставляет изображение качественным даже при вырезании квадранта с координатами
, в остальных случаях изображение имеет шумоподобный вид. Преобразование Хаара оставляет изображение качественным даже при вырезании квадранта с координатами 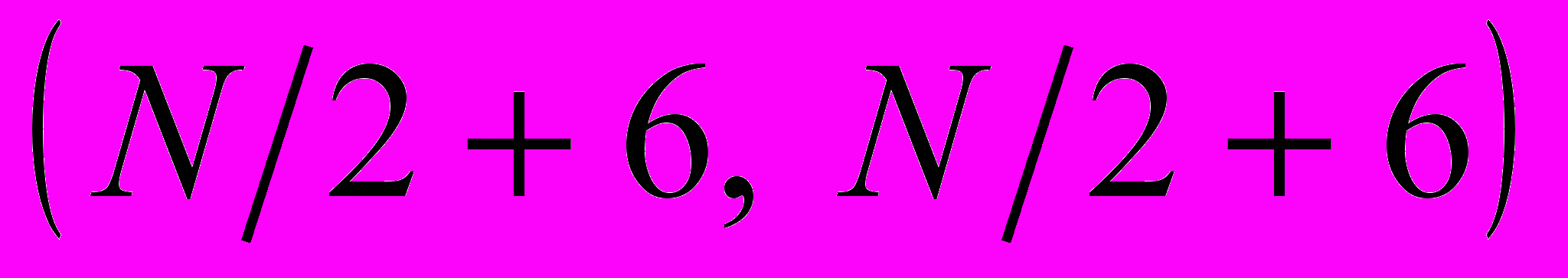 (рис. 6, д). В обоих случаях при передвижении «теневой маски» по спектру на изображении проявляются нескомпенсированные базисные функции. Искажение же изображения, возникающее при перемещении «теневой маски» по спектру является аналогом перемещения двумерного ножа Фуко в плоскости, перпендикулярной линии, соединяющей центры линз оптической системы.
(рис. 6, д). В обоих случаях при передвижении «теневой маски» по спектру на изображении проявляются нескомпенсированные базисные функции. Искажение же изображения, возникающее при перемещении «теневой маски» по спектру является аналогом перемещения двумерного ножа Фуко в плоскости, перпендикулярной линии, соединяющей центры линз оптической системы.Таким образом, в работе показано, что нож Фуко для цифрового изображения можно смоделировать на основе вычислений в пространстве вещественных чисел. Более того, в этом случае возникает возможность получения контуров изображения. Можно предположить, что использование цифрового аналога фазового манипулирования частотными компонентами обрабатываемого сигнального изображения обеспечивает столь же широкое функциональное многообразие, как и в случае когерентно-оптических и голографических систем пространственно-частотной фильтрации изображений.
- Онацкий А.Н., Малов А.Н. Управляемая сенситометрия ПЗС-матриц при регистрации лазерных изображений // // Сборник трудов VII Международной конференции «ГОЛОЭКСПО-2010» - Москва: ВВЦ, 2010. − с. 431 − 437.
- Использование особенностей нелинейной фильтрации ПЗС-матриц при исследовании подповерхностной структуры оптически непрозрачных материалов // Сборник трудов VII Международной конференции «ГОЛОЭКСПО-2010» - Москва: ВВЦ, 2010. − с. 438 − 442.
- Сороко Л.М. Гильберт-оптика – М.: Наука. Главная редакция физико-математической литературы, 1981, 160 с.
- Гонсалес Р., Вудс Р. Цифровая обработка изображений. – М.: Техносфера, 2005, 1072 с.
- Методы компьютерной обработки изображений / Под ред. В.А. Сойфера. – 2-е изд., испр. – М.: ФИЗМАТЛИТ, 2003, 784 с.
Nonlinear laser images digital filtration at registration and processing
Malov A.N., Onatskii A.N.
Irkutsk state university, Irkutsk, Russia
Foucault's knife for the digital image can be simulated on the basis of calculations in real numbers space. Moreover, in this case there is a possibility of the image contours reception. CCD matrixes usage in optoelectronic systems demands special sensitometrical certification of various matrixes types. Thus there is a possibility of a characteristic curve control and possibility of a signs space construction in a combination of integrated transformations with a nonlinear optical filtration colour CCD- matrixes.