И планирование экономики методические указания и задания для выполнения контрольной работы для студентов-заочников высших сельскохозяйственных

Вид материала

Методические указания

Содержание где Ти – темпы инфляции в прогнозируемом периоде К – коэффициент роста потребления сельскохозяйственной продукции за год; Н К – коэффициент роста потребления сельскохозяйственной продукции за год; N Пс – прогноз спроса на сельхозпродукцию, кг; Ц Решение задач по прогнозированию урожайности сельскохозяйственных культур S – выравнивающая функция (прямая, гипербола, парабола и др.); y

Подобный материал:

• Методические указания по выполнению контрольной работы для студентов заочников специальности, 559.27kb.
• Методические указания по изучению дисциплины плодоводство и задание для контрольной, 655.73kb.
• Рабочая программа, методические указания по выполнению курсовой работы, темы курсовых, 1694.43kb.
• Методические указания по изучению дисциплины и задания для контрольной работы для студентов-заочников, 398.39kb.
• Методические указания по выполнению контрольной работы по учебной дисциплине «валютные, 450.92kb.
• Методические указания для выполнения контрольной работы по дисциплине "Налоговое планирование", 278.39kb.
• Методические указания по изучению дисциплины и задание для контрольной работы студентам-заочникам, 610.79kb.
• Методические указания по изучению дисциплины и задания для контрольной работы для студентов-заочников, 386.17kb.
• Методические указания и задания к выполнению контрольной работы по дисциплине, 246.08kb.
• Методические указания и контрольные задания для студентов-заочников средних специальных, 375.78kb.

где Т_и – темпы инфляции в прогнозируемом периоде, %;

J_п – индекс потребительских цен в прогнозируемом периоде;

J_б – индекс потребительских цен в базовом периоде.

Рассчитывают коэффициент скрытой инфляции в прогнозируемом году по формуле

К_cu= J_дн : J_рт ,

где К_cu – коэффициент скрытой инфляции;

J_дн – индекс доходов населения в прогнозируемом периоде;

J_рт – индекс розничного товарооборота в прогнозируемом периоде.

Определяют индекс инфляции (J_и) по формуле

J_и = J_p × К_cu ,

где J_и – индекс инфляции, %;

J_p – индекс потребительских цен;

К_cu – коэффициент скрытой инфляции.

Решение задач по прогнозированию спроса сельскохозяйственной продукции и определение года достижения нормативного потребления сельхозпродукции осуществляется в последовательности, приведенной ниже.

Определяют сложившийся среднегодовой рост потребления сельскохозяйственной продукции за прошедшие годы по формуле

К = ,

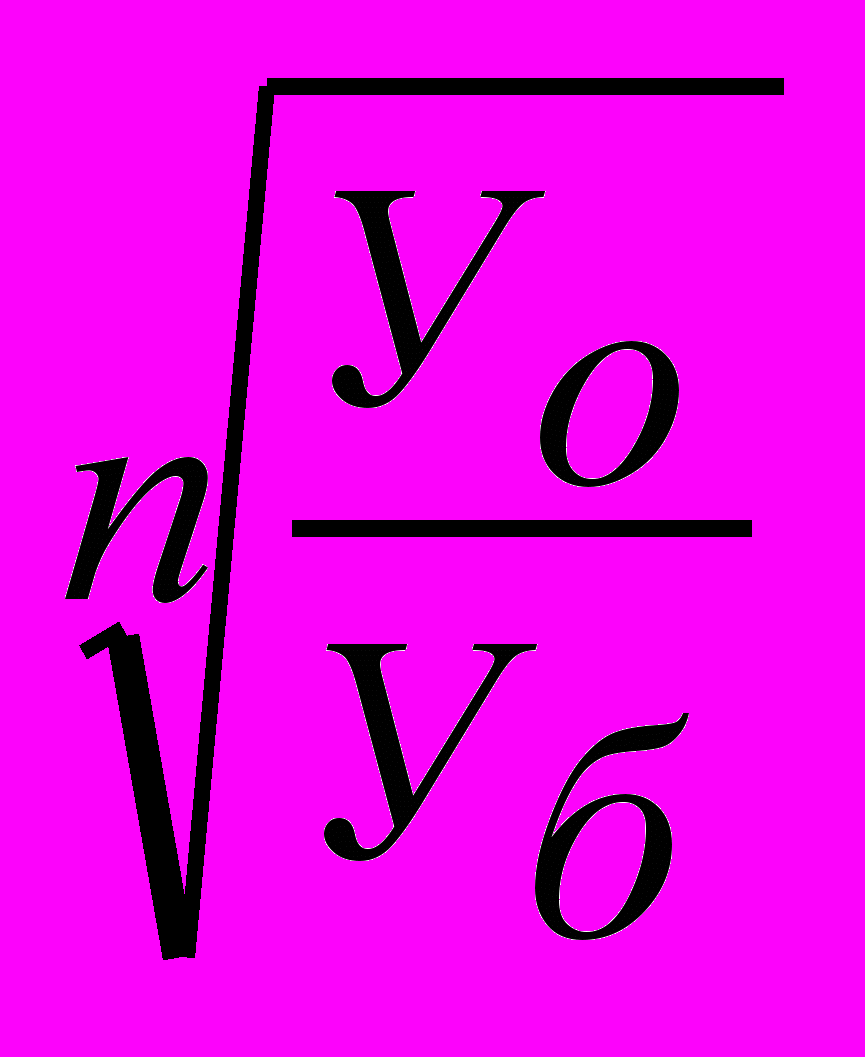где К – коэффициент роста потребления сельскохозяйственной продукции за год;

n – число периодов динамического ряда, т. е. количество периодов между годами в динамическом ряду;

У_о – уровень потребления в отчетном году сельхозпродукции, кг;

У_б – уровень потребления в базисном году сельхозпродукции, кг.

Определяют прогноз спроса на сельхозпродукцию (емкость рынка) с учетом численности населения на 2006 прогнозный год по формуле

П_с = У_о × К³×Н × [(100+П_р) : 100] ,

где П_с – прогноз спроса на сельхозпродукцию, кг;

У_о – уровень потребления в отчетном году сельхозпродукции, кг;

К – коэффициент роста потребления сельскохозяйственной продукции за год;

Н – численность населения;

П_р – процент роста населения от отчетного года до прогнозируемого, %.

Определяют прогноз спроса на сельхозпродукцию (емкость рынка) с учетом численности населения на 2010 прогнозный год по формуле

П_с = У_о × К⁷×Н × [(100+П_р) : 100] ,

где П_с – прогноз спроса на сельхозпродукцию, кг;

У_о – уровень потребления в отчетном году сельхозпродукции, кг;

К – коэффициент роста потребления сельскохозяйственной продукции за год;

N – количество лет от отчетного года до прогнозируемого;

Н – численность населения;

П_р – процент роста населения от отчетного года до прогнозируемого, %;

П_рп – процент роста населения от прогнозируемого года до прогнозируемого периода, %.

Определяют число лет достижения нормы потребления сельхозпродуктов при сложившемся приросте потребления по формуле

,

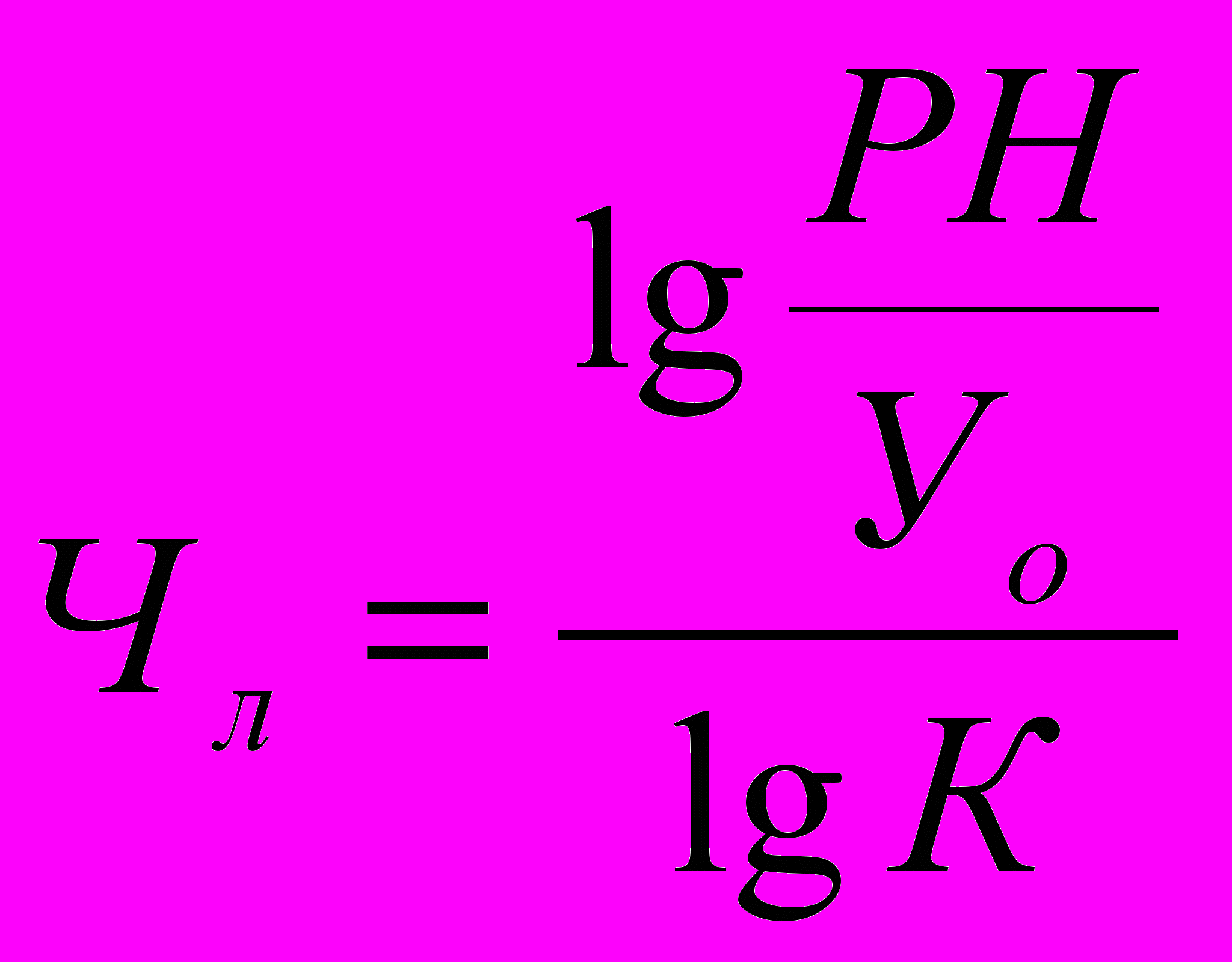где Ч_л – число лет достижения нормы потребления сельхозпродуктов;

РН – рекомендуемая норма потребления сельхозпродуктов на одного человека в год;

У_о – уровень потребления сельхозпродукции в отчетном году, кг;

К – коэффициент роста потребления сельскохозяйственной продукции за год.

Рассчитывают стоимостное выражение спроса на сельхозпродукты (емкость рынка) в ценах отчетного года по формуле

VC = П_с × Ц_i ,

где VC_i – стоимость объема спроса на сельхозпродукты (емкость рынка) в i-м периоде, руб.;

Пс – прогноз спроса на сельхозпродукцию, кг;

Ц_i – цена единицы i-го вида сельхозпродукции, руб/кг.

Решение задач по прогнозированию спроса на мясо и мясопродукты, молоко и молочные продукты.

Определяют норму потребления сельхозпродуктов на краткосрочный период на душу населения (Н_нпк) по формуле

Н_нпк = (Н_пб × Д_днп) : I_пц ,

где Н_пб – норма потребления в базисном периоде на душу населения, кг;

Д_днп – рост доходов населения в прогнозируемом периоде;

J_пц – индекс потребительских цен в прогнозируемом периоде.

Определяют объем спроса на сельхозпродукты в краткосрочном периоде (QС_ппкп) по формуле

QС_ппкп = Н_нпк × Ч_нкп ,

где Н_нпк – норма потребления сельхозпродуктов в краткосрочном периоде на душу населения;

Ч_нкп – численность населения в краткосрочном периоде.

Рассчитывают объем спроса на сельхозпродукты на долгосрочный период (QС_дп) по формуле

QС_дп = РН_пдп × Ч_нкп ,

где РН_пдп – рекомендуемая норма потребления сельхозпродуктов на одного человека в год;

Ч_нкп – численность населения в долгосрочном периоде.

Решение задач по прогнозированию методом "Дефляции", реального и номинального ВВП и определения общего индекса цен.

Определяют реальный ВВП в прогнозируемом периоде по формуле

ВВП_рп = ВВП_б × J_об ,

где ВВП_рп – объем реального ВВП в прогнозируемом периоде;

ВВП_б – объем ВВП в базисном периоде;

J_об – темпы роста объема ВВП в прогнозируемом периоде по сравнению с базисным.

Рассчитывают индекс цен (дефлятор) ВВП по формуле



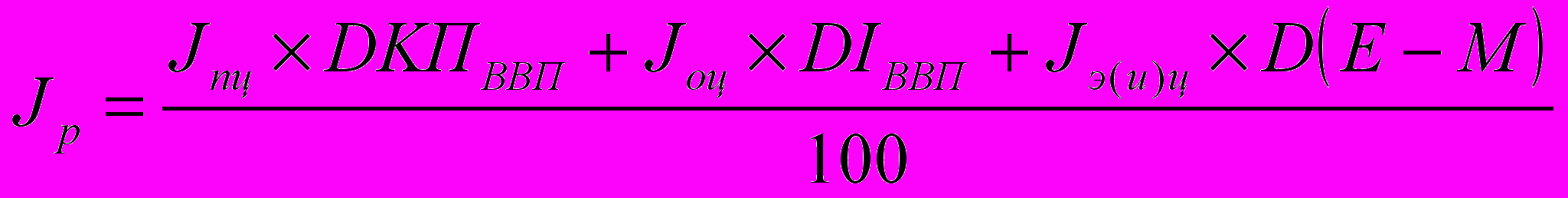
где 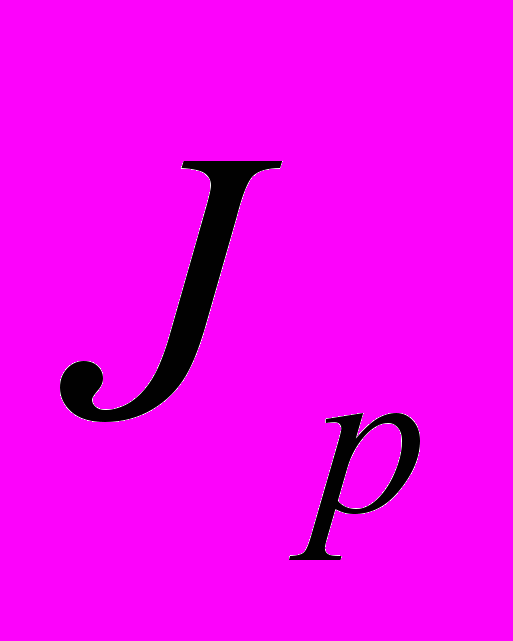– прогнозируемый индекс цен (дефлятор) ВВП. Дефлятор показывает, насколько возрос ВВП исключительно за счет роста цен, т.е. характеризует изменение общего индекса цен;


J_пц, J_оц, J_э(и)ц – потребительские, оптовые (отпускные) цены, цены экспорта и импорта в прогнозируемом периоде, %;

DKП_ВВП, DI_ВВП, D_СЭИ – доля в ВВП конечного потребления; инвестиций; сальдо экспорта (импорта) в прогнозируемом периоде, %.

Определяют номинальный ВВП в прогнозируемом периоде по формуле

ВВП_нн = ВВП_рн ×,

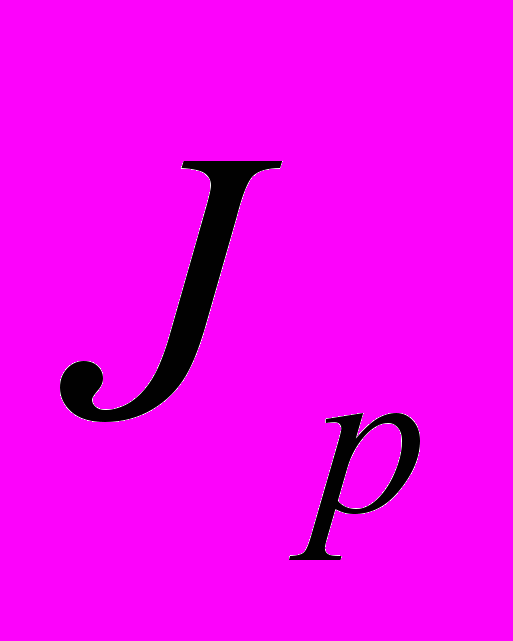где ВВП_рн – объем реального ВВП в прогнозируемом периоде;

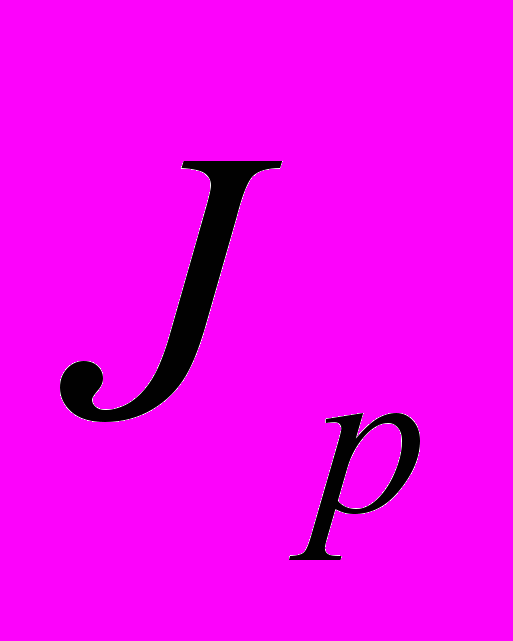– прогнозируемый индекс цен ВВП (дефлятор).

Решение задач по прогнозированию урожайности сельскохозяйственных культур осуществляется с помощью метода подбора функции, входящего в метод прогнозной экстраполяции. Метод подбора функции основан на методе математической экстраполяции, которая в математическом смысле означает распространение закона изменения функции из области ее наблюдения на область, лежащую вне отрезка наблюдения. Суть метода состоит в выборе оптимального вида функции (прямой, параболы, гиперболы и др.), которая наиболее точно описывает тенденцию изменений объекта прогнозирования в будущем.

Выбор функции (прямой, параболы, гиперболы и др.), которая наиболее реально отражает изменения в объекте прогнозирования, проводится с помощью метода наименьших квадратов.

Суть метода наименьших квадратов в том, что выравнивающая функция (прямая, парабола, гипербола и др.) будет занимать такое положение среди точек (фактических значении показателей), при котором суммар­ное отклонение точек от функции будет минимальным, т.е. искомые параметры должны удовлетворять следующему условию:

,


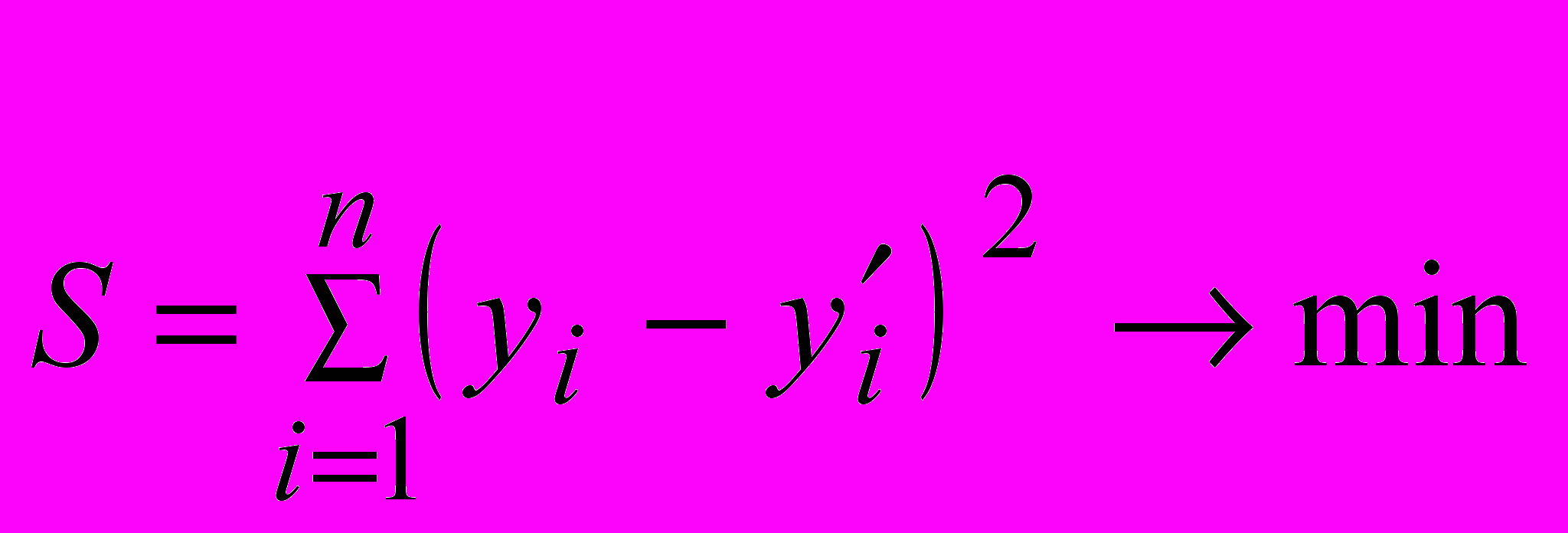где S – выравнивающая функция (прямая, гипербола, парабола и др.);

y_i – фактические уровни показателей в динамическом ряду;

y_i – расчетный ряд прогнозируемых показателей, вычисленный по уравнению функции (прямая, гипербола, парабола и др.);

n – число наблюдений.

Исходной информацией для экстраполяции с помощью метода подбора функций являются временные (динамические) ряды.

Временной ряд представляет собой упорядоченные во времени наборы измерений тех или иных характеристик исследуемого объекта, т.е. множество наблюдений, полученных последовательно во времени.

В наших задачах временной ряд представляет урожайность сельскохозяйственных культур по годам. Например: урожайность пшеницы в 1988 году составила 20,6 ц/га, 1989 г. – 21,7; 1990 г. – 28,5; 1991 г. – 22,0; 1992 г. – 27,4; 1993 г. – 27,2; 1994 г. – 24,8; 1995 г. – 27,3; 1996 г. – 28,2; 1997 г. – 23,2; 1998 г. – 21,1; 1999 г. – 22,0; 2000 г. – 23,9; 2001 г. – 19,1; 2002 г. – 15,0; 2003 г. – 19,4; 2004 г. – 23,2 ц/га. Необходимо с помощью метода подбора функций составить прогноз урожайности на перспективу (2008 г.).

Расчет проводится следующим образом:

1. Составляют таблицу, в которую заносят исходные данные задачи (таблица, гр. 1 и 2), и определяют сумму фактической урожайности зерновых за исследуемый период (Σу) путем её суммирования. В нашем примере с 1988 по 2004 гг. Σу составит 394,6.

2. Строят график фактической урожайности зерновых за исследуемый период с целью определения, к какому виду функции (прямой, параболе, гиперболе и др.) ближе форма кривой фактических данных урожайности сельхозкультур (рис. 1).

Из данных рис. 1 видно, что линия урожайности сельхозкультур за ряд лет по виду напоминает как функцию прямой, так и функцию параболы. Поэтому для обоснованности и достоверности прогноза урожайности дальнейшие расчеты проводят по подбору как функции вида прямой, так и функции параболы с целью более точного выявления имеющейся тенденции в динамическом ряду прогнозирования урожайности сельхозкультур на перспективу (2008 г.).

3. Расчеты по подбору функции прямой линии для определения суммы квадратов отклонений проводят следующим образом.

Определяют уравнение прямой линии как выравнивающей функции по формуле

Y_i = a + bt ,

где Y_i – выравненный уровень урожайности по функции прямой;

a и b – параметры уравнения фактической и прогнозируемой прямой линии;

t – порядковый номер фактического и прогнозируемого уровня.