Geum.ru

Метод принятия решения в выборе варианта реализации алгоритмов при разнородных условиях

Вид материалаДокументы

Содержание


Ксо,i – коэффициент сложности i
Подобный материал:

Метод принятия решения в выборе варианта реализации алгоритмов при разнородных условиях



Litvinskaya O.S.


Выбор варианта реализации алгоритмов будет рассмотрен для алгоритмов последовательной обработки данных. Подобная задача относится к задачам систем поддержки приятия решения.

Задачи принятия решении (ЗПР) встречаются во многих областях знаний и отличаются большим разнообразием..

В зависимости от способа отображения множества допустимых альтернатив во множество критериальных оценок возможных исходов, ЗПР подразделяют на следующие категории:

• задачи в условиях определенности, которые характеризуются полной и точной (как правило, количественной) исходной информацией и детерминированным отображением множества альтернатив в множество критериальных оценок;

• задачи в условиях риска, когда возможные исходы можно описать с помощью некоторого вероятностного распределения, для построения которого необходимо иметь статистические данные или экспертные оценки;

• задачи в условиях неопределенности, когда исходная информация является неполной, неточной, неколичественной, а вид формального отображения является либо слишком сложным, либо не известен. В таких случаях для решения ЗПР привлекаются знания экспертов. Для представления и обработки этих знаний используются различные методы прикладной теории принятия решений и методы искусственного интеллекта.

Предлагаемая работа рассматривается как задача в условиях неопределенности. В работе предполагается применить положения теории систем поддержки принятия решений (СППР) применительно к области оптимального проектирования специализированных цифровых устройств обработки сигналов. В настоящее время СППР успешно развиваются в области экономики и управления. Подходы, используемые в СППР для решения технических задач, развиты слабо.

Выбор средства реализации алгоритмов предполагается осуществить на сравнительной оценке современных интегральных технологий и целевой функции выбора. Сравнительная оценка предполагает наличие оптимизации целевой функции, которая позволяет выразить необходимые характеристики сигналов и алгоритмов в виде числовых зависимостей, а также совокупность средств реализации алгоритмов, например аппаратных и программных, либо выбор может осуществляться среди микроконтроллеров.

Разработан комплекс программных средств, применительно к выбору средства реализации по рассмотренной методике. Комплекс включает в себя два программных средства. Одно осуществляет выбор между аппаратной и программной реализацией (СППР_А_П). Второе - выбор микроконтроллеров (СППР_МК).

Общий вид главной формы ПС СППР_А_П представлен на рисунке 1. Логическая структура программы следующая: На главной форме находятся шесть вкладок: «Исходные данные», «Анализ данных», «Целевая функция», «Отчет», «Справочник», «Файл». Каждая из вкладок содержит определенное количество кнопок-навигаторов и нажатие на каждую из них приводит к отображению подчиненной формы слева.


Рисунок 1 – Главная форма программы СППР_А_П

Метод выбора основан на формировании целевой функции модели вычислительного процесса 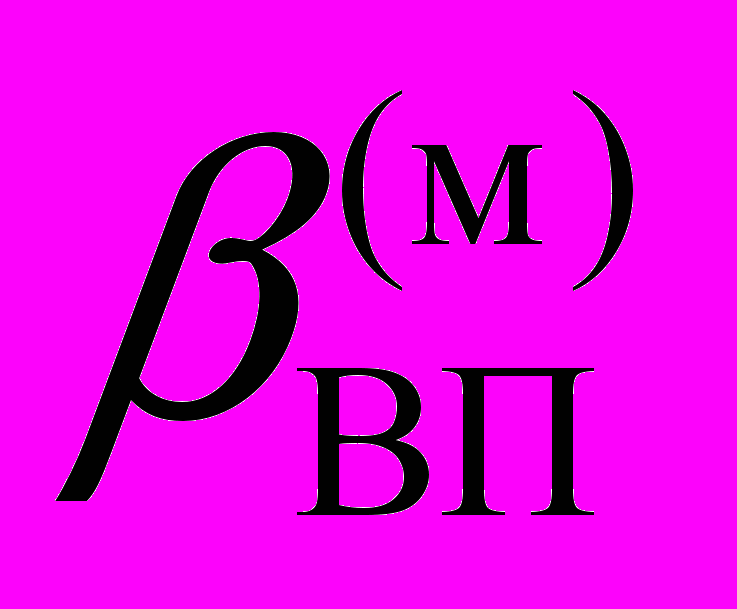, имеющей вид

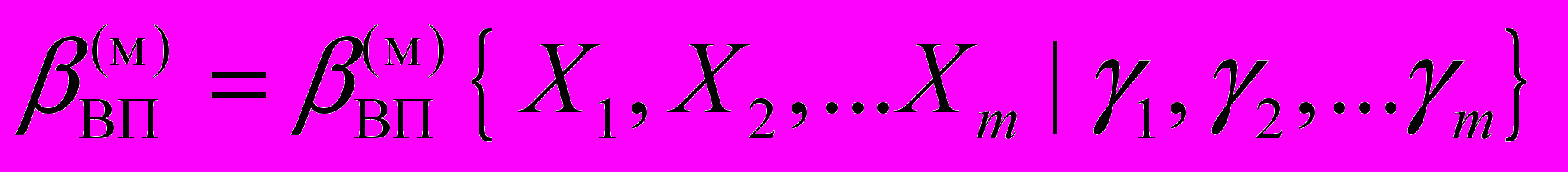, (1)

которая зависит от множества параметров 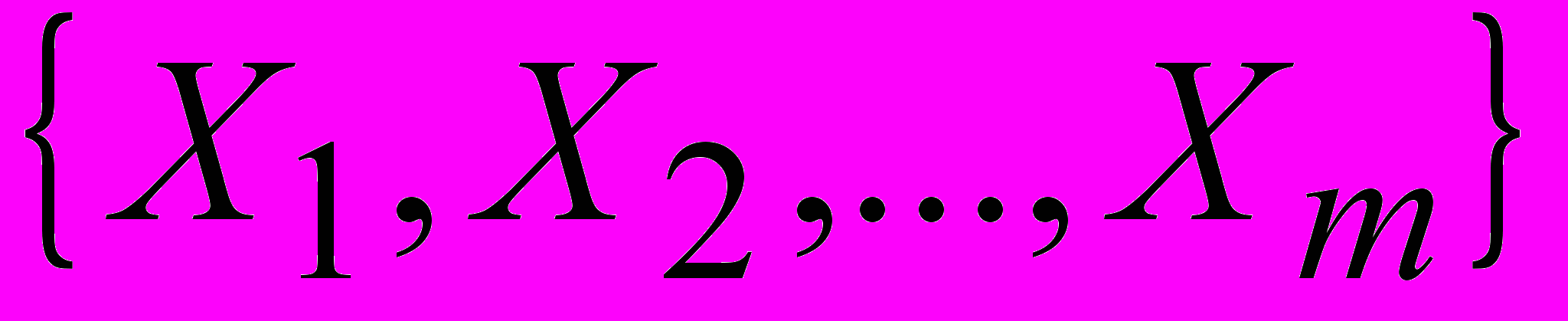и максимальных значений этих параметров .

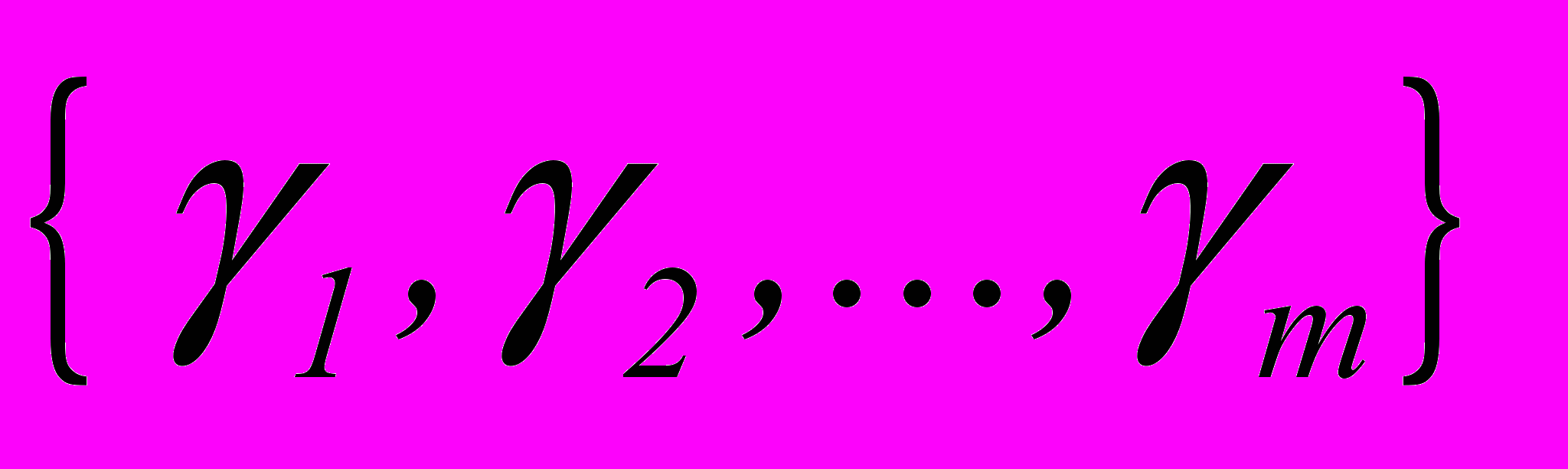Целевая функция будет зависеть от частных параметров моделей алгоритмов и характеристик сигналов, которые являются исходными данными программы. К таким относят: динамический диапазон входного сигнала DS; вид алгоритма КВА; вид преобразования в виде параметра трансформации отсчетов NТО; время выполнения операций в алгоритме ТВО, а также параметры, непосредственно влияющие на выбор средства реализации алгоритмов. На рисунке 2 представлены формы ввода исходных данных.



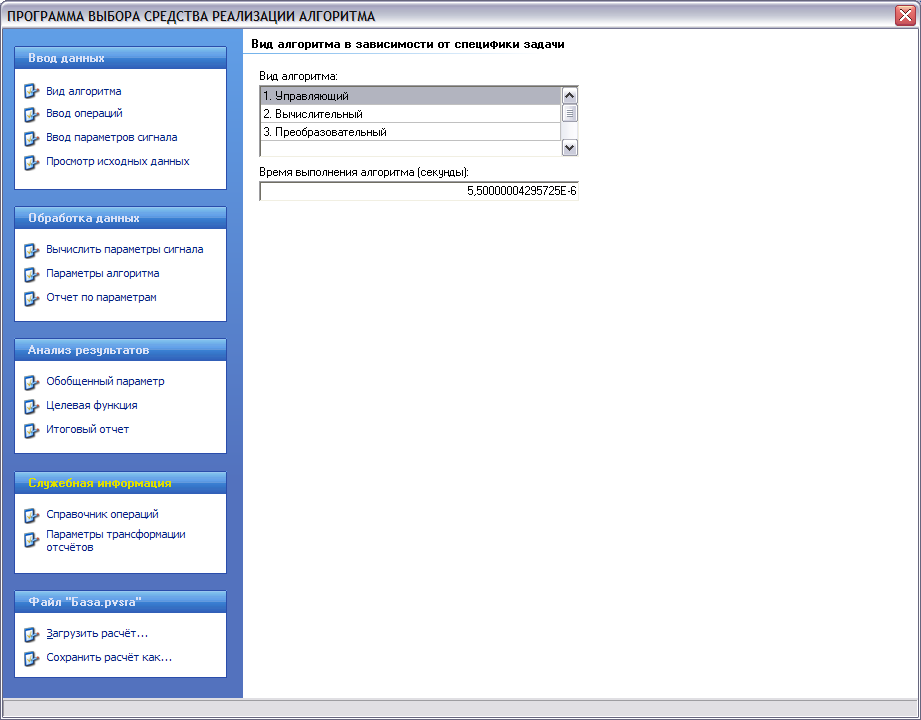
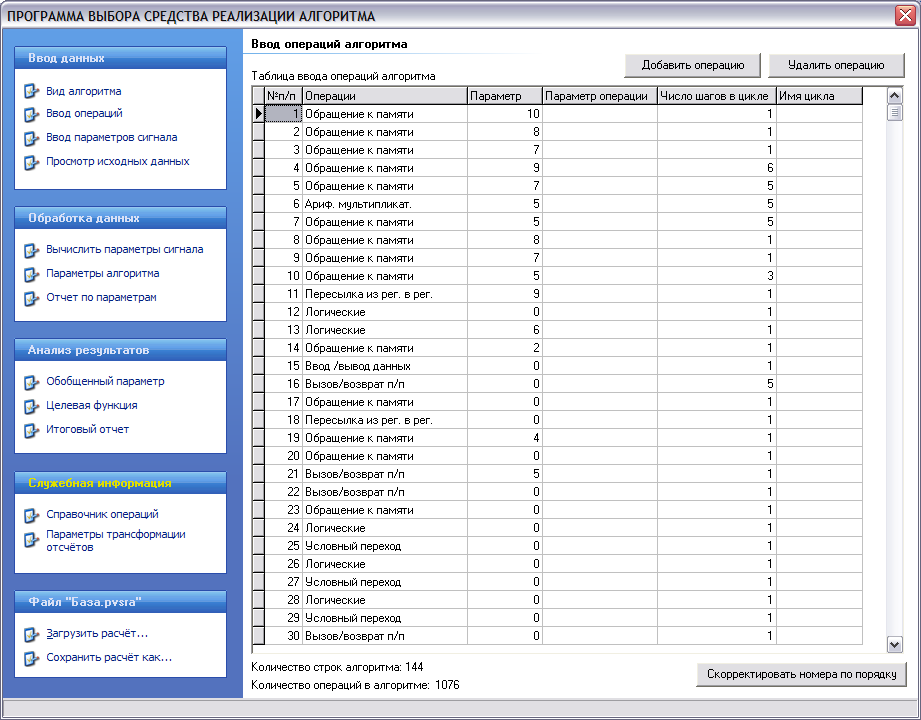
а) б)



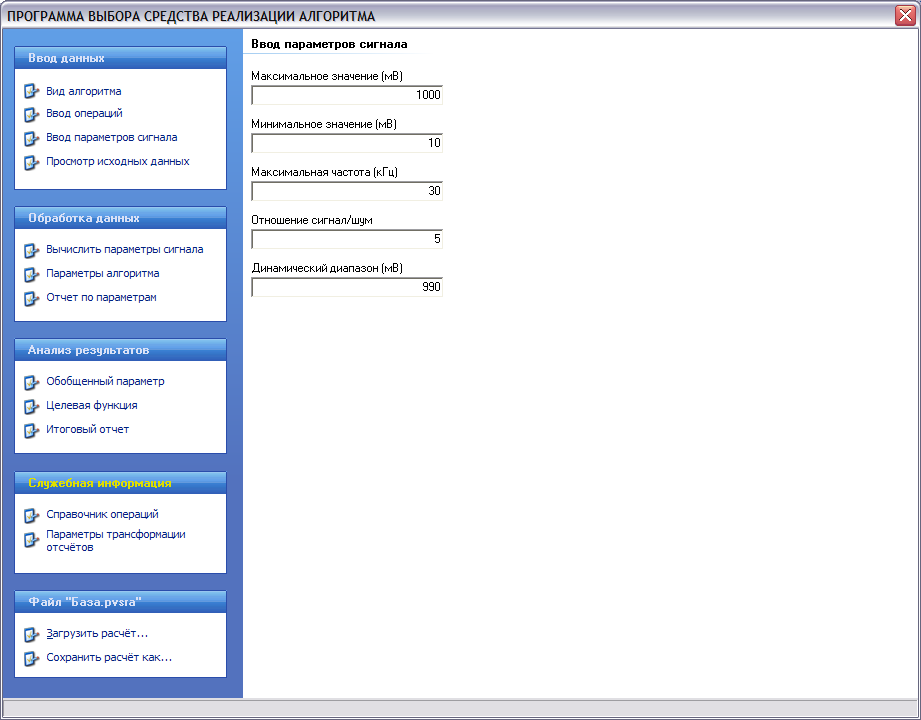
в)

Рисунок 2 – Экранные формы программы: а) форма ввода вида алгоритма и требуемого времени выполнения, б) форма ввода операций алгоритма, в) форма ввода параметров сигнала


При нажатии на кнопку «Вид алгоритма» происходит открытие формы, где вводятся вид алгоритма и время выполнения алгоритма.

При нажатии на кнопку «Операции» открывается форма «Ввод операций». На ней в виде таблицы содержатся данные об операциях алгоритма: порядковый номер операции, название операции, параметр операции, число шагов в цикле, имя цикла. Также в нижней части формы находится поле «Количество операций в алгоритме». Оно рассчитывается как сумма значений в поле «Число шагов в цикле». В таблице разрешается изменять все данные в ней находящиеся, в том числе разрешается добавление или удаление операции.

При выборе кнопки «Параметры сигнала» открывается форма «Ввод параметров сигнала». На ней вводятся следующие данные: максимальное значение, минимальное значение, выраженные в мВ, максимальная частота – в кГц, отношение сигнал/шум, а также поле динамического диапазона, которое рассчитывается как разница между максимальным и минимальным значением автоматически.

Все параметры, входящие в (1), имеют различные физические единицы измерения. Выполнив нормирование проанализированных параметров

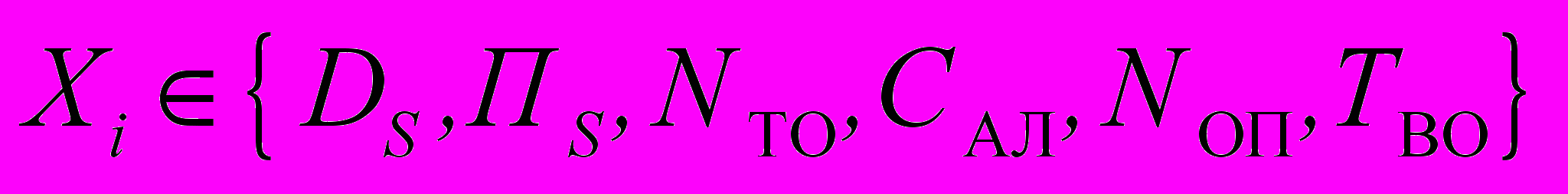, (2)

по множеству их характеристических свойств

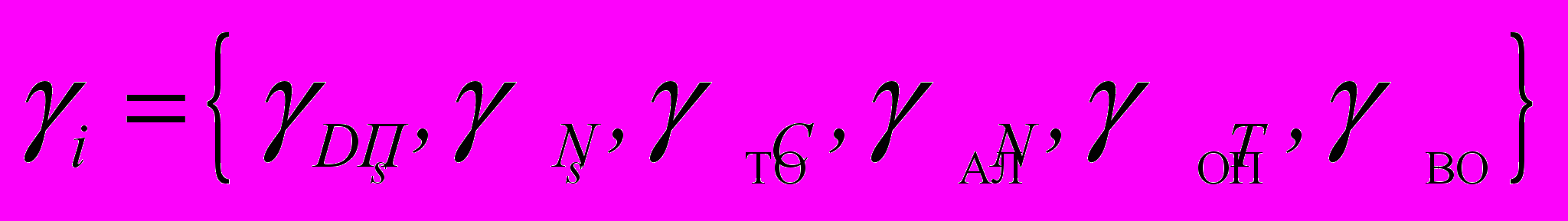, (3)

получим множество нормированных безразмерных параметров:

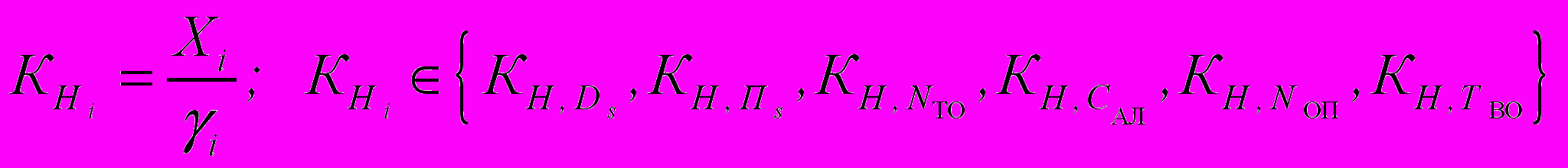. (4)

Множество частных параметров 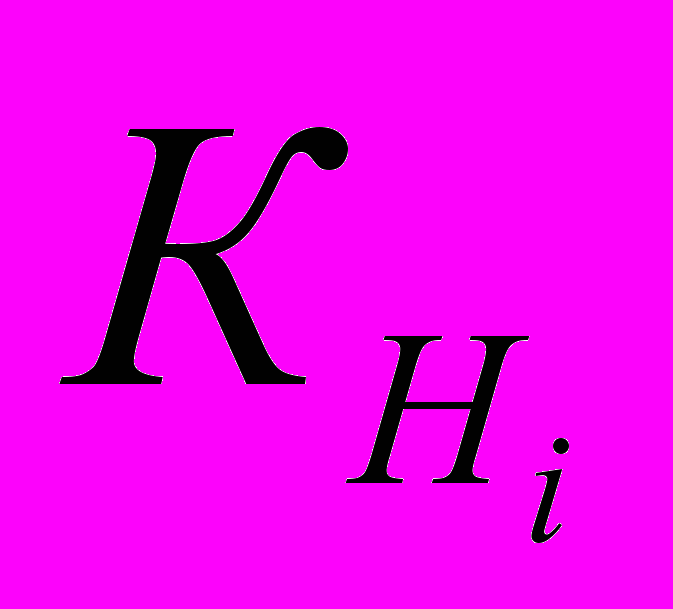рассчитывается по формулам согласно методу, например:

- коэффициент динамического диапазона входных данных:

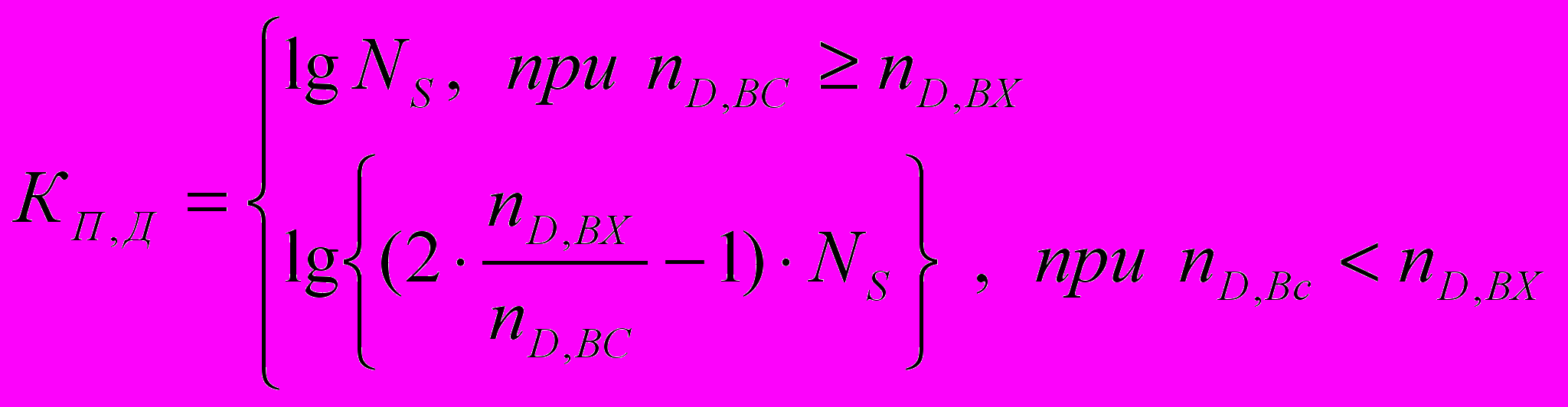, (5)

где NS – число уровней квантования; nD,ВХ – количество разрядов входных данных; nD,ВС, – разрядность вычислительного средства;

- коэффициент последовательного потока данных:

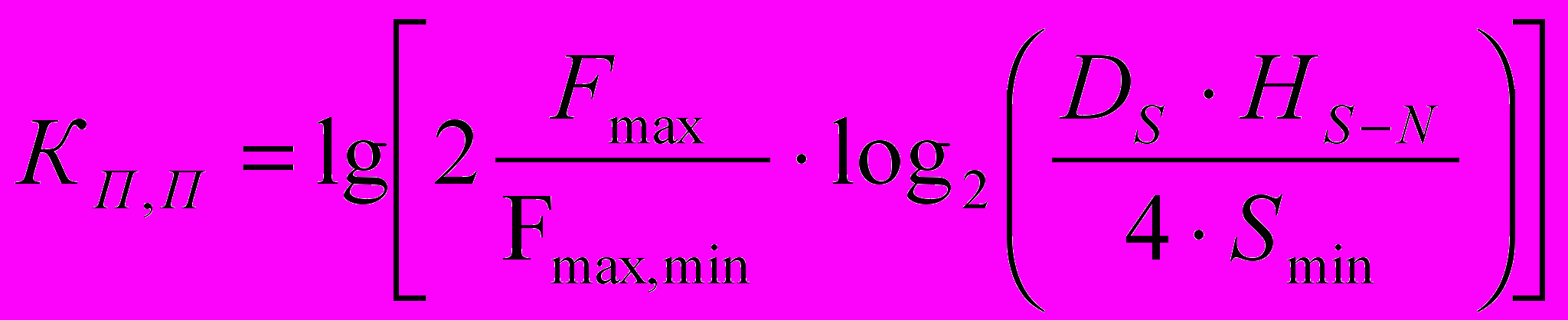(6)

где Fmax – максимальная частота входного сигнала; DS – динамический диапазон входного сигнала; НS-N – отношение сигнал-шум; Smin – минимальное значение входного сигнала.

- коэффициент трансформации отсчетов:

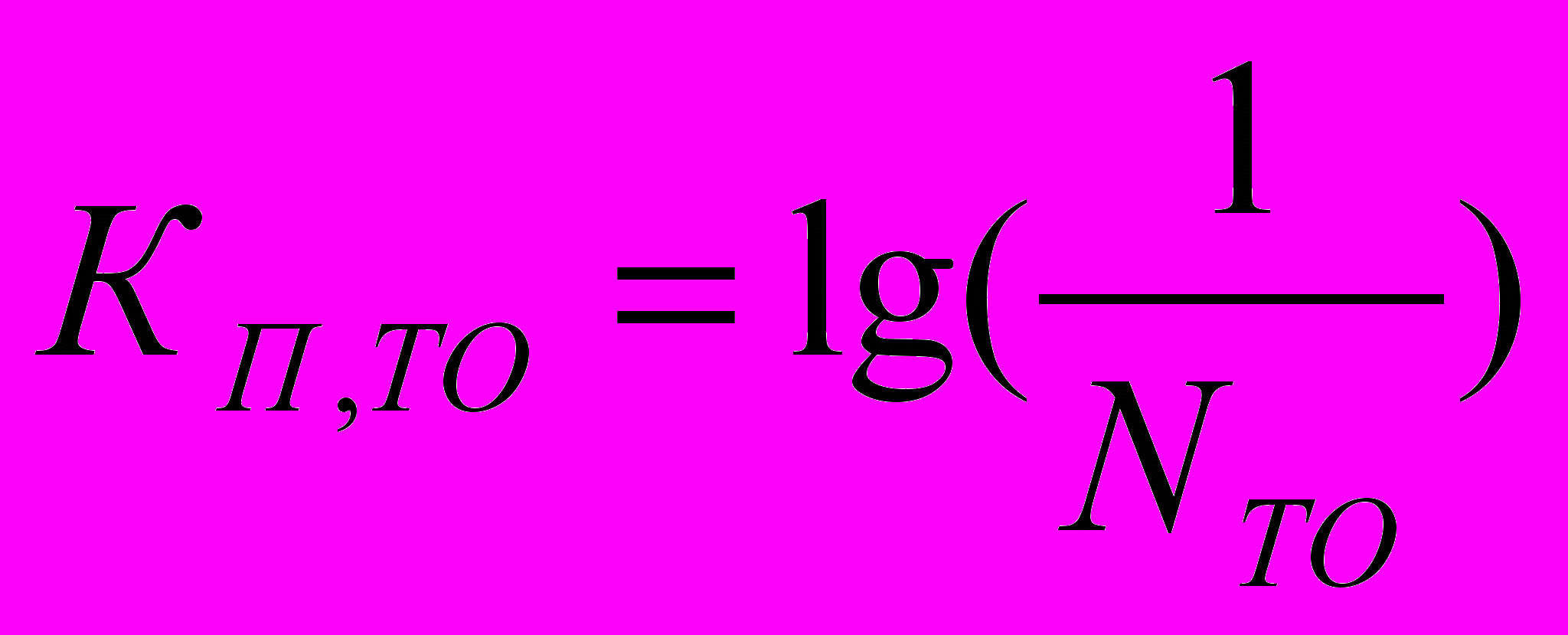(7)

где NТО - параметр трансформации отсчетов входного сигнала;

- коэффициент сложности алгоритма:

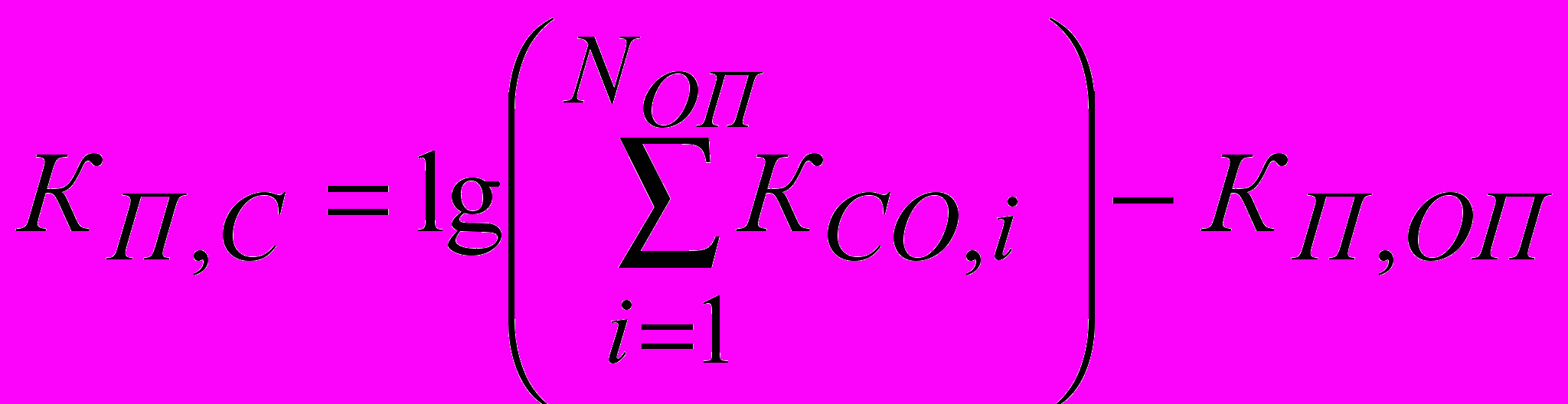(8)

где Ксо,i – коэффициент сложности i-операции; Кп,оп – коэффициент числа операций

и другие коэффициенты, участвующие в описании целевой функции.

Совокупность характеристик алгоритма и сигналов будем называть обобщенной характеристикой формируемой модели 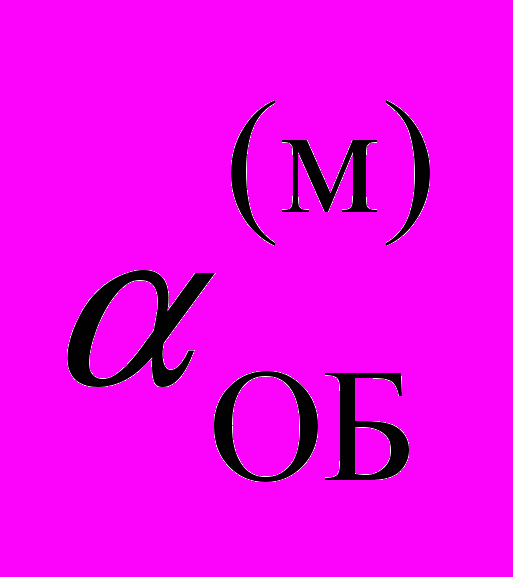. Аналитическое выражение ее имеет вид:

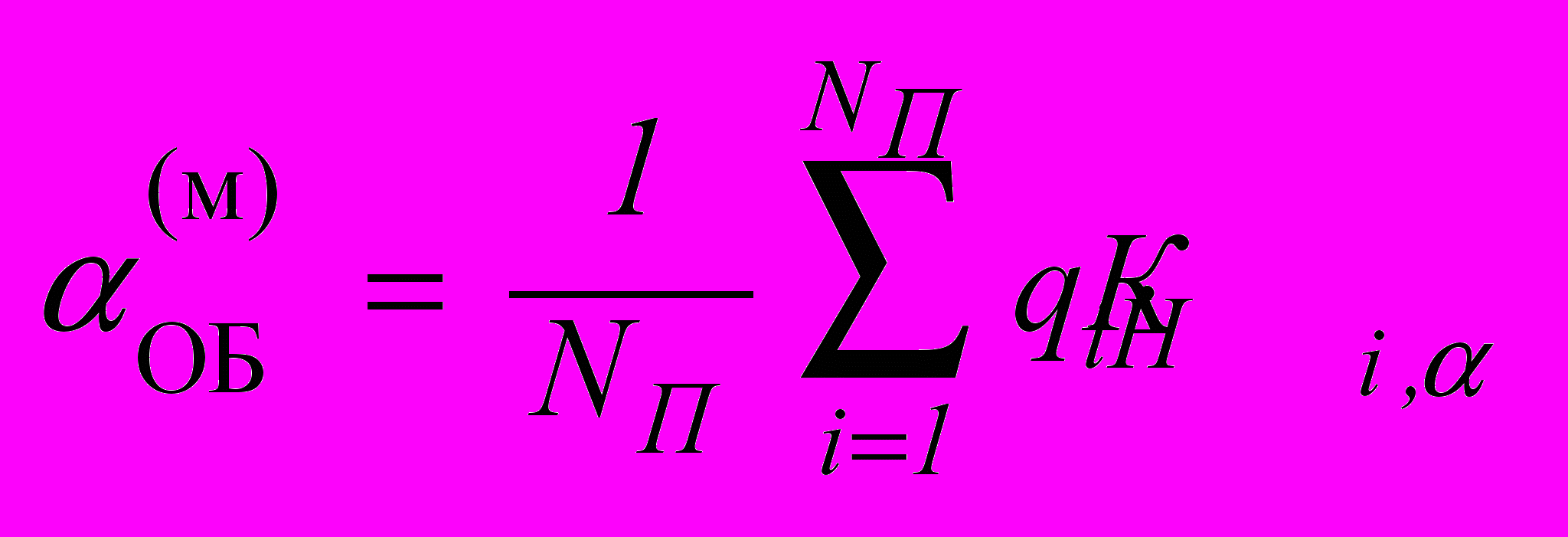(9)

где NП – число параметров; qi – весовой коэффициент параметра.

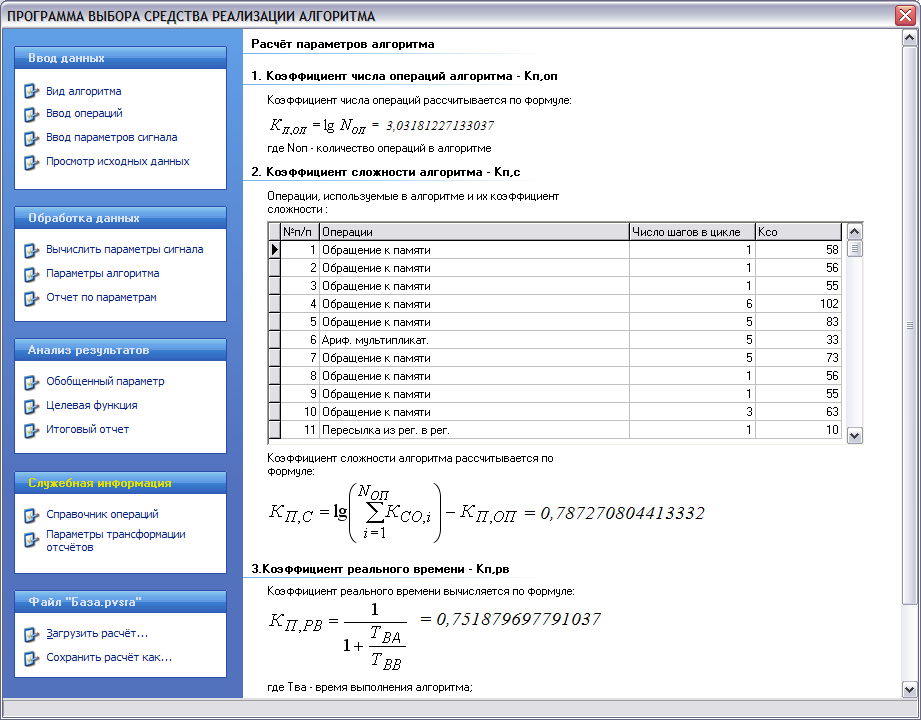
Обработка исходных данных и расчет частных параметров 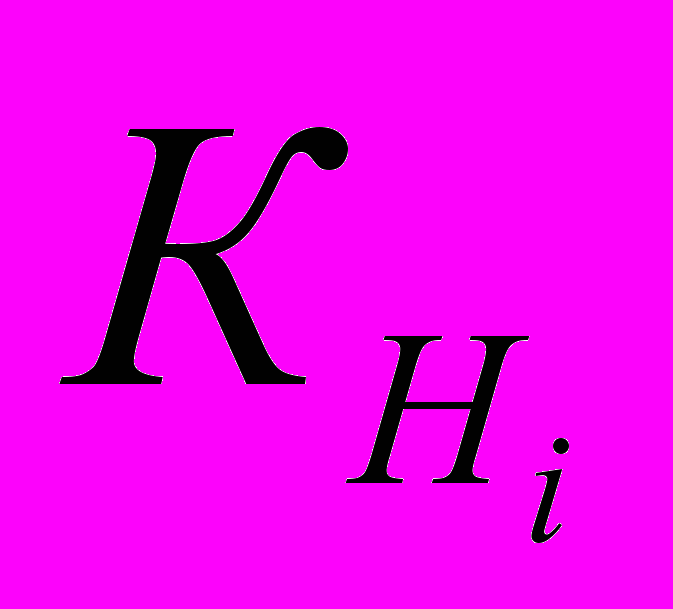представлен на рисунке 3.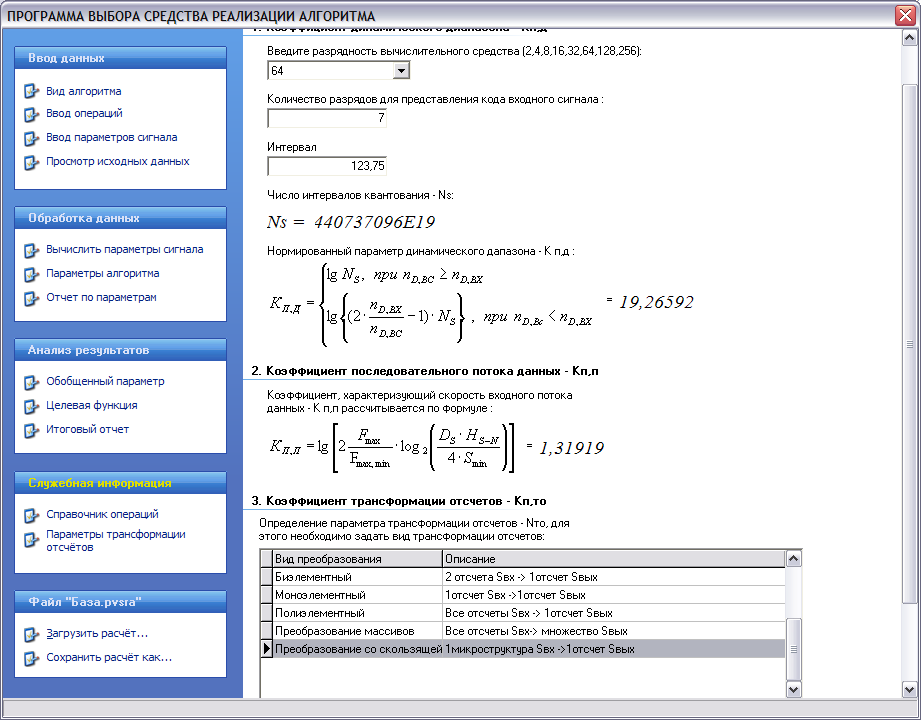



а) б)

Рисунок 3 – Экранные формы пункта «Обработка данных»: а) обработка параметров сигнала, б) обработка параметров алгоритма


Далее, согласно методу, аналитическое выражение целевой функции представлено в виде гладкой экспоненциальной функции:

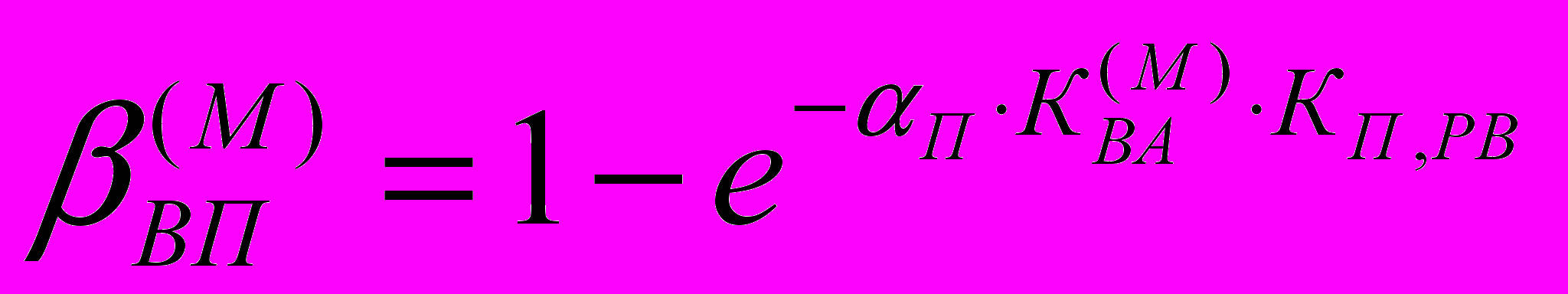(10)

Программная реализация целевой функции представлена на рисунке 4, на вкладке программы «Анализ результатов».



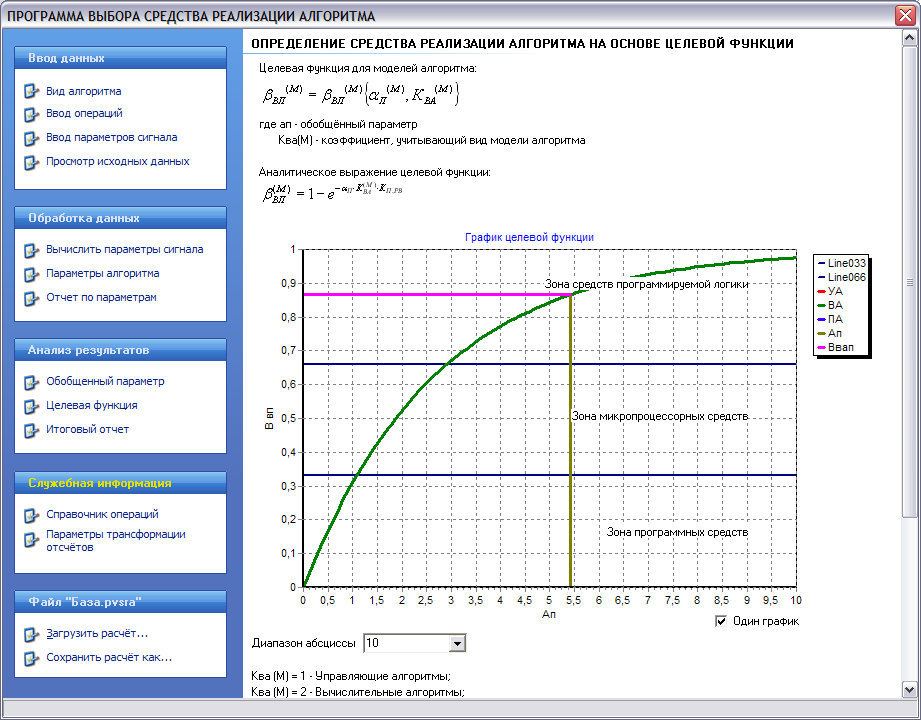
Рисунок 4 – Экранная форма формирования целевой функции


Работа программного средства СППР_МК представлена на рисунках 5, 6. Логическая структура программы следующая: на главной форме находятся шесть вкладок: «Исходные данные», «Анализ данных», «Целевая функция», «Отчет», «Справочник» и «Файл».

Исходные данные программы, а также формы ввода исходных данных аналогичны предыдущей. Обработка параметров алгоритма выполняется аналогично, а обработка параметров сигнала включает добавление параметров, влияющих непосредственно на выбор микроконтроллеров: производительность РМ, разрядность шины данных NШД, разрядность шины адреса NША, и внутренняя память программ микроконтроллера RМ.





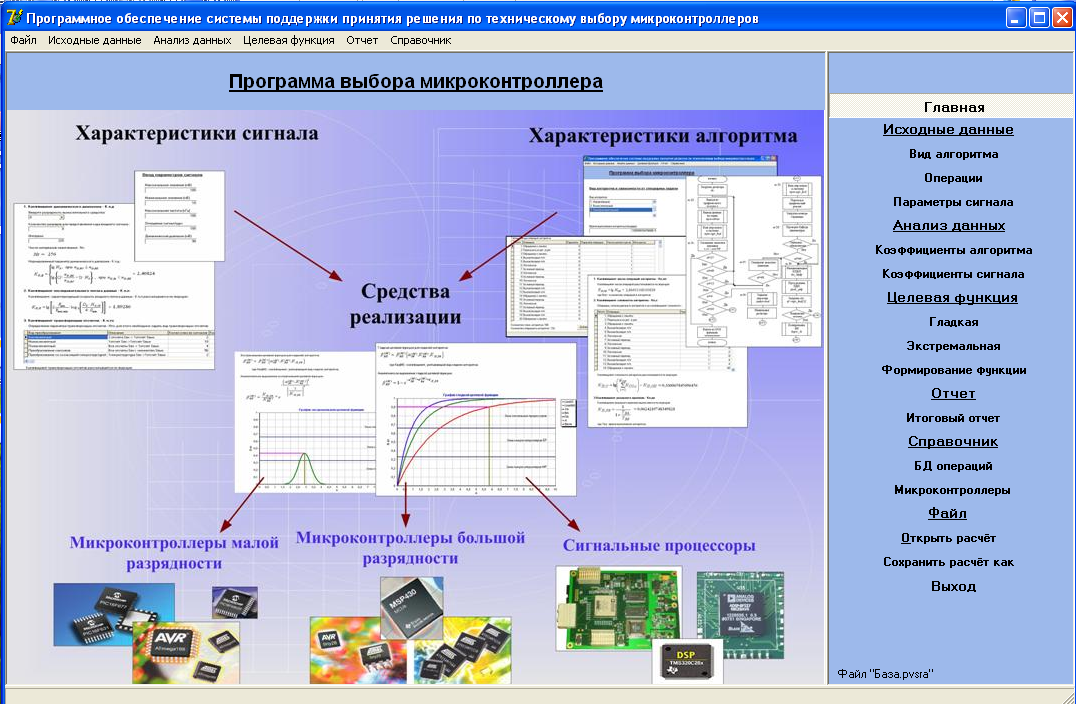
Рисунок 5 – Главная форма программы СППР_МК


Формирование целевой функции выполняется на вкладке «Целевая функция», где расположены три кнопки-навигатора: «Гладкая», «Экстремальная», «Формирование функции».

Нажатие кнопки «Гладкая», приводит к открытию формы расчета целевой функции с аналитическим выражением аналогичным в предыдущем ПС. Внешний вид формы изображен на рисунке 6 (а). Форма содержит расчет значения гладкой целевой функции для конкретного алгоритма, определяет средство его реализации и производит построение графика. Форма только отображает искомый результат, вводить данные не разрешается. Все исправления допускаются только во вкладке «Исходные данные».

Нажатие кнопки «Экстремальная», приводит к открытию форму, содержащую расчет значения экстремальной целевой функции конкретного алгоритма, определяется средство его реализации и производится построение графика. Внешний вид формы изображен на рисунке 6 (б).

Форма «Формирование функции» содержит сгруппированные нормированные коэффициенты сигнала и алгоритма.




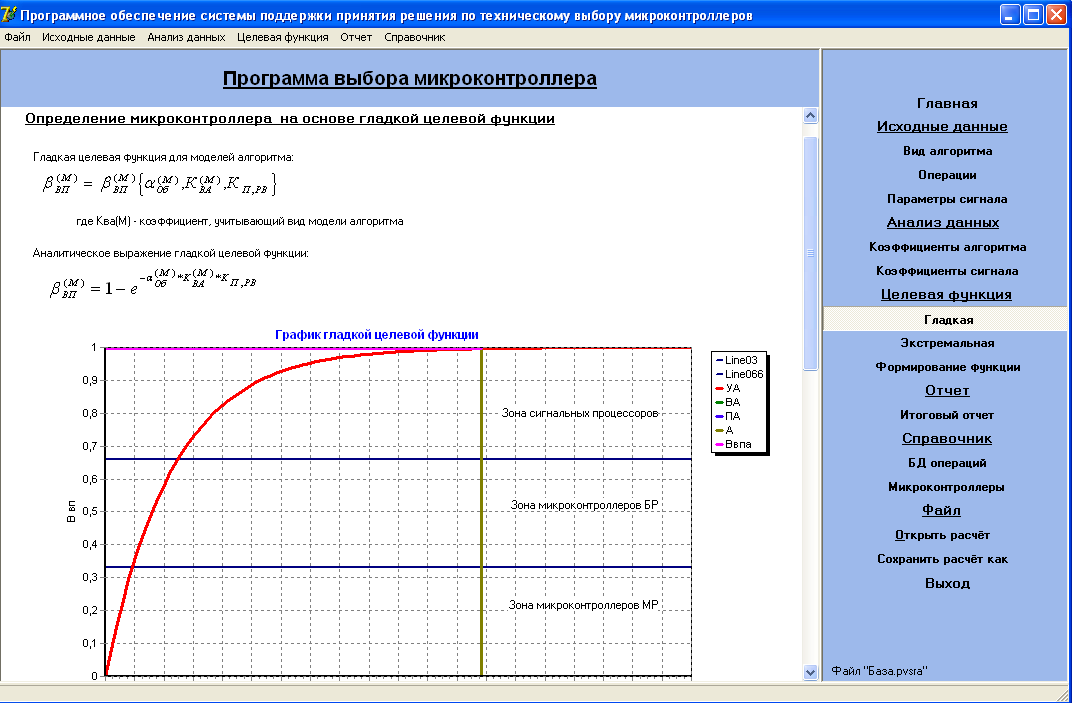
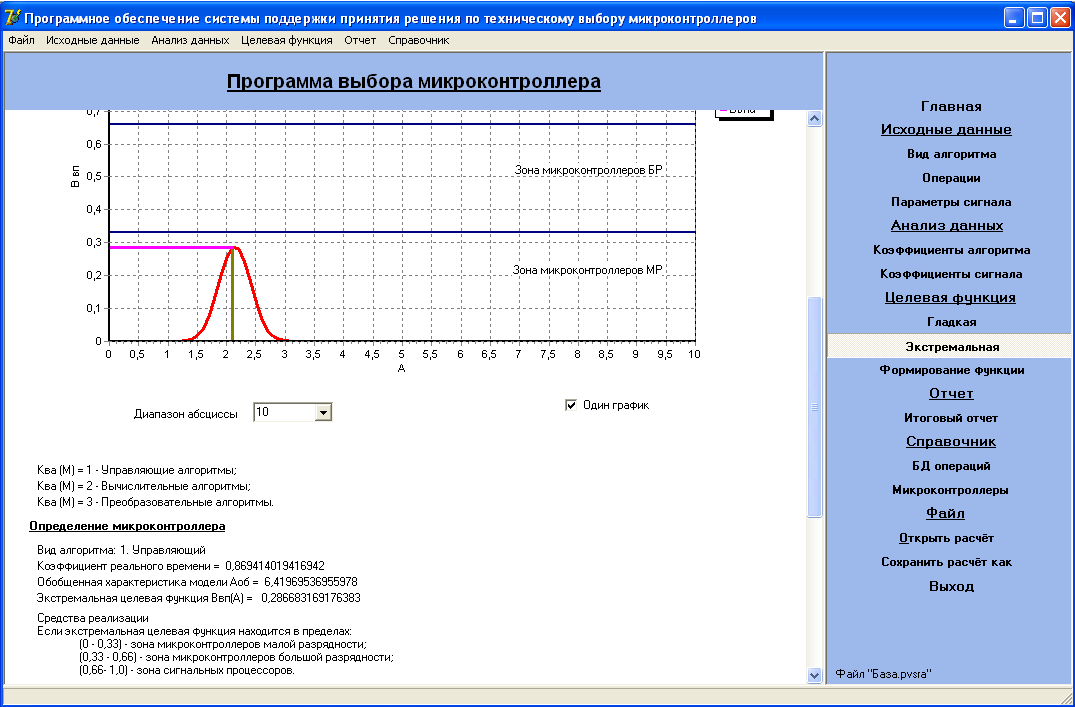
Рисунок 6 – Экранные формы: а) график гладкой целевой функции,

б) график экстремальной целевой функции


Процедура определения средства реализации алгоритма является зональной и представлена на рисунке 7.



Рисунок 7 - Определения средства реализации алгоритма


На вкладке «Справочник» находятся две кнопки: «БД операций» и «Микроконтроллеры». Кнопка «БД операций» позволяет вызывать и справочник операций, используемых в алгоритме.

Кнопка «Микроконтроллеры» вызывает форму, которая отображает БД микроконтроллеров с их характеристиками. Внешний вид формы изображен на рисунке 7.



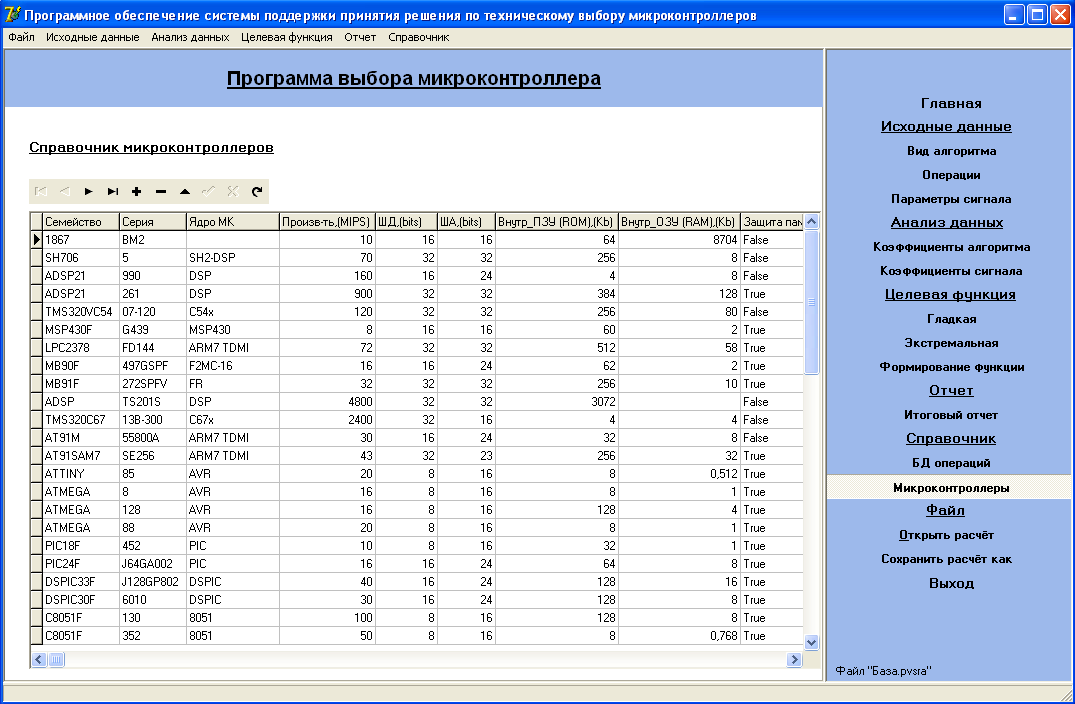
Рисунок 7 – Экранная форма БД «Микроконтроллеры»


Данный комплекс позволяет не только моделировать метод выбора средства реализации алгоритмов, но и исследовать зависимости весовых коэффициентов при формировании обобщенного параметра и выполнять оптимизацию целевой функции. Программный комплекс предполагается наполнять далее методами выбора и по другим средствам реализации.