Ю. В. Малышев Россия, Москва, зао "Главный Вычислительный Центр Интуриста" подход к декомпозиции функции ценности для принятия решения по выбору компьютерной сети и её компонентов доклад

Вид материала

Доклад

Подобный материал:

• К совещанию по экспертным организациям, 81.78kb.
• Лисанов М. В., д т. н., Зао «Научно-технический центр исследований промышленной безопасности»,, 92.54kb.
• «Направления использования служб сети Internet для решения информационных задач», 811.74kb.
• Федеральная налоговая служба главный научно – исследовательский вычислительный центр, 125.75kb.
• Eva2004 Москва Мониторинг икт в сфере культуры г. Москвы Н. В. Браккер, главный специалист, 124.82kb.
• Т. Н. Зайченко Россия, Томск, Томский государственный университет систем управления, 85.43kb.
• План Понятие компьютерной сети, функции, классификация. Топология локальной вычислительной, 64.86kb.
• России Москва Россия 11: 00 11: 40 Перспективы исследования маркеров повреждения мозга, 30.01kb.
• Уроку информатики и икт в 10 классе (базовый уровень) Тема урока: Локальные компьютерные, 139.48kb.
• Годовой отчет открытого акционерного общества «Научно-исследовательский информационный, 252.65kb.

Ю.В. Малышев

Россия, Москва, ЗАО "Главный Вычислительный Центр Интуриста"

ПОДХОД К ДЕКОМПОЗИЦИИ ФУНКЦИИ ЦЕННОСТИ
ДЛЯ ПРИНЯТИЯ РЕШЕНИЯ ПО ВЫБОРУ КОМПЬЮТЕРНОЙ СЕТИ И ЕЁ КОМПОНЕНТОВ

(Доклад)

Настоящее время характеризуется непрерывным развитием локальных вычислительных сетей (ЛВС), появляются всё новые технические разработки и требования пользователей. Поэтому сегодня актуальное значение имеет вопрос оценки качества проекта ЛВС и обоснования решения выбора рационального (а по возможности оптимального) варианта сетевого решения из определённого допустимого множества.

Необходимо отметить, что при сложности современных ЛВС, которую характеризуют многочисленные параметры, трудно дать достаточно быстрый и обоснованный ответ на этот вопрос. Пренебрежение им может способствовать появлению ошибок проектирования, цена исправления которых будет расти со временем разработки и эксплуатации, что может сделать из сети источник постоянных проблем и даже привести к краху всего сетевого проекта.

При построении однотипных сетей можно воспользоваться опытом разработок, измерениями на других сетях. Но об этом не приходится говорить, когда имеем дело с новыми техникой и задачами.

При разработке ЛВС производится анализ предъявляемых к ней требований, соответствующих её назначению, Результаты представляются в виде технических и экономических характеристик технического задания.

Используя эти характеристики, выявляется множество допустимых вариантов решений. Варианты оцениваются по соответствующим критериям и выбирается самый приемлемый рациональный (оптимальный) вариант, обязательно имеющий шансы быть реализованным. Если вариант нереально осуществить, то корректируются требования.

Оценка каждого варианта осуществляется по многим характеристикам ЛВС, некоторые достаточно важные из которых получаются с помощью имитационного моделирования работы рассматриваемого варианта проекта ЛВС, другие в результате автоматизированных расчётов и выявления предпочтений. По результатам выбора производится выработка рекомендаций по предстоящей разработке.

Оценка альтернативных вариантов производится с помощью функции ценности, выражающей результаты предпочтений и расчётов, то есть наиболее существенную информацию о проблеме. Для рассмотрения проблемы в целом формируется иерархия целей, выражающих критерии. Каждому критерию (показателю) ставится в соответствие вес, отражающий степень важности. Однако, число таких показателей может быть достаточно большим и превышать возможности человека воспринимать проблему в полном масштабе. Поэтому обычно производится декомпозиция с помощью традиционного метода анализа иерархий (МАИ) на основе иерархического разделения групп показателей (элементов группы) на подгруппы и определяются отношения между весами элементов.

Пусть в нашей задаче оптимизации существуют критерии C_i, при i=1..n, их вес задаётся компонентами нормированного вектора w=(w₁,w₂,…,w_n) (табл.1). Критерии C_i определяют координатные оси пространства Rⁿ, которое включает область определения D функции ценности v. Вектор x=(x₁,x₂,…x_i,..,x_n), где x_i представляет i-ый критерий. Каждый вариант решения представляется нормированным вектором P_j=(p_1j…p_nj) из D, при j=1..m.

Таблица 1.

критерии	вес критерия	варианты решений
		1	2	…	m
C1	w1	p11	p12	…	p1m
C2	w2	p21	p22	..	p2m
…	…	…	…	…	…
Cn	wn	pn1	pn2	…	pnm

Таким образом, получается множество решений (табл.2).

Таблица 2.

	x1	x2	…	xn
p1	p11	p12	…	p1n
p2	p21	p11	…	p2n
…	…	…	…	…
pm	pm1	pm2	…	pmn

Производится преобразование координат:




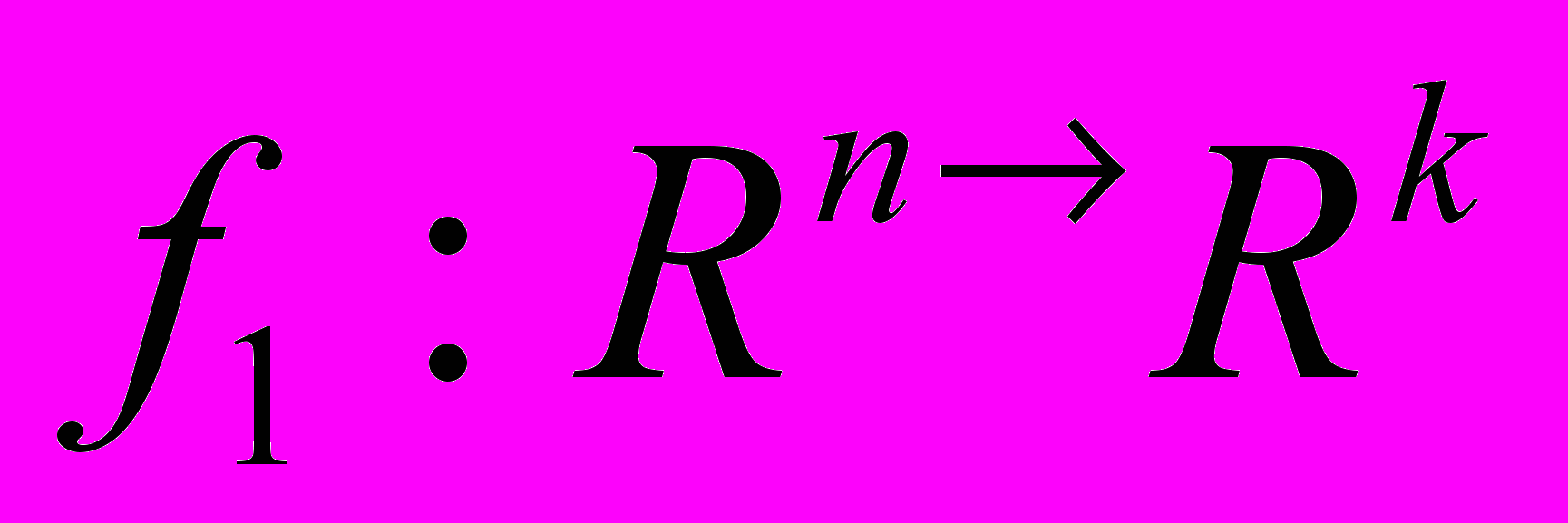
Т
огда функцию ценности можно представить как:

При этом производится декомпозиция k критериев на n подкритериев. Подобную иерархическую декомпозицию можно производить и далее:





Н
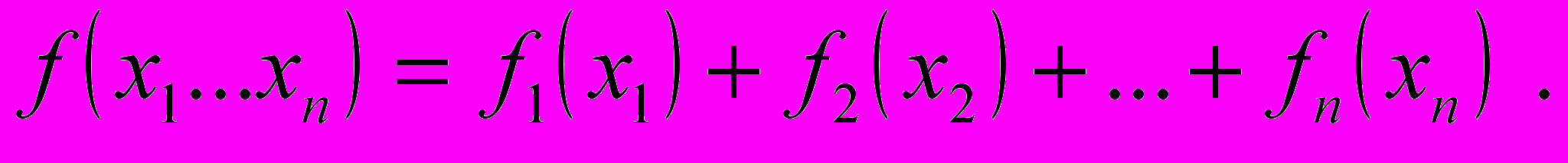
а каждом уровне декомпозиции существуют свои критерии и их веса. По ним строятся функции ценности соответствующих уровней. В нашем случае функцию fi, i=1..s, представляем в аддитивном виде:


Для традиционного подхода МАИ функция ценности имеет вид:




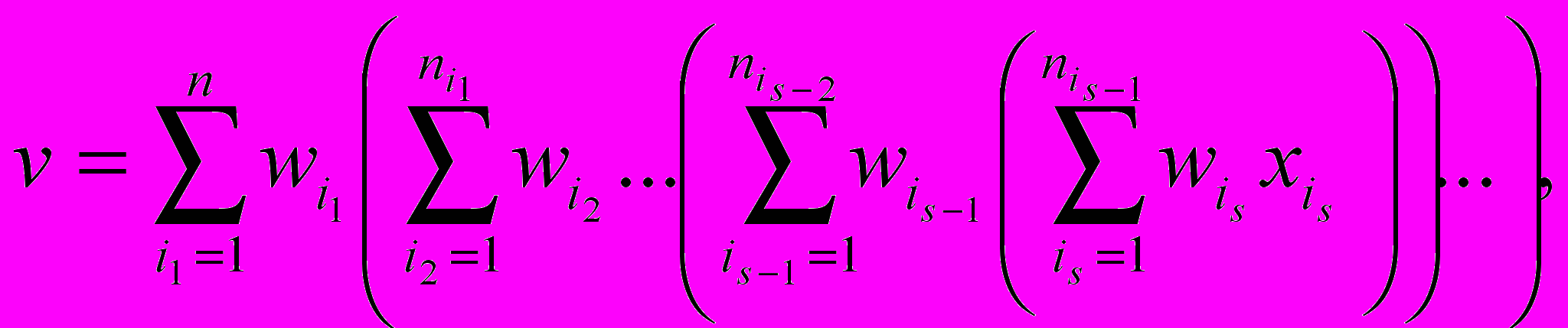
г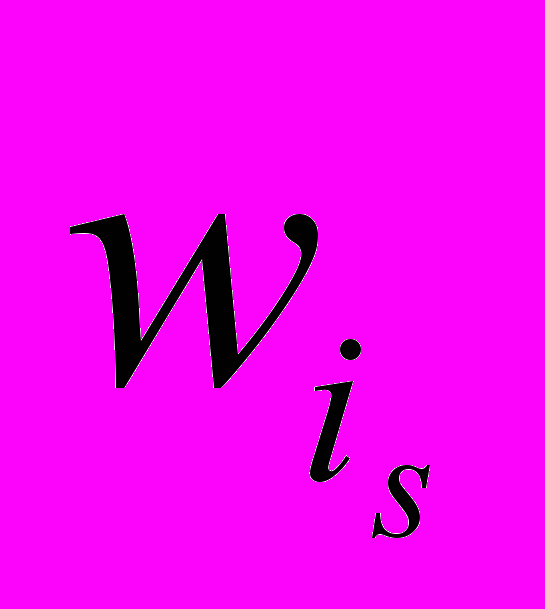де - вес i-ого критерия s-ого уровня декомпозиции;

• з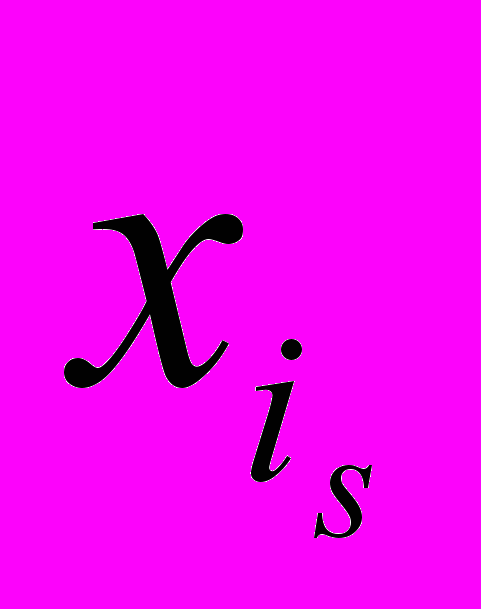начение i-ого критерия s-ого уровня декомпозиции.
  

Для такого синтеза функции ценности необходимо знать веса элементов. Применение МАИ позволяет найти веса по суждениям (отношениям весов). При этом рассматривается матрица суждений из элементов w_i/w_j, где i=1..n, j=1..n. Задаётся матрица возмущений суждений А, состоящая из элементов a_ij, где i=1..n, j=1..n . В идеальном случае a_ij = w_i/w_j и a_ij=1/ a_ij , рассматривается согласованная матрица А. Пусть a_ij = w_i/w_j , тогда w_i = a_ijw_j , где i=1..n, j=1..n . Можем записать:



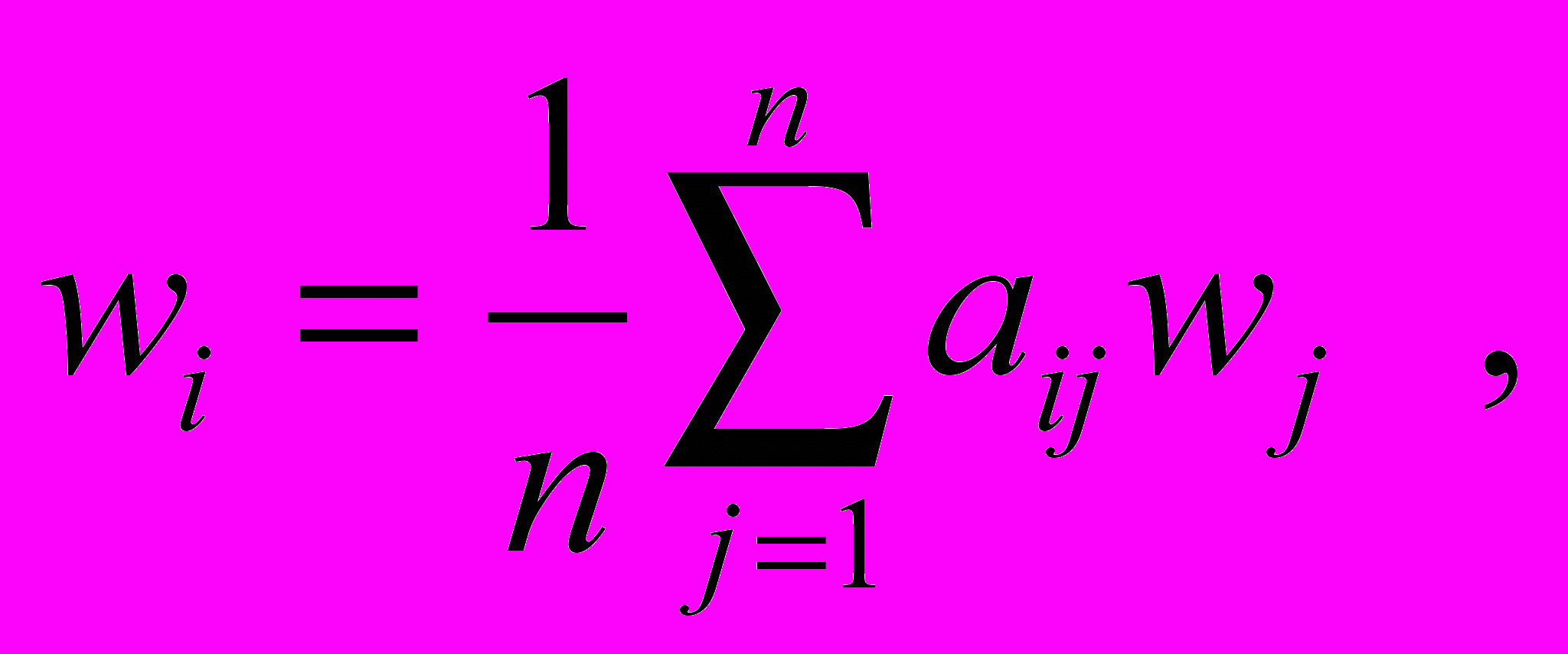
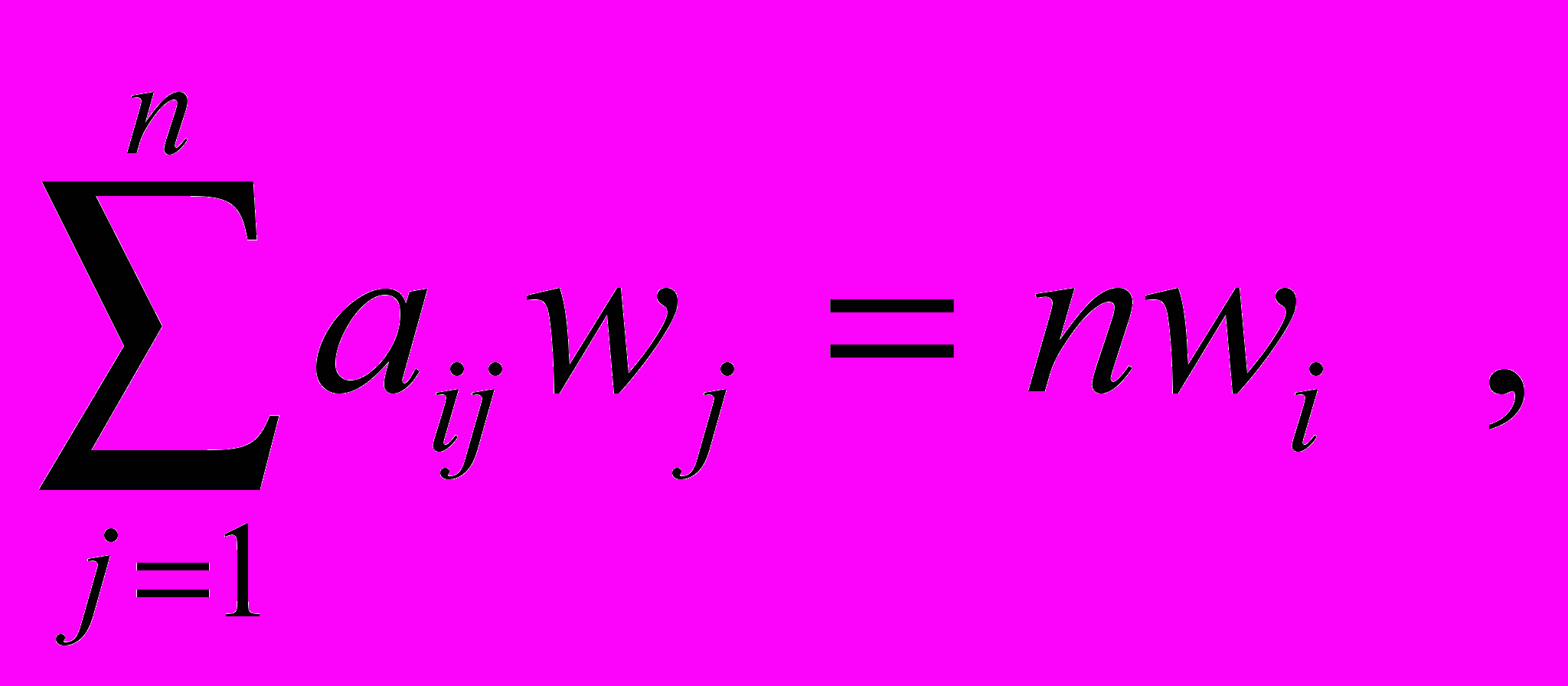
где i=1..n .


При переходе к матричному виду, получается Aw=nw, где w=(w₁,w₂,…,w_n) является собственным вектором (с.в.) матрицы А, n - собственным значением (с.з.) А.

Д
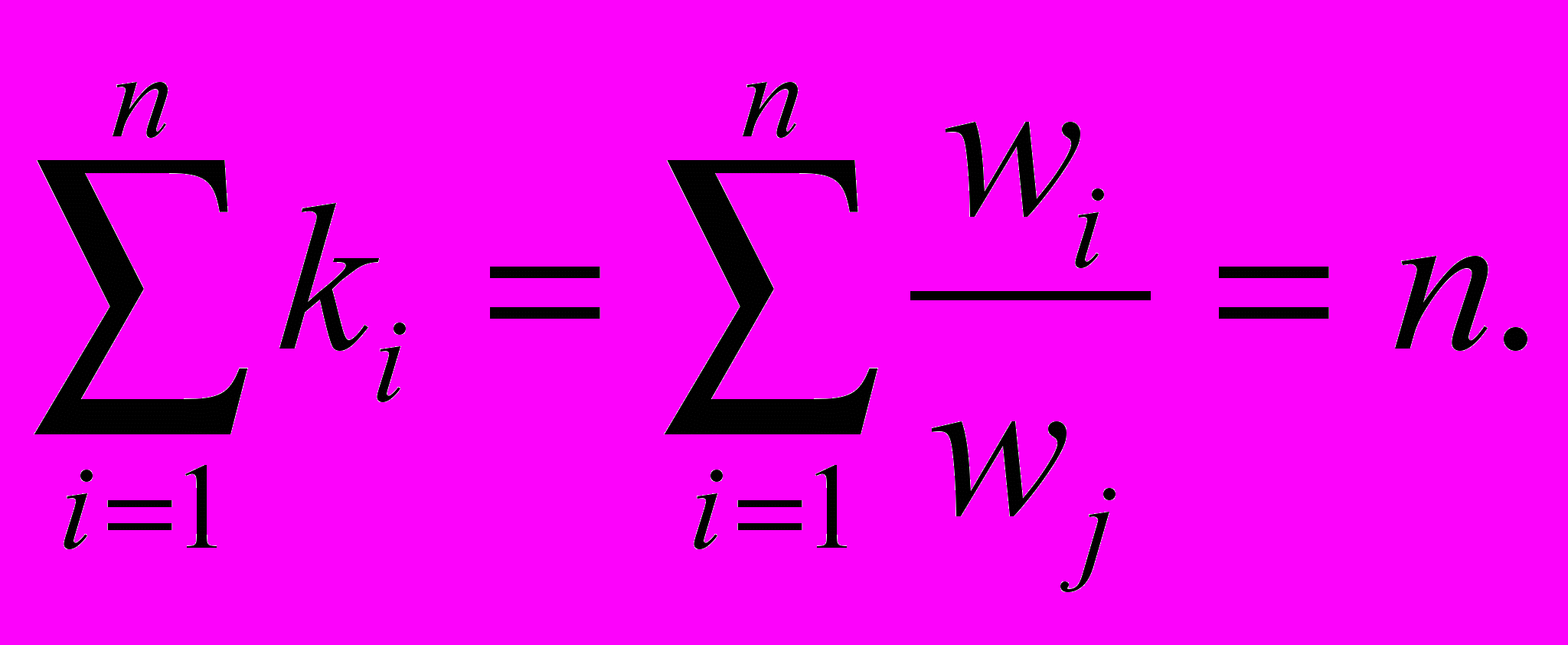
алее используются следующие два математические факта. Первый, что если k_i - с.з. А, где i=1..n, то

Следовательно, для матрицы А с.з. k₁=n, k_i=0, при i=2..n . Второй факт, что так как матрица А положительная обратносимметрическая, то при незначительных изменениях элементов a_i собственные значения изменяются незначительно, причём наибольшее из них k_max остаётся близким к n, а наименьшие - близким к нулю. Для несогласованной А выполняется уравнение: Aw=k_maxw. Можно определить степень её несогласованности по индексу согласованности K:




Значение К 0,1 считается приемлемым.

Однако, существуют случаи, что отмечено в литературе, где невозможно использовать МАИ, в частности из-за того, что он даёт некорректные результаты. Например, в случае построения функции ценности, предлагаемая традиционным подходом схема является применимой, но не вполне корректной. Она неприемлема для нашего случая, так как вес элемента подчинённой группы иерархии существенно зависит как от веса вышестоящего элемента, так и числа самих элементов в подчинённой группе.

Для устранения некорректности и тем самым разрешения проблемы используется следующий подход. Производится иерархическая декомпозиция групп элементов (то есть показателей) на n уровней. В каждой группе k-ого уровня, где k=1..n-1, для каждого элемента выбирается элемент его подчинённой группы k+1-ого уровня с максимальным в ней весом, (т.е. суждением равным 1, о вычислении которого см. далее) и присваивается суждение - отношение веса его выбранного элемента k+1-ого уровня к наибольшему весу среди так же выбранных элементов k+1-ого уровня для другого элемента из той же группы k-ого уровня. Суждение будет меньше или равно 1, если веса не равные, и равно 1, если веса равные. Считается, что на нижнем n-ом уровне у каждого элемента может быть подгруппа уровня k=n+1, состоящая из одного элемента k=n+1 уровня. Его вес считается максимальным в подгруппе (т.к. никакого другого элемента с большим весом в этой группе нет), а суждение равным 1. Элемент разделяется как бы сам на себя и суждение на n-ом уровне есть отношение веса элемента n-ого уровня к наибольшему весу среди элементов той же группы n-ого уровня. Возможно использовать вместо максимальных минимальные веса, но так как у нас элементами являются показатели эффективности, то естественно рассматривать сначала важнейшие и вести декомпозицию по отношению к их (т.е. максимальным) весам. При поэтапной декомпозиции сверху вниз, начиная с первого уровня, рассматриваемый подуровень считаем последним на каждом этапе декомпозиции. То есть показатель ассоциируется в первую очередь с самым главным показателем подчинённой группы.

Таким образом, связь между группами осуществляется не на базе весов элементов, а на базе суждений, причём основополагающими выступают суждения об отношениях весов максимальных по весу элементов подгрупп к максимальному среди них весу. Именно они нас интересуют в вычислениях. Функцию ценности можно строить по схеме МАИ, однако следует использовать не веса элементов, а рассмотренные выше суждения. Следует также отметить, что для вычисления средних весов элементов в пределах группы можно использовать и матрицу суждений МАИ. Однако, если случай идеальный, матрица согласованная (причём это положение является довольно естественным и его не трудно достигнуть), то веса можно рассчитывать по суждениям подхода на основе максимальных весов элементов (это столбец с наименьшими элементами в матрице суждений МАИ), и нет необходимости вычислять с. в. матрицы. Среднее отношение можно получить как среднее арифметическое частных деления строки матрицы суждений на максимальную строку, средний вес - нормированием отношений.

Рассмотренный подход имеет важное практическое значение и может использоваться не только для построения функции ценности для выбора приемлемого варианта структуры ЛВС, но и в других областях исследований.

Литература

1. Саати Т. Принятие решений. Метод анализа иерархий. М.: Радио и связь, 1993.
   
2. Barzilai J. On the decomposition of value functions. Operations Research Letters 22 (1998), pp. 159-170.
   
3. Трахтенгерц Э.А. Компьютерная поддержка принятия решений. М.:СИНТЕГ, 1998.