Методические рекомендации по исследованию строительных конструкций с применением математического и физического моделирования  

Вид материала

Методические рекомендации

Содержание Приложение 4примеры применения ФУНКЦИОНАЛЬНОго модЕЛирования Рис. 1. Расчетная схема стены блока-контейнера Рис. 3. Влияние стеновых панелей на деформативность блока-контейнера Исследования каркаса здания межвидового применения серии Т.020-1/83 Рис. 4. Декомпозиция каркаса многоэтажного здания Рис. 5. Горная панель градирни а - общий вид; б - расчетная схема

Подобный материал:

• Программа курса «Основы математического моделирования» Осень 2007, 25.35kb.
• Аннотация дисциплины «основы математического моделирования», 29.01kb.
• Дефекты изготовления и монтажа строительных конструкций и их последствия, 779.7kb.
• Курс «Основы математического моделирования» реализуется в рамках специальностей 0647, 117.15kb.
• Авдейчиков Г. В. «Испытание строительных конструкций»: Учебное пособие (конспект лекций), 159.67kb.
• Задачи : 1 дать понятие математической модели, раскрыть суть метода математического, 187.03kb.
• Iii международный симпозиум актуальные проблемы компьютерного моделирования конструкций, 77.34kb.
• Пособие по обследованию строительных конструкций зданий, 3072.33kb.
• «Универсальная 32-битная среда для расчета и проектирования строительных конструкций, 23.4kb.
• Вид работ №30 «Монтаж, демонтаж строительных конструкций в подводных условиях», 16.72kb.

Приложение 4
примеры применения ФУНКЦИОНАЛЬНОго модЕЛирования

Исследование блоков-контейнеров

В 1984 - 1985 гг. были проведены комплексные исследования прочности и жесткости базового блока-контейнера, разработанного НИИСК Госстроя СССР, с целью:

разработки расчетной модели блока-контейнера, учитывающей совместную работу элементов каркаса и ограждающих конструкций;

проверки прочности и деформативности. основных несущих элементов отдельного блока и контейнера при действии расчетных нагрузок;

определения внутренних усилий в элементах каркаса от расчетных сочетаний нагрузок при различных конструктивных схемах зданий, собираемых из блоков-контейнеров.

Для решения поставленных задач был использован системный подход, так как применение только экспериментального либо теоретического метода не представлялось возможным из-за чрезвычайно большого объема экспериментов в первом случае и отсутствия достоверной расчетное модели - во втором. Исходя из поставленных целей, исследования проводились в три этапа:

этап I - предварительные численные исследования для получения зависимостей параметров напряженно-деформированного состояния y_i в характерных точках блока-контейнера от неизвестных характеристик расчетной модели x_i типа:

yi = fj(xi)(i = 1, 2,…, n; j = 1, 2,..., m);

(1)

этап II - экспериментальные исследования блока-контейнера при действии расчетных и контрольных нагрузок, определение неизвестных параметров расчетной модели и проверка ее адекватности;

этап III - численные исследования различных типов зданий, собираемых из блоков-контейнеров, для получения расчетных значений внутренних усилий; в элементах.

Численные исследования выполнялись на ЭВМ EC-1030 с применением расчетного комплекса "ПРОКРУСТ". При этом расчетная схема блока-контейнера представляла собой пространственную пластинчато-стержневую систему. Стержни расчетной схемы, элементы каркаса задавались по геометрическим осям и с соответствующими жесткостными характеристиками. Плоскостные элементы - панели стен, пола и потолка - задавались как совокупности прямоугольных плоско-напряженных КЭ с приведенными характеристиками: коэффициент Пуассона υ, модуль упругости Е и толщина t. Соединения ограждающих стеновых панелей с элементами каркаса аппроксимированы в расчетной схеме контактными элементами с неизвестными жесткостями на сдвиг - К_τ, и на растяжение-сжатие К_σ (рис. 1).



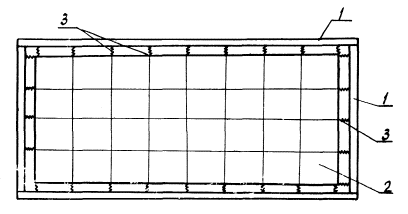
Рис. 1. Расчетная схема стены блока-контейнера

1 - каркас блока - стержневые элементы; 2 - ограждающая конструкция - плоские КЭ; 3 - связь - контактные элементы





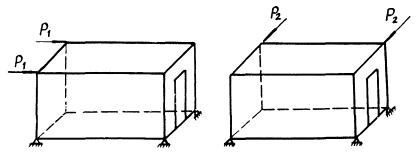
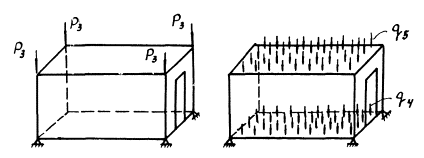
Рис. 2. Схема нагружения блока-контейнера

Для получения уравнений (1) использована матрица планирования типа 2² (см. приложение 1) и формулы (12) настоящих методических рекомендаций. Для получения линейных зависимостей перемещений от жесткостей связей в качестве неизвестных приняты не жесткости связей, а величины им обратные: ; .

При варьировании жесткостей связей принимались уровни K_σmax = K_τmax = 10000 кН/м; K_σmin = K_τmin = 100 кН/м. При выборе вариантов нагружений и характерных параметров напряженно-деформированного состояния блока учитывалось максимальное включение в работу стеновых панелей:

перемещение верхних углов блока вдоль приложенных к ним горизонтальных сил Y⁽²⁾;

прогиб середины продольного элемента панели основания от равномерно распределенной нагрузки на пол Z⁽⁴⁾.

В результате обработки численных экспериментов после отбрасывания малозначимых членов взаимодействий получаем систему уравнений:

(2)

Экспериментальные исследования блока-контейнера были выполнены на натурном образце, изготовленном на заводе и доставленном в НИИСК по железной дороге. Блок испытывался на следующие виды воздействий (рис. 2):

горизонтальная нагрузка, приложенная к верхним углам блока, направленная вдоль длинных Р⁽¹⁾ и коротких Р⁽²⁾ сторон;

вертикальная нагрузка, приложенная к верхним углам блока, - Р⁽³⁾;

равномерно распределенная нагрузка на основание - q⁽⁴⁾;

то же, плюс равномерно распределенная нагрузка на пол - q⁽⁵⁾.

Нагрузки P⁽¹⁾, P⁽²⁾, P⁽³⁾ достигали своих расчетных, а нагрузки q⁽⁴⁾ и q⁽⁵⁾ контрольных значений. Во время эксперимента измерялись перемещения углов и середин ребер блока, а также деформации в наиболее напряженных сечениях элементов каркаса.

При всех схемах нагружения, вплоть до расчетных величин нагрузок, нарастание перемещений в характерных точках было пропорционально росту нагрузки, что свидетельствовало об упругом характере работы конструкции.

Подставив в уравнения (2) экспериментальные значения перемещений - соответственно  - 1,15 мм и  - 5,0 мм, решив их, после соответствующих преобразований получим реальные значения жесткостей связей: K_σ = 900 кН/м; К_τ = 2500 кН/м.

Как показали экспериментальные исследования, стеновые панели, включаясь в работу, существенно разгружают элементы каркаса.

После определения всех неизвестных параметров расчетной модели были проведены численные исследования блока-контейнера.

Сначала исследовалось влияние на напряженно-деформированное состояние элементов каркаса возможных технологических дефектов при реальном осуществлении соединений с элементами каркаса.

Были рассмотрены следующие варианты: связи работают на растяжение и сдвиг; связи работают только на растяжение; связи работают только на сдвиг; связи отсутствуют.

Исследования показали, что качество выполнения связей существенно влияет на напряженно-деформированное состояние элементов каркаса, особенно стоек. При отсутствии связей или при выполнении их с отклонениями от проекта напряжения в элементах каркаса и перемещения существенно возрастают (рис. 3) и в ряде сечений могут превзойти допустимые значения.



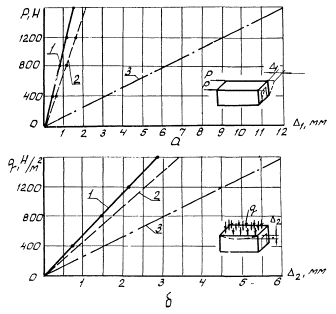
Рис. 3. Влияние стеновых панелей на деформативность блока-контейнера

а - горизонтальная нагрузка; б - вертикальная нагрузка; 1 - эксперимент; 2 - расчет с учетом стеновых панелей; 3 - то же, без учета

Исследовалось также напряженно-деформированное состояние несущих элементов каркаса в зависимости от расположения данного блока в двухэтажном здании, в том числе рассматривались варианты удаления стен (продольных или торцовых) двух смежных блоков. Анализ результатов исследований показал, что из блок-контейнеров данной конструкции можно собирать двухэтажные здания. Причем могут быть применены различные объемно-планировочные решения, в том числе и с удалением двух смежных стен.

Уточнение расчетной модели с включением в работу стен позволило улучшить его технико-экономические показатели, расход металла на блок уменьшился на 140 кг. С учетом наших рекомендаций внесены коррективы в рабочие чертежи и изготовлен по ним экспериментальный блок-контейнер. Испытания облегченного блока контрольными нагрузками подтвердили правильность принятых конструктивных решении.

Исследования каркаса здания межвидового применения серии Т.020-1/83

Каркасы межвидового применения серии 1.020-1/83 предназначены для широкой номенклатуры зданий различного назначения, что обусловливает многообразие конструктивных схем, воздействий и т.д. В этой связи для рационального проектирования конструкций необходимо разработать такие расчетные модели, которые позволяли бы достоверно определять параметры напряженно-деформированного состояния элементов и, в частности, крайних ригелей, как наиболее сложно напряженной конструкции, с учетом их реальной работы в составе диска перекрытия.

Цель исследований:

совершенствование расчетной модели крайних ригелей с учетом их пространственной работы в составе диска перекрытия;

проверка правильности конструктивных решений опирания однополочных ригелей с подрезкой;

исследование влияния на напряженно-деформированное состояние крайних (однополочных) ригелей изменения конструктивных схем здания, характера нагрузок, жесткостей элементов, возможных несовершенств строительного производства, а также ряда других факторов, возникающих в процессе монтажа и эксплуатации здания.

Для решения поставленных задач была использована методика, основанная на системном анализе и функциональном моделировании, в соответствии с положениями которой процесс исследования был разбит на ряд последовательных этапов:

I - разработка расчетной модели каркаса малоэтажного здания, учитывающей факторы, влияющие на напряженно-деформированное состояние элементов (однополочных ригелей);

II - выявление неизвестных параметров расчетной модели и проведение предварительных численных исследований для получения уравнений типа (I);

III - проведение физических экспериментов для получения данных, необходимых для определения неизвестных параметров расчетной модели и проверки ее адекватности;

IV - уточнение расчетной модели и выполнение многовариантных расчетов - численных экспериментов - в необходимом объеме.

Анализ проведенных ранее исследований показал, что расчетная модель однополочного ригеля должна учитывать следующие обстоятельства: пространственную работу; податливость крепления ригеля к колонне; совместную работу ригеля и плит; влияние замоноличивания швов между плитами; возникновение распора в плитах и ригелях; изменение жесткостных характеристик элементов при увеличении нагрузки. Вместе с тем, результат расчета должен быть получен в виде, удобном для проектирования элементов, а сама расчетная модель должна быть четкой, удобной в работе.

С учетом вышеизложенного расчетная схема каркаса с плитами была принята в виде пространственной стержневой системы, в которой основные элементы каркаса (колонны, ригели, плиты) аппроксимированы стержневыми КЭ, оси которых совпадают с физическими осями элементов, а задание реальных расстояний между точками соединения элементов моделируется стержневыми элементами бесконечной жесткости. Соединения ригеля с плитами и плит между собой аппроксимированы дискретными связями (контактными элементами), не имеющими линейных размеров, но обладающими определенной жесткостью на растяжение (сжатие) и сдвиг.

Реализация расчетной схемы выполнена с применением программного комплекса "ПРОКРУСТ" на ЭВМ EC-1030.

Рассмотренная расчетная схема имеет десять неизвестных параметров: жесткость ригеля при изгибе в вертикальной , и горизонтальной  плоскости; жесткость ригеля на кручение D_P; жесткость соединения ригеля с колонной на кручение ; жесткость соединения ригеля с колонной при изгибе в горизонтальной плоскости ; жесткость плиты при изгибе ; жесткость плиты на кручение D_П; высота опорного стержня плиты, определившая наличие распора, h; сдвиговая жесткость шва между плитами и ригелем К_Р.П; то же, между плитами К_П. Таким образом, число уравнений, в системе (1) должно быть не менее десяти.

Поскольку основными параметрами входящими в левые части уравнений (1), будут измеренные в эксперименте перемещения, для получения линейных зависимостей необходимо перейти к новым неизвестным параметрам расчетной модели:





Для упрощения процесса определения неизвестных параметров расчетной модели x_i; (i = 1. 2,…, 10) был применен принцип декомпозиции сложной системы (каркаса) на более простые подсистемы - ригели с опорными узлами и плиты. С учетом этого (1) распалось на шесть независимых систем и отдельных уравнений.

Подсистема - ригель - при действии вертикальной нагрузки:

	(3)
	(4)

Подсистема - плита:

	(5)
	(6)

Подсистема - швы:

(7)

где y_j - параметры напряженно-деформированного состояния конструкций; у₁ - вертикальный прогиб по средине ригеля; у₂ - угол кручения среднего сечения ригеля; у₃ - тоже, опорного; y₄ - горизонтальный прогиб на средине ригеля; y₅ - угол поворота в горизонтальной плоскости опорного сечения ригеля; y₆ - прогиб плиты при шарнирном опирании; y₇ - угол кручения по средине плиты; y₈ - прогиб плиты при реальном опирании; y₉ - прогиб середины ригеля в составе диска перекрытия; y₁₀ - разность вертикальных смещений ребер двух смежных плит; в_ij коэффициенты уравнений регрессии, полученные методом планирования экспериментов в соответствии с матрицами планирования (см. приложение 1).

Для экспериментального определения перемещений y_j были проведены испытания физических моделей со смешанным подобием: простое по отношению к неизвестным параметрам x_i, и функциональное по отношению к остальным.

В соответствии с декомпозицией каркаса на подсистемы были испытаны модели:

ригелей на действие вертикальных и горизонтальных нагрузок (рис. 4,а);

плит при двух вариантах опирания (рис. 4,б);

фрагмента многоэтажного здания (рис. 4,в);

На основании анализа рабочих чертежей ригелей и плит, исходя из сортамента арматуры классов А-III и А-IV, принят масштаб моделирования C_l = 0,5.

Измеренные в эксперименте перемещения  при действии указанных нагрузок подставлялись в соответствующие уравнения (3) - (7), из решения которых определялись неизвестные параметры расчетной модели x_i. Причем, в зависимости от стадии работы конструкции, при которой измерялись перемещения у_j, пара метры x_i были определены для упругой стадии при действии нормативных и расчетных нагрузок и в стадии, близкой к разрушению. Так, например, при действии расчетных нагрузок были определены следующие значения неизвестных параметров в пересчете на натуру в соответствии с масштабами подобия:  = 56000 кН м²;  = 58000 кН м²; D_P = 37000 кН м²;  = 640 кН м²;  = 2100 кН/м²;  = 30000 кН м²; D_П = 31000 кН м²; h = 9 см; К_РП = 18 106 кН; К_П = 13,2·10⁵ кН.

Кроме указанных вариантов испытаний, модель фрагмента испытывалась равномерно распределенной нагрузкой вплоть до разрушения.

После определения неизвестных параметров были выполнены расчеты модели фрагмента и проверена адекватность расчетной модели, которая показала достоверность разработанной расчетной модели.

На отлаженной расчетной модели были выполнены численные исследования и оценено влияние ряда факторов (отклонения в жесткостных характеристиках элементов, изменение высоты этажа, изменение граничных условий, качество замоноличивания, стыков и т.д.) на напряженно-деформированное состояние каркаса здания межвидового применения.



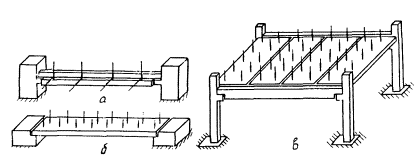
Рис. 4. Декомпозиция каркаса многоэтажного здания

а - подсистема "ригель"; б - подсистема "плита"; в - подсистема "швы"

Исследование панели сборной железобетонной градирни на транспортные нагрузки

Целью исследований было определение оптимального расположения опор на транспортном средстве, обеспечивающем трещиностойкость панелей при перевозке.

По данной методике выполнялись исследований с применением методов математического и физического моделирования следующими этапами: экспериментальные исследования на физической модели, выбор и определение неизвестных параметров расчетной модели, проверка адекватности расчетной модели, численные исследования.

Физическое моделирование осуществлялось на модели из упругого материала, так как при транспортировании возникновение трещин в панелях не допускается. Согласно заданной схеме опирания конструкции в процессе перевозки (рис. 5) в ее элементах возникают, в основном, продольные напряжения, что дает возможность при моделировании не учитывать различие коэффициентов Пуассона материалов модели и натуры. С учетом условия подобия запишем:

(8)

где С_и, С_Е, С_l, С_Р, С_σ, С_М - масштабы соответственно перемещений, модуля упругости, геометрических размеров, нагрузки, напряжений, изгибающих моментов. Поскольку масштабов шесть, а равенств в системе (8) имеем три, то тремя масштабами С_l, С_Е, С_Р, можем задаваться произвольно.

Исходя из технологических условий принимаем С_l = 0,05. Материал модели - эпоксидная смола ЭД-16М, следовательно, С_Е =  = 0,103. Для удобства нагружения принимаем С_Р = 0,0032.

Подставив принятые, значения С_l, С_Е, С_Р в систему (8), получим: С_и = 0,62; С_σ = 1,28; С_М = 1,6·10^-4.

Для изготовления модели применена технология точного литья в размываемые формы.

При экспериментальных исследованиях измерялись прогибы панели в узлах, а также фибровые деформации ребер и поля панели. Значения средних и доверительных оценок результатов прямых измерений прогибов и деформаций определялись по формулам (2).

Определение неизвестных параметров математической модели при транспортировке в горизонтальном положении, когда направление транспортных нагрузок перпендикулярно плоскости панели, выполняется при условии следующих допущений: нагрузка прикладывается в узлах пересечения ребер и воспринимается, в основном, ребрами, так как их жесткость на порядок выше жесткости поля панели. Таким образом, расчетная схема панели представляется в виде стержневой системы, у которой оси стержней совпадают с физическими осями ребер (см. рис. 5). Часть исходных данных известна (координаты узлов, нагрузка). Не известны жесткостные характеристики приведенного сечения ребер.



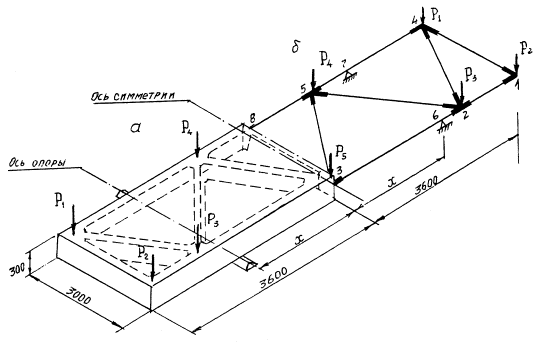
Рис. 5. Горная панель градирни а - общий вид; б - расчетная схема

Для их определения необходимо выявить расчетную ширину полки таврового сечения. В такой постановке задача решалась экспериментально-теоретически с использованием данных тензометрических измерений фибровых деформаций. При этом, если расчетную ширину полки принять за х, то, исходя из гипотезы плоских сечений, получим:

(9)

где  - усредненная по всей ширине х деформация в полке;  =  ε^Р - фибровая деформация ребра; у_Ц.Т(х) - расстояние центра тяжести сечения с шириной полки х до верха плиты.

Решение уравнения (9) получено методом последовательных приближений. Расчетная ширина полки х. определялась для опорных и пролетных сечений ребер.

Проверка адекватности расчетной модели выполнялась сравнением критериев Т и R вычисляемых по формулам (27) и (28) методических рекомендации соответственно. Для этого сначала находили средние значения и доверительные интервалы экспериментальных и теоретических величин сравниваемых параметров соответственно. Для прогибов оценка средних и доверительных значений выполнялась по формуле (2). Для изгибающих моментов аналогичные оценки выполнялись по формулам (8) и (9) с учетом равенства (таблица).

Параметры НДС	Значения				R	Т	Оценка адекватности (+) или неадекватности (-) расчетной модели
	теоретические		экспериментальные
	Средние	Доверительный интервал	Средние	Доверительный интервал
Прогибы, мм
у1	87,1,	18,6	84,3	1,6	2,8	18,7	+
у2	12,4	7,9	19,4	0,9	7	8	+
у3	-16,7.	10,9	-0,1	1;3	16,6	11,3	-
у4	85,2	20,6	88,6	0,9	3,4	20,6	+
У5	-12,5	9,7	0,8	0,6	13,2	9,8	-
Изгибающие моменты, Н·см
М3	10,1	3,4	9,6	2,4	0,5	5,6	+
М7	-34,5	2,8.	-31,4	5	3,1	7,9	+
М8	-2,2	4,6	2,4	0,9	4,6	4,7	+

Доверительные интервалы теоретических значений параметров получены с применением математической теории планирования экспериментов по формулам (11), (12) и (26) настоящих методических рекомендаций на основании численного эксперимента. При этом учитывалась изменчивость следующих факторов:



х₃ - расстояние от торца панели силы Р₄; х₅ - то же, Р₁; х⁴ - расстояние от оси опоры силы Р₅; х₆ -то же, Р₂; х₇ - расстояние опоры от оси панели.

При учете влияния семи факторов численные эксперименты проводились в соответствии с матрицей планирования 3 < n ≤ 7 (см. приложение 1). Значения факторов в центре плана и их доверительные интервалы были соответственно 1,5 ±0,15; 2,23 ±0,33; 6 ±3 мм; 42 ±4 мм; 6 ±3; 21 ±4 мм; 102 ±2 мм. Полученные средние значения и доверительные интервалы параметров напряженно-деформированного состояния: прогибов в точках 1...5 и изгибающих моментов в точках 3...8 - приведены в таблице совместно с результатами вычислений проверки адекватности расчетной модели.

Из таблицы видно, что почти по всем параметрам расчетная модель адекватна физической. В точках неадекватности теоретические значения превышают экспериментальные, кроме того, значения параметров НДС в точках неадекватности гораздо ниже экстремальных показателей. Исходя из этого, а также цели проводимых исследований, делаем вывод о пригодности математической модели для дальнейших численных исследований.

Численные исследования проводились для определения оптимального расположения опор при транспортировании панелей. Критерием оптимальности было условие удовлетворения равнопрочности по трещиностойкости опорных и пролетных сечений. Для натурной конструкции после ряда преобразований оно запишется как:



где М_ОП - изгибающий момент в продольном ребре у опоры; М_ПР - то же, в пролете.

Выполнив серию расчетов, в которых варьировалось расстояние опор от середины продольных ребер, находим их оптимальные значения: 2180 мм по одному продольному ребру и 2340 - по другому. При этом обеспечивается трещиностойкость панели в процессе перевозки.