Методические рекомендации по исследованию строительных конструкций с применением математического и физического моделирования
| Вид материала | Методические рекомендации |
- Программа курса «Основы математического моделирования» Осень 2007, 25.35kb.
- Аннотация дисциплины «основы математического моделирования», 29.01kb.
- Дефекты изготовления и монтажа строительных конструкций и их последствия, 779.7kb.
- Курс «Основы математического моделирования» реализуется в рамках специальностей 0647, 117.15kb.
- Авдейчиков Г. В. «Испытание строительных конструкций»: Учебное пособие (конспект лекций), 159.67kb.
- Задачи : 1 дать понятие математической модели, раскрыть суть метода математического, 187.03kb.
- Iii международный симпозиум актуальные проблемы компьютерного моделирования конструкций, 77.34kb.
- Пособие по обследованию строительных конструкций зданий, 3072.33kb.
- «Универсальная 32-битная среда для расчета и проектирования строительных конструкций, 23.4kb.
- Вид работ №30 «Монтаж, демонтаж строительных конструкций в подводных условиях», 16.72kb.
Нормативные документы размещены исключительно с целью ознакомления учащихся ВУЗов, техникумов и училищ.
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ ГОССТРОЯ СССР (НИИСК)
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ИССЛЕДОВАНИЮ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ С ПРИМЕНЕНИЕМ МАТЕМАТИЧЕСКОГО И ФИЗИЧЕСКОГО МОДЕЛИРОВАНИЯ
Одобрены секцией № 1 Научно-технического совета
НИИСК Госстрой СССР
Протокол № 24 от 17.09.86
КИЕВ 1987
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ 1. СИСТЕМНЫЙ ПОДХОД К ИССЛЕДОВАНИЮ СЛОЖНЫХ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ И СООРУЖЕНИЙ 1.1. Объект исследований как сложная система 1.2. Схема процесса исследования 1.3. Математическое моделирование работы строительной конструкции 1.4. Физическое моделирование 1.5. Определение неизвестных параметров расчетных моделей 1.6. Проверка адекватности расчетных моделей 2. ПОСТРОЕНИЕ МОДЕЛЕЙ ДЛЯ ИССЛЕДОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ 2.1. Расчетные модели строительных конструкций 2.2. Физические модели 2.3. Рекомендации по применению функционального подобия 3. ЭКСПЕРИМЕНТАЛЬНО-ТЕОРЕТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ КОНСТРУКЦИЙ 3.1. Определение констант ортотропии элементов при плоском напряженном состоянии 3.2. Экспериментально-теоретический метод определения элементов матрицы жесткости СЭ Приложение 1 МАТРИЦА ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА Приложение 2 КРИТИЧЕСКИЕ ЗНАЧЕНИЯ Xα ДЛЯ X-КРИТЕРИЯ приложение 3 ФУНКЦИОНАЛЬНОЕ ПОДОБИЕ КАК РАЗВИТИЕ ТЕОРИИ ПОДОБИЯ Приложение 4 примеры применения ФУНКЦИОНАЛЬНОго модЕЛирования литература |
Изложены теоретические предпосылки и практические рекомендации по исследованию прочности и деформативности сложных строительных конструкций, основанные на системном анализе и функциональном моделировании. Применение методики позволит с максимальной эффективностью использовать средства автоматизации научных исследований и существенно сократить стоимость, трудоемкость и сроки их проведения.
Предназначены для научных работников, могут быть полезны инженерам-проектировщикам и аспирантам строительного профиля.
Разработаны кандидатами техн. наук Ф.В. Ярмульником и В.И. Кретовым (НИИСК Госстроя СССР).
ВВЕДЕНИЕ
Ускорение научно-технического прогресса в строительстве тесно связано с сокращением сроков исследований эффективных конструкций. Это обусловливает широкое использование ЭВМ во всем комплексе научных исследований.
Бурное развитие в последнее десятилетие численных методов строительной механики сложных пространственных сооружений, внедрение в инженерную практику разработанных на их основе универсальных программных комплексов показывают, что экономически и методически целесообразно проведение исследований сложных сооружений с применением расчетных моделей. В то же время применение математических методов сдерживается существующей в настоящее время диспропорцией между высоким уровнем автоматизации самого вычислительного процесса и отсутствием алгоритмических приемов построения расчетных схем реальных сооружений, что ставит получение результатов в зависимость от субъективных качеств исследователя.
Достоверные результаты могут быть получены экспериментально. Однако со сложностью конструкций и сооружений существенно возрастают трудоемкость, стоимость и сроки проведения исследований. Это относится и к методам физического моделирования.
В настоящих методических рекомендациях излагаются принципиальные положения оптимизации процесса исследований сложных строительных конструкций на основе системного анализа. При этом в решении поставленных задач рационально сочетаются методы физического и математического моделирования. Основной упор делается на математические методы. Физический эксперимент используется исключительно для уточнения и проверки расчетной модели объекта. Это обусловило применение целенаправленных физических моделей, разработанных на основе функционального подобия, благодаря чему существенно упрощается конструкция моделей, снижаются затраты ресурсов на эксперимент.
Максимально возможное выделение формальных методов при исследовании позволяет снизить влияние субъективных факторов на результаты, использовать автоматизацию. В то же время следует отметить, что роль неформальных методов при исследовании сложных конструкций по-прежнему остается значительной, что делает процесс проведения исследований сочетанием научных методов и искусства экспериментатора.
На современном этапе развития строительной науки, когда исследование сложных конструкций требует снижения затрат труда, времени и материальных средств, разработанные рекомендации вносят определенный вклад в создание комплексных методов исследований, позволяющих за счет ускорения испытаний и повышения информативности результатов создавать новые эффективные конструкции.
1. СИСТЕМНЫЙ ПОДХОД К ИССЛЕДОВАНИЮ СЛОЖНЫХ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ И СООРУЖЕНИЙ
1.1. Объект исследований как сложная система
1.1.1. В целях повышения эффективности исследований сложных строительных конструкций, возможности их максимальной автоматизации и снижения затрачиваемых ресурсов целесообразен подход, основанный на методологической концепции системного анализа [1...3] как одной из основных особенностей современной науки и техники. Это позволит выделить одинаковые для всех типов конструкций процедуры и этапы работ, максимально исключающие субъективность и направленные на оптимальное решение поставленных проблем.
Отсутствие единого теоретического обоснования или даже унифицированной совокупности методов, общих для всех объектов приложения системного анализа вынуждает для каждой проблемы строить свою методологию, впрочем, с обязательным включением общих принципов системности - ряда формальных и неформальных процедур.
1.1.2. Системный подход при исследовании сложных строительных конструкций носит комплексный характер. Объект исследования (конструкция или сооружение) рассматривается как сложная система со всеми необходимыми признаками: наличие подсистем (элементов), объединенных связями (физические, логические, математические), а также выполнение условия целостности функционирования.
1.1.3. В системном анализе при исследовании строительных конструкций выделяются следующие основные логические элементы - исходные категории: цель (или цели); исследования альтернативные средства достижения цели (физическое или математическое моделирование); ресурсы для решения проблемы; система связей между целями, средствами и ресурсами; критерии выбора предпочтительных альтернатив.
1.1.4. При системном подходе выбор методов исследований строительных конструкций производится с учетом их роли в целом. Оптимальные характеристики элементов системы - физических нематематических моделей-- предполагают рассмотрение их как единого средства достижения цели. Поэтому физический и численный эксперименты должны быть с самого начала согласованы между собой, ориентированы на эффективное решение задач исследований, дополняя друг друга.
1.1.5. Исследования строительных конструкций и сооружений выполняются экспериментальными методами на натурных образцах и физических моделях либо теоретическими, с использованием расчетных моделей.
Физическое моделирование, основанное на теории простого или расширенного подобия, по мере усложнения задач исследований все менее целесообразно, так как не решает задач снижения трудоемкости и стоимости изготовления моделей, соблюдения планируемых сроков эксперимента.
1.1.6. Развитием численных методов расчета сложных конструкций, применением ЭВМ, широким внедрением в инженерную практику универсальных и специальных программных комплексов обусловливается экономическая целесообразность широкого использования в исследованиях сооружений расчетных моделей с назначением достоверных расчетных схем сооружений, ориентированных на решение конкретных исследовательских задач. Однако существующей в настоящее время диспропорцией между высоким уровнем автоматизации самого расчета и методикой построения достоверных расчетных схем реального сооружения существенно снижается надежность численных исследований, вносится известная доля субъективности в получаемые результаты.
Традиционно экспериментальные и численные исследования проводятся независимо друг от друга. В лучшем случае сопоставляются результаты. При этом проведенный анализ нисколько не повлияет на саму стратегию и методику эксперимента. Все это исключает существенное ускорение и повышение результативности работ.
1.1.7. Физический и численный (математический) эксперименты рассматриваются как единая система средств (организованный комплекс), направленных на наиболее эффективное решение задач исследования.
Расчетные и физические модели, как элементы системного анализа, по сравнению с аналогичными моделями, используемыми в обычных исследованиях, характеризуются целенаправленностью и ясностью. Системный подход обусловливает применение нового класса физических моделей, разработанных с использованием функционального подобия, что существенно упрощает их конструкцию и уменьшает объем экспериментальных исследований.
1.1.8. Сочетание при исследовании сложных строительных конструкций методов физического и математического моделирования обусловливает целесообразность применения принципа декомпозиции (членения) объекта исследований на более простые элементы, раздельные испытания которых потребуют гораздо меньше ресурсов по сравнению с испытаниями всей системы. Особенно этот принцип эффективен при исследовании сооружений, состоящих из большого количества однотипных элементов и узлов.
Расчетная модель системы может быть получена путем композиции расчетных моделей подсистем с проверкой их адекватности, что существенно упрощает процедуру установления достоверности.
1.1.9. В основу декомпозиции по п. 1.1.8 настоящих методических рекомендаций должны быть положены принципы, обеспечивающие системный подход к организации исследований:
затраты ресурсов на ведение работ должны быть меньше, чем без членения;
принцип декомпозиции должен выполняться с обеспечением независимости результатов исследований отдельных подсистем;
из возможных вариантов декомпозиции предпочтительнее тот, при котором порядок членения, определяемый максимальным количеством неизвестных расчетных параметров в каждой подсистеме, будет наименьшим.
При декомпозиции сложной системы важную роль играют так называемые неформальные методы, основанные на опыте и интуиции исследователя.
1.1.10. Рассматривая процесс исследования строительных конструкций как некоторую систему, необходимо выделить в ней три основные подсистемы:
экспериментальные исследования на физических моделях;
расчетные исследования на математических моделях;
связь между экспериментом и расчетом, включающая идентификацию некоторых параметров расчетной модели, проверку ее адекватности и корректировку.
1.1.11. В научном понимании между физическими и расчетными моделями существует общность (каждая из них представляет собой упрощенное воспроизведение процессов, происходящих в реальной системе и внешней обстановке).
Различие между ними заключается в средствах представления объекта исследований: физические модели - материальные системы, математические или расчетные - знаковые.
Общность физических и математических моделей обусловливает единообразие описания их характеристик и воздействий (входные параметры), а также функциональных параметров их состояния (выходные параметры), для чего используются символика и некоторые основные понятия теорий множеств и алгоритмов.
1.1.12. Признаки, по которым исследуемый объект выделяется из ассортимента других, образуют множество параметров Р. Изменение внешних условий, влияющих на состояние объекта. характеризуется множеством воздействий нагрузок N = {nK}. Естественно, что множества Р и N включают в себя лишь свойства и воздействия, связанные с изучаемой проблемой. Как правило, они определяются вместе с постановкой задачи до начала исследований.
В расчетных моделях объекта исследований множество Р разбивается на два подмножества: М = {т2} (параметры объекта, известные априори) и Χ = {хi} (параметры, подлежащие определению в процессе исследований).
При этом Р = МUX. Таким образом, результат исследований - множество параметров напряженно-деформированного состояния Y = {yi}.
1.1.13. Множества Р, Y должны однозначно характеризовать в интересующем исследователя аспекте, состояние и поведение объекта исследований как до, так и после приложения воздействий N. При решении конкретных исследовательских задач необходимо обращать внимание на корректность их выбора, руководствуясь тем, что между множествами N, Р и У устанавливается функциональное соответствие, которое будет заключаться в следующем:
Каждые
поставлены в соответствие хотя бы одному элементу
;каждому
соответствуют единственные непустые множества
,причем этим подразумевается наличие некоторой функции
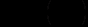,Примечание. В математике слово "функция" употребляется в чрезвычайно широком смысле. В нашем же случае под функцией у = f(х) будем понимать всякое правило (закон), ставящее в соответствие каждому
некоторый единственный элемент 
. Множество χ - область определения функции, Y - множество значений. Основа функции - алгоритм (предписание), позволяющий по каждой совокупности исходных данных из некоторого числа множеств, возможных для данного алгоритма, получить результат, если таковой существует, в противном случае - не получить ничего.Совокупность всех исходных данных, к которым применим данный алгоритм, называется областью его применимости., которая совпадает с областью определения функции, задаваемой им. Два алгоритма считаются равносильными, если совпадают области применимости, а для любого объекта, взятого из этой области, сходятся результаты обоих алгоритмов. Каждый алгоритм может быть записан в конечном счете с помощью слов и необходимых математических символов.