Методические рекомендации по исследованию строительных конструкций с применением математического и физического моделирования  

Вид материала

Методические рекомендации

Содержание 2. ПОСТРОЕНИЕ МОДЕЛЕЙ ДЛЯ ИССЛЕДОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ 2.1. Расчетные модели строительных конструкций Рис. 3. Аппроксимация сечения крестообразной формы EF осевая жесткость, ЕI 6. Стержневая модель ребристой плиты Рис. 7. Аппроксимирующая модель оболочки положительной гауссовой кривизны Рис. 10. Система с нарушенной регулярностью

Подобный материал:

• Программа курса «Основы математического моделирования» Осень 2007, 25.35kb.
• Аннотация дисциплины «основы математического моделирования», 29.01kb.
• Дефекты изготовления и монтажа строительных конструкций и их последствия, 779.7kb.
• Курс «Основы математического моделирования» реализуется в рамках специальностей 0647, 117.15kb.
• Авдейчиков Г. В. «Испытание строительных конструкций»: Учебное пособие (конспект лекций), 159.67kb.
• Задачи : 1 дать понятие математической модели, раскрыть суть метода математического, 187.03kb.
• Iii международный симпозиум актуальные проблемы компьютерного моделирования конструкций, 77.34kb.
• Пособие по обследованию строительных конструкций зданий, 3072.33kb.
• «Универсальная 32-битная среда для расчета и проектирования строительных конструкций, 23.4kb.
• Вид работ №30 «Монтаж, демонтаж строительных конструкций в подводных условиях», 16.72kb.

2. ПОСТРОЕНИЕ МОДЕЛЕЙ ДЛЯ ИССЛЕДОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ

2.1. Расчетные модели строительных конструкций

2.1.1. Исходя из принципов системного подхода к проблеме анализа сложной системы конструкций рекомендуется назначать расчетные схемы на основе анализа их общих закономерностей.

2.1.2. Исследования сложных строительных конструкций следует начинать с анализа объекта исследований, особенностей и условий работы и др., включающего:

изучение рабочих чертежей и другой документации по исследуемому объекту;

рассмотрение функционального назначения объекта, технологических воздействий, условий работы конструкции, вида возможных предельных состояний;

выявление признаков и особенностей, отличающих данный объект от аналогичных, исследования которых проводились ранее;

ознакомление с методиками и результатами проведенных ранее исследований;

оценку новизны и важности проблемы, потенциального экономического эффекта, который может быть получен от внедрения в производство.

2.1.3. Для численных исследований сложных строительных конструкций и сооружений следует применять программные комплексы общего назначения. Наряду с этим для расчета определенных типов сооружений могут использоваться программы, в зависимости от степени специализации которых накладываются ограничения на возможность выбора расчетной схемы. Для программ общего назначения предопределен набор типов расчетных элементов, выбор которых и способ объединения для аппроксимации работы строительной конструкции зависят от инженера-исследователя, исходящего из принципов;

I - расчетная схема сооружения должна назначаться в соответствии со схемой деформирования или разрушения сооружения, подтвержденных строительной практикой;

II - поскольку расчетная схема - аналог механической модели сооружения, в нее вводятся упрощающие гипотезы, позволяющие выделить определяющие факторы, влияющие на работу конструкции (рассчитываемая конструкция находится в менее благоприятных по сравнению с действительностью условиях, кроме того, учитывается требование экономической целесообразности проектируемой конструкций);

III - для расчета некоторых конструктивных элементов или их систем целесообразно иметь несколько расчетных схем, каждая из которых имеет область применения (расчетные схемы отличаются степенью подробности аппроксимации, свойствами расчетных элементов и др.; критерием для выбора той или иной модели служит оценка результата, удовлетворяющего условиям поставленной задачи).

2.1.4. Ввиду того, что здания каркасные или с несущими стенами, массовые конструкции надземного строительства, отдельные конструктивные элементы этих несущих систем рекомендуется рассматривать с точки зрения их аппроксимации расчетными элементами моделируя:

колонны и другие элементы постоянного поперечного сечения - стержневыми конечными элементами (КЭ) с определением их жесткости по известным формулам сопротивления материалов, принимая EF - продольной или осевой жесткостью; ЕI_x, EI_y - изгибными жесткостями; Gl_кр - жесткостью кручения, а GF_x, GF_y - сдвига; при конструктивном обеспечении жесткого узла связи между элементами и при достаточных размерах их поперечных сечений необходимо принимать расчетные стержни с жесткими вставками, размеры которых определяются размерами жесткого узла;

ригели или другие элементы со сложной формой поперечного сечения, кроме стержневых, - набором плоских КЭ, причем потребность в этом возникает при необходимости получения более подробной картины напряженного состояния, а также учета действительных размеров их поперечного сечения; основные габаритные размеры принимаются по исходному поперечному сечению, а толщина КЭ - из решения системы уравнений (например, для крестообразного поперечного сечения по рис. 3 уравнения будут иметь вид:

I_сеч = f₁(в_п, h_n, в_ст, h_ст),

F_сеч = f₂(в_п, h_n, в_ст, h_ст),

где I_сеч., F_сеч. - геометрические характеристики формы исходного поперечного сечения; f₁, f₂ - аналитические функции размеров аппроксимирующего поперечного сечения; в_n, h_ст известные, а в_ст, h_n - определяемые размеры);



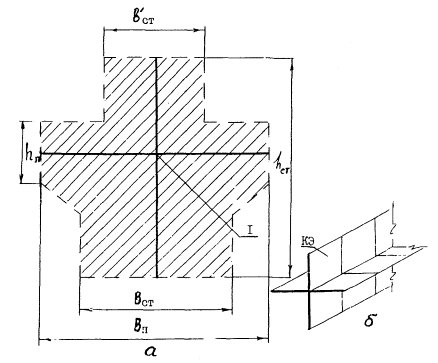
Рис. 3. Аппроксимация сечения крестообразной формы:

а - поперечное сечение; б - расчетная схема; 1 - центр тяжести сечения

балочные и стоечные элементы с отверстиями, регулярно расположенными по длине элемента, - стержневым КЭ, жесткость которого определяется из расчета участка данного элемента на краевые воздействия, как составной части основной системы (рис. 4.) после расчета участка элемента с отверстиями с помощью конечно-элементной аппроксимации на три вида воздействий получим значения перемещений, используемые как правые части системы трех уравнений, решением которых определяем величины трех характеристик жесткости аппроксимирующего стержня:



где EF осевая жесткость, ЕI - изгибная жесткость, GF_СД - сдвиговая жесткость, μ - коэффициент формы сечения;



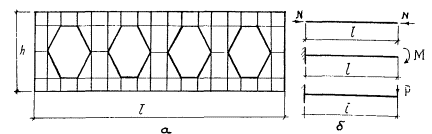
Рис. 4. К определению жесткости перфорированного элемента

а - расчетный участок элемента аппроксимации КЭ; б - единичные состояния элемента основной системы

плиты ребристые - набором КЭ оболочки нулевой кривизны, аппроксимирующих полку плиты, и стержневыми элементами, аппроксимирующими продольные ребра (рис. 5, 6). Связь между КЭ плиты и ребер осуществляется с помощью стержневых или "контактных" элементов с характеристиками жесткости на два порядка выше жесткостей ребер. Плита моделируется одним стержнем, а фактические ее размеры в поперечном направлении - стержневыми элементами повышенной жесткости. Жесткостные характеристика основного стержневого элемента равны жесткости плиты, определяемой теоретически или экспериментально;

плиты пустотные и гладкие - расчетными моделями I и II типа;

цилиндрические поверхности - КЭ оболочки нулевой кривизны прямоугольной формы;

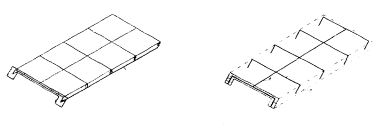Рис. 5. Аппроксимирующая модель ребристой плиты а - поперечное сечение; СЭ - стержневой элемент ребра; КЭ -конечный элемент связи	6. Стержневая модель ребристой плиты а - поперечное сечение плиты; б - основной расчетный стержень; в, г - стержни

оболочки, поверхность которых имеет кривизну в двух направлениях, - КЭ оболочки нулевой кривизны треугольной формы, при отсутствии в библиотеке таковых или по другим соображениям могут быть использованы КЭ прямоугольной формы, при этом три узла каждого КЭ лежат на поверхности, а четвертый, вне ее, - объединяется (рис. 7) с аналогичным узлом на поверхности условием равенства перемещений (происходит незначительное искажение ее формы, однако сохраняется непрерывность функций перемещений по всем сечения оболочки);



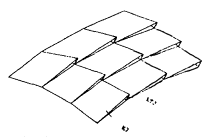
Рис. 7. Аппроксимирующая модель оболочки положительной гауссовой кривизны

КЭ - конечный элемент оболочки нулевой кривизны; KTЭ - контактный элемент, или условие равенства перемещений

эквивалентные системы, когда часть сложной системы необходимо заменить более простой, равнозначной в определенном смысле исходной конструкции (обычно это связано с необходимостью понизить мерность фрагмента или всей конструкции), например, конструкцию инвентарного здания, состоящего из сборных плит основания и металлического каркаса, в которой плиты основания, представляются как трехслойная конструкция - верхние гладкие и нижние ребристые соединены пространственными арматурными каркасами, а примыкание друг к другу и сопряжение с каркасом - точечное согласно рис. 8), - моделью двух однослойных плит, имеющих общие узлы и две группы независимых характеристик: Е_И, t_И, μ - характеристики изгибаемой плиты; Е_П, t_П, μ - характеристики плиты в плоском напряженном состоянии (каждая из них может быть получена из условия эквивалентности трехслойной плиты при расчете на соответствующие виды воздействий), а также когда в расчетных схемах зданий встречаются включения типа ядер или диафрагм жесткости сложной конструктивной формы - сложной моделью, состоящей из большого количества конечных элементов (диафрагма представлена в виде рамной системы; жесткости элементов которой могут быть определены расчетом диафрагмы с помощью подробной схемы на воздействие горизонтальной силы Р единичной величины с определением значений горизонтального смещения Δ_Г верхнего сечения, дополненного расчетом рамы на действие силы Р с определением  при различных соотношениях жесткостей колонн и ригелей (рис. 9);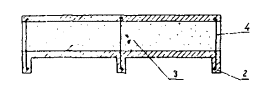



Рис. 8. Поперечное сечение трехслойной плиты

1, 2 - соответственно верхняя и нижняя плита; 3 - утеплитель; 4 - арматурный каркас



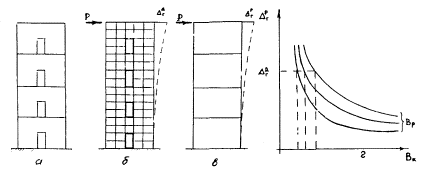
Рис. 9. К расчету диафрагм

а - диафрагма; б - подробная расчетная схема; в - рамная расчетная схема; г - график перемещений рамы

вариантные модели, когда встречаются конструктивные схемы, обладающие слабой нерегулярностью (структура системы регулярна за исключением некоторых локальных особенностей: регулярно и нерегулярно расположенные проемы, отдельные элементы повышенной и пониженной жесткости по сравнению со всей системой, необходимость расчета нескольких вариантов однотипных систем, отличающихся локальными особенностями), - кодированием расчетной схемы для всей системы без учета нерегулярных элементов (рис. 10), которые записываются как дополнительная информация по отношению к основной (при наличии проемов они могут быть описаны как расчетные элементы с отрицательными значениями толщины или модуля упругости, равными положительным значениям этих параметров, использованных при описании регулярной системы; при таком способе описания расчетной модели возможно появление узлов расчетной схемы, к которым присоединены расчетные элементы с нулевой жесткостью и которые необходимо закрепить, в пространстве от возможных смещений; для расчетных элементов, отличающихся по характеристикам жесткости, достаточно ввести в схему дополнительные элементы с тем, чтобы суммарное значение жесткости равнялось заданному, при этом действительное значение усилий необходимо определять как суммарное в исходной системе и добавочных элементах).



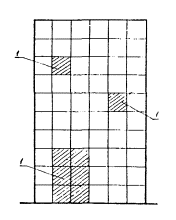
Рис. 10. Система с нарушенной регулярностью

1 - проемы