Методические рекомендации по исследованию строительных конструкций с применением математического и физического моделирования  

Вид материала

Методические рекомендации

Содержание 1.6. Проверка адекватности расчетных моделей Рис. 2. График функции желательности

Подобный материал:

• Программа курса «Основы математического моделирования» Осень 2007, 25.35kb.
• Аннотация дисциплины «основы математического моделирования», 29.01kb.
• Дефекты изготовления и монтажа строительных конструкций и их последствия, 779.7kb.
• Курс «Основы математического моделирования» реализуется в рамках специальностей 0647, 117.15kb.
• Авдейчиков Г. В. «Испытание строительных конструкций»: Учебное пособие (конспект лекций), 159.67kb.
• Задачи : 1 дать понятие математической модели, раскрыть суть метода математического, 187.03kb.
• Iii международный симпозиум актуальные проблемы компьютерного моделирования конструкций, 77.34kb.
• Пособие по обследованию строительных конструкций зданий, 3072.33kb.
• «Универсальная 32-битная среда для расчета и проектирования строительных конструкций, 23.4kb.
• Вид работ №30 «Монтаж, демонтаж строительных конструкций в подводных условиях», 16.72kb.

1.6. Проверка адекватности расчетных моделей

1.6.1. Проверка адекватности разработанных расчетных моделей проводится сопоставлением данных экспериментальных исследований специальной физической модели с результатами численных исследований на расчетной. Так как экспериментальные данные содержат некоторую неопределенность, связанную с погрешностями измерительного комплекса, нагружающих устройств, изменением внешних условий во время эксперимента и т.д., а исходные параметры, закладываемые в расчетную модель, обладают существенной изменчивостью (физико-механические характеристики материалов, жесткости элементов и т.д.), то математически задачу проверки адекватности расчетной модели реальному объекту (физической модели) можно трактовать как проверку некоторой совокупности статистических гипотез.

1.6.2. Для практической реализации единого подхода к решению вопроса о проверке достоверности расчетной модели может быть рекомендован инженерный метод, основанный на сочетании неформальных приемов, отражающих субъективное влияние исследователя, с рядом формальных процедур проверки статистических гипотез.

В соответствии с системным подходом к исследованиям сложных строительных конструкций контроль адекватности расчетных моделей проводится в несколько этапов:

установление адекватности по одному виду параметров напряженно-деформированного состояния y_i в локальной области;

то же, по всему объекту;

проверка адекватности по всем параметрам Y = {y_i}.

Проверка адекватности расчетной модели по одному виду параметров y_i (см. п. 1.6.1) в локальной области основана на сравнении экспериментальных и теоретических значений и их доверительных интервалов методами математической статистики*.

* См. разд. 1.4, формулы (2), (4) и (6).

1.6.3. Для получения доверительных оценок теоретических значений параметров напряженно-деформированного состояния предлагается инженерный метод, основанный на статистической динамике механических систем и математической теории планирования экспериментов, исходя из предположения о том, что, если область определения функции y_i = f_j(x₁, x₂, …, x_n)), где y_i - параметр НДС, x_i - исходные данные расчетной модели, ограничить окрестностями x_i, радиусы которых равны соответствующим доверительным интервалам Δx_i, то эта функция с достаточной точностью может быть аппроксимирована полиномом вида (11) или (13). Тогда доверительные интервалы параметров y_i вычисляются как погрешность функции независимых случайных величин:

(25)

1.6.4. В реальных задачах доверительные интервалы исходных данных в большинстве своем сравнительно невелики, поэтому с точностью, достаточной для практических целей, можно ограничиться аппроксимацией функции f_j полиномами первой степени (11). В этом случае доверительные интервалы y_j вычисляются по более простой формуле:

(26)

где в_ji - коэффициенты уравнений (11), вычисляемые по формулам (12) по результатам численных экспериментов согласно соответствующей матрице планирования (см. приложение 1).

1.6.5. При наличии точечных и доверительных оценок параметра напряженно-деформированного состояния y_i (экспериментальные , Δ и теоретические  и Δ установление адекватности расчетной и физической моделей может быть сведено к проверке статистической гипотезы о равенстве средних. С учетом возможного неравенства дисперсий ()² и ()² применим приближенный метод [20] с несколько преобразованными расчетными формулами, согласно которому вычисляем:

	(27)
	(28)

где  и  - коэффициенты Стьюдента, принимаемые по таблицам t-распределения при доверительной вероятности 0,95 и числе степеней свободы соответственно п - 1 и N - 1, п - количество физических экспериментов при определении Δ; N - количество строк матрицы планирования.

При выполнении условия:

(29)

расчетная модель считается адекватной по параметру y_j в данной точке.

1.6.5. Для проверки адекватности расчетной модели по всему множеству параметра y_j; необходимо определить  проверить неравенство (29) для каждой пары  и  (j =1, 2, ..., m); К = 1,2,…, r, где r - количество пар). Проверка не вызывает затруднений, если условие (29) выполняется для каждой пары. В противном случае необходимо проверить статистическую гипотезу о случайности данного явления с привлечением непараметрических методов (U- или X-критерия), не накладывающих ограничений на функции распределения Δ и Δ.

1.6.6. Проверке адекватности по всему параметру у_j (например по всем изгибающим моментам или всем прогибам и т.д.) должен предшествовать учет превалирования зон с максимальными значениями у_j (по абсолютной величине), связанного с тем, что, исходя из условия обеспечения прочности, надежности и экономичности, расчетная модель сооружения должна, в первую очередь, достоверно описывать напряженно-деформированное состояние конструкции в зонах экстремальных значений параметров НДС введением весовых коэффициентов:

(30)

или:

(31)

где т - количество типов параметров НДС; r - количество зон, на которые разбивается эпюра y_i при проверке адекватности.

1.6.7. С учетом весовых коэффициентов определяется количество сравниваемых пар в каждой зоне:

(32)

где r - общее количество сравниваемых пар.

Для каждой k-той пары  и  находим разность:

ejk = Rjk - Tjk

(33)

Приняв k⁽⁺⁾ за число положительных разностей, а k^(-) - отрицательных, расчетные модели можем считать адекватными при выполнении неравенства:

(34)

где  - критерий Фишера, принимаемый по таблицам F-распределения при доверительной вероятности р = 0,95 и числе степеней свободы m₁ = 2(k⁽⁺⁾+1) и m₂ = 2k^(-).

1.6.8. В ранговом методе (базирующемся на упорядочении сравниваемых величин, в нашем случае - R_jk и Т_jk при k = 1, 2,..., r) с применением X-критерия, имеющем преимущество перед U-критерием по большей эффективности (при сопоставлении с двойным t-критерием он обладает асимптотической эффективностью, равной 1, при эффективности U-критерия 0,64), оценка адекватности сводится к проверке статистической гипотезы: существенно ли значения Т_jk - превышают значения R_jk для всего множества параметров у_j. Сначала упорядочиваются все значения R_jk и Т_jk расположением в порядке их возрастания. Каждому из этих значений присваивается ранговое число, соответствующее порядковому номеру. Затем вычисляется X-критерий:

(35)

где r - число сравниваемых пар; S_k - ранговое число Т_jk;

ψ(y) = x - функция, обратная функции нормированного нормального распределения;



Исходя из этого, ψ(y) = x определяется как аргумент, по значению функции y = Ф(х) таблицы нормированного нормального распределения в [25]. Если статистическая гипотеза подтверждается, модели считаются адекватными:

Χj ≤ Χα

(36)

где Χ_α - критические значения X-критерия, принимаемые по таблице приложения 2 в зависимости от доверительной вероятности и величины 2r.

1.6.9. Один из наиболее удобных и достаточно простых способов установления глобальной адекватности как заключительного этапа проверки тождества расчетных моделей (оценка по всему множеству параметров напряженно-деформированного состояния Y) основывается на применении обобщенной функции желательности Харрингтона [26]. В основе метода - идея преобразования натуральных значений параметров в безразмерные величины dj согласно шкале желательности, или предпочтительности, назначение которой - установление соответствия между физическими и психологическими (умозрительными) параметрам (понимаются чисто субъективные оценки исследователем предпочтительности или желательности того или иного значения параметра).

Шкала желательности имеет интервал dj от 0 до 1, где dj = 1 соответствует идеальная адекватность расчетной модели по параметрам y_i (см. пп. 1.6.7, 1.6.8), d_j = 0 - абсолютное несовпадение расчетных и экспериментальных данных.

Сценка адекватности расчетных моделей по шкале желательности приведена в табл. 2.

Таблица 2

Субъективная оценка исследователем адекватности по параметрам	Очень хорошая	Хорошая	Удовлетворительная	Плохая	Очень плохая
Значение параметра yj по шкале желательности - dj	1…	0,8…	0,63…	0,37…	0,2...
	0,8	0,63	0,37	0,2	0

Выбор оценок 0,63 и 0,37 объясняется удобством вычисления функции желательности , где  - относительное значение параметра в условном масштабе.

1.6.10. В случае, когда проверка адекватности по некоторому параметру y_k дает отрицательный результат, а по другим, наиболее важным, параметрам адекватность моделей установлена, для оценки пригодности имеющейся расчетной модели или выбора лучшей из нескольких альтернативных можно рекомендовать применение коэффициента неадекватности:

(37)

где n_k - коэффициент неадекватности по параметру y_k.

 - наихудшее теоретическое значение параметра с учетом доверительного интервала;

 - экспериментальное значение соответствующего параметра.

Затем принимаем граничные оценки для коэффициентов неадекватности:

0,95 ≤ п_k ≤ 1,05 - очень хорошо;

0,9 ≤ п_k ≤ 0,95; 1,05 < п_k ≤ 1,1 - хорошо;

0,8 ≤ п_k ≤ 0,9; 1,1 < п_k ≤ 1,2 - удовлетворительно;

0,5 ≤ п_k ≤ 0,8; 1,2 < п_k ≤ 1,5 - плохо;

п_k ≤ 0,5; п_k > 1,5 - очень плохо.

Примечание Совершенно очевидно, что могут быть и другие граничные оценки. Для уменьшения влияния субъективного фактора следует воспользоваться мнением нескольких специалистов. При обобщении этих мнений и установлении степени согласованности между различными специалистами можно воспользоваться методом ранговой корреляции [23].

После назначения границ коэффициентов неадекватности определяем частный показатель желательности dj для каждого вида параметров y_j расчетной модели, для чего воспользуемся графиком кривой желательности (рис. 2), на котором по оси ординат нанесены частные показатели желательности d_j, а по оси абсцисс - соответствующие границы коэффициента неадекватности [n_k]

После определения частных показателей функции желательности d_j для каждого вида расчетных параметров вычисляем обобщенный показатель желательности по всем параметрам напряженно-деформированного состояния D, который рассматриваем как формализованную оценку пригодности расчетной модели.



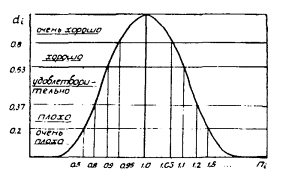
Рис. 2. График функции желательности

Ввиду того, что единого правила вычисления обобщенного показателя желательности нет, рекомендуем определять его как среднее геометрическое частных показателей желательности.

(38)

Обобщенный показатель желательности D может быть использован в качестве критерия оптимальности расчетных моделей.