Свойства оценок параметров, получаемых с помощью наименьших квадратов

Вид материала

Лекция

Содержание Информационные и прогностические способности трендовых моделей. Прогностические способности Приведение некоторых нелинейных моделей к линейному виду. Квадратичная функция. Построение и прогнозирование на основе факторных регрессионных моделей (ФРМ).

Подобный материал:

• Возможности формирования магнитных полей с заданным распределением индукции на центральной, 9.53kb.
• А. Ю. Власов доцент, к Х. н. Математическая обработка результатов эксперимента, 36.78kb.
• И. А. Пахнутов Рассмотрены вычислительные аспекты обобщенного метода наименьших квадратов, 39.76kb.
• Статья посвящена проблеме мониторинга жизненного цикла товаров. Предложена модель жизненного, 80.3kb.
• Лабораторная работа по теме: метод наименьших квадратов, 231.91kb.
• Ф. И. Эджоурт один из известнейших ученых, первый кто попытался применить методы, которые, 243.09kb.
• Решение : Составляем функцию для зависимости, 10.81kb.
• «Математические методы в химии» Общая трудоёмкость дисциплины составляет, 22.21kb.
• Метод наименьших квадратов, 238.98kb.
• Линейная регрессия и метод наименьших квадратов, 177.63kb.

Свойства оценок параметров, получаемых с помощью наименьших квадратов.

1. Свойство несмещенности
   

Оценка a_y параметра α_y называется несмещенной если математической ожидание a_y = линейному значению параметра α_y

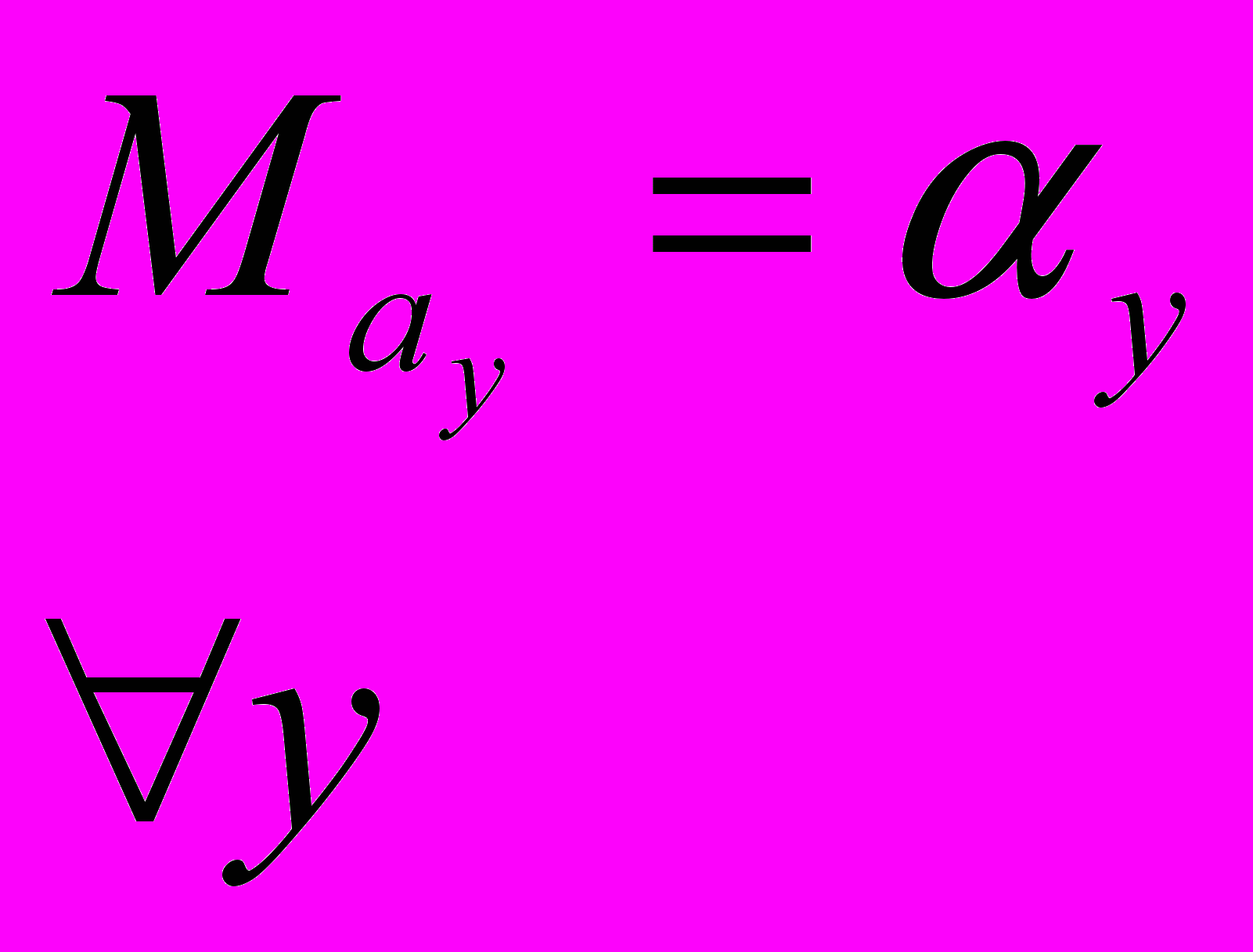Т.е. найденное значение параметра максимально приближено к истинному.

2. Свойство состоятельности
   

Дисперсия оценок параметров стремится к нулю при увеличении наблюдений.

3. Свойство эффективности
   

Оценка a_y называется эффективной параметра α_y в классе оценок A, если ее дисперсия является минимальной среди оценок этого класса.



Если модель линейная априорно, то дисперсия линейна a_y min по сравнению с …


Прогнозирование на трендовых моделях.

1. Строим модель
   
2. Проверяем прогностические способности
   
3. Осуществляем прогнозирование
   

Точечный прогноз.


t_α – табл-ое распределение Стьюдента

- ошибка прогноза

- среднеквадратическое отклонение


Упрощенная формула только для линейного тренда:




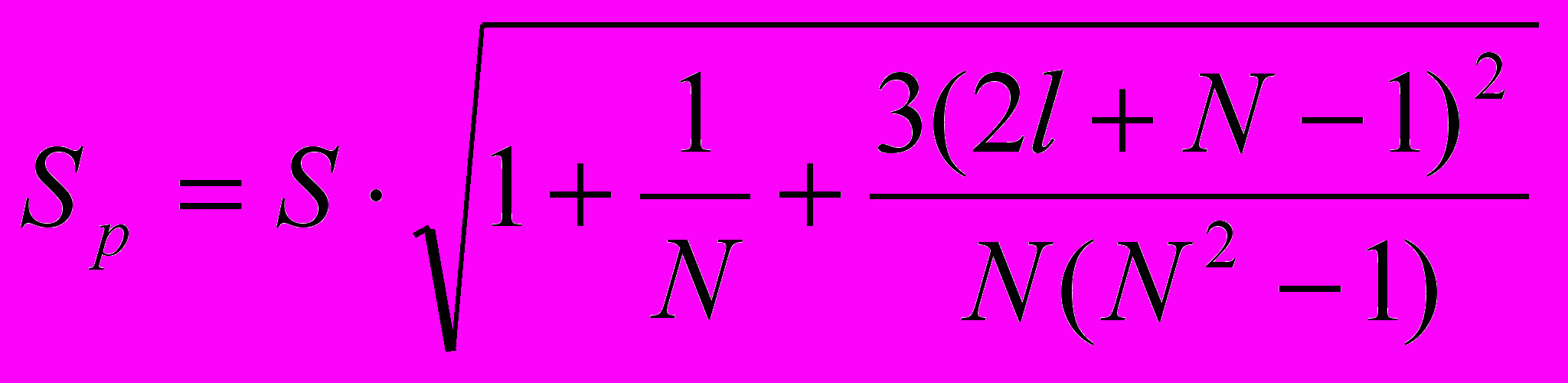
Например:




Информационные и прогностические способности трендовых моделей.

Критерий	Область изменений	Описание
Информационные способности
S	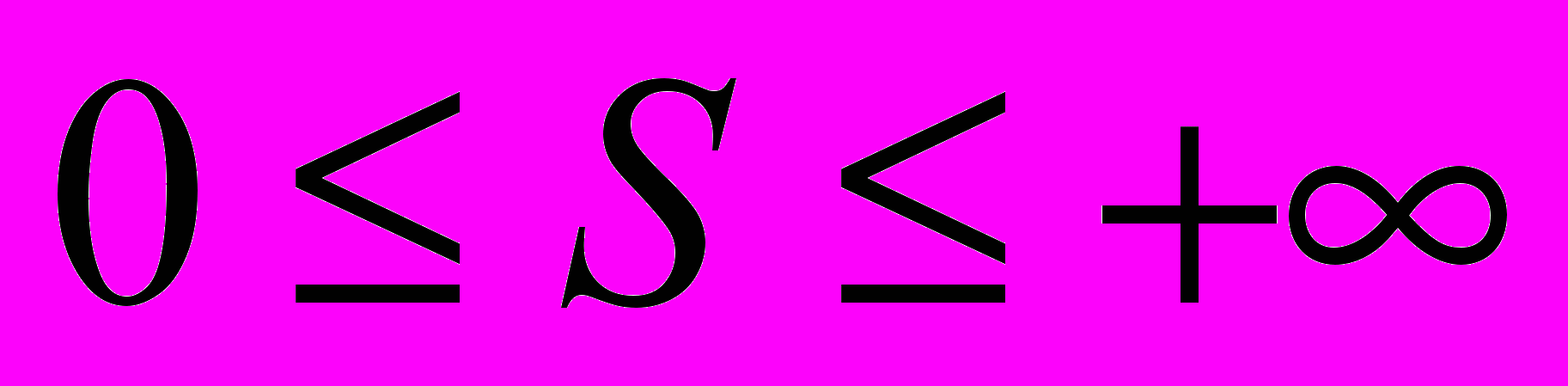модель тем лучше, чем S ближе к нулю	Среднеквадратическое отклонение
F		Критерий Фишера определяет значимость модели в целом. Модель значима если Fрасч>Fкритич. Чем само значение F больше, тем лучше.
R2		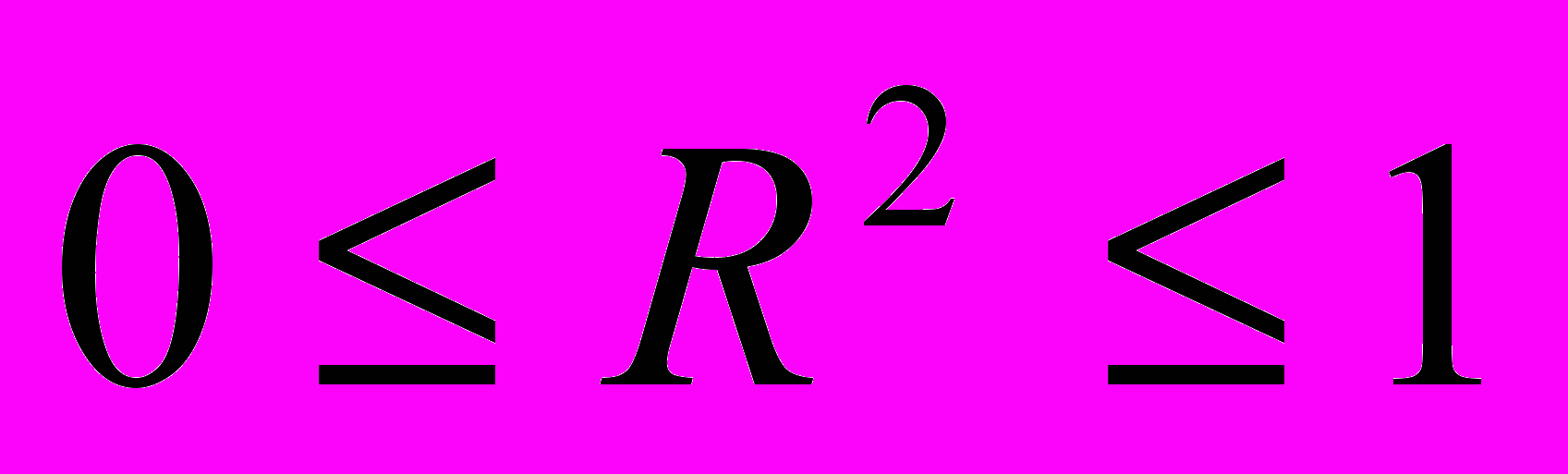Коэффициент детерминации чем ближе к 1, тем лучше. Скорректированный коэффициент детерминации чем ближе к 1, тем лучше. Определяет на сколько наша зависимая переменная объясняется временем.
Прогностические способности
Kt – коэффициент Тейла		Чем меньше, тем лучше.
Sp – ширина доверительного интервала		Чем уже, тем лучше.

Приведение некоторых нелинейных моделей к линейному виду.

Экспоненциальная функция.





Квадратичная функция.





Гипербола.





Построение и прогнозирование на основе факторных регрессионных моделей (ФРМ).


ФРМ – это статистическая зависимость одной переменной от нескольких независимых переменных.




Зависимая переменная = матрица независимых переменных + случайный фактор


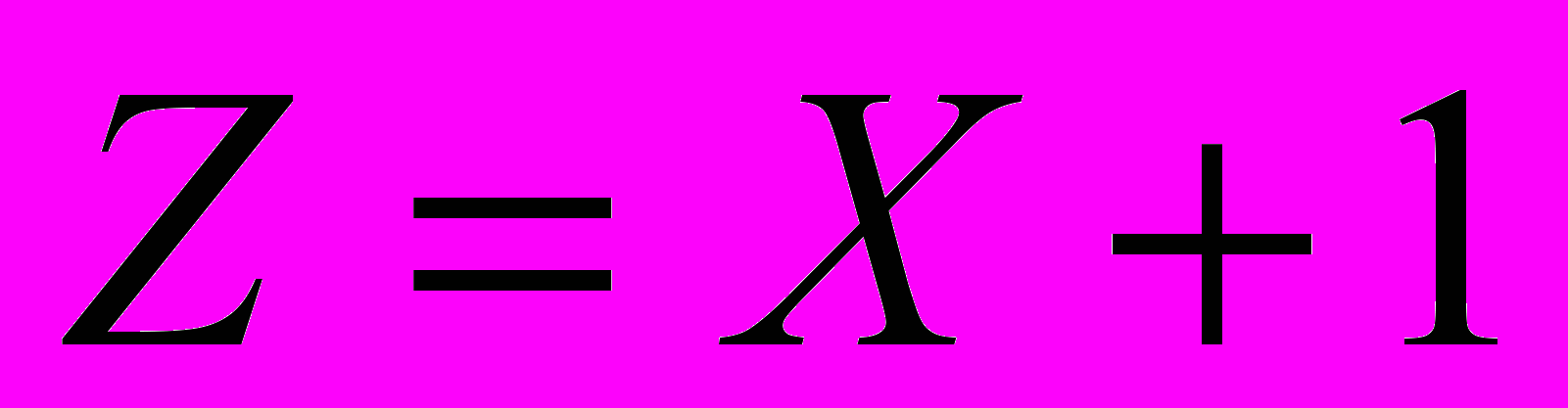(матрица независимых переменных + случайная матрица)


- уравнение регрессии




Тренд – простая регрессия где x – это время (t).

Множественная регрессия:



- случайная компонента


Регрессионная модель может быть и нелинейна.


Построение любой регрессионной модели включает два этапа:

1. определение исходной спецификации модели. Выбор класса функции
   
2. фактическое оценивание параметров регрессии a_y
   

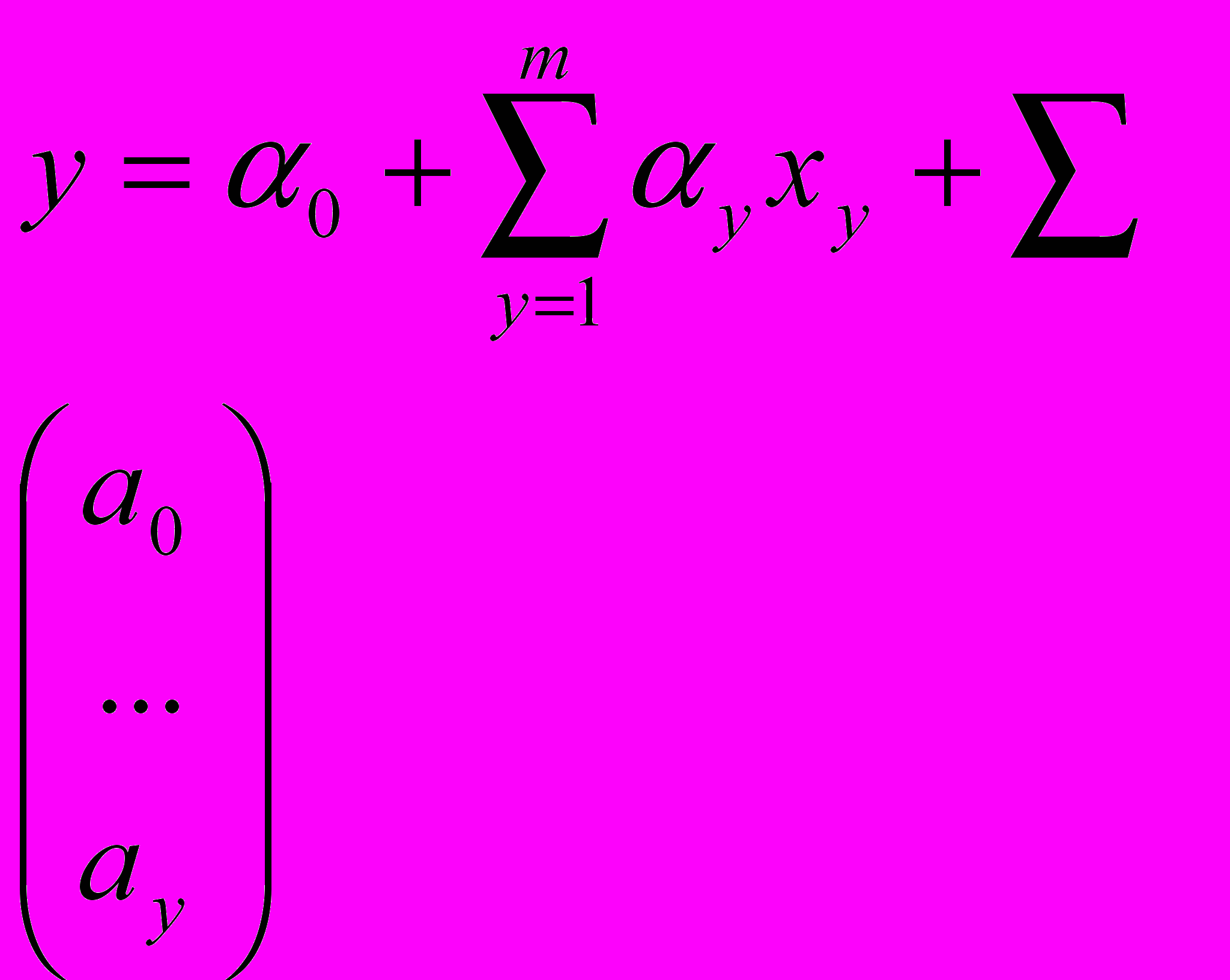
Для оценки параметров 2 метода:

1. метод максимального подобия – ММП – для нормального распределения
   

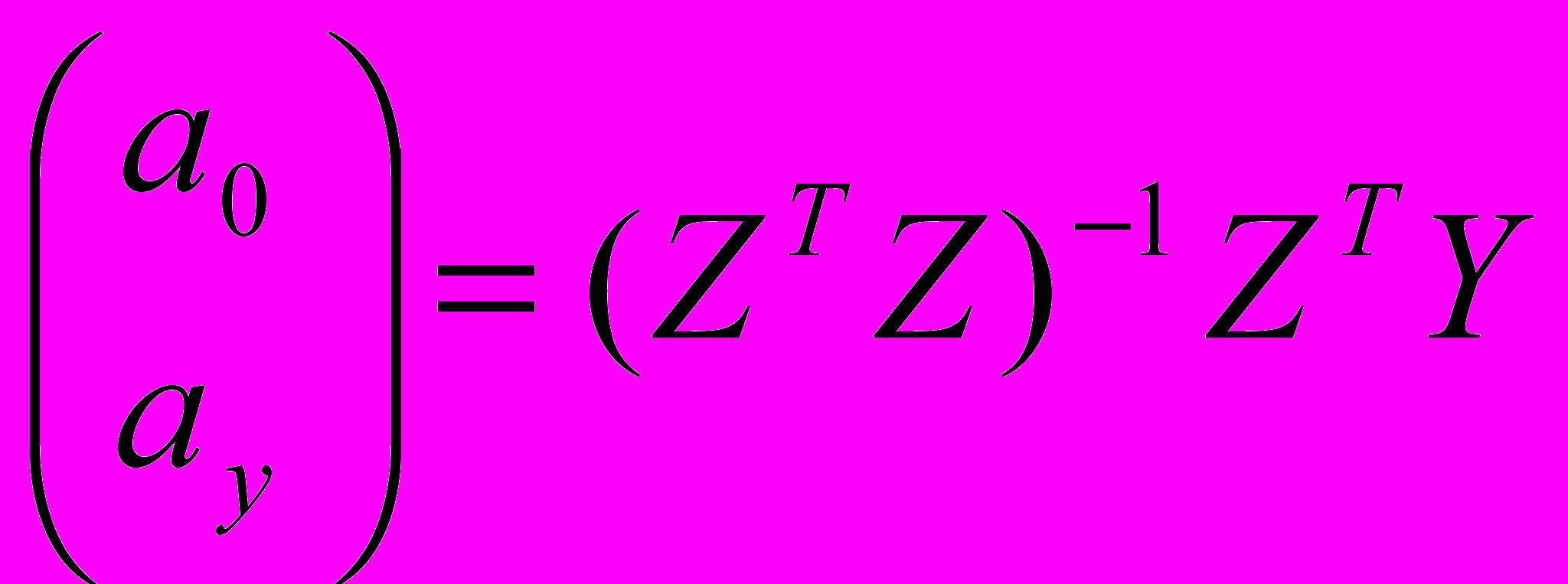
Например:

2. метод Лапласа
   

Корреляционный анализ регрессионных моделей.

Корреляционный анализ – анализ, при котором оценивается степень тесноты статистической связи между анализируемыми переменными.



Зависимость между y и x₁, x₂, x₃,…, x_m – должна быть сильная,

А между x₁, x₂, x₃,…, x_m – не должно быть корреляционной связи.


Корреляция от -1 до 1


Если связь между независимыми переменными существует – мультиколлериальность.

Степень тесноты связи мы определяем с помощью парного коэффициента корреляции - r_xy – тесноту линейной связи.


- коэффициент детерминации – определяет зависимость между зависимой переменной и всей совокупностью независимых переменных.


Для матриц:

- центрированная матрицы


- скалярный вариант





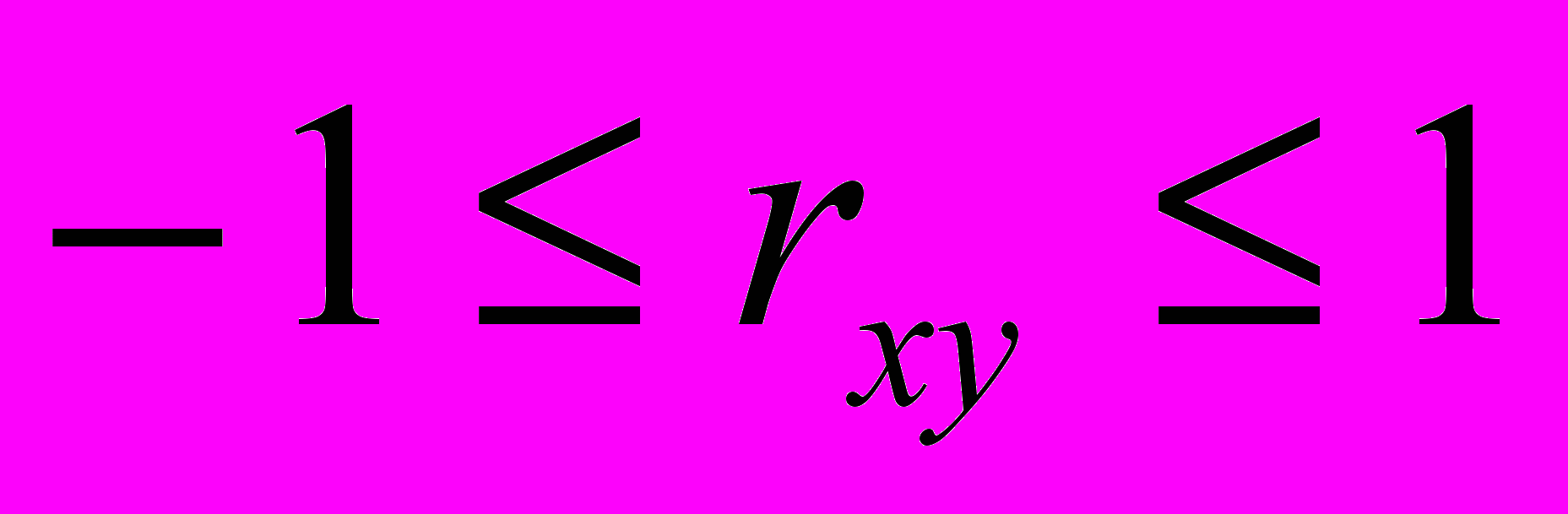
Для проверки значимости коэффициента корреляции используется критерий Стьюдента:



- корреляция случайна

- корреляция существует





Скорректированный коэффициент детерминации:

Критерий проверки значимости коэффициента детерминации Фишера:



- связь несущественна

- связь существенна


Дисперсионный анализ регрессионной модели (см. дисперсионный анализ трендовых моделей).

1. Проверка значимости параметров модели (стр. 26-27):
   

2. Проверка значимости модели в целом (стр. 25):