Р. А. Обозов использование показателя внутренней ставки доходности

Вид материала

Документы

Содержание IRR), ориентированный на увеличение стоимости бизнеса, подходит, наряду с методом чистой настоящей стоимости проекта (NPV E < Ê – положительна. Определенная так IRR IRR, явно нереалистично, было предложено несколько алгоритмов, улучшающих IRR MIRR для заключения об эффективности проекта. Действительно, чтобы сделать вывод об эффективности проекта по показателю IRR IRR является ставка дохода финансового менеджмента (FMRR FMRR такие же, как и у MIRR

Подобный материал:

• Е. В. Безлюдный, А. А. Сергеев, А. В. Григорьев, А. Е. Безлюдный, 46.92kb.
• «экономика информационных ресурсов, технологий и систем», 47.61kb.
• 186422. doc Вопросы «оценка недвижимости», 80.89kb.
• Справочник, 251.37kb.
• Методика расчета Кривой бескупонной доходности по государственным ценным бумагам Термины, 89.72kb.
• Развитие китайской внутренней и внешней экономики по данным сми кнр, 52.31kb.
• Отчет о проделанной работе за 2010 год отделом учета и отчетности управления Алтайского, 56.09kb.
• А. Н. Фоменко Использование переменной ставки дисконтирования при оценке, 118.58kb.
• В. П. Малков Монография представляет собой комплексное процессуально-криминалистическое, 2858.74kb.
• Конференция 'Роль аналитика в управлении предприятием' Критерии выбора ставки дисконтирования, 130.93kb.

УДК 338

Р.А. Обозов


ИСПОЛЬЗОВАНИЕ ПОКАЗАТЕЛЯ ВНУТРЕННЕЙ СТАВКИ ДОХОДНОСТИ

ПРИ ОЦЕНКЕ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ С НЕСТАНДАРТНЫМИ

ДЕНЕЖНЫМИ ПОТОКАМИ


Рассмотрены различные аспекты использования метода внутренней ставки доходности - IRR. Проведено сравнение методов IRR, MIRR, FMRR по принципам простоты применения, информативности, объективности и достоверности.


Ключевые слова: инвестиционный проект, внутренняя ставка доходности, чистая настоящая стоимость проекта, средневзвешенная стоимость капитала.


Метод внутренней ставки рентабельности ( IRR), ориентированный на увеличение стоимости бизнеса, подходит, наряду с методом чистой настоящей стоимости проекта (NPV), для выбора среди независимых проектов и является наиболее распространенным [1]. Эти два метода применяются совместно при оценке одного инвестиционного проекта. Отличительной особенностью метода IRR является то, что все поступления и затраты по проекту приводятся к настоящей стоимости не на основе задаваемой извне средневзвешенной стоимости капитала WACC, а на основе внутренней ставки рентабельности самого проекта. IRR определяется как ставка доходности (предположим, некоторое число Ê), при которой NPV равна нулю и все затраты окупаются. Недостаток определенного так показателя IRR заключается в том, что уравнение NPV(Ê)=0 не обязательно имеет один положительный корень. Оно может вообще не иметь корней или иметь несколько положительных. Такая особенность наблюдается, когда затраты осуществляются не только в начале, но и в середине или конце расчетного периода. В частности, для проекта, имеющего зависимость NPV(E), приведенную на рисунке б, IRR отсутствует [2].


NPV

NPV









E

E




а) б)


Рис. Зависимость NPV от нормы дисконта:

а –стандартные денежные потоки; б – нестандартные денежные потоки


Полученная чистая настоящая стоимость проекта сопоставляется с чистой настоящей стоимостью затрат на привлечение капитала (эта стоимость принимается за минимальный допустимый уровень доходности). Из рассматриваемых проектов предпочтение отдают наиболее прибыльным и инвестиционный портфель формируют с наивысшей суммарной чистой настоящей стоимостью. В то же время метод не лишен недостатков. Во-первых, далеко не всегда, базируясь на IRR, можно выделить самый прибыльный проект. Во-вторых, ситуация, когда все промежуточные положительные денежные потоки будут тотчас реинвестироваться в проект, да еще и по внутренней ставке доходности, кажется малореалистичной. Разумеется, часть средств уйдет на выплату дивидендов, а часть может быть при желании инвестирована в менее доходные, но вместе с тем и менее рискованные объекты.

Рассмотрим различные варианты денежных потоков, и соответствующие возможные ситуации с показателем IRR.

Пример 1:


t=0 t=1 t=2



-10 +25 +25





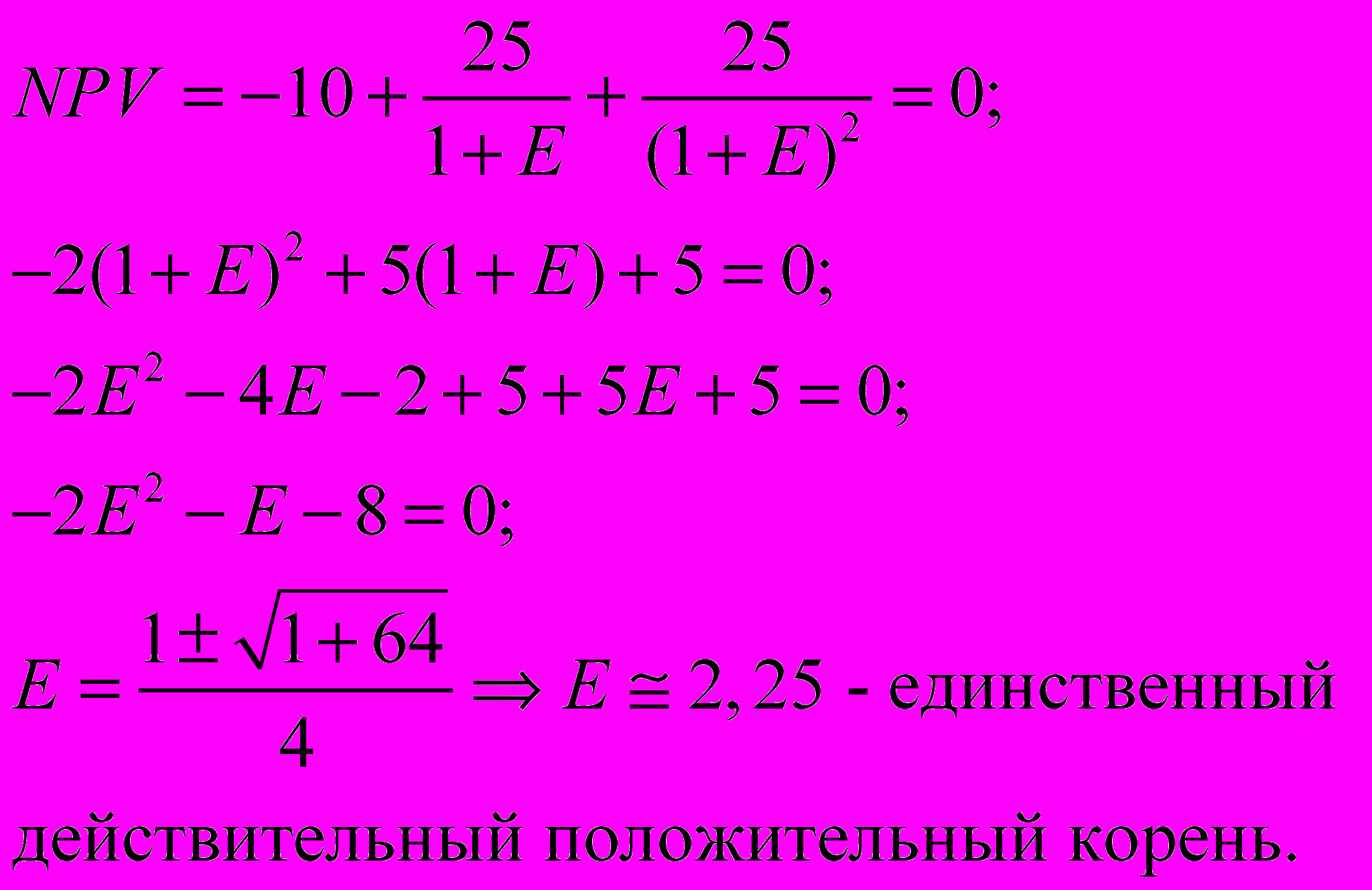
Пример 2:


t=0 t=1 t=2




-10 +25 -25





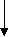
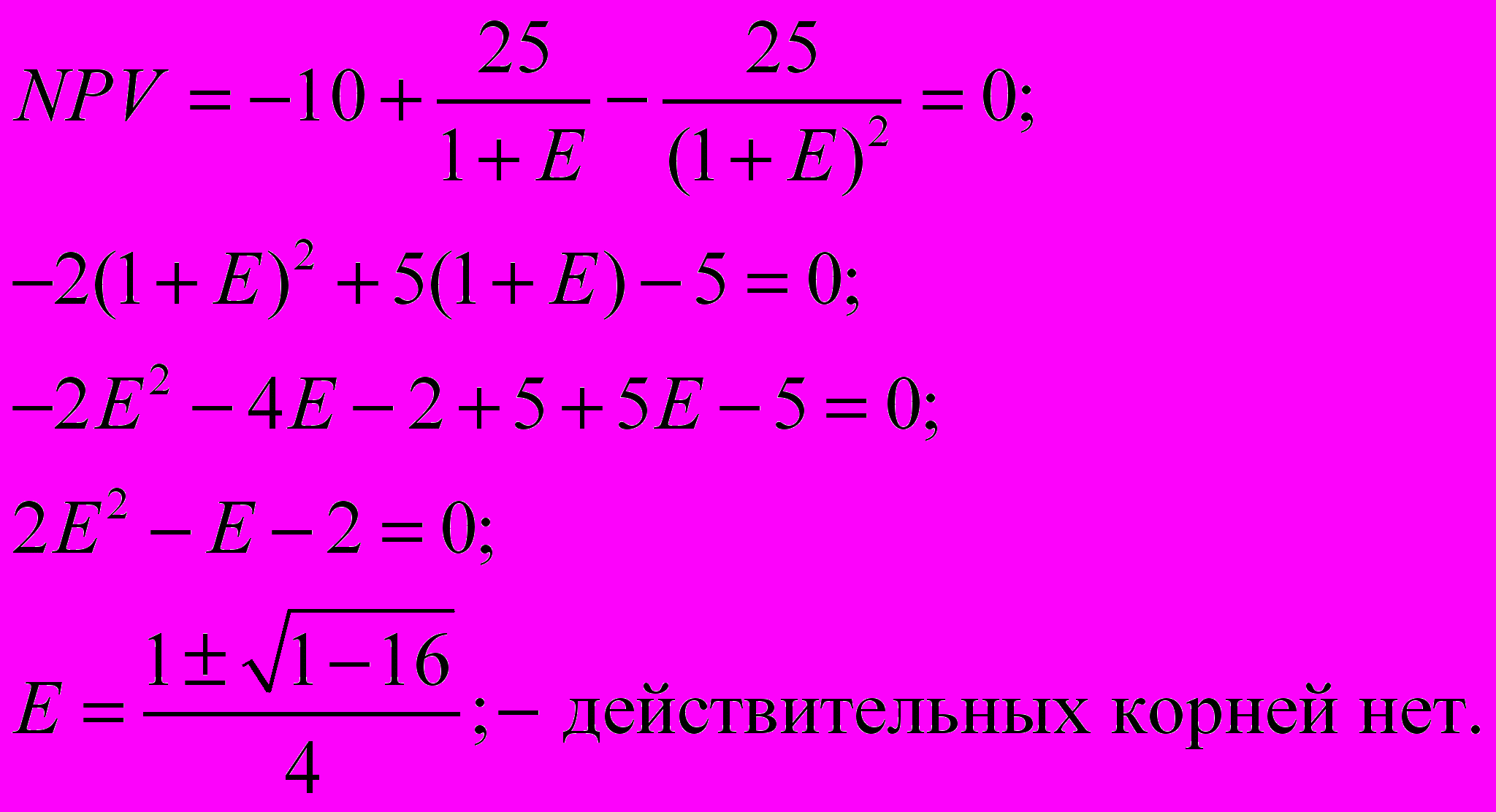
Пример 3:


t=0 t=1 t=2




-5 +25 -25





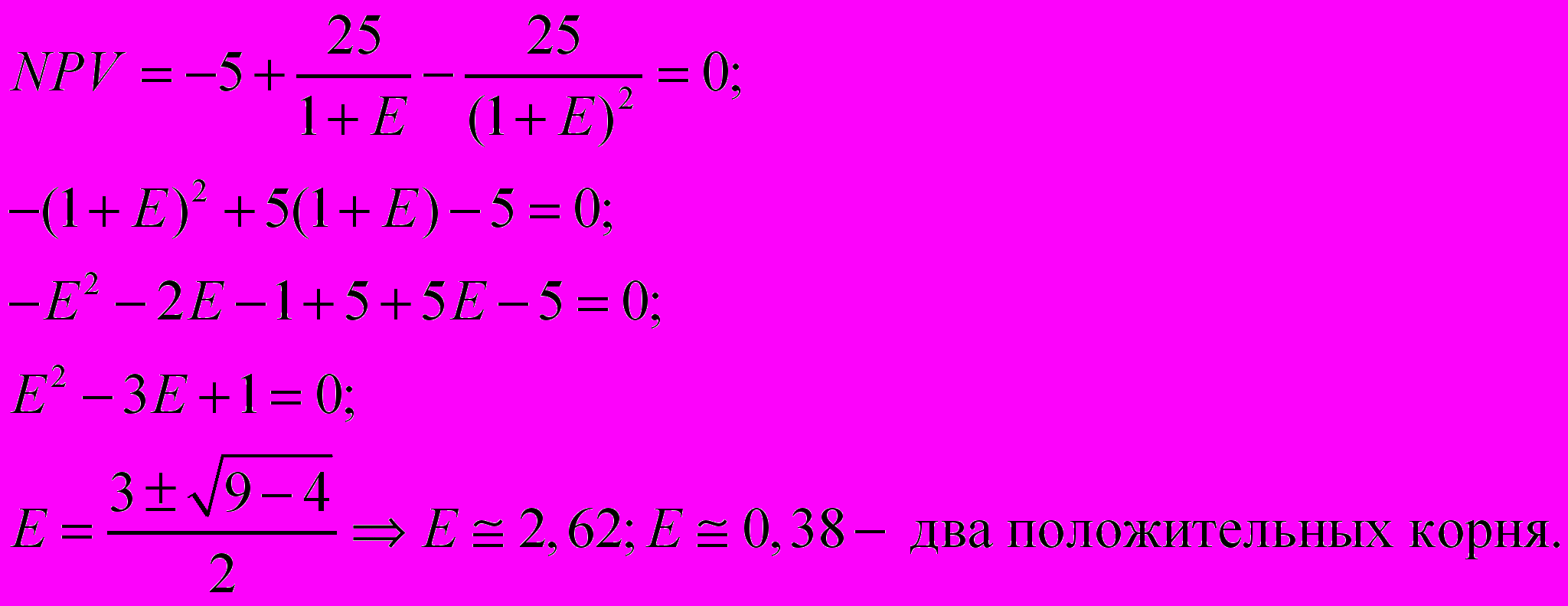
Во избежание этих трудностей выработано более развернутое определение IRR: IRR – это положительное число Ê, если оно существует, такое, что NPV:

- при норме дисконта E= Ê обращается в 0;

• при всех E > Ê – отрицательна;
  
• при всех 0 ≤ E < Ê – положительна.
  

Определенная так IRR, если только существует, всегда единственная.

Кроме того, существуют различные модификации внутренней нормы рентабельности – MIRR, FMRR.

Поскольку условие, согласно которому депозитная ставка «следит» за IRR, явно нереалистично, было предложено несколько алгоритмов, улучшающих IRR. Все они основаны на приведении денежного потока к стандартному виду: вначале отрицательные значения элементов потока, потом неотрицательные (положительные или нулевые). Указанное приведение базируется на дополнительно задаваемой извне (экзогенной) информации, по крайней мере на значениях депозитного процента и/или нормы дисконта. Алгоритм решает задачу определения предельной ставки, под которую можно взять кредит, равный всем внешним по отношению к проекту средствам, с тем чтобы за время существования проекта его можно было вернуть (с процентами). В общем виде данный алгоритм сводится к движению по расчетному периоду (от конца к началу или от начала к концу) и компенсации отрицательных значений денежного потока на каждом шаге, кроме начального (или неразрывной группы шагов, расположенных в начале расчетного периода). Заметим, что метод компенсации отрицательных значений денежного потока применим не только к вычислению варианта IRR. В дальнейшем метод обобщается для использования произвольной схемы финансирования и тем самым становится пригодным для практического применения [3].

Другой путь модифицирования IRR также требует знания депозитной ставки. Обозначим ее через 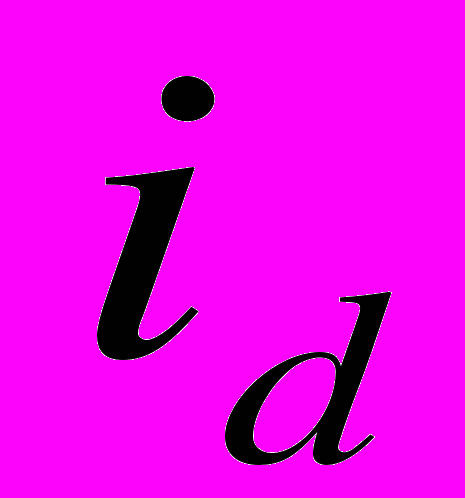(это должна быть ставка наиболее выгодного размещения средств, не обязательно ставка депозита). Существует несколько разновидностей метода МIRR. При одной из них денежный поток преобразуется следующим образом. Все отрицательные значения потока дисконтируются по ставке 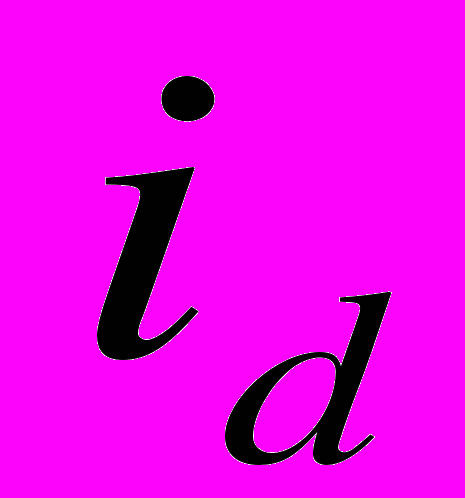к началу расчетного периода. Все положительные значения компаундируются (также по ставке 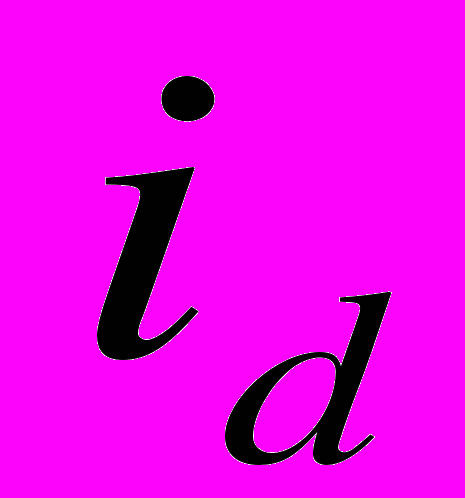) к концу расчетного периода. Получается «двухточечный» поток: на начальном шаге —минус, потом — нули и на конечном шаге — плюс. MIRR — это IRR преобразованного таким способом потока. Ее можно записать и в виде следующей формулы:

,


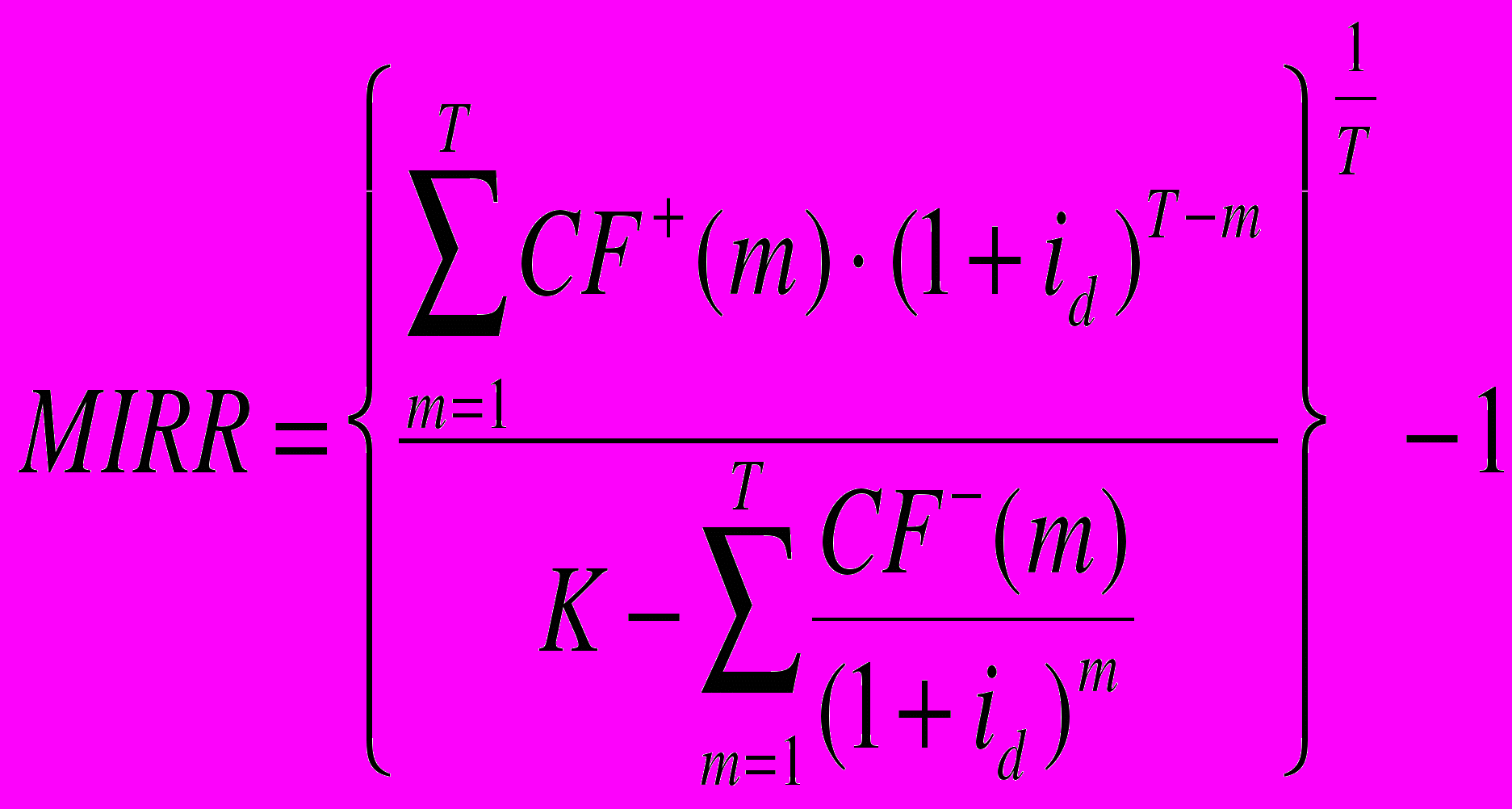где 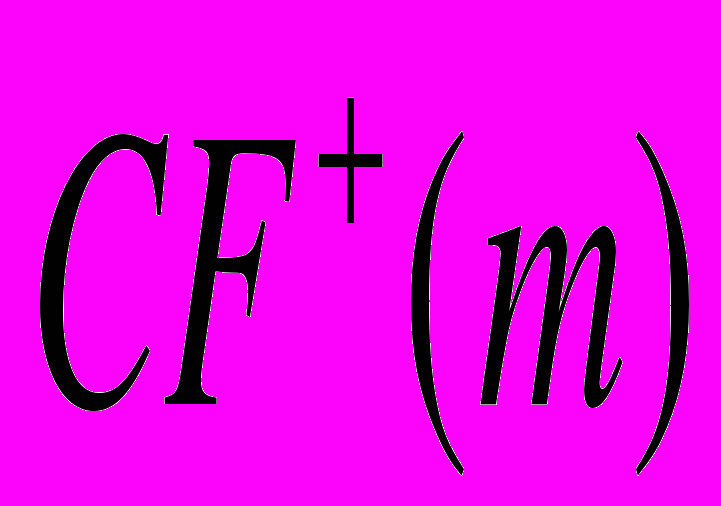и 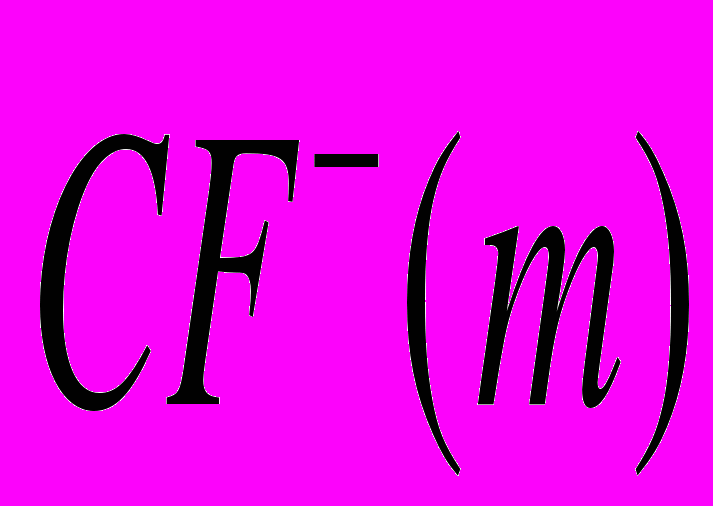- значения денежного потока на шаге m при условии, что они соответственно положительны и отрицательны. Следовательно, 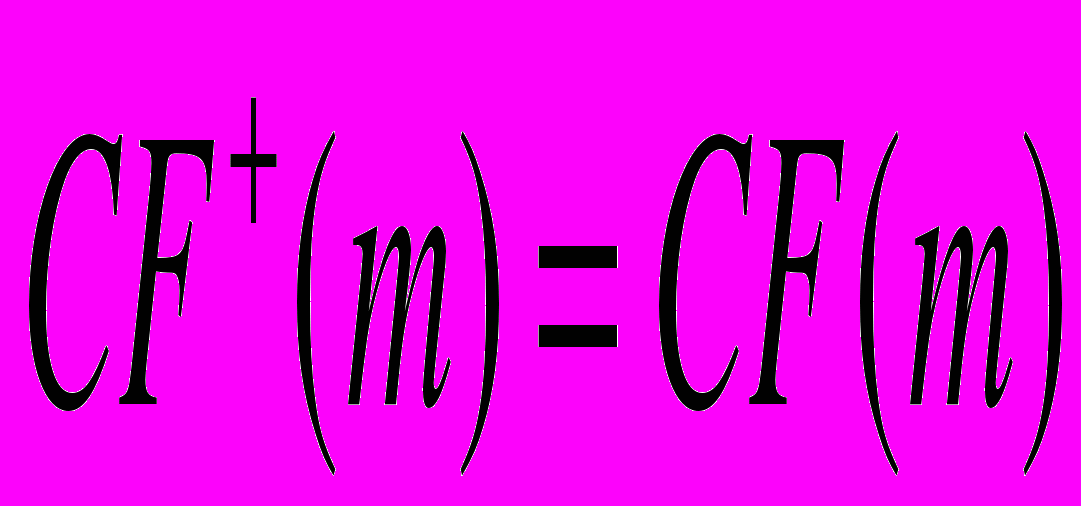, если эта величина положительна.

Основной недостаток метода связан с невозможностью использовать значение MIRR для заключения об эффективности проекта. Действительно, чтобы сделать вывод об эффективности проекта по показателю IRR, надо сравнить его с нормой дисконта. А с чем сравнивать MIRR? Сторонники метода часто сравнивают ее с депозитной ставкой i_d, исходя из того, что если MIRR> i_d, то вложение денег в проект выгоднее, чем на депозит, и проект эффективен. Однако такое сравнение полностью игнорирует риск, который у проекта может быть выше, чем при внесении денег на депозит. Поэтому логично бы было сравнивать MIRR (как и IRR) с заданной извне нормой дисконта E (которая часто и принимается равной сумме депозитного процента и премии за риск). Однако тогда заключения о неэффективности проекта нередко оказываются ошибочными.

Дальнейшим обобщением IRR является ставка дохода финансового менеджмента (FMRR). Как и при вычислении МIRR, для определения значения этого показателя отрицательные элементы денежного потока приводятся к началу расчетного периода (дисконтируются), а положительные - к его концу (компаундируются), но не по одной, а по двум различным ставкам приведения, задаваемым экзогенно (извне). Дисконтирование при этом выполняется по так называемой безопасной, ликвидной посленалоговой ставке (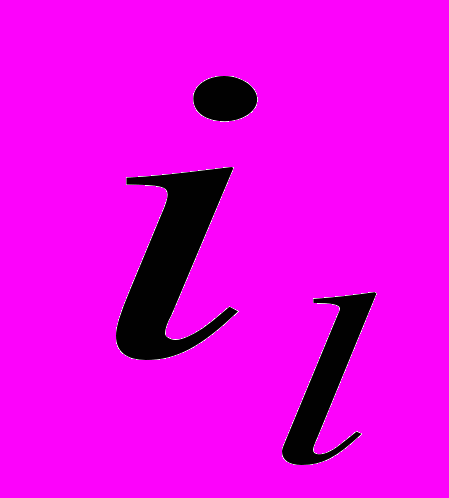), а компаундирование - по другой ставке (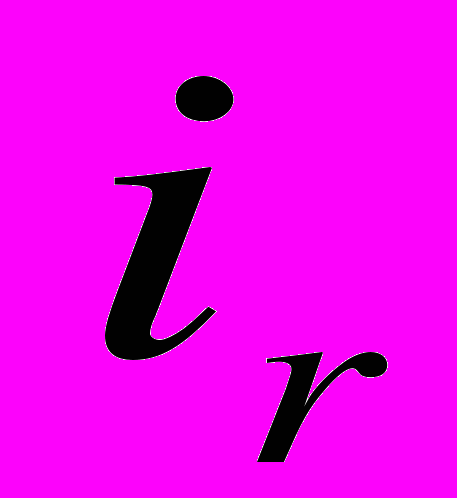), которая называется круговой посленалоговой ставкой. Преобразованный денежный поток вновь становится «двухточечным», а расчетная формула для FMRR принимает вид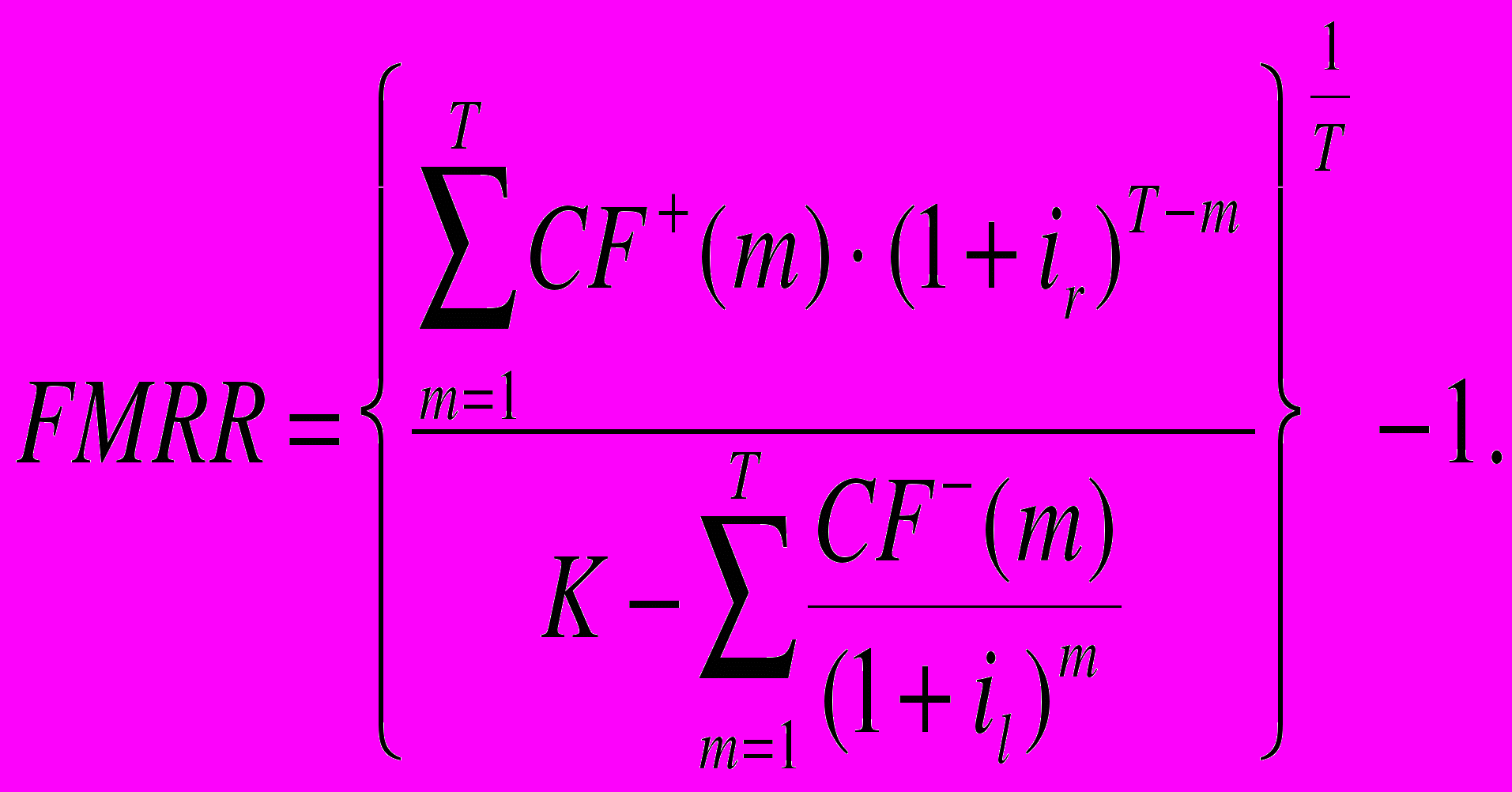





Недостатки FMRR такие же, как и у MIRR. Кроме того, наличие двух экзогенно задаваемых параметров (i_l и i_r) увеличивает степень неопределенности полученного результата. Правда, некоторые авторы считают, что за счет этих двух параметров увеличивается число степеней свободы и гибкость вычислений. Это, конечно, верно, но увеличение числа степеней свободы - достоинство только тогда, когда известно, как ими воспользоваться. В данном случае требуются определенные правила задания ставок i_l и i_r , чего как раз и нет. Несмотря на то, что FMRR применяется в некоторых компьютерных системах для инвестиционных расчетов, например в СОМFАР III Ехреrt, широкого распространения этот показатель не получил (в основном из-за необходимости задавать две априорные ставки).

Все перечисленные модифицированные IRR обладают тем свойством, что при заданном денежном потоке они определяются однозначно.


СПИСОК ЛИТЕРАТУРЫ

1. Сироткин, В. Б. Финансовый менеджмент компаний: учеб. пособие/ В.Б. Сироткин. - СПб.:СПбГУАП, 2001.
   
2. Кулаков, Н. Оценка инвестиционных проектов: сб. науч. тр. / Н. Кулаков, С. Подоляко. - М.: РосЗИТЛП, 2004.
   
3. Коссов, В.В. Методические рекомендации по оценке эффективности инвестиционных проектов/ В.В. Коссов, В.Н. Лившиц, А.Г. Шахназаров. - М.:Экономика, 2000.
   

Материал поступил в редколлегию 5.11.09.