Методы оптимизации запросов в реляционных системах

Вид материала

Документы

Содержание 1. Оптимизатор System R 2. Пространство поиска 2.1 Коммутативность операций 2.1.1 Обобщение последовательности соединений 2.1.2 Внешние и обычные соединения 2.1.3 Группировки и соединения 2.2 Сведение запросов с несколькими блоками к одноблочным запросам 2.2.1 Слияние представлений 2.2.2 Слияние вложенных подзапросов Я предполагаю, что эта операция не устраняет дубликаты. 2.3 Использование техники полусоединений для оптимизации запросов с несколькими блоками 3. Статистики и оценка стоимости 3.1 Статистические сводки данных 3.1.1 Статистическая информация о базовых данных 3.1.2 Оценка статистики базовых данных 3.1.3 Распространение статистической информации 3.2 Вычисление стоимости 4. Архитектуры перебора 5. За пределами основ 5.1 Распределенные и параллельные базы данных ... Полное содержание

Подобный материал:

• Решение задач глобальной оптимизации большой размерности на многопроцессорных комплексах, 143.77kb.
• Петербургский Государственный Университет Математико-Механический Факультет Кафедра, 596.99kb.
• Календарный план учебных занятий по дисциплине Компьютерный дизайн оптических наноструктур,, 39.38kb.
• Рабочей программы дисциплины Системы управления базами данных по направлению подготовки, 20.59kb.
• Методы оптимизации энергопотребления в микроэлектронных системах, 490.32kb.
• Конспект лекций по Методам оптимизации для студентов, обучающихся по специальности, 41.05kb.
• Концепция системного подхода при проектировании сапр. Последовательный метод компоновки, 29.25kb.
• Учебной дисциплины «Методы оптимизации» для направления 010400. 62 «Прикладная математика, 40.12kb.
• Рабочая учебная программа по дисциплине «Методы оптимизации» Направление №230100 «Информатика, 129.28kb.
• Рабочая программа учебной дисциплины (модуля) методы оптимизации, 164.09kb.

Методы оптимизации запросов в реляционных системах


С. Чаудхари,
Системы Управления Базами Данных


С начала 70-х была выполнена значительная работа в области оптимизации запросов. В короткой статье трудно охватить всю эту большую работу вширь и вглубь. Поэтому я решил сосредоточиться прежде всего на оптимизации SQL-запросов в реляционных системах баз данных и представить свое пристрастное и неполное видение этой области. Целью данной статьи не является представление исчерпывающего обзора, а скорее объяснение основ и демонстрация образцов значительных работ в этой области. Я хотел бы принести извинения многим людям, внесшим свой вклад в оптимизацию запросов, которых явно не упоминаю по своему недосмотру или из-за недостатка места. В обзоре для простоты изложения опущены технические детали.

Введение


Реляционные языки запросов обеспечивают высокоуровневый «декларативный» интерфейс для доступа к данным, хранимым в реляционных базах данных. Со временем появился язык SQL [41] как стандарт реляционных языков запросов. Двумя ключевыми подкомпонентами компонента вычисления запросов в SQL-ориентированной системе баз данных являются оптимизатор запросов и подсистема выполнения запросов.

Подсистема выполнения запросов реализует набор физических операций. На вход каждой операции поступают один или несколько потоков данных, и на выходе формируется поток данных. Примерами физических операций являются сортировка (внешняя), последовательное сканирование, индексное сканирование, соединение методом вложенных циклов и соединение сортировкой и слиянием. Я называю эти операции физическими, поскольку они не обязательно связаны один к одному с реляционными операциями. Проще всего представлять физические операции как куски кода, которые используются в качестве строительных блоков для обеспечения возможности выполнения SQL-запросов. Абстрактным представлением такого выполнения является дерево физических операций, пример которого показан на рис. 1. Дуги в дереве операций представляют потоки данных между операциями. Мы используем термины «дерево физических операций» и «план выполнения» (или просто план) в одном и том же смысле. Подсистема выполнения отвечает за выполнение плана, что приводит к формированию ответов на запросы. Следовательно, возможности подсистемы выполнения запросов определяют структуру допустимых деревьев операций. В [21] читатель может найти обзор методов вычисления запросов.


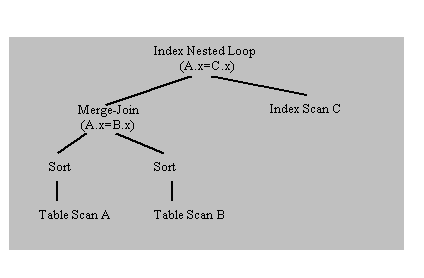
Рис. 1. Дерево операций.

Оптимизатор запросов отвечает за генерацию ввода для подсистемы выполнения. Он принимает на входе представление SQL-запроса после грамматического разбора и отвечает за генерацию эффективного плана выполнения данного SQL-запроса, исходя из тех планов, которые составляют пространство возможных планов выполнения. Задача оптимизатора нетривиальна, потому что для заданного SQL-запроса может существовать большое число возможных деревьев операций:

• Алгебраическое представление данного запроса может быть преобразовано во многие другие логически эквивалентные алгебраические представления; например, Join (Join (A,B),C) = Join (Join (B,C),A)
  
• Для данного алгебраического представления может существовать много деревьев операций, реализующих алгебраическое выражение; например, в системе баз данных обычно поддерживается несколько алгоритмов соединения.
  

Кроме того, пропускная способность, или время ответа системы при выполнении этих планов может весьма различаться. Поэтому здравый выбор плана выполнения, производимый оптимизатором, имеет критическое значение. Таким образом, к оптимизации запросов можно относиться как к сложной поисковой проблеме. Для того чтобы решить эту проблему, нам требуется обеспечить:

• Пространство планов (пространство поиска).
  
• Метод оценки стоимости, чтобы можно было оценить каждый план в каждом пространстве поиска. Интуитивно, это оценка ресурсов, требуемых для выполнения плана.
  
• Алгоритм перебора, который может осуществлять поиск в пространстве планов выполнения.
  

Желаемым оптимизатором является такой, в котором
1) пространство поиска включает планы с низкой стоимостью;
2) метод оценок является точным;
3) алгоритм перебора эффективен.

Каждая из этих трех задача нетривиальна, и из-за этого построение хорошего оптимизатора является громадной работой.

Мы начинаем с обсуждения подхода к оптимизации в System R, поскольку это был необыкновенно элегантный подход, который питал многие последующие работы в области оптимизации. В разделе 4 мы обсудим, что представляет собой пространство поиска, анализируемое оптимизатором. В этом разделе представлены алгебраические преобразования, включаемые в пространство поиска. Раздел 5 посвящается проблеме оценки стоимости. В разделе 6 мы сосредоточимся на теме перебора пространства поиска. Это завершает обсуждение базовых основ оптимизации. В разделе 7 мы обсудим некоторые современные разработки в области оптимизации запросов.

1. Оптимизатор System R


Проект System R существенно улучшил состояние оптимизации запросов в реляционных системах. Идеи [55], внедренные во многие коммерческие оптимизаторы, продолжают оставаться удивительно современными. Я представлю здесь некоторые из этих важных идей в контексте запросов Select-Project-Join (SPJ). Класс SPJ-запросов тесно связан с конъюнктивными запросами, которые обычно изучаются в теории баз данных, и включает эти запросы.

Пространство поиска оптимизатора System R в контексте SPJ-запросов состоит из деревьев операций, которые соответствуют линейной последовательности операций соединения; например, последовательность Join (Join (Join (A, B), C), D) проиллюстрирована на рис. 2(a). Такие последовательности логически эквивалентны, поскольку соединения обладают свойствами ассоциативности и коммутативности. Для реализации операции соединения могут быть использованы методы вложенных циклов или сортировки и слияния. В каждом узле сканирования может использоваться индексное сканирование (на основе кластеризованного или некластеризованного индекса) или последовательное сканирование. Наконец, предикаты вычисляются как можно раньше.


Рис. 2. Линейное (a) и кустовое (b) соединения.

Стоимостная модель присваивает оценочную стоимость любому частичному или полному плану в пространстве поиска. Она также определяет оценочный размер потока данных для вывода каждой операции плана. Эти оценки базируются на следующем:

a) набор статистик, поддерживаемых для отношений и индексов, например, число страниц данных в отношении, число страниц в индексе, число различных значений в столбце;

b) формулы для оценки селективности предикатов и для прогнозирования размера выходного потока данных для каждого узла-операции. Например, размер вывода соединения оценивается путем перемножения размеров отношений-операндов и применения совместной селективности всех относящихся к соединению предикатов;

c) формулы для оценки стоимости расходов ЦП и ввода/вывода при выполнении запроса для каждой операции. В этих формулах принимаются во внимание статистические свойства входных потоков данных операции, существующие методы доступа к данным входных потоков, какой-либо имеющийся порядок данных входного потока (например, если входной поток упорядочен, то стоимость соединения методом сортировки и слияния может быть существенно снижена). Кроме того, проверяется также, не будут ли иметь какой-то порядок данные в выходном потоке.

В оценочной модели механизмы (a)-(c) используются для вычисления для операций плана и связывания с этими операциями следующей информации (вычисление и связывание происходят в направлении от листьев к корню дерева):

1) размер выходного потока данных узла-операции;

2) любая упорядоченность кортежей, создаваемая или сохраняемая в выходном потоке данных узла-операции;

3) оценочная стоимость выполнения операции (и общая стоимость произведенного к этому моменту частичного плана).

Алгоритм перебора в оптимизаторе System R демонстрирует два важных метода: использование динамического программирования и использование интересных упорядочений.

Суть подхода динамического программирования основывается на предположении, что оценочная модель удовлетворяет принципам оптимальности. Более точно - предполагается, что для получения оптимального плана SPJ-запроса Q, состоящего из k соединений, достаточно рассматривать только оптимальные планы для подвыражений Q, которые состоят из (k-1) соединений, и расширять эти планы добавочным соединением. Другими словами, для определения оптимального плана выполнения Q не требуется рассматривать не самые оптимальные планы для подвыражений Q (называемых также подзапросами) с (k-1) соединениями. Соответственно, основанный на динамическом программировании алгоритм перебора представляет SPJ-запрос Q как множество соединяемых отношений { R1, ..., Rn }. Алгоритм перебора работает снизу вверх. В конце j-го шага алгоритм производит оптимальные планы для всех подзапросов размера j. Для получения оптимального плана для подзапроса, включающего (j+1) соединение, мы рассматриваем все возможные способы конструирования плана путем расширения планов, построенных на j-ом шаге. Например, оптимальный план для {R1, R2, R3, R4} получается выбором плана с наименьшей стоимостью из оптимальных планов для:

1) Join ( {R1, R2, R3}, R4} )


2) Join ( {R1, R2, R4}, R3} )


3) Join ( {R1, R3, R4}, R2} )


4) Join ( {R2, R3, R4}, R1} )

Остальные планы для {R1, R2, R3, R4} можно отбросить. Подход динамического программирования работает существенно быстрее, чем «наивный» перебор, поскольку требуется перебрать O(n2n-1) планов вместо O(n!).

Вторым важным аспектом оптимизатора System R является рассмотрение интересных упорядочений. Возьмем теперь запрос, представляющий соединение между {R1, R2, R3} с предикатами R1.a = R2.b = R3.c. Предположим, что стоимости планов для подзапроса {R1, R2} оценены в x и y для методов вложенных циклов и сортировки и слияния соответственно, причем x < y. В таком случае при рассмотрении плана для {R1, R2, R3} мы не принимаем во внимание план, согласно которому R1 и R2 соединяются методом сортировки и слияния. Однако заметим, что если для соединения R1 и R2 используется метод сортировки и слияния, то результат соединения упорядочен по a. Этот порядок сортировки может существенно уменьшить стоимость соединения с R3. Следовательно, отбрасывание плана, включающего соединение сортировкой и слиянием R1 и R2, может привести к неоптимальности глобального плана. Проблема возникает по той причине, что в выходном потоке результата соединения R1 и R2 имеется упорядоченность кортежей, которая полезна для последующего соединения. Однако соединение методом вложенных циклов не обеспечивает такого упорядочения. Поэтому для заданного запроса System R определяет порядок кортежей, который потенциально важен для планов выполнения запроса (отсюда название «интересные упорядочения»). К тому же в оптимизаторе System R два плана являются сравнимыми только в том случае, когда они представляют одно и то же выражение и, кроме того, обеспечивают одно и то же интересное упорядочение. Идея интересных упорядочений позже была обобщена до идеи физических свойств [22] и интенсивно используется в современных оптимизаторах. На интуитивном уровне физическое свойство - это любая характеристика плана, не являющаяся общей для всех планов одного и того же выражения, но могущая влиять на последующие операции. Наконец, заметим, что подход System R принятия во внимание физических свойств демонстрирует простой механизм управления любым отклонением от принципа оптимальности, не обязательно связанным с физическими свойствами.

Несмотря на элегантность подхода System R, его невозможно расширить для включения других логических преобразований (в добавление к изменению порядка соединений), расширяющих пространство поиска. Это привело к разработке более расширяемых архитектур оптимизации. Однако использование оптимизации на основе оценочной стоимости, динамического программирования и интересных упорядочений сильно повлияло на последующие разработки в области оптимизации.

2. Пространство поиска


Как отмечалось в разделе 2, пространство поиска для оптимизации зависит от набора алгебраических преобразований, сохраняющих эквивалентность, и набора физических операций, поддерживаемых в оптимизаторе. В этом разделе я буду обсуждать некоторые из обнаруженных важных алгебраических преобразований. Следует заметить, что преобразования не обязательно снижают стоимость, и поэтому для гарантирования положительного результата их следует применять в стиле основанного на оценочной стоимости алгоритма перебора.

В жизненном цикле оптимизации оптимизатор может использовать несколько представлений запроса. Исходным представлением часто является дерево грамматического разбора, а окончательное представление - это дерево операций. В качестве промежуточного представления используются также деревья логических операций (называемых еще и деревьями запросов), которые изображают алгебраические выражения. На рис. 3 приведен пример дерева запроса. Часто узлы деревьев запроса аннотируются дополнительной информацией.


Рис. 3. Дерево запроса.

2.1 Коммутативность операций


Большой и важный класс преобразований основан на коммутативности операций. В этом подразделе мы рассмотрим примеры таких преобразований.

2.1.1 Обобщение последовательности соединений


Во многих системах последовательность операций соединения синтаксически ограничивается для ограничения размеров пространства поиска. Например, в проекте System R рассматриваются только линейные последовательности операций соединения, и декартово произведение отношений вычисляется только после всех соединений.

Поскольку операции соединения коммутативны, последовательность соединений в дереве операций не обязательно должна быть линейной. В частности, запрос, состоящий в соединении отношений R1, R2, R3, R4, может быть алгебраически представлен и вычислен как Join ( Join (A,B), Join (C,D) ). Соответствующие деревья операций (и запросов) называются кустовыми, пример такого дерева приведен на рис. 2(b). Кустовые последовательности соединений требуют материализации промежуточных отношений. Хотя кустовые деревья могут привести к более дешевому плану выполнения запроса, они значительно увеличивают расходы на перебор пространства поиска. (Наиболее велика не стоимость генерации синтаксических порядков соединений. Интенсивные вычисления требуются для выбора физических операций и оценки стоимости каждого возможного плана.) При наличии некоторых исследований достоинств использования кустовых последовательностей соединений, до сих пор в большинстве систем используются линейные последовательности соединений и только ограниченные подмножества кустовых деревьев соединения.

Откладывание вычисления декартова произведения тоже может привести к плохой эффективности. Для многих запросов категории поддержки принятия решений, у которых граф запроса образует звезду, было замечено, что вычисление декартова произведения соответствующих узлов (таблиц «измерений» в терминологии OLAP [7]) приводит к значительному снижению стоимости.

В расширяемых системах поведение компонента перебора соединений может адаптироваться к конкретному запросу, ограничивая «кустистость» деревьев соединений или разрешая/запрещая вычисление декартовых произведений [46]. Однако нетривиально заранее определить воздействие такой настройки на качество и стоимость поиска.

2.1.2 Внешние и обычные соединения


Одностороннее внешнее соединение - это несимметричная операция языка SQL, которая сохраняет все кортежи одного из отношений-операндов. Симметричное внешнее соединение сохраняет кортежи обоих отношений-операндов. Например, (R LOJ S), где LOJ обозначает левое внешнее соединение R и S, сохраняет все кортежи R. В результирующем отношении этой операции, кроме кортежей, получаемых при естественном соединении, содержатся все кортежи R, которые не удалось соединить с S (заполненные неопределенными значениями для всех атрибутов S). В отличие от естественных соединений последовательность внешних и обычных соединений нельзя произвольно изменять. Однако если имеются предикат обычного соединения между R и S и предикат внешнего соединения между S и T, то действует следующее тождество:
Join (R, S LOJ T) = Join (R,S) LOJ T

Если продолжать применять это правило ассоциативности, мы получим эквивалентное выражение, в котором вычисление «блока обычных соединений» предшествует «блоку внешних соединений». Впоследствии обычные соединения могут произвольно переупорядочиваться. Как и другие преобразования, это тождество следует применять на основе оценок. Тождества, приведенные в [53], определяют класс запросов, в которых можно изменять порядок обычных и внешних соединений.

2.1.3 Группировки и соединения


При традиционном выполнении SPJ-запроса с группировкой вычисление SPJ-компонента запроса предшествует группировке. Набор преобразований, описываемых в этом подразделе, делает возможным выполнять операцию группировки до соединения. Эти преобразования применимы к запросам с SELECT DISTINCT, так что это специальный случай группировки. Выполнение операции GROUP BY потенциально может привести к значительному сокращению числа кортежей, поскольку для каждого раздела отношения, выделяемого операцией группировки, она генерирует только один кортеж. Поэтому в некоторых случаях при выполнении сначала группировки стоимость соединения может быть существенно уменьшена. Более того, при наличии подходящего индекса операция группирования может быть выполнена недорого. Для случая, когда операцию группирования можно выполнить после соединения, существуют двойники таких преобразований. Эти преобразования описаны в [5, 60, 25, 6] (см. обзор в [4]).

В этом подразделе мы кратко обсудим конкретные случаи, в которых применимы преобразования, вызывающие выполнение группировки до соединения. Рассмотрим дерево запроса на рис. 4(a). Пусть R1 и R2 соединяются по внешнему ключу, столбцы агрегирования G все взяты из R1, а в состав набора столбцов группировки входит внешний ключ R1. Для такого запроса рассмотрим соответствующее дерево операций на рис. 4(b), где G1 = G. В этом дереве завершающее соединение может только сократить набор потенциальных разделов R1, созданных G1, но не может повлиять на разделы и на агрегаты, вычисляемые G1 на этих разделах, поскольку каждый кортеж R1 соединяется не более чем с одним кортежем R2. Следовательно, мы можем протолкнуть группировку вниз, как показано на рис. 4(b), и сохранить эквивалентность для произвольных агрегатных функций без побочного эффекта. На рис. 4(c) иллюстрируется пример, где преобразование вводит группировку, и представляется класс полезных примеров, где операция группировки выполняется поэтапно. Например, предположим, что в запросе, дерево операций которого показано на рис. 4(a), агрегатные функции вычисляются только на столбцах R1. В этих случаях введенный оператор группировки G1 разделяет отношение по столбцам R1 и вычисляет агрегатные функции на этих разделах. Однако на рис. 4(a) могут потребоваться истинные разделы, чтобы объединить несколько разделов, образованных G1, в один раздел (отображение много-к-одному). Это обеспечивает оператор группирования G. Такое поэтапное вычисление может быть полезным для уменьшения стоимости соединения по причине сокращения объема данных операцией группировки G1. Для возможности такой поэтапной агрегации требуется, чтобы агрегатные функции обладали тем свойством, что Agg (S U S") можно вычислить на основе AGG (S) и AGG(S"). Например, чтобы вычислить общий объем продаж для всех продуктов каждого отделения, мы можем использовать преобразование с рис. 4(c) для выполнения ранней агрегации и получения общего объема продаж для каждого продукта. Затем нам потребуется еще одна группировка, чтобы сложить объемы продаж всех продуктов, относящихся к одному отделению.


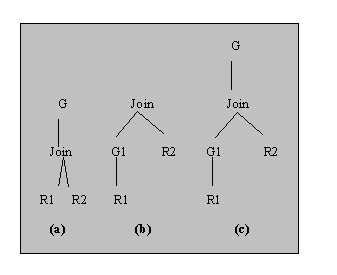
Рис. 4. Группировка и соединение.

2.2 Сведение запросов с несколькими блоками к одноблочным запросам


Описанная в этом подразделе техника в некоторых случаях позволяет сжать SQL-запрос с несколькими блоками в одноблочный запрос.

2.2.1 Слияние представлений


Рассмотрим конъюнктивный запрос с SELECT ANY. Если одно или несколько отношений, к которым адресуется запрос, являются представлениями, но каждое из них определено через конъюнктивный запрос, то определения представлений могут быть просто «раскрыты» для получения одноблочного SQL-запроса. Например, если запрос выглядит как Q = Join (R, V), а представление V определено как V = Join (S, T), то запрос Q может быть раскрыт в Join (R, Join (S,T) ), и его можно свободно переупорядочить. Для выполнения такого шага может потребоваться некоторое переименование переменных в определении представления.

К сожалению, это простое раскрытие не работает, когда представления более сложны, чем SPJ-запросы. Если одно или несколько представлений содержат SELECT DISTINCT, преобразования, перемещающие или поднимающие DISTINCT, нужно производить очень осторожно, чтобы корректно сохранить число дубликатов [49]. В более общем случае, когда представление содержит операцию группировки, для раскрытия требуется возможность поднятия операции группировки и затем свободного переупорядочения не только соединений, но и операции группировки для достижения оптимальности. Например, нам задается запрос типа того, который показан на рис. 4(b), и мы стараемся понять, как преобразовать его к форме рис. 4(a), чтобы R1 и R2 можно было свободно переупорядочивать. Хотя в этом случае могут использоваться преобразования из подраздела 4.1.3, это только подчеркивает сложность проблемы [6].

2.2.2 Слияние вложенных подзапросов


Рассмотрим следующий пример запроса с вложенными подзапросами из [13], где Emp# и Dept# - ключи соответствующих отношений.

SELECT Emp.Name


FROM Emp


WHERE Emp.Dept# IN


SELECT Dept.Dept# FROM Dept


WHERE Dept.Loc = "Denver"


AND Emp.Emp# = Dept.Mgr

Если для ответа на запрос используется семантика последовательного просмотра кортежей, то внутренний запрос вычисляется один раз для каждого кортежа отношения Emp. Очевидная оптимизация применима в том случае, когда внутренний блок запроса не содержит переменных из внешнего блока запроса (отсутствует корреляция). В таких случаях внутренний запрос требуется вычислить только один раз. Если во внутреннем блоке присутствует переменная из внешнего блока, мы говорим, что блоки запроса коррелируют. Например, в приведенном выше запросе Emp.Emp# действует как корреляционная переменная. Ким [35] и впоследствии другие исследователи [16, 13, 44] выявили методы устранения вложенности в SQL-запросе с корреляцией и «уплощения» его до запроса с одним блоком. Например, приведенный запрос со вложенностью приводится к

SELECT E.Name


FROM Emp.E, Dept D


WHERE E.Dept# = D.Dept#


AND D.Loc = "Denver"


AND E.Emp# = D.Mgr

Дайал [13] был первым, кто предложил алгебраическую трактовку устранения вложенности. Сложность проблемы зависит от структуры вложенности, т. е. от того, содержит ли вложенный запрос кванторы (например, ALL, EXISTS) и агрегаты. В простейшем случае, примером которого является приведенный выше пример, семантика перебора кортежей может моделироваться конструкцией Semijoin (Emp, Dept, Emp.Dept # = Dept.Dept#)(Semijoin (A,B,P) обозначает полусоединение A и B, сохраняющее атрибуты A; P - предикат полусоединения.). Опираясь на этот подход, нетрудно заметить, почему может быть произведено слияние запроса, поскольку:

Semijoin ( Emp, Dept, Emp.Dept# = Dept.Dept# ) = Project ( Join (Emp, Dept), Emp* )

Здесь предикатом соединения для Join (Emp, Dept) является Emp.Dept# = Dept.Dept#. Второй операнд операции Project ( Я предполагаю, что эта операция не устраняет дубликаты.) означает, что должны быть оставлены все столбцы отношения Emp.

Проблема становится гораздо более сложной, когда во вложенном подзапросе присутствуют агрегаты, поскольку теперь для слияния блоков требуется вытягивание наверх агрегации без нарушения семантики запроса со вложенными подзапросами. Эту дополнительную сложность иллюстрирует приводимый ниже пример из [44]:

SELECT Dept.name


FROM Dept


WHERE Dept.num-of-machines >= ( SELECT COUNT (Emp.*) FROM Emp


WHERE Dept.name = Emp.Dept_name )

Особенно сложно сохранить дубликаты и неопределенные отношения. Чтобы оценить эти тонкости, обратите внимание, что если для конкретного значения Dept.name (скажем, d) отсутствуют кортежи с совпадающим значением Emp.Dept_name, т. е. если значением предиката Dept.name = Emp.Dept_name является false для всех кортежей Emp, то кортеж отношения Dept со значением d войдет в результат запроса. Однако, если мы применим преобразование, использованное в первой части этого подраздела, то для dept d в результате запроса кортеж не появится, поскольку предикат соединения примет значение false. Поэтому при наличии агрегации мы должны сохранять все кортежи внутреннего блока запроса, используя левое внешнее соединение. В частности, приведенный запрос может быть корректно преобразован к виду

SELECT Dept.name


FROM Dept LEFT OUTER JOIN Emp On (Dept.name = Emp.Dept_name)


GROUP BY Dept.name


HAVING Dept.num-of-machines < COUNT (Emp.*)

Так что для этого класса запросов единственный слитый блок запроса содержит внешние соединения. Если структура вложенности блоков линейна, то этот подход применим и преобразования производят один блок с линейной последовательностью соединений и внешних соединений. Оказывается, что последовательность соединений и внешних соединений такова, что мы можем использовать правило ассоциативности, описанное в подразделе 4.2.1, для вычисления сначала всех соединений, а затем всех внешних соединений из этой последовательности. Другой подход к устранению вложенных подзапросов состоит в преобразовании запроса к такому виду, в котором используются табличные выражения или представления (и, конечно, это не одноблочный запрос). Это было направление работы Kim [35], которая впоследствии была усовершенствована в [44].

2.3 Использование техники полусоединений для оптимизации запросов с несколькими блоками


В предыдущем разделе я представил примеры того, как запросы, содержащие несколько блоков, могут быть свернуты к одному блоку. В этом разделе я обсуждаю дополнительный подход. Цель этого подхода состоит в использовании селективности предикатов за пределами одного блока. (Хотя эта техника исторически является производной от Магических Множеств и побочной передачи информации, я нахожу связь с полусоединениями более интуитивной и менее таинственной.) На концептуальном уровне подход напоминает идею использования полусоединения для распространения из узла A в удаленный узел B информации о подходящих значениях A, чтобы из B в A не посылались ненужные кортежи. В контексте запросов с несколькими блоками A и B находятся в разных блоках запроса, но являются частями одного и того же запроса, и поэтому не стоит вопрос о стоимости передачи данных. Информация, «получаемая от A», используется для сокращения объема вычислений в B, а также для гарантии того, что результаты, производимые в B, являются подходящими для A. Эта техника требует введения новых табличных выражений и представлений. Например, рассмотрим следующий запрос из [56]:

CREATE VIEW depAvgSal AS (


SELECT E.did, Avg (E.Sal) AS avgsal


FROM EMP E


GROUP BY E.did )


SELECT E.eid, E.sal


FROM EMP E, Dept D, DepAvgSal V


WHERE E.did = D.did AND E.did = V.did AND E.age < 30


AND D.budget > 100k AND E.sal > V.avgsal

Метод распознает, что мы можем создать множество подходящих E.did, выполняя соединение E и D в приведенном выше запросе и выполняя проекцию результата на E.did (с устранением дубликатов). Это множество можно передать представлению DepAvgSal для ограничения его вычисления. Это достигается с помощью следующих трех соединений:

CREATE VIEW PartialResult AS


( SELECT E.eid, E.sal, E.did


FROM Emp E, Dept D


WHERE E.did = D.did AND E.age < 30 AND D.budget > 100k)


CREATE VIEW Filter AS


( SELECT DISTINCT P.did FROM PartialResult P )


CREATE VIEW LimitedAvgSal AS


( SELECT E.did, Avg (E.Sal) AS avgsal


FROM Emp E, Filter F


WHERE E.did = F.did GROUP BY E.did )

В приводимом ниже переформулированном запросе эти представления используются для ограничения вычислений.

SELECT P.eid, P.sal


FROM PartialResult P, LimitedDepAvgSal V


WHERE P.did = V.did AND P.sal > V.avgsal

Эта техника может быть использована в запросах с несколькими блоками, содержащими представления (включая рекурсивные представления) и вложенные подзапросы [42, 43, 56, 57]. В каждом случае целью является избежание избыточных вычислений в представлениях или вложенных подзапросах. Важно также осознавать соотношение стоимостей вычисления представлений (представления PartialResult в приведенном примере) и использования таких представлений для снижения стоимости вычислений.

Формальная связь описанных преобразований с полусоединениями была недавно представлена в [56] и может служить основой для интеграции этой стратегии с основанными на оценках оптимизаторами. Заметим, что вырожденное применение этой техники состоит в передаче между блоками предикатов, а не результатов представлений. Этот упрощенный метод используется в распределенных и неоднородных базах данных и получил обобщение в [36].

3. Статистики и оценка стоимости


Для заданного запроса имеется много логических эквивалентных выражений и для каждого из выражений имеется много способов его реализации с помощью операций. Даже если мы игнорируем вычислительную сложность перебора пространства возможностей, остается вопрос принятия решения о том, какое дерево операций потребляет меньше всего ресурсов. В число ресурсов могут входить время центрального процессора, стоимость ввода/вывода, пропускная способность коммуникаций или комбинация всего этого. Поэтому фундаментальную значимость имеет способность точно и эффективно оценивать стоимость данного дерева операций (полного или частичного). Оценка стоимости должна быть точной, потому что оптимизация хороша ровно настолько, насколько хороша оценка стоимости. Оценка стоимости должна быть эффективной, поскольку она входит в самый внутренний цикл оптимизации запросов и много раз вызывается. Основы подхода оценок берут свое начало от System R.

1. Собирать статистические сводки по поводу хранимых данных.

2. Для данной операции на основе статистической информации о входных потоках операции данных определять:

a) статистическую информацию о выходном потоке данных;

b) оценочную стоимость выполнения операции.

Шаг 2 может применяться итерационно для дерева операций произвольной глубины для определения стоимости каждой из операций. Как только мы имеем оценки стоимости для каждого узла-операции, стоимость плана может быть получена путем комбинирования стоимостей узлов-операций дерева. В разделе 5.1 мы обсуждаем используемые при оптимизации на основе оценок статистические параметры хранимых данных и эффективные способы получения такой статистической информации. Мы также обсуждаем, как распространять такую статистическую информацию. Вопрос оценки стоимости физических операций обсуждается в разделе 5.2.

Важно осознавать различие между природой статистического свойства и стоимостью плана. Статистическое свойство выводного потока данных плана - это то же самое, что статистическое свойство любого другого плана того же запроса, но стоимость этого плана может отличаться от стоимости всех других планов. Другими словами, статистическая сводка - это логическое свойство, а стоимость плана - это свойство физическое.

3.1 Статистические сводки данных