Geum.ru

Классификация математических методов статистической обработки

Вид материалаДокументы

Содержание


Меры связи. Корреляционный анализ.
Подобный материал:
Классификация математических методов статистической обработки.

В зависимости от задач, стоящих перед психологом он выбирает те или иные методы обработки данных. Выбор соответствующего метода определяется

1 характеристиками выборки и их количеством (зависимые и независимые выборки, связанные и несвязанные выборки, распределение данных в выборке по соответствующему закону ( характер распределения данных в выборке), количество элементов в выборке, одинаковое количество элементов в разных выборках, количество выборок)

2 от решаемой задачи (задачи на выявление различий, на согласованность изменений, на прогноз изменения параметров характеристики, более полная классификация задач и соответствующих методов приведена в учебнике Ермолаева(приложение №3))

3 используемым типом измерительной шкалы (номинальная,ранговая(порядковая),интервальная, шкала отношений(в психологии используется крайне редко))

Каждому типу шкалы соответствуют свои методы математической обработки.


Этапы принятия статистических решений.

1 формулировка нулевой и альтернативной гипотезы

2 определение объема выборки (с точки зрения возможности сбора данных и остаточности для математической обработки) количество выборок определяется поставленной задачей.

3 выбор уровня значимости

4 выбор метода математической обработки

5 нахождение эмпирического значения критерия по экспериментальным данным.

6 нахождение соответствующих критических значений (соответствующих выбранному методу и уровню значимости)

7 построение оси значимости (и выбор соответствующей гипотезы)

В зависимости от полученных эмпирических данных могут использоваться параметрические и непараметрические методы. К параметрическим методам относятся методы, при расчете которых используются параметры выборки и учитывается закон их распределения. Эта группа методов может применяться для данных, измеренных в интервальной шкале и соответствующих нормальному закону распределения.

К непараметрическим методам относятся методы, использующие в расчетах частоты или ранги.

Использование непараметрических методов допускается при любом распределении данных. Как правило, непараметрические методы проще в расчетах и не требуют проверки соответствия данных закону распределения. Но они не позволяют оценить влияние двух и более признаков одновременно. Параметрические методы являются более мощными и способны выявить различия с большей вероятностью.


Задача

3, 6, 5, 9, 5, 6, 1, 2, 8, 5, 10, 1, 7, 11



Xi
1
2
3
5
6
7
8
9
10
11

Ti(частота встречания)
2
1
1
3
2
1
1
1
1
1



Корреляционный упорядоченный ряд представляет собой таблицу из двух строк, в первой обозначаются встречаемые значения, во второй частота их встречаемости.


Понятие о нормальном законе распределения.

В естественных науках существует понятие «нормы распределения», обладающее следующими характеристиками:

1 Чаще встречается значения, близкие к среднему арифметическому.

2 Большая часть значений лежит в интервале от X-3S(x)до X+3S(x) (правило трех сигм)



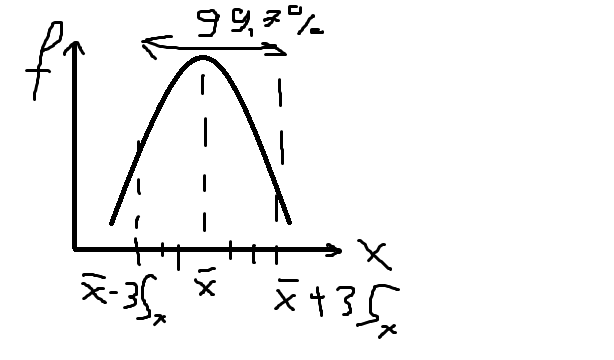
При изменении среднего арифметического форма графика кривой нормального распределения не меняет своей правильной колоколообразной формы, а лишь смещается влево или вправо. При изменении стандартного отклонения (среднеквадратического) меняется только ширина соответствующей кривой.

Для оценки соответствия распределения нормальному, применяется ряд методов:

Критерий Хи квадрат, понятие асимметриии эксцесса


Асимметрияколичественная мера, показывающая симметричность распределения, относительно среднего арифметического значения(при симметричном распределении асимметрии равна нулю. Коэффициент асимметрии рассчитывается по формуле

Эксцесс это количественная мера, определяющая форму верхней части кривой распределения. Обозначается буквой Е. Коэффициент эксцесса рассчитывается по формуле:



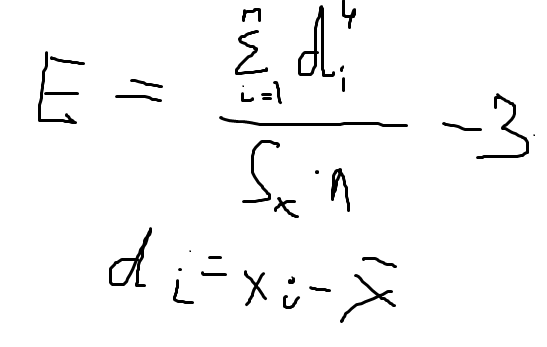
Проверка на соответствие нормальному закону необходима при использование параметрических методов.


Меры связи. Корреляционный анализ.

Под мерой связи понимается показатель определяющий связь между различными переменными.

y=f(x) В Психологии используется понятие статистической связи. Это связь между признаками и явлениями, обуславливающая изменение одного признака при изменениях другого. Одним из видов статистической связи является корреляционная связь. Корреляционная связь это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственно зависимости. Так как корреляционная связь не определяет причину изменений и не может сказать, что причиной изменений значений одного признака является изменение значений другого. Корреляционная связь может быть различных видов. На графиках показано соотношение значений одного психологического свойства или признака Y– уровень тревожности, X–количество задач решенных за время.

20 испытуемых.



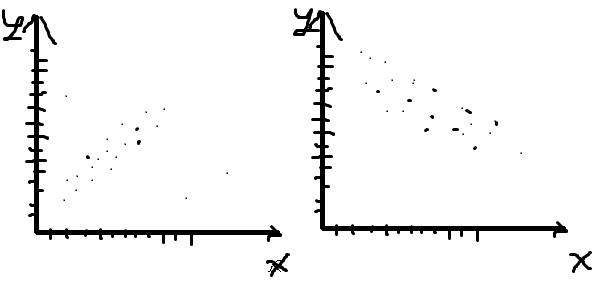
В обоих есть корреляционная связь.



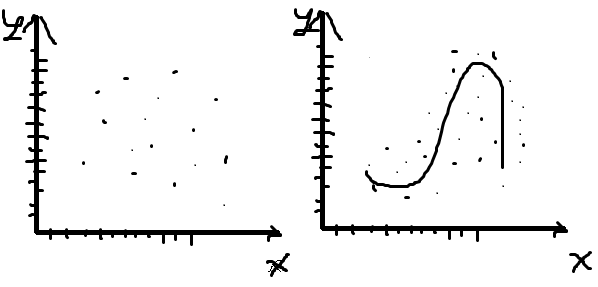
В третьем нет, в четвертом да


Линейная корреляционная связь – если значения переменной увеличиваются или уменьшаются, а значения второй переменной в среднем так же увеличиваются или уменьшаются.

Нелинейная корреляционная связь – если приувеличение значений одной характеристики характер изменения второй описывается любым криволинейным законом.

Линейная корреляционная связь может быть положительной или отрицательной. Положительная – если с увеличением значений первой переменной значения второй в среднем увеличиваются. Отрицательная - если с увеличением значений первой переменной значения второй в среднем убывают.

Анализ корреляционной связи позволяет определить тенденцию изменения результативного признака, при изменении величины факторного признака.

Порядок исследования корреляционной связи:

1 предварительный анализ свойств исследуемой выборки (оценка однородности выборки)

2 установление факта наличия связи, определение ее направления и формы.

3 измерение степени тесноты связи между признаками. Коэффициент корреляции (теснота связи определяется значением коэффициента корреляции)

4 построение регрессионной модели (нахождение аналитического выражения связи) (не всегда востребован)

5 оценка адекватности модели и ее практическое использование (адекватность – соответствие реальной связи аналитическому выражению)


Одним из важнейших условий применения корреляционного анализа является однородность выборки. Количественная оценка однородности проводится с помощью коэффициента вариации. Это выраженное в процентах отношение стандартного отклонения к среднему арифметическому. Выборка считается однородной, если коэффициент вариации не превышает 33%. Значение коэффициента корреляции лежит в пределах от -1 до +1. В зависимости от значения коэффициента корреляции определяется теснота связи.

Если R(xy) <=[0.3] то связи нет

Если [0.3]<=R(xy)<=[0.5]то связь слабая

Если [0.5]<=R(xy)<=[0.7] то связь умеренная

Если [0.7]<=R(xy)<=[1] то связь сильная

Расчет коэффициента корреляции зависит от типа используемых шкал.