Использование программы fieldexpert 3 pro для статистической обработки экспериментальных данных полевого опыта о. И. Акимова, Д. Н. Акимов Хакасский государственный университет им. Н. Ф. Катанова, г. Абакан

Вид материала

Документы

Содержание Данная программа рассчитывает математическую модель однофакторного дисперсионного анализа и содержит расчетные таблицы

Подобный материал:

• Управление внешнеэкономическим потенциалом региона, 83.87kb.
• Пути снижения затрат на производство продукции сельскохозяйственных предприятий, 70.63kb.
• Е. В. Мамаев Хакасский государственный университет им. Н. Ф. Катанова, Абакан, 36.6kb.
• Программа дисциплины «Методы обработки экспериментальных данных», 318.77kb.
• Приглашает студентов принять участие, 30.13kb.
• Этнопоэтическое своеобразие хакасской прозы 1930-1990-х, 268.36kb.
• Управление финансами предприятия, 322.6kb.
• Разработчики программы повышения квалификации: Кисляков В. Е., д т. н., проф., проф, 346.56kb.
• Хакасско алтайские литературные связи в системе взаимодействия литератур народов Российской, 355.75kb.
• Программа вступительных испытаний для лиц, поступающих на направление подготовки 050100., 246.3kb.

ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ FIELDEXPERT V1.3 PRO ДЛЯ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПОЛЕВОГО ОПЫТА

О. И. Акимова, Д.Н. Акимов

Хакасский государственный университет им. Н. Ф. Катанова, г. Абакан

Важнейшую роль в современной агрономической науке игра­ют статистические методы планирования исследований и обработки полученных данных. Современные математические методы составляют неотъемлемую часть процесса обработки и интерпретации результатов наблю­дений и опытов. Они позволяют извлечь максимум информации из исходных данных, оценить, насколько существенны, реальны различия между вариантами, установить коэффициенты уравне­ний регрессий качества продукции, свойств почвы и других показателей (Доспехов, 1967). Для обработки данных полевого опыта при написании курсовых, дипломных и диссертационных работ по агрономическим специальностям используются методы: дисперсионного анализа, корреляционного и вариационного. Сложность математических расчетов, особенно при постановке трех- и четырехфакторных опытов очевидна.

По заданию Аграрного факультета ХГУ им. Н.Ф. Катанова Акимовым Д.Н. была разработана компьютерная программа FieldExpert v1.3 Pro (свидетельство о государственной регистрации № 9455), предназначеная для статистической обработки экспериментальных данных полевого опыта в растениеводстве по методике Б.А. Доспехова (1985). Функциональные возможности пакета FieldExpert v1.3 Pro позволяют быстро и безошибочно провести обработку данных полевого опыта. Что позволит значительно повысить качество и методический уровень научных работ.

Данная программа рассчитывает математическую модель однофакторного дисперсионного анализа и содержит расчетные таблицы:

• «Суммы квадратов отклонений» для расчета:
  

• Количества повторений (l)
  
• Количества вариантов (n)
  
• N - критерия
  
• общей суммы квадратов (C_Y)
  
• суммы квадратов для вариантов (Cv)
  
• суммы квадратов для повторений (Cp)
  
• суммы квадратов для ошибки (Cz)
  
• «Результаты дисперсионного анализа» для расчёта:
  
  • Степеней свободы (n-1)
    
  • Среднего квадрата
    
  • Вклада факторов
    
  • F - фактического
    
  • F – теоретического
    
• «Оценка существенности главных эффектов» для расчёта:
  
  • Двухсторонних критических точек распределения Стьюдента
    
  • Ошибки опыта (Sx)
    
  • Ошибки разности средних (Sd)
    
  • Наименьшей существенной разницы (НСР)
    

При обработке двухфакторного дисперсионного комплекса кроме выше перечисленных показателей рассчитывается: оценка существенности частных различий, главных эффектов для первого и второго факторов и их взаимодействия.

При обработке данных трёхфакторного полевого опыта рассчитываются таблицы:

• «Таблица дисперсионного анализа» для расчёта:
  

• Сумм квадратов
  
• Количества степеней свободы
  
• Средних квадратов
  
• Вклада факторов
  
• F - фактического
  
• F – теоретического
  
• «Оценка частных различий» для расчёта:
  
  • Двухсторонней критической точки распределения Стьюдента
    
  • Наименьшей существенной разницы (НСР)
    
• «Оценка главных эффектов» для расчёта:
  
  • Двухсторонней критической точки распределения Стьюдента
    
  • Наименьшей существенной разницы (НСР)
    
• «Оценка для парных взаимодействий» для расчёта:
  
  • Двухсторонней критической точки распределения Стьюдента
    
  • Наименьшей существенной разницы (НСР)
    
• «Комбинации вариантов».
  

Программа четырехфакторного дисперсионного анализа проводит также оценку существенности тройных взаимодействий.

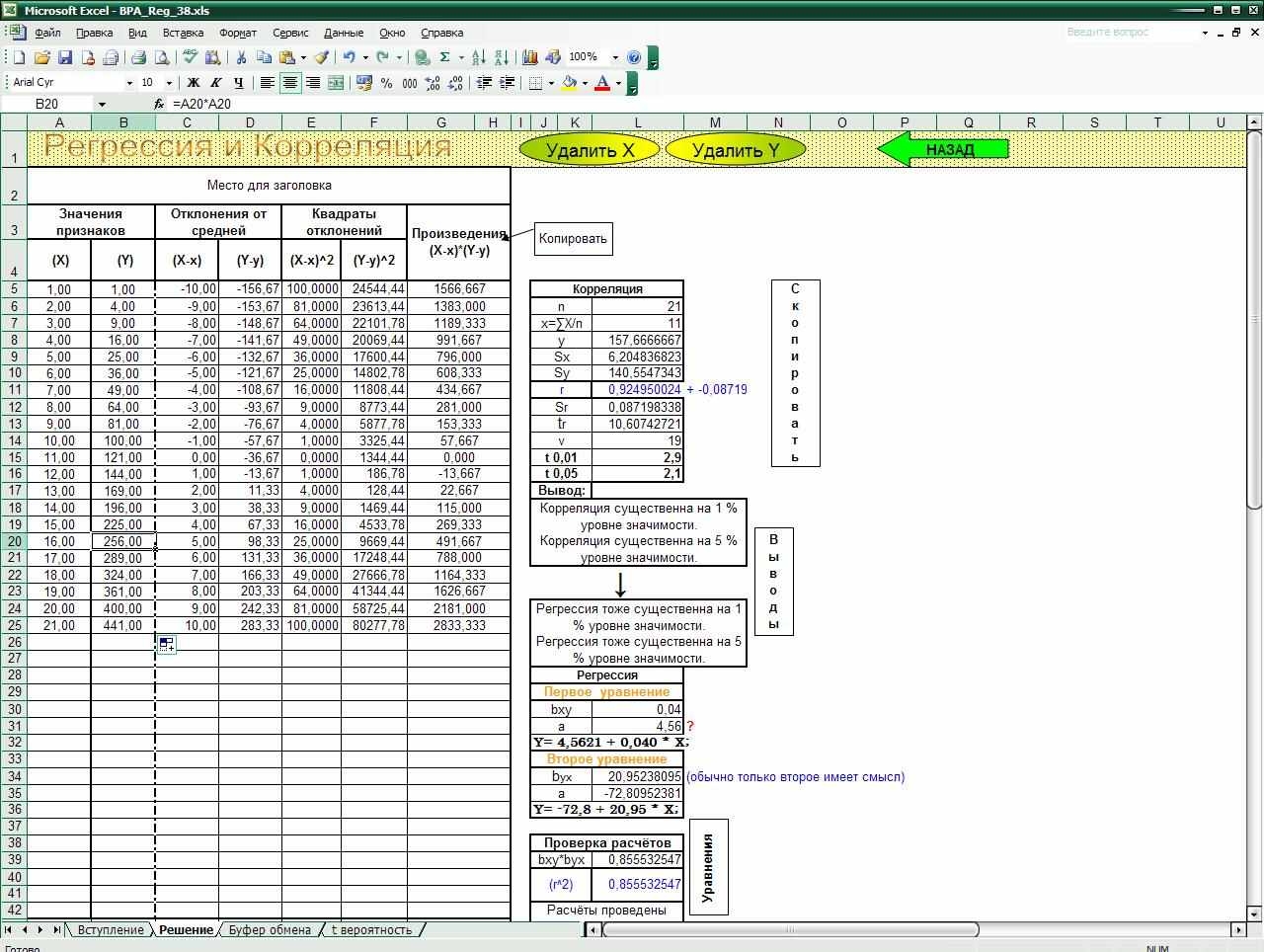
При обработке данных методом корреляционно-регрессионного анализа рассчитываются: коэффициент корреляции – r, ошибка коэффициента корреляции – Sr, критерий существенности – t_r , двухстороння критическая точка распределения Стьюдента на 1%-ном и 5 %-ном уровне значимости, уравнения регрессии, коэффициент детерминации – r² (d), а также строится регрессионная прямая (рис. 1).

Модель вариационного анализа позволяет рассчитать: среднее значения в выборке – X, стандартное отклонения – S², дисперсию – S, коэффициент вариации – V_%, квадратное отклонения – Sx, относительную ошибку средней – Sx%, доверительный интервал среднего значения.

В настоящее время программа FieldExpert v1.3 широко применяется при обработке данных полевого опыта студентами, аспирантами и сотрудниками в Новосибирском государственном аграрном университете, ХГУ им. Н.Ф. Катанова. Используется при преподавании дисциплины «Основы научных исследований в агрономии».

Рис. 1. Программа корреляционно-регрессионного анализа