Методология статистического исследования инвестиций в основной капитал: пространственно-временной аспект

Вид материала

Автореферат диссертации

Содержание Статистически значимые факторы и модели, объясняющие Структура и особенности временного ряда инвестиций Рис. 5. Фазовые диаграммы модифицированных рядов инвестиций Факторы и модели прогнозирования, характеризующие динамику Рис. 6. Динамика инвестиций и приращений основного капитала Модель "правого" двухпараметрического геометрически Рис. 7. Модель "правого" двухпараметрического геометрически

Подобный материал:

• Методология учета и анализа инвестиций в основной капитал, 624.5kb.
• Еженедельный выпуск: «Инновационные технологии в Беларуси: инвестиции, наука, техника», 379.79kb.
• Семинарских/ практических занятий Тема Статистическое наблюдение Методология организации, 113.64kb.
• Восточно-христианское искусство в литургическом контексте (пространственно-временной, 207.11kb.
• Г г. Георгиевск №2 Об анализе и проблемных вопросах привлечения инвестиций в основной, 45.46kb.
• Объем инвестиций в основной капитал и строительство в Беларуси в январе-июле текущего, 269.71kb.
• Методология статистического исследования влияния уровня и качества жизни населения, 657.92kb.
• Структура инвестиций в основной капитал по источникам финансирования, 41.08kb.
• Перечень инвестиционных проектов, предусмотренных к реализации на территории Республики, 706.31kb.
• Инвестиционная активность инвестиции в основной капитал, 231.69kb.

Статистически значимые факторы и модели, объясняющие

объемы инвестиционных расходов в регионах Приволжского ФО


Результаты проведенного анализа устойчивости концентрации инвестиций предопределили выбор Приволжского ФО в качестве наиболее динамичного и устойчивого в своем инвестиционном развитии макрорегиона. На его примере соискателем более детально были исследованы факторы, позволяющие объяснить объемы и динамику региональных инвестиций.

При анализе пространственных статистических данных с помощью инструментария парных регрессий было установлено, что значительная часть вариации инвестиций объяснялась с помощью показателей, характеризующих объемы производимой регионом продукции и оказанных услуг, результаты инвестиционной и внешнеэкономической деятельности, объемы развития строительной индустрии и уровень жизни населения.

Отдельно была выделена группа показателей, обусловливающих развитие финансово-кредитной, страховой региональной систем: величина депозитов юридических и физических лиц; объемы поступлений в бюджеты территориальных фондов обязательного медицинского страхования, фонд социального страхования, пенсионный фонд; задолженности физических и юридических лиц по кредитам; число кредитных организаций; страховые выплаты, взносы и др.

Часть показателей непосредственно была связана с финансами предприятий: дебиторская и кредиторская задолженности, объемы долгосрочных финансовых вложений, финансовые результаты деятельности и др. Направление связи в большинстве случаев было определено как прямое, хотя были выявлены показатели, влияющие на инвестиции противоположным образом. Так, удельный вес убыточных организаций, просроченная дебиторская задолженность, дотации региональных бюджетов от других уровней бюджетной системы, бюджетные кредиты повлияли на объемы инвестиций негативно. На микроэкономическом уровне наилучшим образом объяснила вариацию инвестиций регрессионная модель (1):

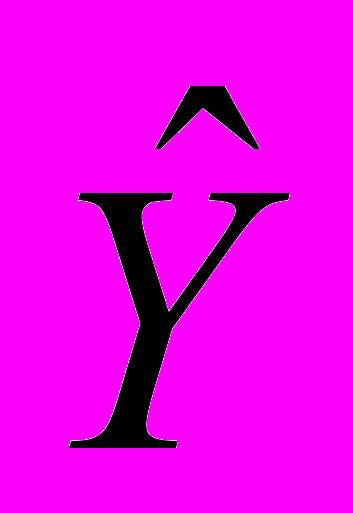= 7,55 + 0,60 Х₁ + 0,08 Х₂


(1)
(c.о.) (0,39) (0,05) (0,02)

R² = 0,96; F = 121,

где Х₁ - сальдированный финансовый результат деятельности предприятий и организаций на душу населения;

Х₂ - объемы прямых иностранных инвестиций на душу населения.


В скобках под параметрами уравнения регрессии, как и в дальнейшем, представлены стандартные ошибки оценок (с.о.), которые показали статистическую значимость независимых переменных. Критерии R² и F подтвердили адекватность множественной регрессионной модели. На макроэкономическом уровне статистически значимой оказалась модель (2).



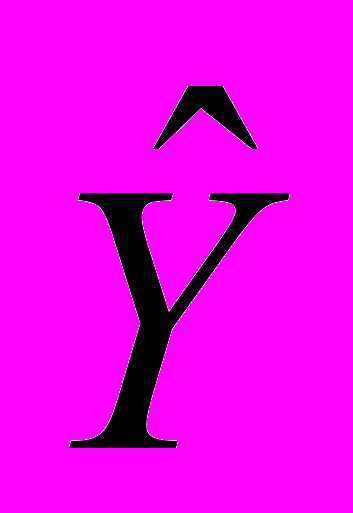
(2)
= 2,71 + 0,12 Х₁ + 28,5 Х₂

(c.о.) (2,11) (0,05) (12,3)

R² = 0,85; F = 31,

где Х₁ - ВРП на душу населения;

Х₂ - объемы экспорта со странами СНГ на душу населения.


Специально обследованные данные бюджетной статистики показали зависимость объемов инвестиционной деятельности от величины доходов, расходов и дефицита бюджетной системы. В частности при объяснении региональных инвестиций значительно увеличилась роль неналоговых доходов, а именно доходов от использования и сдачи в аренду имущества, находящегося в государственной и муниципальной собственности, платежей за пользование природными ресурсами. Выявлена существенная дифференциация местных и региональных бюджетов при формировании инвестиционной политики в регионах Приволжского ФО.

Применение методов множественной регрессии с использованием пространственно-временных данных существенно расширило возможности прогнозирования инвестиционных расходов предприятий и организаций на региональном уровне, когда наблюдалось отсутствие сопоставимой динамики показателей или вовсе невозможно было получить необходимую информацию. Однако незначительный объем выборки не позволил, с одной стороны, одновременно включить в модель более 2-3 независимых переменных, что вызвало необходимость построения комплекса моделей на разных уровнях управления экономикой; с другой стороны, распространить с высокой степенью вероятности полученные выводы на все регионы России. Вместе с тем это позволило региональным и местным властям оперативно реагировать на вновь поступившую информацию об изменениях указанных факторов, учитывая особенности развития данного макрорегиона.


Структура и особенности временного ряда инвестиций

в основной капитал в России


Важной методологической проблемой при предсказании инвестиций является тот факт, что методы, с успехом применяемые в одном случае, в других совершенно не отражают реальную действительность и поэтому не могут считаться адекватными сложившимся условиям. Одним из средств понимания структуры временных рядов инвестиций являлась классическая декомпозиция, позволившая выявить тренд, сезонность, цикличность и нерегулярность. Поведение одних составляющих исследуемого временного ряда, таких, как тренд и сезонность, было достаточно предсказуемым. Другие составляющие, такие как цикличность и нерегулярность, предсказать с высокой степенью точности было практически невозможно.

Для выявления трендовой составляющей была выбрана экспоненциальная кривая, рост которой в геометрической прогрессии определил общую тенденцию изменения объемов инвестиций в текущих ценах с учетом ценового фактора, проявляющегося в инфляционном росте показателя. Сезонная составляющая характеризовала последовательный рост инвестиций в течение каждого года. Причем в первой половине года индексы сезонности оказались меньше единицы, а уровни января каждого года на 40% ниже среднегодового значения. Во второй половине года индексы сезонности были выше единицы, а максимальный рост объемов инвестиций достигался в декабре, когда индекс сезонности на 80% был выше среднего уровня временного ряда.

Несмотря на общую непредсказуемость циклической составляющей, было замечено, что в отдельные периоды значения этой компоненты увеличивались относительно среднего уровня примерно на одну треть (как в январе 1997 г. и ноябре 2000 г.), а затем снижались на ту же величину (в августе 1998 г.), что не противоречило основным положениям теории циклов. Выявленный полный цикл, равный 46 месяцам, в дальнейшем не повторился. Напротив, с конца 2000 г. циклическая составляющая не подвергалась существенным отклонениям в ту или другую сторону от равновесного положения, характеризуя конъюнктурное затишье (стагнацию) на инвестиционном рынке, что обусловлено фактором политической и социально-экономической стабильности. Этот вывод подтвердили результаты проведенной декомпозиции и фазового анализа двух модифицированных рядов инвестиций, первый из которых был скорректирован на экспоненциальный тренд, второй – на накопленный индекс потребительских цен за исследуемый период (рис. 5).





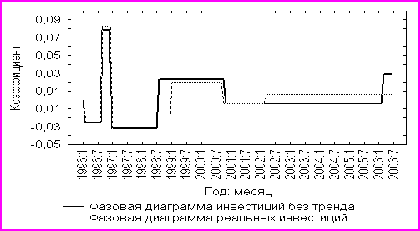
Рис. 5. Фазовые диаграммы модифицированных рядов инвестиций

в РФ за 1996-2006 гг.

Перед проведением фазового анализа предварительно было выполнено несколько преобразований исходных временных рядов, чтобы элиминировать тренды и выделить скрытые в них колебательные процессы в явном виде. Для этого осуществлялся переход к натуральным логарифмам, и вычислялись первые их разности. Исследовать динамику рядов стало возможным путем нахождения отклонений от средних значений, которые выступили в роли некоторого стандарта, от которого измеряются отклонения вверх и вниз, и представляют собой средний темп прироста уровней инвестиций.

Одним из важных выводов при сравнении двух модифицированных рядов явилась невозможность отождествления роста инвестиций в текущих ценах только с величиной инфляционного роста. Несомненно, наряду с инфляцией присутствуют факторы, определяющие динамику инвестиций, связанные с реальным ростом их физических объемов. Как показал анализ поведения случайной компоненты при всевозможных вариантах мультипликативной и аддитивной декомпозиции, в обоих временных рядах инвестиций сохранилась важная неучтенная информация, что подтвердили расчет и анализ выборочных автокорреляционных функций.

Предсказание отдельных составляющих временного ряда инвестиций с целью получения прогноза значений основного ряда не позволило получить точных оценок. Вместе с тем знание структуры ряда помогло глубже понять природу и особенности исследуемого явления. Проведенный анализ привел к выводу о том, что, будучи одним из самых чувствительных критериев к изменениям экономической конъюнктуры, объем инвестиций в РФ также существенно зависит от сезонных ожиданий, особенно в конце каждого квартала (в марте, июне, сентябре и декабре), а максимального его роста следует ожидать в последнем месяце каждого года.


Факторы и модели прогнозирования, характеризующие динамику

инвестиций в основной капитал за 1965-2006 гг.


При исследовании особенностей развития инвестиционного процесса за период 1965-2006 гг. в представленных временных рядах были обнаружены структурные изменения, предполагающие построение кусочно-линейных моделей, что подтвердилось использованием формального теста Чоу. Однако разделение исходной совокупности на две или большее количество частей привело к потере числа наблюдений и степеней свободы, а следовательно, к снижению качества прогнозных оценок (рис. 6).




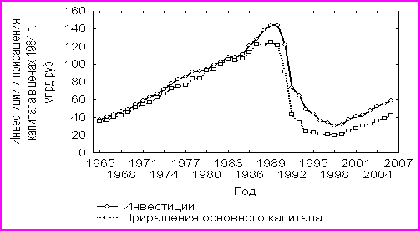
Рис. 6. Динамика инвестиций и приращений основного капитала

в России за 1965-2006 гг. в постоянных ценах 1984 г.

В связи с этим было принято решение исследовать как отдельные периоды исторического развития, так и объединенный период. Как было установлено, в дореформенный период (1965-1990 гг.) и период рыночного реформирования (1991-2006 гг.) выявились некоторые закономерности, присущие обоим этим этапам. Несмотря на существенные изменения в объемных и ценовых соотношениях, практически не изменилась степень влияния инвестиций на приращения основного капитала, и наоборот. Зависимость между ними хорошо описывалась линейной регрессией.

Однако в обоих временных рядах присутствовала автокорреляция в остатках, что не позволило использовать эту взаимосвязь для прогнозирования, так как, с одной стороны, возникло множество неверных толкований результатов регрессионного анализа, с другой стороны, на базе свойств авторегрессии, проявляющейся в инерционности динамики процесса, стало возможным использовать в прогнозировании выявленные особенности.

Дореформенный период характеризовался более устойчивой тенденцией развития, где наряду с приращениями основного капитала на инвестиции влияли темпы экономического роста и темпы роста торговли, причем последние оказывали отрицательное воздействие. Данные показатели помогли улучшить спецификацию регрессионных моделей, так как сделали остатки независимыми.

Несмотря на существенные изменения, коренным образом повлиявшие на условия функционирования рыночной экономики, приращения основного капитала и темпы экономического роста в 1991-2006 гг. продолжали оказывать положительное влияние на объемы инвестиций в основной капитал, причем как текущие, так и с некоторой задержкой во времени. Модель описывала эти взаимосвязи за 1965-2006 гг. следующим образом:


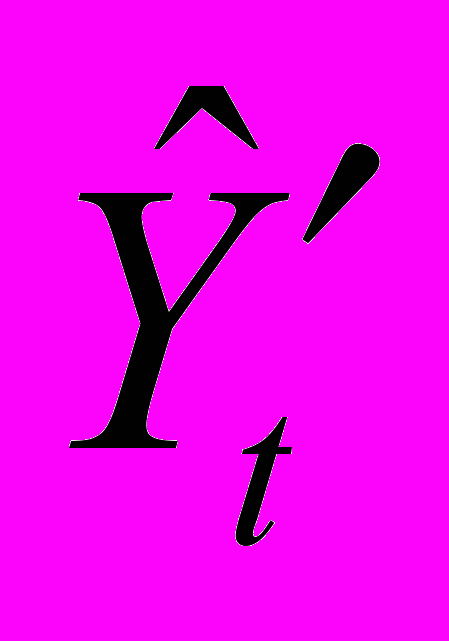
(3)
= – 0,013 + 0,477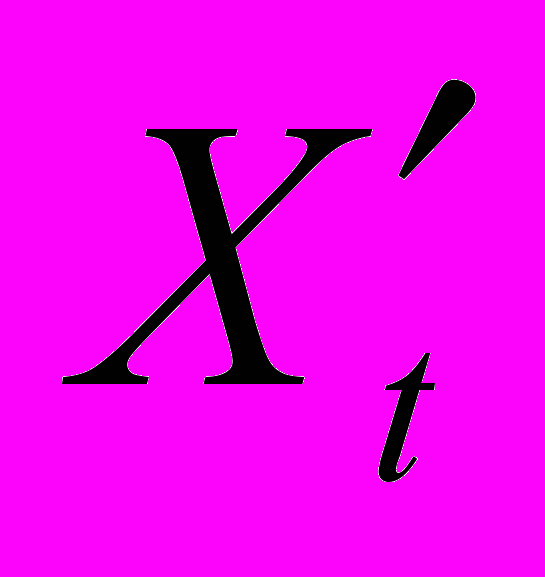+ 0,567 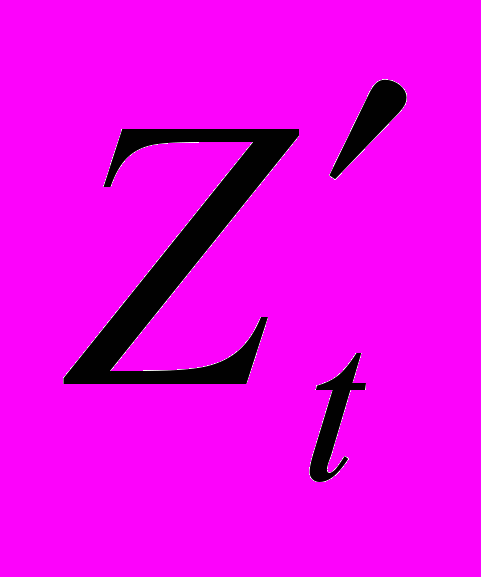+ 0,339

(с.о.) (0,007) (0,073) (0,233) (0,130)

R²=0,93; DW=1,95.

где 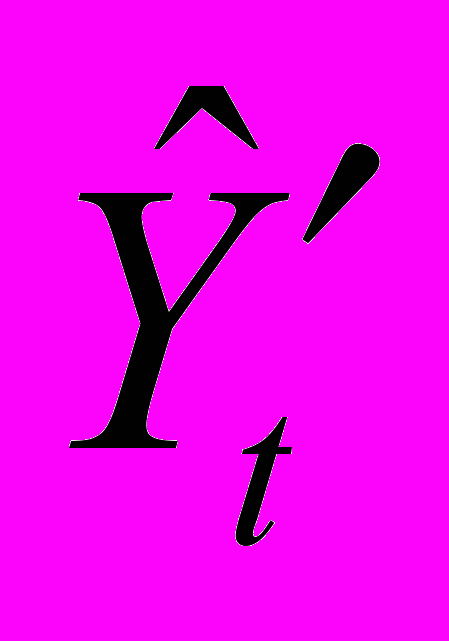- логарифмические разности объемов инвестиций;

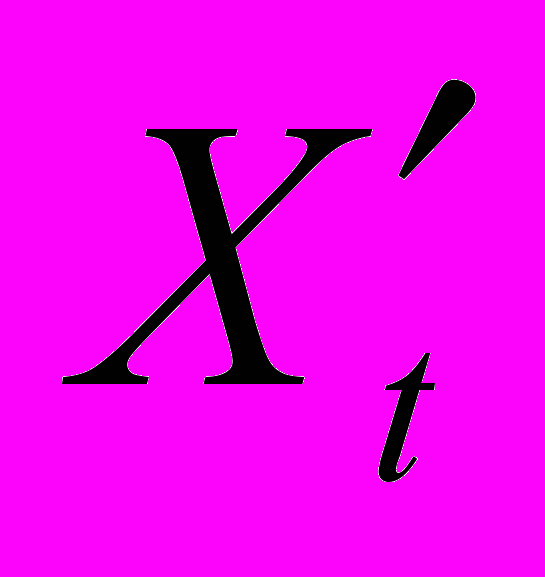- логарифмические разности приращений основного капитала;

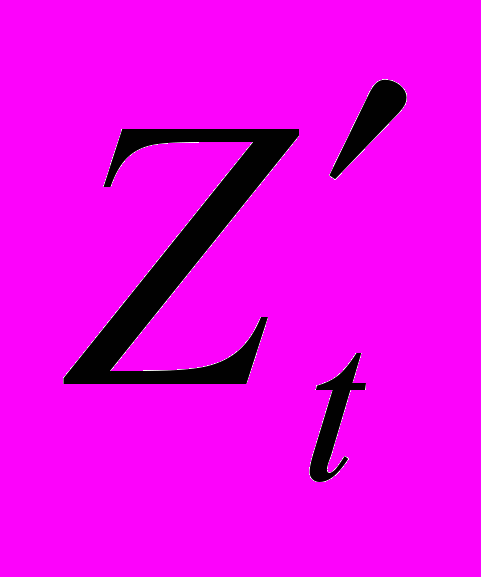- текущие и лагированные темпы роста ВВП;

Штрих означает объединенный период.

Одним из действенных способов устранения автокорреляции в регрессионных остатках инвестиций и приращений основного капитала стало взятие натуральных логарифмов, что существенно снизило вариацию объемных показателей и устранило явление гетероскедастичности, а также нахождение их первых разностей, что сделало ряд стационарным. Регрессия с логарифмическими разностями оказалась вполне пригодной для прогнозирования, так как имела независимые остатки, что подтвердилось расчетом статистики Дарбина - Уотсона (DW).

Корректировка исходных временных рядов на коэффициент автокорреляции первого порядка, а также расчет моделей авторегрессии первого и второго порядков в меньшей степени были пригодны для прогнозирования инвестиций, так как проблема гетероскедастичности полностью не была решена даже с применением обобщенного метода наименьших квадратов и инструментальных переменных.

Несмотря на тесную корреляцию между инвестициями и приращениями капитала, формальный критерий оценки причинности взаимосвязей не позволил установить причинно-следственную обусловленность между этими переменными. При этом использовался двухшаговый процесс для проверки Грэнжер-причинности.

На первом шаге определялись параметры АRIMА-моделей для двух временных рядов по имеющимся данным. Для ряда инвестиций наилучшей по информационным критериям Акайке и Шварца оказалась модель ARIMA (0,1,2), а для ряда приращений капитала – ARIMA (1,1,0). На втором шаге рассчитывались кросс-корреляции, которые показали, что ни при каких лагах k > 0 и k < 0 из 15 перекрестных сдвигов r_k существенно не отлично от нуля. При k = 0 r₀ = 0,87, что позволило сделать вывод о мгновенной взаимной реакции в причинно-следственном соотношении "инвестиции – приращения капитала". Таким образом, инвестиции не могли считаться Гренжер-причиной для приращений капитала, и наоборот.

С учетом оценки причинности при прогнозировании инвестиций в качестве определяющих переменных были установлены темпы роста ВВП, которые с некоторой задержкой во времени оказывали положительное влияние на результативную переменную, а также лагированные уровни инвестиций. Одним из уравнений, описывающих объемы инвестиций 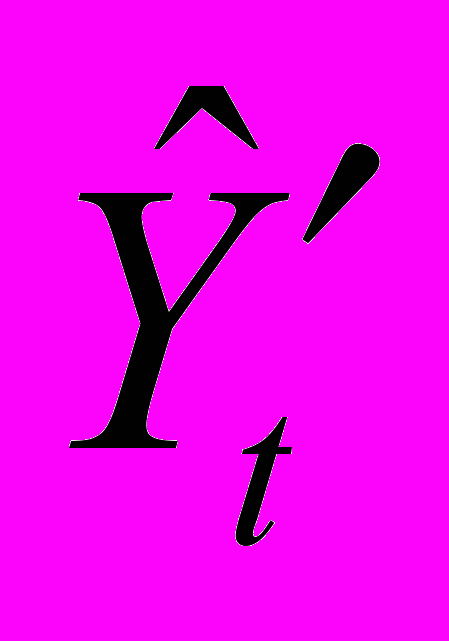на основе собственных лагированных значени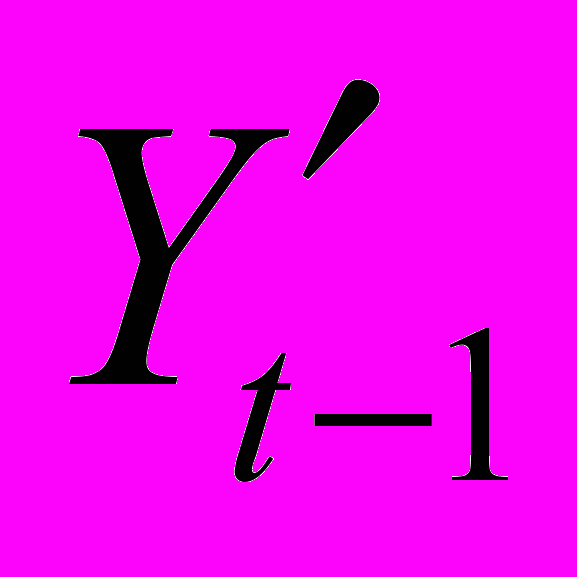й ( и 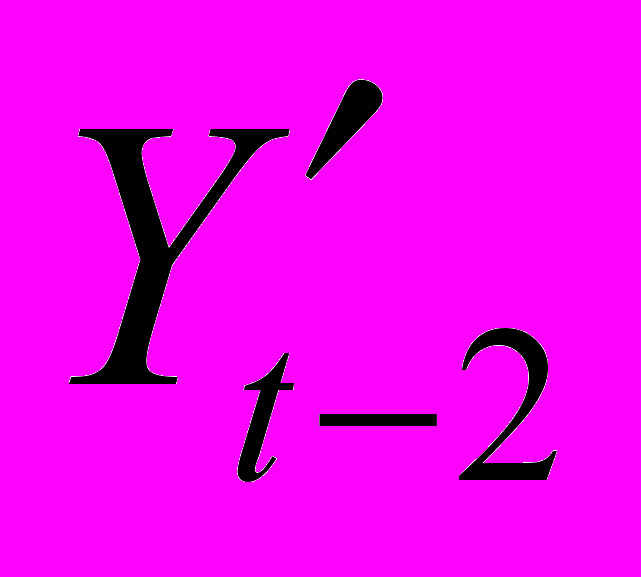) и лагированных значений приростов ВВП (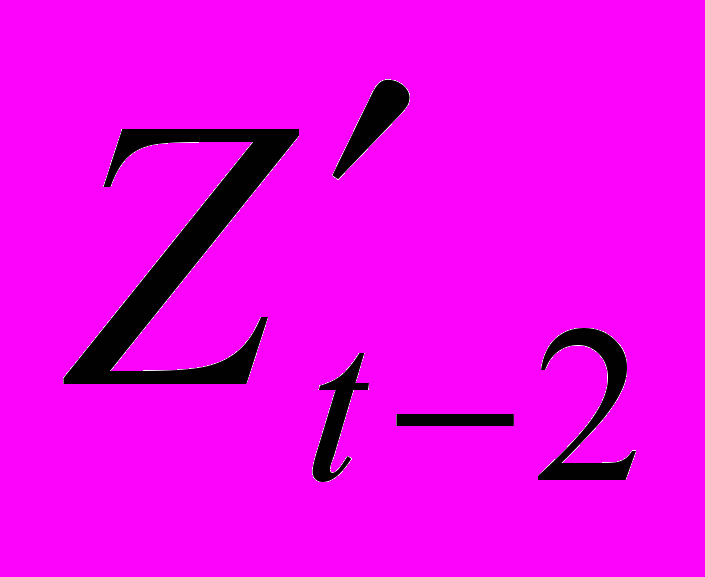, и 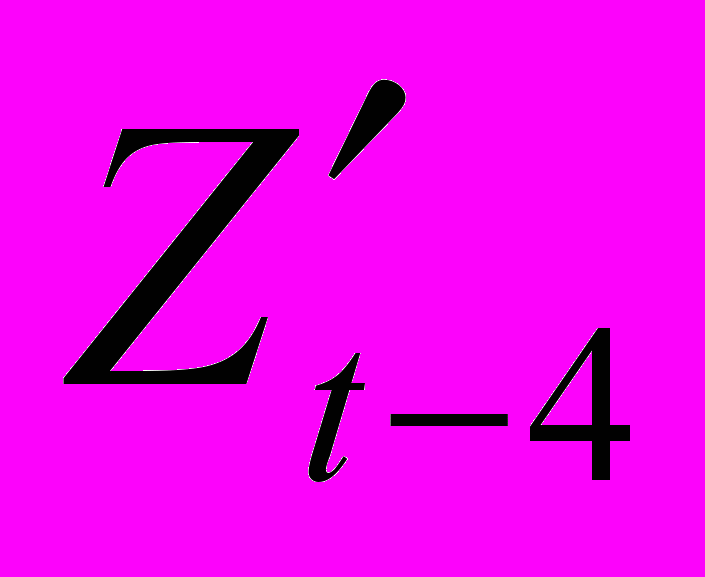), явилась следующая модель:


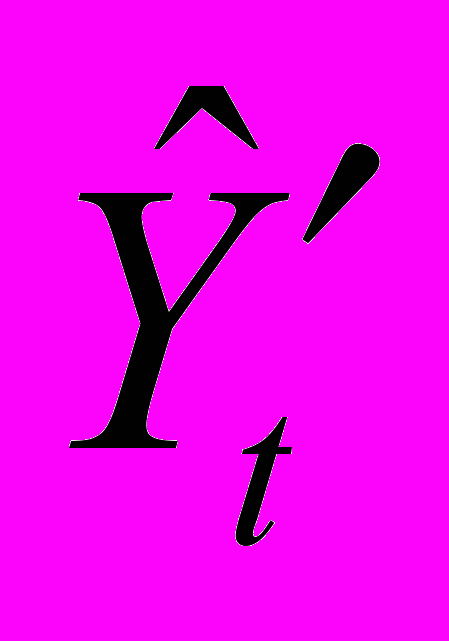= 8,4 + 1,57 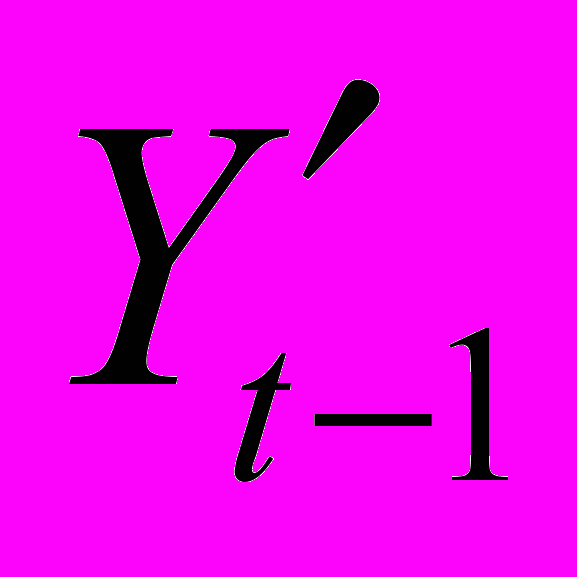– 0,64 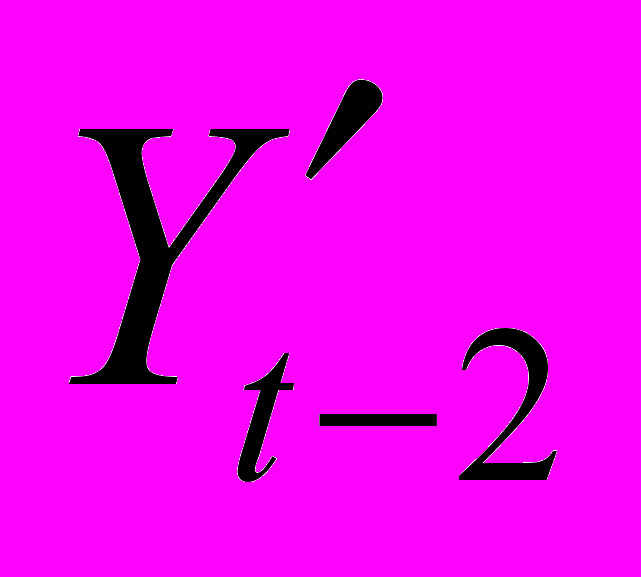+ 0,28 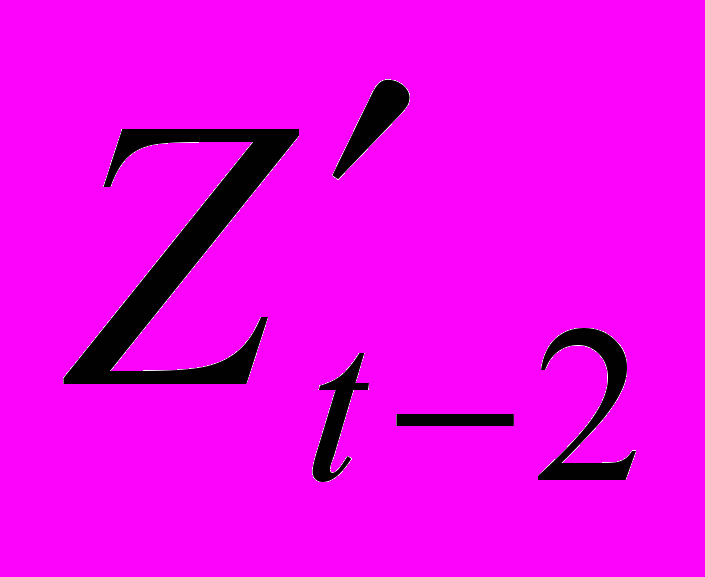– 0,52 + 0,22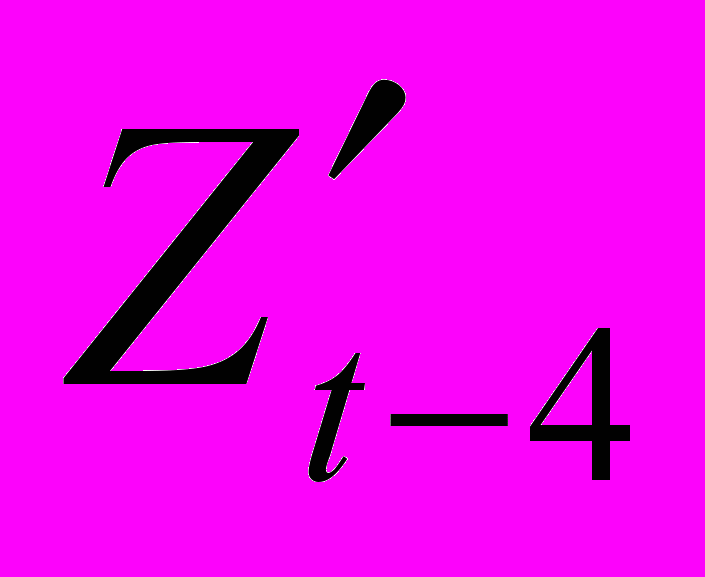


(4)
(с.о.) (5,0) (0,13) (0,13) (0,08) (0,14) (0,09)

R² = 0,96; h-статистика Дарбина = 1,74.

В данном случае вместо традиционной статистики DW для оценки независимости остатков использовалась h-статистика Дарбина, не превысившая критических значений. Исходя из выражения (4), стало возможным заключить: во-первых, влияние и инвестиций, и экономического роста осуществлялось с задержкой в 1–4 года; во-вторых, темпы роста ВВП явились Грэнжер-причиной для инвестиций, так как лагированные значения объяснили дополнительную долю объясненной вариации инвестиций. Вывод о характере причинности подтвердился использованием двухфазовой процедуры проверки причинности. Не было установлено обратной причинно-следственной зависимости. Вместе с тем при исследовании взаимосвязей между приращениями капитала и темпами роста ВВП была установлена как прямая, так и обратная взаимосвязь, т.е. приращения капитала были причиной изменения темпов роста ВВП, и наоборот.

Кроме полученных моделей регрессии, при прогнозировании использовалась методология Бокса - Дженкинса для ежегодных инвестиций за 1965-2006 гг. в постоянных ценах 1984 г. Результаты прогнозирования на основе модели АRIMA (0,1,2) незначительно отличались от прогнозов, полученных по другим методам прогнозирования, и позволили установить, что полученные предсказательные оценки на 2007 г. сопоставимы с объемами инвестиций, осуществленными в 1971 и 1993 гг. Среднесрочный прогноз до 2010 г. в соответствии с выбранной моделью характеризует незначительный ежегодный рост уровней ряда при значительном росте доверительных границ прогнозирования, что, несомненно, снижает качество полученных оценок.


Модель "правого" двухпараметрического геометрически

распределенного лага, объясняющая краткосрочную зависимость между инвестициями и приращениями основного капитала


Как было показано в диссертационном исследовании, хорошее качество оцененных уравнений инвестиций для одного периода не соответствовало параметрам другого периода. Так, модели "левого" распределенного лага, успешно применяемые для 1966-1989 гг., при добавлении всего двух новых наблюдений за 1990-1991 гг. привели к изменению структуры геометрического лага и к ухудшению качества оцениваемых параметров: стандартных ошибок, коэффициентов детерминации, статистики DW. С учетом вновь появившихся условий развития инвестиционного процесса добавление новых наблюдений за 1992-2006 гг. сделало неудовлетворительными для прогнозирования инвестиций модели, которые раньше могли с успехом применяться.

Оценка параметров уравнений инвестиций отдельно для периода реформирования экономики не дала хороших для прогнозирования качеств моделей, так как временной интервал исследования был недостаточно продолжительным. Несмотря на вышесказанное, одна из моделей все же смогла считаться пригодной для прогнозирования инвестиций во всех исследованных периодах, это модель "правого" двухпараметрического геометрически распределенного лага, в которой текущие значения инвестиций определялись текущими и будущими значениями приращений капитала. Модель имеет такое название, поскольку в причинно-следственном соотношении "инвестиции – приращения капитала" распределена во времени его правая часть, а весь прирост капитала происходит на заключительном этапе рассматриваемого периода (рис. 7).





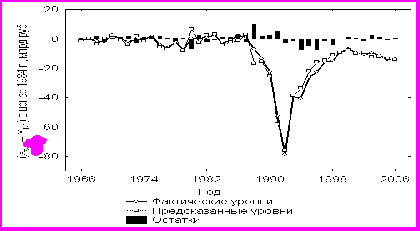
Рис. 7. Модель "правого" двухпараметрического геометрически

распределенного лага за 1966-2006 гг.

Необходимо обратить внимание на существование теоретических предпосылок, серьезно ограничивающих работоспособность и практическую реализацию данной модели. Например, все элементы инвестиций должны перейти в приросты основного капитала, т.е. эти показатели в целом с учетом сдвига во времени должны совпадать. Временная структура инвестиционных процессов должна быть постоянной, т.е. распределение во времени и инвестиций, и приростов основного капитала должно быть одинаковым. Несмотря на указанные ограничения, соискателем были получены статистически значимые оценки параметров, которые хорошо описывали динамику изменения рассматриваемых переменных в сопоставимых ценах. Для 1966-2006 гг. полученная модель описывалась уравнением.

Х_t - Y_t-1 = 0,966 (Х_t - Х_t-1) + 0,965 (Х_t - Y_t)


(5)
(с.о.) (0,055) (0,039)

R² =0,96; DW = 1,71.

Уравнение в преобразованном виде имело следующий вид:


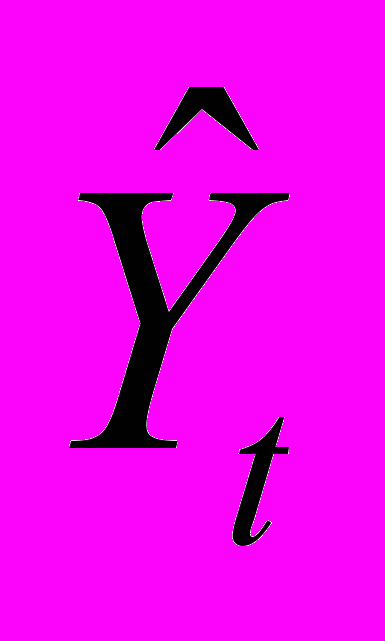
(6)
=0,966 X_t + 0,001208 X_t+1 + 0,001165 X_t+2 + …

В соответствии с уравнением (6) 97% приростов капитала в текущем и двух последующих годах приводили к реализации инвестиций в текущем периоде. Как было показано, добавление новых данных привело к серьезному изменению структуры геометрического лага. Если в 1966–1989 гг. коэффициент при текущей зависимой переменной составил 0,512, то в 1966–2006 гг. – 0,966. Это стало свидетельством более быстрого реагирования изменений объемов инвестиций на изменения приращений капитала в текущем периоде, т.е. существенно возросла роль первого года в реализации инвестиционных проектов.

Полиномиальные распределенные лаги не дали удовлетворительных результатов при объяснении инвестиций в России, и даже подходящая с формальной точки зрения модель "правого" полиномиально распределенного лага в 1966-2006 гг. со степенью полинома m = 2 и длительностью лага n = 4 имела неудовлетворительное качество остатков.