Идентификация параметров упругости и жесткости конструкций из армированных материалов

Вид материала

Автореферат

Содержание Научный консультант Общая характеристика работы Для достижения указанной цели решены следующие задачи Методы исследования Научная новизна работы Личный вклад автора Практическая значимость работы Достоверность результатов Апробация работы. Внедрение результатов. Структура и объем работы. Содержание работы Первая глава Во второй главе Е – матрица упругости материала; Ф(х) – вектор-столбец базисных интерполяционных функций; D Z через обобщенные перемещения q Третья глава Четвертая глава Основные публикации по теме работы

Подобный материал:

• В. П. Николаев, 37.27kb.
• Приказ от 31 августа 2005 г. N 12-п об утверждении положения о проведении ежегодного, 207.04kb.
• А. П. Янковский Институт теоретической и прикладной механики им. С. А. Христиановича, 21.46kb.
• Проект №4504 «Исследование сингулярных проблем нелинейной упругости эластомерных материалов», 22.72kb.
• Рабочая программа дисциплины «Механическое оборудование предприятий строительной индустрии», 248.05kb.
• В. А. Хандожко модернизация автоматизированной системы научных исследований контактной, 48.19kb.
• Научно-практическая конференция «Старт в науку» «Определение жесткости воды водозаборных, 229.45kb.
• Случай и предельные случаи, продемонстрировать графики зависимости координаты маятника, 60.35kb.
• Пластичность, ползучесть и разрушение элементов металлических конструкций, 21.79kb.
• Программа учебной дисциплины "Химия конструкционных материалов" для подготовки, 124.47kb.

На правах рукописи




КАЗНАЧЕЕВА ОЛЬГА КОНСТАНТИНОВНА


ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ УПРУГОСТИ И ЖЕСТКОСТИ КОНСТРУКЦИЙ ИЗ АРМИРОВАННЫХ МАТЕРИАЛОВ


Специальность 05.13.18 – Математическое моделирование, численные методы и комплексы программ


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук


Научный руководитель:

кандидат технических наук, доцент Резниченко А.И.


Научный консультант:

доктор технических наук,

профессор Каледин В.О.


Новокузнецк – 2011

Работа выполнена на кафедре математики и математического моделирования Новокузнецкого института (филиала) ФГБОУ ВПО «Кемеровский государственный университет»

Научный руководитель	кандидат технических наук, доцент Резниченко Александр Иванович
Научный консультант	доктор технических наук, профессор Каледин Валерий Олегович
Официальные оппоненты:	доктор технических наук, доцент Павлова Лариса Дмитриевна
	доктор физико-математических наук, доцент
	Кургузов Владимир Дмитриевич
Ведущая организация	Институт теоретической и прикладной механики им. С.А. Христиановича Сибирского отделения РАН

Защита состоится «15 » ноября 2011 г. в 13.00 час. на заседании диссертационного совета Д212.252.02 в Сибирском государственном индустриальном университете (СибГИУ) по адресу: 654007, Кемеровская обл., г. Новокузнецк, ул. Кирова 42, e-mail sec_nr@sibsiu.ru.

С диссертацией можно ознакомиться в библиотеке СибГИУ.


Автореферат разослан « 6 » октября 2011 г.





Ученый секретарь

диссертационного совета В.Ф. Евтушенко


ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы. Силовые конструкции из армированных материалов, в том числе композиционных, широко распространены в машиностроении и строительстве. Неразрушающий контроль прочности таких конструкций затруднен нестабильностью физико-механических свойств, в особенности при переменных по объему схемах армирования, и невозможностью непосредственного измерения геометрических параметров, определяющих жесткость. Отметим, что неопределенность физико-механических характеристик материала может возникать, как минимум, в двух ситуациях. Одна из них связана с приемочным контролем конструкций из пространственно армированных композиционных материалов, когда материал формируется одновременно с конструкцией, и его свойства существенно зависят от технологических факторов. Вторая ситуация связана с деградацией материала сооружений при сверхпредельных воздействиях, в том числе связанных с пожарами; идентификация свойств армированного материала и интегральной жесткости конструкции необходима для принятия решения о допустимости продолжения эксплуатации.

Повышение достоверности диагностики силовых конструкций представляет актуальную проблему. Так, при выходном контроле качества высоконагруженных ответственных конструкций из углерод-углеродных материалов значительная доля изделий необоснованно отбраковывается при использовании традиционных методов контроля, основанных на оценивании параметров по измерениям характеристик образцов. Повышение объективности диагностики может быть достигнуто определением фактических физико-механических характеристик материала непосредственно в изделии. Поскольку как воздействия, так и отклик при этом являются функциями координат, это приводит к качественно более сложным задачам параметрической идентификации, разработанным в настоящее время недостаточно.

Таким образом, представляется актуальной разработка метода идентификации физико-механических свойств конструкций по данным натурных экспериментов, основанного на интерпретации данных неразрушающих испытаний с использованием их математической модели.

Целью настоящей работы является разработка средств математического моделирования статического деформирования конструкций из армированных материалов применительно к задачам идентификации их физико-механических свойств.

Для достижения указанной цели решены следующие задачи:

• разработать модель статического деформирования конструкции с переменными параметрами упругости и жесткости для вычисления переменных состояния при заданных воздействиях;
  
• построить аппроксимацию функций отклика при переменных физико-механических параметрах материала и переменных геометрических параметрах, определяющих жесткость конструкции;
  
• разработать алгоритм вычисления точечных и интервальных оценок искомых параметров упругости и жесткости по измеренным переменным состояния с учетом случайных погрешностей измерительной системы;
  
• разработать вычислительные программы идентификации физико-механических параметров конструкций по данным натурного эксперимента;
  
• апробировать разработанные алгоритмы идентификации на данных натурного эксперимента по статическому деформированию конструкций из армированных материалов, оценить устойчивость получаемых результатов к случайным погрешностям измерений.
  

Методы исследования включают: метод конечных элементов для построения дискретной модели статического деформирования; методы планирования эксперимента для вычисления коэффициентов функций отклика; методы многомерной оптимизации для вычисления искомых параметров упругости; метод тензометрии для измерения деформаций натурных конструкций; аналитические и численные методы решения и качественного исследования систем уравнений высокого порядка.

Научная новизна работы:

1. Двухуровневая математическая модель статического деформирования конструкций из армированных материалов, состоящая из конечно-элементной модели деформирования и полученной из неё редуцированной модели с явно заданными функциями отклика, отличающаяся тем, что основная и редуцированная модели строятся до проведения натурных испытаний, что позволяет сократить объем вычислений при достаточной точности вычисления функций отклика.
   
2. Численно-аналитический метод построения функций отклика в редуцированной модели, основанный на дробно-рациональном представлении обобщенных перемещений в виде произведений частичных сумм рядов Лорана, в котором особая точка находится аналитически, а коэффициенты определяются на основе факторного вычислительного эксперимента.
   
3. Алгоритм приближенной точечной оценки констант упругости и параметров, определяющих жесткость конструкции, основанный на двухуровневой модели с явным заданием функций отклика по данным факторного вычислительного эксперимента и минимизации суммы квадрата отклонений измеренных и вычисленных перемещений и деформаций.
   
4. Комплекс программ для идентификации параметров упругости и жесткости конструкций, включающий разработанные программы формирования исходных данных для факторного вычислительного эксперимента, программу вычисления коэффициентов аппроксимации функций отклика, программу вычисления точечных и интервальных оценок параметров упругости и жесткости, а также существующие пакеты программ конечно-элементного моделирования и автоматизированного управления измерительной системой.
   

Личный вклад автора заключается в формулировке математической постановки задачи идентификации, уточнении критерия качества идентификации параметров упругости, построении базисных функций аппроксимации отклика, разработке алгоритмов и комплекса компьютерных программ идентификации параметров упругости и жесткости, проведении вычислительных экспериментов и обработке результатов натурных испытаний.

Практическая значимость работы состоит в использовании разработанных методов интерпретации натурного эксперимента при неразрушающем контроле качества конструкций с нестабильными параметрами упругости и жесткости, изготовленных из армированных материалов.

Достоверность результатов обеспечивается корректным применением апробированных теоретических положений и подтверждается согласием теоретических расчетов и экспериментальных измерений, а также результатами имитационного вычислительного эксперимента.

Диссертационная работа выполнялась в рамках госбюджетной темы “Оценивание состояний, оптимизация параметров, режимов функционирования техническими и технологическими системами” (шифр темы ПЗ 838 от 21.05.2003 г.), а также в соответствии с планом НИР ЮРГТУ (НПИ) «Компьютерная оптимизация, ресурсосберегающие расчеты и управление состоянием строительных конструкций и оснований сооружений».

Апробация работы. Основные положения и результаты работы докладывались и обсуждались на научно-практической конференции «Моделирование. Теория, методы и средства», г. Новочеркасск, 2001 г.; Международной научно-практической конференции «Актуальные проблемы строительства и архитектуры», г. Новочеркасск, 2005 г.; XIV Международной конференции «Современные проблемы механики сплошной среды», г.г. Ростов-на-Дону, Азов, 2010 г.; Международной конференции «Наука и образование: архитектура, градостроительство и строительство», Волгоград, 2010; XV Международной конференции «Современные проблемы механики сплошной среды», г.г. Ростов-на-Дону, Азов, 2010 г.; Межрегиональной конференции памяти А.Н. Кабелькова «Современные проблемы механики и её преподавания в вузах Российской Федерации», г. Новочеркасск, 2011 г.; VI Всероссийской школе-семинаре "Математическое моделирование и биомеханика в современном университете", г. Ростов-на-Дону, 2011 г.; XVII Международной конференции по вычислительной механике и современным прикладным программным системам, г. Алушта, 2011 г.; Международной конференции по механике и баллистике «VII Окуневские чтения», Санкт-Петербург, 2011 г.

Внедрение результатов. Результаты исследований (методика, алгоритмы и вычислительные программы для идентификации физико-механических параметров материалов силовых конструкций) внедрены в НИИГрафит (г. Москва), на Московском и Новочеркасском электродных заводах, в учебном процессе ЮРГТУ (НПИ).

Публикации. Основные результаты диссертации изложены в 15 опубликованных статьях, из них 7 статей в ведущих рецензируемых научных журналах и изданиях, рекомендованных Высшей аттестационной комиссией РФ для опубликования, и одной монографии.

Структура и объем работы. Диссертация состоит из введения, четырех глав, заключения, списка литературы из 235 наименований и приложения, включает 33 рисунка и 6 таблиц. Объём основной части составляет 135 страниц.

СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность проблемы, сформулированы цель и задачи диссертационного исследования. Показана научная новизна и практическая значимость исследования. Приведены основные положения, выносимые автором на защиту.

Первая глава содержит аналитический обзор существующих подходов к математическому моделированию статических испытаний конструкций из армированных материалов.

Задачи идентификации параметров упругости конструкций при статических испытаниях сводится к построению расчетно-теоретической модели статического деформирования, построению критерия качества идентификации и его минимизации путем надлежащего выбора пространственного распределения параметров упругости в модели.

Вопросы теоретического описания статического деформирования конструкций из армированных, в том числе композиционных, материалов, и также определения их параметров упругости, явились предметом обширных исследований. Основополагающие результаты принадлежат В.В. Васильеву, Ю.В. Немировскому, Г.А. Ванину, Ю.М. Тарнопольскому, В.В. Болотину, Г.В. Воронцову, Б.Д. Аннину, а также Н. Пагано, О. Зенкевичу и многим другим исследователям. В известных работах найдены определяющие уравнения армированных сред, построены математические модели статического деформирования конструкций с произвольными схемами армирования в форме дифференциальных и вариационных краевых задач и разработаны универсальные методы расчета армированных конструкций. В.В. Болотину принадлежит формализация модели конструкции как отображения пространства воздействий (приложенных нагрузок) на пространство состояний, характеризуемых полями перемещений, деформаций и напряжений. В.С. Зарубиным, А.О. Ватульяном, Н.А. Алфутовым, А.И. Резниченко и многими другими учеными сформулированы критерии и разработаны общие методы идентификации параметров упругости.

Адекватное моделирование поведения конструкций неканонической формы со сложными схемами армирования требует применения универсальных численных методов, таких, как метод конечных элементов. Это приводит к моделям с большим числом степеней свободы, и для вычисления функций отклика необходимо решение систем алгебраических уравнений высокого порядка (от сотен до сотен тысяч неизвестных). С другой стороны, существующие методы идентификации требуют многократных вычислений функций отклика на каждой итерации. Поэтому их практическое использование для идентификации параметров упругости и жесткости реальных конструкций затруднено.

Таким образом, для достижения цели настоящей работы требуется разработать экономичные и достаточно точные алгоритмы вычисления функций отклика, а также экономичные алгоритмы минимизации критерия качества.


Во второй главе формулируется постановка задачи идентификации параметров упругости и жесткости конструкций из линейно и нелинейно упругих материалов. Типичными примерами рассматриваемых объектов являются дорогостоящие изделия из композиционных материалов, жесткая регламентация параметров которых приводит к необоснованной отбраковке большого числа работоспособных изделий, и при выходном контроле качества требуется оценка фактически получаемых модулей упругости во всех точках конструкции.

На рисунке 1 представлена схема, иллюстрирующая постановку задачи.



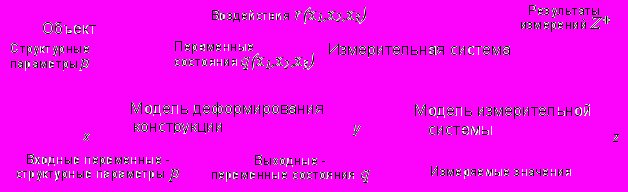
Рисунок 1 – К постановке задачи идентификации параметров
упругости и жесткости

Известно:

- форма, геометрические размеры и структура объекта ;

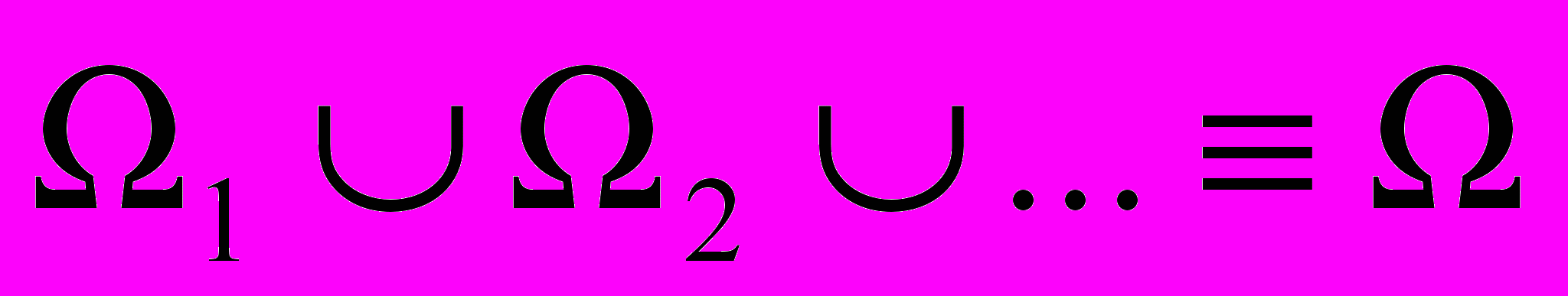- математическая модель статического деформирования в форме вариационной задачи с переменными структурными параметрами 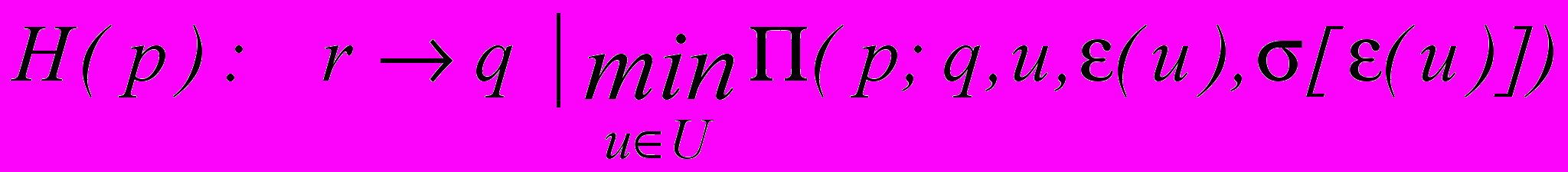, где П – функционал Лагранжа, 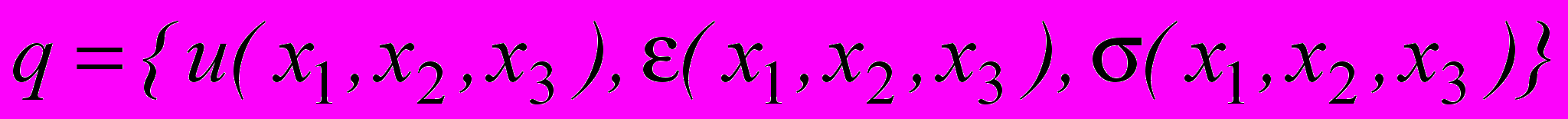- поля параметров состояния (перемещения, деформации и напряжения), - поля внешних нагрузок, U – множество кинематически допустимых полей перемещений, 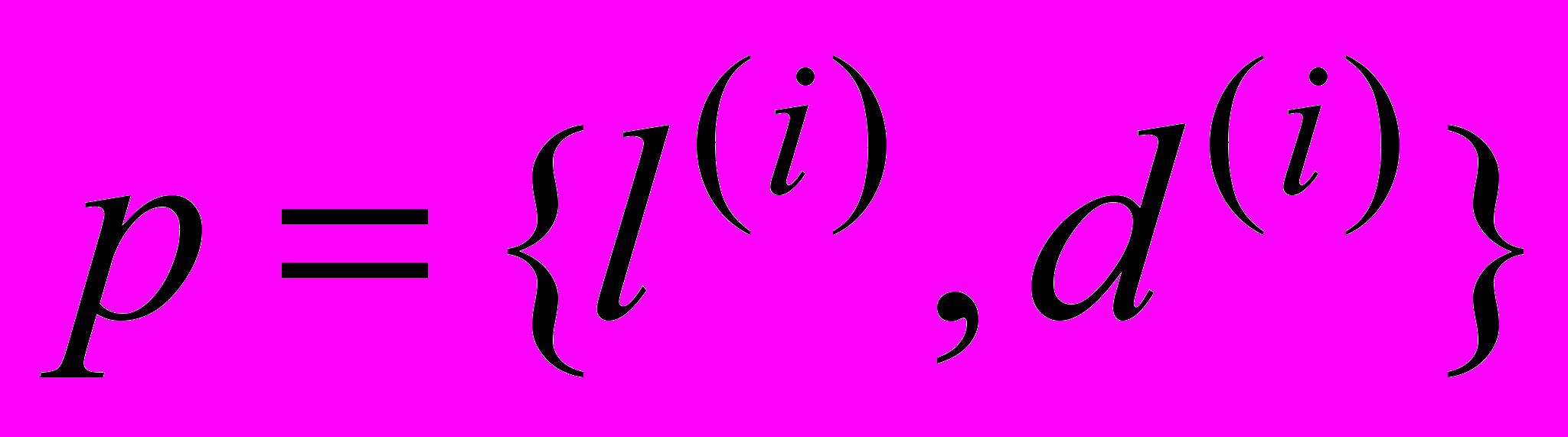- структурные параметры модели (геометрические размеры i-й подобласти l⁽ⁱ⁾ и параметры диаграмм деформирования материалов d⁽ⁱ⁾);

- математическая модель измерительной системы , где С – тарировочная матрица; - вектор случайных погрешностей измерений с известным законом распределений вероятностей компонент;

- приложенные к натурному объекту нагрузки ;

- результаты натурных измерений Z*;

- критерий качества идентификации .

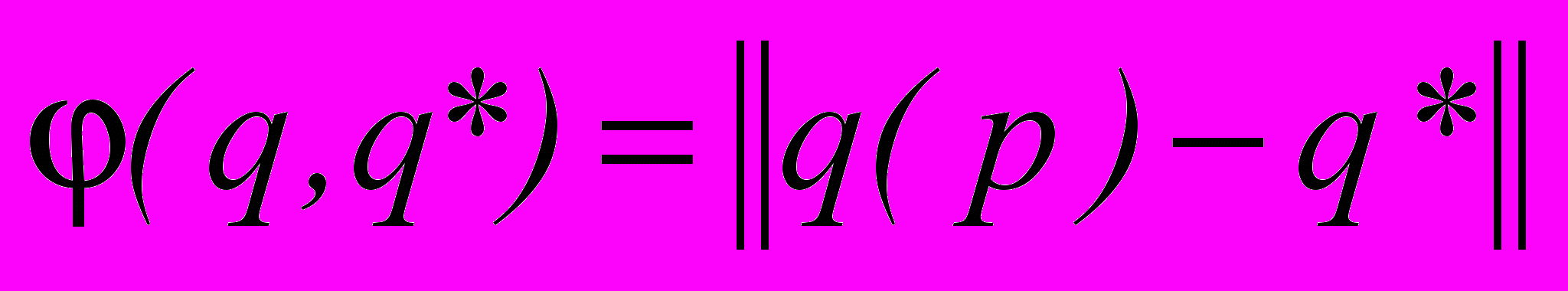Ограничения: двусторонние ограничения на определяемые параметры .

Требуется определить:

- значения структурных параметров , отвечающие минимуму критерия качества;

- доверительные интервалы, покрывающие с заданной вероятностью действительные значения структурных параметров с учетом случайной составляющей измерений .

Особенностью рассматриваемого класса задач является то, что модель строится до проведения натурного эксперимента.

Модель в форме вариационной задачи на практике приводит к неразрешимым математическим проблемам и должна быть заменена более робастным аналогом. Выбор структуры используемой приближенной модели определяется противоречием между точностью и экономичностью расчета. Необходимость адекватного описания и высокой точности вычисления параметров состояния требует использовать дискретную модель, например, основанную на методе конечных элементов, имеющую большое число степеней свободы, не требующую настройки и позволяющую оценить погрешность решения по сравнению с точной вариационной постановкой. Однако минимизация критерия качества идентификации при такой модели приводит к неприемлемым вычислительным затратам. Поэтому выбрана двухуровневая модель, состоящая из конечно-элементной модели статического деформирования (основной модели) и редуцированной модели с явными выражениями для функций отклика.

В основной модели статическое деформирование описывается системой алгебраических уравнений высокого порядка:

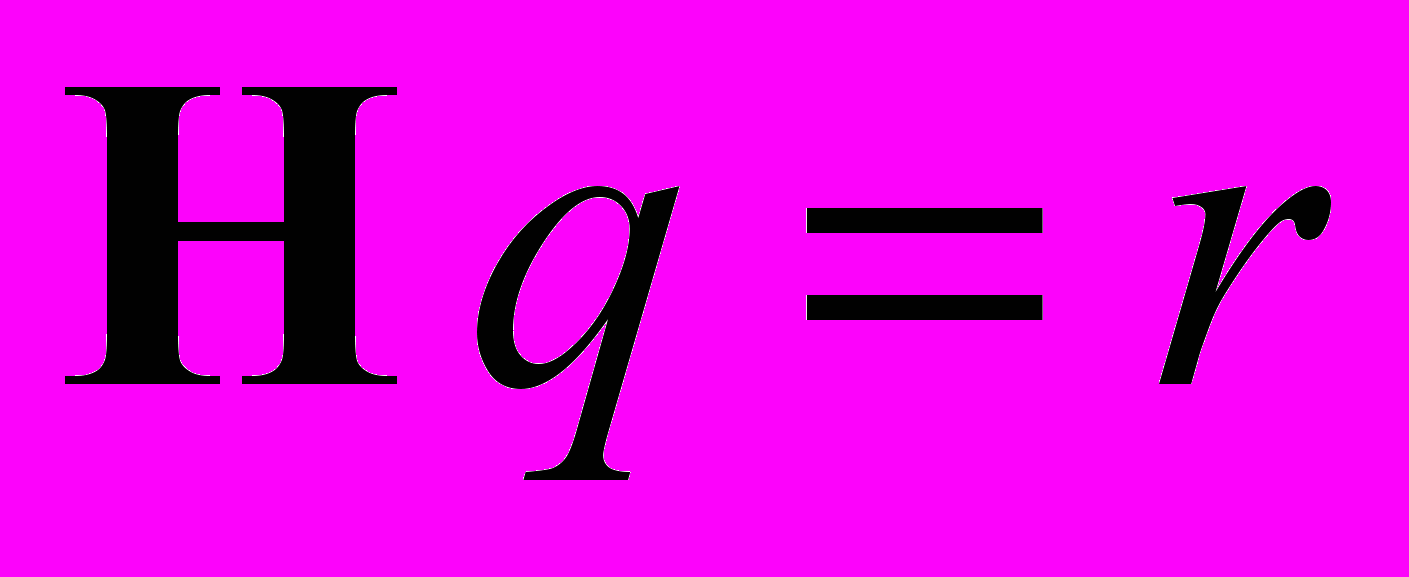, (1)

где H – матрица жесткости; q – вектор обобщенных перемещений; r – вектор внешних воздействий.

Матрица жесткости имеет следующую структуру:

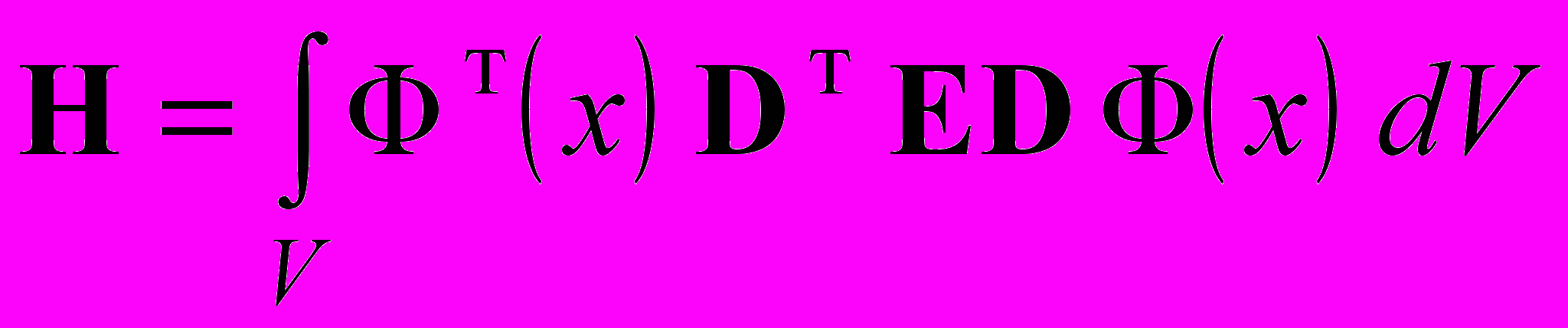, (2)

где интегрирование проводится по объему конструкции. Здесь Е – матрица упругости материала; Ф(х) – вектор-столбец базисных интерполяционных функций; D – дифференциальный оператор, входящий в кинематические соотношения (связь перемещений с деформациями):

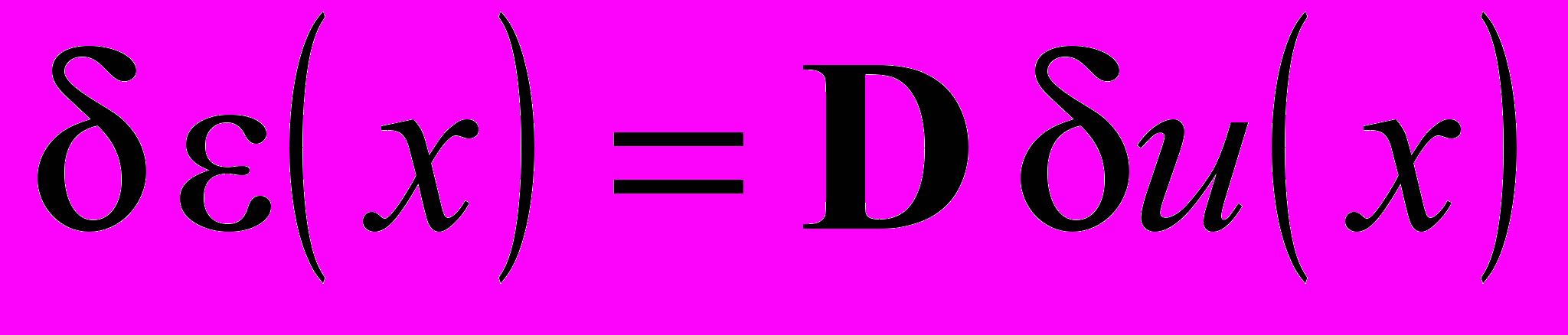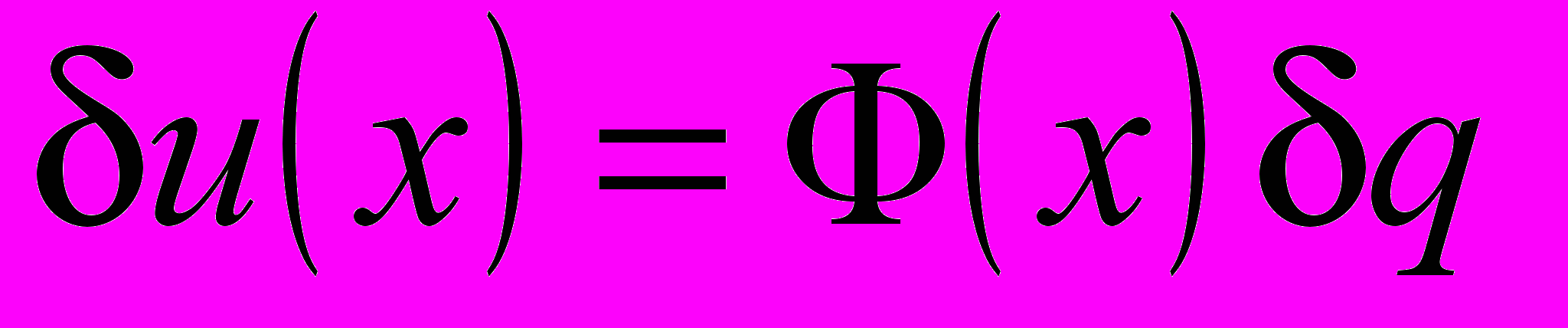, ; (3)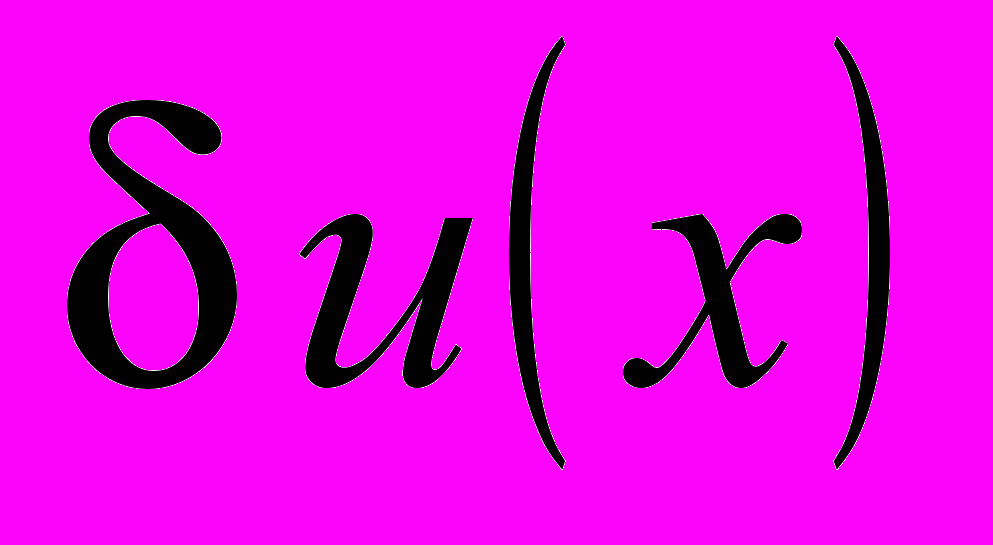

– вариация перемещений, зависящая от координат точки.

Для нелинейно упругого материала в (2) вместо матрицы упругости Е фигурирует матрица секущих модулей Е_cr, зависящая от деформаций:

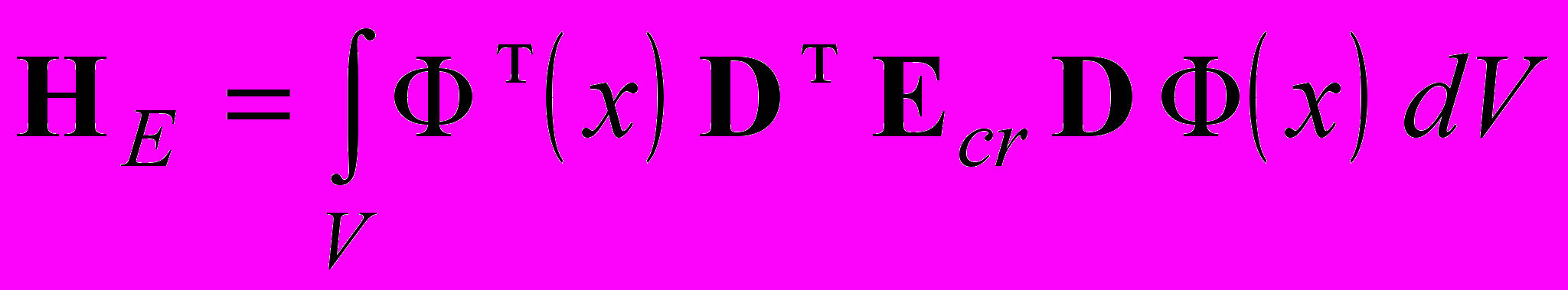, (4)

в силу чего система уравнений (1) становится нелинейной (её матрица зависит от искомого вектора q), и решение может быть получено одним из известных итерационных методов.

Матрицу коэффициентов системы (1) можно представить в виде линейной комбинации нескольких матриц, причем коэффициентами этой комбинации будут варьируемые элементы матрицы упругости:

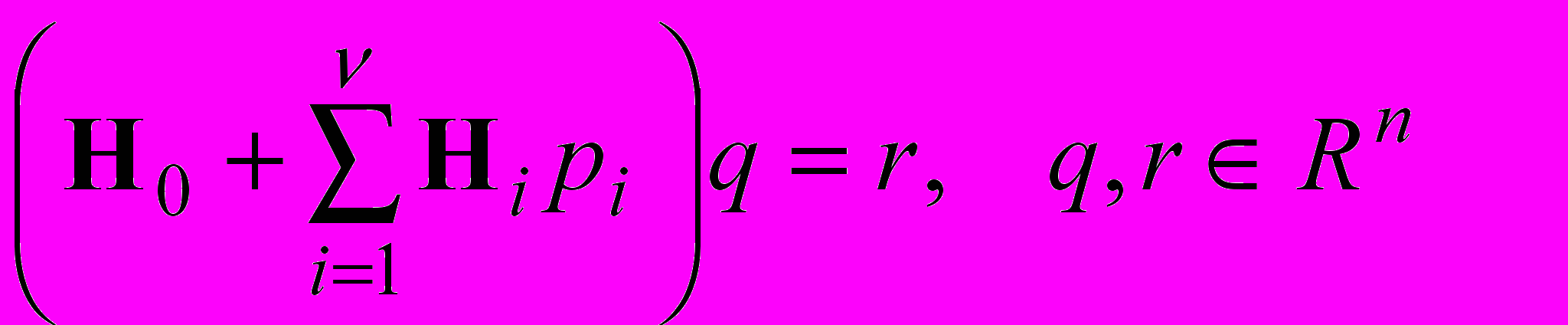. (5)

Здесь p_i – переменные параметры упругости, входящие в матрицу Е;
H₀ – «постоянная» составляющая матрицы жесткости, рассчитываемая по формулам (2) или (4) при некоторых номинальных значениях параметров упругости; – составляющие матрицы жесткости, пропорциональные переменным параметрам упругости p_i.

Положим, что расчетная модель измерительной системы позволяет выразить детерминированную составляющую вектора измерений Z через обобщенные перемещения q:

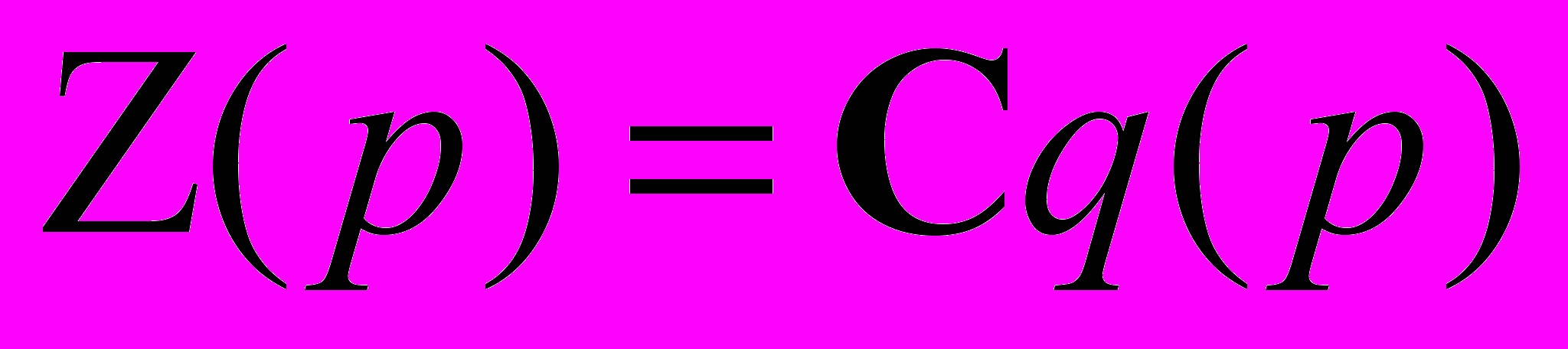. (6)

Эта связь в дальнейшем предполагается линейной.

Критерий качества идентификации должен оценивать отклонение показаний датчиков, рассчитываемых по модели в соответствии с (6), от фактически измеренных показаний датчиков (Z*). Простейший из таких критериев может быть построен как взвешенная сумма отклонений рассчитанных и измеренных величин:

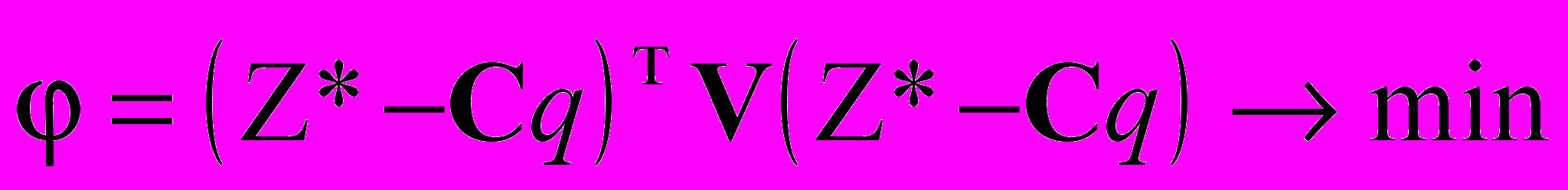, (7)

где V – матрица весовых коэффициентов.

Минимум критерия (7) отыскивается по варьируемым параметрам p, причем функция отклика q находится решением системы уравнений высокого порядка (1) – с постоянной матрицей коэффициентов (2), или, в случае нелинейно упругого материала, нелинейной системы с матрицей коэффициентов (4).

Третья глава содержит разработку экономичных алгоритмов оценивания параметров упругости и жесткости, принципиальная блок-схема которых представлена на рисунке 2.

Условие минимума критерия (7) приводится к виду:

. (8)

После определения перемещений конструкции вычисляем вектор

(9)

и решаем систему уравнений

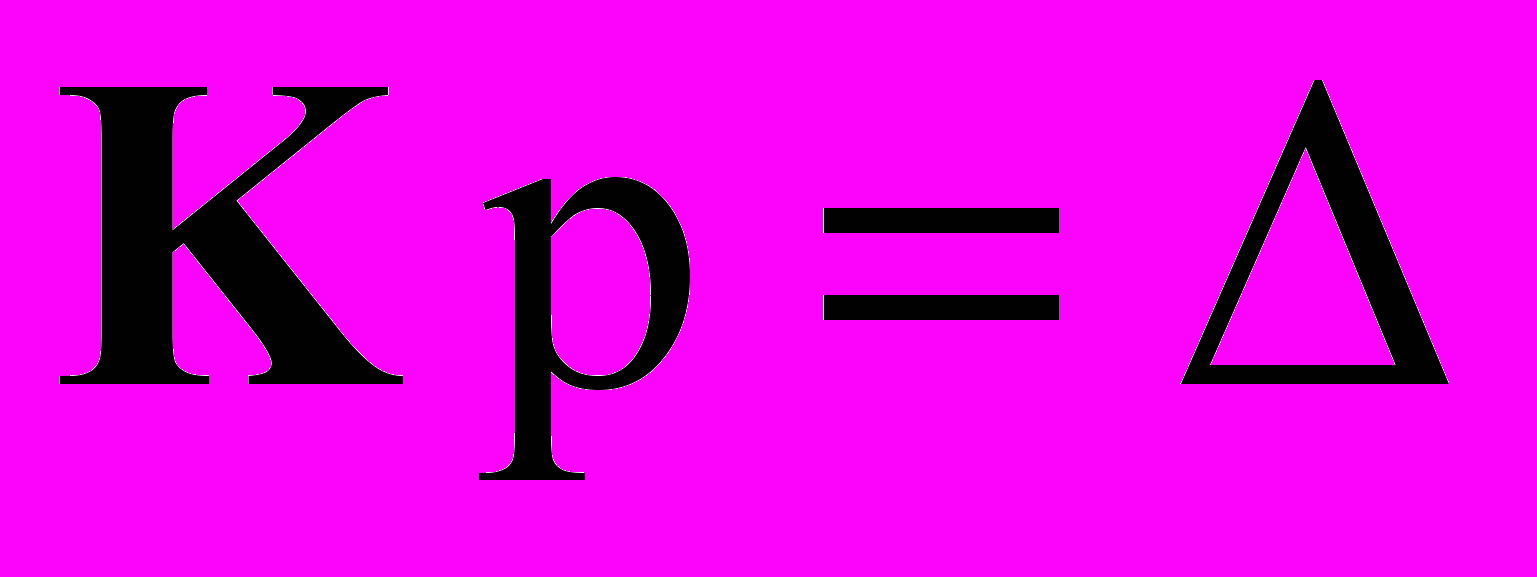, . (10)

Система уравнений (13) переопределена, поэтому необходимо её регуляризовать; окончательно,

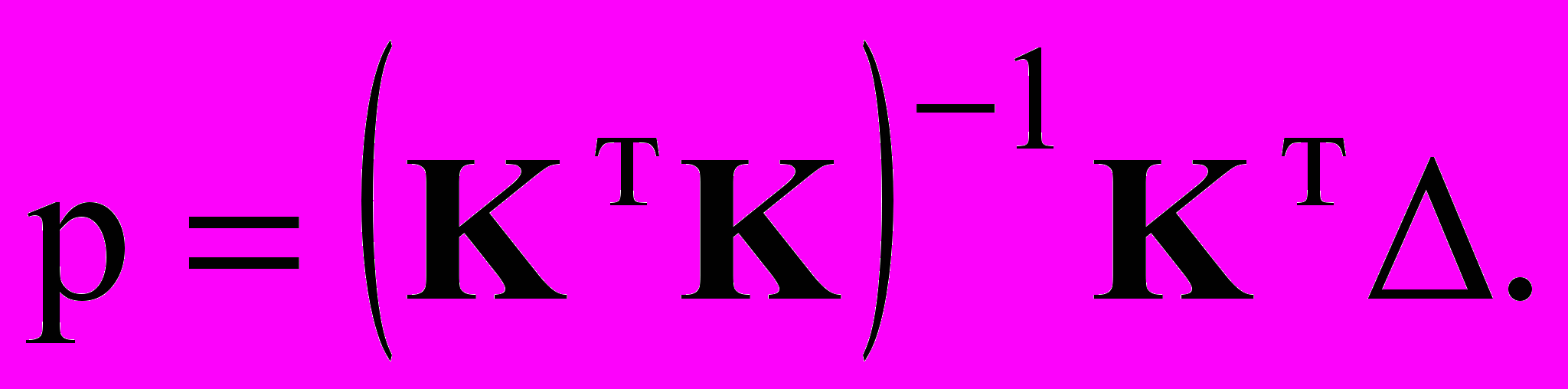(11)

Прямое решение полученной задачи минимизации на дискретной модели с большим числом степеней свободы требует больших затрат вычислительных ресурсов. Сокращение вычислительных затрат на оценку параметров упругости достигается при явном построении аппроксимации функций отклика.



Рисунок 2 – Принципиальная блок-схема алгоритма идентификации параметров упругости и жесткости

Пусть для функции отклика y(x), где x – варьируемые факторы, а y - переменная состояния, построена аппроксимация:

, (12)

где - базисные функции.

После подстановки (12) в критерий (7) он принимает вид функции s переменных A₁, …, A _s. Если число базисных функций невелико, это делает возможным применение точного метода отыскания минимума функции. Задача заключается в построении аппроксимирующего выражения (12) и вычислении коэффициентов A_i.

Выбрав в качестве базисных функций полиномы от параметров x, используем для вычисления коэффициентов факторный вычислительный эксперимент. Для этого требуется проведение N расчетов с варьированием искомых параметров в соответствии с некоторой матрицей планирования. В работе использованы план Хартли, а также простейшие ненасыщенные и насыщенные планы первого и второго порядков.

Проведенные расчеты показали, что полиномиальная аппроксимация дает хорошие результаты при небольшом размахе варьирования, когда имеется априорная информация об оцениваемых параметрах. При увеличении размаха варьирования построение удовлетворительной аппроксимации требует увеличения порядка плана и соответственно увеличения числа расчетов.

Повышение точности аппроксимации проведем на основе качественного анализа решения системы уравнений (1). В работе показано, что зависимость обобщенных перемещений от варьируемых параметров упругости и жесткости может быть точно представлена дробно-рациональной функцией, что позволяет приближенно представить её в виде произведения отрезков рядов Лорана:

, (13)

где - корни характеристического уравнения:

. (14)

Для вычисления коэффициентов разложения необходимо перейти к новым безразмерным факторам :

. (15)

Когда вектор p содержит параметры упругости, корни характеристического уравнения могут быть найдены без фактического решения уравнения (14), поскольку они совпадают с корнями аналогичного уравнения для матрицы упругости материала.

Разработанные алгоритмы реализованы в виде программ на языке Фортран и в среде MathCAD, которые образуют единый комплекс с существующими пакетами конечно-элементного моделирования конструкций. Структура комплекса программ показана на рисунке 3.



Рисунок 3 – Структура комплекса программ

Программы, входящие в комплекс и разработанные в диссертации, реализованы в среде программирования MathCAD, что позволило обеспечить достаточно удобный интерфейс и гибкость алгоритма.

Четвертая глава посвящена исследованию свойств предложенных моделей и алгоритмов и их апробации на задачах оценки параметров упругости и жесткости двух видов конструкций из армированных материалов – балки из армированного железобетона и толстостенной оболочки из углеграфитного композиционного материала.

Балка (рисунок 4), выполненная из керамзитобетона В20, содержит один ряд арматуры A-III. Предполагается, что во время эксплуатации балка испытала огневое воздействие, которое приводит к термодеструкции поверхностных слоев – верхнего и/или нижнего, толщина которых неизвестна и подлежит определению.



Рисунок 4 – Сечение, схема закрепления и нагружения балки

Данный пример является модельным и показывает возможность определения толщины поврежденных слоев. В качестве отклика выбирались прогибы в 9 точках, равномерно отстоящих по всему пролету, и напряжения на верхней поверхности центрального сечения. Вместо результатов измерений принимались вычисленные значения прогибов и напряжений при заданных значениях параметров p₁=0,01, p₂=0,015 м. Варьирование каждого фактора производилось в пределах от 0 до 0,02 м.

При точечной оценке параметров использовались следующие варианты аппроксимации функций отклика: полиномиальная – линейная, билинейная и квадратичная; дробно-рациональная – первого и второго порядков. Коэффициенты определялись двухфакторным вычислительным экспериментом при двух, трех и пяти уровнях.

На рисунке 5 представлены результаты интервальной оценки искомых параметров.



Рисунок 5 – Результаты идентификации сечения армированной балки

Проведено 10000 расчетов, в которых в качестве случайной составляющей измерений принимались сгенерированные векторы с компонентами, равномерно распределенными в интервале полуширины 0,3 мм для перемещений и 0,1 МПа для напряжений. Полученные доверительные интервалы покрывают действительные значения параметров, заложенные в модель.

Толстостенная коническая оболочка из углеграфита УПА-3, показанная на рисунке 6, имела следующие геометрические параметры: высота конуса H=74,3 мм, внешний радиус большего основания 145 мм, внешний радиус меньшего основания 89 мм, толщина стенки 11,2 мм.



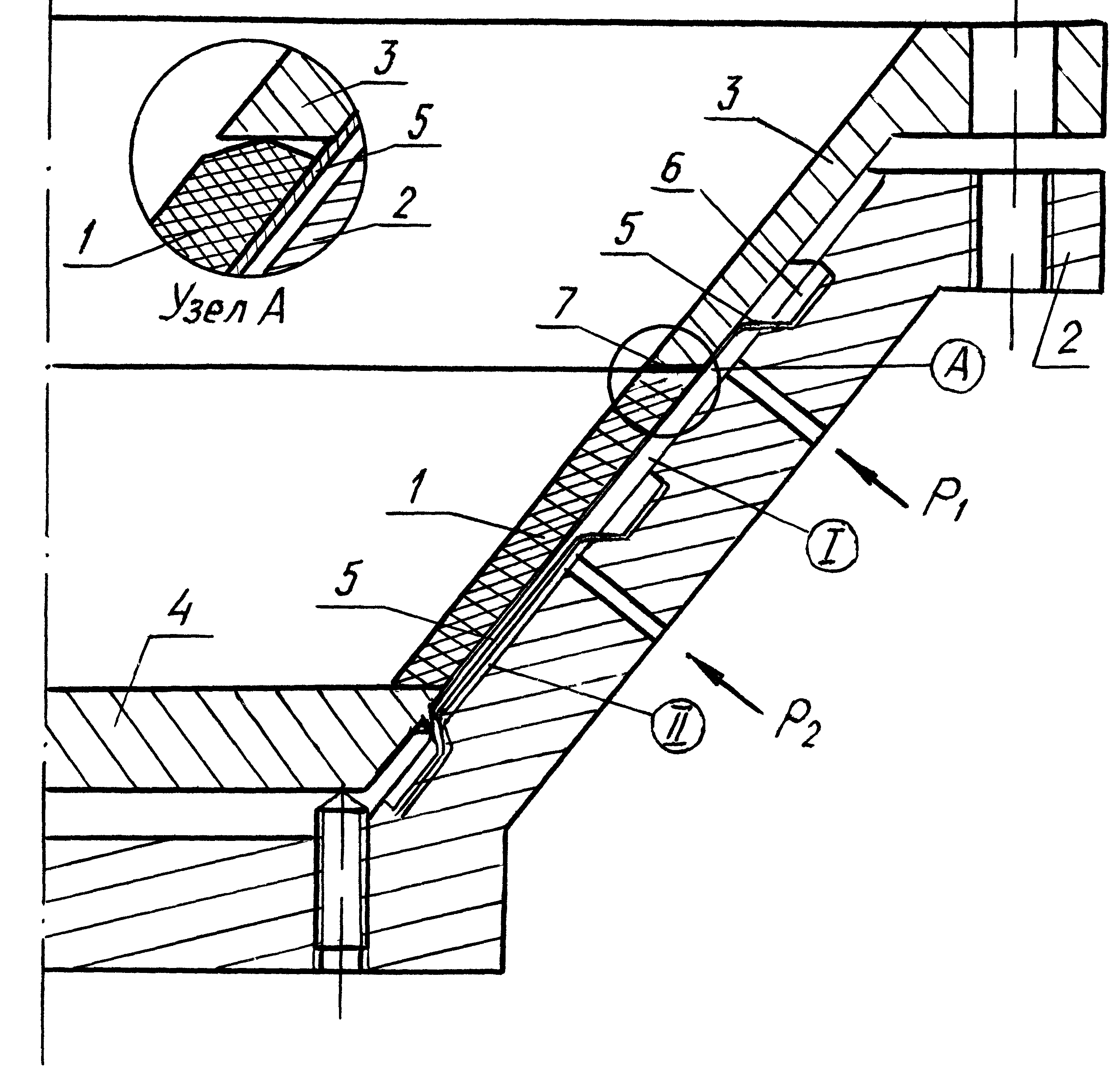
а б в

Рисунок 6 – Оболочка из углеграфита: а – общий вид (половина симметричной конструкции), б – схема нагружающего устройства, в – схема размещения тензодатчиков

Определялись: модуль упругости на растяжение-сжатие вдоль меридиана и вдоль окружности 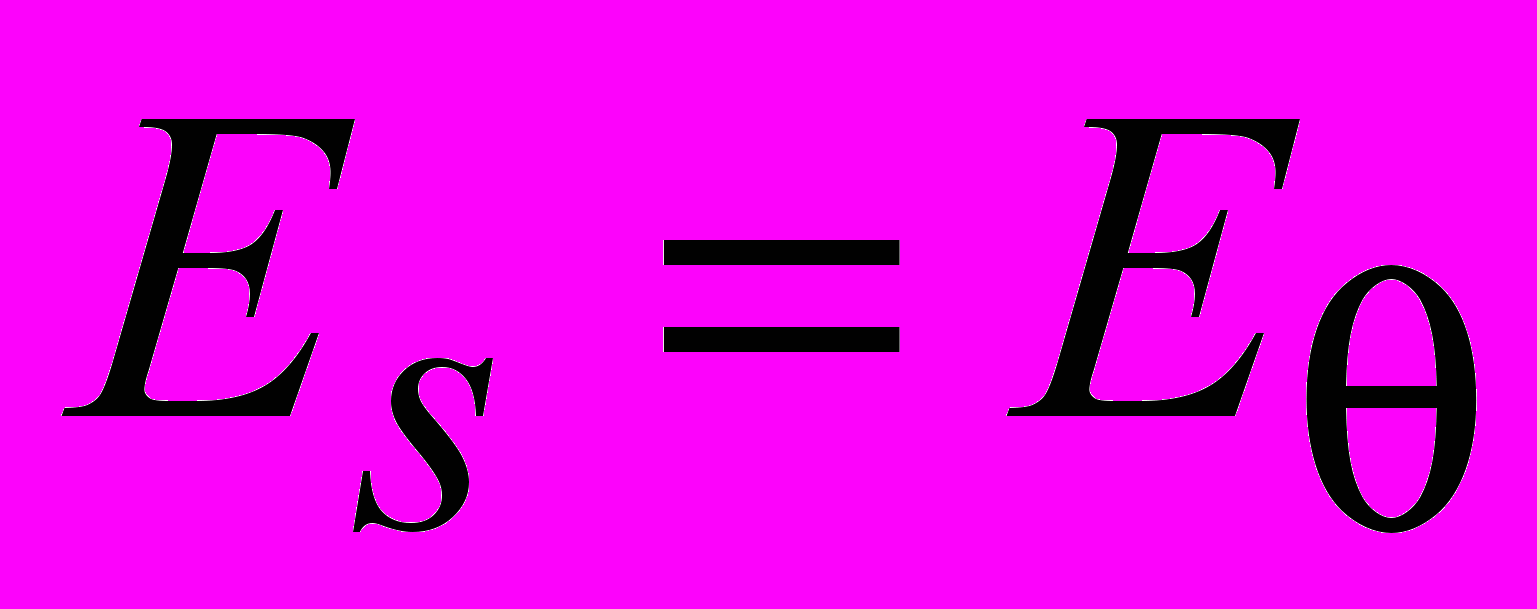, модуль поперечного сдвига 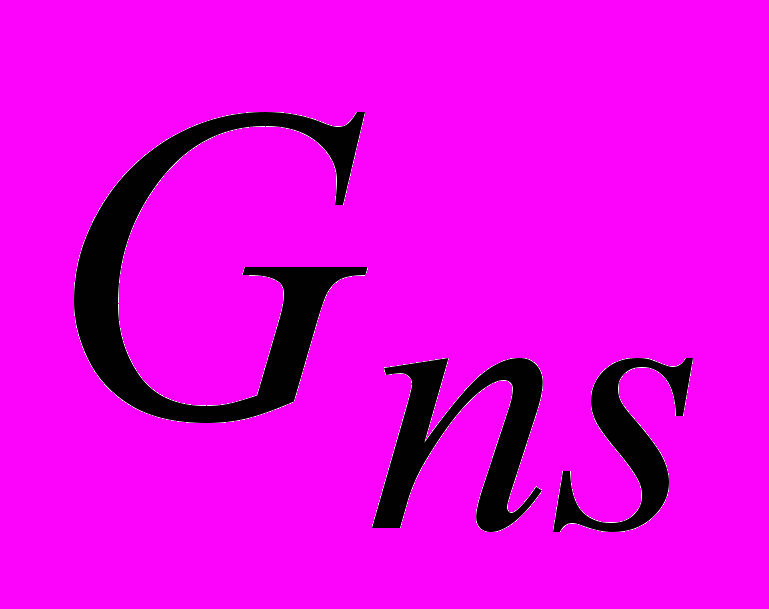и два коэффициента Пуассона и трансверсально изотропного материала. В качестве отклика выбирались окружные и меридиональные деформации в точках установки тензодатчиков (рисунок 6, в).

Натурные испытания проводились на гидравлическом нагружающем устройстве (рисунок 6, б) при внешнем давлении. Деформации измерялись тензорезисторами КФ5П1 с базой 10 мм.

Идентификация параметров упругости выполнялась по описанной выше методике. Найденные значения сопоставлены с результатами испытаний образцов, вырезанных из той же оболочки (таблица 1), и подтверждают достоверность идентификации.

Таблица 1

Наименование		Модули упругости, МПа			Коэффициенты Пуассона
Обозначение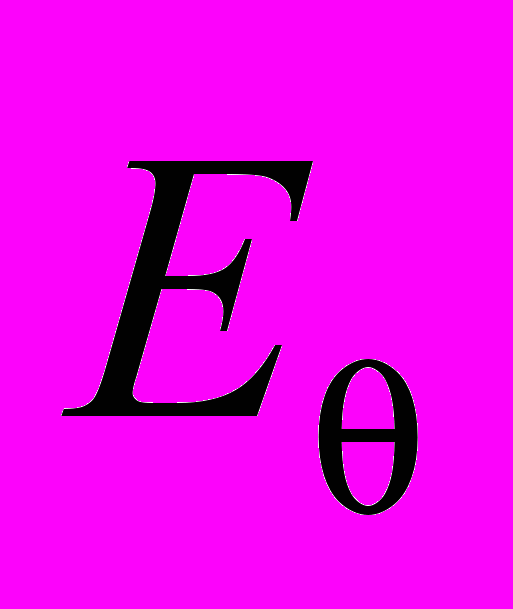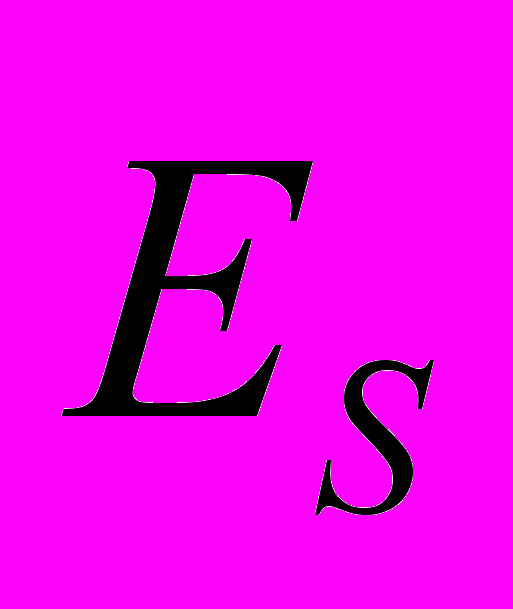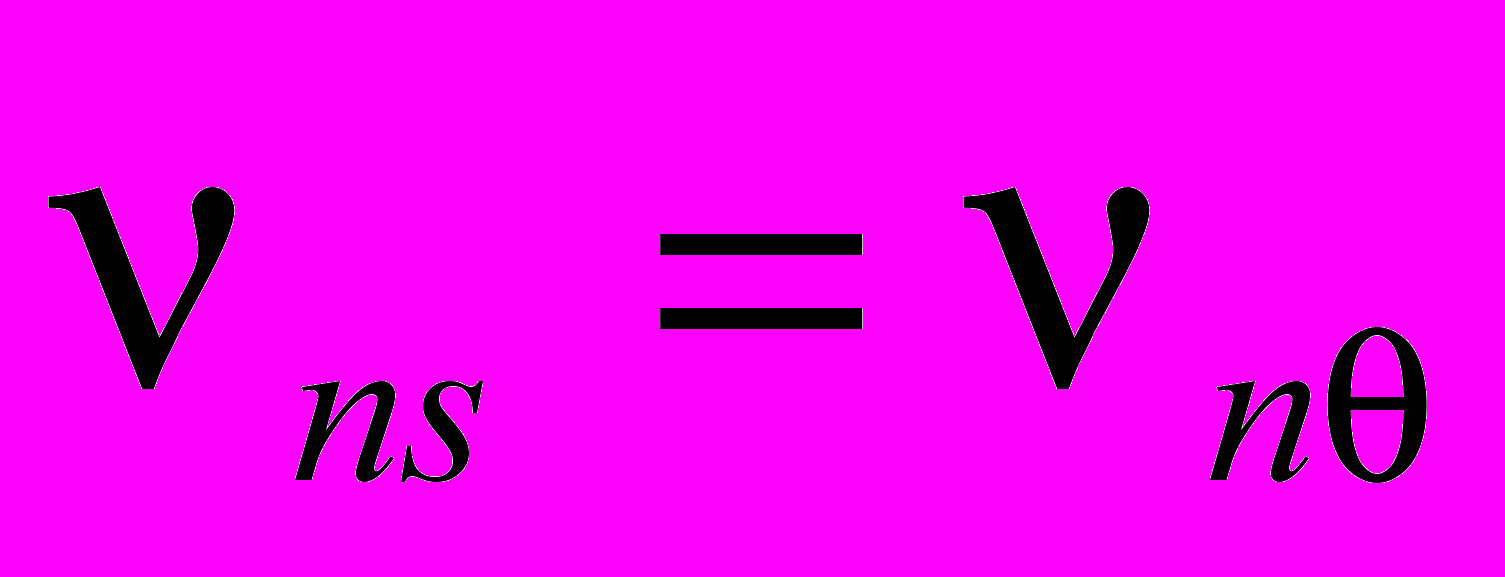
Результаты идентификации		6353	6353	750	0,19	0,12
Результаты измерений на пяти образцах	Среднее значение	5875	6240	656	0,19	0,10
	Разброс, %	10,7	12,2	21,8	20,0	12,8
Относительная погрешность идентификации, % от измеренного		8,1	1,8	14,3	0	20,0

Различие между параметрами, найденными путем идентификации по результатам тензометрирования натурного изделия, и измеренными на образцах, не превышает 15% для модулей упругости и 20% для коэффициента Пуассона, что укладывается в полосу разброса экспериментальных данных. Рассеяние опытных данных в пределах, характерных для используемых тензорезисторов, изменяет значения параметров упругости не более чем на 8 %.

В заключении приведены основные результаты диссертациии:

1. Развит метод параметрического исследования конечно-элементных моделей статического деформирования конструкций из армированных материалов, основанный на разложении обобщенных перемещений в ряд по параметрам упругости и жесткости, в котором предложено использовать отрезок ряда Лорана, а коэффициенты определять из факторного вычислительного эксперимента.
   
2. Построены дробно-рациональные базисные аппроксимационные функции для выражения обобщенных перемещений и деформаций через варьируемые параметры упругости и жесткости для ортотропной оболочки и изгибаемой балки.
   
3. Оценена погрешность численного решения в факторном вычислительном эксперименте, погрешность аппроксимации функций отклика и чувствительность модели к вариации измеряемых переменных состояния.
   
4. Погрешность дробно-рациональной аппроксимации при простейшем четырехточечном плане вычислительного эксперимента составила 1,5%, а погрешность полиномиальной аппроксимации 2,8%. Для получения погрешности 1,6% при полиномиальной аппроксимации потребовалось построить 9-точечный план второго порядка.
   
5. Разработаны алгоритмы интерпретации натурных статических испытаний конструкций из армированных материалов для идентификации параметров упругости и жесткости, в которых используется двухуровневая модель статического деформирования, состоящая из конечно-элементной модели и редуцированной модели в виде аппроксимации функций отклика, а также модели измерительного устройства, имитирующей случайную составляющую измеренных переменных состояния.
   
6. Разработаны алгоритмы точечной оценки кусочно-постоянных параметров упругости и жесткости на основе минимизации квадратичного критерия качества оценивания.
   
7. Разработаны компьютерные программы идентификации параметров упругости и жесткости по данным натурного эксперимента, которые могут использоваться совместно с универсальными и специализированными пакетами конечно-элементного моделирования статики конструкций.
   
8. Достоверность точечных и интервальных оценок параметров жесткости армированной балки, найденных из аппроксимации функций отклика, подтверждена моделированием с имитацией случайных отклонений параметров модели и измеряемых переменных состояния.
   
9. Достоверность результатов идентификации модулей упругости оболочки из углерод-углеродного композиционного материала по измерениям при неразрушающих испытаниях подтверждена сопоставлением с данными прямого экспериментального измерения на образцах, вырезанных из испытанной конструкции. Погрешность идентификации модулей упругости составила 15%, а коэффициентов Пуассона 20%, что укладывается в полосу разброса экспериментальных данных.
   

Основные публикации по теме работы

Статьи, опубликованные в журналах ВАК

1. Резниченко А.И., Казначеева О.К. Исследование физико-ме­ха­ни­чес­ких параметров и уровней остаточных напряжений рентгенографическими методами. Изв. вузов Северо-Кавказский регион. Сер. Технические науки. – 1999. – №2. – С. 125-129.

2. Резниченко А.И., Казначеева О.К., Красюкова И.Ю. Общий алгоритм формирования матриц жесткости конечных элементов для расчета конструкций с учетом геометрической и физической нелинейности. // Изв. вузов. Сев.-Кавк. регион. Сер. Техн. науки. – 2005. – № 3. – С. 60-62.

3. Резниченко А.И., Казначеева О.К., Красюкова И.Ю. Методика и результаты экспериментальных исследований упругопластических свойств полимерного материала. // Изв. вузов. Сев.-Кавк. регион. Сер. Техн. науки. – 2005. Спецвыпуск.– С. 97-99.

4. Казначеева О.К., Резниченко А.И., Ложаев С.М. Формирование матриц жесткости конечных элементов из армированных композитных материалов//Изв. вузов. Сев.-Кавк. регион. Сер. Техн. науки. 2006. – № 10. – С. 21-24.

5. Резниченко А.И., Казначеева О.К., Ложаев С.М. Построение реологических моделей линейно и нелинейно деформируемых упругих тел // Изв. вузов. Сев.-Кавк. регион. Сер. Техн. науки. 2006. – № 12. – С. 112-118.

6. Резниченко А.И., Казначеева О.К., Ложаев С.М. Методика определения приведенных упругих констант в изделиях из вновь созданных композитных материалов. // Научная мысль Кавказа. Северо-Кавказский научный центр высшей школы, 2006. - Спецвыпуск. - №2.-С.89-93.

7. Калашников С.Ю., Казначеева О.К., Бурцева О.А. Алгоритмы оптимального оценивания состояния и внешних воздействий наблюдаемых конструкций. // Вестн. Волгогр. гос. архит.-строит. унив. Сер.: Стр-во и архит. 2011. Вып. 21(40). – С. 5-12.

Статьи и доклады на конференциях

8. Резниченко А.И., Казначеева О.К. Определение приведенных упругих характеристик композитных материалов методом последовательных приближений: сб. ст. и кратк. сообщ. по материалам науч.-техн. конф. студ. и асп. НГТУ / Новочерк. гос. техн. ун-т. – Новочеркасск: НГТУ, 1996. – С. 13-15.

9. Резниченко А.И., Казначеева О.К., Николаев Н.Н. Методика определения приведенных упругих характеристик углерод-углеродного композита (УУКМ) УПА-3М. Моделирование. Теория, методы и средства: материалы междунар. науч.-практ. конф., г. Новочеркасск, 11 апреля 2001 г.: в 8 ч./Юж.-Рос. гос. техн. ун-т.- Новочеркасск: УПЦ «Набла» ЮРГТУ (НПИ), 2001.-Ч.5. − С.46-53.

10. Кабельков А.Н., Казначеева О.К. Алгоритмы экспериментально- теоретического оценивания характеристик некоторых полимерных материалов. // Cовременные проблемы механики сплошной среды. Труды XIV Международной конференции, г.г. Ростов-на-Дону, Азов, 19 − 24 июня 2010 г. Т 2. Ростов н/Д. Изд-во ЮФУ. 2010. − С. 134-136.

11. Казначеева О.К. Об одном методе экспериментального определения упругих характеристик композитных материалов.//Современные проблемы механики и ее преподавания в вузах Российской Федерации: доклады Межрегиональной конференции памяти А.Н. Кабелькова, г. Новочеркасск, 20-23 апреля 2011 г. / Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ(НПИ), 2011. – С. 81-85.

12. Казначеева О.К., Черпаков А.В. Конечно-элементное моделирование НДС оболочки из композитного материала. // Современные проблемы механики и ее преподавания в вузах Российской Федерации: доклады Межрегиональной конференции памяти А.Н. Кабелькова, г. Новочеркасск, 20-23 апреля 2011 г. / Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ(НПИ), 2011. – С. 86-88.

13. Казначеева О.К., Калашников С.Ю., Бобина Е.А. Методика неразрушающего контроля приведенных упругих характеристик в изделиях из композитных материалов. //Наука и образование: архитектура, градостроительство и строительство: материалы Международной конференции, посвященной 80-летию строительного образования и 40-летию архитектурного образования Волгоградской области, 6-10 сентября 2010 г., Волгоград / Волгогр. гос. архит.-строит. унив. – Волгоград: ВолгГАСУ, 2010. – С. 301-308.

14. Казначеева О. К., Бакулин В. Н. Экспериментально-теоретический метод моделирования упругих свойств композитных материалов // Материалы XVII Международной конференции по вычислительной механике и современным прикладным программным системам (ВМСППС'2011), Алушта, 25-31 мая 2011 г. / Моск. авиац. ин-т (гос. техн. ун-т). – М.: Изд-во МАИ-ПРИНТ, 2011. – С. 342-344.

15. Казначеева O.K., Бакулин В. Н., Бобина Е. А. Идентификация параметров в изделиях из вновь созданных композитных материалов // Седьмые Окуневские чтения: материалы докл. Междунар. конф., Санкт-Петербург, 20-24 июня 2011г./ Балт. гос. техн. ун-т, – СПб., 2011. – С. 239-241.

Монография

16. Казначеева О.К. Оптимальное оценивание напряженно-деформированного состояния и идентификация параметров наблюдаемых конструкций: монография. – Новочеркасск: ЮРГТУ, 2010. – 95 с.


Подписано в печать 04.10/2011 г. Формат 60х84 1/16.

Бумага писчая. Ризография.

Усл. печ. л. 1,0. Уч.-изд.л. 1,04. Тираж 100 экз.

Заказ № 135.


Новокузнецкий институт (филиал)

Федерального государственного бюджетного образовательного учреждения

«Кемеровский государственный университет»

654041, г. Новокузнецк, пр. Металлургов, 19, тел. (3843) 74-25-68

Редакционно-издательский отдел