Новиковой Екатерины Николаевны Использование элементов технологии самосовершенствования личности на урок
| Вид материала | Урок |
- Конкурсный урок по теме: «Именем Святой Екатерины», 61.59kb.
- Конкурс «Именем святой Екатерины» «Именем святой Екатерины наречённый», 190.87kb.
- «Именем Екатерины наречённый», 61.49kb.
- Алматинский государственный колледж технологии и экономики использование элементов, 334.93kb.
- Конспект урока в 1 «б» классе моу сош №10 Тема: «Именем Екатерины нареченный», 38.13kb.
- Дракиной Екатерины Анатольевны, учителя физики моу лицея №6 г. Ессентуки Использование, 83.64kb.
- Оздоровительная программа «1000 движений» система Амосова. Практика Йоги как метод, 23.88kb.
- Манукян Владимира Николаевна 2007-2008 уч год урок, 50kb.
- Централизованное тестирование: направления, технологии и содержание, 91.59kb.
- План проведения: 4 Урок по валеологии 4 Интегрированный урок истории и литературы, 617.3kb.
1 2
3. В каком отношении находится подчеркнутое вами слово в каждом из списков к заданию 2 с остальными словами из списка?
В каждом списке лишним предполагается обобщающее слою.
4. Слова из данного ниже списка расставьте в окошки схемы на рис. 1.
Т
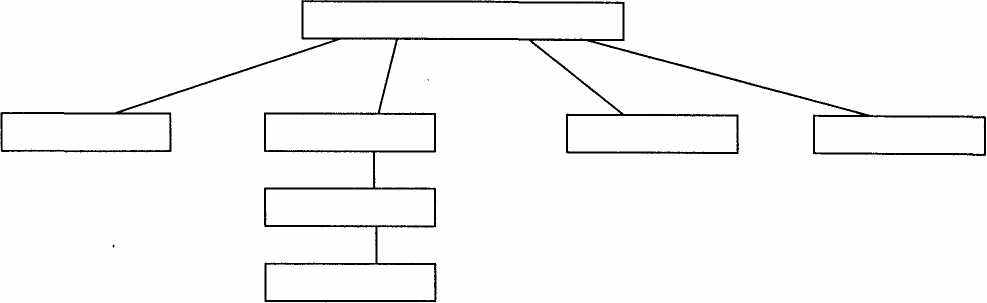 реугольник, четырехугольник, пятиугольник, шестиугольник, прямоугольник, квадрат, многоугольник.
реугольник, четырехугольник, пятиугольник, шестиугольник, прямоугольник, квадрат, многоугольник.Развитие навыка сравнения
Укажите в табл. 1 как можно больше общих свойств понятий «отрезок», «луч», «прямая» и как можно больше различий.
Таблица
| б Общие свойства | Различия | ||
| Отрезок отрезок | луч | прямая | |
| | | | |
Действия с натуральными числами
Классификация
1. Разбейте данные ниже слова на два столбика и озаглавьте каждый столбик.
Слагаемое, вычитаемое, сумма, частное, множитель, уменьшаемое, делитель, произведение, разность.
Один столбик можно озаглавить «действие», а другой - «результаты действий».
2. Даны три ряда чисел. Укажите, по какому правилу составлен каждый ряд чисел, и продолжите его еще на три числа в соответствии с этим правилом.
а)1, 3, 5, 7, 9, 11,....
б)2. 4. 6. 8. 10…
в) 1. 2. 4. 5.

 7. 8. 10. 11. 13….
7. 8. 10. 11. 13….Развитие смысловой памяти
Учитель читает по блокам пары слов, предварительно нацелив детей на
запоминание.
Блок 1 Блок 2
Буквенное выражение. Корень уравнения.
Значение буквы. Неизвестное слагаемое.
Подставить число. Верное равенство.
Решить уравнение. Периметр треугольника.
Затем учитель повторно читает первые слова в парах, а ученики записывают в своих тетрадях второе слово каждой пары.
Проверка проходит так: учитель читает третий раз первое слово каждой пары, а кто-либо из учеников добавляет второе слово.
Корректировка восприятия.
Найти и исправить ошибки, если они есть в следующих действиях:
а) 3,2 4 + 8 = 4,0; г) 29 + 7,1 = 100;
б) 16,6 - 5 = 16,1; д) 25,16 + 0,4 =25,56;
Действия с обыкновенными дробями
Классификация
I. Выделение существенного признака объекта.
Подчеркните два слова из слов, данных в скобках, которые находятся в наибольшей связи с обобщающим словом, стоящим перед скобками.
Доля (апельсин, часть, целое, чеснок).
Дробь (половина, треть, числитель, четверть, знаменатель)
. Круг (арена, центр, солнце, колесо, радиус).
Окружность (диаметр, колесо, кольцо, центр, бублик).
Приложение 2.
4.2.Упражнение для усвоения учащимися 5-6 классов приемов составления задач
1. Составьте задачу, обратную следующей:
«На одной ферме 847 коров, а на другой—на 309 коров больше. Сколько коров на двух фермах?»
2. Составьте задачу по краткой записи:
— Зт
- — на 1 т больше, чем
- — в 2 раза меньше, чем —
3. Составьте задачи по выражениям:
a. 12∙64
b. 18∙79-12∙64
c. (18 ∙79 – 12∙64): 3
4. «Купили 3 кг картофеля, 3 кг свеклы, 4 кг моркови, 5 кг яблок, 6 кг капусты,2 кг груш и 4 кг слив. Сколько было куплено килограммов овощей и сколько килограммов фруктов?» Составьте задачу, решаемую тем же способом, но с другим сюжетом.
5. Составьте задачи, при решении которых:
a. по известным частям находят целое;
b. по целому и его частям находят другую часть.
6. Составьте задачи, используя слова:
a. «ехали, проехали, осталось»;
b. «было, изменили, стало»;
c. «дороже» — «дешевле»;
d. «легче» — «тяжелее».
Приложение 3.
4.3.Нестандартные виды домашних заданий, как элемент технологии саморазвития личности
Одной из важнейших составляющих учебного процесса является домашняя работа учащихся.Определяющее требование к домашним заданиям – не только аккуратность, но и безусловная самостоятельность их выполнения. Знания могут быть глубокими, полными и прочными только в том случае, если они самостоятельно продуманы, прочувствованы, усвоены путем преодоления некоторых трудностей.
Самостоятельный поиск и самостоятельное решение вопросов воспитывает у учащихся убежденность в знаниях, уверенность в своих силах, формирует потребность самостоятельно заниматься учебной деятельностью, воспитывает навыки самообразования.
В процессе самостоятельной домашней работы каждый школьник осуществляет самоконтроль, что предполагает развитие умений анализировать свои знания, находить недочеты и ошибки и затем исправлять их.
Поскольку учебная мотивация детей с ЗПР достаточно низкая, то задания для домашней работы должны быть максимально интересны учащимся – должны пробуждать у них стремление к самостоятельной учебной деятельности, развивать кругозор. Так, это могут быть индивидуальные задания на карточках.
Например:
1 VI класс, тема «Координаты точки на плоскости».
Каждому ученику выдается карточка с набором координат. Отмечая точки по их координатам и соединяя их в порядке записи, ученики получают фигуру и заштриховывают ее. А эта фигура оказывается на что-то похожа! Правда, интересно?!
Карточка №1
А
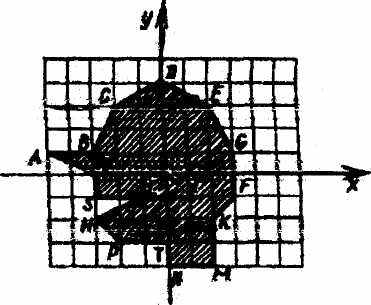 (-5; 1); М (2;-4)
(-5; 1); М (2;-4)В(-3;1); N(0;-4)
С (-2; 3); Т (0;-3)
D(0;4); P(-2;-3) E(2;3); H(-3;-2) G(3;1); L(-1;-1);
F(3;-1); S(-3;-1) К (2;-2); R (-3; 0)
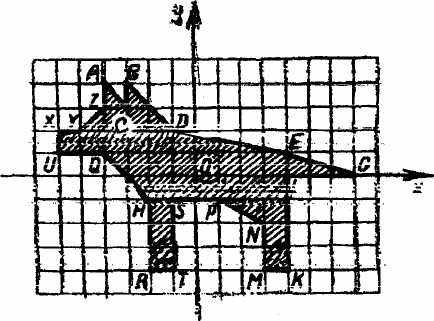
Карточка №2
A (-4; 4); В (-3; 4); С (-3; 3); D (-1; 2); E (4; 1); G (7; 0); L (4; 0); К (4; -4); M (3; -4); N (3; -2); P (-1; -1); S (-1;-1); T (-1; -4); R (-2; -4); H (-2; -1); Q (-4; 1); U (-6; 1); X (-6; 2); Y (-5; 2); 7 (-4; 3),
2.Задание на отработку вычислительных навыков
. Если каплю крови рассмотреть в микроскоп, то в ней станут видны очень мелкие тельца красного цвета. В I мм3 крови, т. е. в одной капле, заключается примерно ... красных телец. Сколько же их всего в вашем теле? Если вы весите 40 кг, то в вашей крови примерно ... триллионов красных кровяных телец. Представим себе, что эта армия кружочков выложена друг за другом. Длина такого ряда составила бы ... км. Нитью такой длины можно было бы обмотать земной шар по экватору более ... раз.
Задания:
l) 3845 :( l0l0-24l) ∙700,
346 - (2486 + 335104:476): 10,
- 507792: 596 + 870-584 + 58093-76,
- 708∙150:450-221,
2035+98765+11088:132∙50,
- (127410:274 + 307200:480-907): 99.
Выполнив дома такое задание, ученики часто не могут дождаться следующего урока математики. Они подходят и спрашивают: «Действительно ли такое может быть? Мы несколько раз перерешали эти примеры. Могут ли быть такие большие числа?». Отсюда следует, что ученик не только сосчитал, но еще и несколько раз проверил расчеты, тем самым, это значит, что закрепление навыков проходит успешно.
2. VI класс, тема «Действия над десятичными дробями».
Каждому ученику выдается карточка с заданием и рисунок.
Задание: Найдите значение буквенного выражения
a∙b:(c+d) при значениях букв, указанных в таблице. Запишите полученные значения в строке «результат» и закрасьте каждую часть своего рисунка цветом, соответствующим в таблице данному результату.
Таблица
| Значения букв | |||||
| а b c d | 7,7 2,21 3,62 13,38 | 24,7 11,9 16,56 38,69 | 14,3 3,23 5,49 5,56 | 1,33 18,7 3,78 6,67 | 9,1 20,9 7,15 7,15 |
| Результат | | | | | |
| Цвет на картинке | красный | желтый | коричневый | черный | серый |
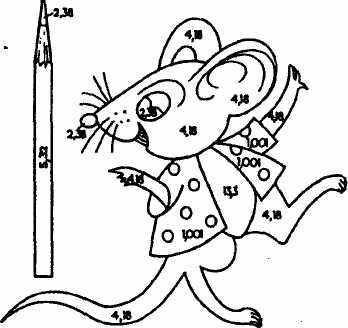
Например, в первом столбце таблицы ученик должен получить результат 1,001
(7,7∙2,21: (3,62 + 13,38) = 1,001).На своей картинке (см. рисунок) он должен закрасить красным цветом те участки, где записано это число, т. е. платьице мышки и ее бантик.
Рисунок детям можно давать один и тот же, а числовые данные или сложность буквенного выражения можно варьировать. Если все ученики правильно выполнят задание, то рисунок у всех будет раскрашен одинаково. Перед уроком рисунки вывешиваются на доске. Туда же учитель помещает и свой рисунок. По этому эталону дети мгновенно видят, кто ошибся и где именно. Обычно обсуждение работы начинается уже на перемене. Не дождавшись звонка на урок, дети делятся своими впечатлениями, выясняют собственные промахи, обсуждают задания и вовлекают в этот разговор учителя.
Школьники часто просят повторить такое задание. На этот случай у учителя есть в запасе дополнительные рисунки и карточки с заданиями.
Математическое же содержание таких заданий может варьироваться от темы к теме.
3. VI к л асе, тема «Действия с рациональными числами».
Учащиеся получают пронумерованные карточки с вычислительными заданиями. В них каждое упражнение шифрует некоторую букву алфавита, а именно: модуль числа, стоящего слева от запятой в результате данного упражнения, есть порядковый номер буквы в алфавите. Например, упражнение 3,8-(-0,25)·4 шифрует букву «В», так как его результат есть -3,8, а |-3|=3, т. е. имеется в виду третья буква алфавита. После выполнения всех упражнений (в порядке их следования) у каждого ученика должна получиться строка из считалочки.
Перед уроком дети записывают на доске каждый свою строчку в соответствии с порядковым номером своей карточки. В результате получаем расшифрованный текст:
Вышли мыши как-то раз
Посмотреть, который час.
Раз, два, три, четыре...
Вдруг раздался страшный звон
Убежали мышки вон.
Данному тексту соответствуют следующие задания.
( Пример)
Карточка №1
3,8- (-0,25)4; -21,75:0.75; -13· (-2);
-39:3; - 49,44:4,8;
2,06∙ (-7,05); -1:0,5+31; (-10,16+4,96)∙5; -2,1∙5;
-6:(-0,5); -2 и т.п.
Идея этого задания возникла после того, как учитель услышала считалочку, которую применяли школьники для начала игры. Текст содержал что-то ужасное и кровожадное, но ей захотелось научить ребят новой считалочке. Но это надо было сделать ненавязчиво. Выход был найден, и теперь многие ребята пользуются этой считалочкой.
Считалочка приносит и дидактическую пользу: ошибки, сделанные учениками, мешают построению текста, поэтому ребята стараются их найти и исправить. Да и на проверку домашнего задания уходят считанные секунды. Кроме того процесс выполнения задания такого типа захватывает ученика, на следующий урок дети часто просят повторить задание, тем самым гарантируют выполнение предстоящей (самостоятельной ) домашней работы.
