Решение задачи о раскрое материала
| Вид материала | Решение |
- При раскрое в нужный, размер, 5621.24kb.
- Программы регионального компонента по истории 5- 9 классы, 175.4kb.
- Языки программирования, 27.65kb.
- Курсовой проект по дисциплине «Теория информационных процессов и систем» тема: Задачи, 258.87kb.
- Решение задачи одним из математических методов, 440.71kb.
- Организационный план : Подготовка к изучению нового материала > Изучение нового материала, 83.57kb.
- Решение задач занимает в математическом образовании огромное место. Умение решать задачи, 270.04kb.
- Программа обсуждена на заседании кафедры Математики фнти, 45.62kb.
- Решение любой задачи является творческим процессом, который состоит из нескольких последовательных, 342.43kb.
- Решение логических задач, 273.53kb.
Муниципальное общеобразовательное учреждение «Лицей»
Секция «математика»
«Графический метод решения задач линейного программирования»
Выполнила:
Смирнова Татьяна.,
учащаяся 9 «А» класса, МОУ «Лицей»
Руководитель:
Полкачева Т.А..
учитель математики,
Моу «Лицей»
г. Междуреченск, 2008г.
Содержание
| 1 | Введение | 3 |
| 2 | Теоретические основы графического метода линейного программирования | 4 |
| 3 | Пример задачи, решаемой этим способом | 10 |
| 4 | Решение задачи о раскрое материала | 15 |
| 5 | Заключение | 18 |
| | Список используемой литературы | 19 |
| | | |
1. Введение
Цель. Решение задачи о раскрое ткани.
Задачи.
1. изучить графический метод линейного программирования.
2. найти оптимальное решение задачи о раскрое материала.
Актуальность. У меня возник интерес сшить односпальные и двуспальные комплекты, но передо мной встал выбор какие комплекты шить и какой ширины использовать для этого ткань.
2. Теоретические основы графического метода линейного программирования.
Введение в исследование операций
Исследование операций — научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами.
Другими словами, исследование операций — научное направление, целевая установка которого - разработка методов анализа целенаправленных действий (операций) и объективная (в частности, количественная) сравнительная оценка решения.
Операция — любое управляемое мероприятие, направленное на достижение цели. Результат операции зависит от способа её проведения, организации, иначе — от выбора некоторых параметров. Всякий определённый выбор параметров называется решением.
Оптимальными считают те решения, которые по тем или иным соображениям предпочтительнее других. Поэтому основной задачей исследования операций является предварительное количественное обоснование оптимальных решений.
Эффективность операции — степень её приспособленности к выполнению задачи — количественно выражается в виде критерия эффективности - целевой функции.
Дня применения количественных методов исследования требуется построить математическую модель операции.
Экономико-математическая модель - достаточно точное описание исследуемого экономического процесса или объекта с помощью математического аппарата (различного рода: функций, уравнений, систем уравнений и неравенств и т.п.).
Этапы исследования операций
Усложнение производства, техники и организационной структуры общества приводит к тому, что принятие решений и эффективное руководство все больше и больше нуждаются в широкой, точной и быстрой информации, количественной оценке и прогнозе результатов, последствий принятых решений. Назначение методов исследования операций — объективно разобраться в каждом явлении, численно оценить предлагаемые целенаправленные действия и, возможно, предложить варианты решений, отличные от тех, которые рассматривали хозяйственные или другие руководители.
Несмотря на многообразие задач, возникающих в экономике (задача оптимального планирования инвестиций, формирование минимальной потребительской корзины, организация рекламной деятельности, составление штатного расписания, определение специализации предприятия и т.д.), при их решении можно выделить некоторую общую последовательность этапов, через которые проходит любое операционное исследование.
Как правило, это:
- Постановка задачи.
- Построение содержательной (вербальной) модели рассматриваемого объекта (операции, процесса). На данном этапе происходит формализация цели управления объектом, выделение возможных управляющих воздействий, влияющих на достижение сформулированной цели, а также описание системы ограничений на управляющие воздействия.
- Построение математической модели, т.е. перевод сконструированной вербальной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.
- Анализ модели или получение решения задачи.
- Анализ решения, т.е. получение информации об изменениях решения при изменении условий (неуправляемых переменных) функционирования системы. Эту часта исследования обычно называют анализом модели на чувствительность.
- Проверка полученных результатов на их адекватность, природе изучаемой системы, включая исследование влияния так называемых внемодельных факторов, и возможная корректировка первоначальной модели.
Реализация полученного решения на практике.
Краткое описание каждого этапа
1,2) Постановка задачи является одним из наиболее важных этапов исследования операций. При постановке задачи исследования операций необходимо определить цель, преследуемую субъектом управления (ЛПР) и установить, значение каких характеристик (управляемых переменных) исследуемой системы (процесса) можно варьировать, а изменение значений каких переменных (неуправляемых) не зависит от решений ЛПР. Кроме того, на данном этапе необходимо определить требования, условия и ограничения на исследуемую операцию. На этом же этапе должны быть решены проблемы информационного обеспечения будущей модели ИО.
3) Построение модели. На этом этапе необходимо выбрать модель, наиболее под ходящую для адекватного описания ИО. При построении модели должны быть установлены количественные соотношения для выражения целевой функции (ЦФ) и ограничений в виде функций от управляемых переменных. Наиболее важным типом моделей ИО являются математические модели (ММ). В основе их построения лежит допущение о том, что все переменные, ограничения, их связывающие, а также целевая функция количественно измеримы. Поэтому если
 представляют собой n управляемых переменных, а условия функционирования исследуемой системы (ИС) характеризуются m ограничениями, то ММ может быть записана в следующем виде:
представляют собой n управляемых переменных, а условия функционирования исследуемой системы (ИС) характеризуются m ограничениями, то ММ может быть записана в следующем виде: - целевая функция
- целевая функция  - ограничения
- ограничения- Анализ модели обычно производится с помощью методов математического программирования.
- Анализ решения или анализ на чувствительность — это процесс, реализуемый после того, как оптимальное решение задачи получено. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели, т.е. фактически рассматривается совокупность моделей, что придает исследуемой операции определенную динамичность.
- Решение, полученное при помощи анализа модели, не может, однако, непосредственно быть рекомендовало для практической реализации. Математическая модель, как и любая другая модель, лишь частично отображает действительность, акцентирует отдельные ее аспекты. Адекватность модели исследуемой операции и, следовательно, качество полученного результата можно проверить, сопоставлял результаты, установленные без использования модели, с результатами, вытекающими из анализа модели.
Работы по исследованию операций имеют смысл, если они завершаются внедрением результатов исследования в практику. Важность задач координации научной и производственной деятельности и трудности, связанные с внедрением научных рекомендаций в производство, заставляют рассматривать эти вопросы как отдельный этап в исследовании операций. При этом следует помнить, что задача исследователя операции - подготовить решение, а не принять его. Руководитель, ответственный за решение, должен учитывать помимо рекомендаций исследователя операций, основанных на количественных оценках, и другие факторы, не поддающиеся формализации.
В исследовании операций используется разнообразный математический аппарат. Чаще других методов для анализа моделей операций и подготовки решений используются методы математического программирования, комбинаторного анализа и статистического моделирования.
Математическое программирование — область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т.е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.
Задача математического программирования (ЗМП) имеет вид:
 — целевая функция
— целевая функция —ограничения
—ограниченияВ зависимости от свойств функций
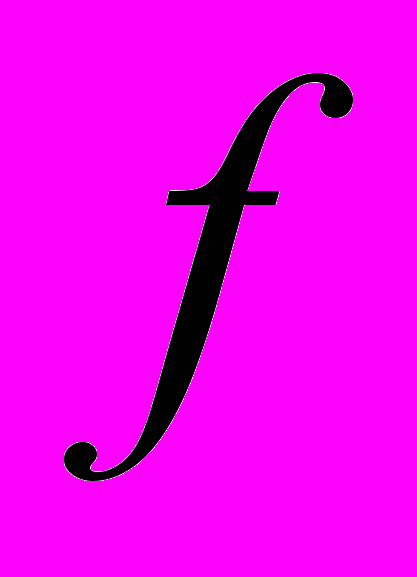 и
и  математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач.
математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач.Прежде всего, задачи математического программирования делятся на задачи линейного и нелинейного программирования. При этом если все функции
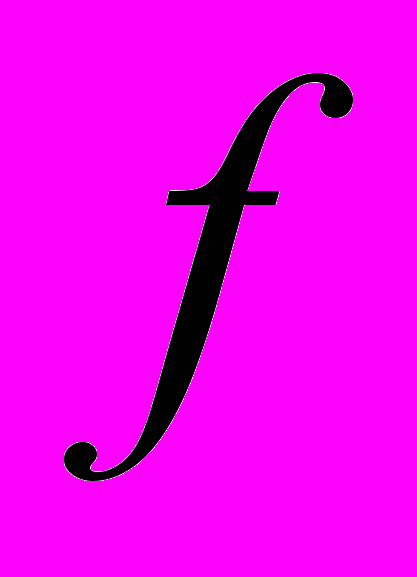 и
и  линейные, то соответствующая задача является задачей линейного программирования. Бели же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.
линейные, то соответствующая задача является задачей линейного программирования. Бели же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач линейного программирования разработан целый ряд эффективных методов, алгоритмов и программ.
Среди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования. Это задачи, в результате решения которых определяется минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования. В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений, либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения.
Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно-линейного программирования.
В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.
В задачах параметрического программирования целевая функция или функции, определяющие область возможных изменений переменных, либо то и другое зависят от некоторых параметров.
В задачах дробно-линейного программирования целевая функция представляет собой отношение двух линейных функций, а функции, определяющие область возможных изменений переменных, также являются линейными.
Выделяют отдельные классы задач стохастического и динамического программирования.
3. Пример задачи, решаемой этим методом
Если в целевой функции или в функциях, определяющих область возможных изменений переменных, содержатся случайные величины, то такая задача относится к задаче стохастического программирования.
Задача, процесс нахождения решения которой является многоэтапным, относится к задаче динамического программирования.
Рассмотрим несколько примеров проведения операционного исследования.
Пример 1.1; Фабрика выпускает продукцию двух видов: П1 и П2. Продукция обоих видов поступает в оптовую продажу. Для производства этой продукции используются три исходных продукта - А, В, С. Максимально возможные суточные запасы этих продуктов составляют 6, 8 и 5 т соответственно. Расходы сырья А, В, С на 1 тыс. изделий П1 и П2 приведены в табл. 1.1.
Таблица 1.1
| Исходный продукт | Расход исходных продуктов на 1 тыс. изделий (т.) П1 П2 | Максимально возможный запас (т.) | |
| А | 1 | 2 | 6 |
| В | 2 | 1 | 8 |
| С | 1 | 0.8 | 5 |
Изучение рынка сбыта показало, что суточный спрос на изделия П2 никогда не превышает спроса изделия П1 более чем на 1 тыс. шт. Кроме того, установлено, что спрос на изделия П2 никогда не превышает 2 тыс. шт. в сутки.
Оптовые цены 1 тыс. шт. изделий П1 равны 3 тыс. руб., 1 тыс. шт. П2 - 2 тыс. шт.
Какое количество изделий (в тыс. шт.) каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Построение математической модели следует начать с идентификации переменных (искомых величин). После этого целевая функция и ограничения выражаются через соответствующие переменные.
В рассматриваемом примере имеем следующее:
Переменные. Так как нужно определить объемы производства каждого вида продукции, переменными являются:
 — суточный объем производства изделия П1в тыс. шт.;
— суточный объем производства изделия П1в тыс. шт.;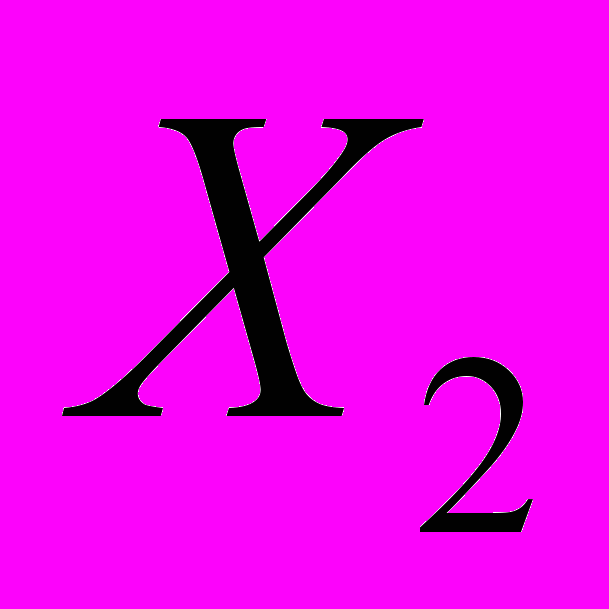 —суточный объем производства изделия П2 в тыс. шт.
—суточный объем производства изделия П2 в тыс. шт.Целевая функция. Так как стоимость 1 тыс. изделий П1 равна 3 тыс. руб., суточный доход от ее продажи составит
 тыс. руб. Аналогично доход от реализации
тыс. руб. Аналогично доход от реализации 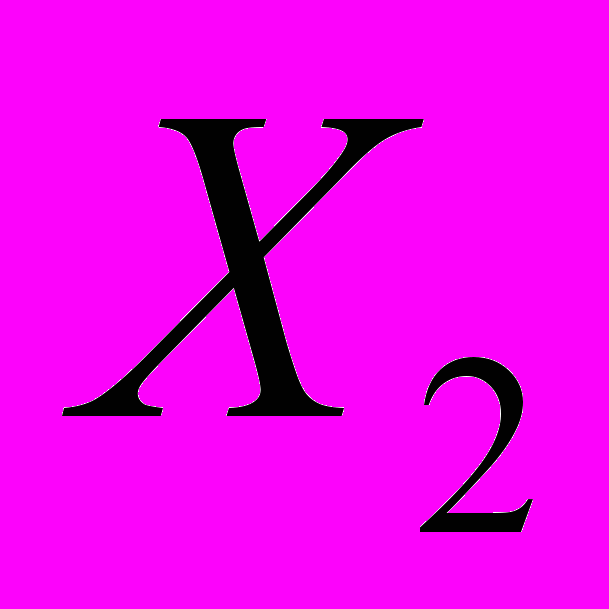 тыс. шт. П2 составит
тыс. шт. П2 составит  тыс. руб. в сутки. При допущении независимости объемов сбыта каждого из изделий общий доход равен сумме двух слагаемых — дохода от продажи изделий П1 и дохода от продажи изделий П2.
тыс. руб. в сутки. При допущении независимости объемов сбыта каждого из изделий общий доход равен сумме двух слагаемых — дохода от продажи изделий П1 и дохода от продажи изделий П2.Обозначив доход (в тыс. руб.) через
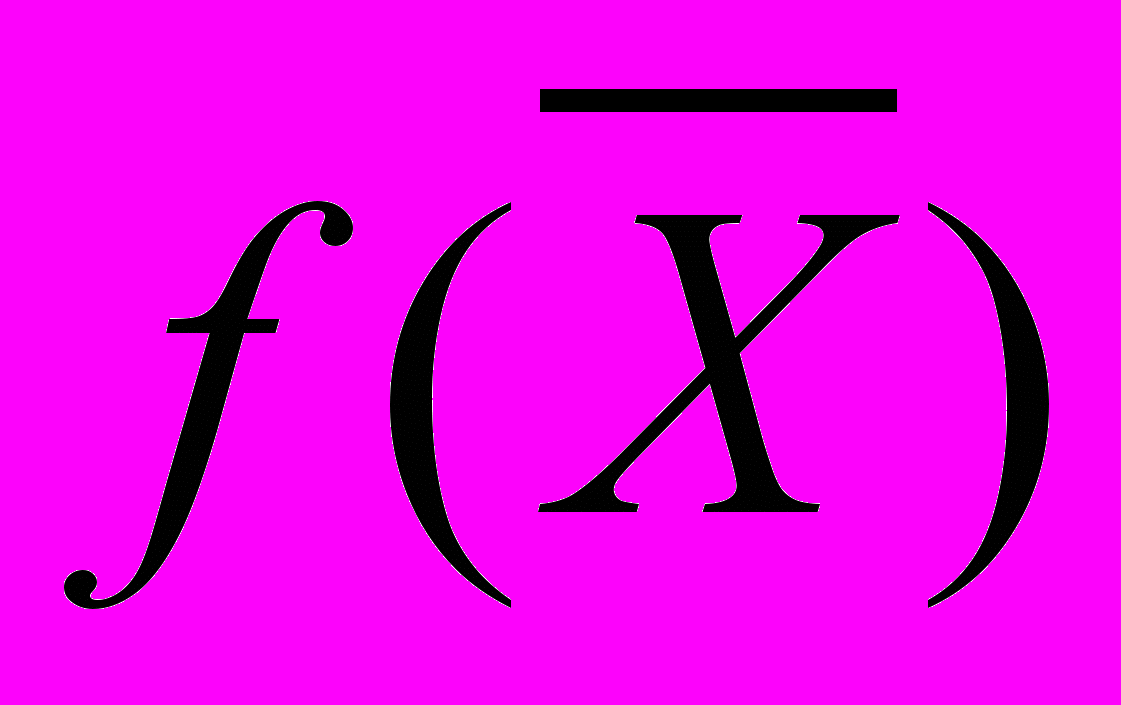 , можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения
, можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения  и
и 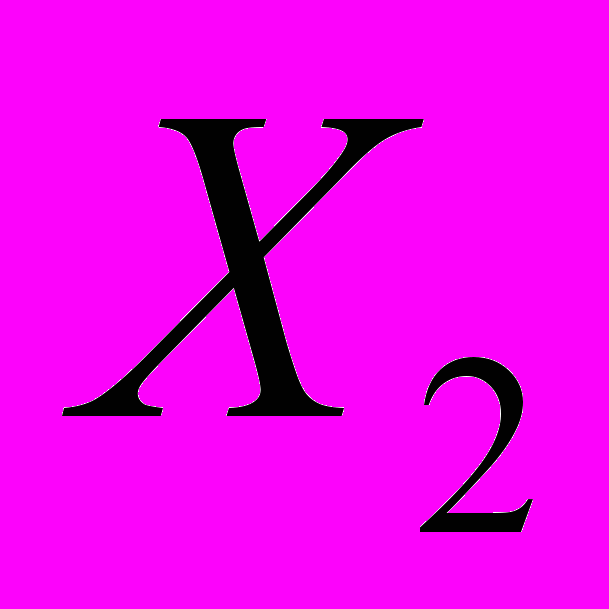 , максимизирующие величину общего дохода:
, максимизирующие величину общего дохода:
Ограничения. При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов А, В и С и спрос на изготовляемую продукцию, что можно записать так:
| Расход исходного продукта для производства обоих видов изделия | ≤ | Максимально возможный запас данного исходного продукта |
Это приводит к трем ограничениям:
 (для А)
(для А) (для В)
(для В)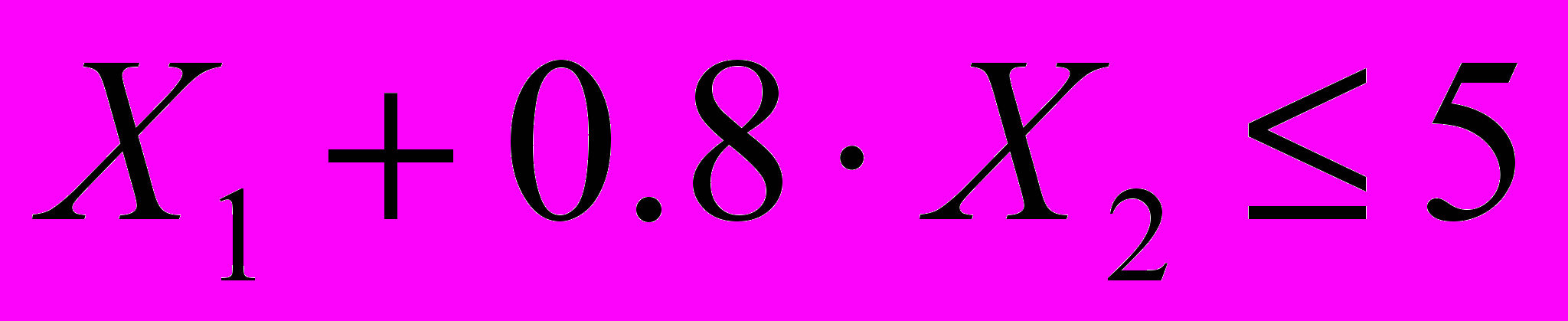 (для С)
(для С)Ограничения на величину спроса на продукцию имеют вид:
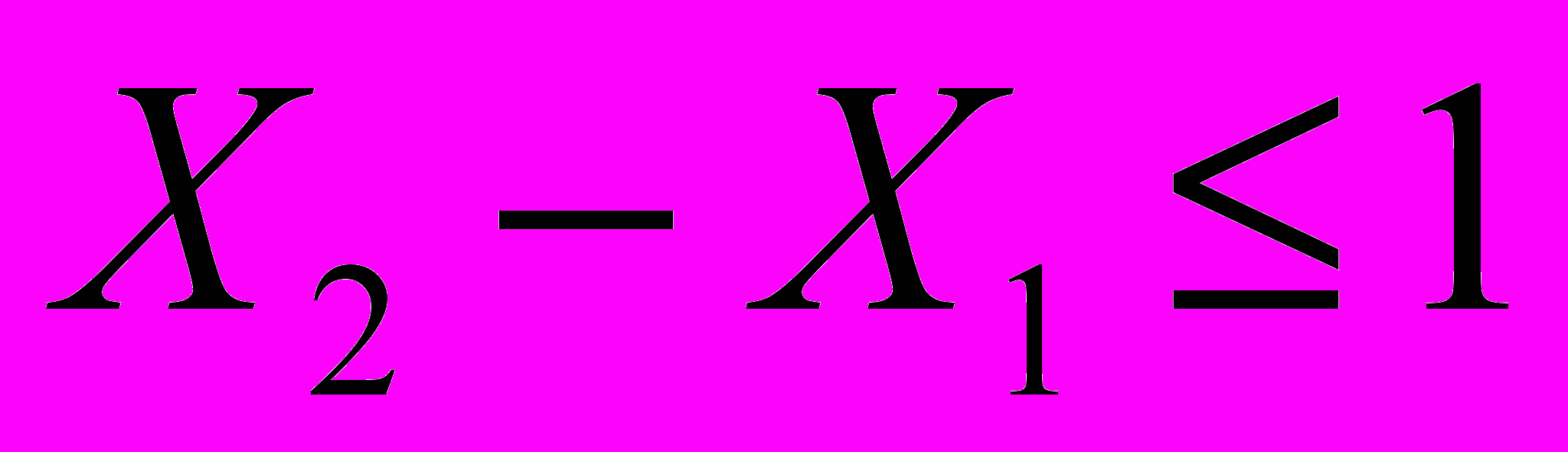 (соотношение величин спроса на изделия П1 и П2),
(соотношение величин спроса на изделия П1 и П2), (максимальная величина спроса на изделия П2).
(максимальная величина спроса на изделия П2).Вводятся также условия неотрицательности переменных, т. е. ограничения на их знак:
 (объем производства П1),
(объем производства П1),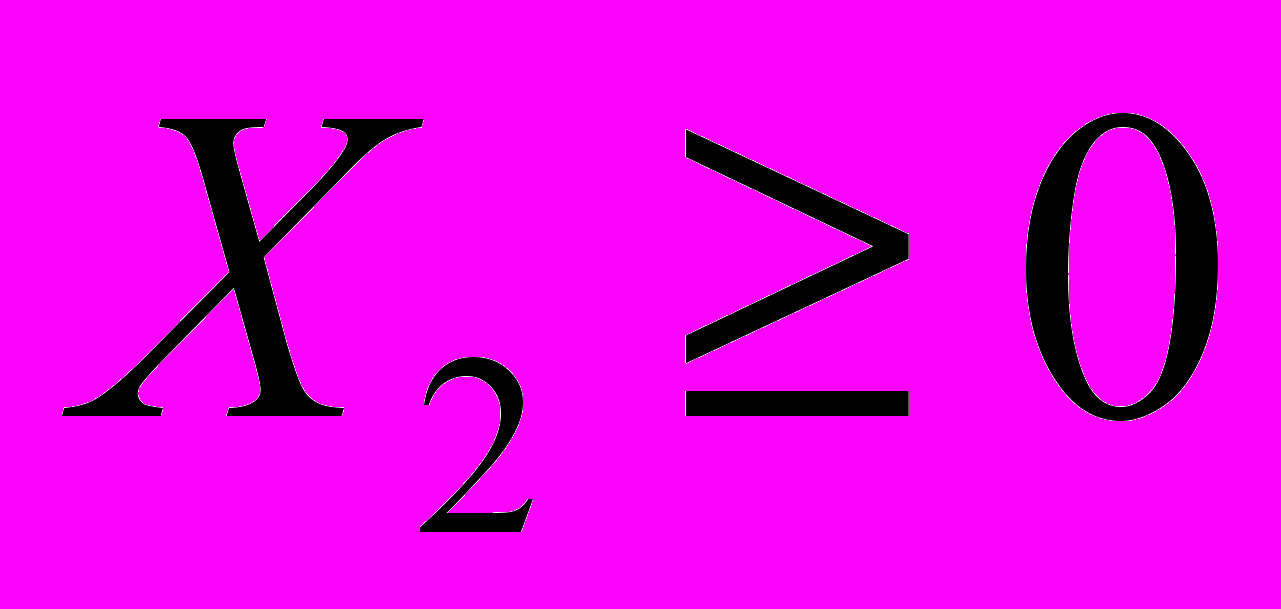 (объем производства П2).
(объем производства П2).Эти ограничения заключаются в том, что объемы производства продукции не могут принимать отрицательных значений.
Следовательно, математическая модель записывается следующим образом.
Определить суточные объемы производства (
 и
и 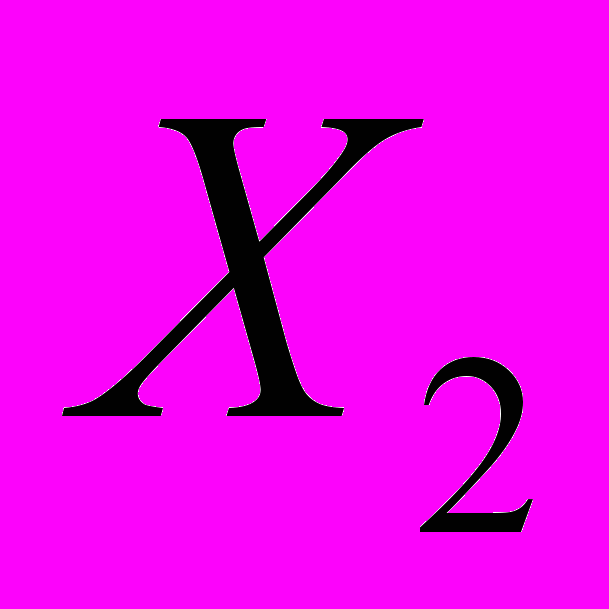 ) изделий П1 и П2 в тыс. шт., при которых достигается
) изделий П1 и П2 в тыс. шт., при которых достигается - (целевая функция)
- (целевая функция) при
-

ограничения
Графический метод решения ЗЛП
Графическим методом целесообразно решать ЗЛП, содержащие не более двух переменных.
Алгоритм графического метода рассмотрим применительно к задаче:

при

Шаг 1. Строим область допустимых решений - область Р, т.е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения ЗЛП. Каждое из неравенств (а)-(д) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми:
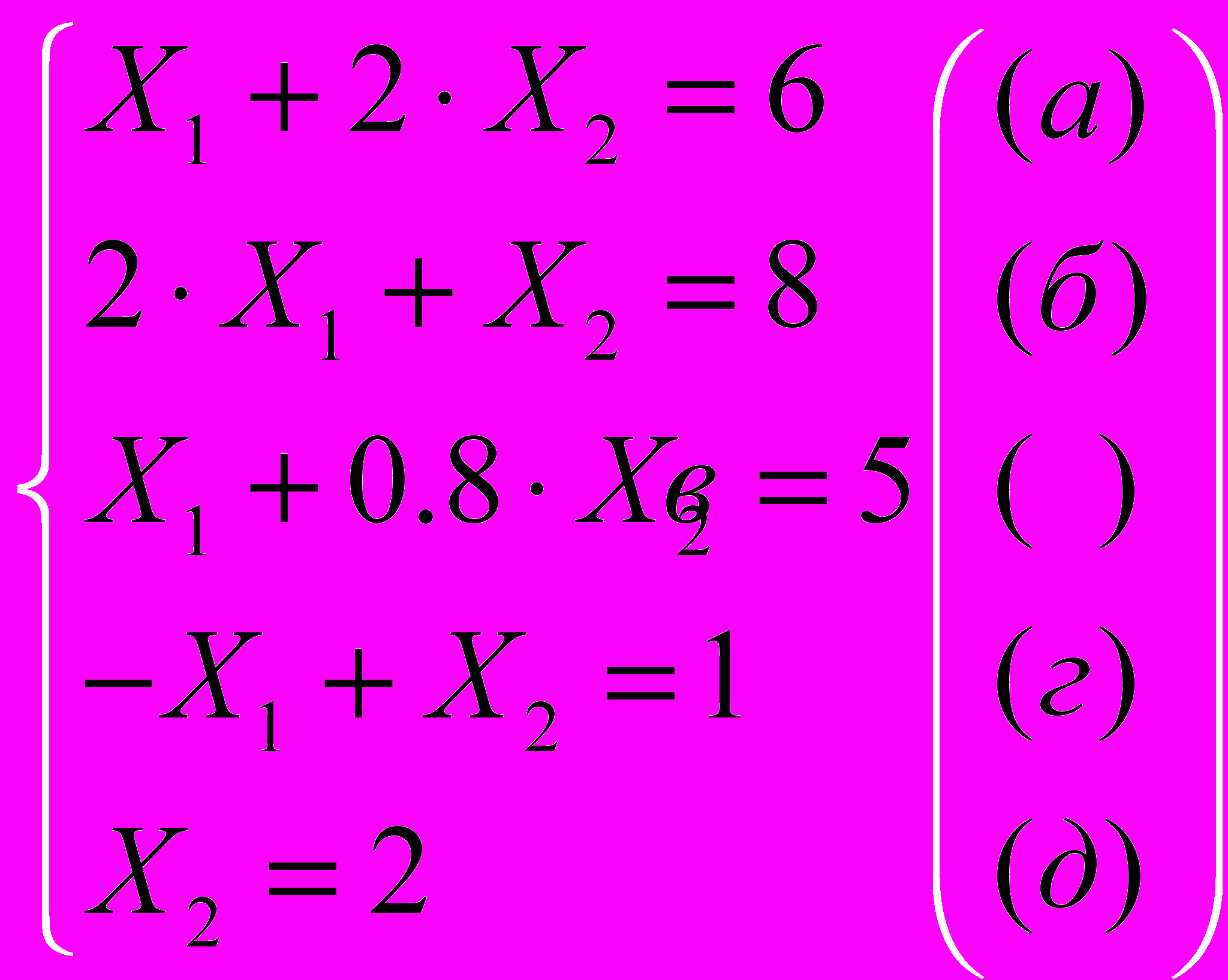
Условия неотрицательности переменных (е) ограничивают область допустимых решений первым квадратом. Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных (см. на рис.).


откуда
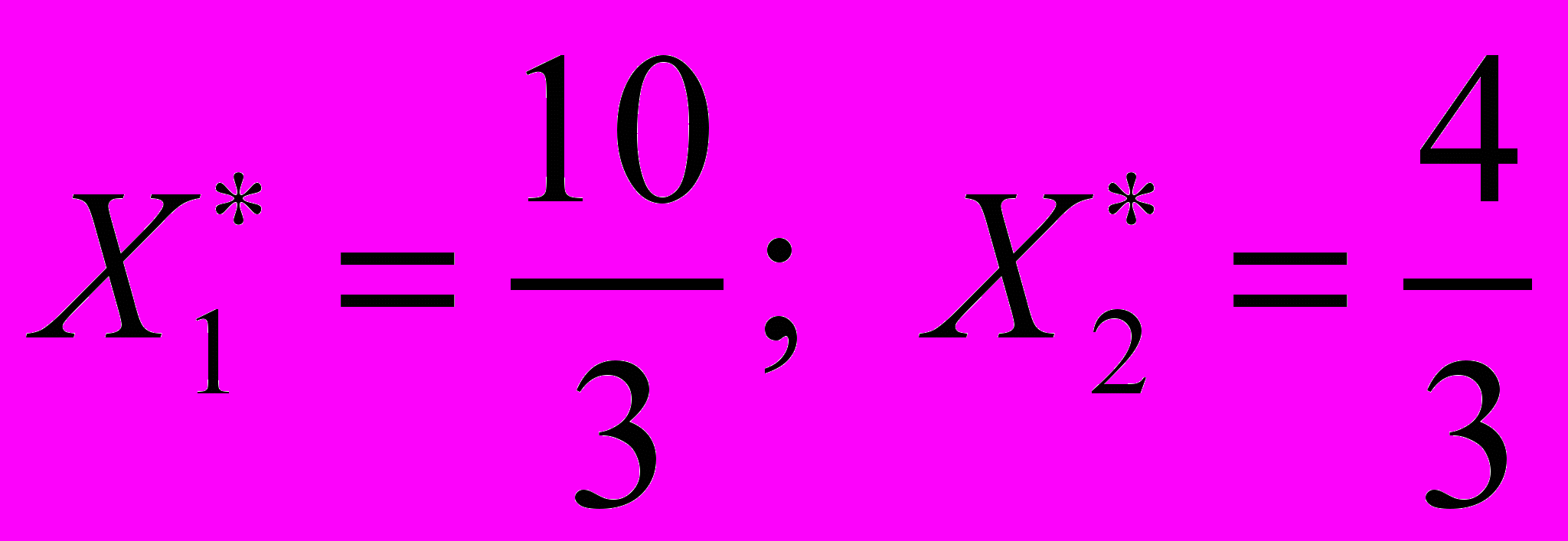 или
или  .
.Подставляя значения
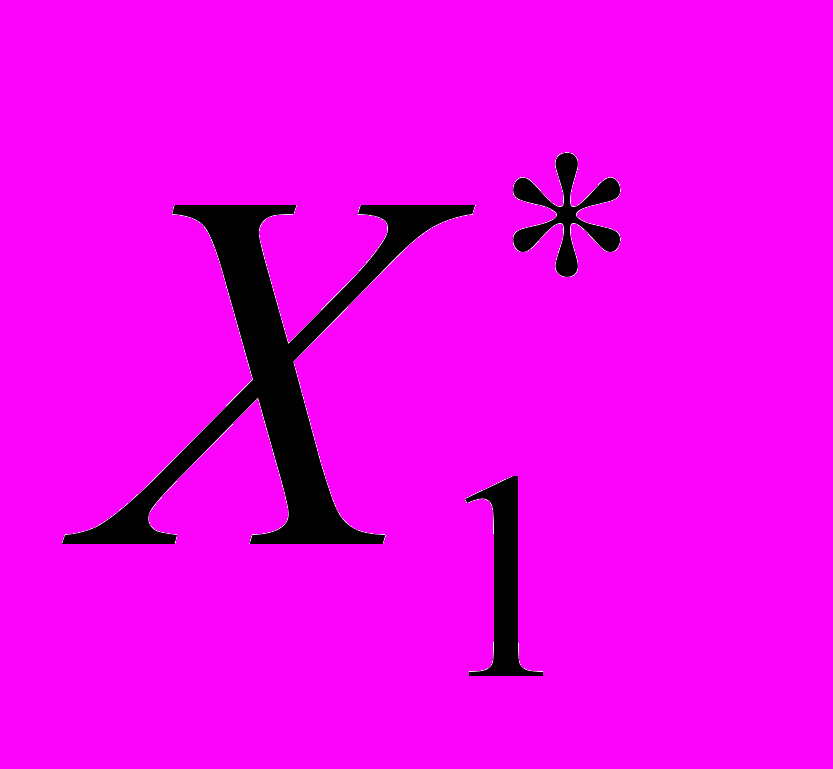 и
и  в функцию
в функцию  , найдем
, найдем  .
.4. Задача о раскрое материала.
Продукция ткацкой фабрики выпускается в виде рулонов ткани шириной 2,20 м. и 1,50 м. Длина ткани в рулоне соответственно 84 м. и 120 м. Из ткани шьют спальные комплекты: односпальные и двуспальные. Цена односпального комплекта 800 руб., а двуспального 1000 руб. Выяснить какое количество комплектов каждого вида нужно изготовить, что бы получить максимальную прибыль от продажи?
Доход ткани
| Ширина (м) | Односпальный комплект (м) | Двуспальный комплект (м) | Количество ткани в рулоне (м) |
| 1,50 | 8,3 | 12,4 | 120 |
| 2,20 | 7 | 8 | 84 |
Постановка задачи
- Построение математической модели начинаем с идентификации переменных (искомых величин). После этого целевая функция и ограничения выражаются через соответствующие переменные.
-
Переменные По условию имеем переменные т. к. нужно выяснить количество комплектов первого и второго видов, переменными являются: X1 – количество односпальных комплектов, X2 - количество двуспальных комплектов.
Целевая функция Т. к. цена односпального комплекта 800 руб., то прибыль от реализации 800 руб. Цена двуспального комплекта 1000 руб., доход от продажи 1000 руб.
Общий доход равен сумме двух слагаемых – доход от продажи односпального комплекта и двуспального. Обозначим доход через
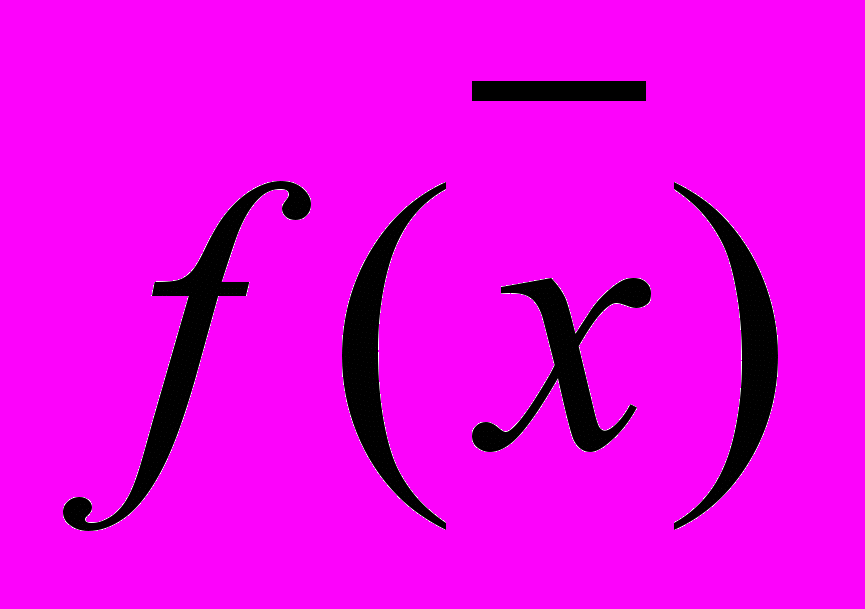 , можно дать следующую формулировку целевой функции: определить допустимые значения
, можно дать следующую формулировку целевой функции: определить допустимые значения  и
и  , максилизирующие величину общего дохода:
, максилизирующие величину общего дохода: ,
,  .
.Ограничения при решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов и спрос на изготовляемую продукцию, что можно записать так:
| Расход исходного продукта для производства обоих видов изделия | 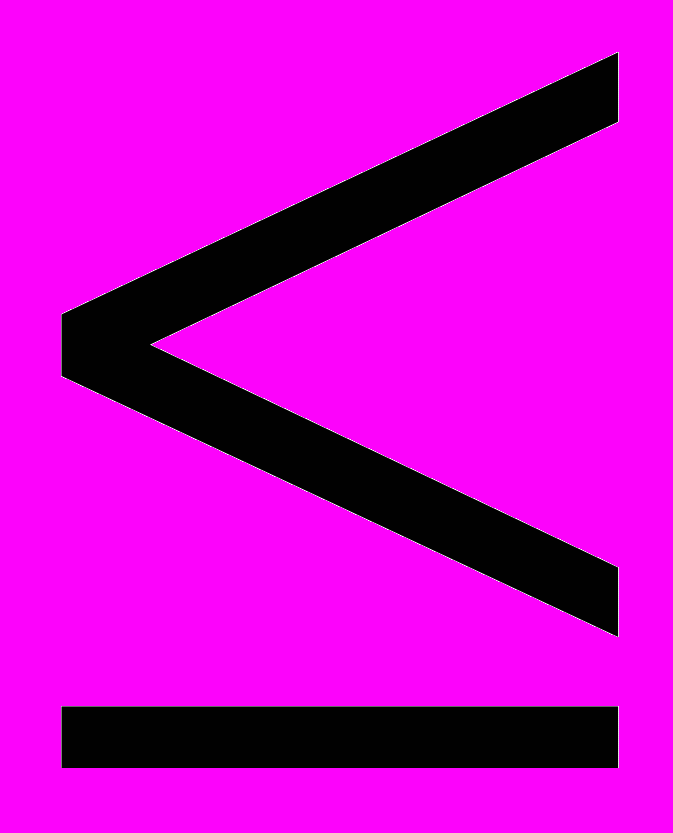 | Максимально возможный запас данного исходного продукта |
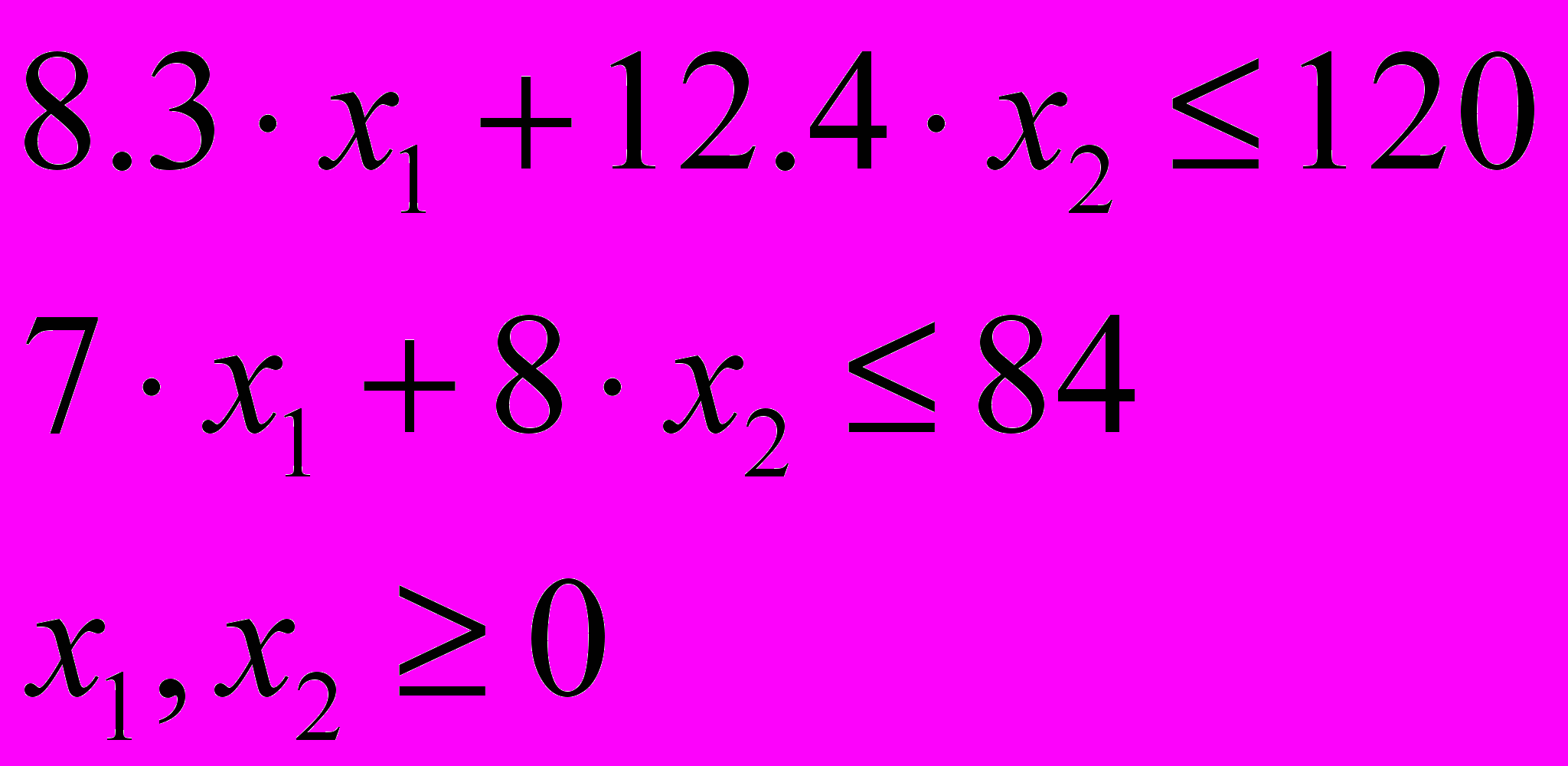
Решим задачу графическим методом
Шаг 1. Построим область допустимых значений, то есть геометрическое место точек, в котором одновременно удовлетворяются все ограничения задачи.
Шаг 2. Строим вектор – градиент
 , указывающий направление возрастание функции.
, указывающий направление возрастание функции.Шаг 3. Строим прямую линию уровня функции перпендикулярную вектору – градиенту
 .
.Шаг 4 . Передвигая линию уровня в направлении вектора, убеждаемся в неограниченном возрастании функции.
Оптимальное решение:

 5. Заключение
5. ЗаключениеВ результате применения графического метода линейного программирования мне удалось решить задачу о раскрое материала: максимальную прибыль я получу, если сошью из данных рулонов ткани 8 односпальных комплектов и 14 двуспальных. При этом выручка от продажи комплектов будет равна 20400 руб. существует еще один метод решения задачи целочисленного программирования, который в дальнейшем я хочу изучить.
Список используемой литературы
1. Н. Ю. Грызина, И. Н. Мастяева, О. Н. Саменихина, П. С. Тимашкова
«Математические методы исследования операции» Москва 2004г.
2. "Математические методы исследования операций" Учебное пособие. М.: 2003
- Алферова З.В, Романников А.Н. "Линейная алгебра", М.:, 2003.
- "Исследование операций в экономике". Под редакцией Н. Ш. Кремера. М., Юнити, 1997.
- Хазанова Л.Э. Математическое моделирование в экономике. М.: Бек, 1998.
- Солодовников А.С. и др. "Математика в экономике" Часть 1. М.:ФиС, 1999.
7. Курицкий Б.Я. "Поиск оптимальных решений средствами Excel 7.0. СПб, BHV, 1997.
- Мастяева И.Н. "Методы оптимизации". М., 1990.
- Таха X. "Введение в исследование операций". М. :ИД "Вильямс", 2001
- Эддоус М., Стэнсфилд Р. "Методы принятия решений". М.: Юнити,
1997.
- Мастяева И.Н., Горбовцов Г.Я., Семенихина О.Н., Турундаевский В.Б
"Прикладная математика". М.:, 2000.
- Васильков Ю.В., Василькова Н.Н. Компьютерные технологии
вычислений в математическом моделировании. М.: Финансы и статистика,
1999.
