Программа учебной дисциплины Математические методы в психологии федерального компонента цикла опд

Вид материала

Содержание

Программа учебной дисциплины Математические методы в психологии
I. Организационно-методический раздел
Генеральная совокупность и выборка.
Таблицы и графики.
Первичные описательные статистики.
Закон нормального распределения.
Коэффициенты корреляции.
Основы статистического вывода (
Классификация методов статистической проверки гипотез.
Дисперсионный анализ (ANOVA).
Общая характеристика многомерных статистических методов.
Многомерные методы прогнозирования.
Методы классификации.
Факторный анализ.
Многомерное шкалирование.
Пример вопроса и вариантов ответа
Наименование тем и разделов
5 курс (9 семестр)
IV. Форма итогового контроля.
V. Учебно-методическое обеспечение курса.
...
Полное содержание

Подобный материал:

Федеральное агентство по образованию

Санкт-Петербургский государственный университет

Факультет психологии

Кафедра педагогики и педагогической психологии

Рассмотрено и рекомендовано		УТВЕРЖДАЮ
на заседании кафедры		Декан факультета
Педагогики и педагогической психологии		Л.А.Цветкова
		(______________)
протокол № __________________
дата _________________________
Зав. кафедрой В.А.Якунин

(_______________)

Программа учебной дисциплины

Математические методы в психологии

федерального компонента цикла ОПД

Разработчик: доцент, кандидат психологических наук А.Д.Наследов

(________________) «_____»____________2009г.

Рецензент:

(________________) «_____»____________2009г.

Санкт-Петербург

2009 г.

Программа дисциплины «Математические методы в психологии» федерального компонента цикла ОПД составлена в соответствии с государственным образовательным стандартом высшего профессионального образования второго поколения по специальности 020400 «Психология», по специальности 022700 «Клиническая психология», по направлению 521000 «Психология».

I. Организационно-методический раздел

Курс «Математические методы в психологии» читается на вечернем отделении в 4 и 9 семестрах.

1. Цель курса.

Курс ориентирован на усвоение студентами основных методологических принципов, теоретических понятий и методических средств использования математики в психологии.

2. Задачи курса.

систематизированное изложение математических средств, применяемых в психологии;
изложение математического аппарата психологической диагностики, проверки гипотез, установления связей между психологическими явлениями;
изложение методов обработки многомерных данных.

3. Место курса в профессиональной подготовке выпускников.

Грамотное применение математических методов является неотъемлемой частью общей культуры научного исследования. Знание математических методов требуется уже на стадии планирования исследования, чтобы заранее знать, какими способами будут обрабатываться полученные данные, избегая ситуации, когда данные уже собраны, но ни один из известных способов обработки применить невозможно. Безусловно, необходимо умение математическими средствами описывать полученные результаты и проводить их предварительный анализ, чтобы в дальнейшем выдвигать и проверять статистические гипотезы, повышая доказательность научных выводов. Математические методы используются также для поиска и описания закономерностей, причин, взаимосвязей, структуры сложных и многомерных психологических явлений.

Усвоение студентами курса «Применение математических методов в психологии» в дальнейшем способствует пониманию тех математических принципов, которые лежат в основе такого важного раздела психологической науки как психодиагностика. Курс вводит необходимые термины, используемые в других учебных курсах, во многих экспериментальных и теоретических работах, таким образом, обеспечивая более глубокое понимание психологических текстов. Курс также готовит студентов и слушателей к самостоятельному написанию дипломной работы, в плане представления и обработки результатов собственного эмпирического исследования.

4. Требования к уровню освоения содержания курса.

В результате освоения содержания курса студенты должны:

приобрести теоретические знания о применении математических методов в психологии;
уметь адекватно применять математические методы к практическим задачам в психологии, и правильно интерпретировать результаты математического анализа данных.

II. Содержание курса

1. Разделы курса.

Содержание дисциплины изложено в двух разделах: 1) основы математической статистики; 2) методы обработки многомерных данных.

2. Темы и краткое содержание.

Введение. Отношение математики и психологии. Исторический экскурс. Специфика научного познания и применение математики. Основные математические модели в психологии: измерительные, описательные и статистического вывода.
Генеральная совокупность и выборка. Гипотеза исследования. Репрезентативность выборки. Выборки: зависимые и независимые.
Измерения и шкалы. Предмет и объект исследования. Операционализация конструкта. Переменная как результат измерения. Специфика психологического измерения. Измерительные шкалы С. Стивенса. Проблема косвенного измерения: идентификация шкалы переменной.
Таблицы и графики. Структура таблицы исходных данных: переменные, объекты, выборки. Таблицы распределения частот. Графики распределения: гистограммы, полигоны, куммуляты. Интерпретация графиков распределения.
Первичные описательные статистики. Параметры и статистики. Меры центральной тенденции: мода, медиана, среднее. Свойства и границы применения мер центральной тенденции. Квантили распределения: квартили, процентили. Меры изменчивости: дисперсия и стандартное отклонение. Свойства и интерпретация дисперсии. Стандартизация переменной (z-преобразование).
Закон нормального распределения. История нормального распределения. Нормальное распределение как стандарт и его свойства. Применение нормального распределения для идентификации шкалы переменной. Проверка нормальности распределения: по графикам распределения и выбросам, по критериям асимметрии и эксцесса, по статистическим критериям. Основы психодиагностики: стандартизация тестовой шкалы.
Коэффициенты корреляции. Связи функциональные и статистические. Ковариация и корреляция Пирсона, их формулы, свойства и интерпретация. Двумерная регрессия, коэффициент детерминации. Ранговые корреляции: Спирмена и Кенделла. Особенности вычисления и интерпретации ранговых корреляций. Границы применения корреляций.
Основы статистического вывода (проверка гипотез). Гипотезы научные и статистические. Логика статистической проверки гипотезы, нулевая и альтернативная гипотезы. Р-уровень значимости, его интерпретация и его зависимость от: величины эффекта, объема выборки, дисперсии. Статистический критерий: теоретическое распределение, формула, число степеней свободы, р-уровень значимости. Принятие статистического решения и вероятности ошибок 1 и 2 рода. Односторонние и двусторонние альтернативы и р-уровни значимости. Статистическая проверка гипотезы в структуре научного исследования.
Классификация методов статистической проверки гипотез. Корреляционный анализ: выбор корреляции, корреляционные матрицы и плеяды. Частотный анализ: методы анализа таблиц распределения частот и сопряженности (Хи-квадрат и точный критерий Фишера), анализ последовательности (критерий серий). Методы сравнения выборок и их классификация. t-Стьюдента для независимых и зависимых выборок. Сравнение дисперсий. Ранговые критерии U Манна-Уитни и Т Вилкоксона. Дисперсионный анализ (ANOVA) для независимых и зависимых выборок. Ранговые аналоги ANOVA: критерии Н Краскала-Уоллиса и Хи-квадрат Фридмана.
Дисперсионный анализ (ANOVA). Основные понятия и виды ANOVA. Однофакторный дисперсионный анализ: гипотеза, последовательность вычислений, результаты, ограничения. Множественные сравнения: парные Post Hoc и метод контрастов. Многофакторный ANOVA: гипотезы о главных эффектах и взаимодействиях, модель, последовательность вычислений, результаты. Многомерный ANOVA: многомерный и одномерный этапы, многомерные критерии, ограничения, результаты. ANOVA с повторными измерениями: модель, гипотезы о внутри- и межгрупповых эффектах, одномерный и многомерный подходы, ограничения, результаты.
Общая характеристика многомерных статистических методов. Многомерные данные. Матрицы. Геометрические представления. Классификация многомерных методов по назначению, по структуре и виду исходных данных.
Многомерные методы прогнозирования. Множественный регрессионный анализ (МРА) в задачах предсказания, его виды. Математико-статистические идеи МРА, требования к исходным данным и основные результаты применения МРА. Множественный дискриминантный анализ (ДА) в задачах предсказания. Математико-статистические идеи метода, вид исходных данных, решение задачи классификации в ДА. Решение задачи интерпретации межгрупповых различий при помощи канонического анализа в ДА.
Методы классификации. Кластерный анализ (КА) в задачах классификации, его виды. Понятие сходства между объектами, меры сходства: прямые оценки, условные и совместные вероятности, меры различия профилей. Иерархические методы кластеризации: одиночной связи, полной связи и средней связи. Примеры применения КА в исследованиях социальных структур групп.
Факторный анализ. Факторный анализ в задачах измерения латентных (скрытых) переменных и задачах уменьшения размерности исследуемого пространства признаков. Основные проблемы факторного анализа и способы их решения: общности, числа факторов, вращения, интерпретации факторного решения и оценки факторов. Матрица факторных нагрузок и соотношения основных показателей. Примеры применения факторного анализа в практических исследованиях.
Многомерное шкалирование. Многомерное шкалирование данных о различии (сходстве) объектов, модели многомерного шкалирования. Метрическая и неметрическая модели многомерного шкалирования. Модель шкалирования индивидуальных различий. Модель шкалирования индивидуальных предпочтений. Примеры применения многомерного шкалирования в психологических исследованиях.

3. Перечень заданий для практической и самостоятельной работы.

Построить гистограмму, преобразовать данные из шкалы в шкалу, вычислить описательные статистики: моду, медиану, среднее, процентили, дисперсию, стандартное отклонение, z-значения.
По таблице стандартных нормальных вероятностей определить вероятность встречаемости значений в заданном диапазоне шкалы с заданным средним и стандартным отклонением.
Проверить нормальность распределения с применением критериев асимметрии и эксцесса.
Сформулировать содержательные психологические гипотезы, представить их на языке статистики, выбрать соответствующие критерии и проверить статистические гипотезы, записав выводы по результатам проверки каждой гипотезы:

- с применением критерия t-Стьюдента для независимых выборок (с предварительной проверкой равенства дисперсий;

- с применением критерия t-Стьюдента для зависимых выборок;

- с применением критерия U Манна-Уитни;

- с применением критерия T Вилкоксона;

- с применением критерия Хи-квадрат Пирсона;

- с применением критерия Н Краскала-Уоллеса;

- с применением критерия Хи-квадрат Фридмана;

- с применением корреляции Пирсона;

- с применением корреляции Спирмена и Тау-Кендалла.

Применить однофакторный дисперсионный анализ с предварительной проверкой гомогенности дисперсии, с последующим множественным сравнением средних Post Hoc и методом контрастов.
Применить двухфакторный дисперсионный анализ и проинтерпретировать его результаты.
Применить многомерный дисперсионный анализ и проинтерпретировать его результаты.
Применить дисперсионный анализ с повторными измерениями и проинтерпретировать его результаты.
Интерпретация результатов множественного регрессионного анализа.
Интерпретация результатов дискриминантного анализа.
Интерпретация результатов кластерного анализа в различных модификациях.
Определение последовательности и интерпретация результатов факторного анализа.
Применение и интерпретация результатов многомерного шкалирования, шкалирования индивидуальных различий и предпочтений.

4. Тематика рефератов, курсовых работ.

Сформулировать для предложенных данных содержательные гипотезы о различии групп по уровню выраженности признака и проверить их с помощью параметрических критериев.
Сформулировать для предложенных данных содержательные гипотезы о различии групп по уровню выраженности признака и проверить их с помощью ранговых критериев.
Для предложенных данных сформулировать содержательные гипотезы о взаимосвязи признаков и проверить их с помощью коэффициента корреляции Пирсона (Спирмена, Кенделла, χ²-Пирсона).
Для предложенных данных сформулировать гипотезу и проверить ее на компьютере с использованием множественного регрессионного анализа (дискриминантного анализа).
Обработать (на компьютере) данные социометрии с применением кластерного анализа.
Обработать предложенные данные при помощи факторного анализа, дать интерпретацию выделенных факторов и сравнить группы испытуемых по уровню выраженности выделенных факторов.
Обработать предложенные данные при помощи многомерного шкалирования, дать интерпретацию выделенных шкал.

5. Перечень тестовых вопросов к зачету и экзамену по всему курсу.

К каждому вопросу предлагается 4 варианта ответа, из которых только один является верным. Для каждого вопроса необходимо указать букву, соответствующую правильному ответу на этот вопрос.

Пример вопроса и вариантов ответа

Такое значение переменной, измеренной на группе испытуемых, меньше которого имеют ровно половина этих испытуемых, называется…

а) мода

б) среднее

в) медиана

г) промежуточное

Правильный ответ: в) медиана

Две выборки являются зависимыми, если
Гипотеза исследования это утверждение о связи двух явлений…
Если 1-я выборка – преподаватели ВУЗа, а 2-я выборка – их студенты, то 2-я выборка по отношению к 1-й является
Основной способ обеспечения репрезентативности выборки относительно генеральной совокупности это
Основное свойство выборки, определяющее ее качество – это:
Цифра, обозначающая номер испытуемого в списке – это измерение в шкале…
Упорядочивание испытуемых по времени решения тестовой задачи – это измерение в шкале…
Время простой сенсомоторной реакции (в мс) – это измерение в шкале
Кодирование испытуемых по воинскому званию (лейтенант, капитан, майор…) для оценки должностного статуса – это измерение в шкале…
Одна из перечисленных характеристик не относится к шкалам (уровням) измерения С.Стивенса:
Для деления выборки на несколько независимых выборок обычно используется следующая переменная:
Если по времени решения тестовой задачи трем испытуемым (из 20) присвоены ранги 1 (самый быстрый), 2, 5, то справедливо следующее утверждение:
Мода как мера центральной тенденции не пригодна для переменных в следующих шкалах:
Медиана как мера центральной тенденции не пригодна для переменных в следующих шкалах:
Среднее как мера центральной тенденции не пригодна для переменных в следующих шкалах:
Графики распределения частот значений признака для группы юношей (1) и группы девушек (2)

Как соотносятся средние значения и дисперсии признака групп (по графику):

Из всех мер центральной тенденции крайние значения (выбросы) в наибольшей степени влияют на…
Абсолютная величина каждого отдельного значения не учитывается для определения значений следующих мер центральной тенденции:
Если для выборки численностью 200 чел., 60-й процентиль некоторого признака равен 12, то справедливо следующее утверждение:
Такое значение признака, измеренного на группе испытуемых, меньше которого имеют ровно половина этих испытуемых, называется…
50-й процентиль соответствует:
Какой из показателей характеризует степень разнообразия испытуемых по значениям переменной:
Чему равна медиана ряда значений 1, 2, 2, 2, 3, 7, 6, 5, 9, 5:
Как соотносятся меры центральной тенденции для данного ряда значений 0, 0, 2, 2, 6, 6, 6, 5, 9:
Как соотносятся стандартные отклонения (сигмы) двух рядов чисел: 1) 9, 15, 12, 24, 21 и 2) 3, 9, 6, 18, 15:
Как соотносятся дисперсии двух рядов чисел:

1) 5, 8, 10, 12, 11 и 2) 1, 4, 6, 8, 7:

Как соотносятся стандартные отклонения возраста выборки детей 2-6 лет (N = 30), выраженные в годах и месяцах:
В группах 1 и 2 измерена некоторая переменная. D₁ = D₂=10, M₁=20, M₂=30. После объединения этих групп дисперсия…
В группах 1 и 2 измерена некоторая переменная. D₁ = D₂=5, M₁=6, M₂=12. После объединения этих двух групп дисперсия…
Если распределение переменной соответствует нормальному виду, то 90% всех ее значений находится:
Если распределение признака соответствует нормальному виду, то 99% всех ее значений находится:
Если распределение переменной соответствует нормальному виду, то 90% всех ее значений находится:
Если распределение переменной соответствует нормальному виду, то в диапазоне М 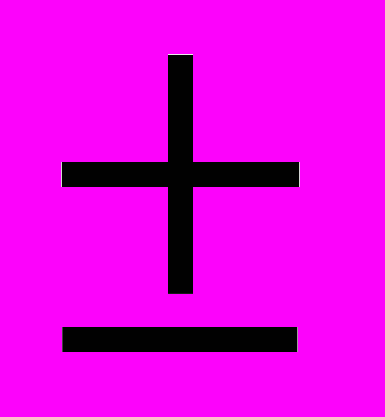1,96σ:
Если распределение переменной соответствует нормальному виду, то 95% всех ее значений находится:
Некоторое свойство измеряется при помощи тестовой шкалы CEEB (М=500, =100). Какая приблизительно доля генеральной совокупности имеет балл от 600 до 700?
Некоторое свойство измеряется при помощи тестовой шкалы Бине (М=100, =16). Какая приблизительно доля генеральной совокупности имеет балл ниже 84?
Для изучения каких связей коэффициенты корреляции не применимы
Для каких переменных допустимо применение коэффициентов корреляции
Если коэффициент корреляции Пирсона r = – 0,5, то коэффициент детерминации равен:
Если y – зависимая, а x – независимая переменные, то R²_xy (коэффициент детерминации) это часть дисперсии…
После z-преобразования выборочных значений переменной среднее и сигма…
Если R_xy=1 и обе переменные x_iи y_i представлены в z-значениях, то уравнение регрессии ŷ_i=bx_i+a принимает вид:
Если R_xy=0, то уравнение регрессии ŷ_i=bx_i+a принимает вид:
Если R_xy= 0, и обе переменные x_iи y_i представлены в z-значениях, то уравнение регрессии ŷ_i=bx_i+a принимает вид:
Если объем выборки N=21, ковариация между двумя признаками Cov₁₂=8, а стандартные отклонения ₁=4; ₂=8, то коэффициент корреляции R₁₂ Пирсона равен
Если изучается взаимосвязь между двумя признаками (₁=5; ₂=6; N = 21), то величина ковариации (Cov₁₂) может быть:
Какая корреляция основана на подсчете разности рангов
Какая корреляция основана на подсчете произведений отклонений от средних
Какая корреляция основана на подсчете пар испытуемых:
Коэффициент корреляции Спирмена основан на подсчете…
Если при переборе всех пар испытуемых в выборке вероятность однонаправленного изменения X и Y (совпадений) составила Р = 0,8, то величина τ-Кенделла равна:
Если при переборе всех пар испытуемых в выборке вероятность разнонаправленного изменения X и Y (инверсий) составила Q = 0,8, то величина τ-Кенделла равна:
При подсчете τ -Кенделла на выборке N = 6 число совпадений составило P=10; τ –Кенделла равно…
Чему равна корреляция Спирмена и Кендалла для двух переменных:

№

X

Y

а) 0

б) -1

в) 1
г) 0,5

1

32

2

2

16

6

3

20

4

4

8

10

5

11

8
Проверяемая содержательная (научная) гипотеза подтверждается, если (при  = 0,05):
Чем больше значение р-уровня, тем…
Вероятность того, что в генеральной совокупности нулевая гипотеза верна, есть показатель…
Результат проверки гипотезы признается статистически достоверным, если…
Уровень статистической значимости это вероятность того, что
Может ли одно и то же численное значение корреляции для разных выборок иметь разную статистическую значимость?
Для 1-ой выборки корреляция R_xy=0,35 (p=0,06), для 2-ой выборки R_xy=0,35 (p=0,03). Почему p-уровень разный?
При сравнении двух средних (М₁=5, М₂=7) значение р-уровня будет тем меньше, чем
При сравнении двух распределений частот с использованием критерия Хи-квадрат значение р-уровня больше, если
Гомогенность (равенство) дисперсий проверяется перед:
Если при сравнении средних для 2-х независимых выборок неравной численности дисперсии статистически значимо различаются, то следует:
Если при сравнении средних для нескольких независимых выборок неравной численности дисперсии статистически достоверно различаются, то следует:
Если при проверке статистической достоверности корреляции (при α = 0,05) р > 0.1, то корректен вывод, что
Если при проверке статистической достоверности корреляции (при α = 0,05) р < 0.05, то корректен вывод, что
Если при проверке статистической значимости различий двух средних р > 0.1, то делают вывод о том, что
Если при проверке статистической значимости различий двух средних (при α = 0,05) р < 0.05, то делают вывод о том, что
Для проверки достоверности различия двух независимых групп, члены которых ранжированы по степени выраженности «тревожности», применяют критерий
Для проверки достоверности различия двух повторных измерений, члены которых ранжированы по степени выраженности «тревожности», применяют критерий
Для проверки достоверности различий студентов 1 и 5 курсов по переменной «семейное положение» (холост – нет) следует применить критерий
Для проверки достоверности различий 2-х выборок по переменной «пол» (муж - жен) следует применить критерий
Для сравнения преподавателей и студентов по «доминантности» (метрическая шкала), следует применить критерий
Для сравнения двух независимых выборок по количественной переменной, имеющей заметные выбросы, применяют критерий
Для проверки различия самочувствия (метрическая шкала) до и после терапии применяют критерий
Если необходимо сравнить два повторных измерения количественной переменной, имеющей заметные выбросы, то применяют критерий
Для проверки достоверности различия двух зависимых выборок по переменной, измеренной в ранговой шкале, применяют критерий
Для проверки достоверности различия старших (1-я выборка) и их младших (2-я выборка) братьев по уровню доминантности, измеренной в метрической шкале, применяют критерий
Гипотезу о взаимосвязи номинативной (2 градации) и ранговой переменных целесообразно проверять при помощи
Гипотезу о взаимосвязи номинативной (2 градации) и метрической переменных целесообразно проверять при помощи
Статистическая значимость улучшения состояния (ранговая шкала) до и после терапии определяется по критерию
Гипотезу о взаимосвязи ранговой и номинативной переменной, имеющей две градации (напр., пол), целесообразно изучать при помощи критерия
Для проверки достоверности различия 2 групп, каждый член которых определен в одну из трех категорий («правый», «левый», «центрист»), применяют критерий
Для проверки гипотезы о различии 2 групп по степени индивидуальной изменчивости (дисперсии) применяют критерий
Гипотезу о взаимосвязи метрической и номинативной переменной, имеющей две градации (напр., пол), целесообразно изучать при помощи критерия
Гипотезу о взаимосвязи метрической и номинативной переменной, имеющей 5 градаций (например, хобби), целесообразно проверять при помощи
Гипотезу о взаимосвязи порядковой и номинативной переменной, имеющей 4 градации (напр., должность), целесообразно изучать при помощи критерия
Гипотезу о взаимосвязи метрической и порядковой переменной, имеющей 15 градаций, целесообразно изучать при помощи
Гипотезу о взаимосвязи 2-х количественных переменных, имеющих заметные выбросы (асимметрии) целесообразно проверять при помощи
Для проверки гипотезы о взаимосвязи одной метрической переменной и двух номинативных переменных целесообразно применять:
Для проверки гипотезы о взаимосвязи одной метрической переменной и одной номинативной переменных с 3 и более значениями целесообразно применять:
Для проверки гипотезы о взаимосвязи одной метрической переменной и трех номинативных переменных целесообразно применять:
Н_о об идентичности зависимых выборок по уровню выраженности переменной, измеренной в ранговой шкале (при α = 0,05) отклоняется, если:
Н_о об идентичности независимых выборок по уровню выраженности переменной, измеренной в ранговой шкале (при α = 0,05) отклоняется, если:
Н_о об идентичности зависимых выборок по уровню выраженности переменной, измеренного в метрической шкале (при α = 0,05) отклоняется, если:
Н_о об идентичности независимых выборок по уровню выраженности переменной, измеренного в метрической шкале (при α = 0,05) отклоняется, если:
Н_о об отсутствии взаимосвязи двух номинативных переменных (при α = 0,05) отклоняется, если:
Н_о об отсутствии взаимосвязи двух номинативных переменных (при α = 0,05) не отклоняется, если:
Н_о об отсутствии взаимосвязи двух порядковых переменных (при α = 0,05) не отклоняется, если:
Н_о об отсутствии взаимосвязи двух порядковых переменных (при α = 0,05) отклоняется, если:
Статистическая гипотеза Н_о о равенстве двух средних значений (N₁=60; N₂=70) не отклоняется (при α = 0,01), если:
Н_о об отсутствии различий двух распределений номинативного признака отклоняется (при α = 0,05), если:
Н_о об отсутствии различий дисперсий двух независимых выборок (при α = 0,05) отклоняется, если:
Н_о об отсутствии различий дисперсий двух независимых выборок (при α = 0,05) не отклоняется, если:
Статистическая гипотеза Н_о о равенстве двух средних значений (N₁=60; N₂=70) отклоняется (при α = 0,01), если:
Статистическая гипотеза Н_о о корреляции двух переменных

(N = 18) отклоняется (при α = 0,01), если:

Статистическая гипотеза Н_о о корреляции двух переменных

(N = 18) не отклоняется (при α = 0,01), если:

Если при сравнении 2-х средних при помощи компьютера получен следующий результат: t=2,48; p=0,045, то различие между соответствующими группами по измеренному признаку (при α = 0,05)
Если при сравнении 2-х средних при помощи компьютера получен следующий результат: t=2,56; p=0,036 (α = 0,05), то различие между соответствующими группами по измеренному признаку
Если при вычислении корреляции на компьютере получен результат: r₃₄=0,49; p=0,11, то взаимосвязь между перменными 3 и 4 (при α = 0,05):
Взаимодействие факторов в дисперсионном анализе обозначает, что влияние одного из этих факторов на зависимую переменную…
Взаимодействие факторов «Пол» и «Группа» в ANOVA обозначает, что различия между группами
Отсутствие взаимодействия факторов в дисперсионном анализе обозначает, что влияние одного из этих факторов на зависимую переменную…
ANOVA предполагает предварительную проверку
Средний квадрат (MS) в ANOVA это
В ANOVA межгрупповая SS это
В ANOVA внутригрупповая SS это
В ANOVA внутригрупповая (случайная) сумма квадратов вычисляется как:
Стандартная таблица результатов ANOVA содержит следующую последовательность столбцов
ANOVA предполагает следующую последовательность вычисления показателей:
Коэффициент детерминации (R², RSQ) в дисперсионном анализе это отношение
Для проверки равенства (гомогенности) дисперсий в ANOVA применяется критерий
Перед проведением ANOVA с неравной численностью выборок необходимо
Для множественного сравнения средних в рамках дисперсионного анализа не применяют
Для множественного сравнения средних в рамках дисперсионного анализа применяют
Метод множественного сравнения средних который требует (не требует) предварительного получения статистически значимого результата дисперсионного анализа это
Метод Post Hoc – это метод
Метод контрастов – это метод
В ANOVA F-отношение – это частное от деления:
При помощи 4-факторного ANOVA проверяется:
Сколько гипотез о взаимодействии проверяется при помощи 4-факторного ANOVA:
Ковариата в дисперсионном анализе это
Многомерный дисперсионный анализ предназначен для изучения влияния
Модель многомерного дисперсионного анализа включает
Многомерный этап многомерного дисперсионного анализа предполагает проверку гипотез
Многомерные критерии След Пиллая и Лямбда Вилкса применяются в многомерном дисперсионном анализе для проверки гипотез
Аналогом критерия Ливина в многомерном дисперсионном анализе (на многомерном этапе) является
Если применение критерия М-Бокса дает статистически достоверный результат, то
Одномерный этап многомерного дисперсионного анализа проводится для
Дисперсионный анализ с повторными измерениями позволяет изучать влияние на зависимые переменные
Внутригрупповым (ВГ) и межгрупповым (МГ) факторам в дисперсионном анализе с повторными измерениями соответствуют выборки:
Сходство этих двух многомерных методов заключается в том, что анализируются различия (сходства) между объектами:
Сходство этих двух многомерных методов заключается в их назначении – классификации объектов:
Сходство этих двух многомерных методов заключается в их назначении – предсказании значений зависимой переменой:
Сходство этих двух многомерных методов заключается в их назначении – анализе структуры с целью выделения латентных переменных:
Различие этих двух многомерных методов заключается в том, в какой шкале представлена зависимая переменная (в первом – метрическая, во втором – номинативная):
Различие этих двух методов классификации заключается в том, что в первом задано число классов и принадлежность некоторых объектов к этим классам, а во втором – не задано ни то ни другое:
Сходство этих двух многомерных методов заключается в том, что анализируются корреляции между признаками:
Часть дисперсии «зависимой» переменной, обусловленная влиянием «независимых» переменных – это…
Если независимая переменная х в множественном регрессионном анализе коррелирует с другими независимыми переменными, то ее вклад в дисперсию зависимой переменной…
Если независимая переменная х в множественном регрессионном анализе не коррелирует с другими независимыми переменными, то ее вклад в оценку зависимой переменной…
Если в многомерном регрессионном анализе (y – зависимая переменная, x₁, x₂ – независимые переменные) r₁₂=0,4; r₁_y = 0,8; r₂_y = - 0,5; β₁ = 0,5; β₂= - 0,2, то коэффициент множественной детерминации R² равен:
Метод «полной связи» («дальнего соседа») в кластерном анализе, по сравнению с методом «одиночной связи» («ближайшего соседа») дает…
Метод «средней связи» (СС) по сравнению с методами «дальнего соседа» (ДС) и «ближнего соседа» (БС) обычно позволяет получить число кластеров:
Иерархический кластерный анализ за (N – 1) шагов кластеризации (N – число объектов кластеризации) дает объединение:
Статистическая значимость вклада каждой переменной в различении классов определяется…
Показателем принадлежности объекта к классу является …
Основной мерой качества решения в многомерном шкалировании является …
Несколько матриц различий одновременно позволяет анализировать
Критерий Кайзера λ > 1 применяют для…
Для предварительной оценки числа факторов в факторном анализе используют…
Величина факторной нагрузки данной переменной по данному фактору свидетельствует …
Квадрат факторной нагрузки переменной по данному фактору есть величина…
Общность в факторном анализе это доля дисперсии…
Какая из перечисленных проблем решается исследователем в процессе проведения факторного анализа
Какая из перечисленных проблем не решается в процессе проведения факторного анализа?
Слева внизу перечислены проблемы факторного анализа. Выберите справа вариант, соответствующий правильной последовательности решения этих проблем.
Слева внизу перечислены шаги факторного анализа. Выберите справа вариант, соответствующий правильной их последовательности.

Слева приведена таблица факторных нагрузок после вращения. Задания (номера в скобках и варианты ответов) – справа.

	Факторы		(171) Факторы следует интерпретировать: а) F1 – по переменной 1, 2; F2 – по переменным 2, 3, 4, 5 б) F1 – по переменным 1, 2; F2 – по переменным 3, 4 в) F1 – по переменным 1, 2, 5; F2 – по переменным 3, 4 г) F1 – по переменным 1, 2, 5; F2 – по переменным 2, 3, 4, 5 (172) Общность переменной № 5 равна: (173) Какой фактор более мощный (по доли дисперсии): (174) Чему равен восстановленный коэффициент корреляции r₁₂
	F1	F2
1
2
3
4
5

III. Распределение часов курса по темам и видам работ.

Наименование тем и разделов		Аудиторных занятий
	2 курс (4 семестр)	Лекции	Семин.
1.	Введение. Отношение математики и психологии. ГС и выборка. Измерения и шкалы. Первичные описательные статистики	2	1
2.	Нормальное распределение	2	1
3.	Корреляции	2	2
3.	Основы статистической проверки гипотез	2	-
4.	Классификация методов статистической проверки (критериев)	4	4
	5 курс (9 семестр)
5.	Основные группы методов статистической проверки гипотез	4	2
5.	Дисперсионный анализ	4	4
6.	Общая характеристика многомерных статистических методов. Многомерные методы прогнозирования	4	2
7.	Факторный анализ	4	2
8.	Дискриминантный и кластерный анализ, многомерное шкалирование	4	2

Итого объем курса: 52 часа. В том числе – лекций: 32 часа,

практических занятий: 20 часов (для одной группы).

IV. Форма итогового контроля.

4 семестр – зачет; 9 семестр - экзамен.

Для сдачи зачета необходимо:

ответить на вопросы теста, состоящего из двух частей:

часть 1: 10 вопросов из пунктов 1 - 54 (см. п. 4. Перечень тестовых вопросов…),
часть 2: 10 вопросов из пунктов 55 – 112 (см. там же);

решить1 практическую задачу из первых 4 заданий (см. п.3 Перечень заданий…).

Требования к сдаче зачета:

не менее 6 правильных ответов по каждой из двух частей теста и правильное решение практической задачи.

Для сдачи экзамена необходимо:

ответить на вопросы теста, состоящего из трех частей:

часть 1: 10 вопросов из пунктов 1 - 54 (см. п. 4. Перечень тестовых вопросов…),
часть 2: 10 вопросов из пунктов 55 – 112 (см. там же),
часть 3: 10 вопросов из пунктов 113 – 174 (см. там же);

решить1 практическую задачу из заданий 5 – 13 (см. п.3 Перечень заданий…).

Критерии оценки результата сдачи экзамена.

За каждый правильный ответ на вопрос теста начисляется 1 балл. За правильное решение практической задачи начисляется 6 баллов. Баллы суммируются.

Отметка «Удовлетворительно»: не менее 21 балла;

отметка «Хорошо»: не менее 26 баллов;

отметка «Отлично»: не менее 31 балла.

V. Учебно-методическое обеспечение курса.

1. Рекомендуемая литература (основная).

Наследов А.Д. Математические методы психологического исследования: анализ и интерпретация данных. СПб, 2004.
Наследов А.Д. SPSS: компьютерный анализ данных в психологии и социальных науках. СПб, 2005.
Наследов А.Д. SPSS15: профессиональный статистический анализ данных. СПб, 2008.

2. Рекомендуемая литература (дополнительная).

Бурлачук Л.Ф., Морозов С.М. Словарь-справочник по психологической диагностике. Киев, 1998.
Гайда В.К., Захаров В.П. Психологическое тестирование. Учебное пособие. Л., 1982.
Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии./ Пер.с англ. Под общ.ред. Ю.П.Адлера. М., 1976.
Гусев А.Н. Дисперсионный анализ в экспериментальной психологии. М., 2000.
Дэйвисон М. Многомерное шкалирование: методы наглядного представления данных. М., 1988.
Дюк В.А. Компьютерная психодиагностика. СПб, 1994.
Закс Л. Статистическое оценивание. М., 1976.
Иберла К. Факторный анализ. М., 1980.
Митина О.В., Михайловская И.Б. Факторный анализ для психологов. М., 2001.
Сидоренко Е.В. Методы математической обработки в психологии. СПб, 1996.
Суходольский Г.В. Основы математической статистики для психологов. Л., 1972.

3. Перечень обучающих, контролирующих компьютерных программ, диафильмов, кино- и телефильмов, мультимедиа и т.п.

Программа SPSS, программа EXEL

Blog

Программа учебной дисциплины Математические методы в психологии федерального компонента цикла опд

Содержание

Кафедра педагогики и педагогической психологии

Программа учебной дисциплины

Математические методы в психологии

Наименование тем и разделов