Г. А. Задание С2: Решаем методом координат
| Вид материала | Документы |
СодержаниеЗадача С2. |
- Ії приймання навігаційної інформації, обчислювання координат супутників, обчислювання, 175.51kb.
- Лекция 4 аксонометрические проекции. Многогранные и кривые поверхности, 219.26kb.
- Положение камеры Преобразования, определяющие положение и ориентацию объекта в мировой, 105.74kb.
- Сочинение на тему «Мы сами решаем свою судьбу», 59.31kb.
- Урок лекция по геометрии в 10 классе по теме «Декартовы координаты в пространстве», 53.59kb.
- Контрольная работа по курсу «Линейной алгебры и математического программирования», 99.84kb.
- Программа курса «Общая физика. Механика», 33.84kb.
- Тема: Карти. Атласи. Визначення географічних координат, 313.96kb.
- Суть метода координат, 16.15kb.
- Задания на курсовую работу по дисциплине программирование на языке высокого уровня, 165.55kb.
РМО учителей математики. Выступление Сморкаловой Г.А.
Задание С2: Решаем методом координат
Особого внимания требуют вопросы, связанные с вычислением расстояний и углов в пространстве применительно к конкретной фигуре. Они остаются трудными для большинства учащихся, причем, даже в тех достаточно типичных ситуациях, которые используются в задачах повышенного уровня. Так, если в задачах высокого уровня сложности рассматривается угол между двумя плоскостями, которые зачастую являются плоскостями боковых граней или плоскостями проведенных сечений, то в задачах повышенного уровня это угол между плоскостью основания и плоскостью боковой грани пирамиды или плоскостью типичного сечения призмы. Задачи, связанные с такими ситуациями, из года в год присутствуют в вариантах ЕГЭ (как и в вариантах многих вступительных экзаменов в вузы), тем не менее, процент их верного решения невысок. Это объясняется двумя причинами. Первая причина связана с тем, что углы между плоскостями (а также другие вопросы, связанные с углами и расстояниями в пространстве) в учебниках часто рассматриваются и проходят первичное закрепление до изучения многогранников и тел вращения. Поэтому еще раз подчеркнем высказанную ранее мысль: очень важно при изучении каждого вида многогранников и тел вращения, а также при повторении материала обращать внимание учащихся на использование изученных ранее геометрических фактов для вычисления элементов рассматриваемой фигуры.
Вторая причина связана с задачами, в которых рассматриваются углы между прямой и плоскостью или между плоскостями, где необходимо применять планиметрический материал, нередко усвоенный непрочно. В данном случае речь идет о решении прямоугольных (реже – косоугольных) треугольников. Поэтому необходимо наиболее часто используемые сведения из планиметрии восстанавливать в памяти учащихся при изучении стереометрии. При этом более продуктивным является постепенное (и возможно, неоднократное) повторение тех вопросов, которые актуальны для изучаемого стереометрического материала. Например, при изучении параллельности прямых и плоскостей целесообразно повторить; свойства углов при параллельных прямых и секущей, свойства средних линий треугольника и трапеции, признаки подобия треугольников, а при изучении перпендикулярности прямых и плоскостей – определения тригонометрических функций острого угла прямоугольного треугольника, свойства треугольников и четырехугольников, связанные с перпендикулярностью. В дальнейшем часть из этих сведений, наиболее важную для решения задач, полезно повторять при изучении многогранников и тел вращения.
Вполне возможно, что часть учащихся, потенциально обладающих уровнем подготовки, достаточным для решения геометрических задач, помещаемых в варианты ЕГЭ, просто не доверяет своим знаниям и умениям и, предполагая, что задачи очень трудные, не пытаются их решить. Здесь, видимо, могло бы помочь более активное ознакомление учащихся с задачами, которые использовались в вариантах прошлых лет. Такие задачи представлены в сборниках, содержащих задания и варианты контрольных измерительных материалов, использованных при проведении ЕГЭ. Знакомясь с ними, учащиеся не только повторят некоторые геометрические сведения и приемы решения, но также увидят, что задачи по планиметрии при рациональном способе решения не требуют длинной цепочки рассуждений и выкладок, а стереометрические задачи повышенного уровня построены на достаточно типичных ситуациях и тоже решаются в 2-3 действия.
В методе координат главная нагрузка приходится на алгебраические выкладки, однако их целесообразность базируется на наглядном осмыслении задачи. Что же требуется , чтобы освоить метод координат? 1)знание определенных формул; 2) умение вычислять координаты вершин многогранников и точек, расположенных на их ребрах и гранях; 3)умение составлять уравнение плоскости, проходящей через три заданные точки.
Задание уровня С 3 . Как предупредить ошибки
(учитель математики МОУ «Клюквинская СОШ» Г. А. Сморкалова)
Анализ результатов экзамена позволил выделить проблемы в обучении математике, которые явно проявляются при сдаче ЕГЭ выпускниками, которые продемонстрировали «удовлетворительный» уровень математической подготовки.
1) Выделяются разделы, темы, вопросы, усвоение которых вызывает серьезные затруднения учащихся. Они допускают грубые ошибки при выполнении заданий базового уровня сложности по следующим темам:
- преобразование тригонометрических выражений, преобразование логарифмических выражений;
- решение иррациональных уравнений;
- решение логарифмических и показательных неравенств с основанием 0<а<1;
- исследование свойств функций элементарными методами (нахождение области определения, множества значений, распознавание четности (нечетности).
2) Анализ ответов на задания базового уровня сложности выявил, что учащимися не усвоены стандартные алгоритмы выполнения изученных преобразований, основных методов решения уравнений и неравенств, элементарных методов исследования свойств функций. Так, например, допускаются следующие ошибки в преобразовании разности логарифмов в логарифм частного: выпускники пишут в ответе логарифм разности, разность чисел, стоящих под знаком логарифма, частное чисел, стоящих под знаком логарифма уменьшаемого и вычитаемого.
Необходимо особо обратить внимание на то, что экзаменационные работы изобилуют так называемыми ассоциативными ошибками. Ошибками, которые появляются в результате нечеткого знания алгоритмов решения типовых задач или их фрагментов и сопряжены с неверным (ассоциированным) переносом алгоритма между типами задач.
Задача С1. Найдите абсциссы всех точек графика функции
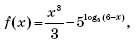
касательные в которых параллельны прямой y = 50x или совпадают с ней.
Одно из возможных решений
1. Df = (– ∞; 6)
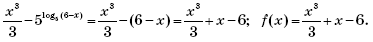 .
.2.
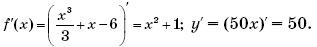
3. Две прямые параллельны или совпадают, если равны их угловые коэффициенты, то есть
x 2 + 1 = 50.
x 2 + 1 = 50; x2 = 49, x = 7 или x = –7.
4. 7
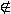 Df, следовательно, (–7) — искомая абсцисса.
Df, следовательно, (–7) — искомая абсцисса.Ответ: –7.
Основные ошибки
1. Ошибка в выполнении порядка действий:
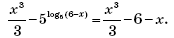
2. В ответ включались оба значения, 7 и –7. То есть не была учтена область определения функции f или учтена формально.
3. Составлялось уравнение x2 + 1 = 50x, в котором производная функции f «приравнивалась» к прямой.
4. Учащиеся сводили задачу к решению уравнения
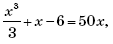 которое после преобразования к виду x 3 – 147x – 18 = 0 либо не решалось, либо решалось путем нахождения дискриминанта (!), либо предлагался следующий путь решения:
которое после преобразования к виду x 3 – 147x – 18 = 0 либо не решалось, либо решалось путем нахождения дискриминанта (!), либо предлагался следующий путь решения: x 3 – 147x – 18 = 0;
x (x2 – 147) – 18 = 0;
x – 18 = 0, x = 18 или x2 – 147 = 0,
x 2 = 147, x » ±12.
Ответ: ±12; 18.
5. Речевые ошибки:
— приравниваем производную функции f и функцию касательной y = 50x;
— записав область определения, мы можем сократить по правилу логарифмирования.
Комментарии
1. На всех этапах изучения функции в школе необходимо подчеркивать, что говорить о свойствах функции или ее значениях в тех точках, где она не определена, — бессмысленно.
2. Для лучшего усвоения учащимися алгоритма составления уравнения касательной, параллельной какой-либо прямой, целесообразно предлагать задачи с разной формой записи прямой (y = 2x + 4, y = 4 + 2x, 0,5y – x = 4 и т.п.).
3. На протяжении уже нескольких лет составители контрольно-измерительных материалов для ЕГЭ по математике в задачах части С предлагают функции, которые сначала необходимо упростить. В связи с этим включение задач с промежуточным этапом решения по упрощению аналитического вида функции при итоговом повторении и на этапах финального закрепления материала представляется весьма оправданным и разумным.
При решении простейших логарифмических неравенств положение еще более плачевное. Около трети учащихся не учитывают область определения логарифма, еще треть учащихся не меняет знак неравенства на противоположный, когда основание логарифма 0
Задача С3. Найдите все значения a > 1, при каждом из которых все значения функции
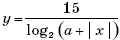
принадлежат промежутку [–3; log2 a – 2).
Одно из возможных решений
1. Поскольку выполнены неравенства | x | ≥ 0
(свойство модуля) и a > 1 (по условию), то в силу того, что функция f(t) = log2 t возрастает на промежутке (0; +∞), имеем следующую цепочку неравенств:
| x | ≥ 0 и a > 1, | x | + a > a,
log2 (| x | + a) > log2 a.
a > 1, log2 a > 0.
2. Пусть log2 (a + | x |) = u. Так как на промежутке (0; +∞) функция
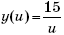 убывает, то
убывает, то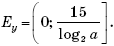
3. Все значения заданной функции y, то есть числа из промежутка
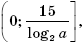 будут принадлежать промежутку [–3; log2 a – 2), если для значений a выполнено неравенство
будут принадлежать промежутку [–3; log2 a – 2), если для значений a выполнено неравенство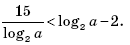
4. Решим неравенство:
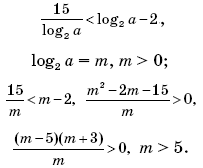
log2 a > 5, log2 a > log2 32, a > 32.
Ответ: (32; +∞).
Основные ошибки
1. Логарифм не может быть отрицательным, поэтому
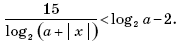
2. Так как 2 > 1, то
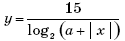 — возрастающая функция.
— возрастающая функция.3. При исследовании функции
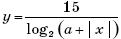
встречались такие записи: (| x |)' = 1.
4
.
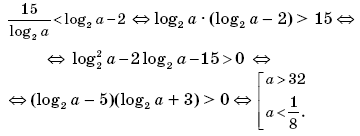
Комментарии
1. Необходимо, чтобы выпускники четко представляли, что знак минус перед числом означает в первую очередь противоположность и уж затем отрицательность. Например, log2 0,1 — число отрицательное, а (–log2 0,1) — положительное.
2. Изучая свойства элементарных функций, было бы правильно при рассмотрении композиций элементарных функций четко выделять, значения какой из них являются аргументом для другой. Это особенно актуально для успешного решения задач с параметрами.
При выполнении заданий базового и повышенного уровня выпускники допускают много вычислительных ошибок.
3) Очень небольшой процент участников экзамена, справляется только с отдельными заданиями повышенного уровня сложности. Обычно для решения таких задач нужно применить не одну формулу или одно свойство, а две формулы или два свойства, или применить изученные знания (формулы, свойства) в несколько измененной ситуации.
С описанными заданиями повышенного уровня сложности справляются лишь около половины выпускников. Им оказываются под силу лишь те задания, где требуется выполнить более сложные вычисления или преобразования, но школьные «хорошисты» испытывают затруднения в тех заданиях, где нужно изменить стандартный алгоритм решения, согласуясь с данными задачи. Так, при нахождении наибольшего и наименьшего значений сложной функции на заданном отрезке (например, «Найдите разность между наибольшим и наименьшим значениями функции y = log 0,1(10-x2) на отрезке [-3; 1]») условие задачи провоцирует выпускника на применение стандартного алгоритма исследования функции с помощью производной. Однако анализ условия показывает, что в силу монотонности логарифмической функции и с учетом значений функции y=10-x2 на отрезке [-3;1] задачу можно решить элементарным методами, найдя разность y(– 3) – y(0). Очевидно, что школьный «хорошист» имеет теоретическую базу, достаточную, чтобы справиться с этой ситуацией. В ходе обучения необходимо ставить перед учениками такие проблемы, решение которых выходило бы за рамки стандартных алгоритмов, но ученики могли бы с ними справиться, применяя самостоятельно изученный ими материал.
4) Особое беспокойство вызывают проблемы, о которых свидетельствует перепроверка ответов учащихся на задания с развернутым ответом повышенного уровня сложности, выполнение которых оценивается максимально 2 баллами. При записи решений этих заданий не требуется каких-либо объяснений, т.к. обычно проверяются известные методы решений. Но вместе с тем выполнение этих заданий требует определенной внимательности выпускников, т.к. в одних случаях нужно учесть область определения выражения, в других - сделать проверку найденных корней уравнения – следствия или отобрать значения, исходя из ограничений данных в условии задачи.
Задача С2. Найдите все значения x, при каждом из которых произведение значений выражения
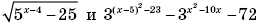 отрицательно.
отрицательно.Решение. Способ I. Задача сводится к решению неравенства
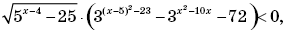 решим его методом интервалов. Рассмотрим функцию
решим его методом интервалов. Рассмотрим функцию 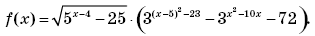
Так как 5x – 4 – 25 ≥ 0, 5x – 4 = 52, x – 4 ≥ 2, x ≥ 6,
то функция f определена и непрерывна на луче [6; +∞). Найдем нули функции f:
1)
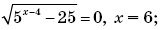
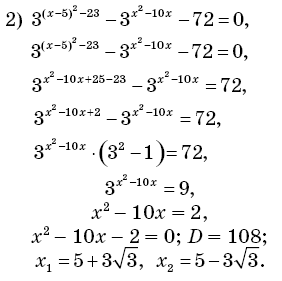
Так как
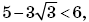 то нулями функции f будут числа 6 и
то нулями функции f будут числа 6 и 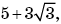 которые разбивают луч [6; + ∞) на два промежутка, в каждом из которых функция сохраняет знак своих значений.
которые разбивают луч [6; + ∞) на два промежутка, в каждом из которых функция сохраняет знак своих значений.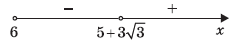
f (10) > 0, f(7) < 0.
Интервал
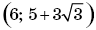 — искомое множество чисел.
— искомое множество чисел.Ответ:
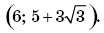
Способ II. 1. Выражение
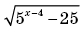 при всех допустимых значениях переменной принимает только неотрицательные значения, следовательно, произведение исходных выражений будет принимать отрицательные значения, если выполняется неравенство
при всех допустимых значениях переменной принимает только неотрицательные значения, следовательно, произведение исходных выражений будет принимать отрицательные значения, если выполняется неравенство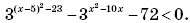
2. Для выражения
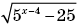 допустимые значения переменной удовлетворяют неравенству 5x – 4 – 25 ≥ 0:
допустимые значения переменной удовлетворяют неравенству 5x – 4 – 25 ≥ 0: 5x – 4 – 25 ≥ 0, 5x – 4 ≥ 52, x – 4 ≥ 2, x ≥ 6.
3. Решим неравенство
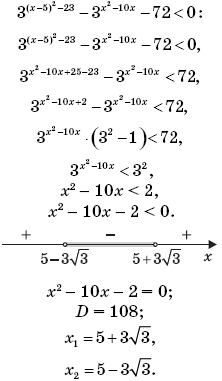
4. Так как x > 6, то
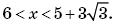
Ответ:
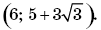
Способ III (метод равносильных преобразований). Искомое множество значений переменной совпадает с множеством решений неравенства
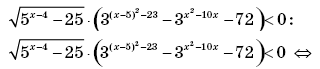
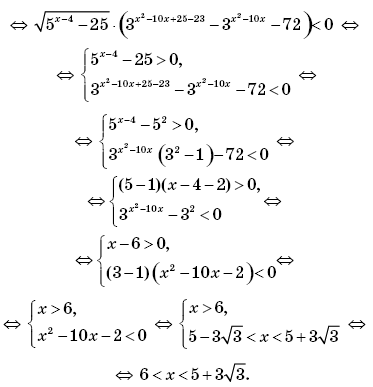
Ответ :
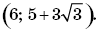
Основные ошибки
1. Не учли область допустимых значений переменной выражения
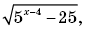 поэтому в качестве ответа указан интервал
поэтому в качестве ответа указан интервал 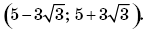
2. Указан нестрогий знак неравенства
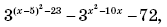
в ответ включено значение, не удовлетворяющее требованию задачи —
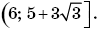
3. Значением, при котором
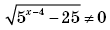 разбивался интервал
разбивался интервал 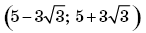
и ответ записывался в виде объединения
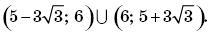
4. Условие задачи записывалось в виде требования:
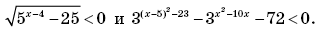
5.
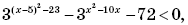
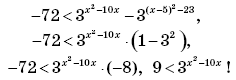
Здесь, как говорится, «уж сколько раз твердили миру...»
6. Задача сведена к решению двух неравенств:
5x – 4 – 25 > 0 и
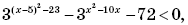
Но после нахождения соответствующих значений и расположения их на числовой прямой, произведено не решение системы неравенств (пусть даже в явном виде и не обозначенной), а чередование знаков.
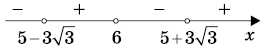
7. Ошибка в проведении равносильного преобразования неравенства:
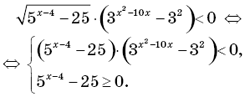
8.
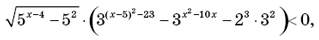
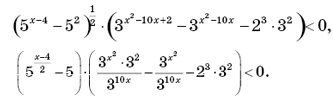
«Сократили» на x:
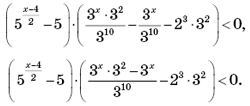
Следующие ошибки относятся к так называемым ассоциированным ошибкам.
9. Для определения области допустимых значений переменной выражения
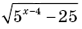 составлено неравенство
составлено неравенство 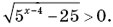 Это характерный пример ассоциированных ошибок школьников, когда возникает путаница между тем, что искать и как искать.
Это характерный пример ассоциированных ошибок школьников, когда возникает путаница между тем, что искать и как искать.10. Условию задачи соответствует неравенство
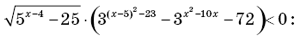
1)
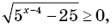
5x – 4 – 25 = 0, 5x – 4 = 25, 5x – 4 = 52, x – 4 = 2, x = 6;
2)
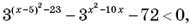
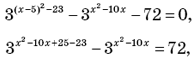
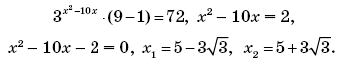
Ответ:
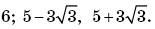
11.
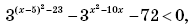
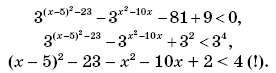
Комментарии
1. Третий способ решения основан на приеме декомпозиции показательных неравенств.
2. Велика доля учеников, которые не смогли по условию задачи просто составить нужное неравенство. Отчасти эта беда определяется тем, что в действующих учебниках слишком мало представлено дидактического материала, который способствовал бы формированию у учащихся таких устойчивых навыков. Поэтому учителю необходимо к урокам составлять подборки задач по сюжетам, например, такого содержания:
1) Найдите все значения переменной, при каждом из которых выражения A(x) и B(x) принимают равные значения.
2) Определите множество всех значений x, при которых функции y = f(x) и y = g(x) имеют одинаковые знаки значений.
3) Определите множество всех значений x, при которых график функции y = f(x) расположен выше графика функции y = g(x).
4) Определите множество всех значений x, при которых график функции y = f(x) лежит ниже биссектрисы I и III координатных углов.
5) Найдите координаты точки пересечения графиков функций y = f(x) и y = g(x).
Не нужно давать и разучивать с учащимися образцы решений, не нужно «канонизировать» какие-то эталоны, решения у разных учеников могут и, по-видимому, должны быть различными, единственным критерием их оценки должна быть математическая грамотность записи решения.
Хотя болевые точки выявлены но, как показывает опыт, положительных результатов трудно ожидать в течение двух и даже трех лет, т.к. математика является таким предметом, где невероятно сильна преемственность в обучении. Чтобы получить высокие результаты в средней школе, нужно добиться успешного овладения теми результатами, которые формируются в основной школе.
К таким важным результатам обучения математике в 5-6 классах и алгебре в 7-9 классах относятся умения:
- выполнять вычисления с обыкновенными и десятичными дробями,
- преобразовывать многочлены, алгебраические дроби, степени с целыми показателями и квадратные корни,
- решать линейные, квадратные и дробно-рациональные уравнения и неравенства,
- читать свойства функций по их графикам, исследовать отдельные свойства функций аналитически.
Учителям математики, начинающим работу в 10 классе и готовящим выпускников к итоговой аттестации, необходимо в начале учебного года получить достоверную информацию об уровне подготовки десятиклассников по основным разделам курса алгебры основной школы и своевременно организовать работу по ликвидации пробелов в знаниях учащихся. Этой цели служит организация вводного повторения материала курса алгебры 7-9 классов. Исходя из результатов, получаемых ежегодно на едином экзамене по математике, можно предложить следующую тематику вводного повторения.
Вполне понятно, что решить проблему ликвидации пробелов в знаниях десятиклассников по курсу алгебры основной школы только с помощью организации вводного повторения не удастся. Поэтому целесообразно организовать еще и индивидуальное повторение, учитывающее пробелы в знаниях и умениях конкретного ученика, и с помощью диагностических работ систематически фиксировать продвижение старшеклассника по пути достижения уровня запланированных требований.
Итак, для успешной подготовки к итоговой аттестации в старших классах необходимо целенаправленное вводное повторение разделов курса алгебры 7-9 классов (математики 5-6 классов) и систематический мониторинг продвижения отдельных учеников по ликвидации пробелов за основную школу.
Вместе с тем не стоит забывать, что курс алгебры и начал анализа отличается не только преемственностью с курсом математики 5-6 классов и курсом алгебры 7-9 классов, но и преемственными связями между различными разделами внутри самого курса. Поэтому для обеспечения прочного овладения всеми выпускниками основными элементами содержания, изучаемыми в старшей школе не только на базовом, но и на повышенном уровне, нужно проводить систематическое повторение пройденного. Во многих учебниках, входящих в федеральный комплект учебников, такое повторение обеспечивается системой упражнений, рекомендованных для домашней работы. Обычно эти упражнения достаточно объемны, трудоемки и требуют письменного выполнения. Одним из возможных альтернативных путей организации текущего повторения может быть использование в ходе обучения устных упражнений.
Устные упражнения традиционно включаются в учебный процесс на уроках математики в основной школе, но, как показывает практика, недостаточно используются в старших классах. Устные упражнения, проводимые обычно в начале урока, имеют своей основной целью актуализацию знаний, необходимых для последующего объяснения учителя. Вместе с тем они могут выполнять и другие функции, например, использоваться для первичного закреплении материала, при опросе (фронтальном и индивидуальном).
При разработке содержания и формы представления устных упражнений следует позаботиться об обеспечении простоты «технических» преобразований и вычислений, необходимых для их выполнения. Этот подход позволит сосредоточить внимание учащихся на смысловой стороне их выполнения, то есть на определении метода их решения. Кроме того, простота технической стороны устных упражнений позволяет с их помощью моделировать различные нестандартные ситуации применения тех или иных знаний (теоретического материала)5, в которых центр тяжести сосредоточен на конструировании нового метода и не осложнен сопутствующими (второстепенными) деталями. Так, подводя учащихся к поиску решения нестандартного уравнения6, можно в устных упражнениях обсудить сущность соответствующего метода решения, например, на заданиях типа:
– решите уравнение
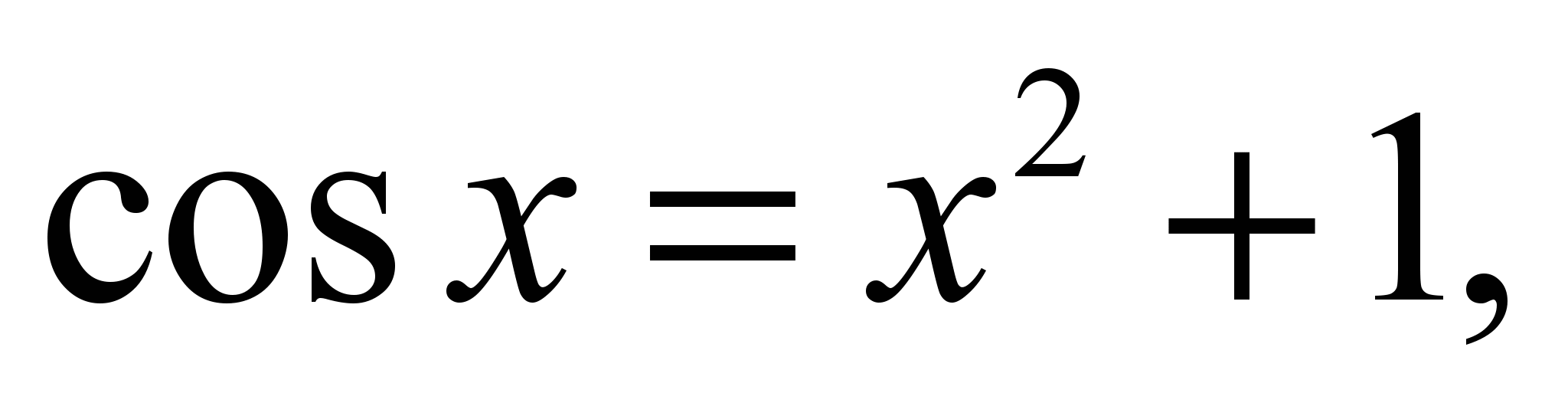
– решите уравнение
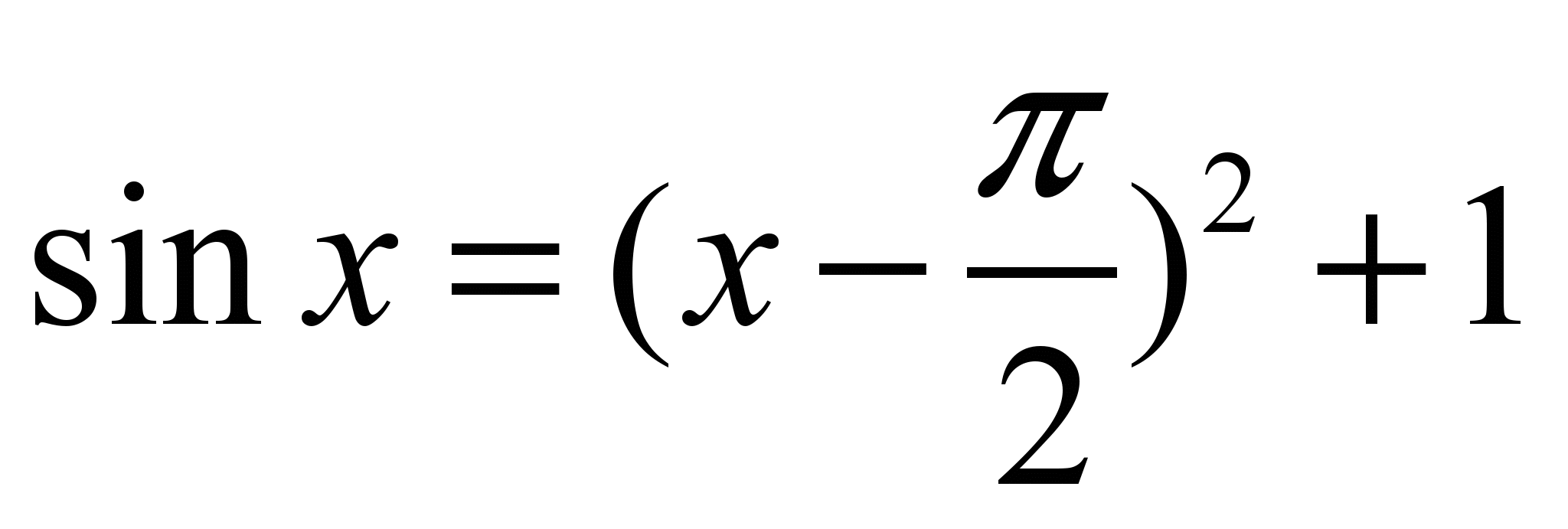 .
.Таким образом, учитель сможет связать учебный материал из различных разделов курса, обеспечивая, с одной стороны, систематическое повторение, а с другой стороны, мотивируя более подготовленных учащихся к решению задач повышенной сложности.
Отдавая должное вводному и систематическому текущему повторению, нельзя переоценить важность и значение итогового повторения, в ходе которого осуществляется систематизация знаний по мере изучения всего курса.
5
6
