Элективный курс для учащихся 11-го класса «Решение иррациональных уравнений и неравенств»
| Вид материала | Элективный курс |
СодержаниеУчебно-тематический план. Пояснительная записка Содержание курса. Учебно-тематический план |
- Элективный курс «Решение уравнений и неравенств» Класс: 11 Профиль класса: общеобразовательный, 47.74kb.
- Элективный курс по математике, 37.2kb.
- Тема: «Рациональные и иррациональные уравнения, неравенства и системы», 199.57kb.
- Элективный курс «Уравнения и неравенства с модулем» 10 класс разработан учителем моу, 93.7kb.
- Никонова Марина Николаевна Учитель математики высшей категории г. Кировск 2011 г элективный, 81.49kb.
- Элективный курс по географии для 8-9 класса «Многонациональный Костромской край», 61.14kb.
- Элективный курс по химии для 10 класса профильного уровня. Тема: «Избранные вопросы, 93.44kb.
- Трубчаниновой Татьяной Евгеньевной пояснительная записка, 59.76kb.
- Пояснительная записка Элективный курс «Природа тел Солнечной системы» предназначен, 50.52kb.
- Волжска Республики Марий Эл Разработала и провела учитель математики Попова Л. З. Уравнения, 33.26kb.
Элективный курс для учащихся 11-го класса
«Решение иррациональных уравнений и неравенств».
Пояснительная записка
Значение предпрофильного элективного курса в 11-ом классе очень велико, так как он ориентирует учащихся в выборе профиля для дальнейшего обучения. Данная программа предусматривает расширение и углубление знаний учащихся, проявивших интерес к изучению математики. В процессе работы учащиеся ознакомятся с различными методами решений иррациональных уравнений и неравенств. Широко будет практиковаться защита лучшего способа решения. В процессе работы приобретенные знания, умения и навыки по данному курсу будут фиксироваться с помощью промежуточных контрольных и зачетных работ, будут проводиться семинарские занятия.
Учащиеся расширят свой кругозор, рассматривая решения уравнений и неравенств с параметрами.
Одна из целей курса дать возможность ученикам самоутвердиться и самореализоваться в ходе обучения.
Цели и задачи:
- Учащиеся должны приобрести навыки решать задачи более высокой по сравнению с обязательным уровнем сложности.
- Ознакомить учащихся с основными методами и приемами решения уравнений и неравенств, решения системы уравнений.
- Ознакомить учащихся с нестандартными приемами решения неравенств: обобщенным и эффективным.
- Обеспечить сознательное овладение учащимися системой математических знаний, умений и навыков, необходимых для продолжения учебы более высокого уровня.
Программа.
- Решение иррациональных уравнений. (15 часов)
- Решение иррациональных неравенств. (8 часов)
- Решение иррациональных уравнений и неравенств с параметрами. (7 часов)
Содержание программы.
Тема «Решение иррациональных уравнений» считается самой трудной. Одним из способов решения иррациональных уравнений заключается в последовательном возведении обеих частей уравнения в степень.
Если степень, в которую возводится уравнение четная, то полученное уравнение может иметь посторонние корни, в таких случаях нужна проверка решений.
Умножение обеих частей уравнения на множитель зависящий от переменной, не всегда является равносильным преобразованием, поэтому нужно доказать, что это множитель определен и не обращается в нуль на области определения уравнения.
При решении уравнений и неравенств с несколькими радикалами лучше всего найти область определения и постоянно следить за равносильностью преобразования.
Умелое использование формул сокращенного умножения позволяет многие уравнения и неравенства решать проще, а некоторые уравнения без применения этого способа неразрешимы.
Метод мини-максов основан на использовании свойства функций, неравенство Коши. Умелое использование этого метода позволяет быстро и эффективно решать комбинированные уравнения и неравенства, которые часто встречаются при сдаче ЕГЭ. Дискриминантный метод широко применяется, особенно при решении уравнений и неравенств с параметрами, в виду простоты его применения.
Все методы прекрасные, но к каждому иррациональному уравнению при решении, нужно иметь определенный метод. Поэтому данный курс рассчитан на расширение кругозора учащихся и на развитие нестандартного мышления.
При решении иррациональных неравенств следует помнить, что при возведении обеих частей неравенства в нечетную степень, всегда получается неравенство, равносильное исходному, а в четную - равносильно исходному, и имеющее тот же знак лишь в случае, если обе части исходного неравенства неотрицательны.
В данном курсе учащиеся знакомятся с решением неравенств обобщенным м эффективным методами, что позволяет быстро и эффективно решать целый класс неравенств повышенной сложности, переводя их тем самым в разряд «стандартных» задач. Центральным методом в данном случае является метод замены переменных. Решение уравнений и неравенств с параметрами буду вести параллельно с методами решений.
Учебно-тематический план.
| № п/п | Тема занятия | Кол-во часов | Виды деятельности | Форма контро-ля | ||||||
| Решение иррациональных уравнений. | ||||||||||
| 1. | Возведение в степень. | 1 | Практическая работа по решению примеров | | ||||||
| 2 | Уравнение вида  | |||||||||
| 3. | Метод замены | 2 | Лекция. Решение примеров | Тест | ||||||
| 4. | Использование формул сокращенного умножения | 2 | Лекция. Практическая работа | Само-стоятель-ная работа | ||||||
| 5. | Уравнения со сложными радикалами | 2 | Лекция. Практическая работа. | | ||||||
| 6. | Уравнения, содержащие несколько радикалов | 1 | Решение примеров | Зачетная работа | ||||||
| 7. | Использование производной пропорции | 1 | Лекция решение примеров | | ||||||
| 8. | Применение тригонометрической подстановки | 2 | Лекция. Решение примеров. | Контроль-ная работа | ||||||
| 9. | Комбинированные уравнения | 2 | Лекция. Решение примеров. | | ||||||
| 10. | Метод геометрической подстановки | 1 | Лекция | | ||||||
| 11. | Метод мини-максов | 1 | Лекция. Решение примеров. | | ||||||
| 12. | Дискриминантный метод | |||||||||
| 13 | Итоговое семинарское занятие | 2 | | Зачет | ||||||
| Решение иррациональных неравенств. | ||||||||||
| 1. | 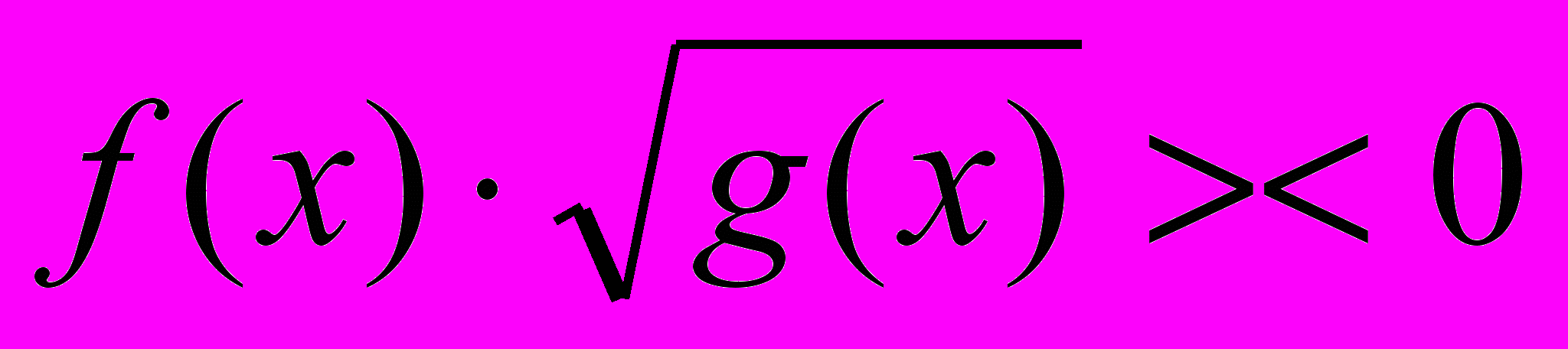 | 1 | Практическая работа | | ||||||
| 2. | 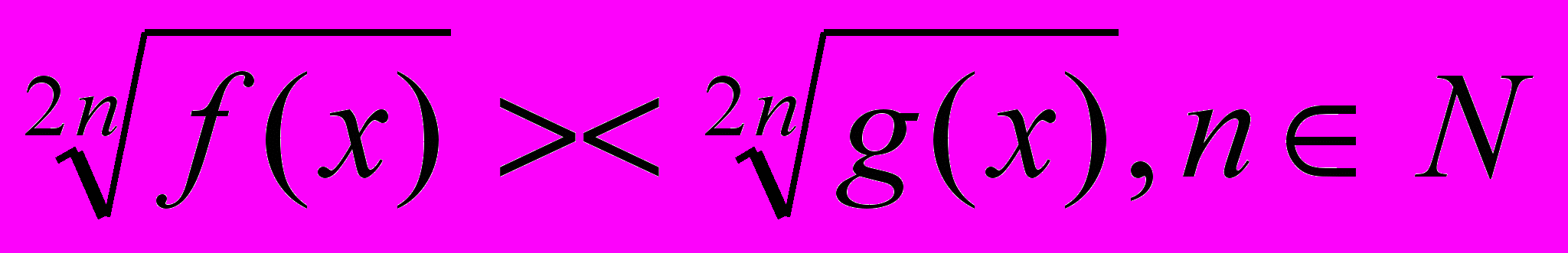 | 1 | Практическая работа | | ||||||
| 3. | 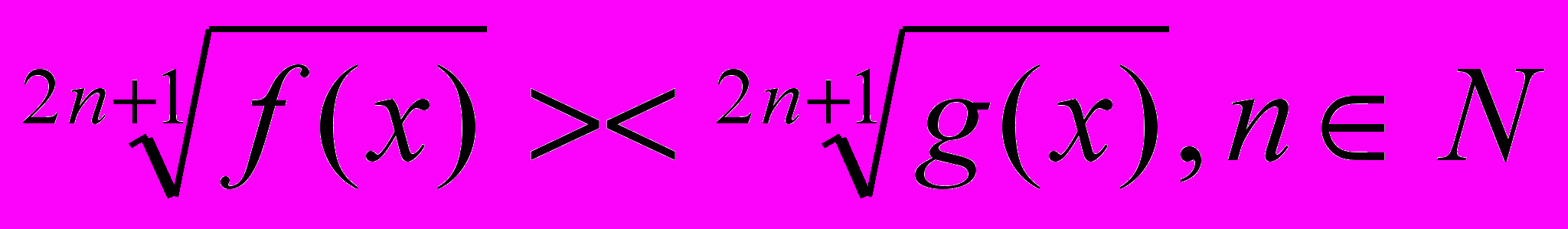 | 1 | Практическая работа | | ||||||
| 4. |  | 1 | Практическая работа | | ||||||
| 5. | 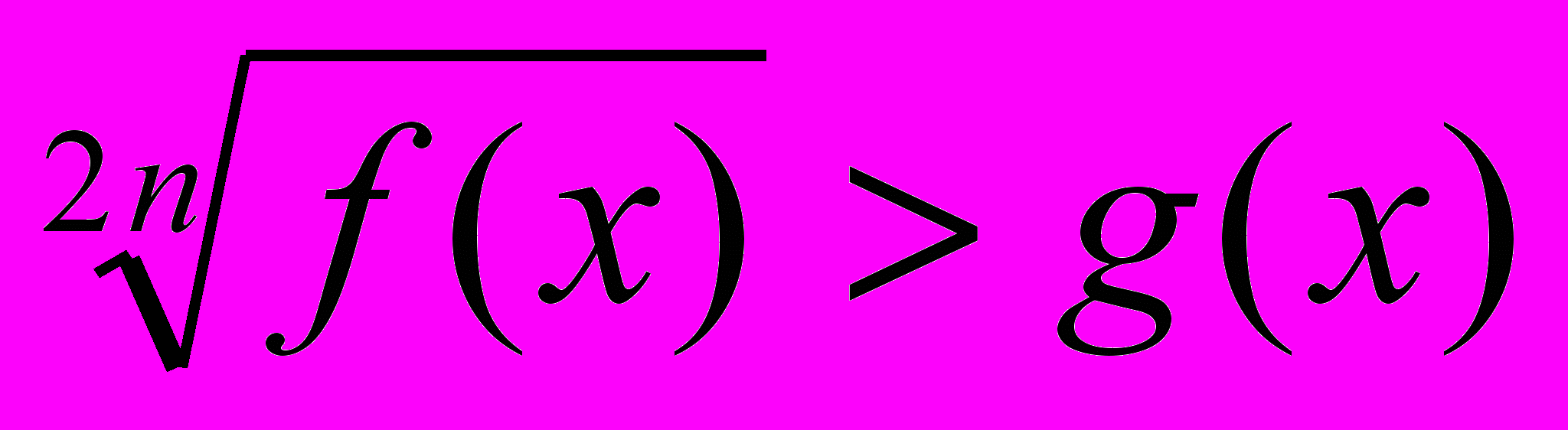 | 1 | Практическая работа | | ||||||
| 6. |  | 1 | Практическая работа | | ||||||
| 7. |  | 1 | Практическая работа | | ||||||
| 8. | Неравенства с несколькими радикалами | 3 | Лекция | | ||||||
| 9. | Обобщающий и эффективный метод | 6 | Лекция | | ||||||
| | Итого | 34 | | Защита реферата | ||||||
Планируемый результат курса.
- Учащиеся должны освоить основные методы решения
- Применять полученные знания в поисках решения сложных заданий.
Литература:
- А.Г.Цыпкин «Справочник по методам решения задач по математике»
- М.Е. Подтягин «Элементарная математика»
- И.Ф.Шарыгин «Факультативный курс по математике»
- В.В.Вавилов «Задачи по математике»
- Т.Дорофеев, М.Потапов «Математика для поступающих в вузы»
- Т.Дорофеев, М.Потапов «конкурсные задачи по математике»
- Н.А.Бобылева «Конкурсные задачи по математике»
- О.Ю.Чернов, А.Г.Якушев «Математика»
- М.И.Сканави «Сборник задач по математике для поступающих в вузы»
- М.И.Шабунин «Математика для поступающих в вузы»
- Ф.Ф.Лысенко «Математика».
Содержание
- Пояснительная записка 1
- Цели и задачи 2
- Программа 3
- Содержание программы 4
- Учебно-тематический план 5-6
- Планируемый результат курса 7
- Литература 8
Элективный курс для учащихся 11-ых классов
«Решение геометрических задач по определению расстояния между элементами многогранников и решение комбинированных задач»
Пояснительная записка
Задачи по стереометрии вызывают большие затруднения у учащихся . Это связано с тем, что для успешного решения пространственных задач требуется не только знание основных определений и теорем, но и развитое геометрическое воображение, умение выполнять необходимые построения. Эффективно использовать алгебру и тригонометрию.
Умение решать задачи – один из основных показателей математического развития учащихся, глубины усвоения ими учебного материала, четкости в рассуждениях, понимании логических аспектов различных вопросов.
Данный элективный курс предназначен для учащихся 11 классов, которые желают научиться решать задачи из группы С4 ЕГЭ.
Пространственные представления учащихся развиваются в процессе решения большого числа задач, при этом часто приходится вычислять расстояния между различными точками, плоскостями и расстояния между скрещивающимися прямыми. Учащиеся испытывают большие затруднения, особенно, при вычислении расстояния между скрещивающимися прямыми.
Поэтому данный курс будет построен по принципам модульного дополнения действующего учебника геометрии 10-11 классов под редакцией Л.С.Атанасяна, естественным образом примкнет к курсу, углубляя и расширяя его. Зная, определения расстояния между любыми элементами геометрии, легко можно справиться с комбинированными задачами на вычисления объемов, площадей и задачами, связанными с нахождением экстремальных значений.
Одна из целей данного курса найти оптимальные способы решения геометрических задач, вовлечь учащихся в групповые и индивидуальные работы, найти нестандартные поиски решений.
Основные цели и задачи:
- Ознакомить учащихся с основными методами и приемами решения геометрических задач
- Сформировать умение решать проблемные задачи, выискивать новые приемы.
- Расширить пространственное воображение и применять ранее изученное к решению задач
- Показать взаимосвязь геометрии и алгебры
Содержание курса.
При решении многих стереометрических задач приходится вычислять расстояние между точкой и прямой, прямой и плоскостью, расстояние между скрещивающимися прямыми. Ученики затрудняются даже в построении чертежа. Поэтому данный курс поможет ученикам как в построении и нахождении искомого элемента, решать более сложные задачи, чем задачи, решаемые в классе. При сдаче ЕГЭ всего несколько процентов справляются с заданиями С4. Целью проведения курса, заинтересовать учащихся в решении задач, найти более эффективные методы решения.
Учебно-тематический план
| № п/п | Тема занятия | Кол-во часов | Виды деятельности | Форма контроля |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | Определение расстояния между точками в пространстве. Векторный метод. Расстояние от точки до прямой Определение расстояния между параллельными плоскостями Расстояние между скрещивающимися прямыми. Построение длины отрезка, нахождение расстояния векторным методом Комбинации круглых тел, определение площади поверхности и объема Цилиндры и многогранник Конус и многогранник Комбинации многогранников Сфера и многогранники Сфера и цилиндр Сфера и конус Экстремальные задачи на комбинации тел. Решение задач с использованием производной Приложения векторов и метода координат к решению задач по геометрии. | 2 2 2 3 2 3 2 3 3 2 2 4 4 | Лекция. Практическая работа Лекция. Практическая работа Лекция. Практическая работа Лекция. Практическая работа Лекция. Практическая работа Решение задач Решение задач Решение задач Лекция. Решение задач Лекция. Решение задач Лекция. Решение задач Лекция. Решение задач Лекция. Решение задач | Самостоятель-ная работа Зачет Семинар Защита рефератов Итоговая контрольная работа |
| | ИТОГО | 34 | | |
Литература:
- Т.Дорофеев, М.Потапов «Математика для поступающих в вузы»
- М.И.Сканави «Сборник задач по математике для поступающих в вузы»
- С.Л. Евсюк «Решение задач повышенной сложности»
- И.В. Пархимович «Математика для поступающих в вузы»
- Г.Г.Мамонтова «Математика»
- О.Ю.Чернышев, В.Т.Якушев «Математика для поступающих в вузы»
- Ф.Ф.Лысенко «Математика для абитуриентов»
