Урок математики в 6-м классе по теме: «Отношения и пропорции»

Вид материала

Урок

Содержание II. Проверка теоретического материала. Устная работа III. Самостоятельная работа Задание для слабых учащихся. IV. Решение задач V. Задание на дом

Подобный материал:

• Урок математики  в 6 классе по теме: Пропорции, 20.43kb.
• Урок. Математика 6 класс. «Длина окружности», 95.5kb.
• Урок математики во 2 классе по теме: «Прямой угол», 77.07kb.
• Урок по математике в 5 классе по теме тип: интегрированный урок подготовила и провела, 85.18kb.
• Урок в 8-м классе по теме: "Тепловой баланс. Решение задач", 94.3kb.
• Урок по алгебре и началам анализа в 10г классе учителя математики моу «сош №32 г. Энгельса», 97.37kb.
• Урок в 6-м классе с использованием презентации по теме "Математическая география" или, 244.98kb.
• Урок математики в 6 классе по теме «Нахождение числа по его дроби», 28.07kb.
• Урок обществознания в 8 классе по теме: «Нации и межнациональные отношения», 119.79kb.
• Урок математики в 7-м классе по теме "Решение задач с помощью систем уравнений", 63.6kb.

Автор: Жаркова И.В. учитель математики


Обобщающий урок математики в 6–м классе по теме: « Отношения и пропорции »


Цели урока:

• закрепить знания и умения по данной теме;
  
• развивать воображение, математическую интуицию, память, мышление;
  
• активизировать познавательную и творческую активность учащихся.
  

Оборудование:

карточки для устного счета, карточки для самостоятельной работы.

ХОД УРОКА

I. Организационный момент:

• проверка готовности класса к уроку;
  
• сообщение темы и цели урока.
  

II. Проверка теоретического материала.


Учащимся предложены карточки с теоретическим материалом, в которых нужно вставить пропущенные слова. Затем обсудить данным материал с учащимися.





Пропорция – это равенство двух _____________________________.

В пропорции а : m = k : b а и ___ - ____________ члены; ___ и

___ - ___________ члены.


Основное свойство пропорции: ______________________________

средних членов равно произведению ___________________________

членов.


Устная работа:


На доске карточки с заданиями. Необходимо выяснить какие пропорции верные, а какие нет. Найти неизвестный член пропорции.

1) Верна ли пропорция:

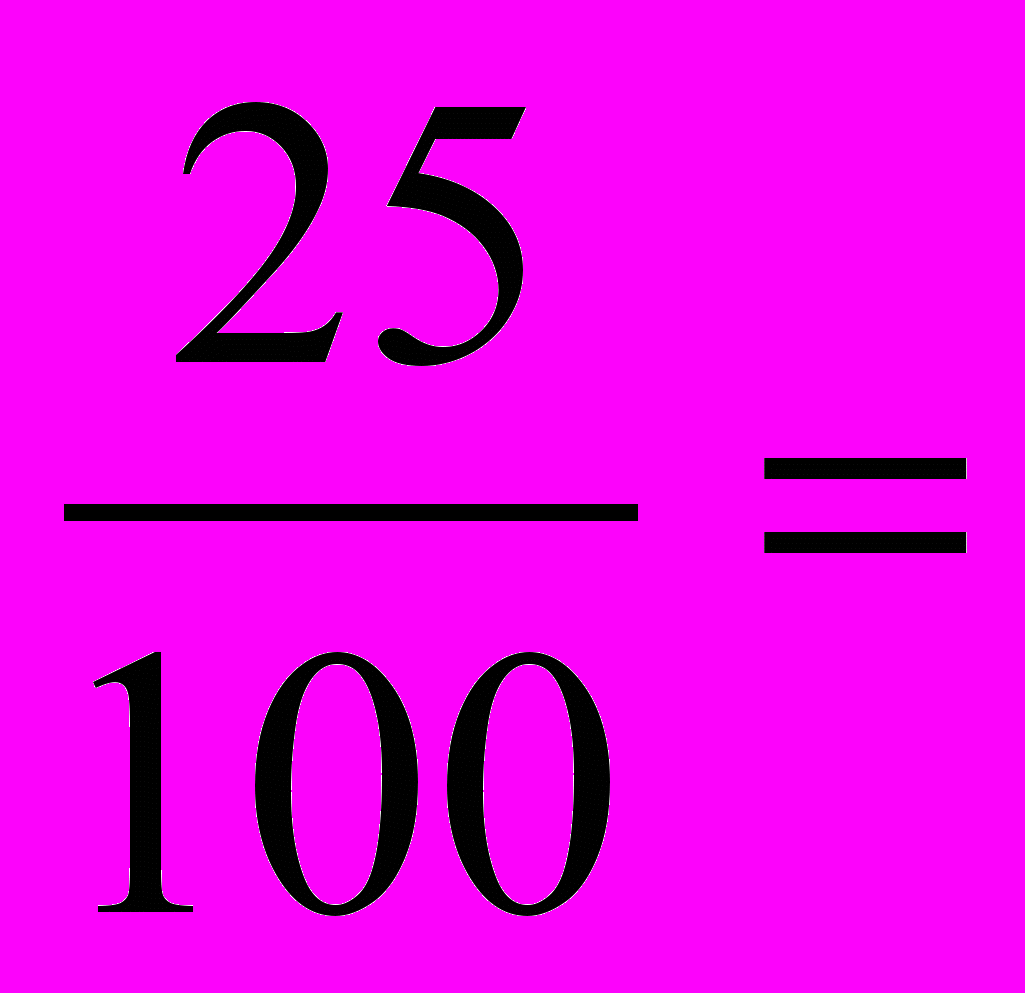
а) 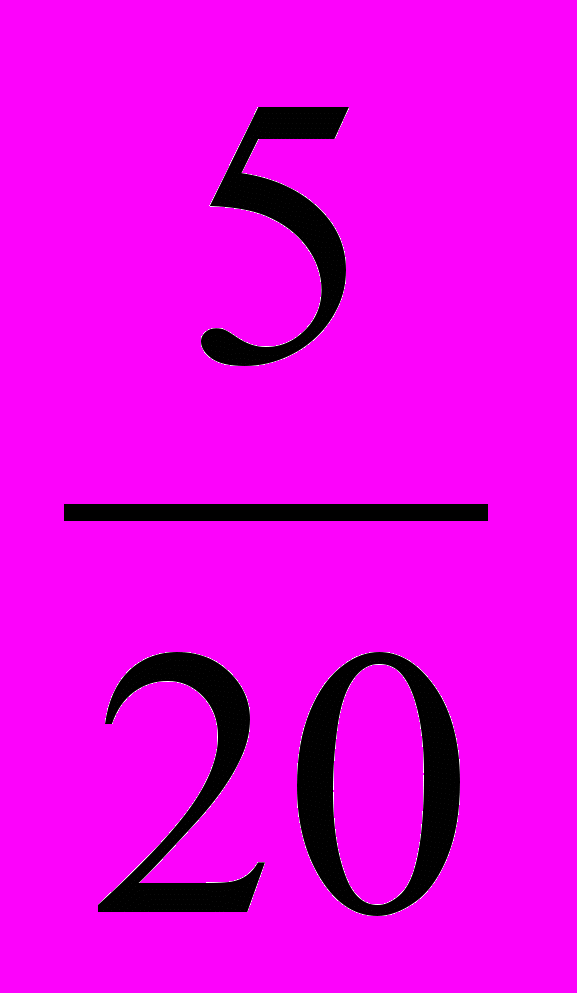( верна );

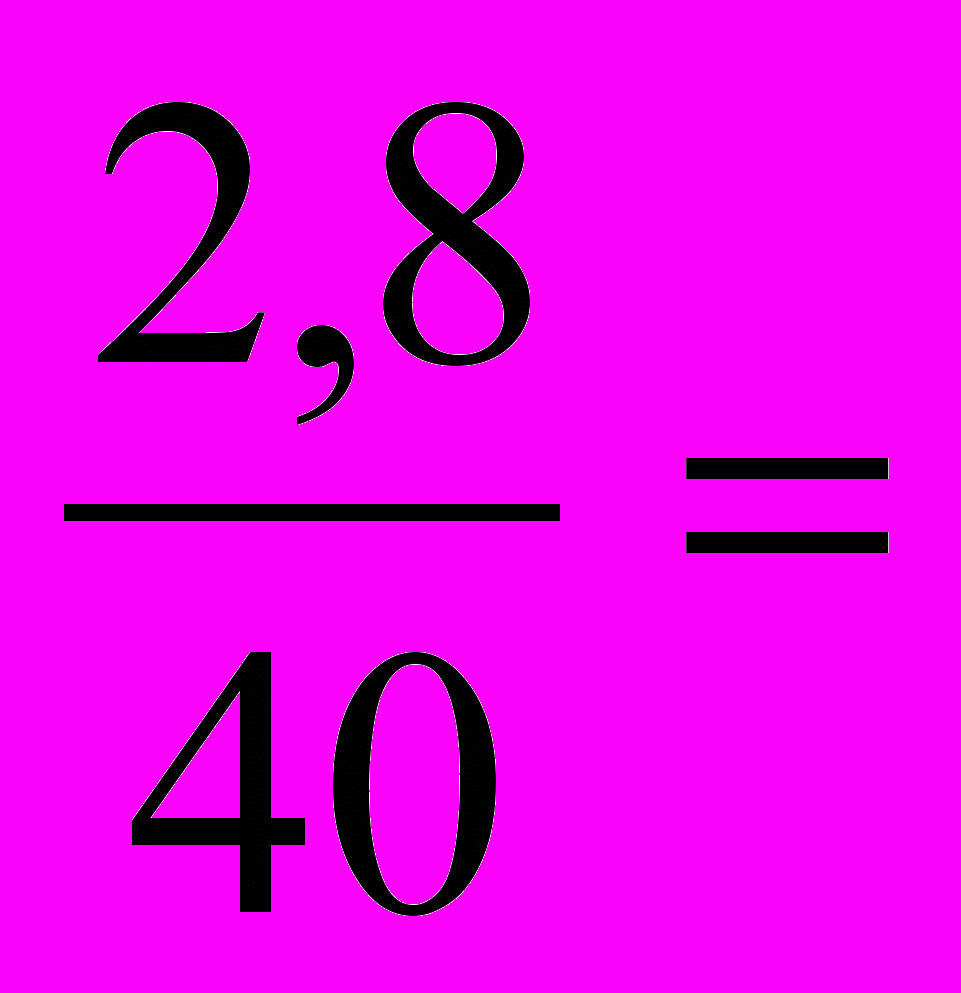
б) 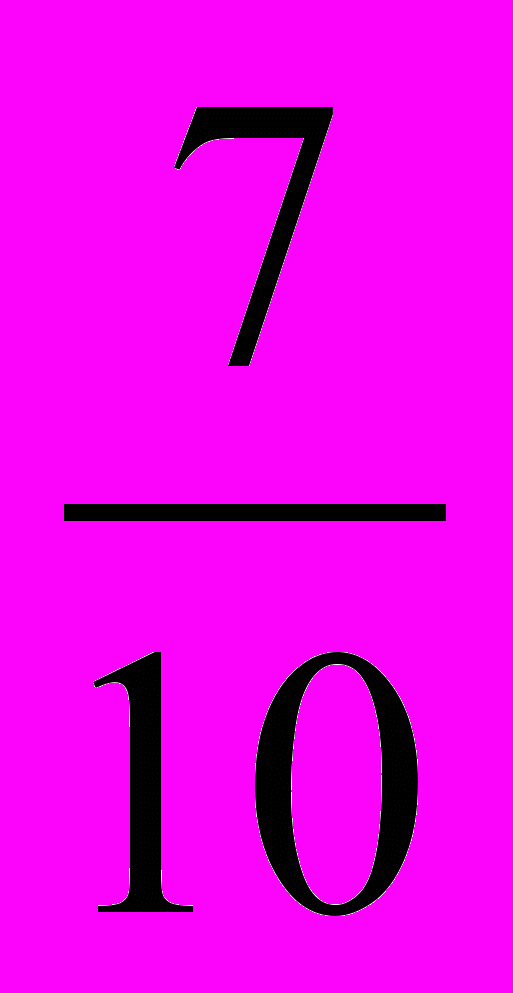( нет );


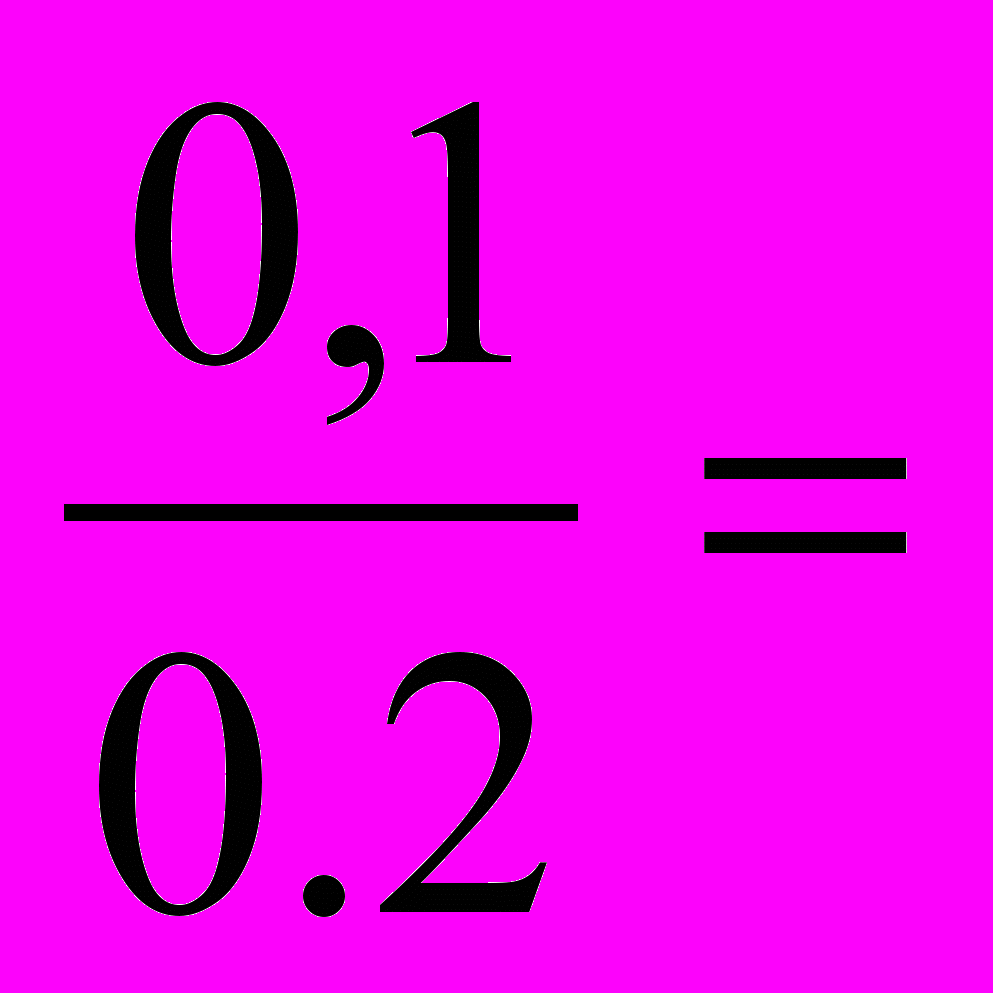
в) 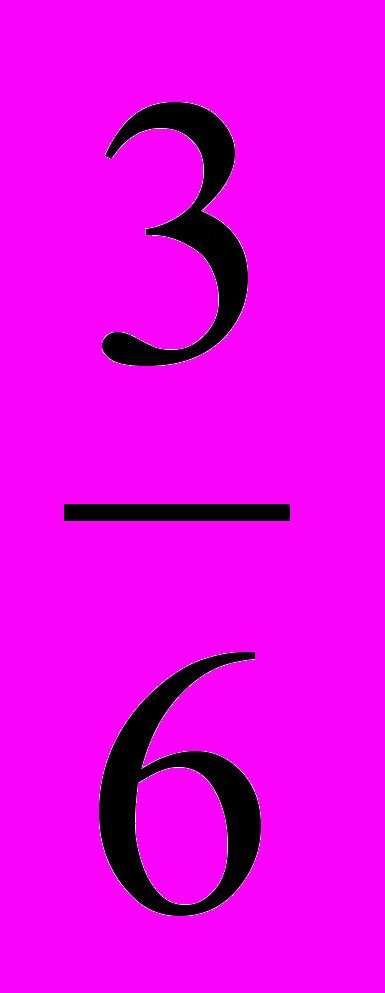( верна );


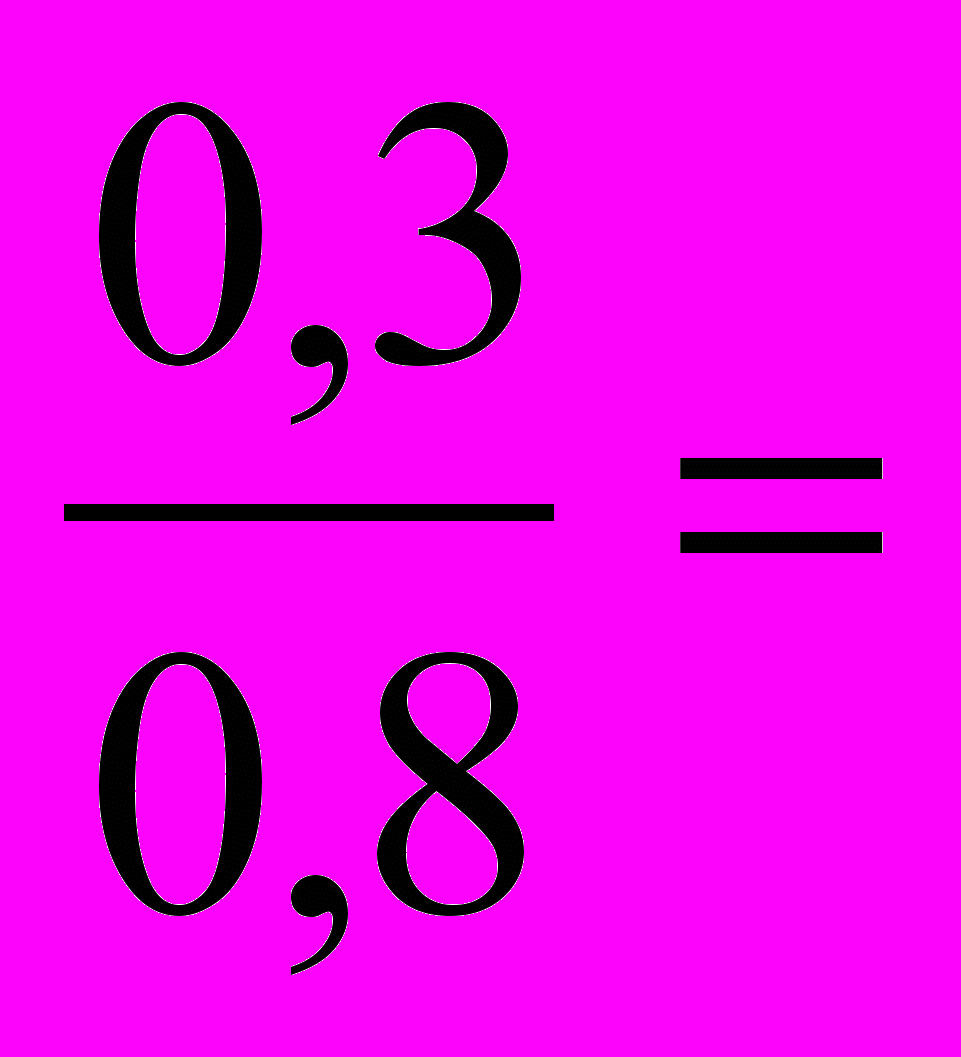
г) 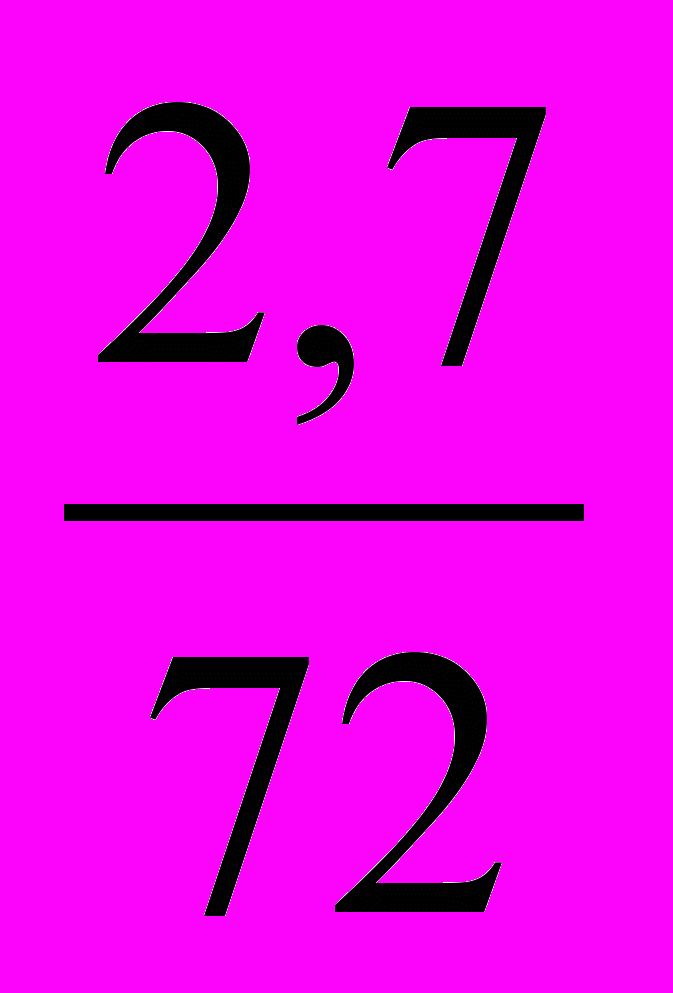( нет ).

2) Найти неизвестный член пропорции:


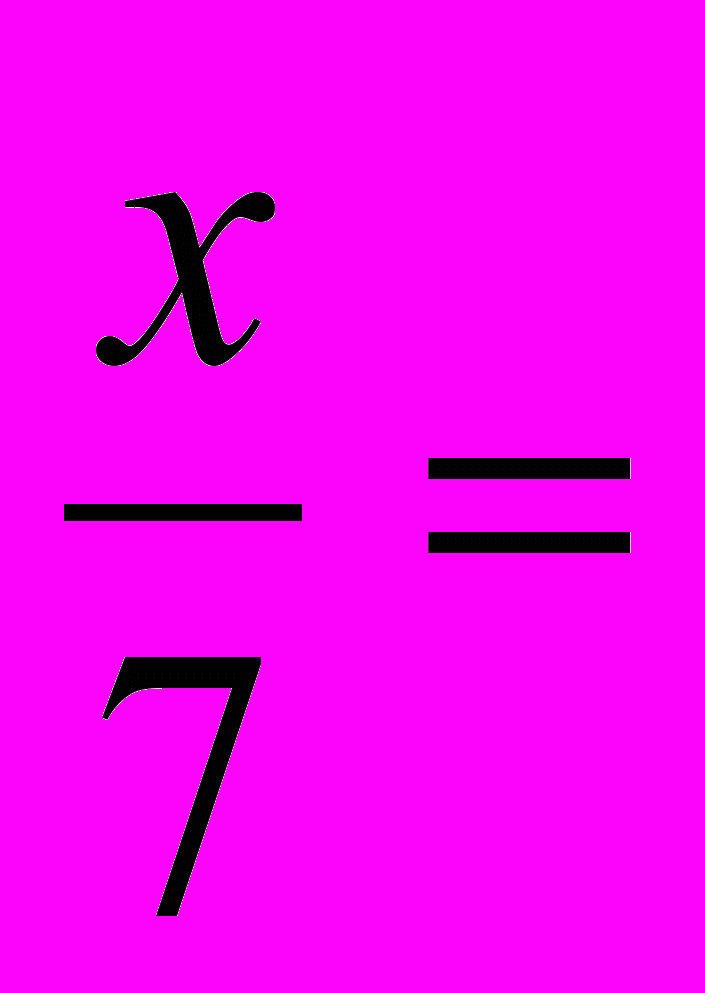
а) 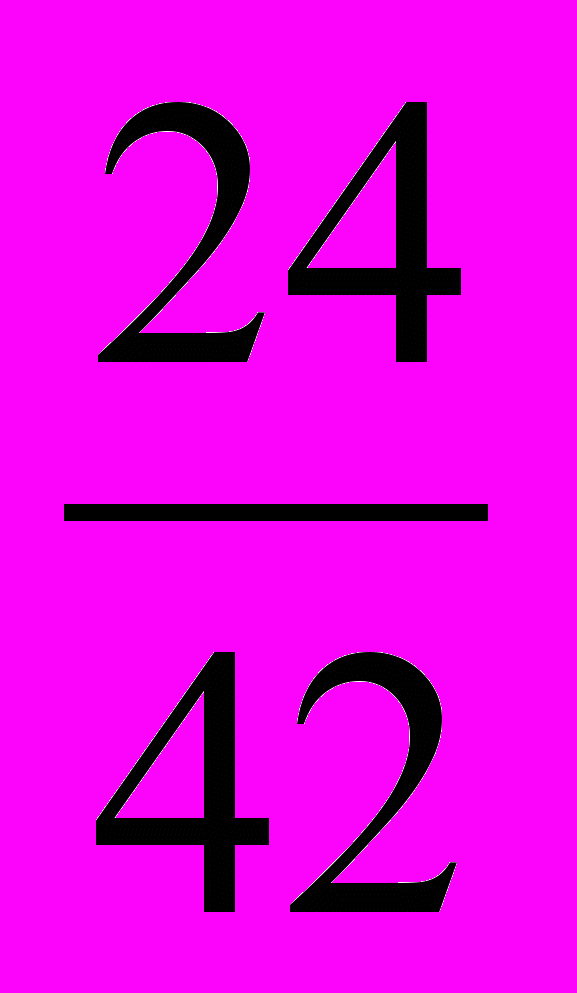[ 4 ];

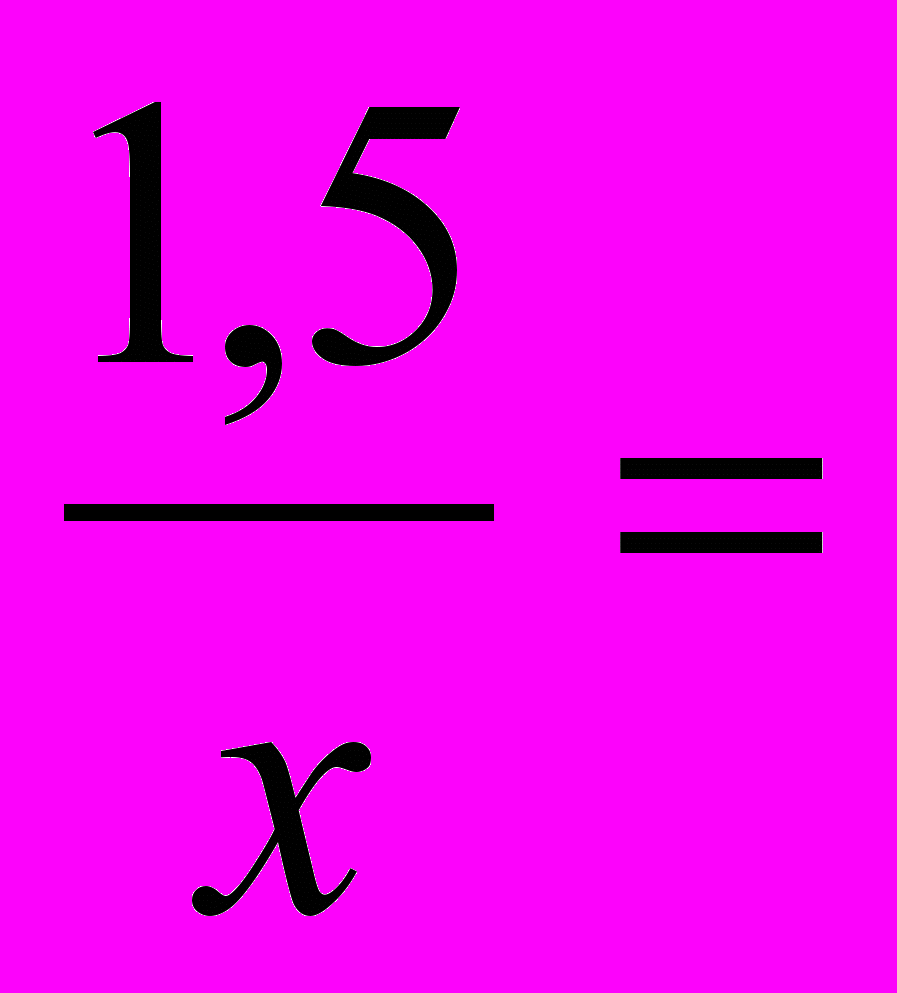
б) 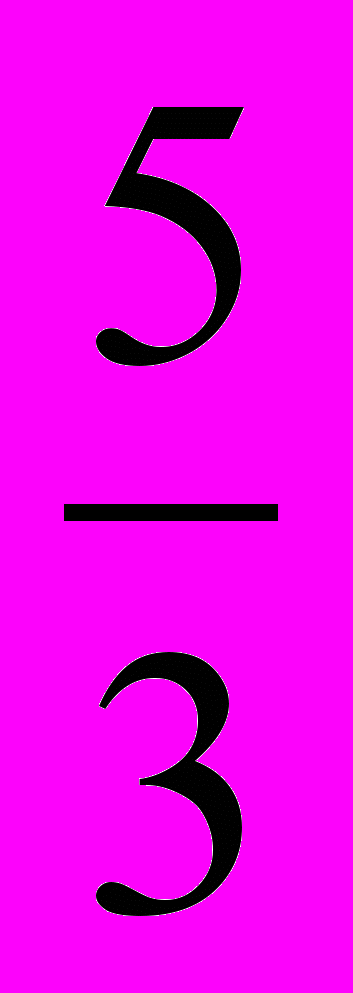[ 0,9 ];

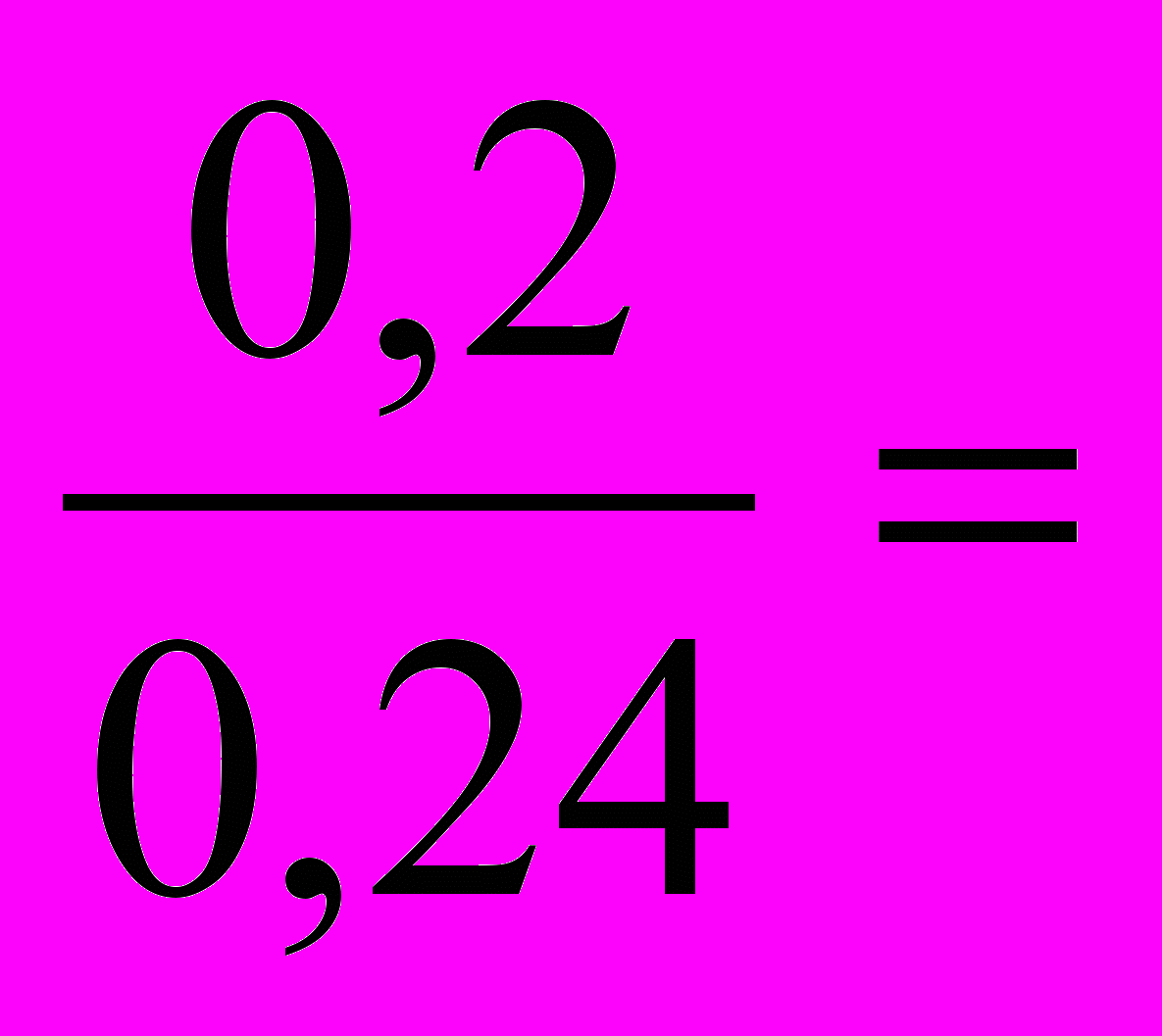
в) 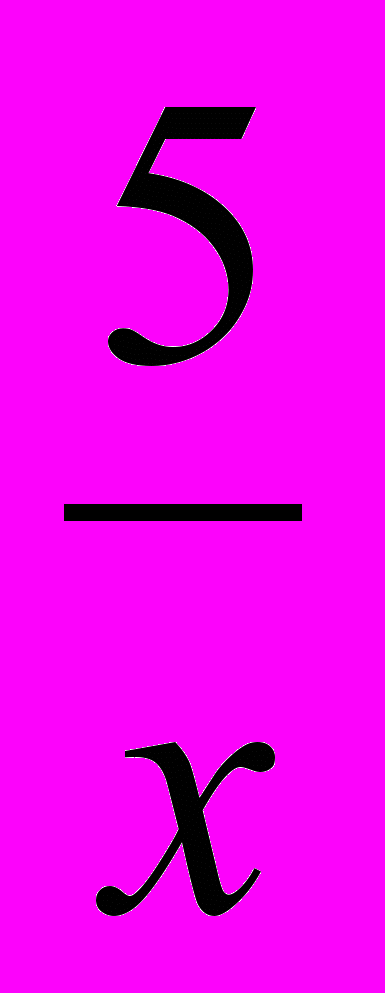[ 6 ];


г) 1 : 2 = 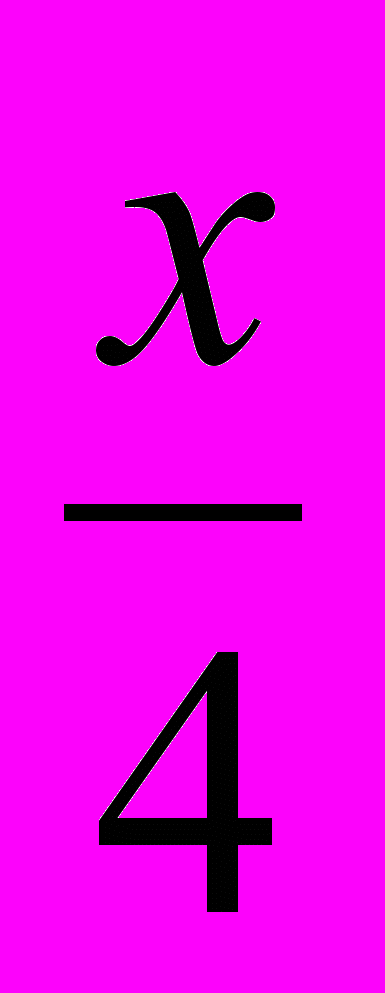[ 2 ].


III. Самостоятельная работа:


Учащимся предложена самостоятельная работа на карточках по вариантам. Учащиеся заранее рассажены по принципу « сильный – слабый », и им предлагаются задания I – го и II – го уровней, т.е. для слабых учащихся с « подсказкой ».


Задание для слабых учащихся.





Решите уравнение: 41,8 : b = 3,8 : 2,2.

Решение. Уравнение представляет собой пропорцию, у которой ____

и 2,2 - ___________________ члены, ___ и ___ - _________________

члены. Воспользуемся ______________ свойством пропорции:

запишем, что равно произведение средних и _____________ членов

пропорции.

b ∙ ___ = _____ ∙ _____;

b ∙ 3,8 = ________;

b = _____ : _____;

b = ______ .

Задание для сильных учащихся.





Решите уравнения, используя основное свойство пропорции.

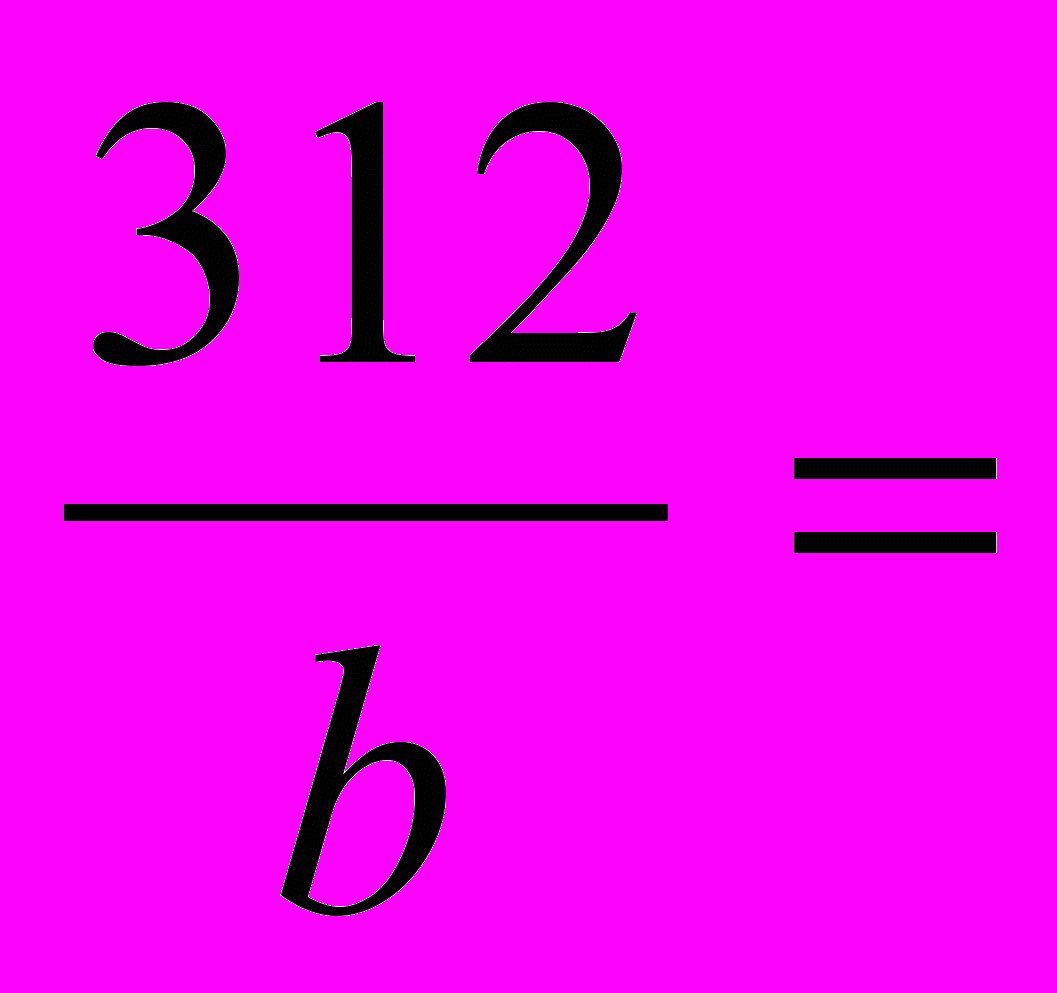
а) ; б) .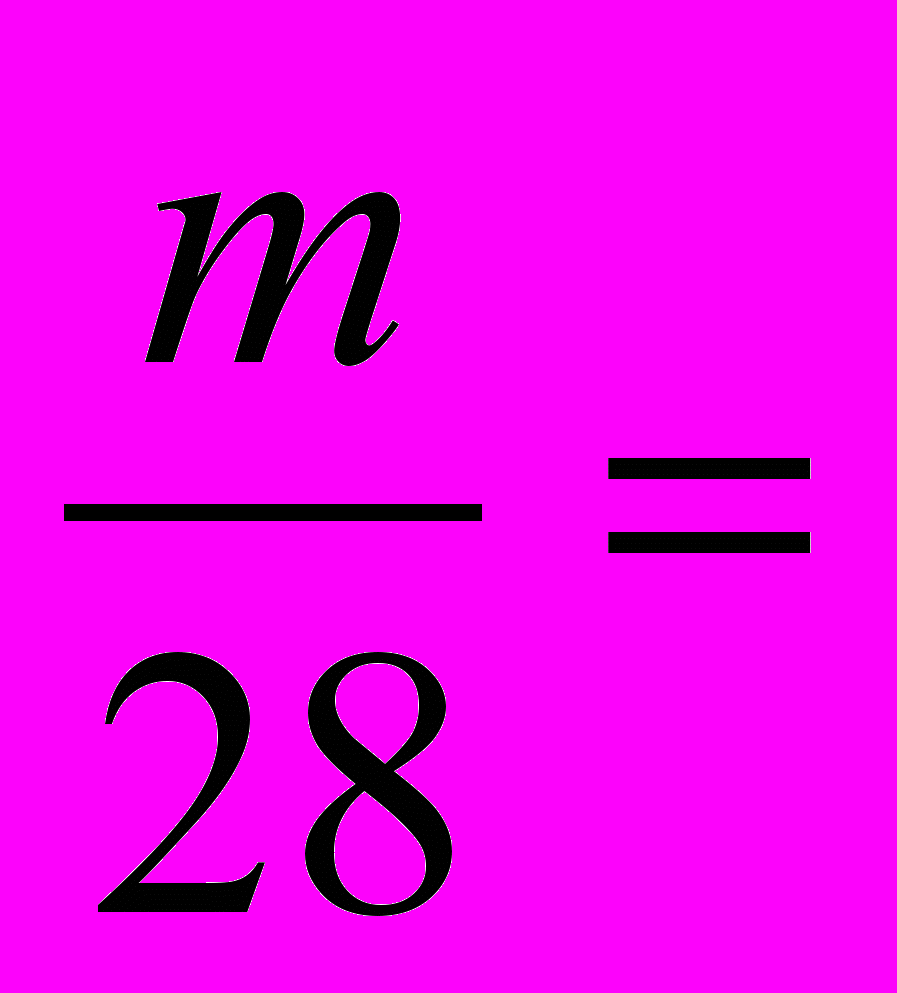

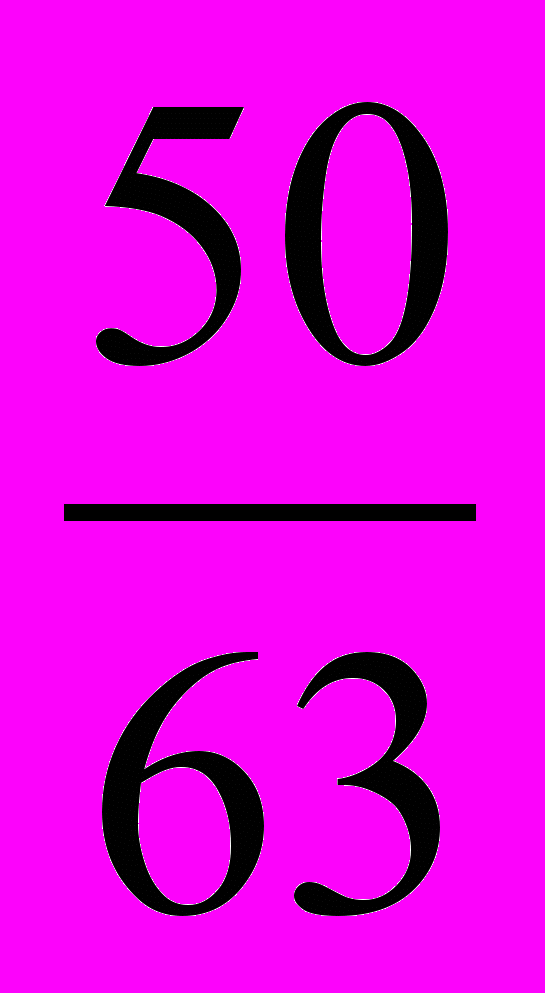Решение. а) В данном уравнении крайние члены ____ и ____ ,

средние члены ___ и ___ .

а) 312 ∙ ___ = ____ ∙ ____;

b = ______ : ______;

b = _______ .

б) 50 ∙ ____ = ____ ∙ ____;

m = _______ : _______;

m = _________ .


IV. Решение задач


На предыдущих уроках учащимся были введены понятия прямой и обратной пропорциональности, отработаны данные понятия на задачах. На данном уроке решаем задачи с помощью пропорций. В процессе устного обсуждения выделяем две величины, устанавливаем вид зависимости. Уменьшение величины показываем стрелкой вниз, а увеличение – стрелкой вверх. Затем составляем пропорцию и решаем задачу.


1. Для приготовления борща на каждые 100 г мяса надо взять 60 г свеклы. Сколько свеклы надо взять на 650 г мяса?

Решение.


Составим краткую запись условия задачи:

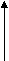
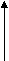мясо свекла

650 г Х г

100 г 60 г


Краткая запись заранее оформляется на плакате или на слайде. В процессе устного обсуждения выясняем, что масса продуктов увеличивается в одно и то же число раз, следовательно, величины прямо пропорциональны.


Затем, составляем пропорцию и решаем её:

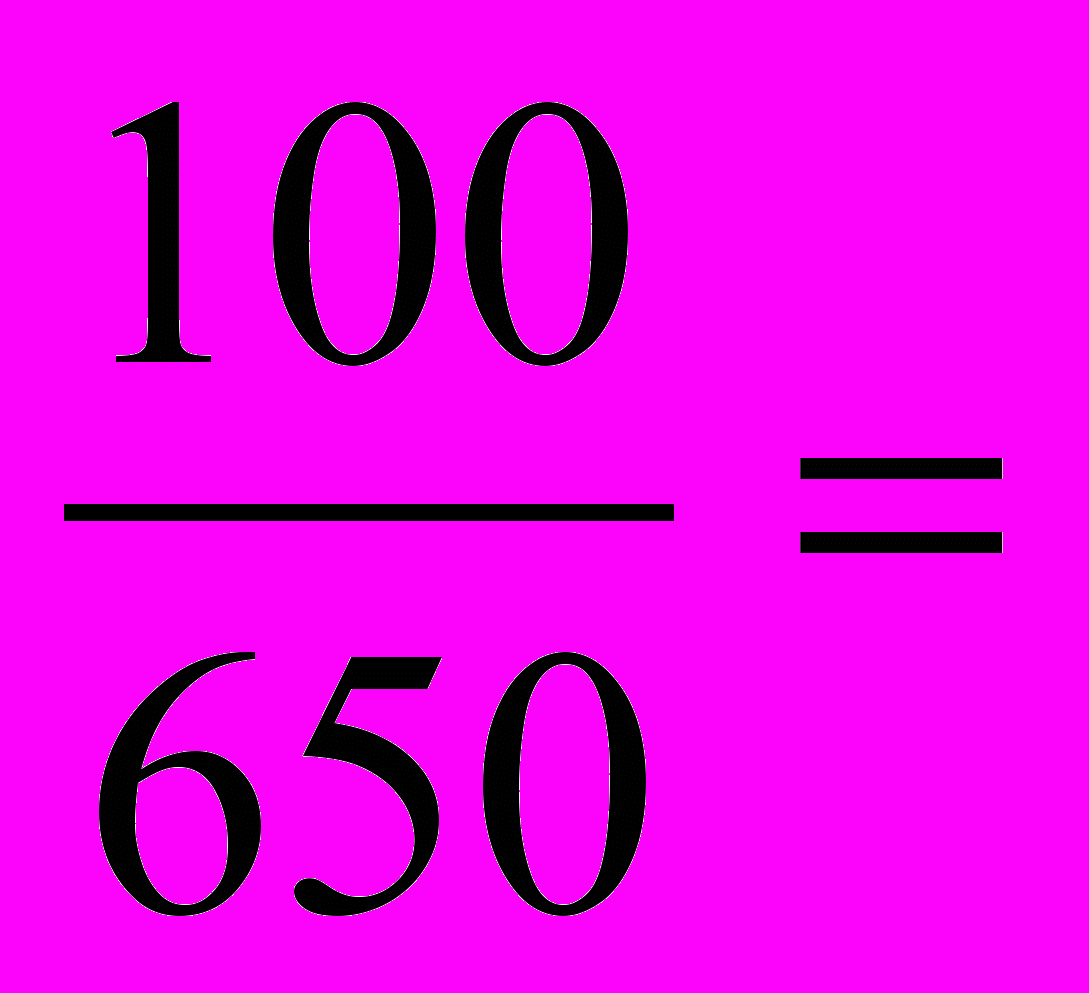
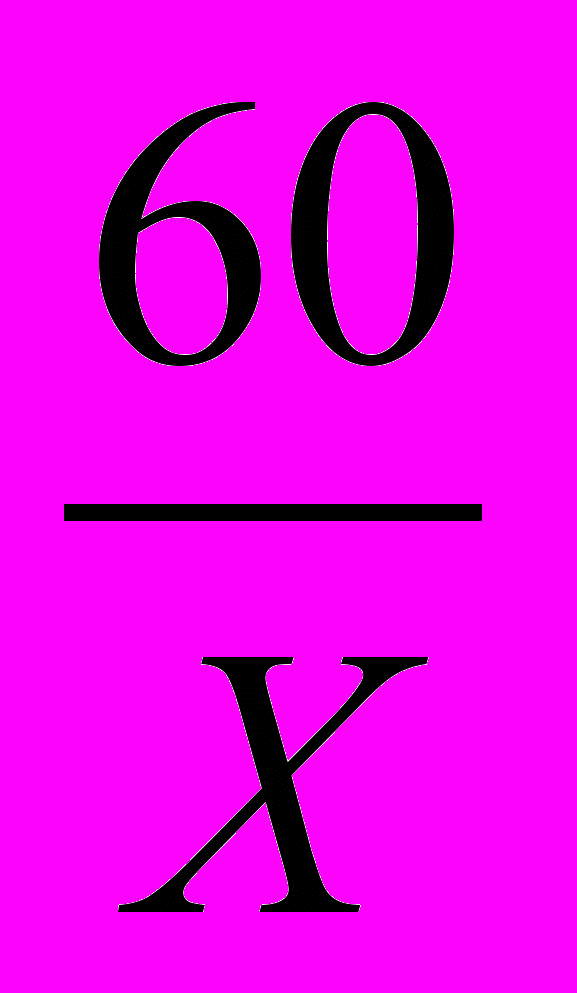; Х = 390 ( г )


2. Трое маляров могут закончить работу за 5 дней. Для ускорения работы добавили еще двух маляров. За какое время они закончат работу, если все маляры работают с одинаковой производительностью?


Решение.


Маляры Дни

3 ч. 5

5 ч. Х


В процессе устного обсуждения выясняем, что число людей увеличилось, а количество дней уменьшилось, следовательно, эти величины при одной и той же производительности являются обратно пропорциональными.


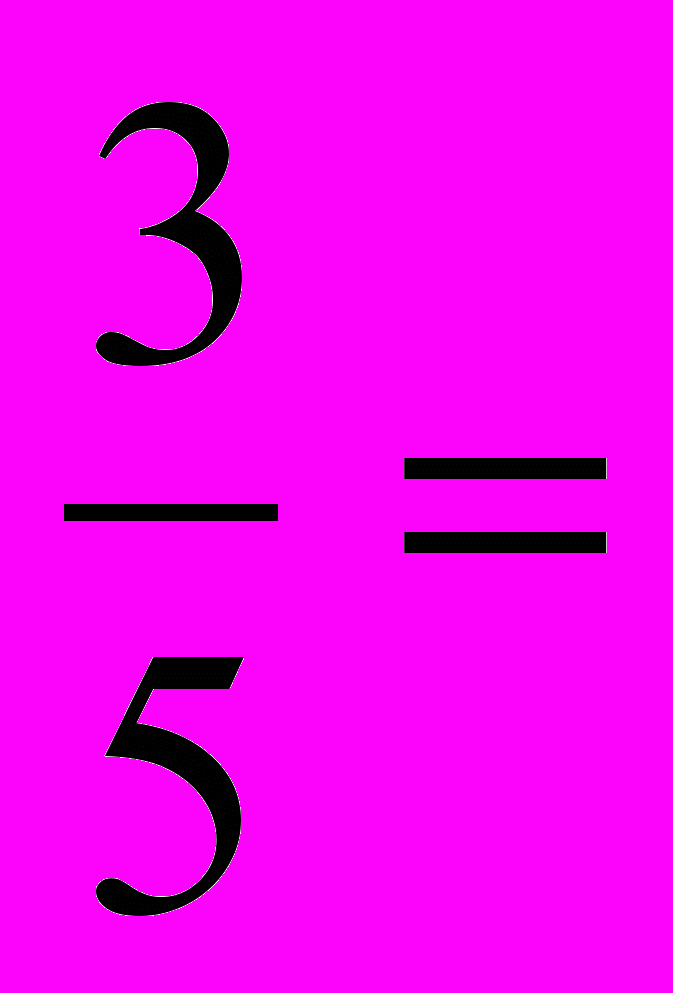
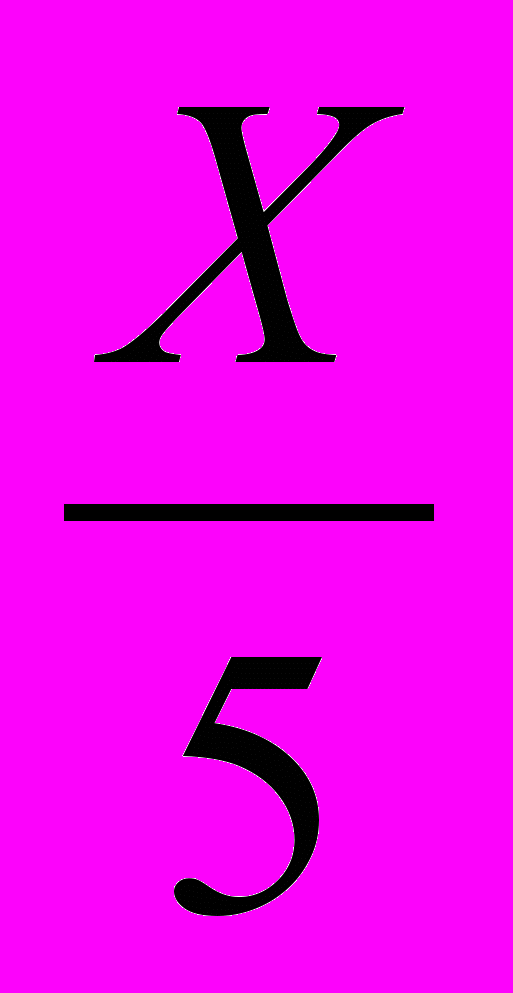; Х = 3 ( дня )


3. Два прямоугольника имеют одинаковую площадь. Длина первого прямоугольника 3,6 м, а ширина 2,4 м. Длина второго прямоугольника 4,8 м. Найдите ширину второго прямоугольника.

( Задача дается на самостоятельное решение, но перед этим устное обсуждение задачи ).


V. Задание на дом


Домашнее задание учащимся предлагается в виде теста, в котором предусмотрены задания для сильных и слабых учеников.


Вариант I

• 1. Укажите верную пропорцию.
  

а) 2 : 3 = 5 : 10; в) 5 : 10 = 8 : 4;

б) 2 : 3 = 10 : 15; г) 12 : 18 = 3 : 2.

• 2. Найдите неизвестный член пропорции
  

7,5 : 3,5 = х : 14.

а) 19,6; б) 3; в) 7; г) 30.

• 3. Три ученика пропололи грядку за 4ч. За сколько часов выполнят
  

работу два ученика?

а) 2 ч 40 мин; б) 8 ч; в) 10 ч; 6 ч.


4. Со 125 гусей можно получить 4 кг пуха. Сколько пуха можно

получить с 875 гусей?

а) 28 кг; б) 57,4 кг; в) 21,8 кг; г) 25 кг.


5. Из 1,75 т золотоносного песка намывают в среднем 0,7 золота. Сколько золота можно намыть из 2170 т золотоносного песка.7

а) 564,5 г; б) 542,5 г; в) 642 г; г) 868 г.


VI. Подведение итогов урока.