Тепловые двигатели и нагнетатели

Вид материала

Документы

Содержание 6. Струйные однофазные насосы 6.15), затрачивается минимальный перепад давлений рабочей среды на работу СН. На основе (6.15) Gc = 11 кг/с. При этом гидравлические потери составляют Dр Кавитационная эрозия Кавитационный режим сопла Кавитационный режим камеры смешения. 7. Струйные аппараты для гидротранспорта зернистых материалов 8. Жидкостно-газовые струйные аппараты Расчет ЖГСА. K — эмпирический коэффициент (для водовоздушного СА равный 0,85); D р

Подобный материал:

• Интегрированный урок «Тепловые двигатели» Цели урока, 28.56kb.
• Выбор рациональных параметров конструкции опор газотурбинных двигателей с межроторными, 218.67kb.
• Пособие по выполнению контрольных работ №1 и №2 Одобрено методической комиссией фбо, 1130.33kb.
• Учебник : С. В. Громов, Н. А. Родина 8 класс, 66.62kb.
• Совершенствование рабочего процесса дизеля с объемно-пленочным смесеобразованием при, 190.09kb.
• Конвертирование рабочего процесса транспортных двс на природный газ и водород 05. 04., 459.6kb.
• Урок по физике. 8 класс Тема: «Тепловые двигатели. Двигатель внутреннего сгорания», 113.91kb.
• Конспект урока физики в 10 классе По теме: «Тепловые двигатели и их роль в жизни человека», 37.82kb.
• Тепловые двигатели. Двигатель внутреннего сгорания, 139.75kb.
• «О структуре естественно-научного факультета», 54.97kb.

6. Струйные однофазные насосы

Уравнение характеристики струйных насосов (СН или СОН, см. рис. 5.1, д), согласно [14], имеет вид

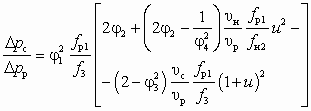, (6.1)

где ; ; ;

; ; ;

.

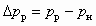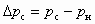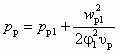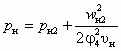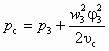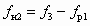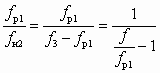Уравнение (6.1) — результат применения теоремы об изменении количества движения для цилиндрической камеры смешения (см. рис. 4.3, б) с использованием коэффициентов j₁, j₂, j₃ и j₄, названных коэффициентами скорости сопла, камеры смешения, диффузора и входного участка камеры смешения (конфузора). Основное допущение при выводе — это неизменность сечения рабочего потока, т. е. f_p1 = f_p2 = idem. Значения коэффициентов j₁, j₂, j₃ и j₄ рекомендуется принимать [14] соответственно 0,95; 0,975; 0,9 и 0,925.

При расчете высоконапорных СН, характеризующихся отношением 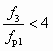, уравнение (6.1) дает завышенную величину 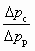в области повышенных значений u. Поэтому расчет таких СН должен проводиться по более точному уравнению (6.2), учитывающему изменение сечения рабочего потока на входном участке камеры смешения ( f_p2  f_p1), вызванное снижением статического давления на этом участке (р₂ = р_р2 = р_н2  р_н):

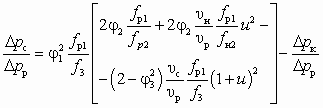, (6.2)

где Dр_к = р_н – р₂ — снижение статического давления на входном участке камеры смешения; р₂ = р_р2 = р_н2 — статическое давление во входном сечении камеры смешения;

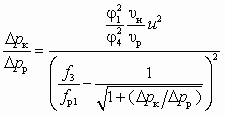; (6.3)

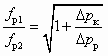; (6.4)

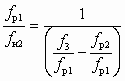. (6.5)

Как следует из анализа соотношений (6.3)–(6.5), отношения сеченийвеличины 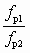и 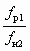являются величинами переменными, зависящими от u. Характер зависимости показан на рис. 6.1.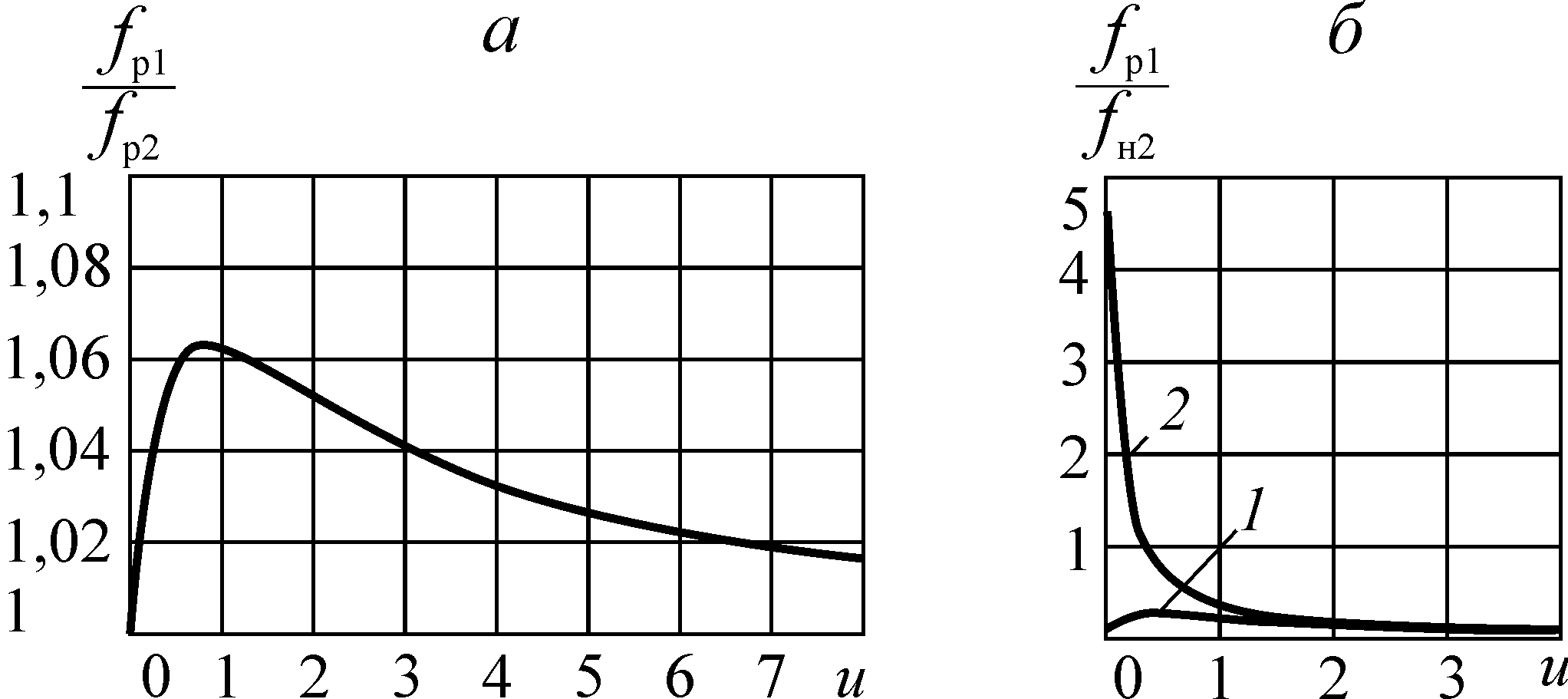



Рис. 6.1. Зависимости (а) и (б) от u:
1 — без учета снижения статического давления;
2 — с учетом снижения статического давления

При расчете характеристики по уравнению (6.3.6.2) следует предварительно для каждого значения u найти любым численным методом , а затем 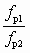и .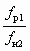

Совершенство струйного насоса (СН) определяется величиной КПД. В применении к СН выражение (5.38) преобразуется к виду:

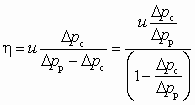. (6.6)

Определение достижимых параметров и оптимального отношения сечений .

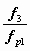При заданных величинах Dр_р и u оптимальное отношение сечений 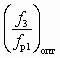соответствует максимальному значению перепада давлений Dр_с, развиваемого СН, и поэтому находится аналогично СА для пневмотранспорта зернистых материалов:

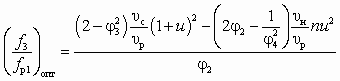, (6.7)

где

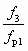
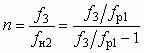. (6.8)

Из совместного решения (6.7)–(6.8) следует зависимость для однозначного определения :

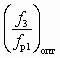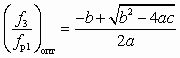, (6.9)

где



При подстановке 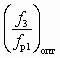в (6.1) находят достижимый перепад давлений D р_с.

Совместное решение (6.7) и (6.1) дает зависимость для непосредственного расчета достижимого относительного перепада давлений СН без необходимости предварительного расчета :

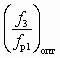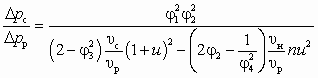. (6.10)

Характер зависимостей достижимых параметров 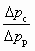, , 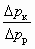h пр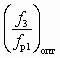и и 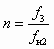для каждого значения u представлен на рис. 6.2, что позволяет осуществить приближенный выбор СН.

Если задан Dр_с, а искомой величиной является достижимый коэффициент инжекции u, то, предварительно определив из совместного решения (6.7) и (6.10)

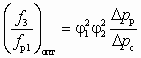, (6.3.6.11)

а также n из (6.8), после преобразований (6.10) нетрудно получить

,

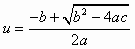где ;

;

.

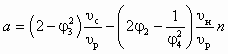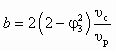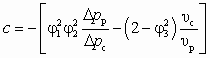На рис. 6.3 показана расчетная кривая достижимых параметров 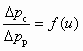, построенная с помощью (6.9) и (6.10). Там же приведены характеристики СН с различным отношением 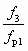. Как видно из рис. 6.3, кривая оптимальных параметров является огибающей семейства характеристик СН с различным отношением 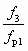и касается этих характеристик в точках, соответствующих оптимальным режимам их работы.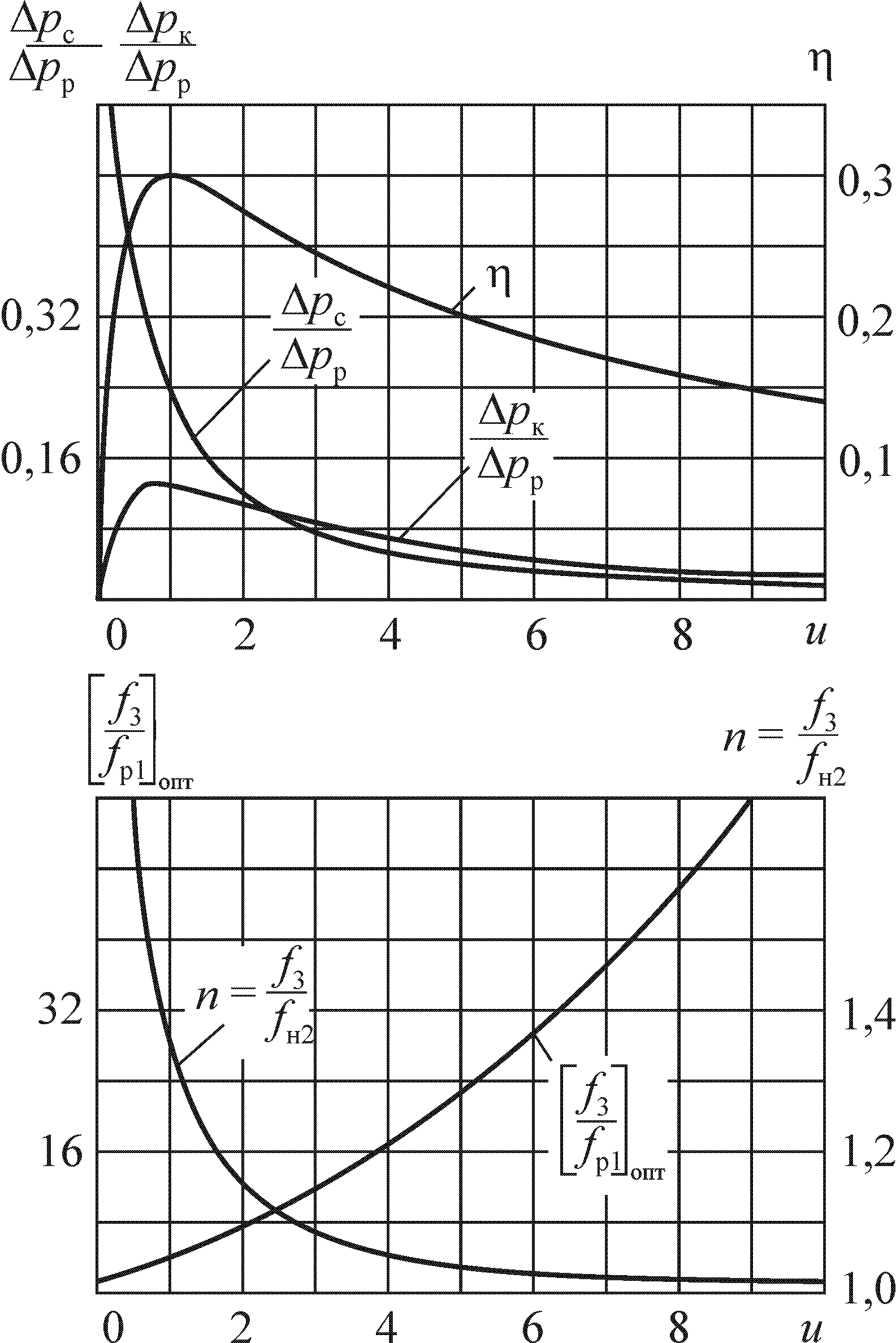



Рис. 6.2.Зависимость , , , n и h от коэффициента инжекции u струйного насоса



Рис. 6.3. Характеристики СН  при различных

Расчет геометрических размеров СН.

Выходное сечение рабочего сопла находят по формуле

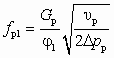. (6.12)

Осевые размеры СН определяются по тем же формулам, что и в случае расчета СА. Однако, согласно [14], опытная константа для водоструйных насосов а = 0,16.

При работе СН на замкнутый контур, например, в качестве смесительного аппарата в узлах присоединения отопительных установок к водяным тепловым сетям, либо диспергатора для приготовления водотопливной эмульсии, или в установках с лопастными насосами (см.рис. 6.4), р_с можно представить в виде:,

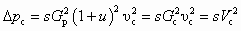, (6.13)

где s — сопротивление системы, в которой струйный насос создает циркуляцию жидкости, Па · с²/м⁶; V_c — объемная подача СН, м³/с.

Совместное решение уравнений (6.7), (6.10), (6.12), и (6.13) или (6.1), (6.12), (6.13) дает

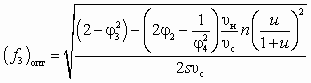; (6.14)

, (6.15)

где .

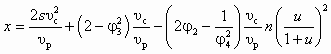На основе этих зависимостей в [14] приведена номограмма для подбора размеров СН конструкции ВТИ—Теплосеть Мосэнерго, широко используемых на практике. Там же приведены конструкция и основные размеры СН.



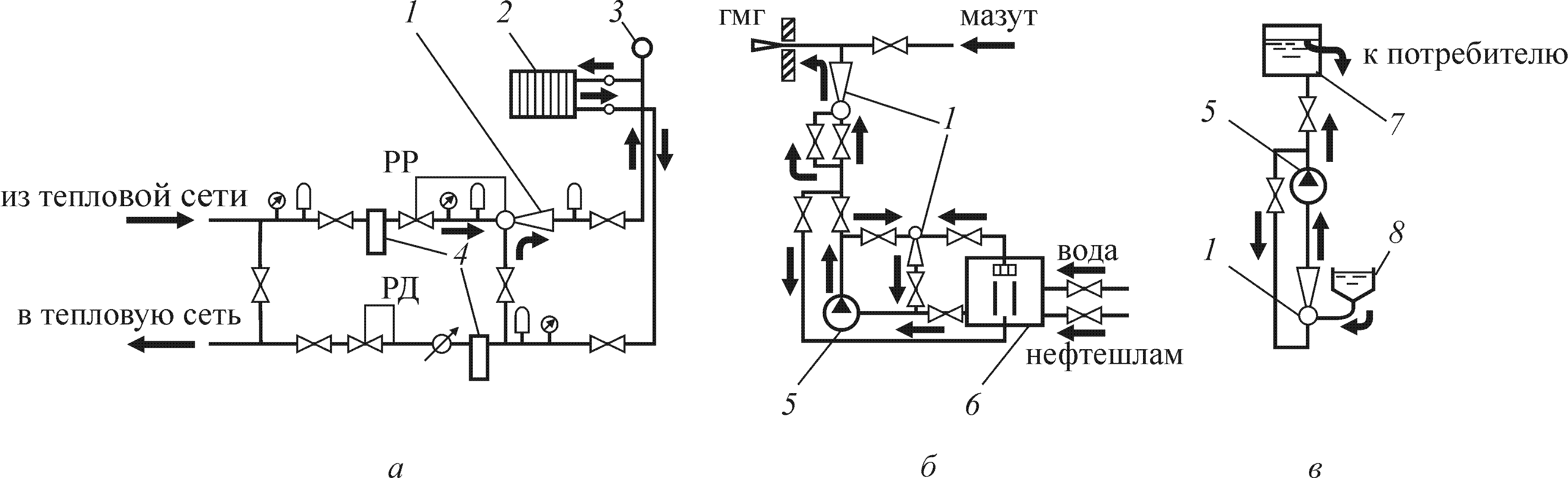
Рис. 6.4.Принципиальные схемы работы СН на замкнутый контур:
а)— присоединение отопительной установки к тепловой сети по зависимой схеме;
б)— система подготовки к утилизации нефтешлама в котельной установке; в) — установка для подъема жидкости с большой глубины
1 — СН; 2 — радиатор; 3 — воздухосборник; 4 — грязевик; 5 — центробежный насос; 6 — емкость для перемешивания;
7 — бак; 8 — источник (резервуар); РР — регулятор расхода; РД — регулятор давления до себя; ГМГ — газомазутная горелка

При установке сопла, рассчитанного по ( 6.15), затрачивается минимальный перепад давлений рабочей среды на работу СН. На основе (6.15) основан производится пересчет диаметра сопла СН, работающего на замкнутый контур. Если СН имеет диаметр сопла d₁ и развивает при этом коэффициент инжекции u, то для получения на этом же насосе при работе на тот же контур другого коэффициента инжекции u¢ необходимо установить новое сопло диаметром :

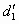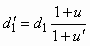. (6.16)

Из совместного решения (6.1), (6.12), (6.13) выводится также формула для расчета ожидаемого коэффициента инжекции

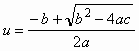, (6.17)

где ; ;

.

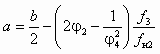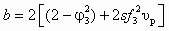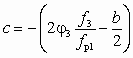Это соотношение оказывается весьма полезным при работе насоса с заданными сечениями камеры смешения f₃ и сопла f_p1 на замкнутую систему с заданным сопротивлением s. Из анализа (6.17) следует, что при уменьшении f_p1 растет абсолютное значение с, а с ним и коэффициент инжекции СН. В реально возможном диапазоне изменения f_p1 отношение 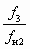практически не меняется,. и на этом Поэтому на основе этой зависимости основано применение СН с регулируемым сечением рабочего сопла для местного количественного регулирования отопительной нагрузки. Уменьшение полезной площади выходного сечения сопла ведет к снижению объемного расхода рабочего потока, однако благодаря увеличению при этом коэффициента инжекции расход циркулирующей жидкости снижается не столь значительно. Коэффициент скорости сопла с регулирующей иглой определяется эмпирической формулой 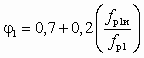, где f_р1и — площадь сечения сопла при введенной в него игле.

Наличие иглы приводит также к увеличению потерь во входном участке камеры смешения, в результате чего рекомендуется, согласно [14], принимать j₄ = 0,9.

Пример 6.1. Подобрать СН для присоединения отопительной установки здания к тепловой сети, определить требующийся перепад давлений в сопле Dр_р, построить характеристику СН Dр_с = f (V_с) и рассмотреть режимы работы отопительной установки при изменении действующего рабочего перепада давлений в сети перед СН, а также при изменении сопротивления отопительной установки (пример заимствован из [14], где при расчете допущены ошибки).

Расчетный массовый расход воды в отопительной установке G_c = 11 кг/с. При этом гидравлические потери составляют Dр_с = 10⁴ Па. Расчетный коэффициент инжекции u = 2,2. Удельные объемы воды u_р = u_н = u_с = 1,03 ∙ 10^–3.

Из (5.23) нетрудно выразить необходимый массовый расход рабочего потока 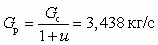. В соответствии с (6.13) сопротивление отопительной установки s = 7,79 · 10⁴ кПа ∙ с²/м⁶.

В результате совместного решения методом итераций (6.14), (6.15) и с учетом (6.8) определим ( f₃)_опт = 2,188∙10^–3 м², (f_p1)_опт = 2,711 ∙ 10^–4 м², n = 1,141 и 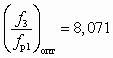и n = 1,141. Тогда, соответственно: d₃ = 0,053 м и d_р1 = 0,0186 м. В этом случае необходимый перепад давлений в сопле найдем из (6.12): .

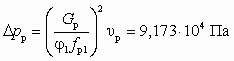Согласно [14], ближайший размер серийного СН: d₃ = 0,047 м, что дает f₃ = 1,735 ∙ 10^–3 м². Тогда в соответствии с (6.8), (6.15) будем иметь f_p1 = 2,672 ∙ 10^–4 м², d_р1 = 0,0184 м, n = 1,182 и 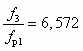. Уменьшение 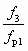по отношению к 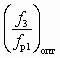вызывает снижение достижимого коэффициента инжекции при одновременном увеличении относительного перепада давлений (см. рис. 6.2 и 6.3). Для обеспечения заданных условий уменьшение диаметра рабочего сопла естественно приводит к увеличению p_p   9,446 10⁴ Па.

На основе (6.1) легко построить характеристику Dр_с = f (V_с) для разных значений Dр_р, а также характеристику отопительной установки Dр_с = sV_с² при двух значениях s (см. рис. 6.5).

Анализ рис. 6.5 достаточно наглядно показывает закономерности и возможности регулирования работы СН на замкнутый контур.



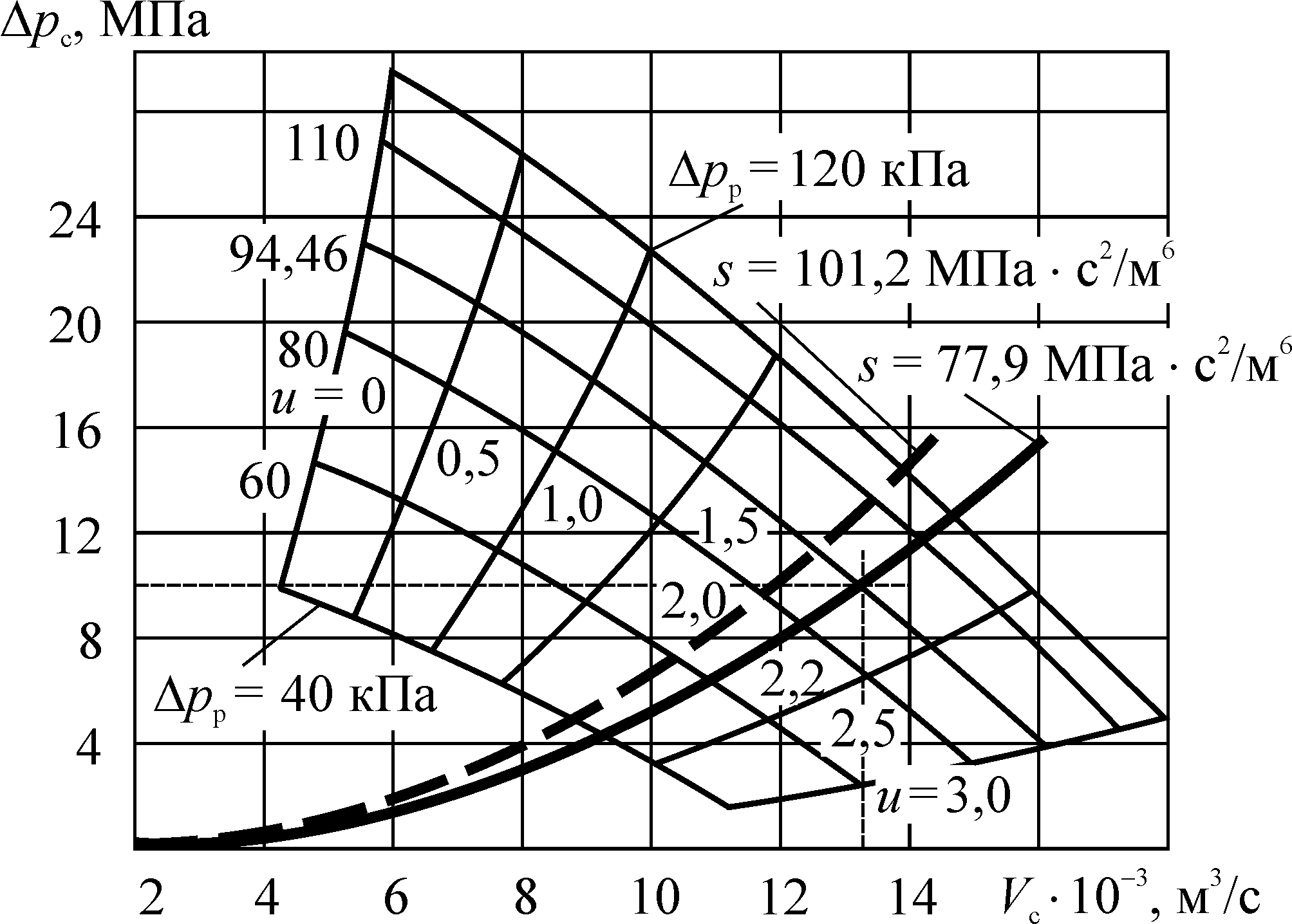
Рис. 6.5. Совмещенные характеристики D р_с  f (V_c) СН и отопительной установки
при различных D р_р и сопротивлении s

Предельные (кавитационные) режимы струйных насосов.

Если статическое давление на каком-либо участке проточной части СН снижается до давления насыщенных паров текущей жидкости, то в ней возникает парообразование (холодное кипение). Образовавшаяся паро-жидкостная смесь при последующем перемещении попадает в область повышенного давления, где происходит быстрая конденсация паров. Жидкость мгновенно заполняет остающиеся полости, вызывая гидравлические удары. Это явление называют кавитацией, а режим работы СН — кавитационным. Возникновение такого режима наиболее вероятно на участках с наиболее высокой температурой и наиболее низким статическим давление. Такими участками в СН являются выходной участок рабочего сопла и входной участок камеры смешения. Для первого из них характерно струйное истечение высоконапорной вскипающей жидкости, для второго — струйное кавитационное течение инжектируемой или смешанной жидкости.

Кавитация в СН сопровождается режимами так называемого предельного расхода среды, характерными тем, что снижение давления за участком кавитации не сопровождается увеличением расхода; при этом внешние возмущения после участка кавитации не передаются через этот участок. Это обстоятельство свидетельствует о том, что скорость среды на участках кавитации равна местной скорости звука.

Кавитационная эрозия проточной части СА рассмотрена в [16].

Кавитационные струйные течения — одно из перспективных направлений ускорения химических реакций, смешения жидкости с жидкостями и газами, получения эмульсий, диспергирования и испарения жидкостей, интенсификации массообменных процессов [32]. Например, в случае использования СН в качестве диспергатора [17] для получения водотопливной эмульсии (ВТЭ) или при подготовке к сжиганию загрязненных вод отмечается благотворное влияние кавитации на качество смешения и качество ВТЭ.

Кавитационный режим сопла. Подобный режим в СН с сужающимся соплом имеет место при истечении однородной «недогретой» или насыщенной рабочей среды с высокой температурой. Задача по определению предельного расхода среды в этом случае является одной из ключевых с точки зрения анализа аварийных ситуаций на атомных электростанциях, в аппаратах химической технологии, нефтепроводах и других установках современной техники [15, 33].

Кавитационный режим сопла реализуется также в случае выполнения сопла в виде трубы Вентури и рассмотрен в [32], где предлагается физико-математическая модель кавитации и процесса эжекции.

Кавитационный режим камеры смешения. Минимальное давление инжектируемого или смешанного потока имеет место во входном сечении 2–2 цилиндрической камеры смешения (см. рис. 4.3, б). Это минимальное давление р₂ = р_н – Δр_к, где Dр_к — падение давления на входном участке камеры смешения, определяемое по (6.3). При давлении р₂, равном давлению насыщенного пара смешанного потока р_нп, проходящего через камеру смешения, в насосе возникает кавитационный режим. Давление р_нп зависит от температуры смешиваемых потоков t_p и t_н и коэффициента инжекции u. При одинаковых теплоемкостях взаимодействующих сред (с_р = с_н = с_с) температура смешанного потока

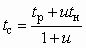. (6.18)

Принимая р₂ = р_нп, из (6.3) нетрудно получить зависимость для расчета кавитационного коэффициента инжекции u_к в виде

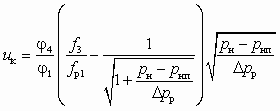. (6.19)

Как видно из (6.19), u_к растет с увеличением 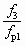и р_н, а также при снижении р_нп и Dр_р.

При заданных температурах рабочего и инжектируемого потоков и одинаковых теплоемкостях взаимодействующих сред каждой температуре смешанного потока t_c согласно (6.18) соответствует коэффициент инжекции .

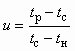Кавитация в насосе наступает при u ³  u_к. Если t_p = t_н = t_c, давление насыщенного пара р_нп = f(t_c) — величина постоянная.

Пример 6.2. Основной геометрический параметр струйного насоса 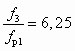. Параметры рабочей воды: р_р  1100 кПа; t_р  150 °C; u_р = 0,0011 м³/кг, ; р_нп  476,2 кПа. Параметры инжектируемой воды: р_н = 500 кПа; t_н = 130 °C; u_н  0,00107 м³/кг. Проверить возможность возникновения кавитационного режима и построить характеристику Dр_с = f (u) (пример заимствован из [14]).

С целью проверки возможности возникновения кавитационного режима на входном участке камеры смешения зададимся рядом значений коэффициента инжекции u. Для каждого из них по (6.18) найдем среднюю температуру смешанного потока t_c и соответствующее ей давление насыщенного пара р_нп. Далее по найденным р_нп и заданным р_р, р_н и 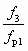найдем по формуле (6.19) кавитационные коэффициенты u_к. Кавитационный режим на входном участке камеры смешения возникает при u = u_к.

Результаты расчета приведены в таблице и представлены графически на рис. 6.6.

u	tc	pн, кПа	uк
0	150,0	476,2	1,023
0,5	143,3	396,7	2,152
1,0	140,0	361,1	2,505
2,0	136,7	328,2	2,758
3,0	135,0	312,7	2,925
4,0	134,0	303,7	2,998

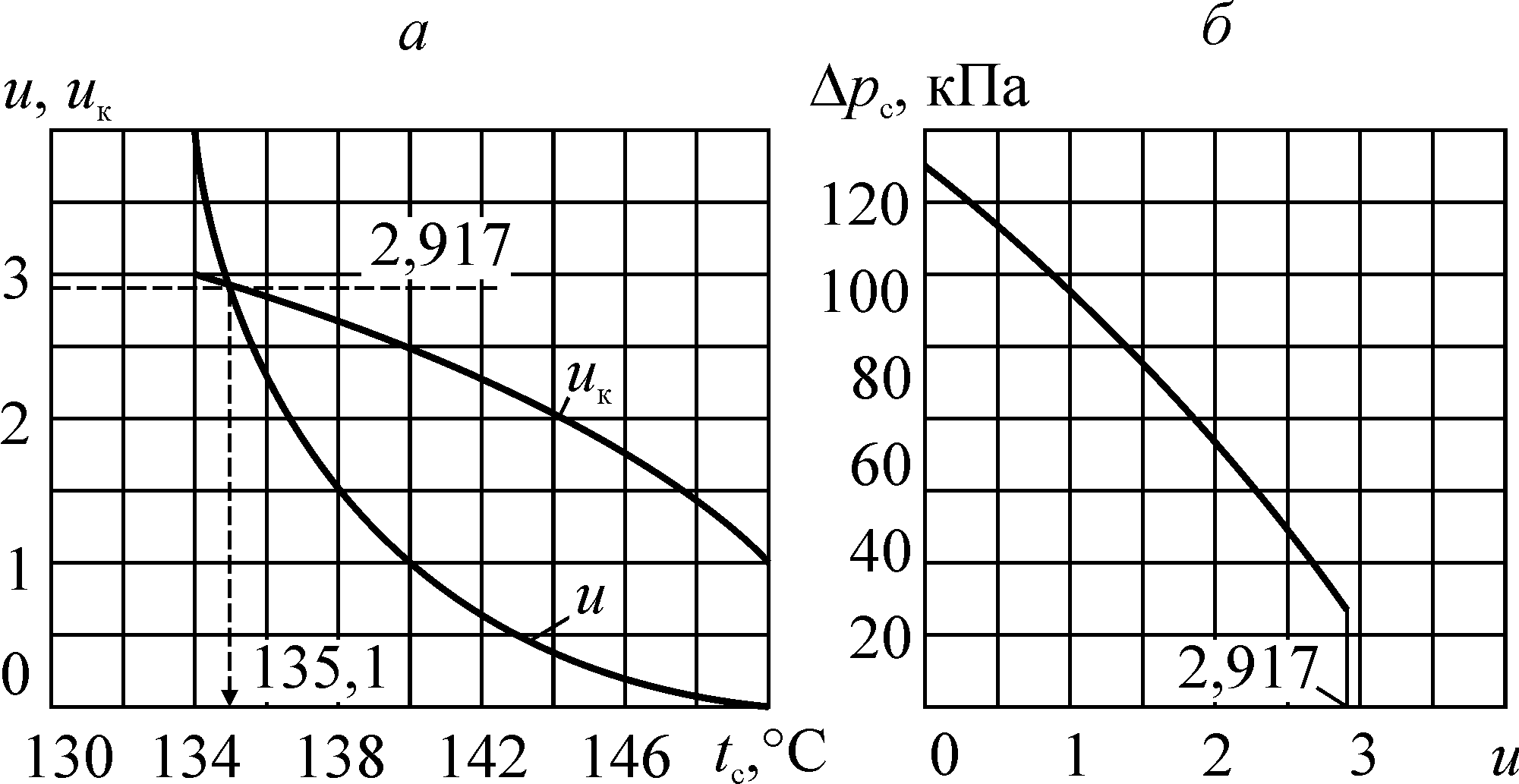
Рис. 6.6. К расчету кавитационного режима камеры смешения:
а) определение кавитационного коэффициента инжекции u, u_к = f (t_c);
б) характеристика струйного насоса

Как видно из графика (рис 6.6, а), кавитационный режим во входном сечении камеры смешения возникает при t_c = 135,1 °С, когда u = u_к = 2,917. Характеристика СН (рис. 6.6, б) построена по (6.1). При u = 2,917 в насосе возникает кавитационный режим. Снижение создаваемого перепада давлений Dр_с не приводит к увеличению коэффициента инжекции.

7. Струйные аппараты для гидротранспорта зернистых материалов

В струйных аппаратах в качестве рабочей среды используется обычно вода, поступающая с большой скоростью из сопла в приемную камеру. Инжектируемой средой является твердое тело (песок, шлак и др.) или смесь воды и твердого тела. Если допустить равномерность распределения твердой фазы в движущемся потоке жидкости и отсутствие относительной скорости между фазами, то можно воспользоваться соотношениями (5.49) и (5.52), в которых целесообразно заменить u_г на .

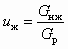Основным уравнением для расчета СА для гидротранспорта зернистых материалов является уравнение характеристики СН (6.1), которое с учетом (5.48), (5.50)–(5.51) преобразуется к виду:

, (7.1)

где ; .

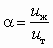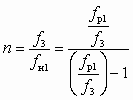Обычно в струйных аппаратах для гидротранспорта зернистых материалов удельные объемы рабочей, инжектируемой и смешанной жидкостей одинаковы, т. е. u_р = u_нж = u_сж.

В предварительных расчетах струйных аппаратов для гидротранспорта задаются теми же значениями коэффициентов скорости, что и в случае пневмотранспорта. Затем указанные коэффициенты должны быть скорректированы на основе испытания аппаратов в лабораторных или промышленных условиях.

При заданных значениях Dр_р = р_р – р_н и коэффициенте инжекции u оптимальное отношение сечений 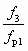СН находится из совместного решения уравнений (6.7) и (6.8) или непосредственно из (6.9). Применительно к СА для гидротранспорта уравнение (6.7) записывается в виде

,  (7.2)

а коэффициенты a, b и c в уравнении (6.9) имеют вид:



Если задан перепад давлений Dр_с, развиваемый СА, а искомой величиной является достижимый коэффициент инжекциии аппарата, то, предварительно определив 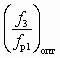и n на основе (6.11) и (6.8), после преобразований (6.10) нетрудно получить

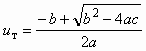, (7.3)

где ;

; .

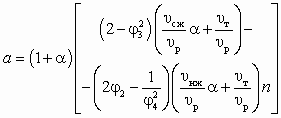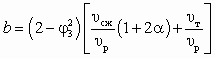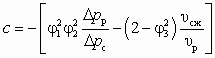Выходное сечение рабочего сопла определяется по (6.12).

Для расчета осевых размеров СА для гидротранспорта могут быть использованы формулы (5.27)–(5.30).

Пример 7.1.. Рассчитать СА для гидротранспорта песка. Производительность аппарата по песку G_т = 30 кг/с. Аппарат должен развивать избыточное давление D р_с = р_с – р_н = 1× 10⁵ Па. Инжектируемой средой является смесь песка и воды 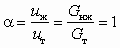. Давление инжектируемой среды р_н = 1 × 10⁵ Па. Располагаемое избыточное давление рабочей воды Dр_р = р_р – р_н = 1 × 10⁶ Па; 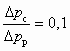. Удельный объем воды u_нж = u_сж = u_р = 1·10^–3 м³/кг. Удельный объем песка u_т = 5·10^–4 м³/кг. Коэффициенты j₁ = 0,95; j₂ = 0,875; j₃ = 0,81; j₄ = 0,83 (пример заимствован из [14]).

Согласно (6.11) и (6.8), найдем 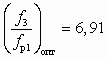и n = 0,145.

Достижимый коэффициент инжекции по твердому телу u_т определим по (7.3): а   2,985; b   4,704; c   5,566; u_т   0,789.

Задаваясь рядом значений u_т, построим рабочую характеристику СА (см. рис. 7.1).



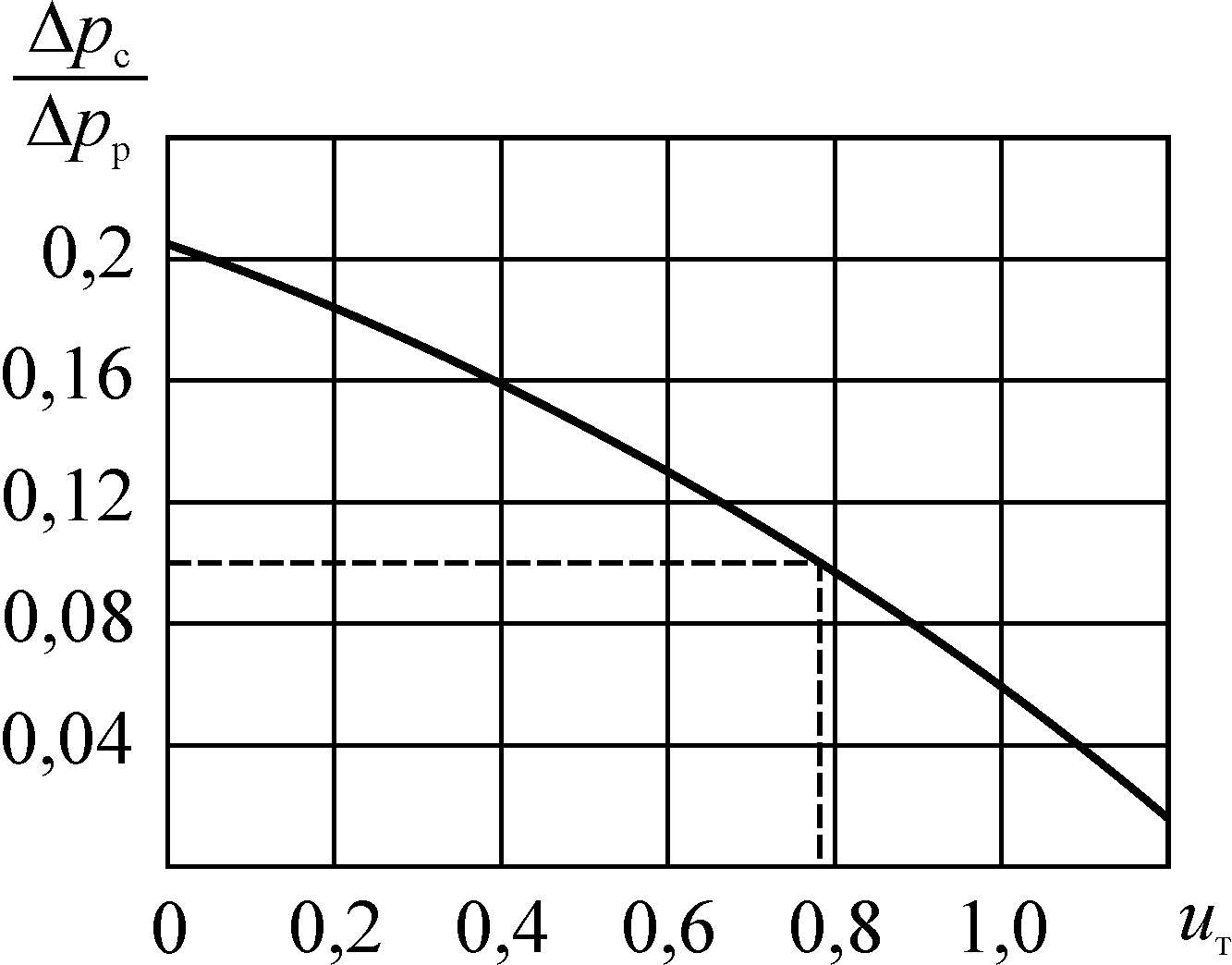
Рис. 7.1. Рабочая характеристика 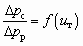D р_с/D р_р = f(u_т) струйного аппарата для гидротранспорта песка: 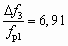f₃/f_p1 = 6,91; a = 1

Для расчетного режима определим основные сечения аппарата. Согласно формуле (6.12) и с учетом равенства 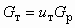имеем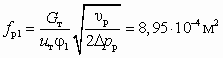

,

 .

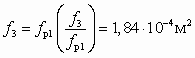Соответствующие диаметры рабочего сопла и камеры смешения равны: d_p1 »  34 мм; d₃ »  89 мм.

8. Жидкостно-газовые струйные аппараты

В таких аппаратах рабочий (жидкость) и пассивный (газ) потоки находятся в разных агрегатных состояниях, почти не изменяющихся в процессе смешения. В силу большой разницы плотностей взаимодействующих сред массовый коэффициент инжекции имеет величину порядка 10^–5, а объемный коэффициент инжекции 0,2–3,0.

В зависимости от типа струи различают жидкостно-газовые аппараты с компактной и с диспергированной струей. В зависимости от соотношения температур рабочей и пассивной сред рассматриваемые аппараты разделяют также на две группы: термодинамическую, в которой смешиваемые потоки имеют существенно разные температуры, и изотермическую, когда разница температур незначительна и ею можно пренебречь при расчете гидравлических процессов эжектирования.

В большинстве случаев аппараты с компактной струей относятся к изотермической группе. Наряду с традиционной формой проточной части (рис. 4.1, а) применяются ЖГСА, в которых рабочая жидкость подается в камеру смешения через несколько рабочих сопел или одно сопло (многоструйное, рис. 4.1, г) с несколькими отверстиями (многоструйное сопло). Увеличение поверхности контакта фаз взаимодействующих сред приводит к увеличению коэффициента инжекции при прочих равных условиях. Эффективность ЖГСА возрастает также в случае увеличения длины камеры смешения до 40–50 вместо 8–10 калибров для однофазных СА. Это связано с тем, что образование однородной газо-жидкостной эмульсии требует большей длины пути перемешивания, чем выравнивание профиля скорости однофазного потока. В этом случае отпадает необходимость в диффузоре.

ЖГСА с диспергированной струей в качестве рабочего сопла используют различные распылители жидкости (форсунки). Эти аппараты нашли широкое применение в химической, микробиологической, пищевой промышленности, системах очистки воды [34–36].

Расчет ЖГСА. Существующие методики расчета ЖГСА (все они разработаны для водовоздушных эжекторов, применяемых в основном в энергетике как вакуумные струйные насосы) являются эмпирическими, справедливыми в достаточно узком диапазоне режимных и конструктивных параметров. Анализ этих методик выполнен в [18].

Течение в камере смешения представляется следующим образом. Струя жидкости поступает в камеру смешения, сохраняя свою первоначальную цилиндрическую форму. Примерно на расстоянии 2 – 3 калибров d₃ от начала камера смешения оказывается заполненной молочно-белой водовоздушной эмульсией (пеной), причем у стенок камеры смешения наблюдаются обратные токи водовоздушной эмульсии, которая снова захватывается струей и увлекается ею. Это возвратное движение обусловлено повышением давления по длине камеры смешения. Давление р_н в начале камеры смешения равно давлению в приемной камере. При низких противодавлениях повышение давления в цилиндрической камере смешения сравнительно невелико. Основное повышение давления происходит в диффузоре. При увеличении противодавления эта картина изменяется: степень повышение повышения давления в диффузоре уменьшается, а в камере смешения — резко увеличивается, причем оно это происходит на сравнительно небольшом участке камеры смешения скачкообразно. Чем меньше отношение 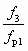, тем более резко выражен скачок давления. Место скачка хорошо различимо, т. к. после него движется уже не молочно-белая эмульсия, а прозрачная вода с пузырьками воздуха.

Чем больше отношение 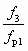, тем более развиты обратные токи водовоздушной эмульсии. С увеличением противодавления скачок давления перемещается против течения струи и, наконец, при определенном противодавлении (р_с)_max достигает начала камеры смешения. При этом эжекция воздуха водой прекращается, вся камера смешения заполнена прозрачной водой без пузырьков воздуха. Аналогичные явления имеют место, если при неизменном противодавлении снижается давление рабочей воды перед соплом.

Согласно [14], отношение объемных расходов инжектируемой и рабочей сред сохраняется достаточно стабильным при изменении в широких пределах параметров его работы (p_p, p_н, р_с и G_р). Поэтому, в отличие от рассмотренных выше СА, в ряде методик расчета используются объемные коэффициенты инжекции (подсоса) по паровоздушной смеси и сухому воздуху:

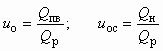, (8.1)

где Q_пв, Q_н и Q_р — объемные расходы соответственно инжектируемой (паровоздушной), воздушной и рабочей (жидкостной) сред, м³/с.

В камере смешения происходит насыщение воздуха парами воды. Температура пара в эмульсии практически равна температуре воды T_p. Поэтому газовая фаза эмульсии представляет собой насыщенную паровоздушную смесь, полное давление которой в начале камеры смешения равно давлению инжектируемого сухого воздуха в приемной камере р_н. Парциальное давление воздуха р_в в смеси меньше этого давления на давление насыщенного пара р_нп при температуре рабочей жидкости T_p, т. е. р_в = р_н – р_нп.

Поскольку сжимаемый в СА воздух входит в состав паровоздушной смеси, то Q_пв в (8.1) представляет собой объемный расход паровоздушной смеси. Воспользовавшись законом Дальтона и уравнением Менделеева — Клайперона, нетрудно выразить массовый расход инжектируемого сухого воздуха в виде

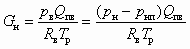. (8.2)

Тот же расход ,можно выраженныйзить через параметры инжектируемого сухого воздуха:

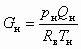, (8.3)

где Q_н, T_н — объемный расход и абсолютная температура сухого воздуха на всасывании.

Из этих уравнений нетрудно установить взаимосвязь между u_o и u_oс

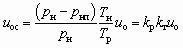, (8.4)

где 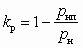; k_т = T_н/T_p.

В случае р_н   р_нп и T_н » T_р имеем u_oс » u_o.

При G_н = 0 (u_oс = 0) р_н = р_нп, т. е. давление всасывания равно давлению насыщенного пара при температуре рабочей воды T_р. Несмотря на равенство u_oс = 0 u_o  0, т. к. в приемной камере эжектора происходит вскипание рабочей воды и выделившийся пар отсасывается этой же рабочей водой.

Для расчета ЖГСА с компактной струей и короткой цилиндрической камерой смешения (длиной около 10 калибров) можно воспользоваться формулами для СН.

Если предположить одинаковые удельные объемы рабочей и сжатой сред, скорость эжектируемой среды равной нулю, то после замены массового коэффициента инжекции u объемным u_o будем иметь следующие уравнения, определяющие:

- достижимый объемный коэффициент инжекции

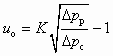, (8.5)

где K — эмпирический коэффициент (для водовоздушного СА равный 0,85); D р_р = р_р – р_н — располагаемый перепад давления рабочей воды; Δр_с = р_с – р_н — перепад давления, создаваемый эжектором;

- отношение

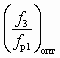
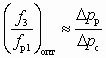; (6.3.8.6)

- характеристику ЖГСА, аналогичную СН (см. уравнение (6.1) при условии р₂ = р_н, чему отвечает f_н2 = ¥   и, соответственно, ))

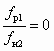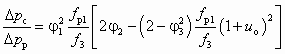. (8.7)

Уравнение (8.7) может быть представлено в следующей модификации

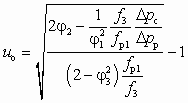, (8.8)

которой удобно пользоваться для определения объемного коэффициента инжекции ЖГСА по заданным отношениям сечений 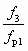и перепадов давлений .

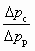Из уравнения (8.8) следует, что для аппарата данных размеров 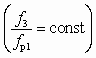в области глубокого вакуума, когда при постоянных значениях р_р и р_с существенные изменения р_н практически не меняют отношения 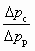, объемный коэффициент инжекции остается постоянным. Поскольку при этом расход рабочей воды практически не меняется, то и объемный расход паровоздушной смеси также остается постоянным.

Наряду с изложенной предлагаются и другие методики расчета ЖГСА с короткой камерой смешения, приведенные в [15, 18].

В [14] содержится информация для расчета ЖГСА с удлиненной цилиндрической камерой смешения, а также многоструйного ЖГСА.

Методы расчета ЖГСА с диспергированной струей, как и других типов гидроструйных аппаратов, основываются также на эмпирических или полуэмпирических моделях. Законченной теории расчета в настоящее время нет.

Несмотря на большую работу по исследованию СА, эффективность ЖГСА осталась на уровне, достигнутом в 1920-е годыг., что объясняется сложностью внутренних процессов в ЖГСА и их недостаточной изученностью. Поэтому весьма важной задачей является дальнейшее изучение механизма рабочего процесса ЖГСА с целью разработки более строгой методики расчета.

Очевидно, что эмпирический подход к решению этой задачи малоперспективен.

Полуэмпирический подход, включающий в себя ту или иную физико-математическая математическую модель с разной степенью приближения к реальному физическому процессу, которая затем коррелируется эмпирическими данными, более перспективен.

В этой связи отметим работу [37], в которой Достаточно успешно в рамках теории взаимопроникающих континуумов осуществлено моделирование гидродинамики в ЖГСА с диспергированными и компактными струями в [37].