Тепловые двигатели и нагнетатели

Вид материала

Документы

Содержание 5. Струйные аппараты для пневмотранспорта зернистых материалов и жидкости 1— СА с центральным соплом; 2 П(l) — относительное давление, т. е. отношение давления р Таблица 5.1 Взаимосвязь основных газодинамических функций для упругой и неупругой сред Расчет СА с большой степенью расширения (рр / рн ³ 1/П*) и умеренной степенью сжатия Расчет поля рабочих характеристик СА. Расчет СА с малой степенью сжатия (р Расчет СА для пневмотранспорта зернистых материалов. Газодинамические функции 5.5 представлены рабочие характеристики СА. Из приведенных данных видно, что (рис. 5.5, а)

Подобный материал:

• Интегрированный урок «Тепловые двигатели» Цели урока, 28.56kb.
• Выбор рациональных параметров конструкции опор газотурбинных двигателей с межроторными, 218.67kb.
• Пособие по выполнению контрольных работ №1 и №2 Одобрено методической комиссией фбо, 1130.33kb.
• Учебник : С. В. Громов, Н. А. Родина 8 класс, 66.62kb.
• Совершенствование рабочего процесса дизеля с объемно-пленочным смесеобразованием при, 190.09kb.
• Конвертирование рабочего процесса транспортных двс на природный газ и водород 05. 04., 459.6kb.
• Урок по физике. 8 класс Тема: «Тепловые двигатели. Двигатель внутреннего сгорания», 113.91kb.
• Конспект урока физики в 10 классе По теме: «Тепловые двигатели и их роль в жизни человека», 37.82kb.
• Тепловые двигатели. Двигатель внутреннего сгорания, 139.75kb.
• «О структуре естественно-научного факультета», 54.97kb.

5. Струйные аппараты для пневмотранспорта зернистых материалов и жидкости

В зависимости от принципа действия пневмотранспортной установки (ПУ) СА устанавливается в начале, в конце, а в некоторых случаях и в середине пневмотрассы [14, 25, 30]. В установках нагнетательного действия возможны различные варианты применения эжектора (см. рис. 5.1).

Так, например, СА, изображенные на рис. 5.1, а и 5.1, б представляют собой устройства, обеспечивающие необходимые параметры пневмотранспортного потока а именно, — давление и расход газа. Причем в обоих случаях возможен подсос атмосферного воздуха. Из рис. 5.1, б следует, что применение эжектора с кольцевым соплом весьма актуально в ПУ всасывающе-нагнетательного действия, причем крупность материала не имеет принципиального значения. На рис. 5.1, в СА играет роль тягового эжектора. В этом качестве СА широко используется при разработке различных пневмонасосов [25], а также при проектировании всасывающих сопел (см. п. 2 и рис. 3.2).



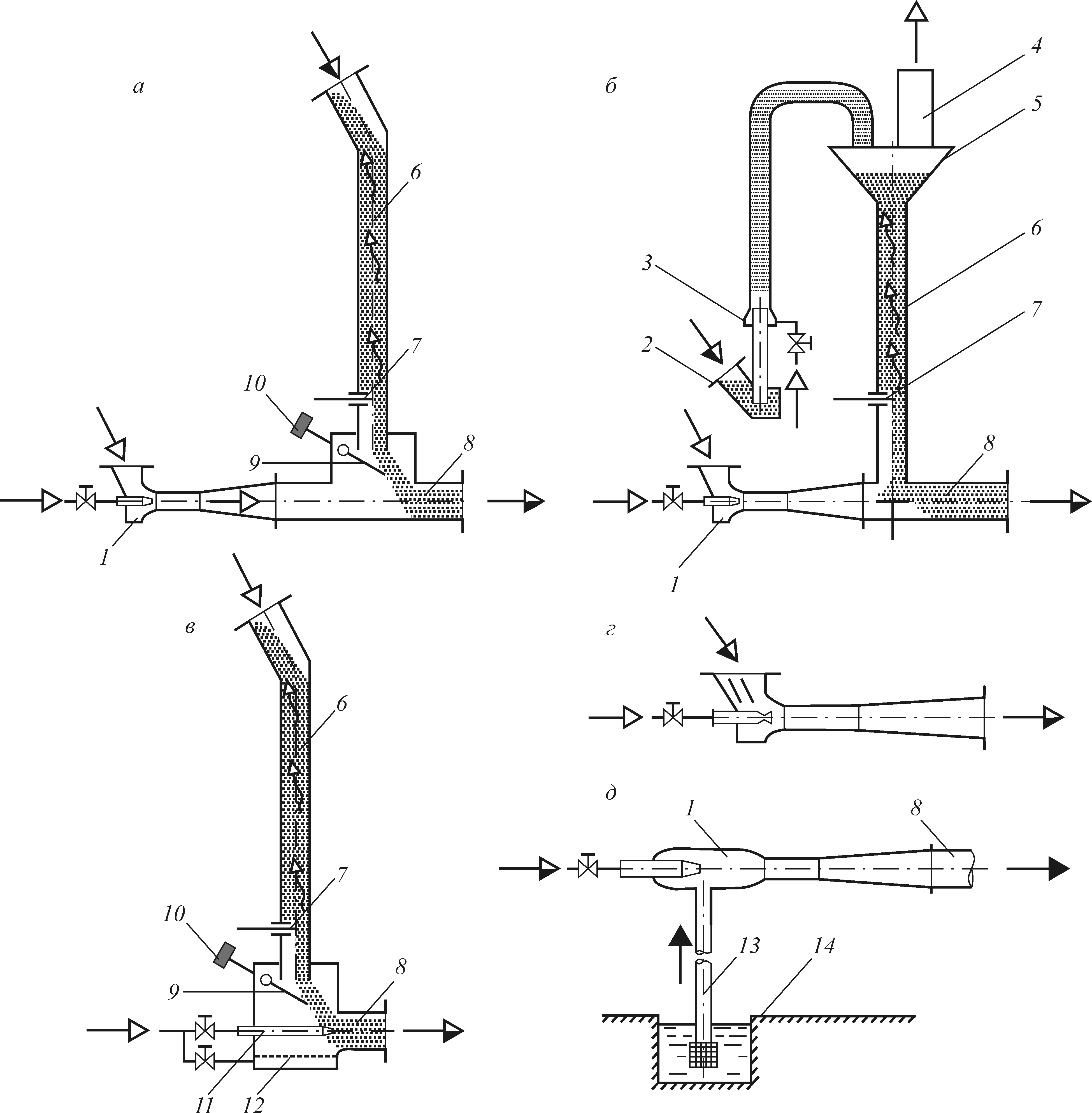
Рис. 5.1. Применение СА для пневмотранспорта зернистых материалов (а, б, в, г) и жидкости (д):
а) в ПУ нагнетательного действия; б) в ПУ всасывающе-нагнетательного действия;
в),г),д) в качестве тягового эжектора, питателя и струйного однофазного насоса соответственно;
1— СА с центральным соплом; 2 — загрузочное устройство; 3 — СА с кольцевым соплом; 4 — фильтр;
5 — промежуточная емкость; 6 — шахта; 7 — задвижка; 8 — транспортный трубопровод; 9 — обратный клапан;
10 — противовес; 11 — сопло; 12 — пористое днище; 13 — всасывающий трубопровод; 14 — колодец

СА, изображенные на рис. 5.1, а и 5.1, б, следует отнести к аппаратам с большой степенью расширения (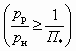) и достаточно высокой степенью сжатия (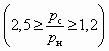), т. е. рабочая и инжектируемая среды являются упругими. В СА, изображенных на рис. 5.1, г и 5.1, д, в качестве рабочей среды также используется упругая среда — газ, а инжектируемой средой является неупругая среда — сыпучее твердое тело или жидкость. Степень расширения рабочего потока может быть как сверхкритической (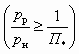), так и докритической ( 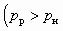и одновременно 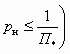). Степень сжатия, напротив, мала (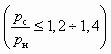), т. к. инжектируемая среда представляет собой смесь сыпучего твердого материала и газа (чаще воздуха) или жидкости.

СА на рис. 5.1, г представляет собой питатель, в который материал, подлежащий транспортировке, подается непосредственно в приемную камеру, а далее увлекается струей воздуха, выходящей с большой скоростью из рабочего сопла. Общее сопротивление ПУ не должно превышать (0,2÷0,4) · 10⁵ Па.

СА, принципиальная схема которого представлена на рис. 5.1, д, применяется для перекачки жидкости из резервуаров и колодцев и других целей.

Поскольку уравнения, характеризующие состояние упругой (1) и неупругой (2) сред, имеют вид

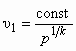и 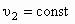, (5.1)

то, очевидно, условию неупругости (несжимаемости) соответствует показатель адиабаты k.

При расчете любого СА широко используются газодинамические функции, связывающие термодинамические параметры потока (температуру, давление, плотность и др.) с его приведенной скоростью l , представляющей собой отношение скорости газа при его адиабатном течении w к критической скорости а_*: т. е.

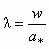. (5.2)

Поскольку для упругой среды

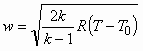, (5.3)

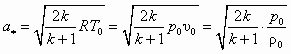, (5.4)

то

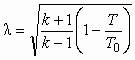. (5.5)

может изменяться от 0 до 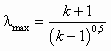при Т = 0, т. е. при истечении потока в абсолютный вакуум.

В свою очередь, Для условно несжимаемой среды будем иметь

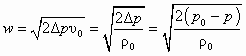, (5.6)

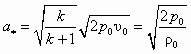, (5.7)

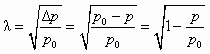. (5.8)

По смыслу выражения (5.7) критическая скорость неупругой среды равна скорости истечения этой среды в абсолютный вакуум, когда внешнее давление р = 0.

Наиболее часто используются следующие функции:

- функция П(l) — относительное давление, т. е. отношение давления р адиабатно движущегося газа в данном сечении к давлению торможения р₀;

- функция e(l) — относительная плотность, т. е. отношение плотности ρ адиабатно движущегося потока в данном сечении к его плотности ρ₀ в заторможенном состоянии;

- функция q(l) — относительная массовая скорость, т. е. отношение массовой скорости r w адиабатно движущегося потока в данном сечении к массовой скорости этого потока r _*а_* в критическом сечении, определяемая как

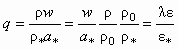. (5.9)

Взаимосвязь основных газодинамических функций для упругой и неупругой сред приведена в табл. 5.1.

Исходные данные для расчета:

- G_н (G_р или G_с) — расход газа в инжектируемом (рабочем или смешанном) потоке, кг/с или u;

- p_p p_н (p_н или р_с) — статические давления рабочего, (инжектируемого или (смешанного) потоков, Па;

- T_p, T_н — температуры рабочего и инжектируемого потоков, К;

- r _р (r _н (или r _с) — плотности рабочего, (инжектируемого (или смешанного) потоков, кг/м³;

- k_p = k_н = k — показатель адиабаты;

- R_р = R_н = R — газовая постоянная, Дж/(кг · К);

Основные задачи расчета СА:

1. Определение максимально достижимого коэффициента инжекции или максимально достижимого давления сжатия при заданных параметрах рабочего (от компрессора) (р_р, Т_р) и инжектируемого (р_н, Т_н) потоков перед СА и заданном либо давлении сжатия р_с, либо коэффициенте инжекции u;

2. Определение геометрических размеров СА;

3. Расчет поля рабочих характеристик СА.

Решение первой задачи существенно зависит от степени расширения и сжатия, что связано с возникновением так называемого предельного режима работы. В наибольшей мере это относится к СА с большой степенью расширения 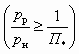и умеренной степенью сжатия 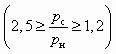. К таким аппаратам относятся, согласно [5], газо (паро)-струйные компрессоры.

Таблица 5.1

Взаимосвязь основных газодинамических функций для упругой и неупругой сред

Функция	Основные соотношения		Значения газодинамических функций
			 = 0	 =1,0	 =  max
λ	λ		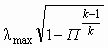0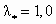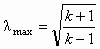
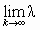	λ		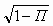0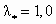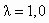
П		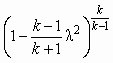П	1,0		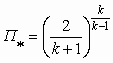0
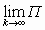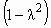		П	1,0	0	0
ε		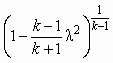	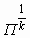1,0		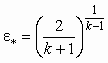0
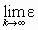	1	1	1,0		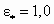1,0
q		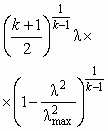	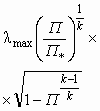0		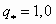0
	λ		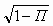0		1,0

Решение первой задачи существенно зависит от степени расширения и сжатия, что связано с возникновением так называемого предельного режима работы. В наибольшей мере это относится к СА с большой степенью расширения 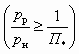и умеренной степенью сжатия 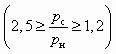. К таким аппаратам относятся, согласно [5], газо- и пароструйные компрессоры.


Расчет СА с большой степенью расширения (р_р / р_н ³ 1/П_*) и умеренной степенью сжатия

(21,52 £ р_с / р_н £  12,25). Критические скорости рабочего и инжектируемого потоков a_р* и a_н*, равные местной скорости звука, находят из выражения (5.6). Далее по величине относительного давления П_рн = р_н / р_р, воспользовавшись соотношениями, приведенными в табл. 5.1, находят параметры рабочего потока на входе в камеру смешения — l_рн и q_рн.

Поскольку максимально достигаемый коэффициент инжекции u зависит от параметров потоков в сечениях 2–2 и 3–3 камеры смешения (см. рис. 4.3), то решение задачи, связанной с его определением, возможно лишь методом перебора целого ряда значений l_с3 в выходном сечении 3–3 камеры смешения (см. рис. 4.3). Интервал возможных значений l_с3 ограничивается рядом условий, приведенных ниже.

Прежде всего, этот интервал находится в области l_с3 £  1, т. к. скорость смешанного потока не может быть больше критической. Скорость инжектируемого потока должна соответствовать аналогичному требованию в любом сечении s–s цилиндрической камеры смешения, т. е. l_нs  1. Поэтому реальный интерес имеют лишь те значения l_с3, при которых это условие выполняется. Если l_нs = 1 и q_нs = 1, то в аппарате как уже отмечалось выше, возникает второй предельный режим, характеризующийся максимально возможным коэффициентом инжекции:

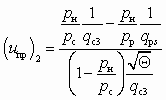, (5.10)

где 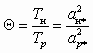. В этом случае

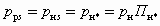, (5.11)

а величина q_c3 должна отвечать условию

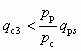. (5.12)

В противном случае работа СА невозможна. Параметры рабочего потока в этом сечении (l_рs и q_рs) находят также по величине относительного давления П_ps, для которой с учетом (5.11) можно записать

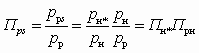, (5.13)

где П_н* = П_*.

Расчет достижимого коэффициента инжекции для ряда значений l_с3 осуществляется методом последовательных приближений по следующей схеме.

Задаваемая величина l_с3 однозначно определяет остальные газодинамические функции П_с3 и q_с3, характеризующие смешанный поток (см. табл. 5.1). Невыполнение условия (5.12) означает переход к следующему более низкому значению l_с3. В противном случае находят (u_пр)₂, воспользовавшись формулой (6.3.5.10). Этот параметр определяет взаимосвязь между газодинамическими функциями смешанного потока в сечении 3 – 3 (см. рис. 4.3) и аналогичными функциями инжектируемого потока в некотором сечении s – s, где l_нs = 1 и q_нs = 1. Принимая эту величину в качестве предварительного значения u' = (u_пр)₂, можно найти приведенную массовую скорость q_н2 инжектируемого потока на входе в камеру смешения из выражения

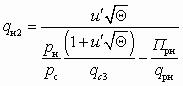. (5.14)

Воспользовавшись зависимостью q(l) (см. табл.  5.1), можно записать

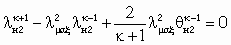. (5.15)

Разрешая уравнение (5.15) любым численным методом, следует иметь в виду неравенство l_н2  1, т. к. q неоднозначным образом определяет l. Зная l_н2, нетрудно найти П_н2. Далее, воспользовавшись методом итераций, находят уточненное значение u. При этом расчеты проводятся в следующей последовательности:

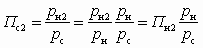; (5.16)

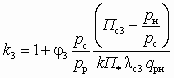; (5.17)

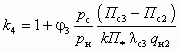; (5.18)

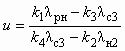, (5.19)

где k₁ = j₁j₂j₃; k₂ = j₂j₃j₄. В свою очередь j₁; j₂; j₃; j₄ — эмпирические коэффициенты, численные значения которых рекомендуется принимать соответственно 0,95; 0,975; 0,9 и 0,925. При этом k₁ = 0,834; k₂ =  0,812.

Если полученное значение u  (u_пр)₂, то окончательно принимают u = (u_пр)₂. Если u  (u_пр)₂, то задаются u' = u и по формулам (5.14)–(5.19) продолжают вычисления до тех пор, пока не будет достигнуто |u' – u| £ 10^–3.

Аналогичные расчеты проводятся и для других значений λ_с3. Затем из полученных данных осуществляется выбор оптимальных параметров l_н2, q_н2, l_с3 и q_с3, при которых u = u_max.

Таким же образом решается задача по определению достижимой степени сжатия в случае, когда задан коэффициент инжекции u, только вместо (u_пр)₂ находят :

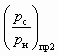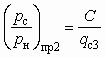, (5.20)

где

. (5.21)

Величина 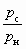определяется соотношением:

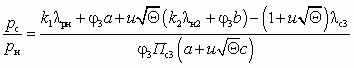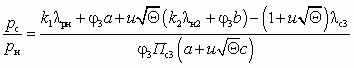., (5.22)

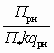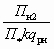где a = , b = , c = .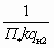

Принимая предварительно искомое значение (р_с / р_н)′ = (р_с / р_н)_пр2, находят q_н2 по (5.14), а затем аналогично предыдущему l_н2 и, наконец, П_н2. Уточненное значение р_с/р_н определяется из выражения (5.22).

Если полученное по (5.22) значение р_с / р_н >  (р_с / р_н)_пр2, то принимают р_с / р_н  =  (р_с / р_н)_пр2. В противном случае задаются (р_с / р_н)′ = р_с / р_н и продолжают вычисления по приведенному алгоритму до тех пор, пока не будет достигнуто |(р_с / р_н)′ – р_с / р_н | £ 10^–3.

Полученная информация является основой для расчета геометрических размеров СА.



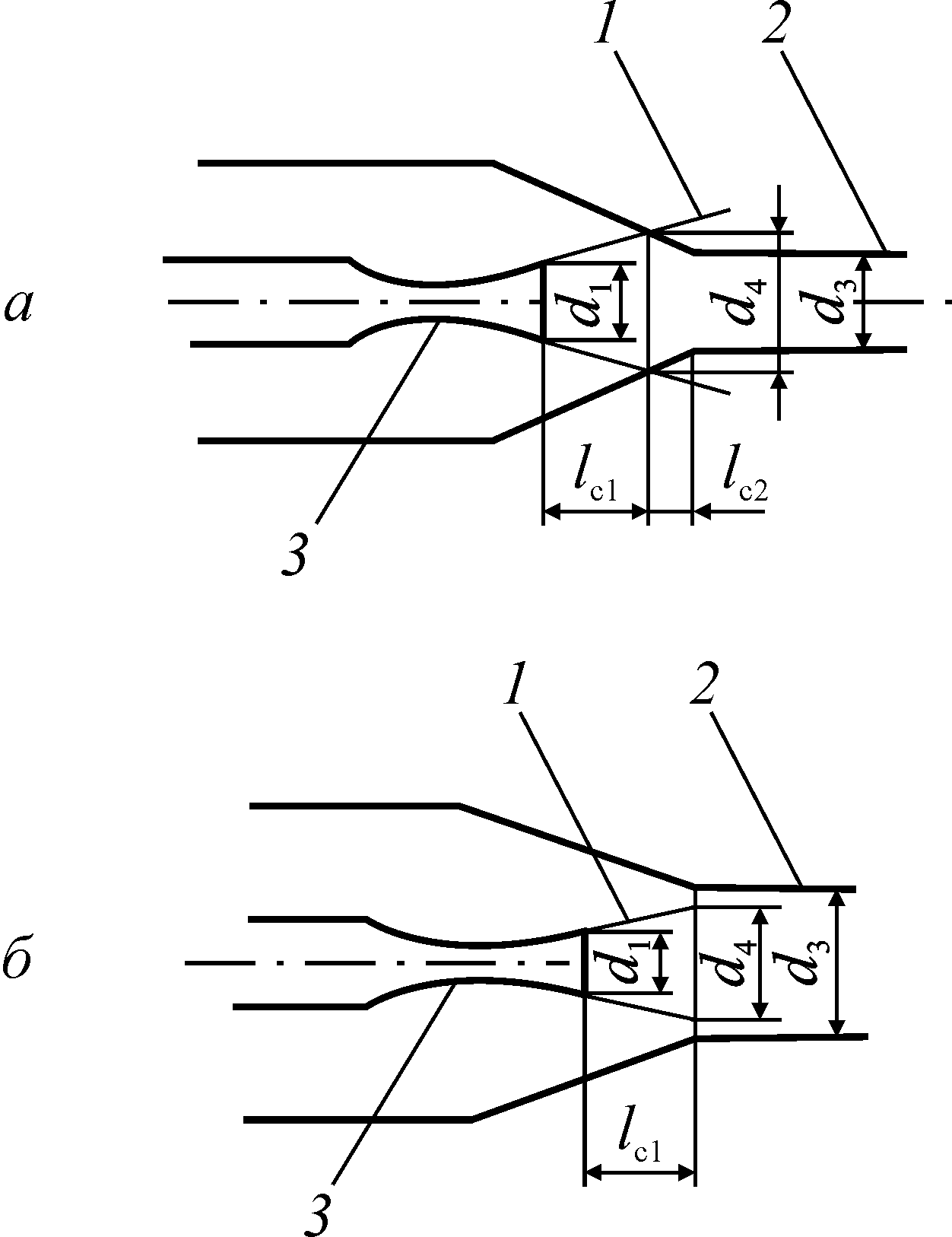
Рис. 5.2. К определению положения сопла относительно входа в камеру смешения в зависимости
от диаметра свободной струи d₄:
а) d₄  d₃; б) d₄  d₃
1 — свободная струя; 2 — камера смешения; 3 — рабочее сопло

Определение геометрических размеров СА.

Зная G_н = r _нQ_н и u, нетрудно найти массовые расходы газа в рабочем и смешанном потоках:

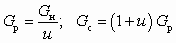. (5.23)

Площади критического и выходного сечений расширяющегося сопла (сопла Лаваля) можно выразить из уравнений расхода и неразрывности, соответственно

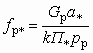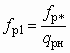; . (5.24)

Площадь входного сечения сопла f_p определяется по скорости в подводящем трубопроводе:

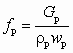. (5.25)

В свою очередь, площадь сечения камеры смешения находят из уравнения

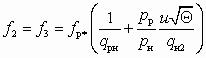. (5.26)

Сечения f_p*, f_p1 и f₂ определяют все основные поперечные размеры эжектора.

Положение рабочего сопла зависит от длины свободной струи l_c1 и соответствующего этой длине диаметра струи d₄ (см. рис. 5.2), которые определяются формулами:

при u  > 0,5



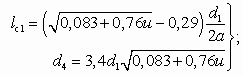
при u ³  0,5

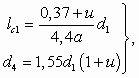(5.27)

где а — опытная константа, лежащая для упругих сред в пределах 0,07–0,09 (меньшее значение опытной константы рекомендуется принимать при u  0,2).

Если d₂  d₄ (см. рис. 5.2, а), то расстояние l_c от входного сечения сопла до входного сечения камеры смешения принимают равным l_c1. В этом случае более близкая установка сопла (l_c  l_c1) практически не влияет на работу сопла. Удаление же сопла от камеры смешения (l_c  l_c1) существенно ухудшает работу СА.

Если диаметр камеры смешения d₂  d₄ (рис. 5.2, б), то l_c принимается равной

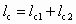, (5.28)

где l_c2 — длина входного участка камеры смешения, на которой диаметр струи меняется от d₄ до d₂:

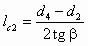. (5.29)

Здесь b — угол между образующей входного участка камеры смешения и осью эжектора, обычно принимаемый равным 45 °.

Длина цилиндрической камеры смешения выбирается в пределах l_к = (6 ¸  10)d₂. Длина диффузора определяется исходя из угла его раскрытия a  = 8 ¸  10° по формуле

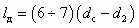, (5.30)

где .

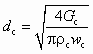Определившись с геометрией эжектора, можно перейти к решению третьей задачи, алгоритм которой зависит от условий работы СА.

Расчет поля рабочих характеристик СА.

Если СА применяется в качестве побудителя тяги для пневмотранспорта и установлен в конце ПУ, то p_с, как правило, постоянно, а давление в инжектируемом потоке газа p_н будет переменным, т. к. сопротивление ПУ существенно зависит как от концентрации, так и от характеристики транспортируемого материала. Давление газа в рабочем потоке p_p также может изменяться в зависимости от нагрузки на компрессор. Однако в этом случае целесообразно иметь возможность регулирования для поддержания оптимальных условий эксплуатации СА. Рабочая характеристика СА определяется уравнением

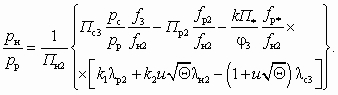  (5.31)

Если эжектор установлен в начале ПУ, то p_н, как правило, постоянно, а p_p и p_с могут изменяться по тем же соображениям. В этом случае рабочая характеристика определяется уравнением

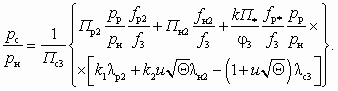(5.32)

Расчет характеристики заключается в определении p_н или p_с для целого ряда значений коэффициента инжекции u.

В том и другом случае задача решается методом итераций. В качестве примера приведем алгоритм определения p_н.

Вначале задаются предварительно ожидаемым давлением p_н при известных значениях u и р_р. Значения массовых скоростей рабочего, инжектируемого и смешанного потоков определяют по уравнениям:

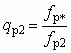; (5.33)

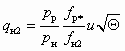; (5.34)

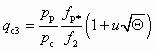. (5.35)

Соответствующие значения l_р2, l_н2 и l_с3 находят на основе уравнения (6.3.5.15). Поскольку каждому значению q (кроме q = 1) соответствуют два значения l , то l_р2 ³  1, если степень расширения рабочего потока в сопле (р_р / р_н) ³  1/П_р*. Приведенные же скорости l_н2 и l_с3 всегда меньше единицы.

Определив l_р2, l_н2 и l_с3, находят соответствующие им значения П_р2, П_н2 и П_с3, а затем по уравнению (5.31) — текущее значение 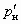, которое сравнивают с предварительно заданным p_н. Если

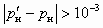, (5.36)

то p_н присваивают значение 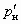. Итерационный процесс заканчивается, если условие (5.36) не соблюдается. Определив зависимость p_н от u, проводят аналогичные расчеты для других возможных значений p_р.

Предельные режимы СА.

Увеличение коэффициента инжекции, сопровождающееся уменьшением степени сжатия, возможно до тех пор, пока его величина не достигнет своего предельного значения u = u_пр. При этом СА определенных размеров развивает производительность, максимальную для данных начальных параметров рабочего и инжектируемого потоков, т. е. начинает работать на предельном режиме. Такой режим характеризуется тем, что скорость какого-либо потока (инжектируемого или смешанного) в произвольном сечении камеры смешения s–s достигает критического значения. Это возможно при в следующих условияхслучаях: 1) w_н2 = a_*; 2) w_нs = a_*; 3) w_c3 = a_*. Соответствующие коэффициенты инжекции определяются как:

; ;

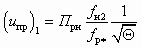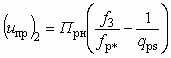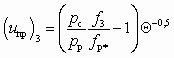.  (5.37)

где 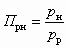; q_рs — массовая скорость рабочего потока в сечении s–s. При этом производительность СА ограничивается тем предельным режимом, который наступает при наименьшем коэффициенте инжекции. Эти ограничения должны учитываться в алгоритме расчета СА, что нетрудно сделать, определив предельные расходы газа в инжектируемом потоке (G_нпр)₁, (G_нпр)₂ и (G_нпр)₃ по уравнению (5.23).

При цилиндрической камере расширения первое условие не реализуется, так как второе условие наступает обычно раньше первого.

Совершенство СА характеризуется величиной КПД, определяемым как

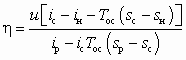, (5.38)

где i_p, i_н, i_c, s_p, s_н, s_c — удельные энтальпии и энтропии рабочего, инжектируемого и сжатого потоков в заторможенном состоянии; Т_ос — температура рабочего тела в состоянии равновесия с окружающей средой (обычно Т_ос = 293 К). В свою очередь

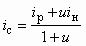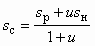; . (5.39)

Оценка эффективности СА особенно целесообразна в тех случаях, когда аппарат работает в системе, не являющейся замкнутой.

Пример 6.3.5.1. Определить геометрические размеры СА и построить его рабочую характеристику для обеспечения процесса пневмотранспортирования гранитной крошки, используемой в качестве посыпки в производстве рубероида, из сушилки кипящего слоя в бункер готовой продукции (см. рис. 5.3).



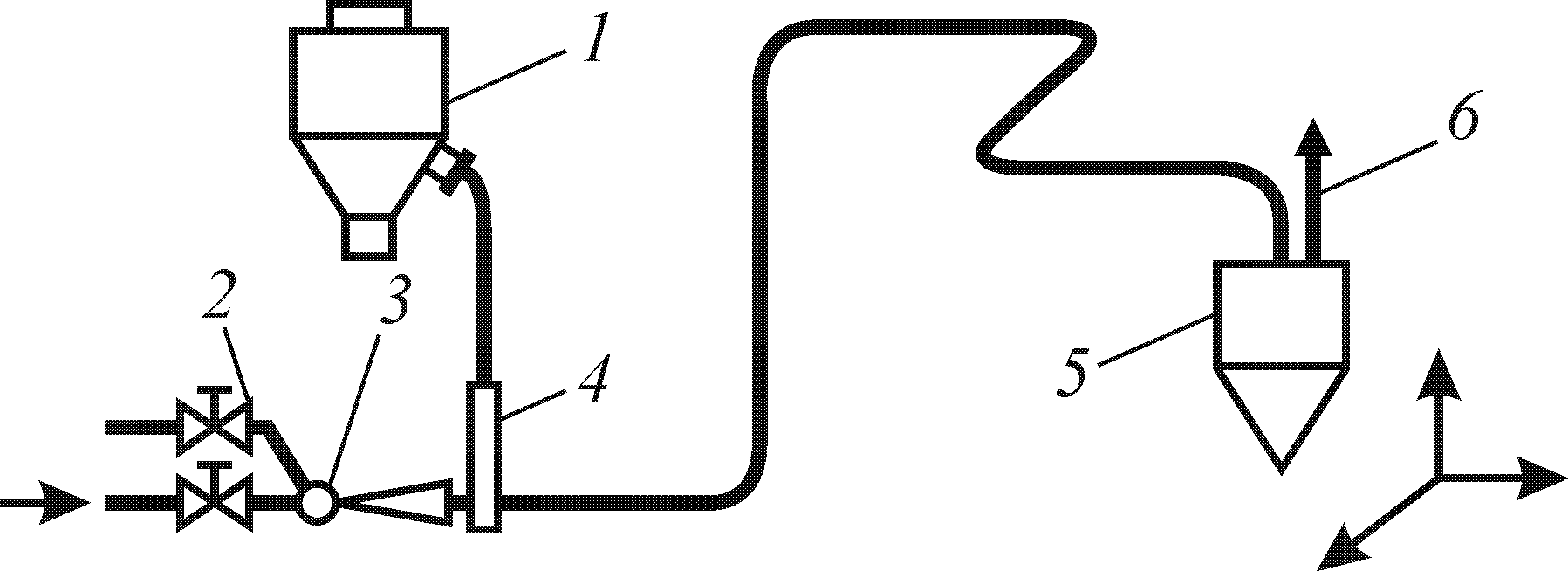
Рис. 5.3. Схема ПУ:
1 — сушилка КС – 1 – 0,16; 2 — регулировочный вентиль
подсоса воздуха; 3 — струйный аппарат СА;
4 — шахтный затвор; 5 — бункер готовой продукции;
6 — сброс воздуха в систему пылеулавливания

Исходные данные: производительность по материалу G₂ = 4,2·10^–4 кг/с; плотность материала r₂ = 2600 кг/м³; дисперсионный состав: d = 3÷0,5 мм; приведенная длина транспортирования L = 65 м; диаметр трубопровода D_у = 68 мм; концентрация дисперсной фазы m  4,8 кг/кг; необходимый массовый расход несущей среды, с учетом 20 % запаса, G₁ = 0,0861 кг/с; общие потери давления Dр = 0,203·10⁵ Па. Максимальное давление в сети сжатого воздуха р_р = 6 ·10⁵ Па.

Выбор схемы включения СА для организации пневмотранспортного процесса осуществляется с учетом сопротивления трассы. В данном случае, учитывая возможность изменения рабочего давления, предпочтение следует отдать схеме, изображенной на рис. 5.1, а. Особенностью решения данной задачи является определение минимального рабочего давления р_р, при котором коэффициент инжекции u максимален, т. е. постановка задачи отличается от изложенных выше. Поэтому в алгоритме решения должен быть предусмотрен анализ различных вариантов расчета, в которых задаваемые величины р_р и u обеспечивали бы необходимую степень сжатия 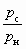, т. е. Dр_с = Dр. Кроме этого надо иметь в виду, что на предприятиях рабочее давление воздуха не превышает 6 атм. Поэтому при незначительных степенях расширения 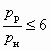и степенях сжатия 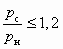достижимый коэффициент инжекции не больше 2, а (l_с3)_опт находится в диапазоне от 0,5 до 0,6. При этом, чем меньше величина (l_с3)_опт, тем меньше p_с, u и отношение 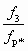, что в некоторых случаях является весьма существенным обстоятельством. В табл. 5.2 приведены результаты расчета расчетов, выполненных при р_н = 0,1 МПа и р_р = 0,3 и 0,4 МПадля двух случаев приведены ниже в виде таблицы.

На рис. 5.4 представлены рабочие характеристики СА для вариантов 1 и 2. Пунктирными линиями (линии 3 и e; 4 и e соответственно) обозначены расчетные варианты.

Вертикальными пунктирными линиями обозначен необходимый расход газа для обеспечения пневмотранспорта. Пологие участки характеристик описываются уравнением (5.32). Вертикальные участки характеристик соответствуют третьему предельному режиму. Из анализа данных табл. 5.2 и рис. 5.4 следует, что второй вариант расчета предпочтительнее как с точки зрения геометрии (размеры меньше), так и с точки зрения потребности в количестве рабочего газа для обеспечения заданного перепада давления.

Расчет СА с малой степенью сжатия (р_с / р_н  1,2). К таким аппаратам, согласно [14], можно отнести инжекторы, а также СА для пневмотранспорта зернистых материалов и жидкости (см. рис. 5.1, г и д). Алгоритм расчета этих аппаратов менее трудоемок, поскольку в них, как правило, предельные режимы не имеют места.

Таблица 5.2

Влияние степени расширения рабочего потока  на геометрию СА

№ п/пварианта		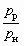	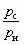lс3	fp1 / fp*	f3 / fp*	dp*, мм	dp1, мм	d3, мм	d4, мм	dд, мм	lc, мм	lксм, мм	lд, мм
1	3	1,164	0,54	1,093	8,57	7,9	8,2	23	32	68	43	184	270
2	4	1,204	0,59	1,218	10,371	6,8	7,52	22	29	68	39	176	276

Принципиально для расчета достижимых параметров таких СА применимы уравнения, приведенные выше. Однако, поскольку в этом случае инжектируемый и смешанный потоки практически проявляют себя как неупругие среды (удельный объем газа мало меняется в отличие от рабочего потока), то небольшая неточность в величине степени сжатия приводит к существенной ошибке в определении достижимого коэффициента инжекции. В этих условиях полезная мощность, сообщаемая инжектируемому потоку в СА, без большой погрешности может быть определена как

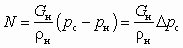. (5.40)

Поэтому в качестве расчетного показателя в данном случае принимают абсолютный или относительный перепад давлений инжектируемой среды:

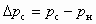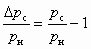; . (5.41)

Уравнение рабочей характеристики можно получить из выражения (5.32), если принять:

- на основе зависимостей (5.4) и (5.7) —

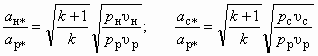; (5.42)

- на основе зависимостей (6.3.5.35), (6.3.5.36), (6.3.5.10) и соотношений, приведенных в таблице 5.1, —.

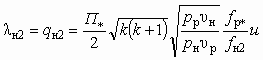; (5.43)

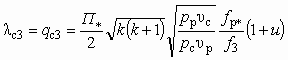; (5.44)

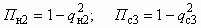. (5.45)

После соответствующих преобразований (5.32) получим уравнение характеристики газоструйного инжектора для условий сверхкритической степени расширения :

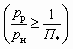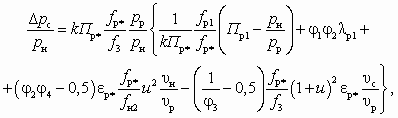. (5.46)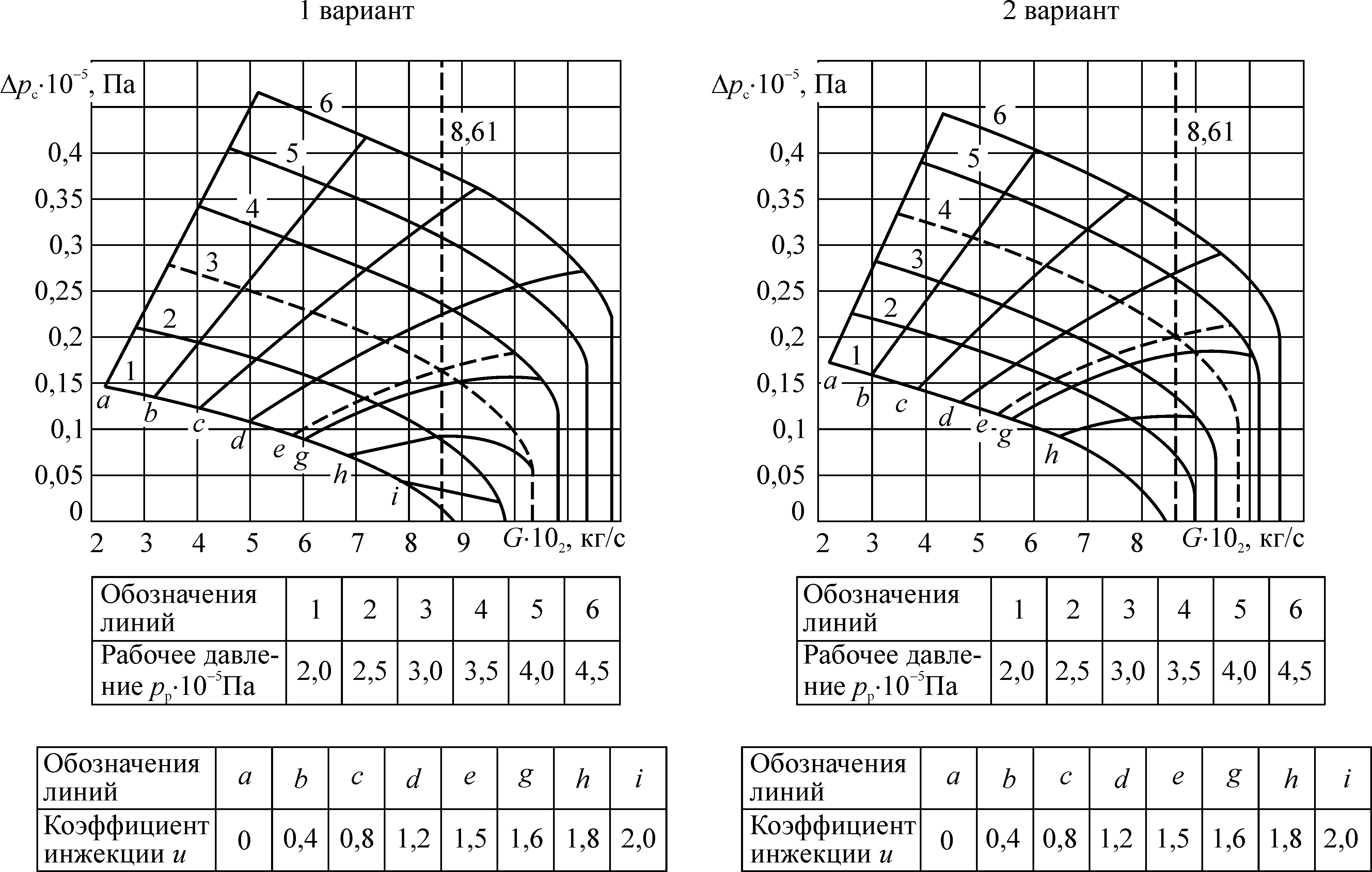



Рис. 5.4. Рабочие характеристики СА

В условиях докритической степени расширения 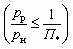– имеем 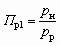, а замена f_p* равнозначной величиной q_рн f_p1 дает

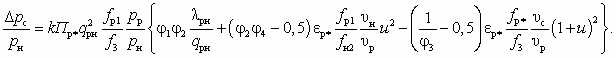(5.47)

Отношения удельных объемов 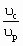и 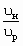в случае одинаковых газовых постоянных и теплоемкостей рабочего и инжектируемого потоков, т. е. при R_р = R_н и с_р = с_н, можно найти из очевидных соотношений

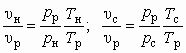, (5.48)

где 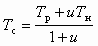Т_с = (Т_р  uТ_н) / (1  u).

Если СА используется для пневмотранспорта (см. рис. 5.1, г, д), то, как инжектируемая, так и смешанная среда представляют собой смесь газа с сыпучим твердым телом (зернистый или порошкообразный материал) или с жидкостью. При условии равномерности распределения твердой фазы в движущемся потоке газовой фазы и отсутствии относительной скорости между фазами, воспользовавшись понятием массовой расходной концентрации, можно записать: 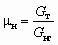/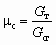_, . В свою очередь из баланса массы нетрудно получить:

- для инжектируемой среды

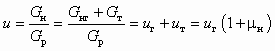, (5.49)

- а для смешанной среды

 (5.50)

Тогда удельные объемы инжектируемой и смешанной сред можно выразить как

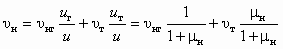; (5.51)

(5.52)

где 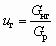— коэффициент инжекции по газу;  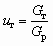— коэффициент инжекции по твердому телу; u_н — удельный объем инжектируемой среды, м³/кг; G_нг, u_нг — расход, кг/с, и удельный объем инжектируемого газа, м³/кг; G_т, u_т — расход, кг/с, и удельный объем инжектируемого твердого тела, м³/кг; G_p — расход рабочего газа кг/с; u_с — удельный объем смешанного потока, м³/кг; G_сг, u_сг — расход, кг/с, и удельный объем сжатого газа на выходе из СА, м³/кг.

Отметим, что Параметры u_нг и u_сг определяются уравнениями (5.48). Подставляя (5.49), (5.51)–(5.52) в (5.46) и в (5.47), не трудно получить:

(5.53)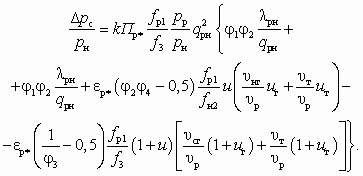

(5.54)

Эмпирические коэффициенты j₁; j₂; j₃; j₄ принимают указанные выше значения, если инжектируемый и рабочий потоки однофазны. Если же потоки разнофазны, то в случае пневмотранспорта зернистых материалов рекомендуется принимать: j₁ = 0,95; j₂ = 0,875; j₃ = 0,81; φ₄ = 0,83, а в случае жидкости: j₁ = 0,95; j₂ = 0,875; j₃ = 0,83; j₄ = 0,925. Испарением жидкости при этом можно пренебречь.

Расчет СА для пневмотранспорта зернистых материалов.

При сверхкритической степени расширения рабочего потока 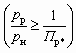газодинамические функции П_р1 и l_р1 находятся однозначно по 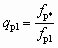. Если заданы величины p_н, p_р и u, то оптимальное отношение сечений 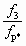соответствует максимальному перепаду давлений Dр_с, развиваемому СА. На основании (5.53) из условия

(5.55)

следует

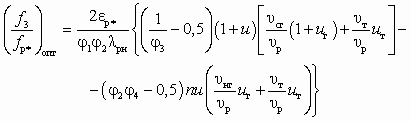, (5.56)

где

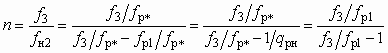. (5.57)

Совместное решение (5.56) и (5.57) дает

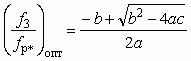, (5.58)

где ;

;

.

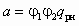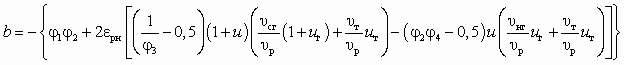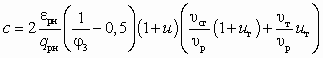Газодинамические функции l_рн, e_рн и q_рн однозначно определяются по известному относительному давлению рабочего потока на выходе из сопла 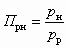. При подстановке 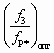в (5.53) находят достижимое Dр_с.

Для условий докритического расширения рабочего потока 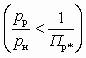по аналогии следует

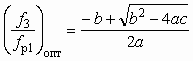, (5.59)

где



.

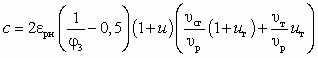При подстановке 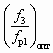в (5.54) находят достижимое Dр_с.

Если заданной величиной является Dр_с, а искомой величиной — достижимый коэффициент инжекции u, то весьма удобными для расчета оказываются зависимости

;

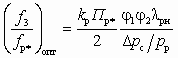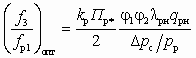. (5.60)

Тогда, с учетом (5.53) или (5.54), в условиях 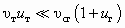и 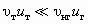, а также при равенстве температур рабочего и инжектируемого потоков (Т_р = Т_н = Т_с), достижимый коэффициент инжекции по твердому телу u_т в обоих случаях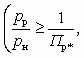 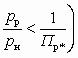можно найти из уравнения

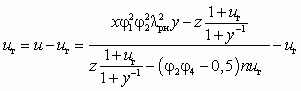, (5.61)

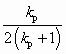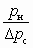где x = , y = , z = .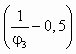

При расчете по (5.61) u_г должен быть заранее задан или выбран.

При сверхкритической степени расширения рабочего потока 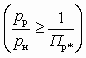основные размеры рабочего сопла ( f_p, f_p*, f_p1) рассчитываются по формулам (5.24), (5.25). При докритической степени расширения рабочего потока 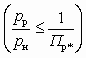рабочие сопла имеют коническую форму, а выходное сечение сопла рассчитывается по формуле, являющейся модификацией соотношений (5.24):

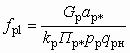. (5.62)

Для определения осевых размеров СА следует воспользоваться выражениями (5.27)–(5.30).

Пример 5.2. Определить геометрические размеры СА для пневмотранспорта песка. Построить рабочую характеристику аппарата Dр_с / р_н = f(u_т). Расход песка G_т = 1,39 кг/с. Параметры рабочего воздуха перед струйным аппаратом: р_р = 2,943∙10⁵ Па; t_р = 20 °C. Песок поступает в аппарат в состоянии рыхлой насыпки, т. е. вместе с воздухом, защемленным между зернами песка, при давлении р_н = 9,81∙10⁴ Па. На выходе смешанной среды из аппарата должно быть создано при расчетном режиме давление р_с = 1,0791∙10⁵ Па. Истинная плотность песка r_т = 2600 кг/м³. Насыпная плотность песка r_тн = 1400 кг/м³.



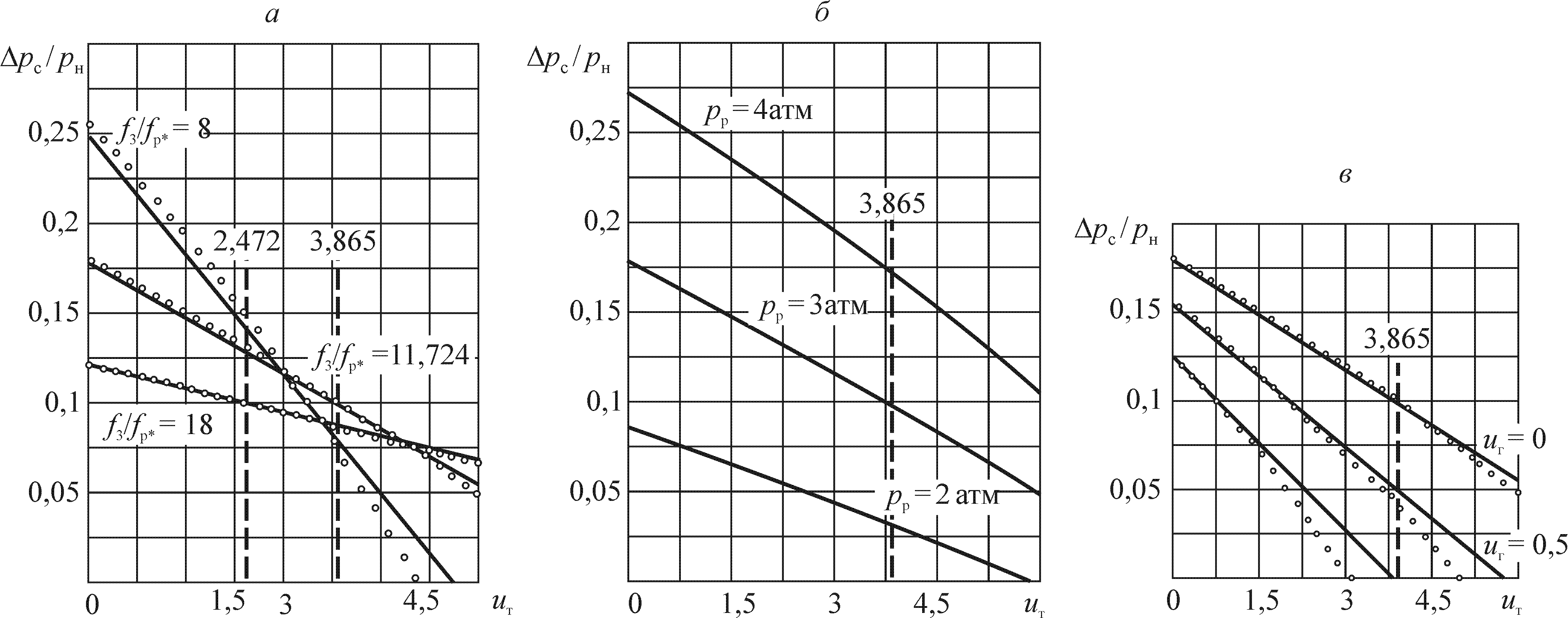
Рис. 5.5. Характеристики СА для пневмотранспорта песка:
а) р_р = 3 атм; u_г = 0; (  f₃ / f_p*)_опт = 11,724; б) u_г = 0; ( f₃ / f_p*)_опт  = 11,724; в) р_р = 3 атм; ( f₃ / f_p*)_опт = 11,724
Сплошные линии — при постоянстве _сг; точки — с учетом изменения _сг

Оценим количество воздуха, поступающего в СА (см. рис. 5.1, г) вместе с песком. Пористость песка в рыхлой насыпке 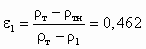. Тогда 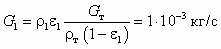, что на 3 порядка меньше расхода песка. Это означает, что u_г = 0 и u_н = u_т. Результаты расчета приведены в таблице :

Gp, кг/с	0,36	dp1, м	0,027
pp·105,Па	2,943	d3, м	0,088
pн·105,Па	0,981	dд, мм	0,134
pс·105,Па	1,079	lc, м	0,344
fp1/fp*	1,093	lксм, м	0,703
f3/fp*	11,72	lд, мм	0,275
dp*, м	0,026

На рис.  5.5 представлены рабочие характеристики СА. Из приведенных данных видно, что (рис. 5.5, а) достижимый коэффициент инжекции при заданном р_с ниже, чем при(f₃ / f_p*)_опт. Влияние изменения удельного объема υ_сг проявляется в наибольшей степени при f₃ / f_p*  ( f₃ / f_p*)_опт как при f₃ / f_p*  ( f₃ / f_p*)_опт, так и при f₃ / f_p*  ( f₃ / f_p*)_опт. Увеличение давления (рис. 5.5, б) рабочего воздуха при одном и том же создаваемом перепаде давлений приводит к ощутимому росту коэффициента инжекции по твердому телу. Влияние изменения удельного объема u_сг на характер зависимости D р_с / р_н = = f(u_т) становится тем заметнее, чем больше примесь воздуха в инжектируемом потоке (рис. 5.5, в).