Кочетковой Ольги Валентиновны моу «сош №2» Салиной Натальи Петровны Г. Балаково г. Саратов 2009г. Содержание Введение 2 Ι. решение
| Вид материала | Решение |
СодержаниеМетод разложения на множители. Метод замены переменной. Введение вспомогательного аргумента. Универсальная тригонометрическая подстановка. Уравнение вида |
- Аналитический отчет учителя биологии моу гимназии №32 города Калининграда Федосеевой, 327.4kb.
- Анализ работы городского методического объединения учителей биологии г. Боготола, 171.67kb.
- Ефремовой Натальи Вячеславовны учителя начальных классов моу сош №5 г. Мытищи. 1 слайд., 38.73kb.
- Биюшкиной Лидии Петровны. Тема урок, 56.57kb.
- Милешиной Натальи Петровны, и, именуемый в дальнейшем Поставщик, в лице, действующего, 1503.17kb.
- Приказ №344 от 19 апреля 2011г. Об итогах районной научно- практической конференции, 52.66kb.
- Погодина Марина Викторовна, учитель русского языка и литературы моу сош №26 г. Балаково., 157.47kb.
- Чеботаревой Татьяны Валентиновны моу «сош №1» 2008 год. Тема урок, 95.14kb.
- Программа прилагается. Директор моу сош №1 Шармазанян Л. С. Приложение 1 Областная, 188.28kb.
- Моу мук 2008-2009 уч год, 106.71kb.
Министерство образования Саратовской области
ГОУ ДПО «Саратовский институт повышения квалификации и переподготовки работников образования»
Кафедра математического образования
Методические рекомендации по изучению
тригонометрических уравнений, в рамках
подготовки учащихся к единому государственному экзамену по математике.
Творческая работа слушателей курсов повышения квалификации по профессиональной образовательной программе
«Теория и методика преподавания математики»,
учителей математики
МОУ «Лицей№1» Кочетковой Ольги Валентиновны
МОУ «СОШ №2» Салиной Натальи Петровны
Г.Балаково
г.Саратов – 2009г.
Содержание
| Введение | 2 |
| Ι. Решение простейших тригонометрических уравнений | 3 – 7 |
| ΙΙ. Общие методы решения тригонометрических уравнений | |
| 1. Метод разложения на множители | 8 – 10 |
| 2. Метод введения новой переменной | 10 – 14 |
| 3. Функционально-графические методы | 15 – 17 |
| ΙΙΙ. Решение комбинированных уравнений | 18 – 23 |
| ΙV. Решение тригонометрических уравнений с параметром | 24 – 25 |
| V. Тесты для самостоятельного решения | 26 – 27 |
| Литература | 28 |
Введение
Как подготовить учеников к экзамену по математике и научить их решать задачи?
Казалось бы, для этого нужно решать задачи, предлагавшиеся на экзаменах в прошлые годы. Однако, если следовать только этому рецепту, то результат может оказаться вовсе не тем, который ожидается.
В каждом новом году зкзаменационные задачи отличаются от задач прошлых лет, и из того, что вы узнали, как решаются задачи, предлагаемые на экзаменах в прошлые годы, не следует, что вы сможете решить другие задачи.
Важно, чтобы задачи, которые вы решаете, готовясь к экзамену, носили развивающий, системный характер, создавали базу для решения других задач.
На приемных экзаменах во втузы, университеты и институты неизменно отмечаются как один из серьезных недочетов в знаниях выпускников школ слабые навыки и ошибки в решении тригонометрических уравнений.
Отчасти это обьясняется тем, что не существует общего метода, который был бы применим для решения любого тригонометрического уравнения, и поиск решения в каждом конкретном случае требует определенных навыков в выполнении тригонометрических преобразований, умении найти и применить нужную тригонометрическую формулу. Общее направление преобразований, применяемых для решения таких задач, состоит в большинстве случаев в том, чтобы свести рассматриваемое уравнение к нескольким простейшим уравнениям.
Технические ошибки в преобразование тригонометрических выражений и в записи решений простейших тригонометрических уравнений часто являются существенной преградой на пути к решению.
Многолетний опыт работы многих учителей показывает, что учащиеся значительно лучше овладеваю приемами решения тригонометрических уравнений, если их решать систематически, начиная с введения понятия тригонометрической функций на протяжении изучения всего тригонометрического материала в курсе алгебры и начал анализа.
Ι. Решение простейших тригонометрических уравнений
Все тригонометрические уравнения сводятся к простейшим. Поэтому особое внимание следует уделять решению простейших уравнений. Начинать нужно с самых простых.
К простейшим тригонометрическим уравнениям относятся уравнения вида:

Для каждого из простейших тригонометрических уравнений определены формулы, справедливость которых обосновывается с помощью тригонометрического круга и с учетом периодичности тригонометрических функций.
| sinx=а, |а|>1, решений нет; sinx=0, x= πn, nєZ sinx =–1, x= –  +2πn, nєZ; +2πn, nєZ;sinx =1, x=  +2πn, nєZ; +2πn, nєZ;sinx=а, |а|<1, x= arcsinа +2πn, nєZ; x= π–arcsinа +2πn, nєZ. В последнем случае для сокращения записи используют формулу: x=(–1)narcsinа + πn, nєZ. | cos x=а, |а|>1,решений нет; cos x=0, x= –  +πn, nєZ; +πn, nєZ;cos x=–1, x= π +2πn, nєZ; cos x=1, x=2πn, nєZ; cos x=а, |а|<1, x= ± arccosа +2πn, nєZ. |
Решения уравнения tg x=а и ctg x=а записываются существенно проще:
x= arctgа +πn, nєZ и, соответственно, x= arcсtgа +πn, nєZ .
Пример 1. Решить уравнение sinx =
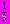 .
.Решение: так как
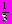 <1, значит x=(–1)narcsin
<1, значит x=(–1)narcsin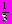 + πn, nєZ.
+ πn, nєZ. Ответ: (–1)narcsin
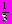 + πn, nєZ.
+ πn, nєZ. Пример 2. Решить уравнение cos x =
 .
. Решение: так как
 >1, значит уравнение не имеет решения.
>1, значит уравнение не имеет решения. Ответ: нет решения.
Пример 3. Решить уравнение tg x+
 = 0.
= 0.Решение:
tg x+
 = 0
= 0 tg x = –

x = arctg (–
 ) + πn, nєZ
) + πn, nєZ x = – arctg
 + πn, nєZ
+ πn, nєZ x = –
 +2πn, nєZ;
+2πn, nєZ;Ответ: –
 +2πn, nєZ.
+2πn, nєZ. Пример 4. Решить уравнение 2cos x = –
 .
. Решение:
2cos x = –

cos x = –

x= ± arccos (–
 )+2πn, nєZ
)+2πn, nєZx= ±( π – arccos
 )+2πn, nєZ
)+2πn, nєZ x= ±( π –
 )+2πn, nєZ
)+2πn, nєZx = ±
 + 2πn, nєZ
+ 2πn, nєZОтвет: ±
 + 2πn, nєZ.
+ 2πn, nєZ.Для отработки общих формул решения простейших уравнений можно предложить для устного решения задания такого вида.
Образуют ли арифметическую прогрессию расположенные в порядке возрастания положительные корни уравнения : sinx =0; cosx = 0,5; tg x=1.
На начальном этапе, пока не отработаны навыки использования общих формул решения простейших уравнений желательно прописывать эти формулы, чтобы учащиеся быстрее их запомнили.
Далее нужно переходить к решению более сложных уравнений, которые чаще всего встречаются в вариантах ЕГЭ в разделе А.
Пример 5. Решить уравнение cos
 =
=  .
. Решение: cos
 =
= 
Это уравнение сводится к простейшему cos t =
 заменой t =
заменой t = , которую можно не прописывать.
, которую можно не прописывать. = ± arccos
= ± arccos  +2πn, nєZ
+2πn, nєZ  = ±
= ±  +2πn, nєZ
+2πn, nєZх = ±
 + 10πn, nєZ
+ 10πn, nєZОтвет: ±
 + 10πn, nєZ.
+ 10πn, nєZ.Пример 6. Решить уравнение: sin (2x–
 ) =
) =  .
. Решение: sin (2x–
 ) =
) = 
2x–
 = (–1)narcsin
= (–1)narcsin  + πn, nєZ
+ πn, nєZ 2x–
 = (–1)n
= (–1)n + πn, nєZ
+ πn, nєZ2x–
 = +
= + + 2πn, nєZ
+ 2πn, nєZ2x–
 = –
= –
 + (2m + 1)π,mєZ
+ (2m + 1)π,mєZ2x =
 + 2πn, nєZ
+ 2πn, nєZ2x =π + 2πm, mєZ
x =
 + πn, nєZ
+ πn, nєZ
x =
 + πm, mєZ
+ πm, mєZ Ответ:
 + πn,
+ πn,  + πm, n,mєZ.
+ πm, n,mєZ.Так же нужно обратить внимание учащихся на то, что довольно часто исходное уравнение приводится к простейшему лишь после различных тождественных преобразований и применения формул тригонометрии.
Пример 7. Решить уравнение 4 sin3x cos 3x =1.
Решение: 4 sin3x cos 3x =1
2(2sin3x cos 3x) =1
2sin6x =1
sin6x =
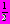
6x = (–1)n
 + πn, nєZ
+ πn, nєZx = (–1)n
 +
+  n, nєZ
n, nєZОтвет: (–1)n
 +
+  n, nєZ.
n, nєZ. Часто предлагается решить тригонометрическое уравнение на некотором промежутке. Целесообразно начинать решать такие уравнения до вывода общих формул решения простейших тригонометрических уравнений.
Рассмотрим примеры.
Пример 8. Найдите корни уравнения 2cosx = –1, принадлежащие промежутку [0;2π].
Решение:
2cosx = –1
cosx = –
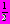
Выбор значений x , которые принадлежат указанному промежутку можно выполнить различными способами.
Наиболее рационально это делать с помощью единичной окружности.
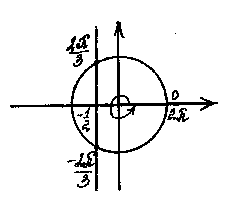
x1 =
 ; x2 =
; x2 =  .
. Ответ:
 ;
; .
.В тестах часто требуется не просто найти корни, принадлежащие данному промежутку, а вычислить их сумму или разность; определить наибольший или наименьший корень; указать количество корней.
Пример 9. Найдите сумму корней уравнения (cos 2 x –1)(2 sin
 – 1) = 0, принадлежащих промежутку [–
– 1) = 0, принадлежащих промежутку [– ; π ).
; π ).Решение:

 x1 = 0; x2 =
x1 = 0; x2 =  , x1 + x2 =
, x1 + x2 = 

Ответ:
 .
. Решите самостоятельно.
Решите самостоятельно.1. Найдите сумму корней уравнения 2sinx = –1 на указанном промежутке

2. Найдите количество корней уравнения 4cos 22х = 1 на указанном промежутке
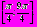
3. Найдите сумму наименьшего положительного и наименьшего отрицательного корней уравнения sinx cos
 + sin
+ sin  cos х =
cos х = 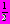 на указанном промежутке
на указанном промежутке 
Уже при решение простейших тригонометрических уравнений полезно предлагать нестандартные уравнения.
Пример 10. Решить уравнение cos x2 = 1.
Можно дать это уравнение для самостоятельного решения.
Найдутся ученики, которые решат его в одну строчку:
х2 = 2πk, kЄZ
х =
 , kЄZ.
, kЄZ.Целесообразно продемонстрировать это решение на доске и предложить ученикам найти допущенные ошибки.
В случае затруднений, чтобы внести полную ясность, решить для начала уравнение
х2 = a.
Его решение имеет вид х = ±
 при а
при а 0.
0.Если а <0, то уравнение не имеет решений. Значит решением исходного уравнения является х = ±
 , kЄZ, k
, kЄZ, k 0.
0.Ответ: ±
 , kЄZ, k
, kЄZ, k 0.
0.Пример 11. Решить уравнение sinsinx = 1.
Решение: sinsinx = 1.
sinx =
 +2πn, nєZ
+2πn, nєZВыражение |
 +2πn | > 1 при любых значениях n , nєZ.
+2πn | > 1 при любых значениях n , nєZ. Поэтому исходное уравнение не имеет решений.
Ответ: нет решений.
ΙΙ. Общие методы решения тригонометрических уравнений
- Метод разложения на множители.
Этот метод заключается в том , что исходное уравнение сводится к уравнению вида
f (x)g(x)h(x) = 0, которое можно заменить совокупностью уравнений, каждое из которых сводится к простейшему.
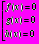
Решив уравнения совокупности нужно взять только те решения, которые принадлежат области определения исходного уравнения, а остальные корни отбросить.
Пример 1. Решить уравнение sin4x = 3 cos2х.
Решение:
sin4x = 3 cos2х.
2 sin2x cos2х = 3 cos2х
Получив такое уравнение, ученики достаточно часто делают ошибку, «сократив» левую и правую части уравнения на cos2х. Некоторые из них при этом оговаривают, что cos2х
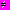 0,но одной оговорки здесь, увы, недостаточно. Необходимо ещё рассмотреть случай, когда cos2х = 0, и проверить, не являются ли значения х, удовлетворяющие этому равенству, корнями исходного уравнения. Разумеется, лучше всего не делить левую и правую части уравнения на cos2х, а разложить на множители
0,но одной оговорки здесь, увы, недостаточно. Необходимо ещё рассмотреть случай, когда cos2х = 0, и проверить, не являются ли значения х, удовлетворяющие этому равенству, корнями исходного уравнения. Разумеется, лучше всего не делить левую и правую части уравнения на cos2х, а разложить на множители(2 sin2x – 3) cos2х = 0.
Полученное уравнение равносиьно совокупности двух уравнений
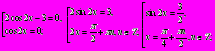 х =
х =  , nЄZ.
, nЄZ.Первое уравнение решения не имеет, так как функция синус не может принимать значений по модулю больших единицы. К сожалению, не все ученики это понимают, а из тех, кто понимает, не всякий вспоминает вовремя.
Ответ:
 , nЄZ.
, nЄZ.Пример 2. Решить уравнение sin2x = sin4x
Решение: некоторые учащиеся, встретив такое уравнение, решительно записывают
2х = 4х или 2х = 4х + 2πn, nЄZ, что приводит к потере решений исходного уравнения.
Решение исходного уравнения состоит в переходе к уравнению sin2x – sin4x = 0
и последующем применении формулы для преобразования разности тригонометрических функций в произведение
2cos
 = 0
= 0cos3x (–sinx) = 0

Ответ:

Пример 3. (ЕГЭ 2009г. Вариант 1, С2.).
Найдите все значения
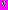 , при каждом из которых выражения
, при каждом из которых выражения принимают равные значения.
принимают равные значения.Решение:
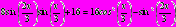
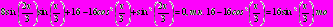
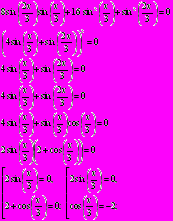


Ответ:

Пример 4. (ЕГЭ 2009г. Вариант 2, B7.).
Найдите наименьший корень уравнения

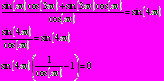 Решение:
Решение: 
Ответ:
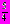
- Метод замены переменной.
В школьном курсе в основном рассматриваются уравнения, которые после введения нового неизвестного t = f(x),где f(x) – одна из основных тригонометрических функций, превращаются в квадратные либо рациональные уравнения с неизвестным t.
Пример 5. Решить уравнение cos2 πx + 4sinπx + 4 =0
Решение: 1 – sin 2 πx + 4sinπx + 4 =0
– sin 2 πx + 4sinπx + 5 =0
Заменим sin πx = t , -1
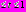
–t 2 + 4t +5 = 0
t 2 – 4t – 5 = 0
t1 = –1, t2 = 5
t2 не удовлетворяет условию -1
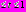
sin πx = –1
πx = –

х = –

Ответ: –

Решение однородных тригонометрических уравнений.
Уравнение вида аsinx +bcosx =0, где а и b –некоторые числа, называются однородными уравнениями первой степени относительно sinx и cosx.
Уравнение вида аsin 2 x +bcos 2 x + с =0, где а,b,с – некоторые числа, называются однородными уравнениями второй степени относительно sinx и cosx.
Пример 6. Решить уравнение sinx – cosх = 0.
Решение: легко убедиться, что cosx = 0 не является корнем исходного уравнения.
В самом деле, если cosx = 0, то, в силу исходного уравнения, и sinx = 0, что противоречит основному тригонометрическому тождеству. Этот факт позволяет разделить левую и правую части уравнения на cosx.
Получим уравнение tg x = 1, откуда х =

Ответ:

Пример 7. Решить уравнение sin 2 x – 3sinx cosх + 2cos 2 x = 0.
Решение: поскольку cosx = 0 не является корнем tg x данного уравнения,
разделим левую и правую части уравнения на cos 2 x. В результате приходим к квадратному уравнению относительно tg2 x – 3 tg x + 2 = 0,
решив которое, получим
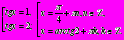
Ответ:
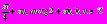
Введение вспомогательного аргумента.
Уравнение вида аcosx + b sinx = с, где а, b, с –некоторые числа, причем
 называют линейными тригонометрическими уравнениями.
называют линейными тригонометрическими уравнениями. Для решения таких уравнений используют введение вспомогательного аргумента.
Так как а 2 + b2 >0, то можно разделить обе части уравнения на
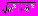 , получим
, получим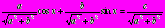
Введём в рассмотрение угол
 такой, что
такой, что
Угол
 , удовлетворяющий этим двум условиям, принято называть дополнительным (или вспомогательным) аргументом. Для любых значений а и b такой угол существует, так как
, удовлетворяющий этим двум условиям, принято называть дополнительным (или вспомогательным) аргументом. Для любых значений а и b такой угол существует, так как 
Вообще, полезно напомнить учащимся, что любые числа p и g такие, что
p2 + g2 = 1 можно рассматривать как косинус и синус некоторого угла.
Теперь исходное уравнение можно записывать в виде
cos
 cosx + sin
cosx + sin sinx =
sinx = 
cos (x –
 ) =
) = 
Аналогично можно вводить вспомогательный угол
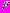 такой, что:
такой, что:
Тогда исходное уравнение можно привести к виду
sin
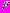 cosx + cos
cosx + cos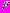 sinx =
sinx = 
sin (x +
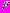 ) =
) = 
Полезно также обратить внимание учащихся, что умение преобразовывать выражения вида а cosx + b sinx может понадобиться не только при решении уравнений, но и для построения оценок, нахождения наибольших значений и т. д.
Пример 8. Решить уравнение 3 sinx – 4cosх = 5.
Решение. 3 sinx – 4cosх = 5
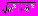 =
= =5
=5
 , cosx =
, cosx =  ,
,cos(x +
 ) = –1
) = –1x +
 = π + 2πn, nЄZ
= π + 2πn, nЄZx = –
 + π + 2πn, nЄZ
+ π + 2πn, nЄZ x = –arcsin
 + π + 2πn, nЄZ
+ π + 2πn, nЄZОтвет: –arcsin
 + π + 2πn, nЄZ.
+ π + 2πn, nЄZ.Пример 9. Решить уравнение 2cosх = 1– 2cos 2х –
 sin2x.
sin2x. Решение. Воспользуемся формулой 2cos 2х – 1 = cos 2x,
получим 2cosх = – cos2х –
 sin2x.
sin2x.Применим к правой части процедуру введения вспомогательного аргумента.
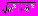 =
=
2cosх = – 2(
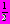 cos2х +
cos2х + sin2x)
sin2x)2cosх = – 2 (сos
 cos2х + sin
cos2х + sin sin2x), где
sin2x), где 
2cosх = – 2(cos2х –
 )
)cosх + cos (2х –
 ) = 0
) = 0Последнее уравнение легко решить, преобразовав сумму косинусов в произведение:
2cos
 cos
cos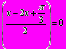
cos


Необходимо обратить внимание учащихся на то, что в тригонометрических системах и совокупностях при записи имеет смысл употреблять разные буквы, обозначающие целые числа.
Ответ:
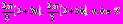 .
.Универсальная тригонометрическая подстановка.
Универсальная тригонометрическая подстановка позволяет перейти от синуса и косинуса аргумента х к тангенсу половинного аргумента:
sin
 , cos
, cos 
При таком переходе возможна потеря решений, следует помнить, что
 (в этих точках tg
(в этих точках tg 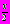 не существует). Поэтому всякий раз, когда приходится пользоваться универсальной подстановкой, значения х = π + 2πn, nЄZ необходимо проверять отдельно, подставляя в исходное уравнение.
не существует). Поэтому всякий раз, когда приходится пользоваться универсальной подстановкой, значения х = π + 2πn, nЄZ необходимо проверять отдельно, подставляя в исходное уравнение.Пример 10. Решить уравнение sinx + cosх = –1.
Решение:
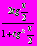
 = –1, заменим tg
= –1, заменим tg 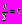 , получим
, получим2t +1 – t2 = –1– t2
2t = – 2
t = – 1
tg
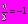

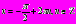
Подставим теперь в исходное уравнение значение
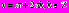 и убедимся, что они действительно являются его решениями.
и убедимся, что они действительно являются его решениями. Ответ:


Уравнение вида
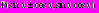
Уравнение вида
 где
где 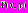 - многочлен, удобно решать при помощи введения новой переменной
- многочлен, удобно решать при помощи введения новой переменной 
Тогда можно получить выражение для произведения из формулы

Пример 11. Решить уравнение

Решение: введем новую переменную


Тогда
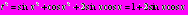
Следовательно,
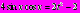 и исходное уравнение принимает вид
и исходное уравнение принимает вид 
Для определения переменной
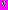 получаем два уравнения
получаем два уравнения 
Для решения таких уравнений используют введение вспомогательного аргумента.

Ответ:

После завершения изучения рассмотренных методов, при наличии времени, рекомендуем провести урок-практикум – «Урок решения одного уравнения»
3. Функционально-графические методы
- Использование свойств ограниченности функций, метод оценок.
Часто приходится иметь дело с уравнениями, имеющими вид f(x) = g(x), где f и g – некоторые функции, составленные с помощью тригонометрических выражений, такие, что можно исследовать области значений Е(f) и Е(g) и доказать, что эти области либо не пересекаются, либо имеют небольшое число общих точек. В таких случаях решения уравнения f(x) = g(x) следует искать среди таких x , которые удовлетворяют более простым уравнениям f(x) = a, g(x) = a , где а – такое действительное число, что

Пример 12. Решить уравнение
 .
.Решение:

Ответ: нет решения.
Пример13. Решить уравнение
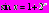 .
.Решение:

Ответ: нет решения.
Пример14. Решить уравнение
 .
.Решение:

Ответ:
 .
.Пример15. Решить уравнение
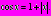
Решение:

Ответ:

Пример16. Решить уравнение
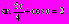
Решение.
Заметим, что сумма в левой части полученного уравнения может принимать значение 2, только если
 одновременно, т.е. наше уравнение равносильно системе уравнений
одновременно, т.е. наше уравнение равносильно системе уравнений
И должно выполняться равенство
 Поскольку
Поскольку 
Ответ:

- Использование графиков.
Суть метода использования графиков для решения уравнения f(x) = g(x) проста: нужно построить графики функций y = f(x) и y = g(x) и найти все точки их пересечения, абсциссы которых и будут являться корнями нашего исходного уравнения.
Пример 17. Сколько корней имеет уравнение:

Решение: в данном примере для решения уравнений используются свойства графиков функций.

Ответ: 1 решение.
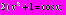
Ответ: 1 решение.


Ответ: 7 решений.
ΙΙΙ. Решение комбинированных уравнений
Пример1. Решите уравнение

Решение:
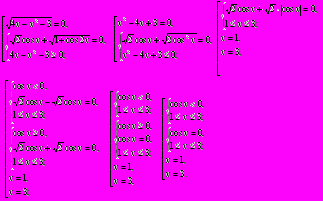
Ответ:
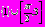 .
.Пример 2. Решите уравнение

Решение:


Ответ:
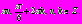
Пример 3. Решите уравнение

Решение:

Решим первое уравнение системы с использованием универсальной тригонометрической подстановки:
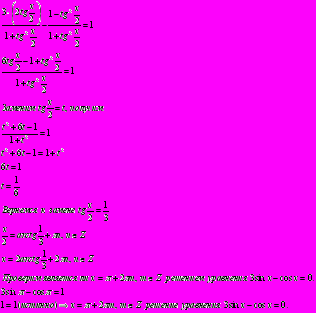
С учетом неравенств системы имеем:
Ответ:

Пример 4. Решите уравнение
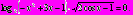
Решение:

Ответ:

Пример 5. Решите уравнение

Решение:
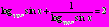

Ответ:
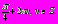
Пример 6. Решите уравнение

Решение:


Ответ:
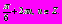
Пример 7. Решите уравнение

Решение:

Ответ:
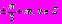
Пример 8. Решите уравнение

Решение: воспользуемся формулой понижения степени
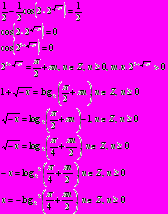
Ответ:

Пример 9. Решите уравнение
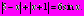
Решение:

Решим полученное уравнение графически, для этого в одной системе координат построим графики функций


Ответ:

Пример 10. Решите уравнение

Решение: введем функцию
 тогда получим
тогда получим 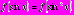
Исследуем функцию на монотонность
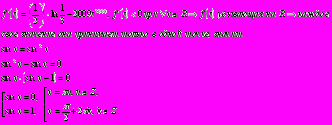
Ответ:
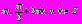
Пример 11. Решите уравнение

Решение: данное уравнение равносильно системе

Ответ:

ΙV. Решение тригонометрических уравнений с параметром.
Пример1. Найти все значения параметра
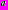 , при которых уравнение
, при которых уравнение  имеет решение.
имеет решение.Решение:


Пример 2. Найти все значения параметра
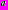 , при которых уравнение
, при которых уравнение имеет на отрезке
имеет на отрезке  ровно три корня.
ровно три корня.Решение:

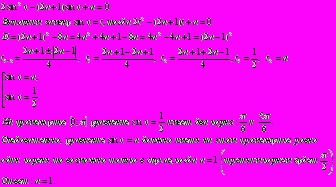
Пример 3. Решите уравнение
 .
.Решение:

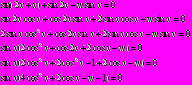


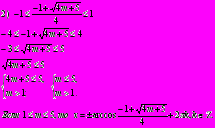

V. Тесты для самостоятельного решения
Данные тесты предназначены для проверки умений решения тригонометрических уравнений различными способами.
Вариант№1.


Вариант№2.

Вариант№3.

Вариант№4.
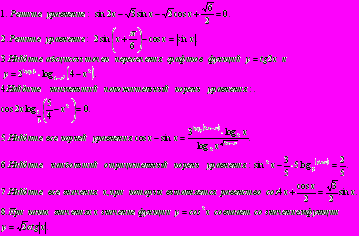
Литература
- Алгебра и начала анализа: дидактические материалы для 10 класса / М.К.Потапов, А.В.Шевкин.-2-е изд.-М.:Просвещение,2007.
- Алгебра и начала анализа: дидактические материалы для 11 класса: базовый и профильные уровни / М.К.Потапов, А.В.Шевкин.-2-е изд.-М.:Просвещение,2007.
- Бурмистрова Н.В.,СтаростенковаН.Г.Математика.11класс. Подготовка к экзамену.
-Саратов: Лицей,2005.
- Единый государственный экзамен: Математика: контрольные измерительные материалы: 2006-2007.-М.:Просвещение: СПб.: Просвещение,2007.
- ЕГЭ-2009.Математика: Сдаём без проблем!/ О.А.Креславская, В.В.Крылов, В.И.Снегурова, В.Е.Ярмолюк.-М.:Эксмо.2008.
- ЕГЭ. Репетитор. Математика.Эффективная методика./ Л.Д.Лаппо, А.В.Морозов, М.А.Попов.-М.:Издательство «Экзамен»,2007.
- Панчишкин А.А.. Шавгулидзе Е.Т. Тригонометрические функции в задачах - М.:Наука. Главная редакция физико – математической литературы,1986.
- Самое полное издание типовых вариантов реальных заданий ЕГЭ:2009:Математика /
авт.-сост. В.И.Ишина, В.В.Кочагин, Л.О.Денишева и др.-М.:АСТ: Астрель,2009.
- Сборник заданий для подготовки и проведения письменного экзамена по математике
(курс А) и алгебре и началам анализа (курс В) за курс средней школы.11 класс/
Г.В,Дорофеев, Г.К.Муравин ,Е.А.Седова.-10-е изд.,стереотип.-М.:Дрофа,2007.
- Тематические тесты. Математика. ЕГЭ-2009.Часть2.10-11 классы/ Под редакцией Ф.Ф.Лысенко. - Ростов-на-Дону:Легион,2008.
- Макеева А.В.Карточки по тригонометрии.10-11 класс: Дидактический материал
для учителей. - Саратов:Лицей.2002.
- Макарова Л.В. Уроки-практикумы в системе работы учителя. //Математика в школе,1998,№3.
- Математика: интенсивный курс подготовки к экзамену.-4-е изд.испр. и доп.-М.:Рольф:Айрис-пресс,1999.
- Математика: Тематическое планирование уроков подготовки к экзамену / А.В.Белошинстая.-М.:Издательство «Экзамен»,2007.
- Шаммин В.М. Тематические тесты для подготовки к ЕГЭ по математике. Изд.3-е.-
Ростов н/Д: Феникс,2004.
