Один из важнейших аспектов модернизации содержания математического образования включение в школьные программы элементов статистики, комбинаторики и теории вероятностей
| Вид материала | Документы |
- Программа семинара для слушателей курсовой подготовки «Формы и методы преподавания, 66.17kb.
- Алгебра- 9 класс Пояснительная записка, 250.35kb.
- Алгебра, 9 класс Пояснительная записка, 307.04kb.
- Методика изучения темы: «Элементы статистики, комбинаторики и теории вероятностей, 1031.61kb.
- Урок №1 тема: история развития теории вероятностей. Предмет теории вероятностей, 71.79kb.
- Беляева Светлана Борисовна учитель математики пояснительная записка, 192.79kb.
- Программа дисциплины ''Модели региональной экономики'' для направления 521600 Экономика, 87.19kb.
- Календарно-тематический план учебная дисциплина: «Математика», 40.92kb.
- Программа курса для студентов, 38.52kb.
- Рабочей программы учебной дисциплины «основы теории вероятностей и математической статистики», 46.75kb.
Один из важнейших аспектов модернизации содержания математического образования – включение в школьные программы элементов статистики, комбинаторики и теории вероятностей. Это обусловлено ролью, которую играют вероятностно-статистические знания в общеобразовательной подготовке современного человека. Без минимальной вероятностно-статистической грамотности трудно адекватно воспринимать социальную, политическую, экономическую информацию и принимать на ее основе обоснованные решения. Современная физика, химия, биология, весь комплекс социально-экономических наук построены и развиваются на вероятностно-статистической базе. Без соответствующей подготовки невозможно полноценное изучение этих дисциплин уже в средней школе.
В течение последних лет материалы по комбинаторике, теории вероятностей, статистике появились в учебниках математики, однако не во всех УМК они являются систематическими.
Как показывает анализ учебников и учебных пособий, содержащих материал по данной теме, существуют проблемы как в вопросах изложения этого достаточно сложного материала в школьном курсе, так и в определении содержания, необходимого для успешного усвоения и понимания основ теории вероятностей и статистики, и его соответствия содержанию и требованиям ФГОС по математике. Включение элементов комбинаторики, статистики и теории вероятностей в государственный стандарт общего образования требует более тщательного осмысления методики преподавания этих разделов математики.
При разработке общего подхода к преподаванию статистики и теории вероятностей в лицее мы руководствовались следующими положениями:
- Наглядность и простота изложения.
- Минимальный формализм в записи выражений и определениях.
- Использование сквозных примеров и задач при обсуждении разных тем.
- Подчеркнутая ясность и простота формулировок большинства задач.
- Выделение более сложных задач, которые помещены в конце обсуждаемой темы и отмечены символом.
- Отсутствие однозначного ответа в некоторых задачах и вопросах. (В основном, эти задачи предполагают обсуждение в классе и требуют от учащихся разумного обоснования своего мнения)
- Подбор примеров и задач с учетом различных интересов и возрастных особенностей развития учащихся.
- Проведение небольших практических исследований (измерений) и экспериментов для лучшего понимания природы случайной изменчивости и смысла вероятности.
- Возможность повторения и закрепления на новом материале пройденного ранее.
- Дать законченное элементарное представление о теории вероятностей и статистике и их тесной взаимосвязи.
- Подчеркивать тесную связь этих разделов математики с окружающим миром, как на стадии введения математических понятий, так и на стадии использования полученных результатов;
- Избегать утративших свою актуальность для общества примеров и задач, в том числе задач из азартных игр.
- Иллюстрировать материал яркими, доступными и запоминающимися примерами.
На наш взгляд, все это должно способствовать усвоению простых, но принципиально новых для учащихся понятий, росту интереса учащихся к математике в целом, формированию современного мировоззрения и умения ориентироваться в изменчивом информационном мире.
Для полноценного и качественного усвоения данного материала учителя лицея учитывают принципы дидактики:
1. Используют средства наглядности, опытную работу с учащимися.
2. Сопровождают изучение иллюстративными задачами и примерами.
3. Рекомендуют учащимся дополнительную литературу по данной теме, доступную для их понимания.
4. Предусматривают задачи для самостоятельной работы учащихся.
5. Учитывают индивидуальные особенности школьника при решении различных задач и примеров.
6. Добиваются прочности знаний с помощью решения задач, опирающихся на ранее изученный материал.
Изучение элементов комбинаторики, вероятности, статистики целесообразно начинать в 5 классе и продолжать в течение всего дальнейшего периода обучения (постепенный переход от простого к сложному).
На всех ступенях обучения фактически формируются одни и те же виды деятельности, но на разных уровнях и различными средствами.
Рассмотрим примерное содержание материала для каждого этапа обучения.
5-6 классы
Существование и построение комбинаций с какими-либо заданными свойствами. Перебор возможных вариантов.
Достоверное, невозможное, случайное событие. Сравнение шансов наступления случайных событий на основе интуитивных соображений, на классической, статистической основах, с помощью геометрических соображений.
Представление данных. Чтение таблиц, диаграмм.
7—9 классы
Комбинаторные правила произведения и сложения. Решение комбинаторных задач на правила умножения и сложения.
Эксперимент со случайными исходами, случайное событие. Операции над событиями. Частота события. Вероятность события. Вычисление вероятности наступления случайных событий на классической, статистической, геометрической основах.
Первичная обработка статистических данных. Наглядное представление статистической информации. Статистические характеристики. Статистические исследования. Статистическое оценивание и прогноз.
10—11 классы
Размещения, перестановки, сочетания. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Вероятностное пространство. Вероятность события. Вероятности суммы и произведения событий. Решение задач.
[Случайные величины и их характеристики. Понятие о законе больших чисел.]
В результате изучения данных тем учащиеся должны:
- понимать вероятностный характер многих закономерностей окружающего мира;
- решать комбинаторные задачи методом перебора, с использованием известных комбинаторных правил и формул;
- использовать комбинаторные схемы для вычисления вероятностей случайных событий в классической модели;
- вычислять вероятности наступления случайных событий на статистической основе, с помощью геометрических соображений;
- использовать приобретенные знания и умения для анализа реальных числовых данных, представленных в виде таблиц, диаграмм, графиков, для сбора и анализа информации статистического характера, для решения учебных и практических задач.
1. Изучение стохастической линии в 5-6 классе по учебнику «Математика-5», «Математика-6» (авторы: Н. Я. Виленкин, В. И.Жохов и др.) производится не параллельно с изучением основного материала, а отдельным блоком. Для этого отводится 15 часов в IV четверти (за счёт компонента образовательного учреждения). Тематическое планирование прилагается.
Знакомство с элементами теории вероятностей мы начинаем с изложения на интуитивном уровне понятий случайного события и его вероятности. На этом этапе мы никак не связываем эти вопросы с комбинаторикой как таковой, не делаем первостепенного упора на комбинаторику, как это часто делается в так называемой схеме "классической теории вероятностей". Учащиеся должны знать и понимать, что основным способом определения вероятности события в содержательных примерах на практике является частотный подход, но что порой определение вероятности события – это довольно сложная или даже неразрешимая задача.
Преподавание данного курса 7-9 классов и профильных 10-11 классах ведётся в соответствии с тематическим планированием под редакцией А. Г. Мордкович.
В лицее № 34 учащиеся 10-11 классов знания, полученные на уроках по данной теме, применяют при решении практических задач на семинарах и практикумах в КГУ им. Н. А. Некрасова. Считаем, что данная практика позволяет успешно решать задачи ЕГЭ по данной теме и в дальнейшем легче усваивать комбинаторику, теорию вероятности в ВУЗах.
При организации и планировании итогового контроля нами используются тексты контрольных работ под редакцией А.Г. Мордковича, а также самостоятельные работы Александрова. Используемые тексты контрольных работ и список используемой литературы прилагается.
Введение элементов комбинаторики по нашему мнению должно быть подчинено вероятностным задачам, а не наоборот. Важно научить учащихся перебору различных комбинаций, подходам к этому перебору, а не доказательства комбинаторных теорем и формальным преобразованиям выражений, включающих число сочетаний или перестановок. Важно показать, что без использования комбинаторных подходов во многих вероятностных задачах трудно описать все элементарные события. Важно дать наглядное, запоминающееся представление о тех практических ситуациях, где используются комбинаторные принципы подсчета, а не заучивать "схему урн с различными или неразличимыми шарами разного цвета", которая сама по себе является уже обобщенной моделью многих различных практических задач, и усваивается с трудом.
Тема перехода от элементарных событий к произвольным событиям и операциям с ними изложены нами без привлечения понятия "множества". Хотя по сути дела операции над событиями полностью аналогичны операциям над множествами. Мы надеемся, что для части учителей это облегчит процесс преподавания. Очень наглядны и полезны диаграммы Эйлера, показывающие, как соотносятся друг с другом различные события.
В заключении нам хочется ещё раз обратить внимание на особую значимость данной темы в школьном курсе математики. не только в плане развития познавательных способностей учащихся ,но и в плане подготовки к успешному решению задач по теории вероятности, комбинаторики и статистики при прохождении итоговой аттестации за курс 9класса ( ГИА) и 11 класса (ЕГЭ)
Приложение.
Тематическое планирование 5 класс
Тема: «Элементы статистики, комбинаторики и теории вероятностей» 15 часов
| № урока | Содержание изучаемого материала | Тип урока | Дата проведения |
| 1 | Что изучает теория вероятностей. | | |
| 2 | Случайные, невозможные и достоверные события | | |
| 3 | Случайные, невозможные и достоверные события. Самостоятельная работа. | | |
| 4 | Что вероятнее? Сравнение шансов. | | |
| 5 | Вероятность случайного события. Классическое определение вероятности. | | |
| 6 | Решение задач на определение вероятности случайного события. | | |
| 7 | Решение задач. Самостоятельная работа. | | |
| 8 | Комбинаторные задачи. | | |
| 9 | Дерево возможных вариантов. | | |
| 10 | Комбинаторное правило умножения. | | |
| 11 | Практикум по решению комбинаторных задач. | | |
| 12 | Решение задач. Самостоятельная работа. | | |
| 13 | Среднее арифметическое. (Повторение) | | |
| 14 | Повторительно-обобщающий урок по теме: «Элементы статистики, комбинаторики и теории вероятностей» | | |
| 15 | Контрольная работа по теме: «Элементы статистики, комбинаторики и теории вероятностей» | | |
Тематическое планирование 6 класс
Тема: «Элементы статистики, комбинаторики и теории вероятностей» 15 часов
| № урока | Содержание изучаемого материала | Тип урока | Дата проведения |
| 1 | Факториал. | | |
| 2 | Нахождение значений выражений, содержащих знак факториала. Самостоятельная работа. | | |
| 3 | Перестановки. | | |
| 4 | Решение задач по теме: «Перестановки». | | |
| 5 | Решение задач. Самостоятельная работа. | | |
| 6 | Размещения. | | |
| 7 | Решение задач по теме: «Размещения» | | |
| 8 | Решение задач. Самостоятельная работа. | | |
| 10 | Виды диаграмм. Чтение диаграмм. | | |
| 11 | Построение столбчатых и круговых диаграмм. | | |
| 12 | Построение различных диаграмм с применением ИКТ | | |
| 13 | Практикум по построению диаграмм с применением ИКТ | | |
| | Построение диаграмм. Самостоятельная работа. | | |
| 14 | Повторительно-обобщающий урок по теме: «Элементы статистики, комбинаторики и теории вероятностей» | | |
| 15 | Контрольная работа по теме: «Элементы статистики, комбинаторики и теории вероятностей» | | |
Учебники, включающие элементы комбинаторики, статистики, теории вероятностей:
5-6 классы
1. Математика: Учеб. для 5 кл. общеобразоват. учреждений /Под ред. Г.В. Дорофеева, И.Ф. Шарыгина.- М.: Просвещение, Дрофа, 2000-2003.
Математика: Учеб. для 6 кл. общеобразоват. учреждений /Под ред. Г.В. Дорофеева, И.Ф. Шарыгина.- М.: Дрофа, Просвещение, 2000-2003.
2. Арифметика: Учеб. для 5 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.- М.: Просвещение, 1999-2002.
Арифметика: Учеб. для 6 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.- М.: Просвещение, 2000-2002.
3. Зубарева И.И., Мордкович А.Г. Математика: Учеб. для 5 кл. общеобразоват. учреждений. - М.: Мнемозина, 2002.
Зубарева И.И., Мордкович А.Г. Математика: Учеб. для 6 кл. общеобразоват. учреждений. - М.: Мнемозина, 2003.
4. Математика: Учебник-собеседник для 5 кл. общеобразоват. учреждений / Л.Н. Шеврин, А.Г. Гейн, И.О. Коряков, М.В. Волков.- М.: Просвещение, 2000-2002.
Математика: Учебник-собеседник для 6 кл. общеобразоват. учреждений / Л.Н. Шеврин, А.Г. Гейн, И.О. Коряков, М.В. Волков. - М.: Просвещение, 2000-2002.
7-9 классы
5. Математика: Арифметика, алгебра, анализ данных: Учеб. для 7 кл. общеобразоват. учреждений / Под ред. Г.В. Дорофеева.- М.: Дрофа, 2000-2003.
Математика: Алгебра, функции, анализ данных: Учеб. для 8 кл. общеобразоват. учреждений / Под ред. Г.В. Дорофеева.- М.: Дрофа, 2000-2003.
Математика: Алгебра, функции, анализ данных: Учеб. для 9 кл. общеобразоват. учреждений / Под ред. Г.В. Дорофеева.- М.: Дрофа, 2000-2003.
6. Алгебра: Учеб. для 7 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.- М.: Просвещение, 1999-2002.
Алгебра: Учеб. для 8 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.- М.: Просвещение, 2000-2002.
Алгебра: Учеб. для 9 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.- М.: Просвещение, 2001-2002.
Вкладыши к учебникам:
7. Мордкович А.Г., Семенов П.В. События. Вероятность. Статистика: Дополнительные материалы к курсу алгебры для 7-9 кл. – М.: Мнемозина, 2002. (к учебникам А.Г. Мордковича)
8. Ткачева М.В., Федорова Н.Е. Алгебра, 7-9: Элементы статистики и вероятность. - М.: Просвещение, 2003. (к учебникам А.Ш. Алимова и др.)
Дополнительная литература:
9. Бунимович Е.А., Булычев В.А. Вероятность и статистика, 5-9 кл. – М.: Дрофа, 2002.
10. Бунимович Е.А. Вероятностно-статистическая линия в базовом школьном курсе математики.- Математика в школе, №4, 2002.
11. Бунимович Е.А., Суворова С.Б. Методические указания к теме «Статистические исследования».- Математика в школе, №3, 2003.
12. Мордкович А.Г., Семенов П.В. События, вероятности, статистическая обработка данных.- Математика (приложение к газете «Первое сентября»), №34, 35, 41, 43, 44, 48, 2002, №11, 17, 2003.
13. Селютин В.Д. О формировании первоначальных стохастических представлений.- Математика в школе, №3, 2003.
14. Селютин В.Д. О подготовке учителей к обучению школьников стохастике.- Математика в школе, №4, 2003.
15. Ткачева М.В., Федорова Н.Е. Элементы статистики в курсе математики 7-9 классов основной школы.- Математика в школе, №3, 2003.
16. Ткачева М.В. Анализ данных в учебниках Н.Я. Виленкина и других.- Математика в школе, №5, 2003.
Материалы для организации переподготовки учителей
17. Изучение теории вероятностей и статистики в школьном курсе математики. Программа для курсов повышения квалификации учителей/ В.А. Булычев, Е.А. Бунимович - Математика в школе, №4, 2003.
Приложение № 2
Самостоятельные и контрольные работы по теории вероятностей и статистике
С-1 Вариант 1
1. На уроке рисования первокласснику надо раскрасить прямоугольник, треугольник и круг в один из четырех цветов (желтый, синий, красный или зеленый) так, чтобы все три фигуры были разных цветов.
а) Сколько существует способов раскрашивания этих трех фигур?
б) Сколько среди них способов раскрашивания, в которых круг будет зеленым?
2. Сколько двузначных чисел можно составить из пяти цифр: 2; 3; 5; 7; 8? Сколько среди них чисел, кратных 3?
Вариант 2
1. Ученик на уроке труда вырезает из цветной бумаги звезду, квадрат и круг. У него имеется пять листов бумаги разных цветов (желтый, зеленый, красный, синий и фиолетовый). Ученик хочет вырезать все три фигуры разного цвета, но при этом звезда должна быть непременно красной или синей.
а) Сколько существует способов вырезания фигур заданным образом?
б) Сколько среди них способов, в которых круг будет фиолетовым?
2. Сколько трехзначных чисел можно составить из четырех цифр: 1; 4; 5; 8? Сколько среди них чисел, кратных 5?
С-2 Вариант 1
1. На соревновании по фигурному катанию фигурист за произвольную программу получил следующие баллы:
4,8; 4,6; 4,1; 4,6; 4,5; 4,3; 4,6; 4,5; 4,5; 4,3.
а) Составьте таблицу распределения данных.
б) Найдите объем выборки, кратность и частоту каждой варианты.
Вариант 2
1. На соревновании по фигурному катанию фигурист за произвольную программу получил следующие баллы:
5,9; 5,9; 5,7; 6,0; 5,8; 5,9; 5,8; 5,7; 5,8; 5,9.
а) Составьте таблицу распределения данных.
б) Найдите объем выборки, кратность и частоту каждой варианты.
С-3 Вариант 1
Таблица распределения баллов за контрольную работу по математике имеет вид:
| Варианта | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 14 | 15 | 16 | 17 | Всего 12 вариант |
| Кратность | 2 | 1 | 2 | 4 | 3 | 3 | 5 | 2 | 4 | 1 | 2 | 1 | Сумма — 30 |
По данным таблицы:
а) составьте многоугольник распределения кратностей;
б) определите моду, размах и среднее значение;
в) постройте гистограмму частот (в %), если отметка «5» ставилась за 15 –17 баллов, «4» — за 11–14 баллов, «3» — за 8–10 баллов, «2» — менее 8 баллов.
Вариант 2
Таблица распределения цен на хлеб в ряде магазинов имеет вид:
| Варианта | 6,9 | 7,3 | 7,5 | 7,9 | 8,3 | 8,5 | 8,9 | 9,5 | 10 | Всего 9 вариант |
| Кратность | 6 | 8 | 12 | 9 | 10 | 6 | 5 | 4 | 3 | Сумма — 63 |
По данным таблицы:
а) составьте многоугольник распределения кратностей;
б) определите моду, размах и среднее значение;
в) постройте гистограмму частот (в %) ценовых категорий на хлеб:
№ 1 — менее 7 р.,
№ 2 — от 7 до 8 р.,
№ 3 — от 8 до 9 р.,
№ 4 — более 9 р.
С-4Вариант 1
1. В мешке лежат 7 синих, 8 красных и 6 зеленых одинаковых по форме шаров. Не глядя, вынимают один шар. Какова вероятность того, что шар окажется зеленым?
2. В коробке «Ассорти» лежат 30 одинаковых по виду шоколадных конфет, из которых 18 штук со сливочной начинкой и 12 штук — с ореховой. Выбираются наугад две конфеты. Какова вероятность того, что обе конфеты окажутся с ореховой начинкой?
Вариант 2
1. Выпускники девятого класса выбрали для продолжения образования следующие профили обучения: 7 человек — юридический, 12 человек — экономический, 6 человек — математический и 10 человек — гуманитарный. Какова вероятность того, что случайно встреченный выпускник этого класса выбрал математический профиль обучения?
2. Ученику надо выучить к зачету 32 вопроса. Он выучил 24 вопроса. На зачете он вытягивает два билета из 32, по одному вопросу в каждом. Какова вероятность того, что ответ хотя бы на один вопрос он знает?
С-7. Вариант 1
1. По статистике ежедневных продаж в одном из супермаркетов чеки со скидкой составляют 15%. В течение дня супермаркет посетило 2055 человек. Сколько человек приблизительно получили скидку?
2. Вероятность того, что семена огурцов взойдут, равна 0,84. Сколько семян приблизительно было взято для проращивания, если взошло 140 семян?
Вариант 2
1. Во время распродажи цена на оргтехнику была снижена в среднем на 30%, при этом цена на принтеры была снижена на 12% от среднего снижения цен на всю оргтехнику. Какова была цена принтера во время распродажи, если до распродажи он стоил 5400 рублей?
2. Вероятность брака при использовании современных высокоточных технологий равна 0,0015. Сколько качественных изделий выпускает предприятие, если число бракованных изделий за исследуемый период было равно 2?
Контрольная работа
Элементы комбинаторики, статистики и теории вероятностей
Вариант 1
1. Сколько различных двузначных чисел можно составить из цифр 0, 2, 4, 5, 7? Сколько среди них будет нечетных чисел?
2. Вычислите:
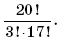
3. Сколькими способами можно обозначить вершины восьмиугольника буквами C, D, M, N,U, V, T, Q?
4*. Случайным образом выбрали двузначное число. Какова вероятность того, то остаток от деления этого числа на 8 равен 5?
5*. На детской метеостанции ученик производил замеры температуры воздуха в течение 15 дней мая в одно и то же время и получил следующий ряд значений (в °C):
12,4; 12,4; 12,8; 14,1; 15; 15; 14,8; 14,1; 13,9; 13,5; 15; 15; 14,8; 14,1; 12,4.
а) Составьте таблицу распределения данных и распределения частот.
б) Найдите размах, моду и среднее значение данного ряда чисел.
Вариант 2
1. Сколько различных трехзначных чисел можно составить из цифр 0, 3, 6, 7 при условии, что цифры в числе не повторяются? Сколько среди них четных чисел?
2. Вычислите:
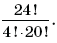
3. Команда девятиклассников в количестве 7 человек принимала участие в соревнованиях по мини-футболу. Перед началом матча они построились на поле следующим образом: капитан, вратарь, а остальные игроки в произвольном порядке. Сколько существует способов построения команды?
4*. Случайным образом выбрали трехзначное число. Какова вероятность того, что сумма его цифр равна 21?
5*. На экзамене учащиеся класса получили следующие результаты по 100-балльной шкале: 36, 38, 45, 48, 48, 49, 52, 53, 55, 53, 48, 63, 67, 69, 67, 72, 72, 69, 53, 55, 69, 72, 70, 53, 67.
а) Постройте графики распределения данных и распределения частот.
б) Найдите размах, моду и среднее значение данного ряда чисел.
