Программа курса для студентов

Вид материала

Программа курса

Содержание Содержание курса

Подобный материал:

• Программа курса «политическая география. Формирование политической карты мира» для, 309.98kb.
• Программа курса, 383.76kb.
• Программа курса Новосибирск 2005 Программа составлена в соответствии с Государственным, 77.33kb.
• Программа курса для студентов По специальности 030501- "Юриспруденция", 807.97kb.
• Программа лекционного курса для студентов 5 курса спец. «история», 413.6kb.
• Программа курса для студентов вузов специальности 050501, 130.04kb.
• Программа курса общая психология для студентов 3 курса физического факультета мгу тематический, 176.66kb.
• Программа курса Для студентов направления «Управление муниципальное», 407.8kb.
• Шаповалов Александр Васильевич I. Oрганизационно-методический раздел Цель курса программа, 107.74kb.
• Шаповалов Александр Васильевич I. Oрганизационно-методический раздел Цель курса программа, 67.82kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ


УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯНКИ КУПАЛЫ»


УТВЕРЖДАЮ

Ректор _______________ Е.А. Ровба


«___ » ____________________ 200 ___ г.


ВЫСШАЯ МАТЕМАТИКА

раздел

Теория вероятностей и математическая статистика

ПРОГРАММА КУРСА


ДЛЯ СТУДЕНТОВ

СПЕЦИАЛЬНОСТИ 1-25 01 03 «Мировая экономика», 1-25 01 10 «Коммерческая деятельность», 1-25 01 07 «Экономика и управление на предприятии», 1-25 01 04 «Финансы и кредит»


Гродно 2006 год


Предисловие


Целью курса является изучение математического обоснования методов теории вероятностей и математической статистики.

Кроме того, современные методы обработки результатов эксперимента и подготовки отчетов требуют умения работы со стандартными статистическими пакетами. Целью курса является также приобретение навыков работы со статистическим пакетом Statistica for Windows.


Введение


Курс «Теория вероятностей и математическая статистика» является основой еще нескольких курсов по экономической статистике. Кроме того, курсовое и дипломное проектирование может основываться на статистической обработке экономических данных. В этой связи важно научить студентов пользоваться недетерминированными методами в научном исследовании.

Изучение основных методов теории вероятностей необходимо для понимания построения методов математической статистики.

Знания и умения из раздела «Математическая статистика» должны основываться на понимании природы изучаемых данных и обоснованном выборе методов.

Реализация методов математической статистики осуществляется с помощью статистического пакета Statistica for Windows с целью устранения ошибок вычислительного характера, а также экономии времени для анализа полученных результатов.

Содержание курса

1. Случайные события. Действия над событиями. Классическая вероятность и ее свойства. Формулы комбинаторики. Примеры.
   
2. Условная вероятность. Независимость событий. Формула полной вероятности. Формула Байеса.
   
3. Схема независимых испытаний Бернулли. Формула Бернулли.
   
4. Дискретные и непрерывные случайные величины. Функция распределения вероятностей и ее свойства. Плотность распределения вероятностей и ее свойства.
   
5. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение, моменты, коэффициент корреляции.
   
6. Основные распределения случайных величин.
   
7. Многомерные случайные величины.
   
8. Закон больших чисел. Центральная предельная теорема.
   
9. Шкалы измерения. Понятие выборки. Графическое изображение выборки. Эмпирическая функция распределения.
   
10. Точечное оценивание. Требования, предъявляемые к точечным оценкам. Несмещенные оценки математического ожидания и дисперсии.
    
11. Интервальное оценивание. Доверительные интервалы для оценки параметров нормального распределения. Минимальный объем выборки для получения оценок заданной надежности и точности.
    
12. Проверка статистических гипотез. Уровень значимости и мощность критерия. Ошибки первого и второго рода.
    
13. Критерии 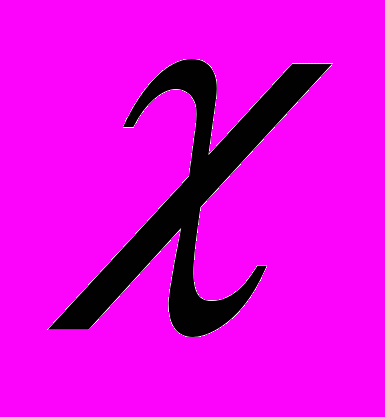-квадрат проверки гипотезы о виде распределения.
    
14. Дисперсионный анализ. Однофакторный и двухфакторный дисперсионный анализ.
    
15. Элементы регрессионного и корреляционного анализа. Парная линейная и нелинейная регрессия. Множественная линейна регрессия. Парный и множественный коэффициент корреляции, коэффициент детерминации. Проверка гипотез о достоверности этих коэффициентов.
    

Литература.

№ п/п	СПІС
1	Булдык Г.М. Теория вероятностей и математическая статистика. – Мн.: Выш. школа, 1989.
2	Гмурман В.Е. Теория вероятностей и математическая статистика.- М.: Высшая школа, 1977.
3	Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.- М.: Высшая школа, 1978.
4	Гурский Е.И. Сборник задач по теории вероятностей и математической статистике.- Мн.: Выш. школа, 1984.
5	Лихолетов И.И., Мацкевич И.П. . Руководство к решению задач по выс- шей математике и математической статистике.- Мн.: Выш. школа, 1976.
6	Мацкевич И.П., Свирид Г.П. Высшая математика: Теория вероятностей и математическая статистика.- Мн.: Выш. школа, 1993.
7	Мацкевич И.П., Свирид Г.П., Булдык Г.М. Сборник задач по высшей математике: Теория вероятностей и математическая статистика.- Мн.: Выш. школа, 1996.
8	Основные возможности пакета Statisticа for Windows. Учебно-методические рекомендации для студентов нематематических специальностей / Сост. Ляликова В.И., Макарова Н.П. - Гродно, 1997.
9	Сборник задач математике для вузов. В 3 ч. Ч. 3. Теория вероятностей и математическая статистика/Э.А.Вуколов, А.В.Ефимов, В.Н.Земсков и др. - М.: Наука, 1990.