Методика изучения числовых систем
| Вид материала | Документы |
- Методика изучения учебной мотивации по итогам обучения в 1-м классе 1 Методика изучения, 417.39kb.
- Методика изучения мотивов участия школьников в деятельности, 1409.71kb.
- Методика изучения ориентировочно-исследовательского поведения мышей в «открытом поле», 165.24kb.
- Реферат электронная таблица Excel, 324.13kb.
- Методика преподавания экономики в высшей школе Код, 19.08kb.
- Правила работы и некоторые операции: (p,q) = (s,w) (p,w) = (q,s); (p,q) + (s,w), 31.59kb.
- Методика обучения алгоритмам умножения и деления на двузначное и трехзначное число., 77.64kb.
- Программа дисциплины дпп ф. 09 «числовые системы» Специальность 032100 (050201. 65), 121.39kb.
- Методика грамматики. Задачи изучения грамматики в школе. Роль грамматики в формировании, 19.02kb.
- Методика словообразования. Значение, содержание и задачи изучения словообразования, 35.75kb.
Методика изучения числовых систем
Изучение чисел в школьном курсе математики ведется в такой последовательности: натуральные числа, нуль, дроби (положительные), отрицательные чисел и множество рациональных чисел, иррациональные числа и множество действительных чисел. Эта последовательность отражает исторический путь развития понятия числа в математике: N
 Q+
Q+ Q
Q R (историческая схема развития понятия числа). В математике дроби возникли значительно раньше, чем отрицательные числа. В современной математике принята другая последовательность: N
R (историческая схема развития понятия числа). В математике дроби возникли значительно раньше, чем отрицательные числа. В современной математике принята другая последовательность: N Z
Z Q
Q R (логическая схема развития понятия числа). От исторической она отличается более ранним введением отрицательных чисел. Поэтому в такой последовательности после натуральных чисел изучаются целые числа. Приверженность школьного курса исторической схеме объясняется тем, что понятие дроби доступнее, чем понятие отрицательного числа.
R (логическая схема развития понятия числа). От исторической она отличается более ранним введением отрицательных чисел. Поэтому в такой последовательности после натуральных чисел изучаются целые числа. Приверженность школьного курса исторической схеме объясняется тем, что понятие дроби доступнее, чем понятие отрицательного числа. п.1. Методика изучения натуральных чисел. Множество натуральных чисел изучается с начальной школы. Без понимания структуры множества N нельзя достичь понимания структуры множеств Z, Q, R. Уже в начальных классах учащиеся понимают, что отношение «меньше» устанавливает определенный порядок в множестве N. Это объясняется с помощью упражнения: «b следует за a или a предшествует b, если
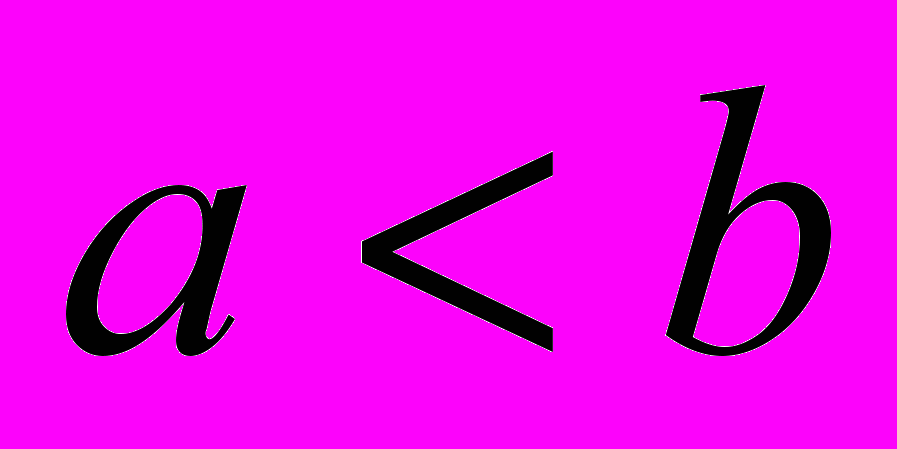 ». Далее на базе отношения «меньше» разъясняются более сложные отношения: «лежит между» и «непосредственно следует за» - это определяет свойство дискретности (то есть между ними нет ничего).
». Далее на базе отношения «меньше» разъясняются более сложные отношения: «лежит между» и «непосредственно следует за» - это определяет свойство дискретности (то есть между ними нет ничего). Правильная ориентация в методике изучения натуральных чисел в 5 классе предполагает знание, с одной стороны, связи данной темы с курсом 1-4 классов, с другой стороны – знание нового в содержании учебного материала и методике его изложения в 5 классе. Необходимо также учитывать общие особенности учебника математики 5 класса. В этом учебнике усиливается роль теоретического материала: приводятся определения, математические термины и обозначения, формулируются факты и законы, отдельные факты получают теоретическое объяснение. В учебниках соответствующий теоретический материал излагается в виде небольших фрагментов, после чего приводятся упражнения и задачи.
В 5 классе даются определения (или описания) понятий: натурального числа, десятичной записи числа, миллиарда, координатного луча, координаты точки, суммы двух чисел, слагаемых, числового выражения, значения выражения, разложения числа по разрядам, разрядных слагаемых, разности двух чисел, уменьшаемого, вычитаемого, произведения двух чисел, множителей, частного двух чисел, делителя числа, кратного числа и др. При этом учителю необходимо различать, в каком случае в учебнике приводится полноценное в логическом отношении определение, а в каком – описание понятия, не претендующее на строгость.
Пример 1. Понятие натурального числа. В учебнике говорится, что «числа, употребляемые при счете предметов, называются натуральными числами». Это описание. В математике при аксиоматическом построении теории натуральных чисел понятие натурального числа является неопределяемым (исходным). В тех случаях, когда понятие вводится описанием, заучивать соответствующую формулировку с учащимися не нужно.
Пример 2. В учебнике говорится: «Вычесть из числа a число b – значит найти такое число х, которое в сумме с числом b дает a:
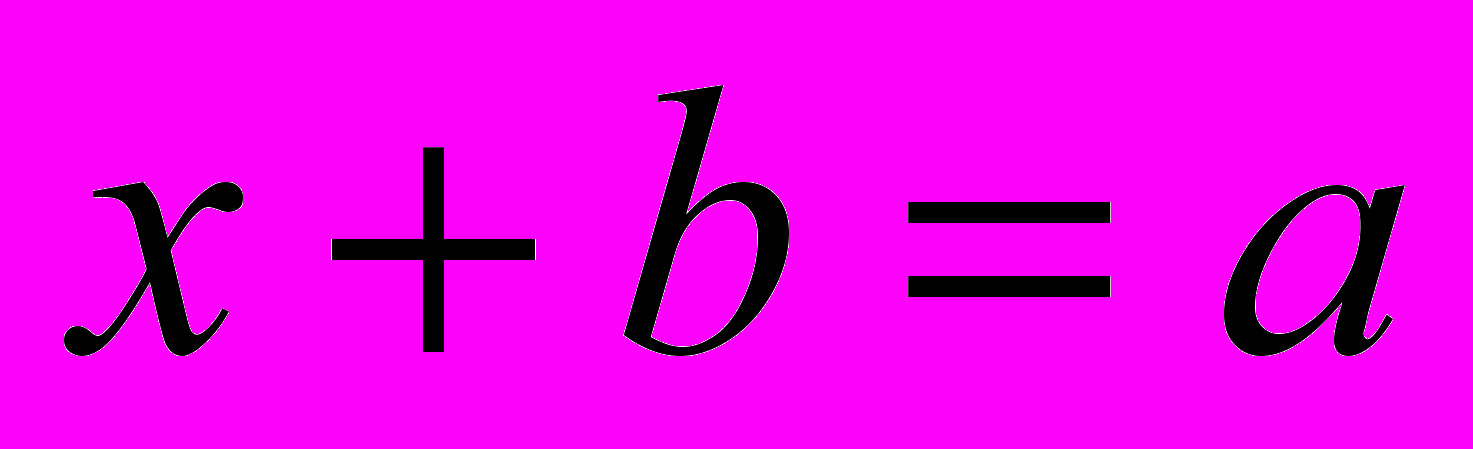 . Число х называют разностью чисел a и b, число a - уменьшаемым, а число b – вычитаемым». Это пример настоящего определения, которое именно в таком виде широко используется в математической науке. Наличие определений в 5 классе является одним из признаков повышения теоретического уровня изложения учебного материала. Понятие разности двух чисел должно быть разъяснено, а формулировка определения – тщательно отработана. Таким образом, учителю важно выяснить для себя, какие понятия, относящиеся к натуральным числам, вводятся в учебнике описанием, а какие – определением. Это позволит четче выделить элементы нового подхода в методике изучения натуральных чисел в 5 классе (по сравнению с методикой изучения числового материала в начальных классах). Усиление роли теоретических объяснений проявляется в сочетании индукции и дедукции.
. Число х называют разностью чисел a и b, число a - уменьшаемым, а число b – вычитаемым». Это пример настоящего определения, которое именно в таком виде широко используется в математической науке. Наличие определений в 5 классе является одним из признаков повышения теоретического уровня изложения учебного материала. Понятие разности двух чисел должно быть разъяснено, а формулировка определения – тщательно отработана. Таким образом, учителю важно выяснить для себя, какие понятия, относящиеся к натуральным числам, вводятся в учебнике описанием, а какие – определением. Это позволит четче выделить элементы нового подхода в методике изучения натуральных чисел в 5 классе (по сравнению с методикой изучения числового материала в начальных классах). Усиление роли теоретических объяснений проявляется в сочетании индукции и дедукции. п.2. Методика изучения обыкновенных и десятичных дробей. Первое знакомство с обыкновенными дробями происходит в 3 классе параллельно изучению натуральных чисел. Систематическое изучение дробей начинается в 5 классе. Десятичные дроби не являются новыми числами по сравнению с обыкновенными дробями. Они представляют лишь другую запись ранее известных обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. В математических вычислениях и практических расчетах более удобными являются десятичные дроби. Обыкновенные дроби в вычислениях используются гораздо реже.
В методике математики существуют различные подходы к порядку изучения обыкновенных и десятичных дробей: 1) вначале изучаются обыкновенные дроби, затем – десятичные (традиционный подход), 2) вначале изучаются десятичные дроби, затем – обыкновенные, 3) смешанный вариант, при котором изучение обыкновенных и десятичных дробей чередуется. В учебнике Виленкина придерживаются смешанного варианта. Вначале в нем вводится понятие обыкновенной дроби. Затем рассматриваются вопросы сравнения, сложения и вычитания дробей с одинаковыми знаменателями. После этого осуществляется переход к десятичным дробям и рассматриваются все четыре арифметических действия над ними. Изучение десятичных дробей начинается и заканчивается в 5 классе. После этого в 6 классе вновь возвращаются к обыкновенным дробям: изучают сравнение произвольных дробей, арифметические действия над ними. Понятие процента примыкает к понятию десятичной дроби. Проценты – это новая форма записи десятичных дробей со знаменателем 100: 1%=
 =0,01, 15%=
=0,01, 15%=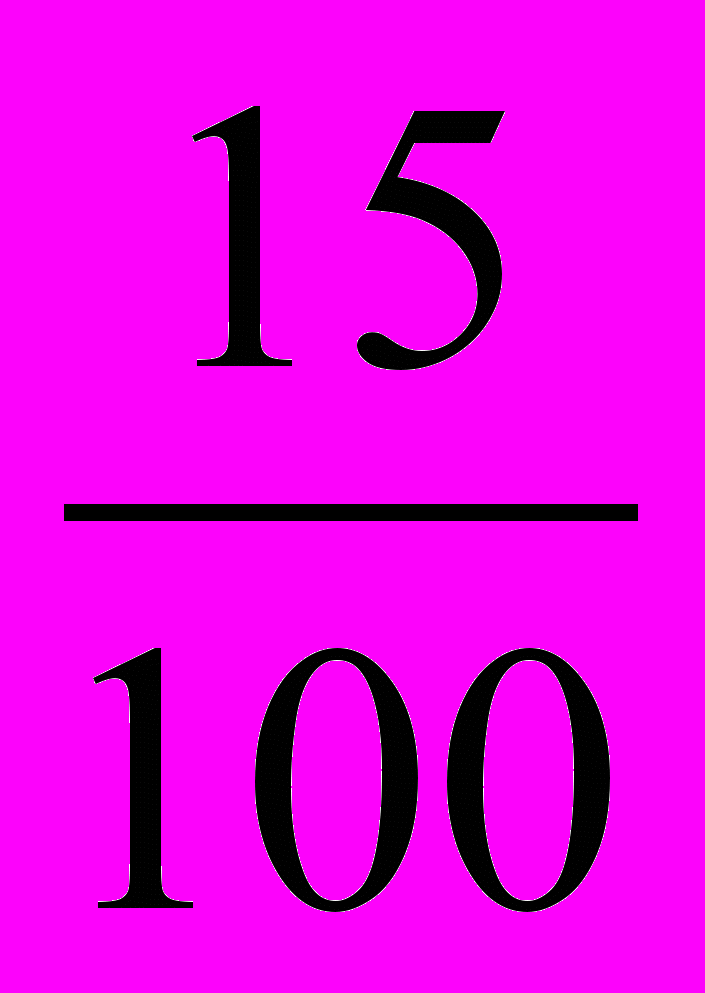 =0,15 и т.д..
=0,15 и т.д..Центральным в теме «Дробные числа» (5 класс) является понятие обыкновенной дроби. Оно вводится таким описанием (аналогично тому, как это делалось в 3 классе): приводится рисунок с изображением пирога, разрезанного на четыре равные части. Одна из них лежит на одной тарелке, а три части – на другой. Говорят: «На первой тарелке лежит одна четвертая часть пирога, а на второй – три четвертых части пирога». Пишут: «
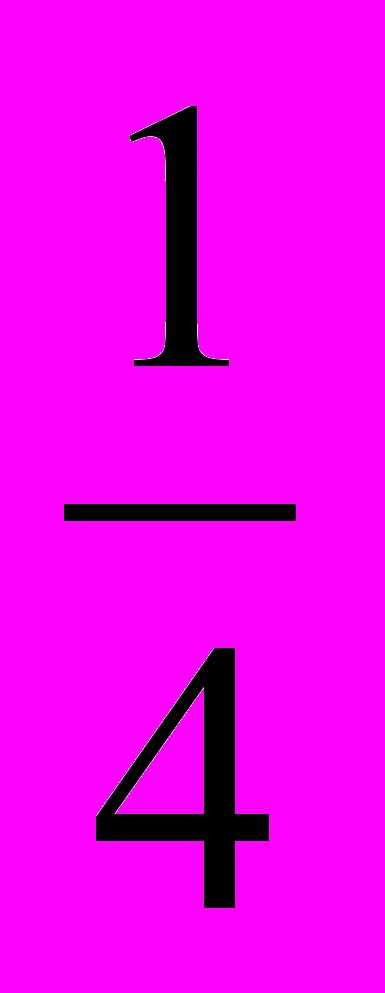 пирога,
пирога, 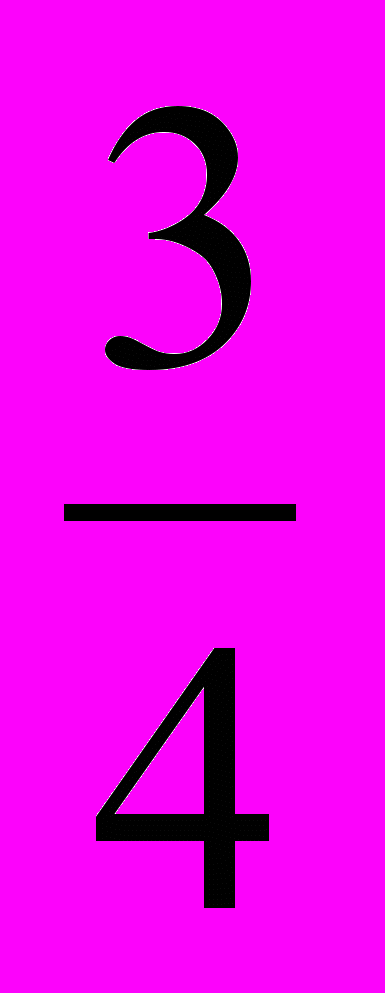 пирога». Далее сообщают, что такие числа как
пирога». Далее сообщают, что такие числа как 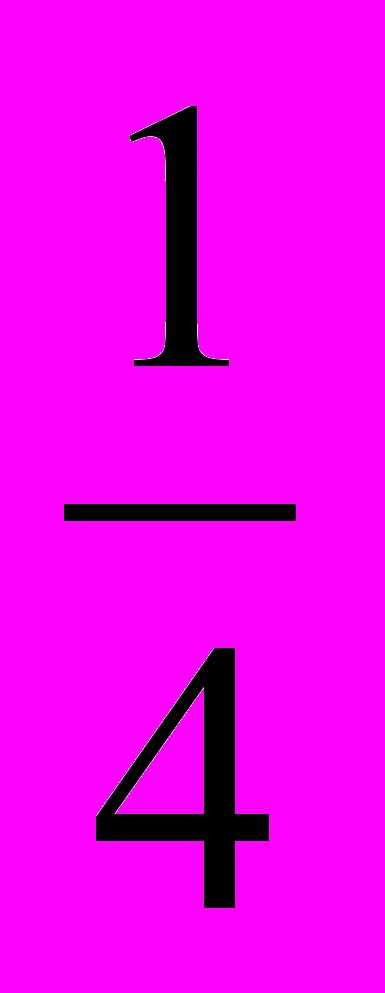 и
и 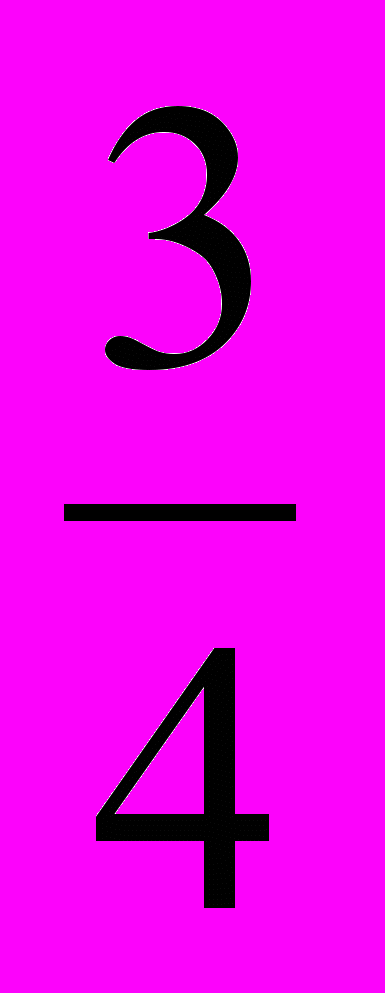 , называют обыкновенными дробями. В дроби
, называют обыкновенными дробями. В дроби 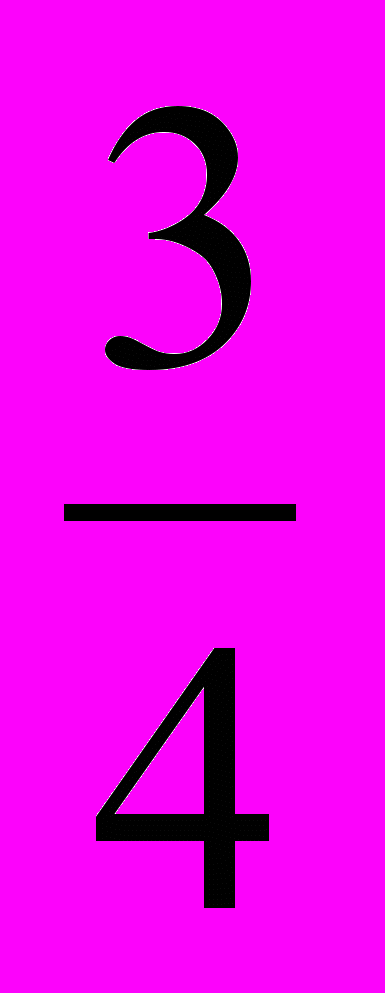 число 3 называют числителем дроби, а число 4 – ее знаменателем. Характеристика дроби начинается со знаменателя: знаменатель показывает, на сколько равных частей разрезан пирог, а числитель – сколько надо взять таких частей. Числитель пи шут над чертой, а знаменатель – под чертой. Проведенные разъяснения повторяются на других примерах. Вместо пирога может быть взят круг (отрезок, прямоугольник, квадрат), разделенный на шесть(восемь, семь восемнадцать) равных частей.
число 3 называют числителем дроби, а число 4 – ее знаменателем. Характеристика дроби начинается со знаменателя: знаменатель показывает, на сколько равных частей разрезан пирог, а числитель – сколько надо взять таких частей. Числитель пи шут над чертой, а знаменатель – под чертой. Проведенные разъяснения повторяются на других примерах. Вместо пирога может быть взят круг (отрезок, прямоугольник, квадрат), разделенный на шесть(восемь, семь восемнадцать) равных частей. Методическая схема введения понятия обыкновенной дроби в 5 классе:
- выполнить материализованные действия по делению предмета на 4 равные части;
- сообщить термины «одна четвертая», «три четвертых»;
- ввести записи:
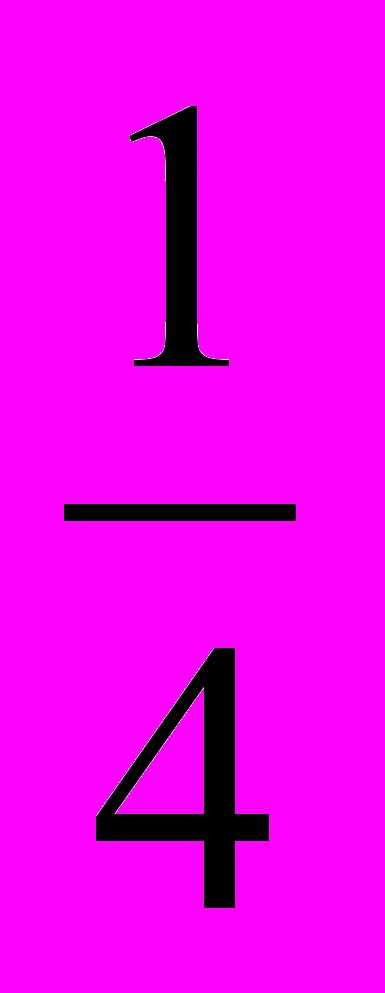 ,
, 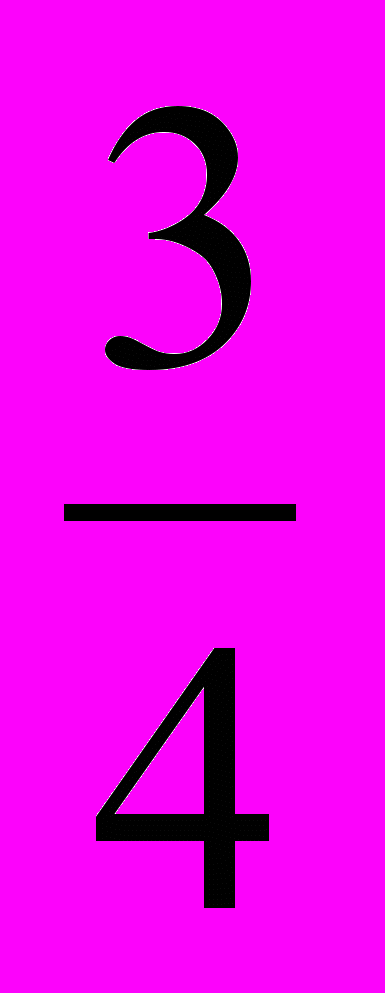 ;
;
- сообщить термины «обыкновенная дробь», «числитель дроби», «знаменатель дроби»;
- дать содержательную характеристику дроби (что показывает знаменатель дроби, что показывает ее числитель);
- привести другие примеры дробей, записать и прочитать их.
Важным элементом методики изучения чисел является убеждение учащихся в целесообразности введения новых чисел. Возможность записать доли с помощью обыкновенных дробей является одним из приемов убеждения учащихся в полезности таких дробей. Помимо этого существуют еще два других приема, показывающих необходимость введения дробных чисел. Мотивировать введение дробных чисел можно также тем, что с их помощью операция деления натуральных чисел делается всегда выполнимой. Пример. В множестве натуральных чисел число 2 не делится на число 3. Дополним это множество дробями и вновь рассмотрим деление числа 2 на 3. Пусть требуется разделить 2 яблока между тремя учениками. Как это сделать? Разрежем каждое яблоко на три равные части. Одна такая часть выражается дробью
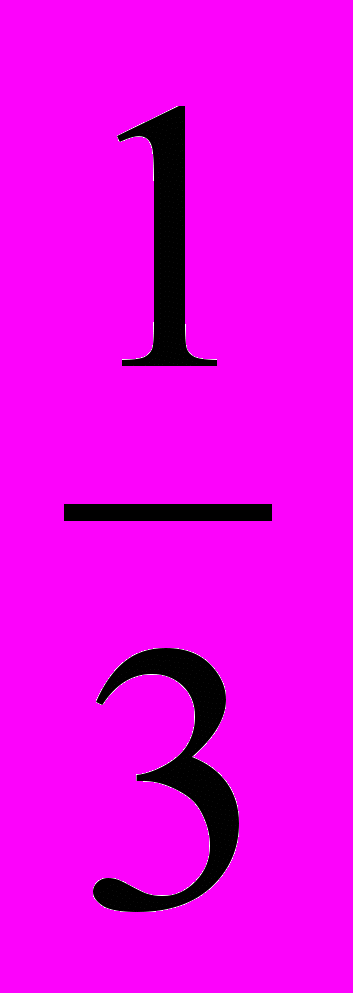 . Если каждому ученику дать по две таких части, то два яблока будут поделены поровну между 3 учащимися. Две части выражаются дробью
. Если каждому ученику дать по две таких части, то два яблока будут поделены поровну между 3 учащимися. Две части выражаются дробью 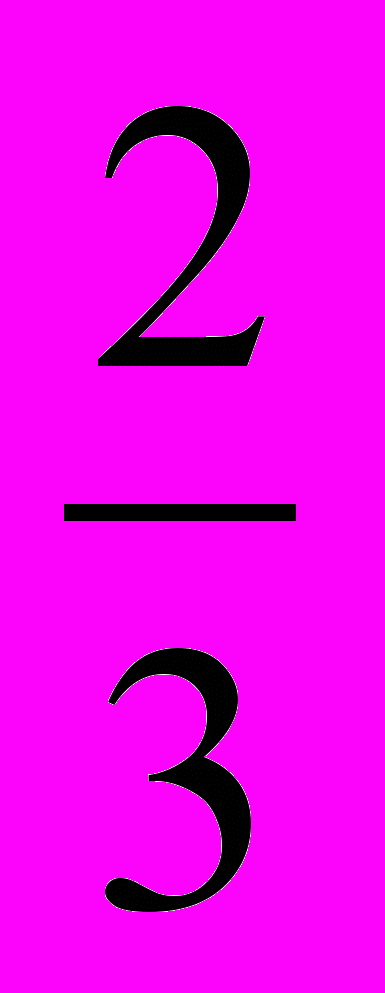 . Значит каждый ученик получает
. Значит каждый ученик получает 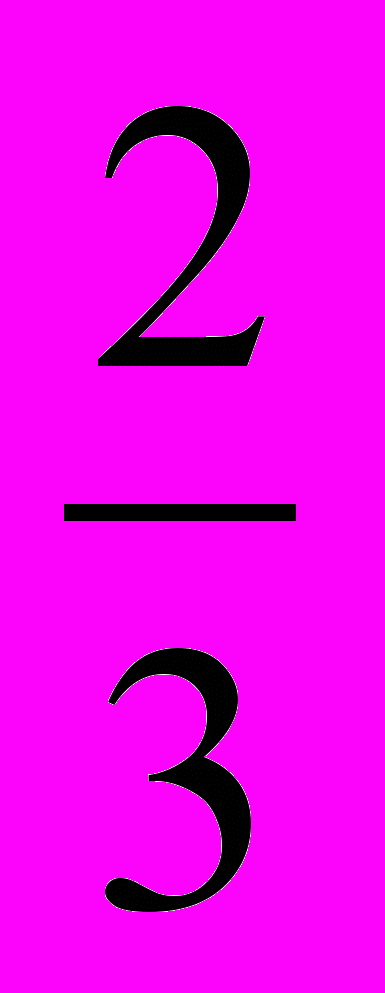 яблока, т.е.
яблока, т.е.  . Делается вывод о том, что деление натурального числа 2 на натуральное число 3 возможно, только при делении получается не натуральное число, а дробное
. Делается вывод о том, что деление натурального числа 2 на натуральное число 3 возможно, только при делении получается не натуральное число, а дробное 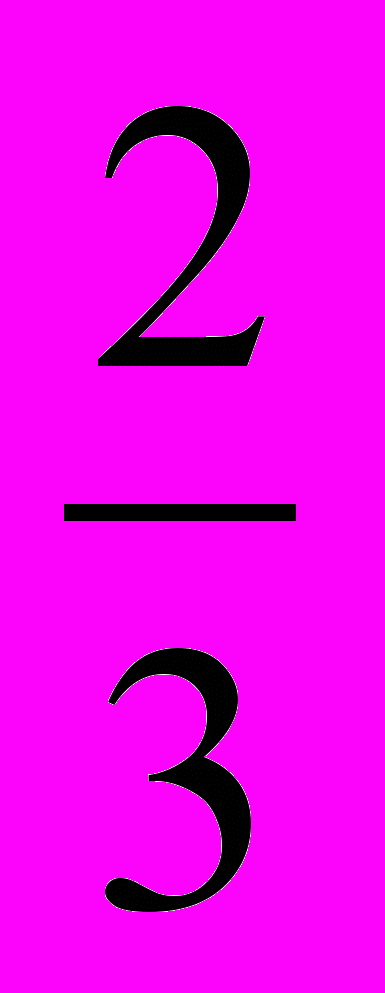 . Третий прием мотивации введения дробных чисел связывается с задачей измерения величин. Пример. Пусть требуется измерить длину отрезка в сантиметрах (выбирается отрезок, длина которого меньше одного сантиметра). При измерении учащимися отрезка обнаруживается, что его длина меньше 1 см. Для измерения такого отрезка удобно привлечь доли 1 см – миллиметры, при этом учитывая, что 1 мм =
. Третий прием мотивации введения дробных чисел связывается с задачей измерения величин. Пример. Пусть требуется измерить длину отрезка в сантиметрах (выбирается отрезок, длина которого меньше одного сантиметра). При измерении учащимися отрезка обнаруживается, что его длина меньше 1 см. Для измерения такого отрезка удобно привлечь доли 1 см – миллиметры, при этом учитывая, что 1 мм = 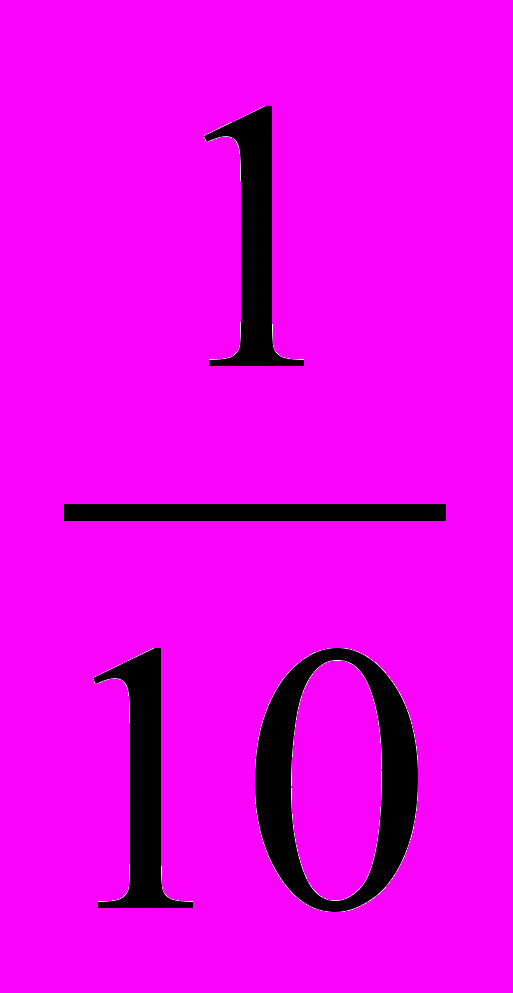 см. Пусть длина отрезка оказалась равной 9 мм. Это означает, что отрезок содержит
см. Пусть длина отрезка оказалась равной 9 мм. Это означает, что отрезок содержит 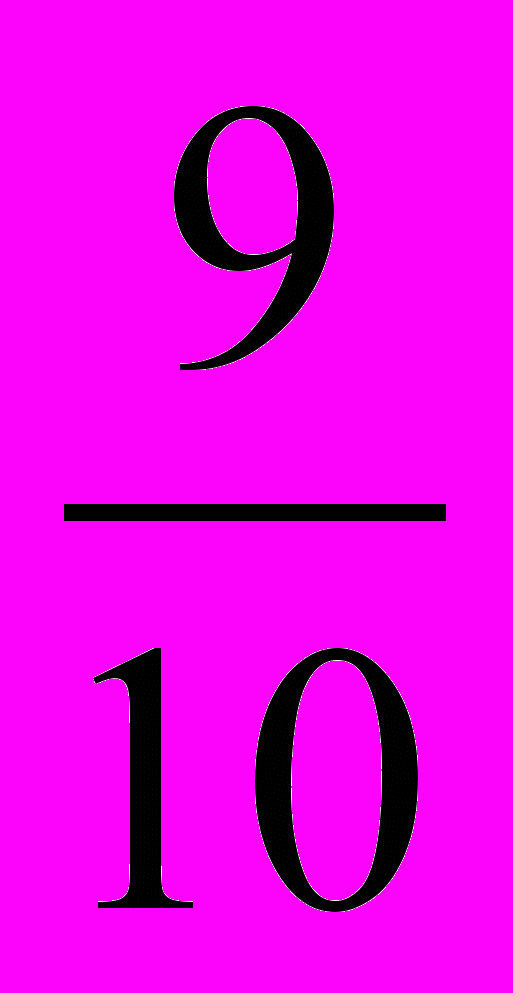 см. Как видно, длина данного отрезка выражается в сантиметрах дробным числом. Без дробных чисел измерение его в сантиметрах невозможно.
см. Как видно, длина данного отрезка выражается в сантиметрах дробным числом. Без дробных чисел измерение его в сантиметрах невозможно.Тенденция на усиление роли теоретических объяснений имеет место и при изучении темы «Дробные числа». По аналогии с натуральными числами объяснение правила сложения десятичных дробей может быть построено следующим образом.
Пусть требуется сложить две десятичные дроби 3,14 и 2,83. Воспользуемся разложением числа в виде суммы разрядных слагаемых, сочетательным и переместительным законами сложения обыкновенных дробей с одинаковыми знаменателями.
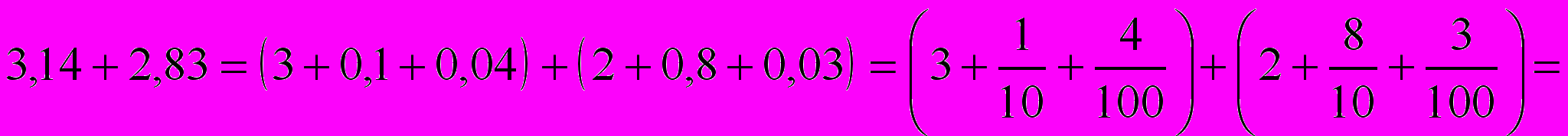
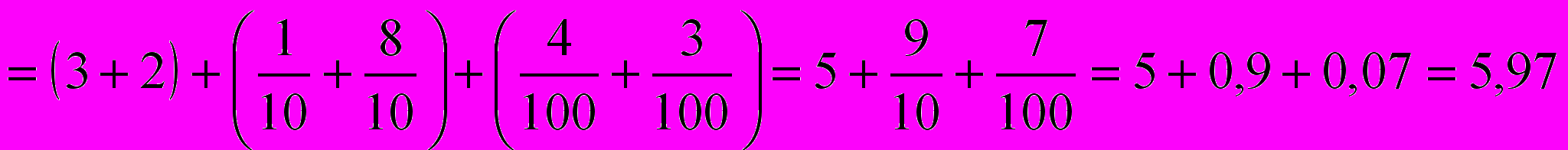 .
.Поэтому для того, чтобы сложить две десятичные дроби «столбцом», необходимо записать их одну под другой так, чтобы единицы одинаковых разрядов находились друг под другом. Затем провести сложение единиц одинаковых разрядов, начиная с наименьшего для данных чисел разряда, и в полученном результате целую часть отделить от дробной запятой:
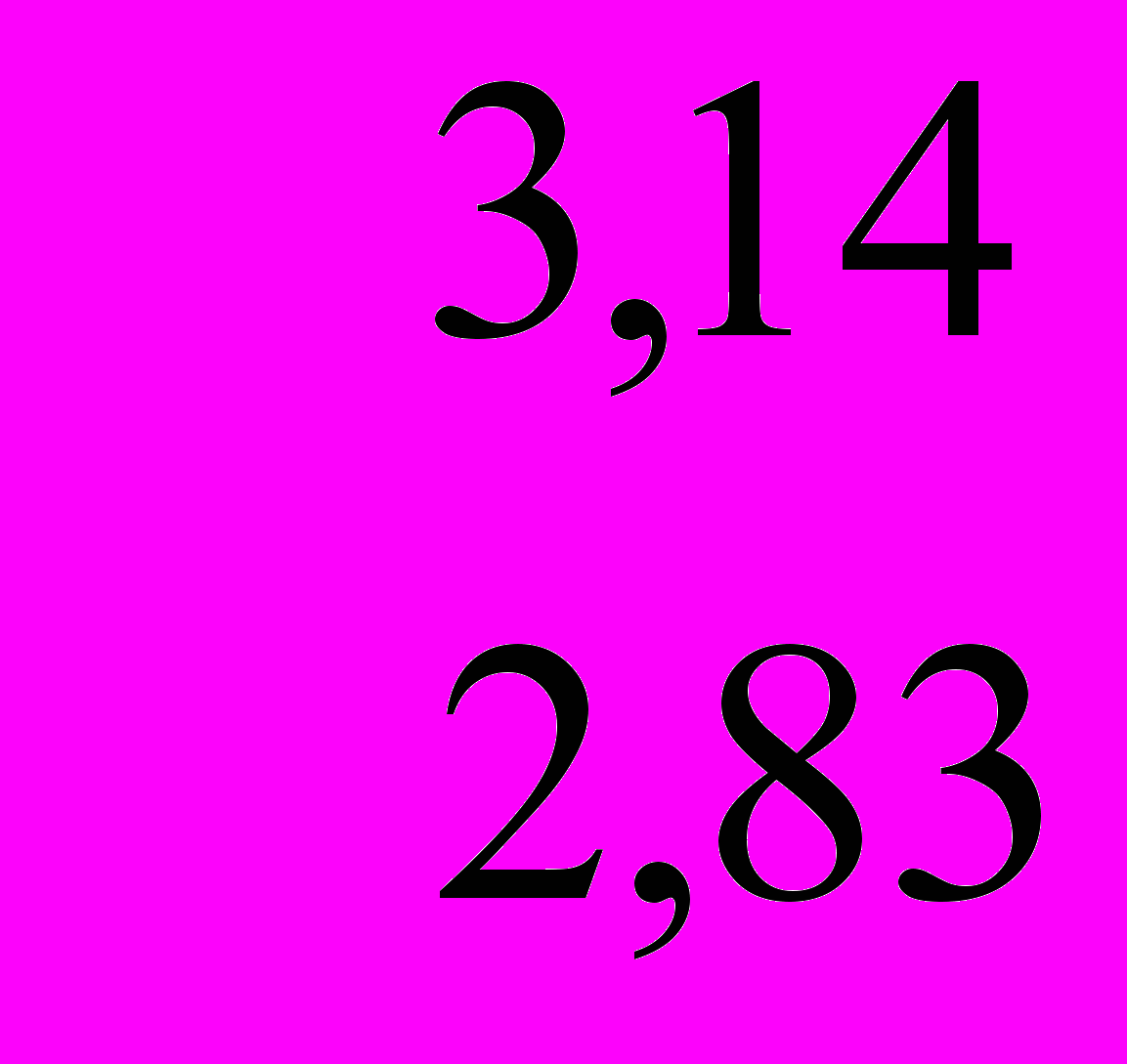
5,97
п.3. Методика изучения отрицательных чисел. Первая методическая задача, возникающая при введении отрицательных чисел, состоит в том, чтобы убедить учащихся в необходимости введения новых чисел. Достигается это с помощью целесообразно подобранных задач. Примеры:
Белка вылезла из дупла и бегает по стволу дерева вверх и вниз. Покажите на рисунке:
1) где будет находится белка, если она удалена от дупла на 3 м (Можно ли указать местоположение белки единственным образом?);
2) где окажется белка, если она будет: а) выше дупла на 2 м; б) ниже дупла на 3 м; в) ниже дупла на 1,5 м; г) выше дупла на 2,5 м.
При решении этих задач устанавливается, что для того, чтобы определить местоположение белки на дереве, необходимо знать: расстояние. на которое она удалена от дупла, и направление, в котором она переместилась (выше дупла, ниже дупла). Выясняется, что известных чисел недостаточно для того, чтобы охарактеризовать ими и расстояние, и направление. Необходимы новые числа.
Рассмотренные задачи полезно представить в более математизированной форме. Для этого достаточно вместо дерева взять прямую, вместо дупла – некоторую фиксированную точку этой прямой, вместо белки – произвольную точку прямой. Созданию наглядно-геометрической основы для введения новых чисел служит такая задача.
Проведите прямую слева направо и отметьте на ней точку О. изобразите на этой прямой точки A, B, C, K, если известно, что точка А расположена правее О на 6 клеток, точка В – правее О на 5,5 клетки, точка С – левее О на 2 клетки и точка К – левее О на 7,5 клетки.
В результате учащиеся будут подготовлены к восприятию понятия «координатная прямая». Учителю останется лишь ввести термины: «начало отсчета», «положительное направление прямой», «отрицательное направление прямой». Если положительное направление обозначить знаком «+», а отрицательное – знаком «–», то ясно, что положение точки А в предыдущей задаче определяется числом +6, положение точки В – числом +5,5, положение точки С – числом – 2, положение точки К – числом – 7,5, положение самой точки О – числом 0. Числа +6, +5,5, 0 были известны ранее, числа – 2, – 7,5 – новые. Числа +6, +5,5, … называются положительными (их можно записывать и без знака «+»), числа – 2, – 7,5, … – отрицательными. С помощью положительных, отрицательных чисел и числа 0 можно полностью охарактеризовать положение точки на прямой.
Важно, чтобы учащиеся осознали не только необходимость введения новых чисел, но и правильно понимали их смысл. В этих целях полезны упражнения на чтение и запись положительных и отрицательных чисел, на изображение их точками на координатной прямой. Полезны задания и на обратный перевод (с математического языка на естественный).
Правила выполнения действий над положительными и отрицательными числами устанавливаются на основании решения содержательных задач (например, задач на определение температуры). Математические формулировки этих правил опираются на понятие модуля числа.
Методическая схема введения правила сложения положительных и отрицательных чисел (в основу ее положено индуктивное обобщение):
- показать, что результат изменения температуры находится с помощью действия сложения;
- на основании измерений температуры с помощью термометра выполнить следующие действия: + 2 + (+3) = + 5, – 2 + (– 3) = – 5, – 2 + (+3) = +1, + 2 + (– 3) = – 1;
- ввести установку: каждое число определяется своим модулем и знаком; с помощью этой установки высказать догадки о том, как найти модуль суммы и ее знак (соответствующие записи полезно оформить в виде таблицы):
+ 2 + (+3) = + (
 ) = + 5, – 2 + (–3) = – (
) = + 5, – 2 + (–3) = – (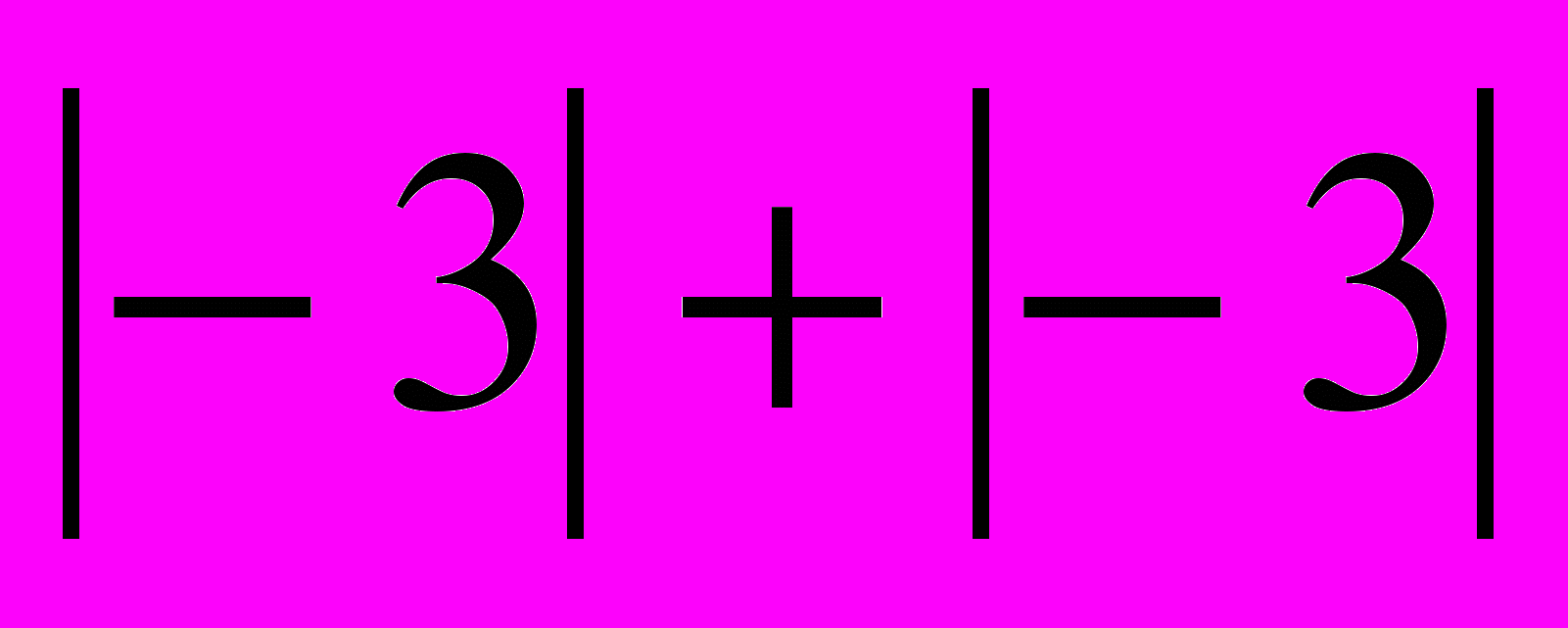 ) = – 5,
) = – 5, – 2 + (+3) = + (
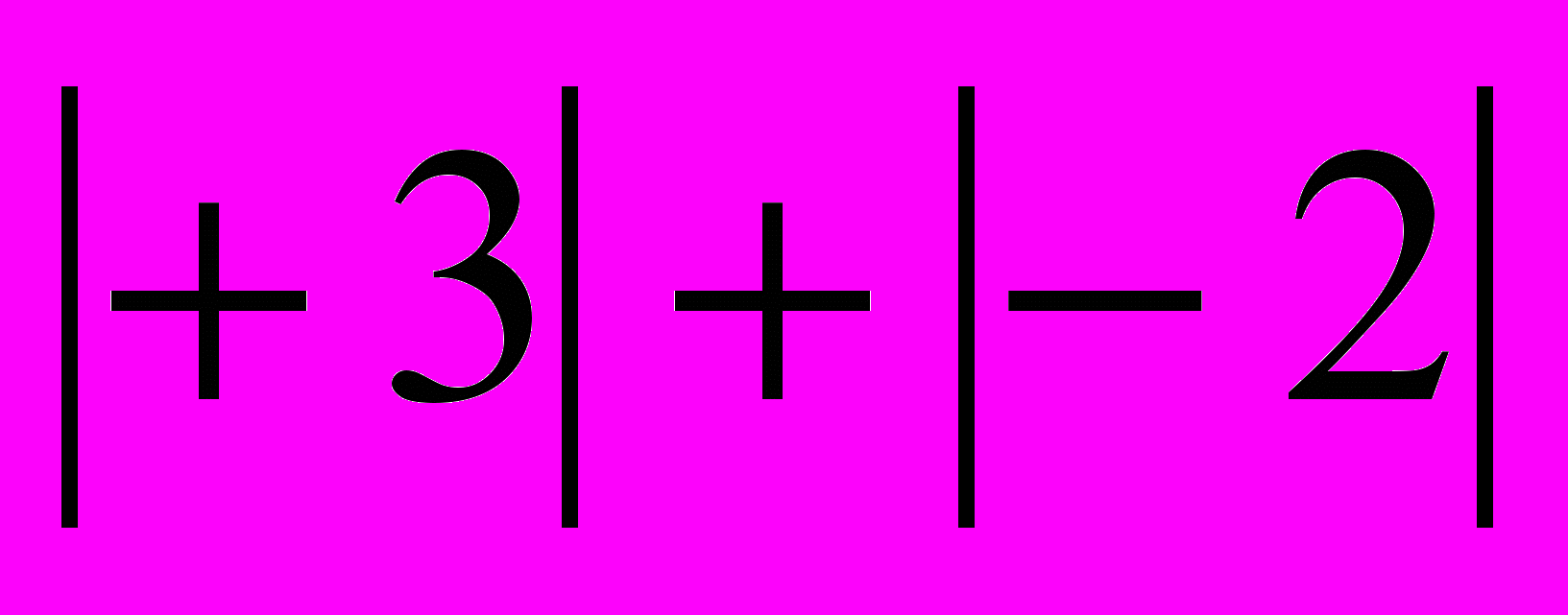 ) = + 1, + 2 + (– 3) = – (
) = + 1, + 2 + (– 3) = – (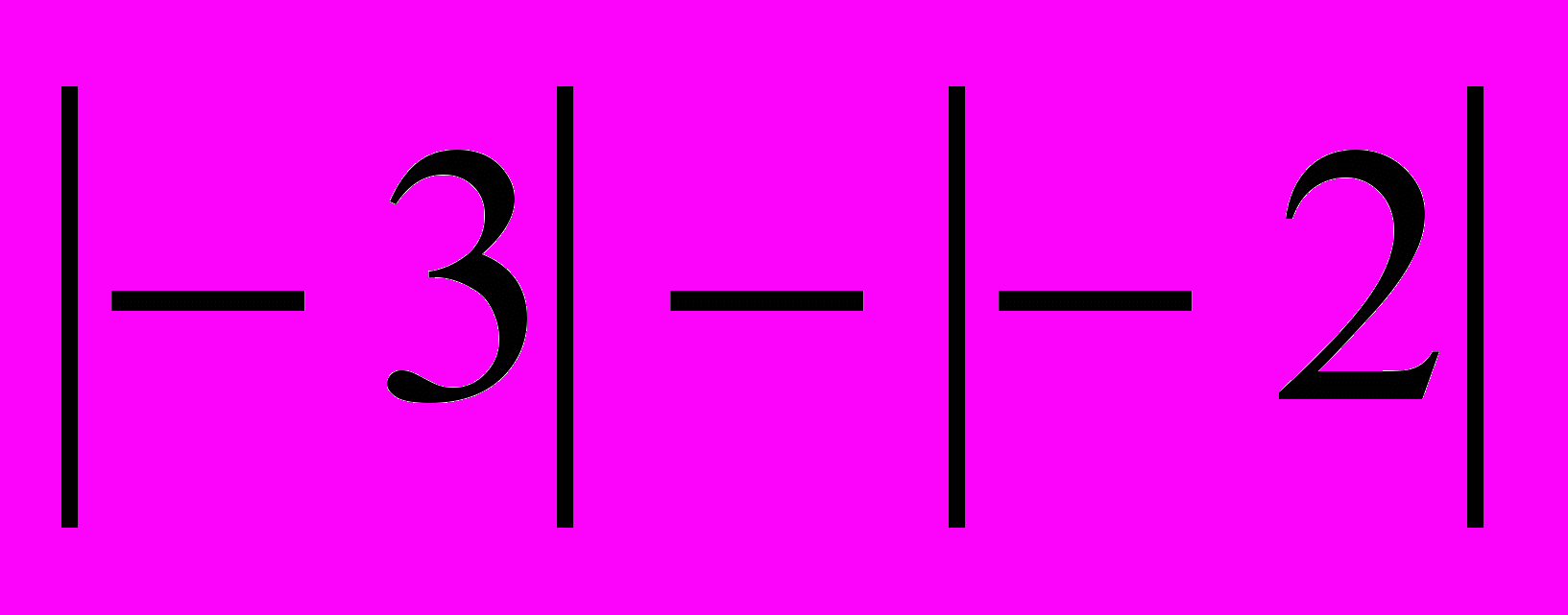 ) = – 1;
) = – 1;- сформулировать правило сложения чисел с одинаковыми и разными знаками;
- закрепить это правило письменными упражнениями с подробными записями;
- осуществить переход к более сокращенным записям вычислений, сопроводив их полным устным комментарием;
- на следующем уроке (в качестве повторения и закрепления правила) привести схему соответствующего алгоритма.
Методическая схема введения правила умножения положительных и отрицательных чисел:
1) предложить задачу: «Температура воздуха изменяется в течение b суток, причем в каждые сутки на a градусов. Как изменится температура через b суток (по сравнению с настоящим моментом), если а) a = 2, b = 3, б) a = – 2, b = 3, в) a = 2, b = – 3, г) a = – 2, b = – 3?»
2) выяснить смысл высказываемых в задачах предложений: что означает утверждение о том, что температура воздуха изменилась на a градусов, если a равно 2, – 2, объяснить смысл утверждения о том. Что температура изменяется в течение b суток, если b равно 3, – 3;
3) провести решение задачи для случая а: «За трое суток температура повысится в 2 раза; увеличение в 2 раза находится умножением на 2; отсюда искомое изменение температуры получим, если 2 умножим на 3:
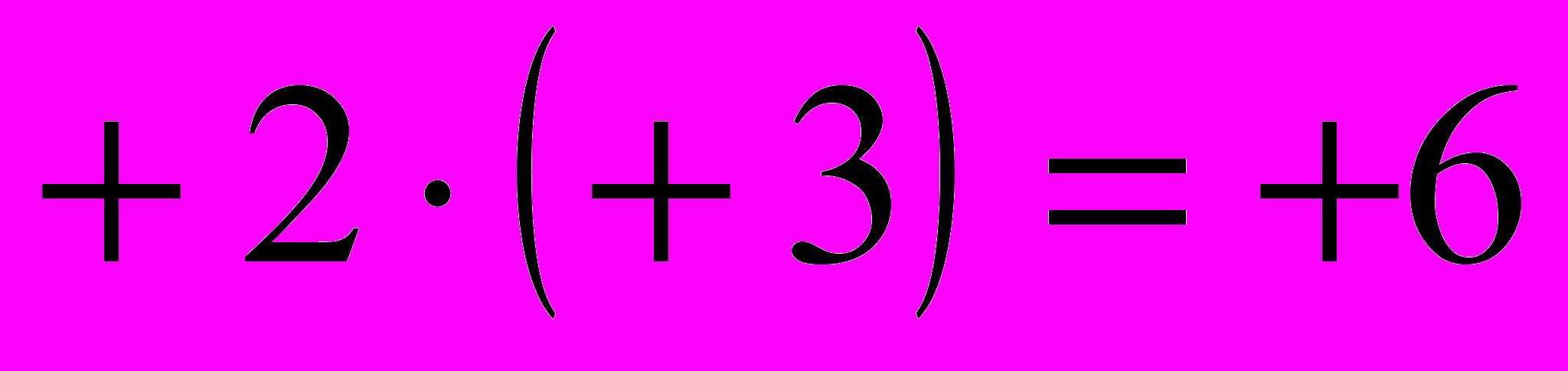 ». Так как остальные задачи аналогичные, то делается вывод, что они также должны решаться с помощью умножения. Поэтому возникает необходимость научиться выполнять умножение с положительными и отрицательными числами;
». Так как остальные задачи аналогичные, то делается вывод, что они также должны решаться с помощью умножения. Поэтому возникает необходимость научиться выполнять умножение с положительными и отрицательными числами;4) сформулировать задачу для случая б: «Как изменится температура воздуха через 3 суток, если каждые сутки она понижается на 2 градуса?» и привести ее решение: «Вначале устанавливается, что температура воздуха через 3 суток понизится на 6 градусов. Это понижение характеризуется числом – 6 и делается запись
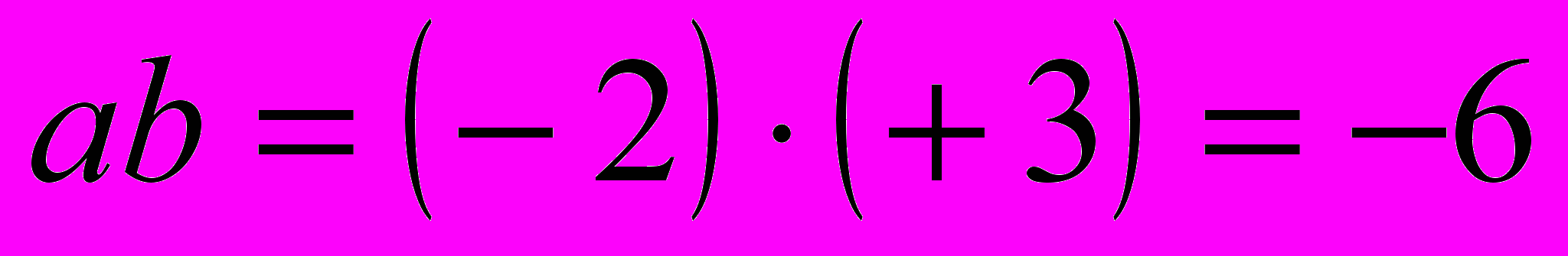 »;
»;5) поставить и решить задачи для остальных случаев, сделать аналогичные записи:
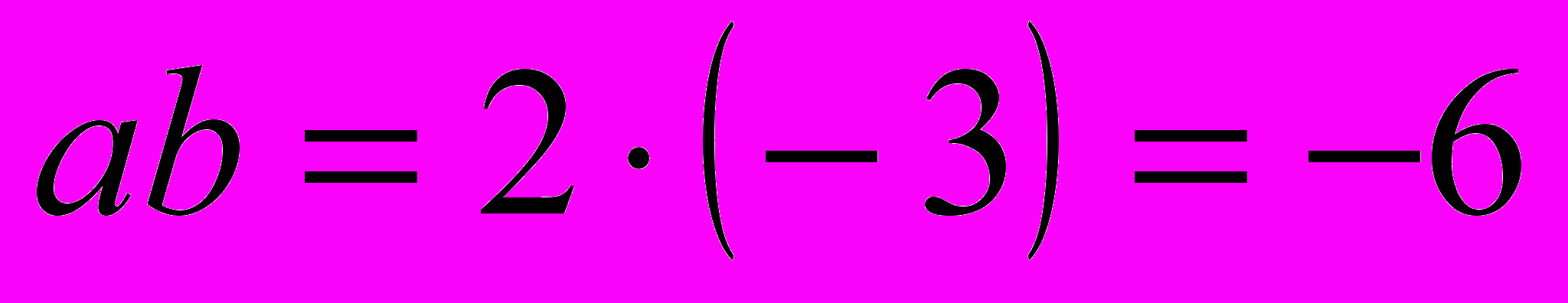 ,
, 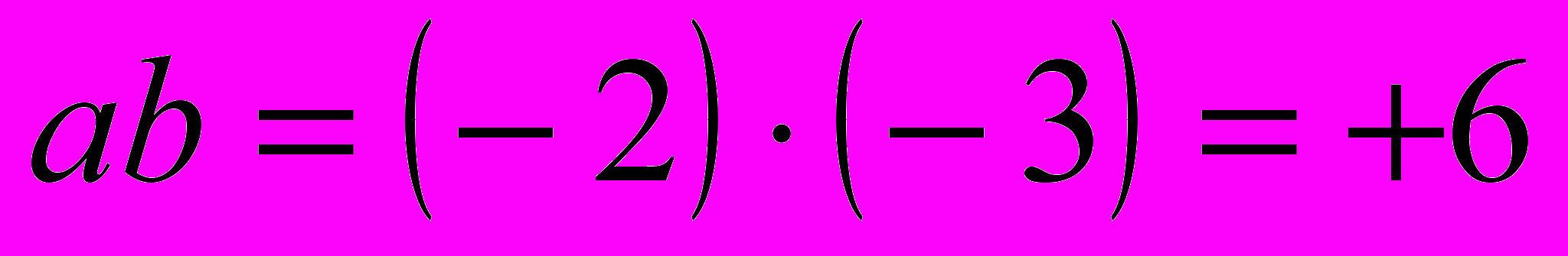 ;
;6) высказать догадку о том, как найденные произведения можно получить математическим способом;
7) сформулировать правило умножения положительных и отрицательных чисел;
8) закрепить это правило составлением схемы соответствующего алгоритма и письменными упражнениями с подробными записями, показывающими, как выбирается знак произведения и находится его модуль;
9) осуществить постепенный переход к сокращенным записям вычислений.
