Значение элективных курсов по математике в рамках предпрофильной подготовки и профильного обучения
| Вид материала | Документы |
СодержаниеЦели курса |
- I. общие положения, 94.94kb.
- Использование элективных курсов как новое направление естественнонаучной подготовки, 949.47kb.
- Программа элективного курса для профильного обучения учащихся 10-11 классов Ильина, 214.21kb.
- Элективные курсы (курсы по выбору) играют важную роль в системе профильного обучения, 138.92kb.
- Задачи: провести проблемно-ориентированный анализ для введения предпрофильной подготовки, 37.69kb.
- Программа элективного курса предпрофильной подготовки и профильного обучения «Введение, 91.03kb.
- Программа элективного курса предпрофильной подготовки и профильного обучения «ссср, 149.31kb.
- Элективных курсов по математике в рамках реализации программы «Одаренные дети» в общеобразовательной, 95.67kb.
- Программа элективного курса предпрофильной подготовки и профильного обучения «История, 160.13kb.
- Курс предназначен для подготовки учащихся и обучения их в рамках гуманитарного профиля, 385.09kb.
Муниципальное общеобразовательное учреждение
«Пролетарская средняя общеобразовательная школа №2»
Ракитянского района Белгородской области
Б
 елоконева Людмила Платоновна,
елоконева Людмила Платоновна,учитель математики высшей категории, Почетный работник общего образования РФ.
Значение элективных курсов по математике в рамках предпрофильной подготовки и профильного обучения.
Мы живём в период серьёзных изменений в системе образования. Эти изменения заявлены в «концепции модернизации российского образования на период до 2010 года». Модернизация образования - это не политическая компания, а жизненная необходимость. Развитие информационного общества, научно-технические преобразования, рыночные отношения требуют от каждого человека высокого уровня профессиональных и деловых качеств, предприимчивости, способности ориентироваться в сложных ситуациях, быстро и безошибочно принимать решения.
Профильное обучение - одно из важных направлений модернизации образования.
В школе уже три года работают либо класс углубленного изучения экономики, либо классы социально-экономического профиля. Экономическая образованность и экономическое мышление формируются не только при изучении курса экономики, но и на основе всего комплекса предметов, изучаемых в школе. Математике здесь принадлежит особая роль. Это объясняется тем, что многие экономические проблемы поддаются анализу с помощью того математического аппарата, который изложен в курсе алгебры VII - XI классов. Взаимодействие математики и экономики приносит обоюдную пользу: математика получает широчайшее поле для многообразных приложений, а экономика - могучий инструмент для получения новых знаний.
Однако государственные программы, хоть и для профильного обучения, не дают полной возможности для такого взаимодействия экономики и математики. Элективные же курсы как бы «компенсируют» во многом достаточно ограниченные возможности и базовых, и профильных курсов в удовлетворении разнообразных образовательных потребностей старшеклассников. Причем начинается эта работа уже с 9 класса при проведении курсов в рамках предпрофильной подготовки.
С другой стороны, проведение элективных курсов по математике не только помогает разобраться с экономическим материалом, но и дает большие возможности учителю в создании системы подготовки учащихся к итоговой аттестации: в 9 классе – к новой форме, в 10 и 11 классах – к ЕГЭ по математике.
При организации профильного обучения с использованием элективных курсов учащиеся лучше овладеют изучаемым предметом; расширятся возможности развития их мыслительной деятельности, привитие им исследовательских навыков по сравнению с обычными формами организации учебного процесса. Таким образом, проведение таких курсов предоставляет ученику возможность работать на уровне повышенных требований, а также от них зависит и мера подготовленности учащихся к успешной сдаче единых государственных экзаменов и перспективы на продолжение образования после школы.
Поэтому уже в 9 классе я проводила 2 элективных курса по 17 часов: «Проценты» и «Модуль».
Выбор темы «Проценты» обусловлен непродолжительным изучением данной темы на первом этапе основной школы, когда учащиеся в силу возрастных особенностей еще не могут получить полноценные представления о процентах, об их роли в повседневной жизни. На последующих этапах обучения повторного обращения к этой теме не предусматривается, хотя и есть задачи на проценты. Текстовые задачи включены в материалы итоговой аттестации за курс основной школы, в КИМы и ЕГЭ, а также в дидактические материалы, контрольные работы, в сам учебник С.М. Никольского, по которому идет обучение алгебре и началам анализа в старшем звене. Кроме того, прикладное значение этой темы очень велико и затрагивает финансовую, социологическую сторону нашей жизни, что является одной из сторон экономики, изучаемой в классах социально-экономического профиля. Данный курс способствует развитию познавательных интересов, экономической грамотности, мышления, предоставляет возможность подготовиться к сознательному выбору профиля обучения и дальней специализации.
Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа. Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешности приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы, ЕГЭ.
Понятие модуля рассматривается еще в 6 классе, и больше о нем не упоминается. Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях, их свойствах, полученных учащимися за весь период обучения. В обязательном минимуме этот материал представлен, но в школьном курсе алгебры такие задачи рассматриваются пока крайне редко, бессистемно. У девятиклассника возникает страх перед заданиями с модулем. Поэтому, начав работать по курсу «Модуль», поставила перед собой следующие задачи:
- показать красоту математики;
- развивать настойчивость и внимательность в нахождении правильного решения, умения применять полученные знания в нестандартных ситуациях;
- развивать активно-познавательную деятельность учащихся;
- уточнить готовность и способность ученика осваивать выбранный предмет (математику) на повышенном уровне.
Вместе с этим я стремилась к тому, чтобы данный курс позволил школьникам систематизировать, расширить и укрепить знания, связанные с абсолютной величиной, подготовиться для дальнейшего изучения тем, использующих это понятие, научиться решать разнообразные задачи различной сложности.
Исходя из этого, поставила следующие цели и задачи курса:
Цели курса:
обобщение и систематизация, расширение и углубление знаний по теме абсолютная величина, обретение практических навыков выполнения заданий с модулем, повышение уровня математической подготовки школьников.
Задачи курса
- вооружить учащихся системой знаний по теме абсолютная величина;
- сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;
- подготовить учащихся к аттестации;
- сформировать навыки самостоятельной работы, работы в малых группах;
- сформировать умения и навыки исследовательской работы;
- способствовать развитию алгоритмического мышления учащихся;
- способствовать формированию познавательного интереса к математике.
Элективные курсы в 10 профильном классе продолжают расширять и углублять знания учащихся по математике и экономике. Курс «Процент» продолжает курс «Математика в экономике», который ведет учитель экономики Присада И.В.. По математике ученикам мною предложены два курса по 0,5 часа «Функции и их графики» и «Нестандартные задачи по математике», которые как бы, как отмечала выше, «компенсируют» во многом достаточно ограниченные возможности курса алгебры. Одним из недостатков упражнений школьного курса математики является их однофункциональность. Часто они направлены на достижение одной цели, выполняют одну функцию (освоение введенных понятий, закрепление способов действий). Между тем этого недостаточно.
Например, теме «Множество значений функций» в курсе алгебры уделяется внимание при изучении каждой функции, однако задания, входящие в КИМы значительно отличаются от тех, которые рассматриваются согласно программе и материалам учебника, причем задания предлагаются и во всех частях КИМов:
Задания А
- Найдите множество значений функции
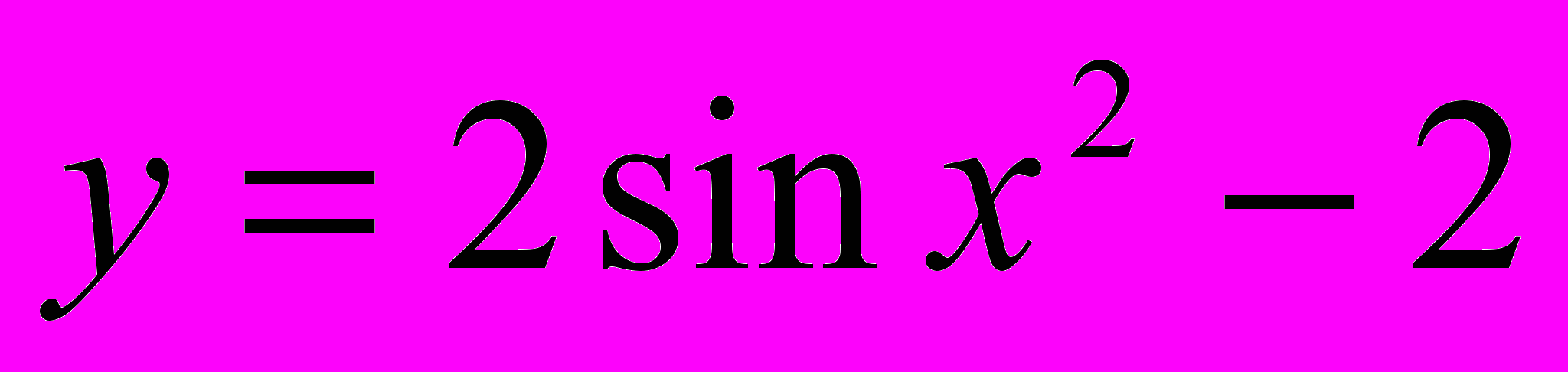
1)
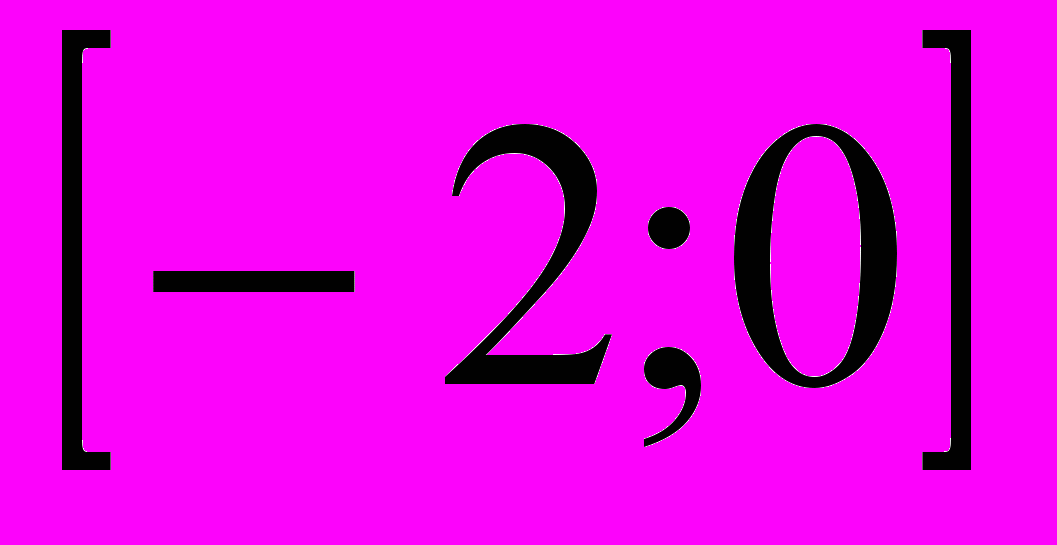 2)
2) 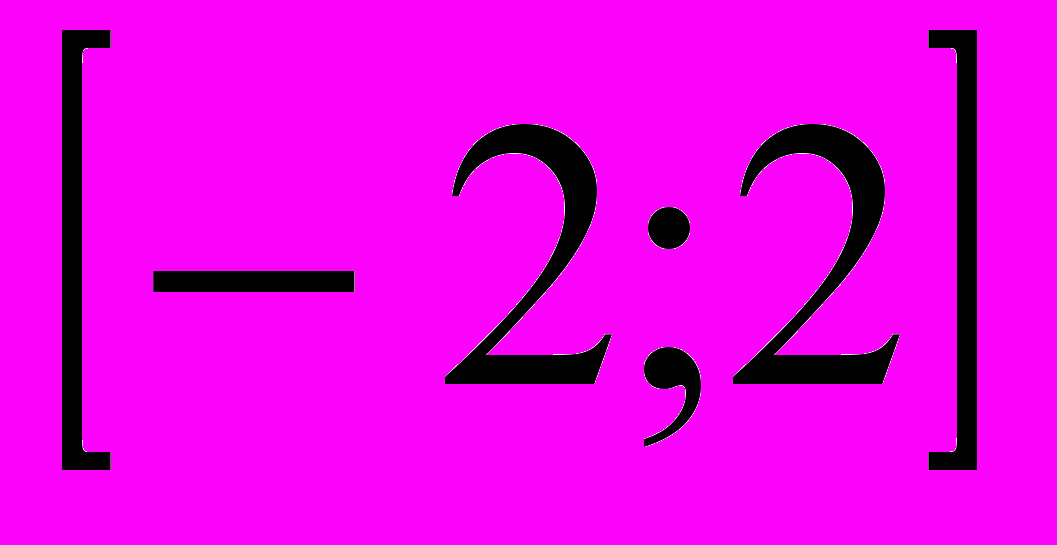 3)
3) 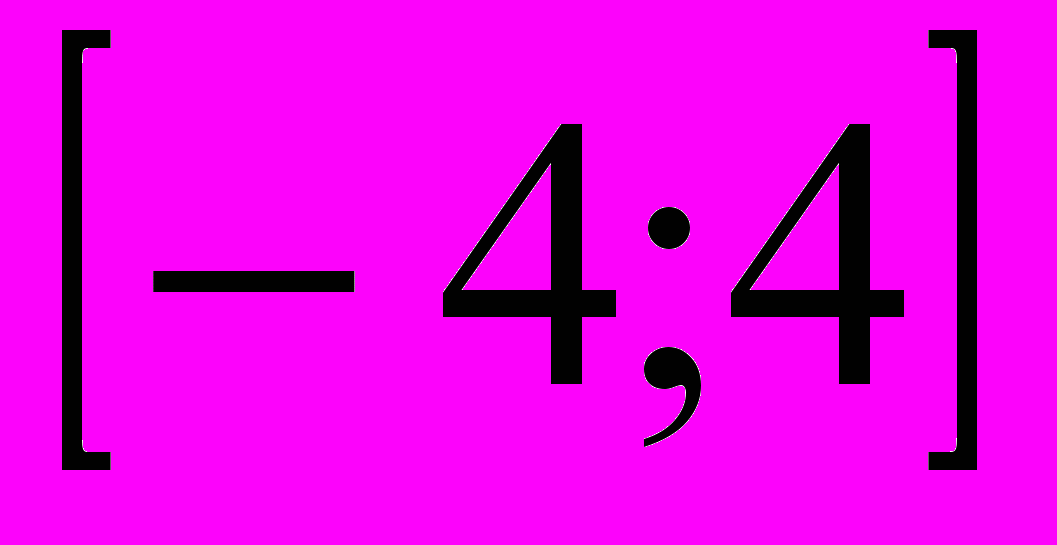 4)
4) 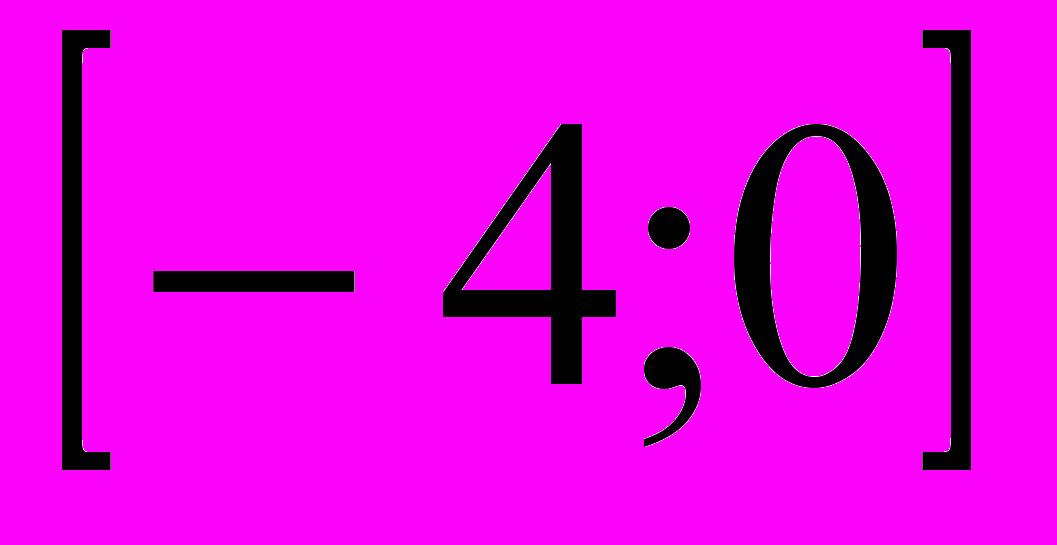
- Найдите множество значений функции:
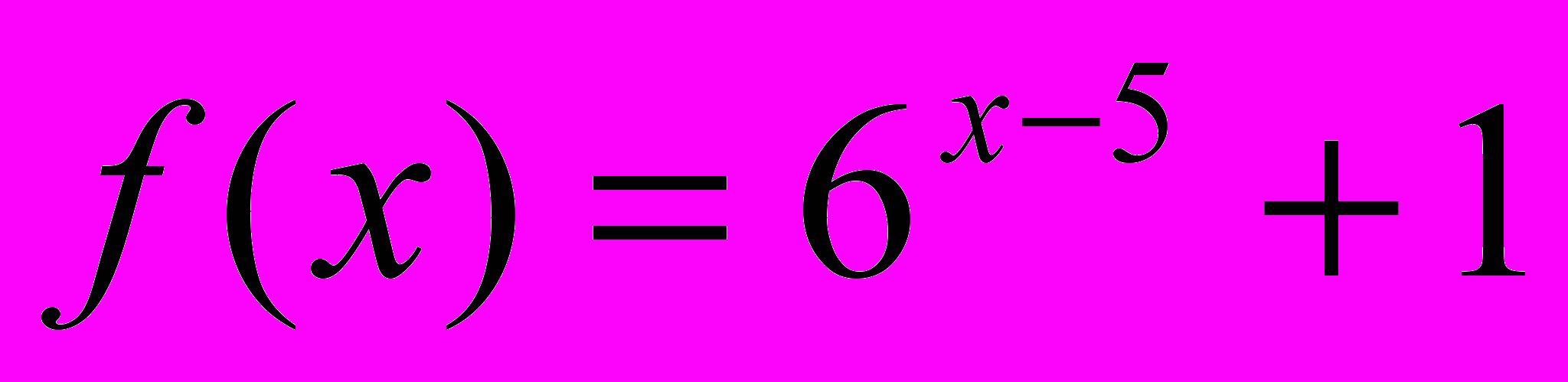
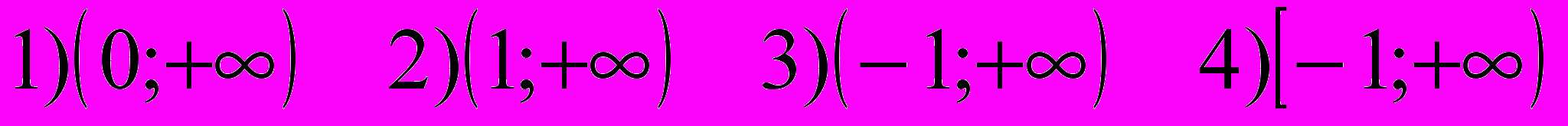
Задания В
- Найти наибольшее значение функции
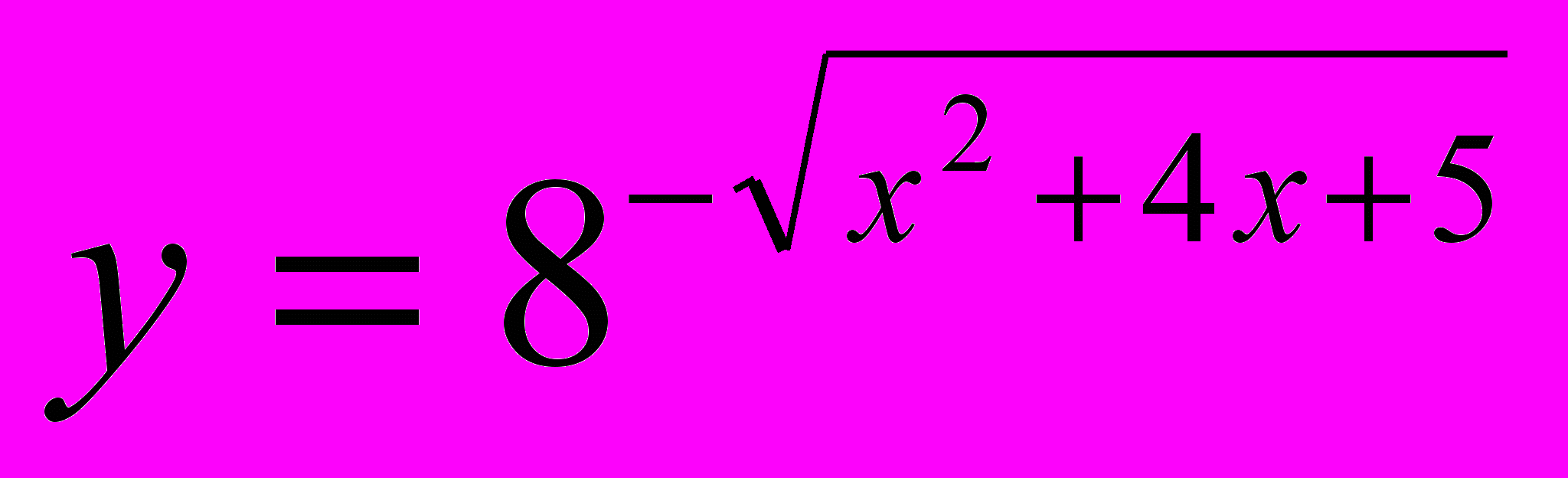
- Найдите наибольшее значение функции
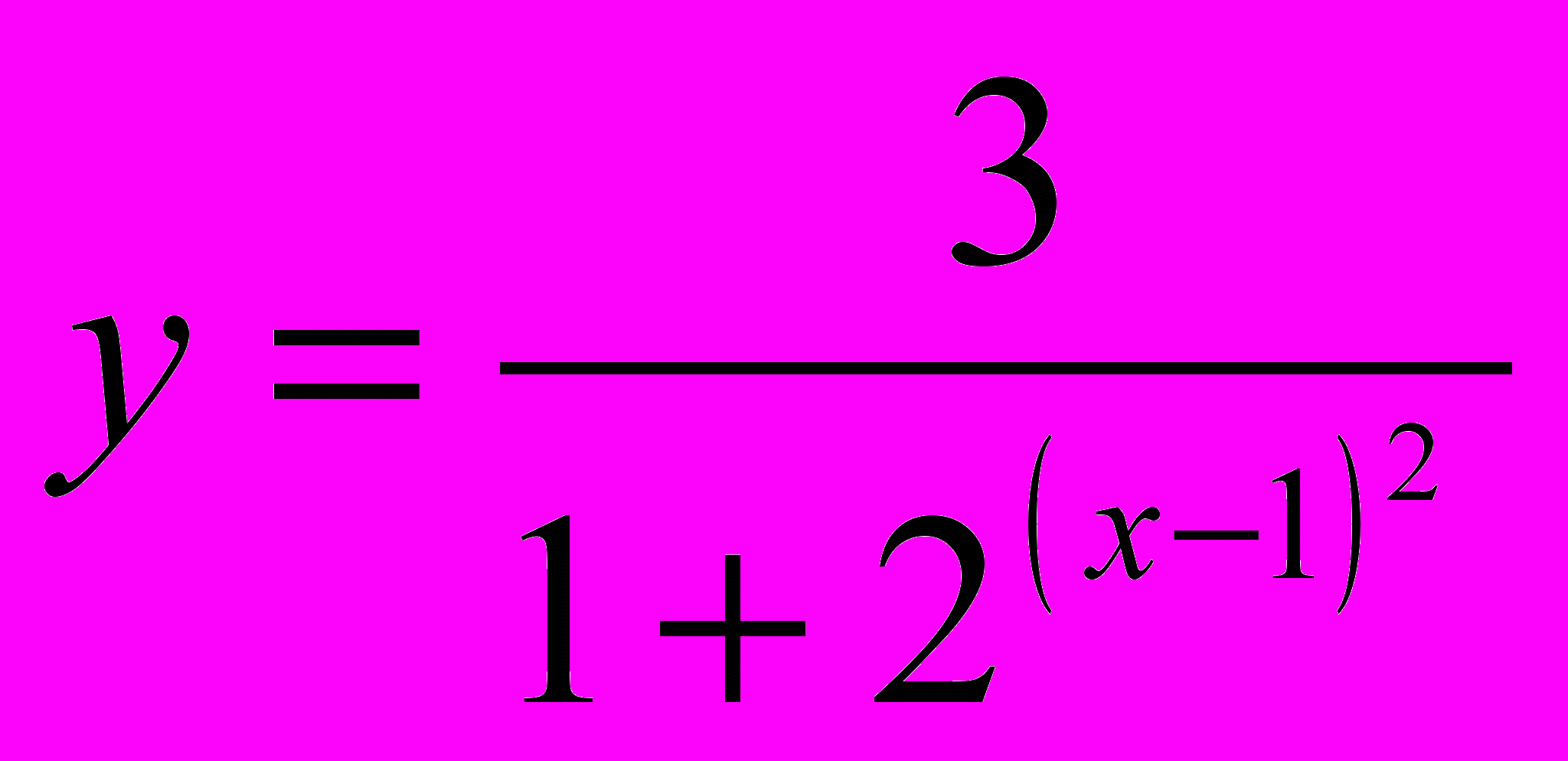
- Найдите наибольшее целое значение функции:
у = 1,5
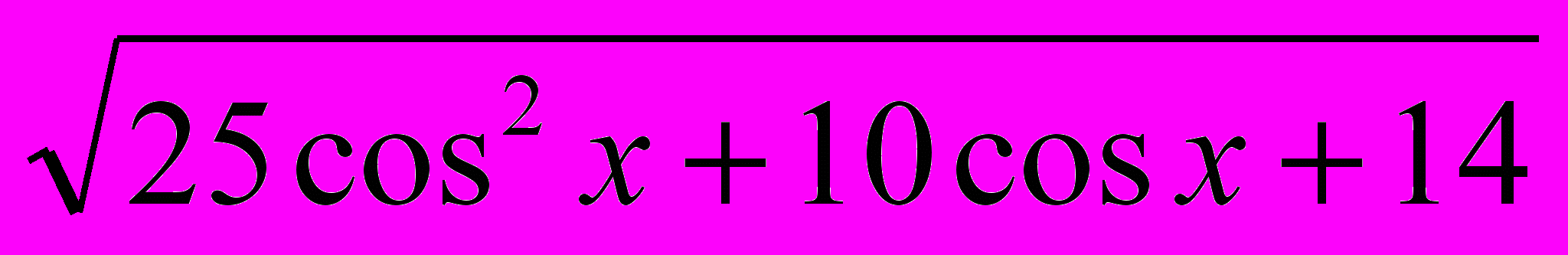
Задания С
- Найдите наименьшее и наибольшее значения функции
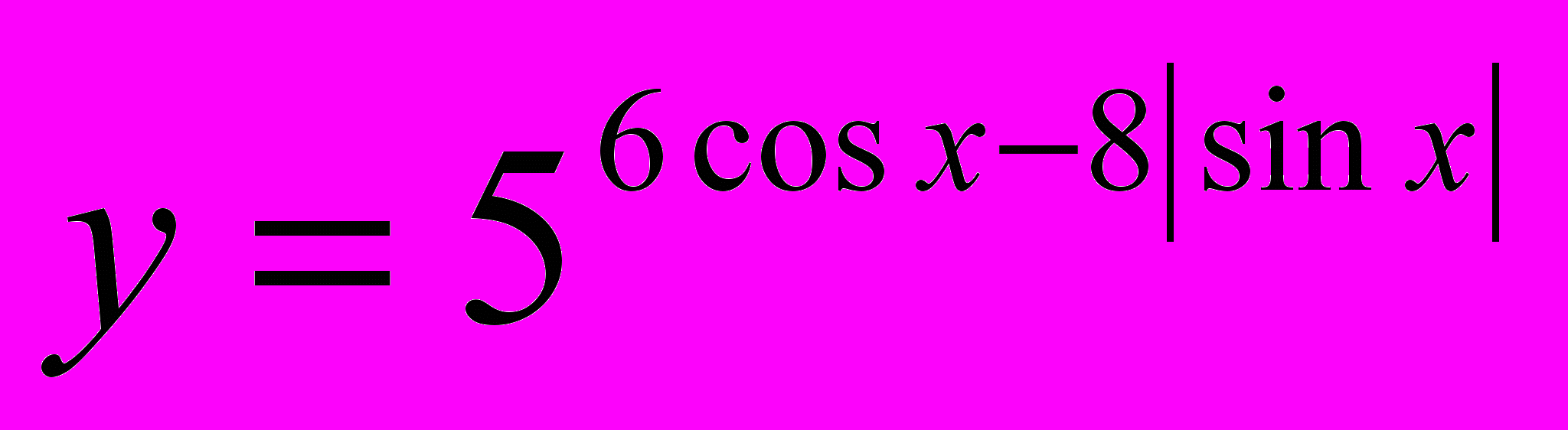 .
.С введением ЕГЭ на учителя математики явно или неявно возлагается еще большая ответственность, поэтому преподаватель независимо от профиля стремится к увеличению числа учебных часов по своему предмету. Естественно, что одно лишь увеличение числа часов не может поднять изучение школьной математики на качественно иной уровень.
«Компенсация» ограниченных возможностей курса алгебры через программы элективных курсов играет, конечно, большую роль в повышении математических знаний школьников, развитии их познавательного интереса, в подготовке учащихся к ЕГЭ. Однако вводя элективные курсы в предпрофильное и профильной обучение необходимо обязательно учитывать, что речь идет не только об их программах и учебных пособиях, но и о всей методической системе обучения этим курсам в целом. Ведь профильное обучение - это не только дифференцирование содержания образования, но, и главное по-другому построенный учебный процесс.
Изменяющаяся методика обучения в профильных классах (особенно на элективных курсах) должна постепенно развивать у учащихся навыки организации умственного труда и самообразования. Основная функция учителя состоит в «сопровождении» учащегося в его познавательной деятельности, коррекции ранее полученной информации, помощи в извлечении из полученных ранее знаний тех, которые актуализируются в изучаемом курсе. Работа учителя индивидуализируется, ориентируясь на обеспечение активной познавательной деятельности самих обучающихся. Иными словами, не учитель теперь призван обучать математике школьников, а сами ученики в созданных учителем обучающих ситуациях, самостоятельно или в сотрудничестве друг с другом (или с учителем) должны овладевать системой математических знаний, умений и навыков.
Учитель профильной школы обязан не просто быть специалистом, соответствующим профилю и специализации своей деятельности, но и должен обеспечивать:
- вариативность и личностную ориентацию образовательного процесса (проектирование индивидуальных образовательных траекторий);
- практическую ориентацию образовательного процесса с введением интерактивных, деятельностных компонентов (освоение проектно-исследовательских и коммуникативных методов);
- завершение профильного самоопределения старшеклассников и формирование способностей и компетентностей, необходимых для продолжения образования в соответствующей сфере профессионального образования.
Основными формами проведения элективного курса являются изложение узловых вопросов курса в виде обобщающих лекций, семинаров, дискуссий, практикумов по решению задач, рефератов учащихся. Например, можно провести такие дискуссии:
- «Легко ли определить знак числа или найти наибольшее из двух чисел, если числа заданы как значения некоторых числовых значений?»
- «Можно ли использовать вычислительную технику (микрокалькулятор) для сравнения числовых выражений? Ожидания и заблуждения?»
- «Самое лучшее решение. За и против»
Главное, формы и методы обучения математике на элективных курсах должны быть направлены на продуктивное усвоение школьниками системы ведущих знаний, на эффективное их воспитание и развитие. Необходимо шире использовать обучение в сотрудничестве, метод проектов, лекционно-практическую систему обучения.
Возможны и разные формы индивидуальной или групповой деятельности учащихся, как «Допишем учебник», отчетные доклады по результатам «поисковой» работы на страницах книг, журналов и сайтов в Интернете и т.д. Или можно, например, провести аукцион «Что я знаю об абсолютной величине?», защиту проектов опорных сигналов по способам решения уравнений и неравенств с модулем, разработать (по указанной учителем литературе) один из вариантов обоснования конкретного неравенства с переменными и подготовить сообщение в защиту данного способа установления этого неравенства. Главное необходимо учитывать интересы школьников, все предпочтения и вводить в процесс обучения упражнения, которые включают учеников в осмысленную, продуктивную деятельность. Основное внимание следует уделять накоплению у школьников опыта самостоятельного поиска решений заданий, чтобы на том же ЕГЭ каждый ученик был готов к полной самостоятельности в работе.
В зависимости от времени и места его применения, особенностей сочетания в нем различных способов, приемов и средств один и тот же метод обучения может оказаться эффективным или неэффективным. Найти удачный метод обучения в каждом конкретном случае означает найти удачную комбинацию различных приемов и средств, позволяющих достичь поставленной заранее цели (или целей) наиболее оптимальным в данных условиях путем.
