«Текстовые задачи и методы их решения»

Вид материала

Программа курса

Содержание Задача №8. Задача №10 Ответ: 187,5 кг.Мы решили вторую задачу путём составления таблицы, помогающей зрительно воспринимать задачу. Вывод Арифметическая и геометрическая прогрессии Задачи для курса по выбору «Текстовые задачи и приёмы их решения» Задачи на работу

Подобный материал:

• Задачи и их решение Стандартные и нестандартные задачи Задачи «на работу» Задачи «на, 157.13kb.
• Как научить младших школьников решать текстовые задачи?, 124.64kb.
• Урок №15. Тема: «Текстовые редакторы», 75.16kb.
• Лябина Татьяна Ивановна 2009 год Введение Необходимость введения курса «Текстовые задачи, 274.98kb.
• Задачи нелинейной и дискретной оптимизации. Методы решения. Постановка и экономико-математическая, 25.18kb.
• Прикладная лингвистика. Моделирование языковых процессов. Лингвистические аспекты искусственного, 576.91kb.
• Задачи нелинейной и дискретной оптимизации. Методы решения. Постановка и экономико-математическая, 24.28kb.
• Лекции 7 8, 31.73kb.
• Текстовые процессоры (или текстовые редакторы), 184.62kb.
• Секция “Краевые задачи механики сплошной среды, численные и численно-аналитические, 67.85kb.

Задача №8.

В каких пропорциях нужно смешать раствор 50%-й и 70%-й кислоты, чтобы получить раствор 65%-й кислоты?

Решение.

1 способ

Пусть х г – масса 50%-й кислоты, y г – масса 70%-й кислоты, 0,5х г – масса чистой кислоты в первом растворе, (x+y)г – масса смеси, 0,65(x+y)г - масса чистой кислоты в смеси. Составим уравнение (рис. 6а):

0,5x+0,7y=0,65(x+y)

Получаем соотношение 1:3.

Ответ: 1:3.


Существует и другой способ решения этой задачи. Он называется арифметическим (или старинным) способом.

2 способ

Обоснуем старинный способ решения задач «на смеси».

Пусть требуется смешать растворы а%-й и b%-й кислот, чтобы получить

с%-й раствор.

Пусть х г – масса а%-го раствора, y г – масса b%-го раствора, 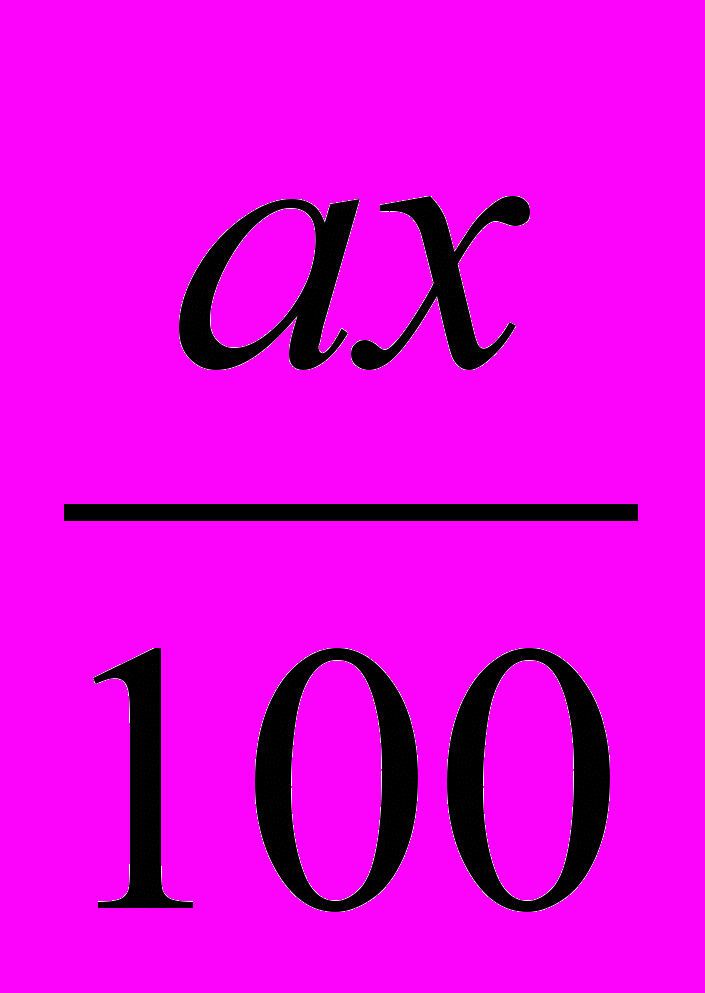г – масса чистой кислоты в первом растворе, а 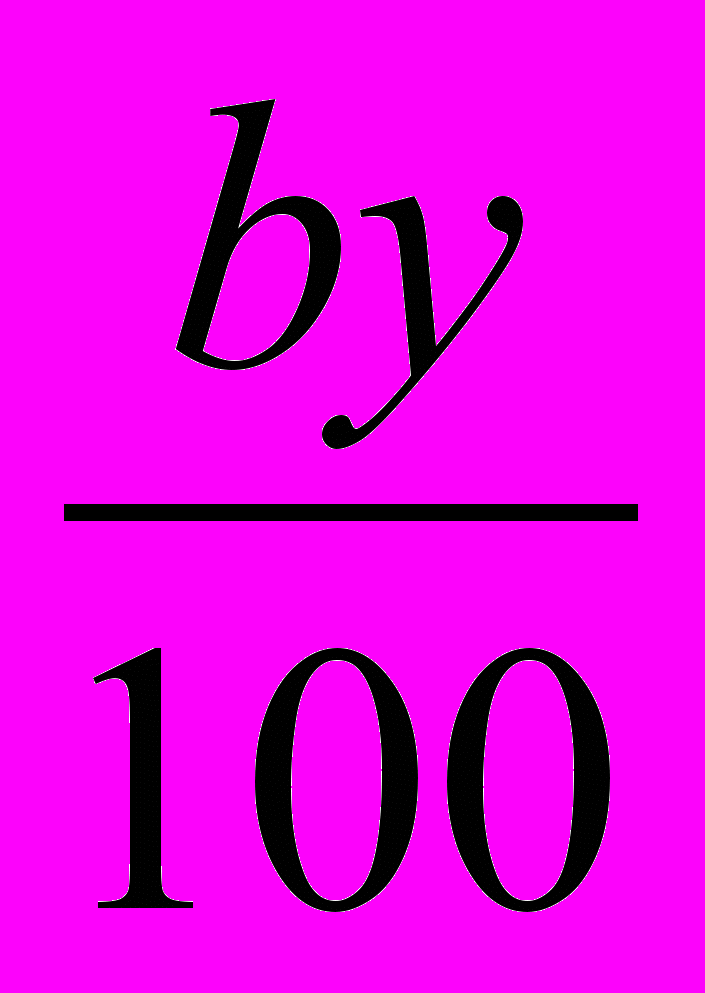г – масса чистой кислоты во втором растворе, 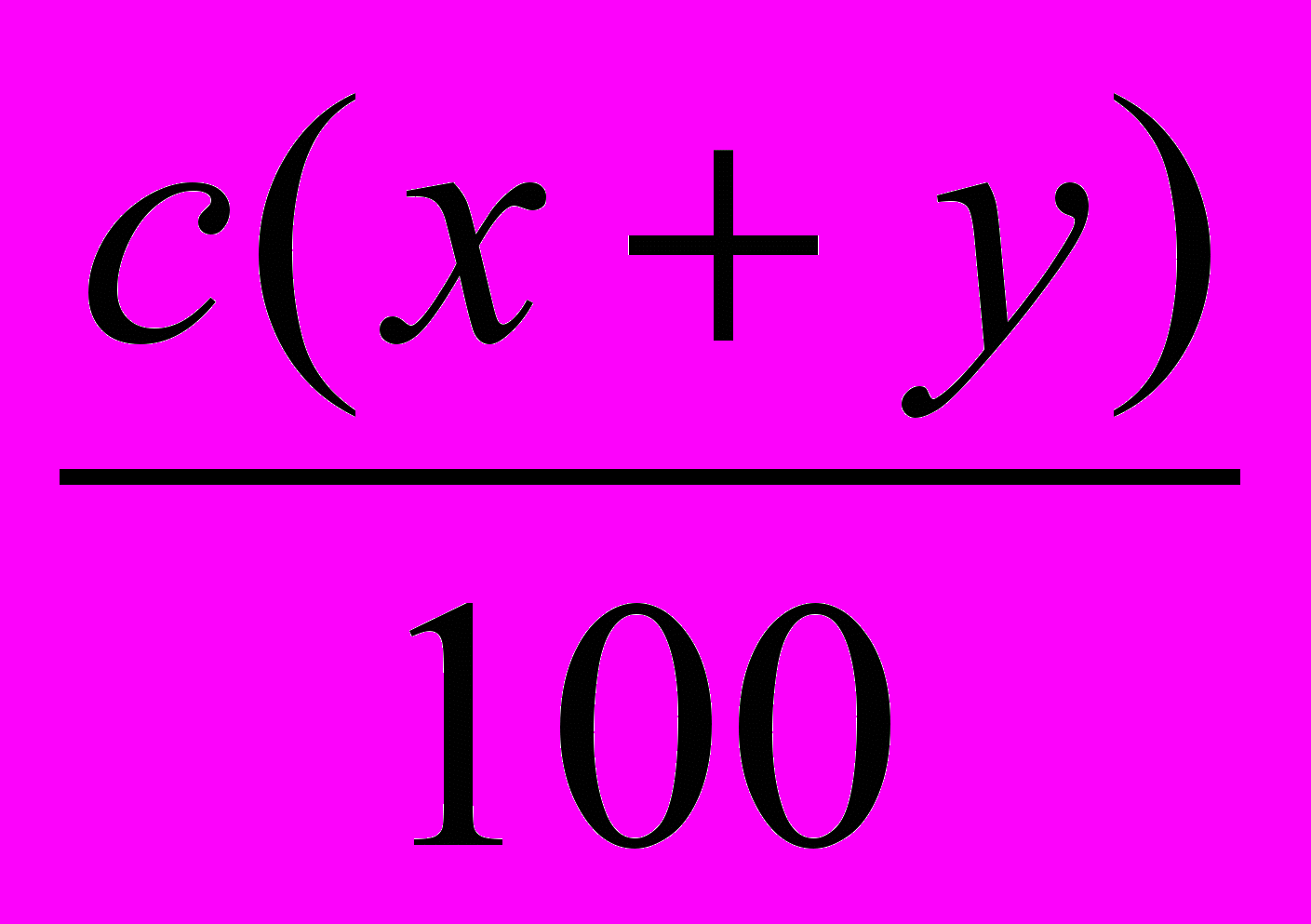г – масса чистой кислоты в смеси.

,

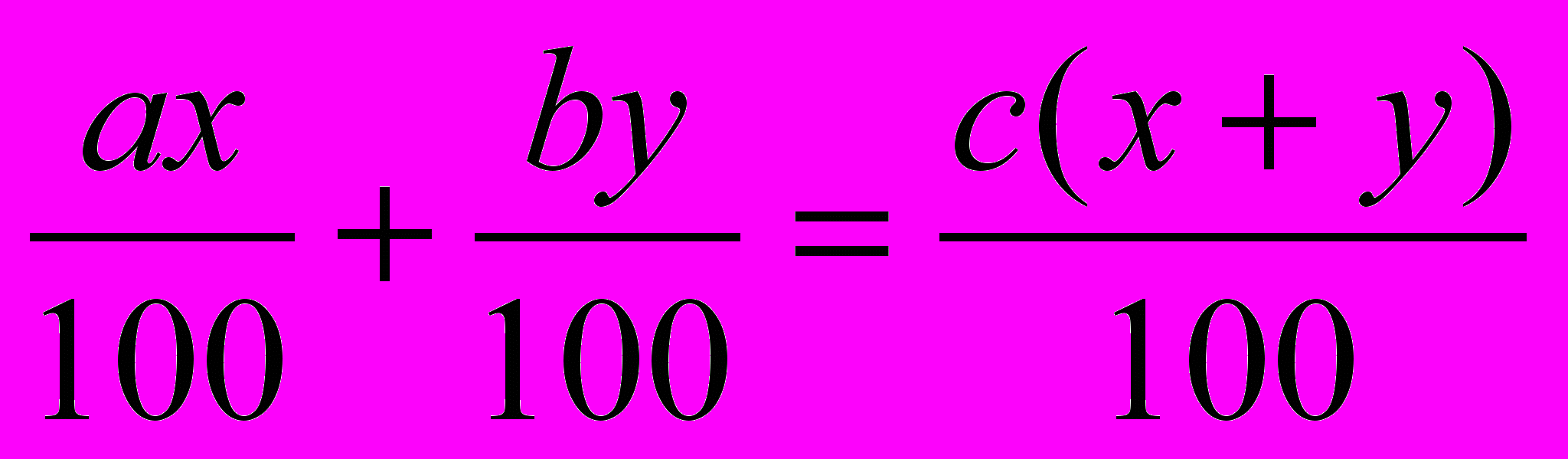при упрощении которого станет ясно, что x:y=(b-c):(c-a). Такой же вывод даёт схема:




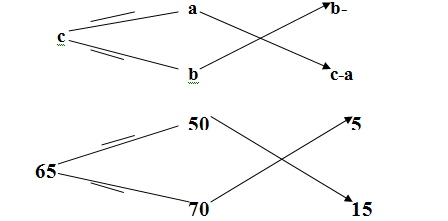
Задача №9

Имеется два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй – 26% меди. Процентное содержание цинка в первом и во втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Определите, сколько килограммов олова содержится в получившемся новом сплаве.

Решение.

Пусть х кг – количество олова в новом сплаве. Так как новый сплав весит 400 кг и в нём находится 30 % цинка, то он содержит 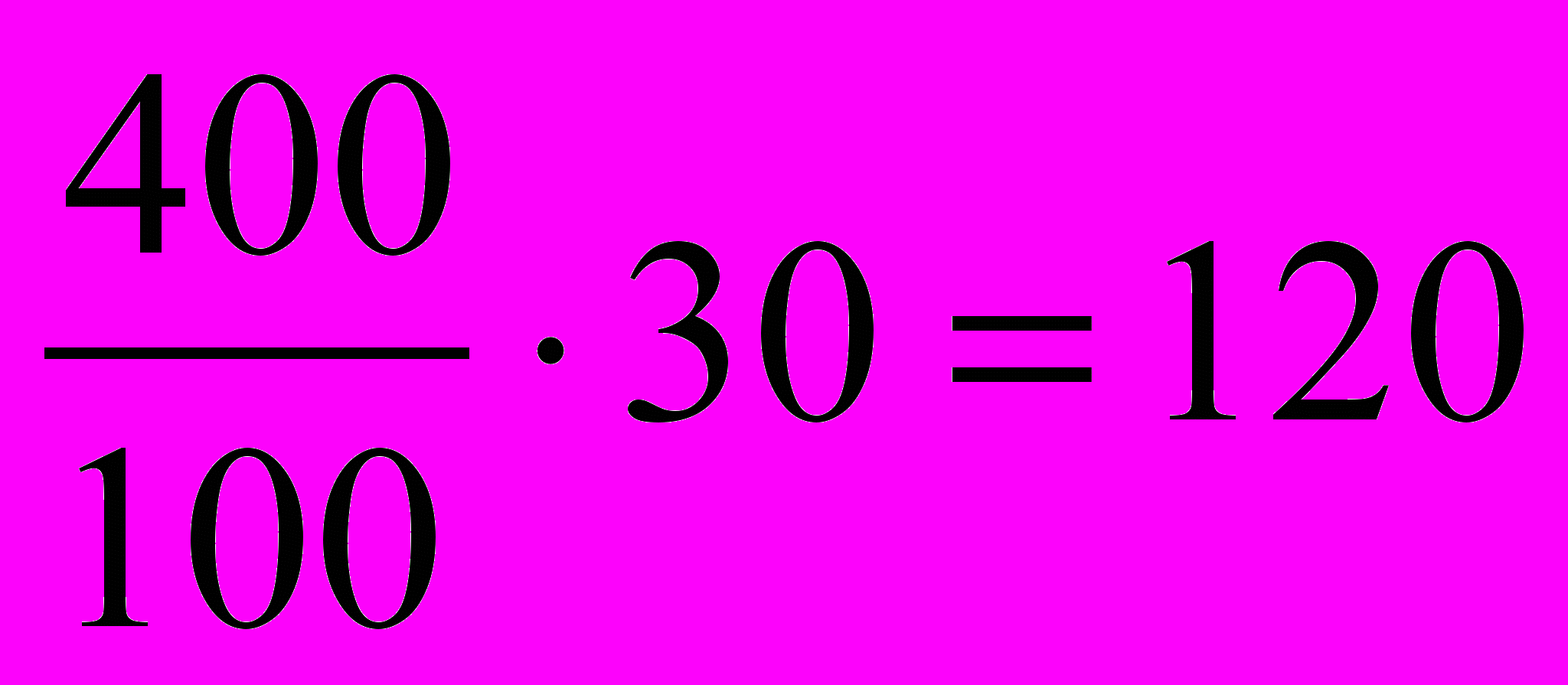кг, а во втором сплаве (120-y) кг цинка. По условию задачи процентное содержание цинка в двух сплавах равно, следовательно, можно составить уравнение: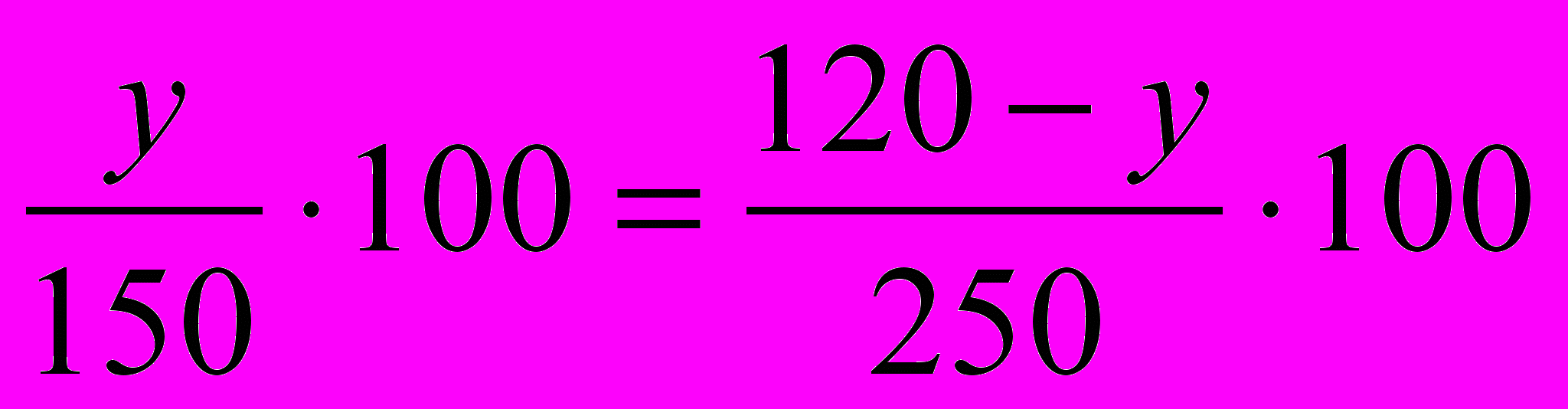



Из этого уравнения находим, что у=45. Поскольку первый сплав содержит 40% олова, то в 150 кг первого сплава олова будет 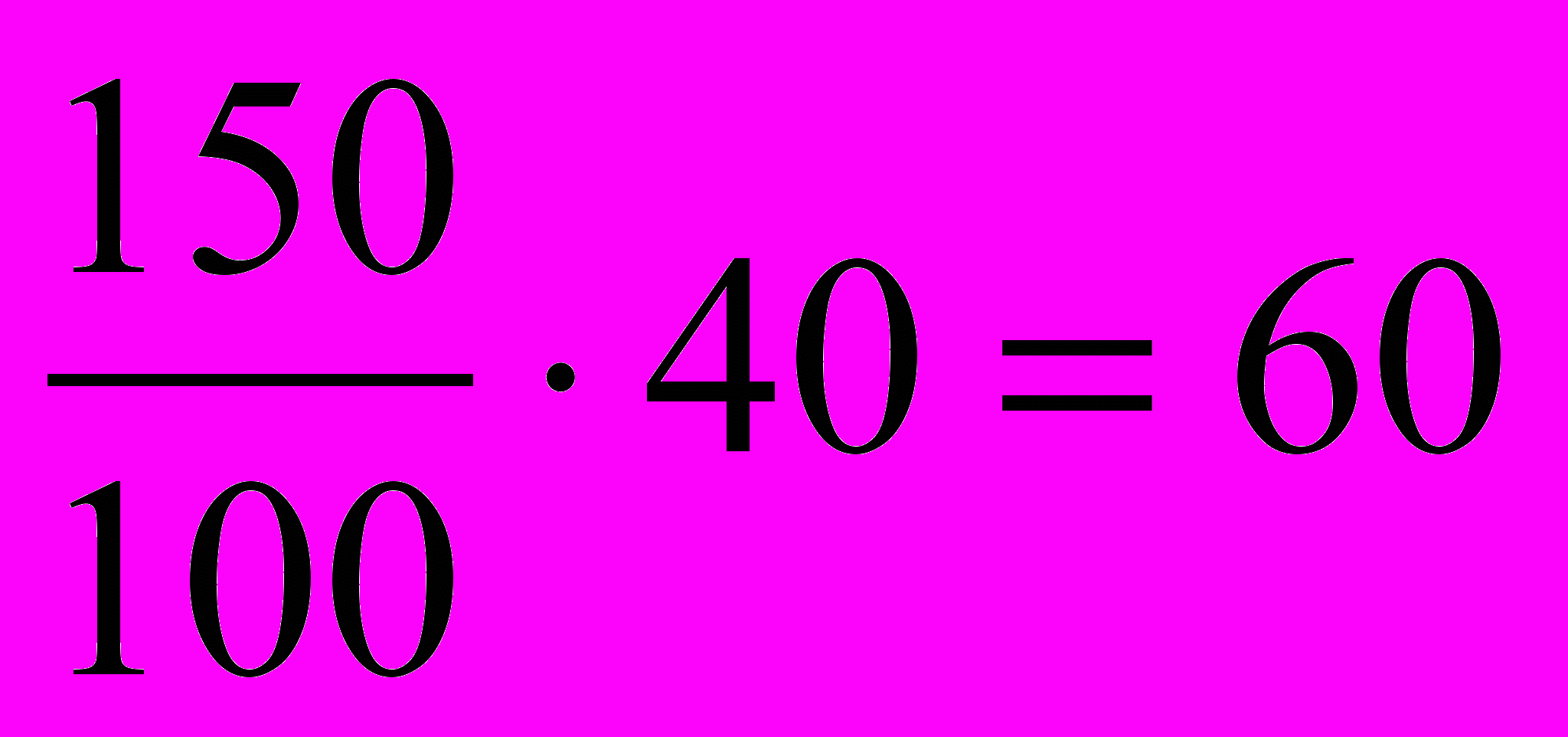кг, а во втором сплаве олова будет (х-60) кг. Поскольку второй сплав содержит 26% меди, то во втором сплаве меди будет 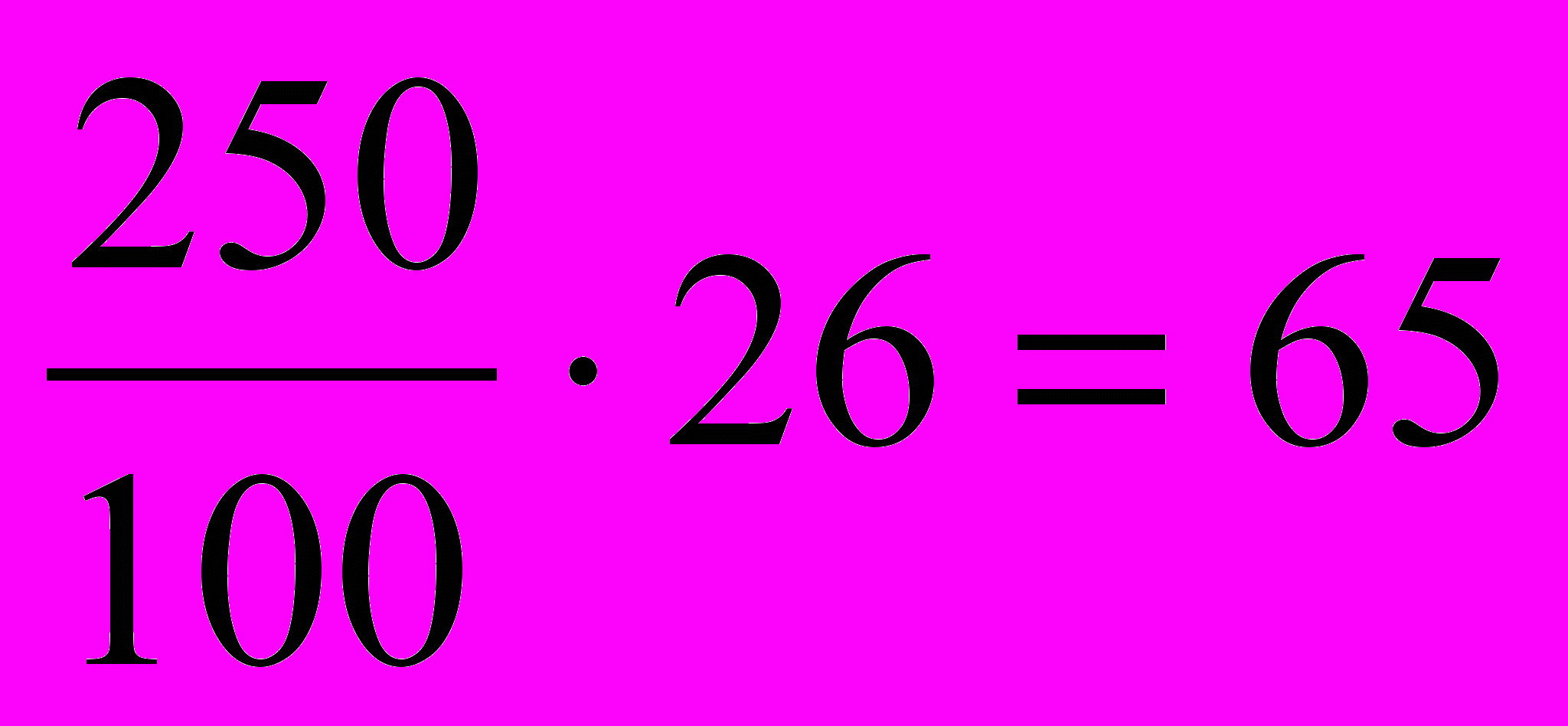кг. Во втором сплаве олова содержится (х-60) кг, цинка 120-45=75 (кг), меди 65 кг и, так как весь сплав весит 250 кг, то имеем:

х-60+75+65=250, откуда х=170 кг

Ответ: 170 кг.


Задача №10

В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20 %. Определите, какое количество железа осталось ещё в руде?

Решение.

Сначала составим таблицу, в которой напишем массу руды, массу железа, концентрацию (долю железа в рудеапишем массу руды, массу железа, концентрацию () руде?

нем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20) до и после удаления примесей.

	Масса руды, кг	Масса железа, кг	Концентрация (доля железа в руде)
Руда	500	х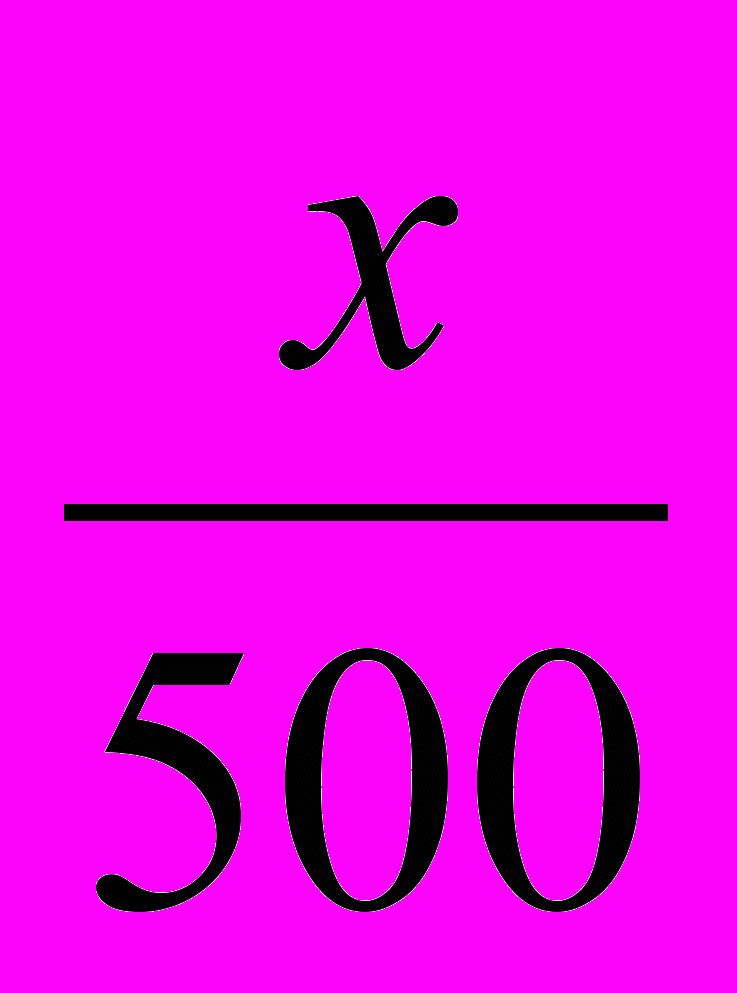
Руда после удаления примесей	500-200=300	х-0,125200=x-25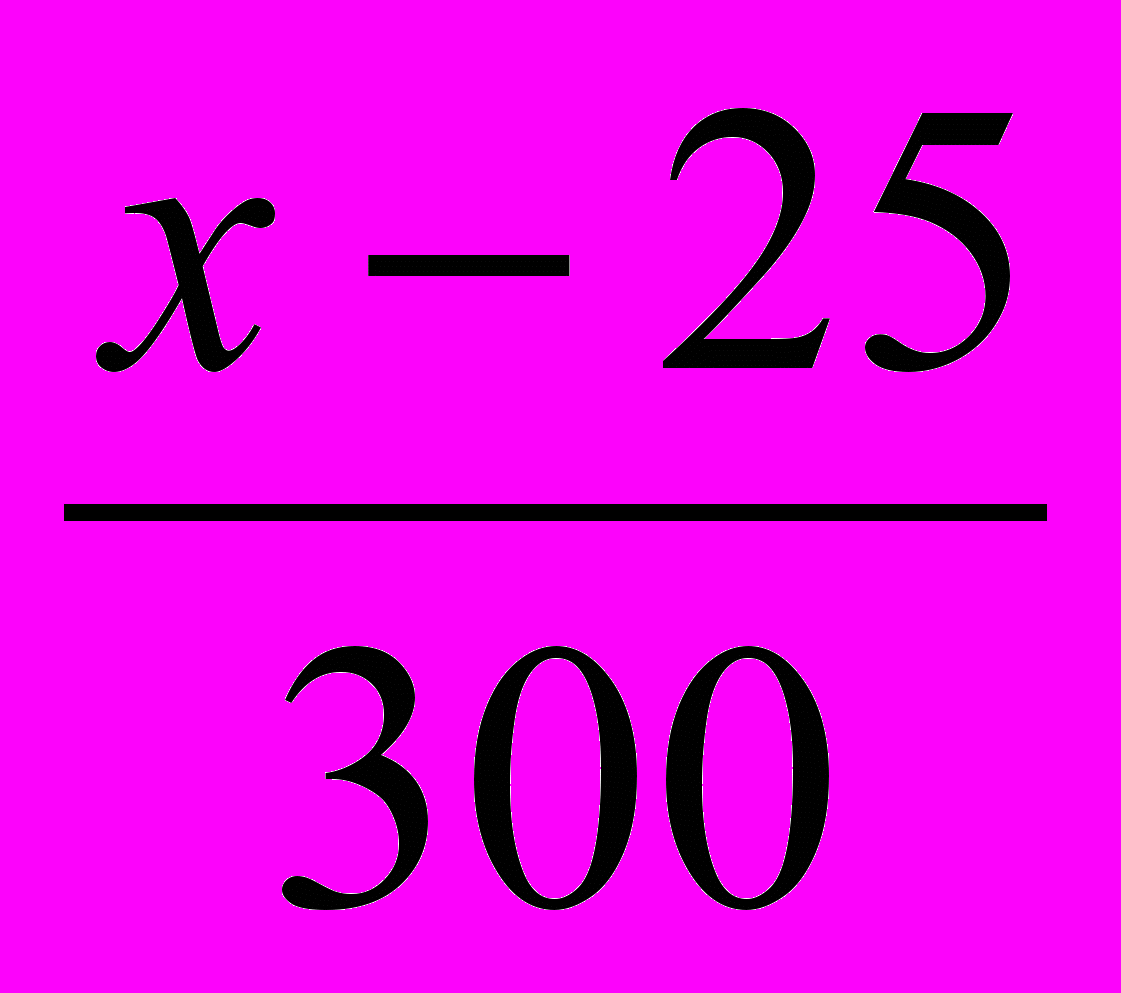

Пусть х кг – масса железа в руде. Так как масса всей руды равна 500 кг, то концентрация железа в ней равна .

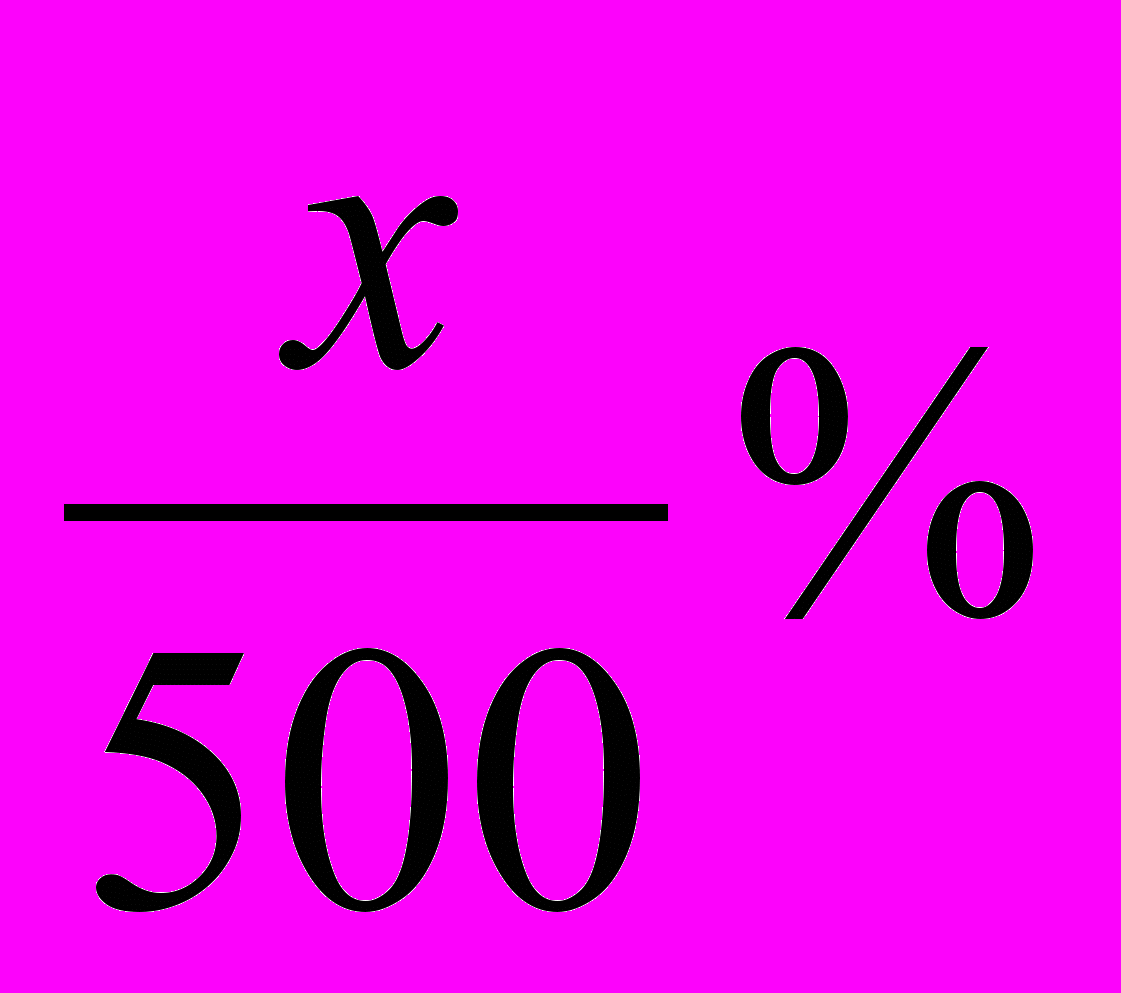Так как масса железа в 200 кг примесей равна 0,125200=25 (кг), то его масса в руде после удаления примесей равна (х-25) кг. Из того, что масса оставшейся руды равна 500-200=300 кг следует, что концентрация железа в ней равна .

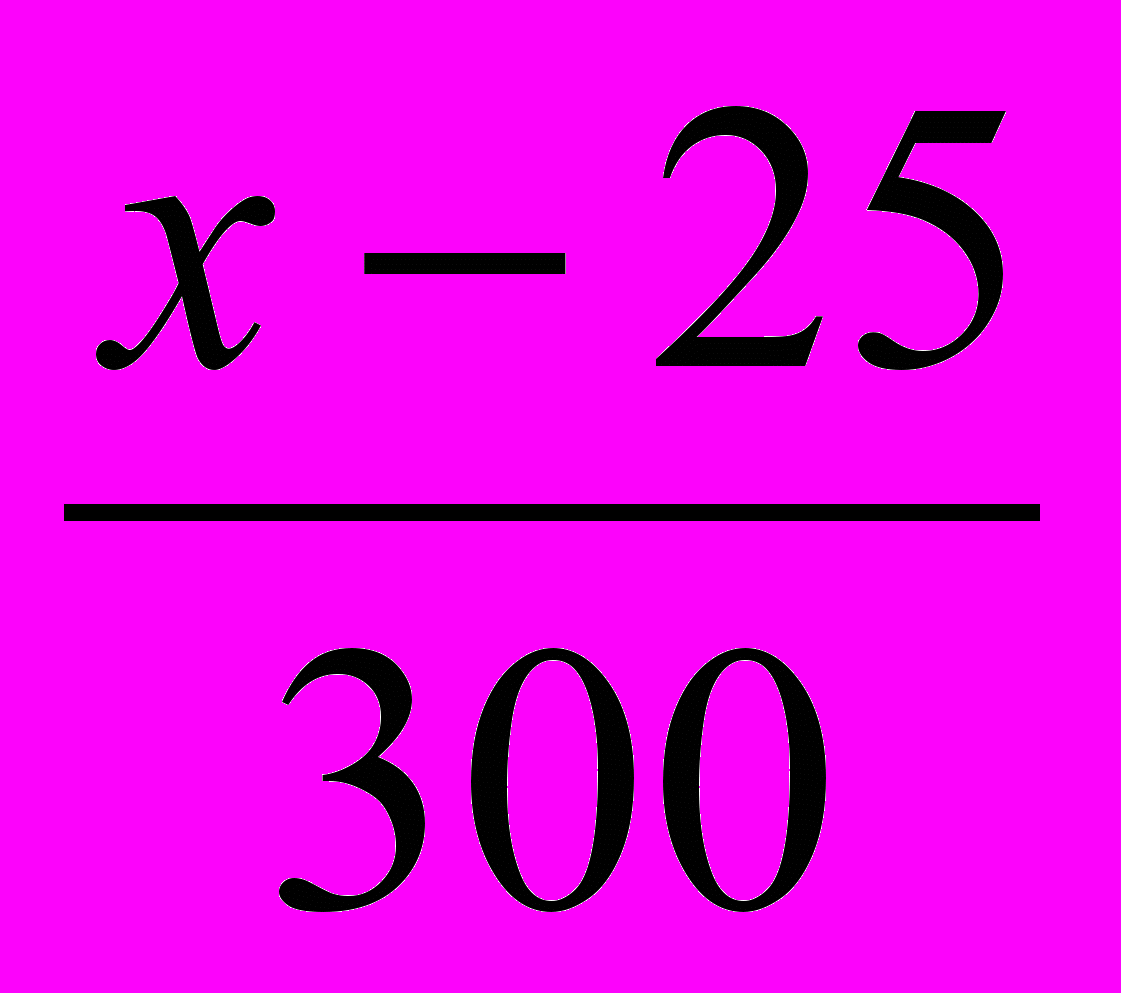По условию, содержание железа в оставшейся руде повысилось на 20%=1/5. Составим уравнение:



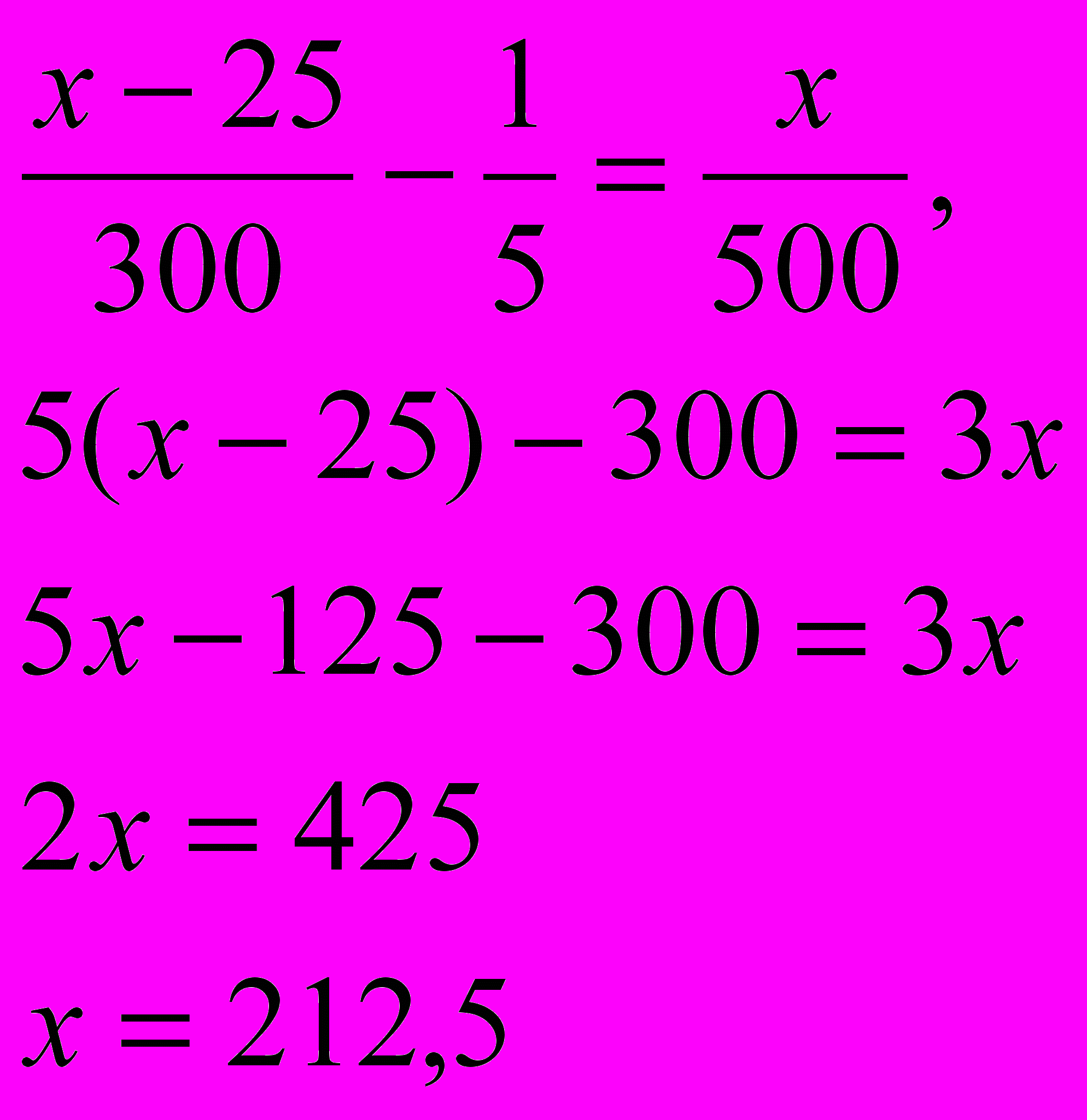
Найдём, что х=212,5 кг – масса железа в руде.

Найдём остаток железа в руде после удаления примесей:

212,5-25=187,5 (кг)

Ответ: 187,5 кг.


Мы решили вторую задачу путём составления таблицы, помогающей зрительно воспринимать задачу.

Вывод: задачи «на смеси и сплавы» решаются множеством способов, но в них всегда присутствует концентрация (доля содержания одного вещества в другом), и они всегда решаются путём составления уравнений.


Арифметическая и геометрическая прогрессии

Определение: Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией. Обозначение: a_1,. a₂ a_3, a_4,…..,a_n.

Из определения арифметической прогрессии следует, что разность между любым ее членом и ему предшествующим равна одному и тому же числу, т.е. a₂-a₁=a₃-a₂=...=а_k–a_k-1. Это число называется разностью арифметической прогрессии и обозначается буквой d.

Для того чтобы задать арифметическую прогрессию (а_п), достаточно знать ее первый член a₁ и разность d. Если разность арифметической прогрессии — положительное число, то такая прогрессия является возрастающей; если отрицательное число, то убывающей. Если разность арифметической прогрессии равна нулю, то все ее члены равны между собой и прогрессия является постоянной последовательностью.

Формула n-го члена арифметической прогрессии имеет вид:

a_n = a₁ - d(n— 1)

Формула суммы п первых членов арифметической прогрессии имеет вид:

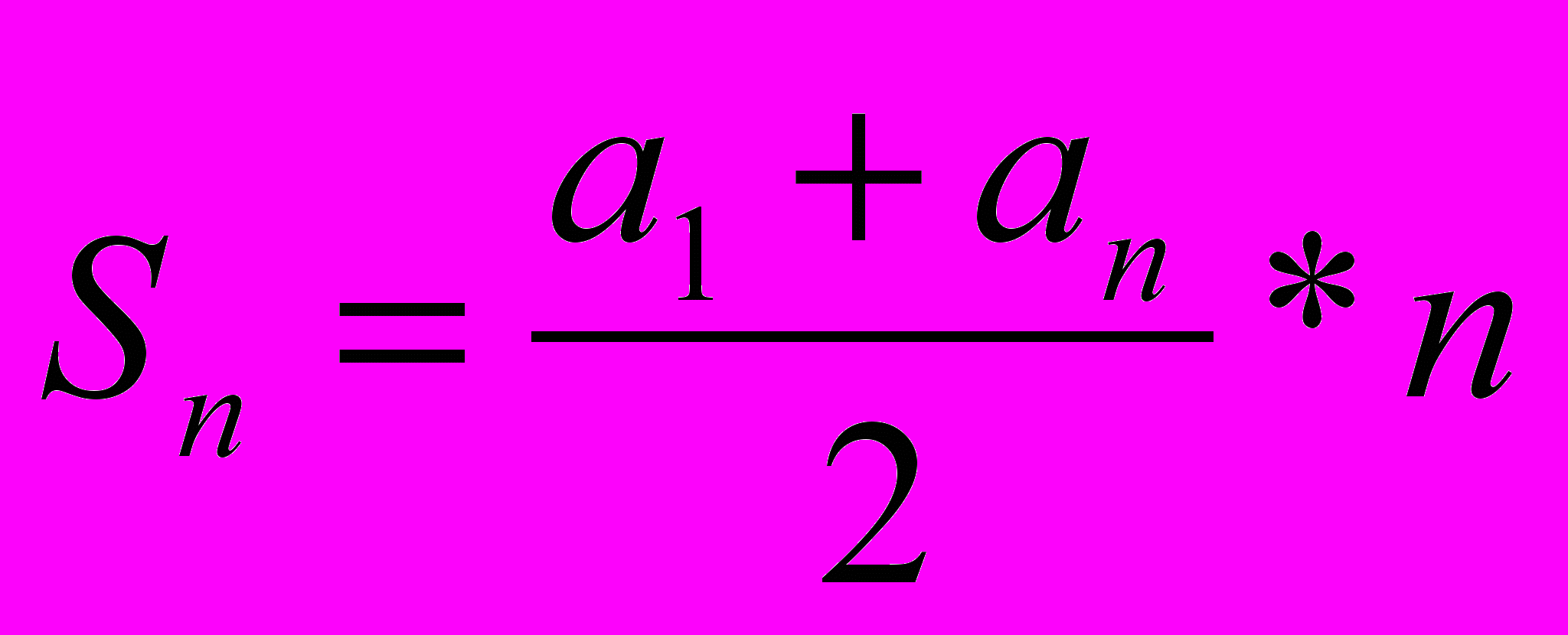или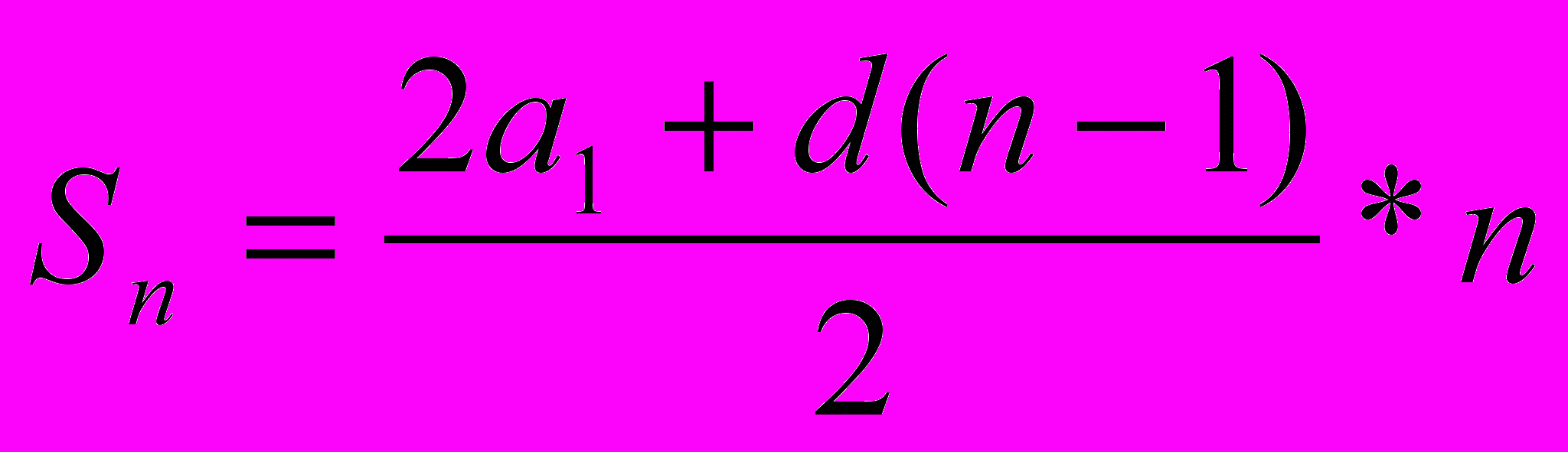

Определение:: Числовая последовательность, первый член которой отли­чен от нуля, а каждый член, начиная со второго, равен пред­шествующему члену, умноженному на одно и то же не равное нулю число, называется геометрической прогрессией.

Из определения геометрической прогрессии следует, что от­ношение любого ее члена к предшествующему равно одному и тому же числу, т.е.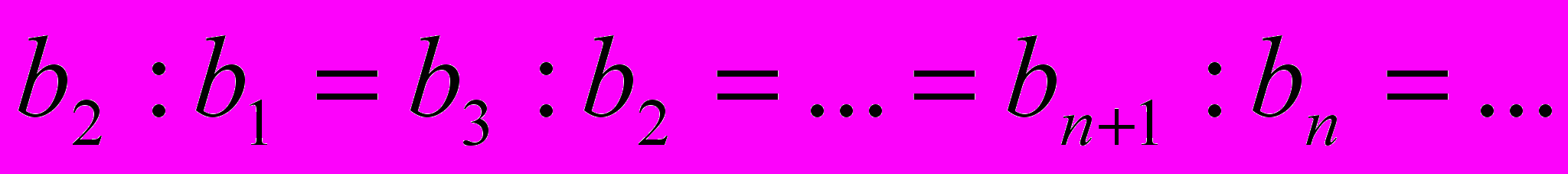. Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q.

Для того чтобы задать геометрическую прогрессию (b_п), достаточно знать ее первый член b₁ и знаменатель q.

Если q>0 (q≠1), то прогрессия является монотонной последовательностью. Пусть, например, b₁= - 2, q = 3, тогда гео­метрическая прогрессия -2, -6, -18,... есть монотонно убываю­щая последовательность.

Если q=1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последователь­ностью.

Формула n-го члена геометрической прогрессии имеет вид:

b_n = b_1* q

Формула суммы п первых членов геометрической прогрессии имеет вид:

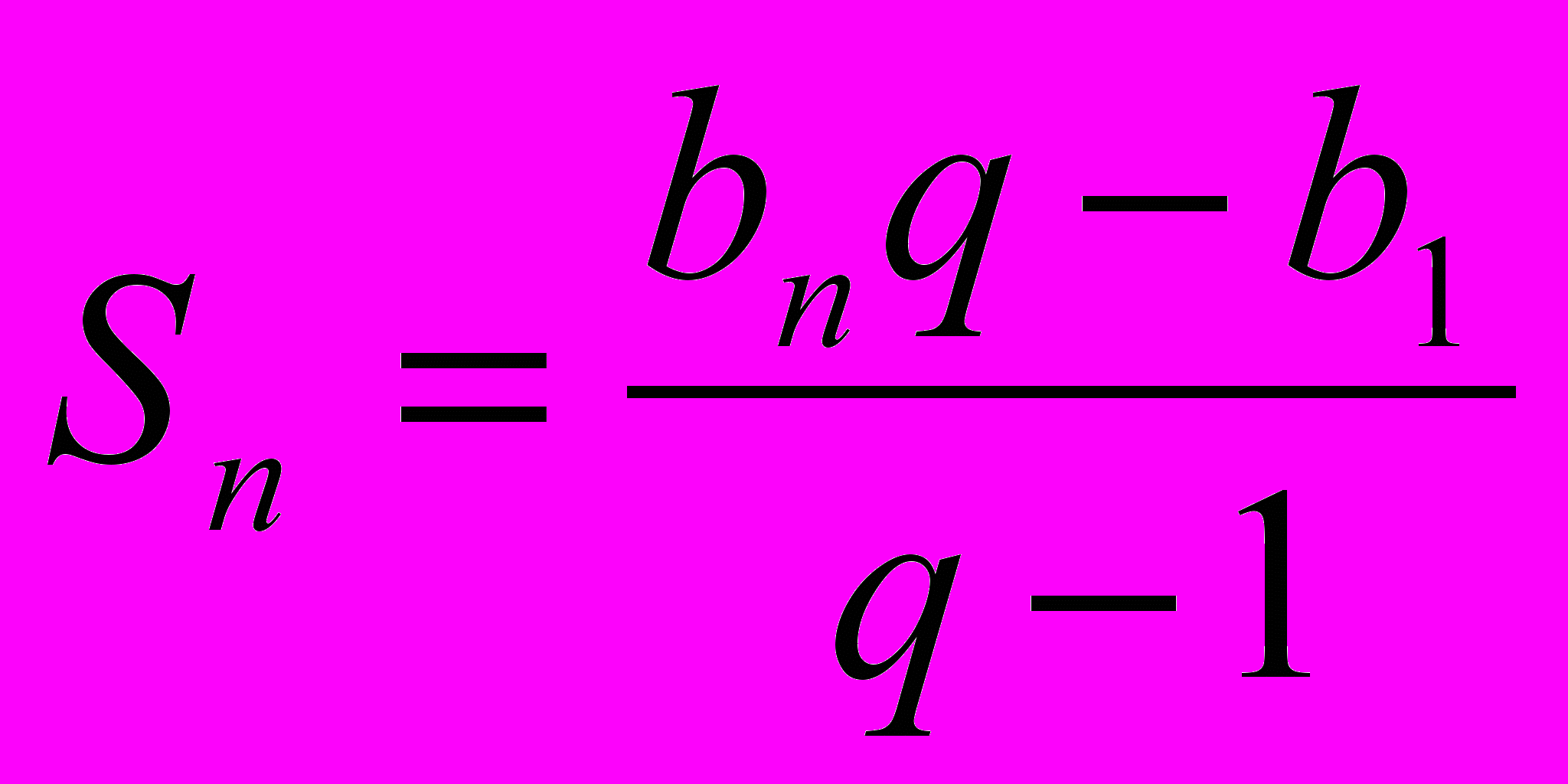или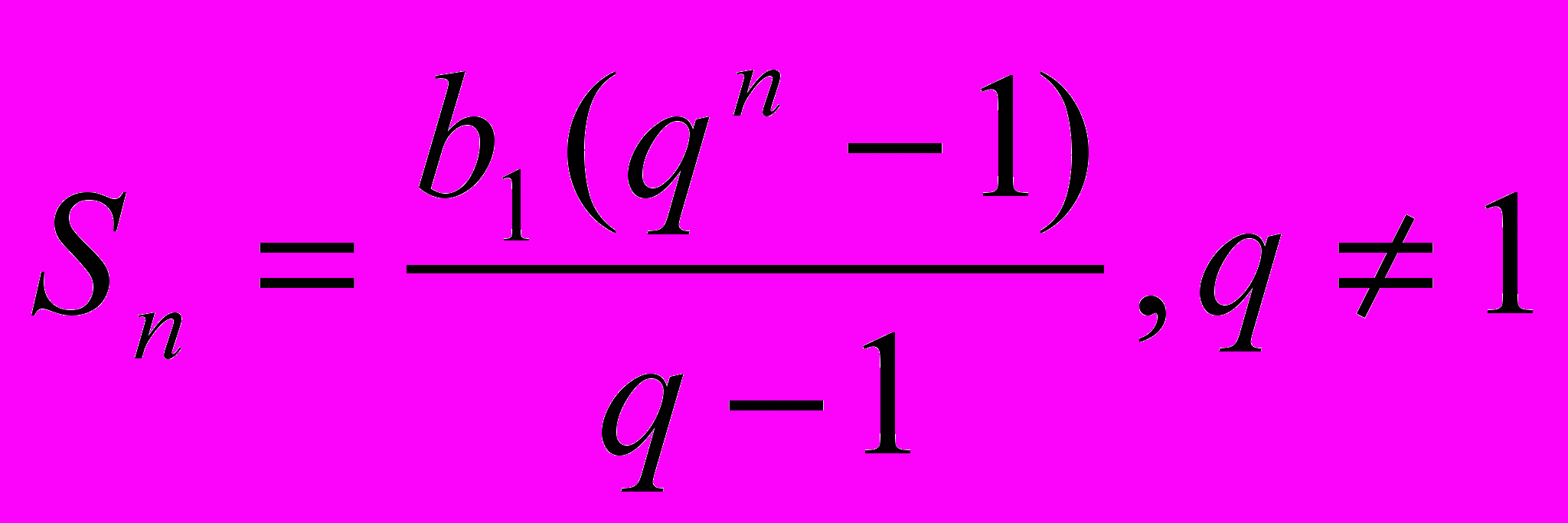

Задачи для курса по выбору «Текстовые задачи и приёмы их решения»

Задачи на движение

Уровень А

№1

а) Из двух городов, расстояние между которыми рав­но 363 км, навстречу друг другу выехали два авто­мобиля. Через сколько часов автомобили встретятся, если их скорости равны 57 км/ч и 64 км/ч?

б) Из двух городов, расстояние между которыми рав­но 108 км, навстречу друг другу выехали два вело­сипедиста. Через сколько часов велосипедисты встре­тятся, если их скорости равны 15 км/ч и 12 км/ч?

№2

а) Города А, В и С соединены прямолинейным шос­се, причем город В расположен между городами А и С. Из города А в сторону города С выехал легковой автомобиль, и одновременно с ним из города В в сто­рону города С выехал грузовик. Через сколько часов после выезда легковой автомобиль догонит грузовик, если скорость легкового автомобиля на 23 км/ч боль­ше скорости грузовика, а расстояние между городам и А и В равно 92 км?

б) Города А, В и С соединены прямолинейным шос­се, причем город В расположен между городами А и С. Из города А в сторону города С выехал легковой автомобиль, и одновременно с ним из города В в сто­рону города С выехал грузовик. Через сколько часок после выезда легковой автомобиль догонит грузовик, если скорость легкового автомобиля на 17 км/ч боль­ше скорости грузовика, а расстояние между городам и А и В равно 102 км?

№3

а) Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 52 км/ч, а вторую половину времени — со скоростью 62 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

б) Половину времени, затраченного на дорогу, автомо­биль ехал со скоростью 48 км/ч, а вторую половину времени — со скоростью 68 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Уровень В

№4

а) Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 3,5 км от места отправления. Один идет со скоро­стью 2,7 км/ч, а другой — со скоростью 3,6 км/ч. Дой­дя до опушки, второй с той же скоростью возвраща­ется обратно. На каком расстоянии от точки отправ­ления произойдет их встреча?

б) Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 16 км. Пешеход прошел путь из А в В за 6 часов. Время его движения на спуске составило 2 часа. С какой скоростью пешеход шел на спуске, если скорость его движения на подъеме меньше скорости движения на спуске на 2 км/ч?

№5

а) Из пункта А круговой трассы, длина которой равна 80 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого автомобилиста равна 92 км/ч, скорость второго автомобилиста равна 68 км/ч. Через сколько минут первый автомоби­лист будет опережать второго ровно на 1 круг

б) Из пункта А круговой трассы, длина которой равна 57 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого автомобилиста равна 81 км/ч, скорость второго автомобилиста равна 63 км/ч. Через сколько минут первый автомобилист

будет опережать второго ровно на 1 круг?

№6

а) Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо придорожного столба за 36 с. Найдите длину поезда.

б) Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 24 с. Найдите длину поезда.

Уровень С

№7

а) Из пункта А в пункт В, отстоящий от пункта А на 27 км, отправился пешеход со скоростью 5 км/ч. Через 36 минут после этого навстречу ему из В вы­ шел другой пешеход со скоростью 3 км/ч. Найдите расстояние от пункта В до места их встречи.

б) Из пункта А в пункт В, отстоящий от пункта А на 11 км, отправился пешеход со скоростью 4 км/ч. Через 15 минут после этого навстречу ему из В вы­ шел другой пешеход со скоростью б км/ч. Найдите расстояние от пункта В до места их встречи.

№8

а) Из пункта А в пункт В по течению реки отпра­вились одновременно моторная лодка и байдарка. Скорость течения реки равна 3 км/ч. Последнюю часть пути моторная лодка шла с выключенным мо­тором, и ее скорость относительно берега была равна скорости течения. На той части пути, где моторная лодка шла с включенным мотором, ее скорость была на 5 км/ч больше скорости байдарки. Найдите ско­рость байдарки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.

б) Из пункта А в пункт В по течению реки отправились одновременно моторная лодка и байдарка. Скорость течения реки равна 2 км/ч. Последнюю часть пути моторная лодка шла с выключенным мотором, и ее скорость относительно берега была равна скорости течения. На той части пути, где моторная лодка шла с включенным мотором, ее скорость была на 7 км/ч больше скорости байдарки. Найдите скорость байдар­ки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.

№9

а) Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 88 км. Возвращаясь из В в А, он ехал понача­лу с той же скоростью, но через 2 ч пути вынужден был сделать остановку на 10 мин. После этого он про­должил путь в А, увеличив скорость на 2 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

б) Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 32 км. Возвращаясь из В в А, он ехал понача­лу с той же скоростью, но через 1 ч пути вынужден был сделать остановку на 12 мин. После этого он про­должил путь в Л, увеличив скорость на 4 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

Уровень D

№10

а) Два бегуна одновременно стартовали из одного и того же места в одном направлении. Спустя 1 час, когда одному из них оставалось бежать 1 км до промежуточного финиша, ему сообщили, что второй бе­гун миновал промежуточный финиш 5 минут назад. Найдите скорость каждого бегуна, если известно, что скорость первого на 2 км/ч меньше скорости второго,

б) Два бегуна одновременно стартовали из одного и того же места в одном направлении. Спустя 1 час, когда одному из них оставалось бежать 1,5 км до промежуточного финиша, ему сообщили, что второй бе­гун миновал промежуточный финиш 5 минут назад. Найдите скорость каждого бегуна, если известно, что скорость первого на 3 км/ч меньше скорости второго.

№11

а)Если велосипедист увеличит скорость на 5 км/ч, то получит выигрыш во времени 12 минут при прохождении некоторого пути. Если же он уменьшит скорость на 8 км/ч, то потеряет 40 минут на том же пути. Найдите скорость велосипедиста и длину пути.

б) Если велосипедист увеличит скорость на 9 км/ч, то получит выигрыш во времени 27 минут при прохождении некоторого пути. Если же он уменьшит скорость на 5 км/ч, то потеряет 29 минут на том же пути. Найдите скорость велосипедиста и длину пути.

№12

а) Из пункта А в пункт В со скоростью 80 км/ч вы­ ехал первый автомобиль. Через некоторое время по тому же маршруту с постоянной скоростью отправил­ся второй автомобиль. После остановки на 20 минут в пункте В второй автомобиль поехал с той же ско­ростью назад и через 48 км встретил первый автомобиль. В момент прибытия в В первого автомобиля второй автомобиль был в 120 км от В. Найдите расстояние от А до места первой встречи автомобилей, если расстояние между пунктами А и В равно 480 км.

б) Из пункта А в пункт В с постоянной скоростью выехал первый автомобиль. Через некоторое время по тому же маршруту со скоростью 100 км/ч отправился второй автомобиль. Обогнав первый автомобиль через 150 км, второй автомобиль остановился на 1 час в В, затем поехал с той же скоростью назад и был на расстоянии 200 км от В в момент прибытия в В первого автомобиля. Найдите расстояние от В до места
второй встречи автомобилей, если расстояние между А и В равно 600 км.

Задачи на работу

Уровень А

№13

а) Один мастер может выполнить заказ за 28 ч, а дру­гой — за 21 ч. За сколько часов выполнят заказ оба мастера, работая вместе?

б) Один мастер может выполнить заказ за 9 ч, а дру­гой — за 18 ч. За сколько часов выполнят заказ оба мастера, работая вместе?

№14

а) Первая труба наполняет бак объемом 820 литров, а вторая труба – бак объемом 790 литров. Известно, что одна из труб пропускает в минуту на 3 л воды больше, чем другая. Сколько литров воды в минуту пропускает каждая труба, если баки были наполнены за одно и то же время?

б) Первая труба наполняет бак объемом 790 литров, а вторая труба – бак объемом 750 литров. Известно, что одна из труб пропускает в минуту на 4 л воды больше, чем другая. Сколько литров воды в минуту пропускает каждая труба, если баки были наполнены за одно и то же время?

№15

а) Олег отвечает за час на 8 вопросов теста, а Ники­та—на 9. Они одновременно начали отвечать на вопросы теста, и Олег закончил позже Никиты на 10 ми­нут. Сколько вопросов содержит тест?

б) Сергей отвечает за час на 10 вопросов теста, а Иван — на 12. Они одновременно начали отвечать на вопросы теста, и Сергей закончил позже Ивана на 30 минут. Сколько вопросов содержит тест?

Уровень В

№16

а) Беллетрист хочет набрать на компьютере рукопись объемом 480 страниц. Если он будет набирать на 8 страниц в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько страниц в день планирует набирать беллетрист?

б) Прозаик хочет набрать на компьютере рукопись объемом 450 страниц. Если он будет набирать на 5 страниц в день больше, чем запланировал, то закон­чит работу на 3 дня раньше. Сколько страниц в день планирует набирать прозаик?

№17

а) В помощь садовому насосу, перекачивающему 9 л воды за 4 мин, подключили второй насос, перекачива­ющий тот же объем воды за 7 мин. Сколько времени эти два насоса должны работать совместно, чтобы перекачать 99 л воды?

б) В помощь садовому насосу, перекачивающем 5 л воды за 2 мин, подключили второй насос, перекачива­ющий тот же объем воды за 3 мин. Сколько времени эти два насоса должны работать совместно, чтобы пе­рекачать 25 л воды?

№18

а) Саша и Стае вскапывают грядку за 10 минут, а один Стае - за 15 минут. За сколько минут вскапы­вает грядку один Саша?

б) Даша и Вита пропалывают грядку за 12 минут, а одна Вита - за 20 минут. За сколько минут пропалывает грядку одна Даша?

Уровень С

№19

а) Игорь и Паша могут покрасить забор за 3 часа. Паша и Володя могут покрасить этот же забор за 6 часов, а Володя и Игорь - за 4 часа. За какое время мальчики покрасят забор, работая втроем?

б) Маша и Настя могут вымыть окно за 20 минут. Настя и Лена могут вымыть это же окно за 15 минут, а Маша и Лена - за 12 минут. За какое время девочки вымоют окно, работая втроем?

№20

а) Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали строить два одинаковых летних домика. В первой бригаде бы­ло 7 рабочих, а во второй — 13 рабочих. Через 8 дней после начала работы в первую бригаду перешли 7 рабочих из второй бригады, в результате чего оба домика были построены одновременно. Сколько дней потребовалось бригадам, чтобы закончить работу в новом составе?

б) Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали строить два одинаковых летних домика. В первой бригаде было 8 . рабочих, а во второй —14 рабочих. Через 7 дней после начала работы в первую бригаду перешли 10 рабочих из второй бригады, в результате чего оба домика были построены одновременно. Сколько дней потре­бовалось бригадам, чтобы закончить работу в новом составе?


Уровень D

№21

а) Два насоса разной производительности наполня­ют резервуары объемом 432 л каждый. Насосы были включены одновременно, и спустя некоторое время воды в двух резервуарах оказалось 432 л. Через 6 минут после этого первый насос заполнил свой резервуар, а второй насос закончил работу на 18 минут позже. Сколько литров воды в минуту перекачивает каждый насос? Какой объем воды накачал бы первый на­сос за то время, которое требуется обоим насосам для заполнения одного резервуара при совместной работе?

б) Два насоса разной производительности наполняют резервуары объемом 504 л каждый. Насосы были включены одновременно, и спустя некоторое время воды в двух резервуарах оказалось 504 л. Через 7 минут после этого первый насос заполнил свой резервуар, а второй насос закончил работу на 21 минуту позже. Сколько литров воды в минуту перекачивает каждый насос? Какой объем воды накачал бы первый насос за то время, которое требуется обоим насосам для заполнения одного резервуара при совместной работе?

№22

а) Три трактора разной производительности вспахивают два поля разной площади. Третий трактор вспахивает второе поле на 5 часов быстрее, чем первый вспахивает первое поле, но на 2 часа медленнее, чем второй вспахивает первое поле. Первый и второй тракторы, работая совместно, вспахивают первое поле на 11 часов быстрее, чем третий вспахивает второе поле. За сколько часов третий трактор вспахивает второе поле?

б) Три трактора разной производительности вспахивают два поля разной площади. Третий трактор вспахивает второе поле на 4 часа быстрее, чем первый вспахивает первое поле, но на 3 часа медленнее,
чем второй вспахивает первое поле. Первый и второй тракторы, работая совместно, вспахивают первое поле на 12 часов быстрее, чем третий вспахивает второе поле. За сколько часов третий трактор вспахивает второе поле?

№23

а) Трава на всем лугу растет одинаково густо и быст­ро. 70 коров съедают всю траву за 24 дня, а 30 коров – за 60 дней. За сколько дней съедят всю траву 20 коров?

б) Трава на всем лугу растет одинаково густо и быст­ро. 50 коров съедают всю траву за 36 дней, а 80 ко­ров – за 20 дней. Стадо коров съело всю траву на лугу за 100 дней. Сколько коров было в стаде?