Применение информационных технологий при изучении школьного курса стереометрии

Вид материала

Документы

Содержание Математический конструктор Стереометрия 10-11 1С: Школа. Математика. 5-11 классы. Практикум Компас-3d lt 9.0 2. Использование ИТ с точки зрения конструирования урока. 3. Использование программы «Стереометрия» для решения задач на построение. C к плоскости BDG BDG, построив отрезки ее пересечения с гранями куба. Затем построим точку K 4. Практикум «Решение задач на построение сечений с помощью ЭУМК «Стереометрия»

Подобный материал:

• «Применение современных информационных технологий при изучении вопросов нетарифного, 316.46kb.
• Применение информационных технологий в исторических исследованиях, 413.67kb.
• Программа дисциплины Моделирование информационных систем для направления 080700., 244.82kb.
• Тема 1: Первые уроки стереометрии, содержание и методика изучения некоторых вопросов, 148.41kb.
• Применение компьютерных технологий на уроках биологии Слюсарь, 60.39kb.
• Использование информационных технологий при изучении школьных предметов и во внеклассной, 126.89kb.
• Евсеев В. И., Вафин Ф. Ф., Горохов, 20.88kb.
• Использование информационных технологий в организации самостоятельной работы студентов, 44.5kb.
• «Применение информационных технологий при решении задач высшей алгебры», 159.09kb.
• Использование Mathcad и Excel при изучении школьного курса физики, 67.71kb.

Применение информационных технологий

при изучении школьного курса стереометрии

Кузьмина И.А., учитель математики МОУ СОШ №5 г.Нарьян-Мара

1. Целесообразность применения ИКТ на уроке стереометрии.

Опыт преподавания геометрии показывает, что для многих школьников наибольшие затруднения вызывают стереометрические задачи. Учителю, ведущему математику в старших классах, известны трудности, которые возникают в процессе преподавания стереометрии буквально с первых уроков. При знакомстве с аксиомами стереометрии пространственные представления учащихся развиты очень слабо. Начальные сведения по стереометрии имеют абстрактный характер, усвоение материала строится на заучивании. Ученики теряют интерес к предмету, и многие из них считают стереометрию трудным школьным предметом.

Трудности в изучении стереометрии вызваны тем, что зрительное восприятие геометрических объектов не всегда соответствует тем закономерностям, которыми этот объект обладает. Отображение пространственных фигур в виде чертежа на листе бумаги приводит к тому, что очень многие закономерности представляются в искаженном виде. Например, скрещивающиеся прямые могут выглядеть как пересекающиеся или как параллельные прямые, прямой угол может выглядеть как острый или тупой угол, равные отрезки могут выглядеть как отрезки разной длины, и т.д. В реальной жизни человек приучается зрительно распознавать закономерности за счет наблюдений над объектами, находящимися в движении.

Т.к. при работе над стереометрическими задачами используются плоские чертежи, сделанные на бумаге или на доске, то возникают объективные трудности, связанные с поиском необходимых закономерностей на основе схематического чертежа, который отражает далеко не все особенности пространственных фигур. На чертеже изображения элементов пространственных фигур выглядят искаженно и не соответствуют действительности. Некоторые важные для решения задачи линии или точки могут оказаться на чертеже слишком близкими или совпадающими. Другие важные точки могут попасть за край листа бумаги. Кроме того, при работе на бумаге трудно без следа стереть ненужную или неудачно проведенную линию. Все эти факторы приводят к неправильному восприятию учащимися пространственных фигур в самом начале курса стереометрии.

Если при решении задачи по формированию образов пространственных фигур, таких как куб, шар, пирамида, учитель опирается на вещественные модели, что может обеспечить успешность решения первоначальных стереометрических задач, то для решения сложных задач, таких как построение линейного угла двугранного угла, построение сечения многогранника плоскостью на помощь должен прийти чертеж. Для чтения условного чертежа, на котором искажены линейные и угловые размеры, нужно иметь хорошо развитое пространственное мышление.

Выполнение нужного чертежа для большинства стереометрических задач обычно требует несколько попыток. Лишь после того, когда решающему удается увидеть в чертеже ключевые соотношения, чертеж приобретает требуемый вид. Полученный чертеж являет­ся внешним источником, из которого черпаются идеи решения задачи.

К сожалению, почти все школьные учебники геометрии, включенные в федеральный перечень, не пре­дусматривают специального обучения выполнению чертежей, подразумевается, что учащийся необходимые чертежи научится строить самостоятельно, следуя образцам, приведенным в учебнике (или с помощью учителя).

Только выход на другую наглядность может помочь учащимся справиться с задачами, для решения которых нужно видеть «внутренность» тел, изменять их строение и расположение частей.

Эту группу наглядности образуют изображения геометрических тел с помощью современных компьютерных технологий. Существующее сегодня программное обеспечение позволяет строить перспективное изображение, поворачивать его и рассматривать под разными углами, что помогает формировать умение у учащихся воссоздавать целостный пространственный образ.

При проведении уроков в современной школе большое распространение получили презентации. Например, при доказательстве теоремы о трех перпендикулярах возможно опираться на соответствующие слайды. При этом остается проблема трудности восприятия пространственных фигур через плоскостной чертеж.

Для изучения стереометрического материала педагогом могут создаваться и использоваться Flash-анимации. Они придают телам объем, позволяя наделять их свойствами пространства. В этом случае педагог должен затратить много времени для подготовки к уроку, создавая анимационные фильмы.

В настоящее время создано определенное количество компьютерных программ, позволяющих ученикам осуществить выход в пространство. Возможно некоторые из них вам уже знакомы. Среди программного обеспечения есть платные ресурсы, есть свободно распространяемые в сети Интернет.

В начале изучения курса стереометрии перед учителем возникает проблема переноса пространственного тела в плоскость. Часто приходится строить чертежи многогранников. Если при этом возникают трудности с мысленным представлением фигуры и пониманием того, как ее можно изобразить на плоскости, из каких фигур она состоит, поможет программа Poly32. Она содержит огромную базу многогранников, каждый из которых можно визуализировать 11 способами.

В курсе стереометрии определенное месте отводится построению сечений пространственных фигур. Правда, в учебнике Атанасяна этому вопросу уделяется недостаточно внимания, а именно построение сечений позволяет развивать пространственное воображение учащихся. Здесь можно отметить программу построения сечений SecBuilder 1.0. Выбирая один из стандартных трехмерных объектов, можно его двигать, вращать, приближать, удалять, строить сечения. Результаты можно применять в качестве иллюстраций к геометрическим задачам.

Среди распространенных платных программ можно выделить Математический конструктор, который позволяет работать в плоскости осуществлять выход в пространство. Программная среда предназначена для создания интерактивных моделей по математике, работа с которыми сочетает конструирование, эксперимент, решение задач.

Учебник-справочник Стереометрия 10-11, разработанный авторским коллективом Кудиц, содержит теоретическую информацию в объеме курса средней школы, дополнительные теоремы и формулы для изучения каждой темы, задачи с указаниями к решению и ссылками, конструктор трехмерных чертежей и мультипликаций, трехмерные интерактивные иллюстрации. Данный электронный учебник построен на широком использовании возможностей современного персонального компьютера для удобного и наглядного представления учебной информации.

Входящий в учебник СтереоКонструктор позволяет учителю совместно с учащимися дополнить материал издания собственными разработками, зада­чами и их решениями и даже подготовить собственное мультимедийное пособие по математике.

Распространяемое в образовательных школах России электронное издание 1С: Школа. Математика. 5-11 классы. Практикум представляет собой комплекс лабораторных работ по геометрии, алгебре, алгоритмике и теории вероятностей, предназначенный для поддержки курсов практическими заданиями творческого характера. В состав комплекса входит известная система динамического моделирования Живая Геометрия 3.1, которая позволяет выполнять конструирование, моделирование, математический эксперимент.

В последние годы распространены различные программы с использованием возможностей языко программирования Delphi и Java. Интересна демонстрация OpenGL 3D Demonstration, которая представляет собой практическую реализацию основных методов построения трехмерных объектов, позволяет легко управлять параметрами построения и выбирать требуемый объект из 5 многогранников для построения которых она используется. Для представленных многогранников имеется возможность динамического изменения различных параметров их отображения: угла поворота объекта и его размера, уровня поперечной и продольной детализации, модели построения.

Подсистема КОМПАС-3D LT 9.0, распространяемая сегодня в школах в рамках ПНП «Образование», предназначена для создания трехмерных параметрических моделей, ориентирована на формирование трехмерных моделей конкретных тел, содержащих как типичные, так и нестандартные, уникальные конструктивные элементы. Программа позволяет строить красивые и выразительные модели пространственных конструкций. Результатом работы в данном редакторе может стать анимированный ролик или статическое изображение, просчитанное программой.

Современные мультимедийные средства предоставляют широкие возможности для построения изобра­жений геометрических фигур. Вместе с тем, использование этих средств при самостоятельном выполнении чертежей не освобождает пользователя от знакомства с теоретическими основами теории изображений.

2. Использование ИТ с точки зрения конструирования урока.

Среди новинок, приходящих сегодня в школу, особое место занимают современные технические средства обучения, позволяющие педагогу сделать процесс обучения ярким, наглядным, динамичным, варьировать частные решения с опорой на имеющиеся готовые «шаблоны», а также более эффективно осуществлять «обратную связь». Из моего опыта применения ИТ на уроках наиболее эффективным является использование технических средств на уроках стереометрии 10 класса, а также на уроках алгебры, посвященных функциям и графикам функций.

Рассмотрим, за счет чего происходит это повышение эффективности урока.

1. На этапе актуализации знаний учитель задает вопрос, который тут же отображается на экране. При необходимости проецируется иллюстрация к вопросу, что позволяет рассмотреть чертеж. Чертежи, вопросы появляются на доске последовательно, что позволяет избежать ненужного нагромождения. Появляется возможность поэкспериментировать с условием задачи, изменяя чертеж и рассматривая различные случаи, что ведет к развитию геометрических представлений учащихся и лучшему пониманию темы.

На классическом уроке учащиеся на слух воспринимают заданный учителем вопрос, что снижает степень его понимания некоторыми учащимися. На выполнение иллюстрации к задаче необходимо время, кроме того, чертеж, выполненный на плоскости, не всегда наглядно передает истинную картину, а значит, возникает необходимость использования различных моделей. Чертежи на доске, конечно, могут быть заготовлены заранее. Но при этом большое количество рисунков на доске мешает некоторым учащимся сосредоточиться на конкретной задаче, на доске остается мало места для дополнительных выкладок к каждой конкретной задаче, что может привести к непониманию каких-то моментов решения. Теряется время на стирание чертежей.

2. На этапе проверки домашнего задания возможен вариант проверки путем сканирования либо с помощью документ-камеры. Работа ученика выводится на доску, он поясняет свое решение. При необходимости учитель или другие ученики исправляют допущенные ошибки. Если задача имеет несколько решений, на доску выводятся другие варианты, и учащиеся имеют возможность быстро сравнить различные способы решения задачи. Основное время используется непосредственно на разбор заданий.

На классическом уроке ученик переписывает решение на доску из тетради, а затем объясняет его другим ученикам. При этом тратится в среднем от 5 до 10 минут в зависимости от скорости письма ученика. Если задача решена несколькими способами, то время на воспроизведение этих заданий на доске увеличивается.

3. При объяснении нового материала возможно использование презентации, раздаточного материала с комментариями, дополнениями, ответами на вопросы учащихся. Отработку материала можно разнообразить примерами из различных источников. Здесь информационные технологии остаются лишь дополнением к объяснению учителя.

На классическом уроке материал выносится на доску, учащиеся также записывают его в тетради. Если учащийся не очень внимателен, при списывании решения с доски он может допустить ошибки, которые затем затруднят понимание материала или приведут к ошибкам при решении заданий подобного типа. Использование дополнительного материала ограничено наличием достаточного на класс числа сборников.

4. На этапе закрепления материала ученикам могут быть предложены разноуровневые задания. Хорошо организуется момент проверки правильности выполнения задач.

На классическом уроке основная часть учащихся выполняет задания в тетрадях, а двое или трое учащихся одновременно решают задания своего варианта на доске, а затем эти задания комментируются. Ответы проверяются с помощью доски, где возможно неправильное решение.

5. При подведении итогов урока всю информацию, появлявшуюся в процессе урока на экране, можно просмотреть, повторить основные моменты, сделать выводы.

На классическом уроке, если у учащихся возникает в конце урока вопрос по какой-либо решенной задаче или при формулировке выводов, чертеж к задаче или этапы рассуждений приходится восстанавливать на доске заново.

Следует отметить, что время на предварительную подготовку учителя при использовании компьютера на первом этапе, несомненно, увеличивается, однако постепенно накапливается методическая база, создаваемая совместно учителями и учениками, что значительно облегчает эту подготовку в дальнейшем.

Также замечено, что использование компьютера позволяет повысить заинтересованность, а значит и внимание учеников за счет новизны способа изложения материала. Повышается интерес и к математике в целом. Учащиеся активно включаются в поиск и подготовку материалов к урокам, что в свою очередь развивает у них навыки учебно-исследовательской деятельности и позволяет добиться лучших результатов не только в изучении математики, но и в информатике и информационных технологиях.


3. Использование программы «Стереометрия» для решения задач на построение.

В большинстве стереометрических задач набольшую трудность представляет начальный этап решения. Этот этап чаще всего основан на некоторой геометрической конструкции, получающейся путем проведения некоторых дополнительных линий и приводящей к цепочке вычислительных задач, которые позволяют получить ответ на поставленный в задаче вопрос. Важно осознавать, что все дополнительные построения выполняются не произвольно, а в соответствии с теми закономерностями, которые изучаются в теоретической части школьного курса стереометрии.

Осуществлять пространственные построения на экране компьютера с возможностями перемещений или поворотов изображения, и тем самым облегчающий приобретение навыков решения стереометрических задач на трудной начальной стадии решения позволяет электронный учебно-методический комплекс (ЭУМК) «Стереометрия», созданный как вспомогательный инструмент для изучения стереометрии, педагогами из Новосибирска Ю.В.Михеевым, А.В.Овчинниковым, Г.Б.Чернецовой. Задачник программы позволяет решать задачи на пересечение прямой с многогранником, построение сечений многогранников, угол между плоскостями, угол между прямой и плоскостью, построение перпендикуляра к плоскости, сложные задачи на перпендикулярность, задачи повышенной трудности. Предусмотрена также возможность экспорта текущего состояния чертежа в графический файл, что удобно для создания иллюстраций к текстам или презентациям.

При запуске клиентской части программы на экране компьютера слева вверху расположена строка панели меню, ниже расположена панель для чертежа, справа – панель для текста задачи, слева внизу остается место для появления дополнительных панелей меню. Выбрав в меню кнопку «Файл», можно загрузить локальную задачу. На появившейся вкладке можно выбрать конкретный раздел задачника и в этом разделе конкретную задачу. После выбора конкретной задачи на экране появляется условие задачи и исходный чертеж, становятся доступными кнопки меню, позволяющие перейти к поиску решения задачи.

При решении большинства стереометрических задач, имеющих отношение к многогранникам, при выполнении геометрических конструкций достаточно применять всего два режима: строить прямые и отмечать точки пересечения прямых. Поэтому для формирования ответа при решении задач с помощью программы «Стереометрия» предусмотрено выполнение следующих элементарных действий: строить или стирать точку, строить или стирать отрезки прямых, строить многоугольник по его вершинам. Указанные действия реализуются путем применения одного из следующих режимов, позволяющих построить:

– точку пересечения двух прямых;

– точки пересечения некоторой прямой со всеми прямыми, имеющимися на чертеже;

– точку на отрезке, делящую его в заданном рациональном отношении;

– точку на продолжении отрезка, находящуюся от его конца на расстоянии, пропорциональном длине отрезка с рациональным коэффициентом пропорциональности;

– отрезок прямой, соединяющий две заданные точки;

– отрезок прямой с одним из концов в данной точке, который параллелен данной прямой;

– отрезок прямой с одним из концов в данной точке, который перпендикулярен данной прямой (перпендикуляр к прямой);

– отрезок луча, представляющий биссектрису данного плоского угла.

Названия точек при построениях могут быть введены с клавиатуры, а могут быть внесены при помощи клика по правой кнопке мыши в момент, когда курсор мыши подведен к нужной точке.

Ответом в задаче может быть точка, отрезок, угол или многоугольник. Это означает, что, выбрав соответствующий пункт в меню, можно ввести ответ задачи в виде геометрической фигуры, обозначенной названиями точек из числа точек, имеющихся на чертеже. Программа анализирует введенный вариант на правильность ответа и выдает соответствующее сообщение.

1. Чтобы построить точку пересечения двух прямых, необходимо ввести их обозначения. При этом нужная прямая может обозначаться любыми двумя различными точками этой прямой из числа имеющихся на чертеже. В случае, когда обозначение некоторой прямой вводится некорректно, программа выдает соответствующее сообщение. После ввода данных программа производит анализ и либо строит их точку пересечения, либо выдает сообщение, по каким причинам такое построение не реализуемо (прямые скрещивающиеся, параллельны, совпадают).

2. Чтобы построить точку X на отрезке AB, необходимо ввести обозначение отрезка и отношение в виде m/n, которому равно отношение AX/XB. При этом концы отрезка должны существовать на чертеже и быть различными точками, а числа m и n должны быть натуральными.

3. Чтобы построить прямую, параллельную данной, а точнее, отрезок такой прямой, сначала необходимо ввести обозначение точки, через которую проводится нужная прямая, а затем любые две точки на прямой, параллельно которой строится искомая прямая.

4. Чтобы построить отрезок перпендикуляра к прямой, необходимо ввести обозначение точки, из которой проводится перпендикуляр, и любые две точки на прямой, к которой проводится перпендикуляр. Не предусмотрено построение перпендикуляра к прямой, который проходит через точку этой прямой, потому что такое построение чаще всего приводит к некоторой неопределенности.

6. Чтобы построить биссектрису плоского угла, достаточно ввести обозначение этого угла. В программе предусмотрено построение биссектрисы плоского угла, величина которого заключена в пределах от 0 до 180.

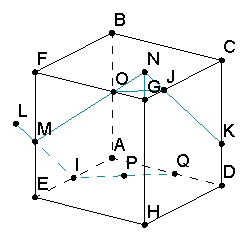
В процессе выполнения указанных действий исходный чертеж преобразуется за счет добавления новых точек, отрезков или прямых. Иногда чертеж может оказаться неудобным.

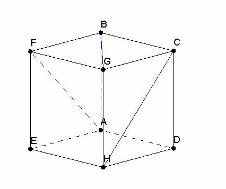Сливающиеся линии АВ и GH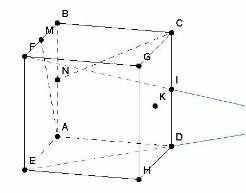

Построенная точка J оказалась вне чертежа

В таком случае предусмотрены возможности видоизменения чертежа. В любой момент решения задачи можно покрутить исходную фигуру вокруг одной из координатных осей. Для этого нужно, зажав левую кнопку мыши, перемещать курсор мыши вправо-влево или вверх-вниз. Можно также изменять масштаб и выполнять некоторые перемещения изображения.

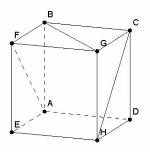После поворота линии уже не сливаются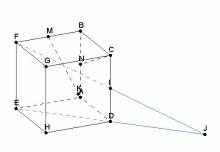

После поворота точка J уже внутри чертежа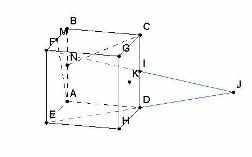

После изменения масштаба точка J уже внутри чертежа

Если на некотором этапе обнаружится, что Вас не удовлетворяет текущий ход решения, можно выбрать пункт меню «Начать заново», при этом восстанавливается начальный чертеж к задаче, а все ранее выполненные построения аннулируются. Работают также кнопки «Шаг назад» и «Шаг вперед».

Применение ЭУМК «Стереометрия» к решению задач непосредственно связано с использованием закономерностей трехмерного пространства. Поэтому теоретическую основу для работы с программой «Стереометрия» составляет учебный материал, который изучается в соответствии со школьным курсом стереометрии:

– аксиомы стереометрии, отражающие основные свойства взаимного расположения точек, прямых и плоскостей в пространстве;

– определения параллельности прямых в пространстве, параллельности прямой и плоскости, параллельности плоскостей;

– определения перпендикулярности прямой и плоскости, расстояния от точки до плоскости, угла между плоскостями, угла между прямой и плоскостью;

– признаки параллельности прямых, параллельности прямой и плоскости, параллельности плоскостей;

– признаки перпендикулярности прямой и плоскости, перпендикулярности плоскостей;

– теорема о трех перпендикулярах.

На основе перечисленных свойств с помощью возможностей ЭУМК «Стереометрия» удается реализовать решение задач по всем принципиальным направлениям школьного курса стереометрии. Укажем эти направления и приведем некоторые примеры.

I. Начальный этап изучения стереометрии относится к определению взаимного расположения точек, прямых и плоскостей в пространстве. Для этого нужно освоить решение задач следующего вида:

– найти пересечение данных прямых;

– найти пересечение данной прямой с данной плоскостью;

– найти пересечение данных плоскостей.

Решение перечисленных задач основывается на аксиомах стереометрии и простейших следствиях из них.

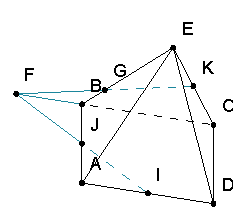
Пример 1. В правильном тетраэдре ABCD построить сечение, проходящее через центр грани BCD и точки M, N на ребрах AB и AC такие, что AM:MB=CN:NA=1:2. («Сечение тетраэдра через 2 точки на ребрах и центр грани»)

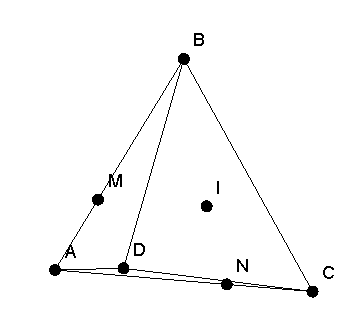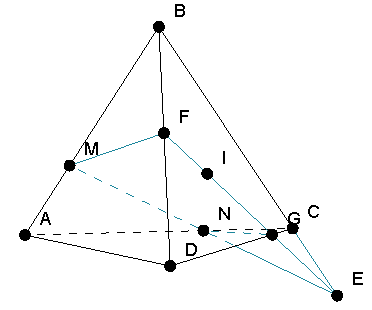Решение. Заметим, что точки M и N лежат в одной плоскости ABC, причем отрезок MN не параллелен отрезку BC. Построив отрезок MN, заметим, что точка I не лежит ни с одной из данных точек в одной плоскости. Чтобы изменить указанную ситуацию, будем искать дополнительную точку секущей плоскости, принадлежащую одной из граней тетраэдра, на которых уже имеется одна точка сечения. Например, построим точку пересечения прямой MN с плоскостью грани BCD. Для этого построим точку E пересечения прямых MN и BC. Точки F и G пересечения прямой FE с прямыми CD и BD являются точками секущей плоскости, которые находится в плоскости грани BHDG. Многоугольник MFGN является искомым сечением тетраэдра плоскостью MNI.

II. Очередной этап изучения стереометрии относится к изучению параллельности в пространстве. Для этого нужно освоиться с определениями параллельности прямых, параллельности прямой и плоскости, параллельности плоскостей и с решением задач следующего вида:

– построить прямую, которая проходит через данную точку и параллельна данной прямой;

– построить плоскость, которая проходит через две данные точки и параллельна данной прямой;

– построить плоскость, которая проходит через данную точку и параллельна двум данным прямым;

– построить плоскость, которая проходит через данную точку и параллельна данной плоскости.

Решение всех перечисленных задач основывается на определениях параллельности, свойствах параллельности, признаках параллельности прямых, параллельности прямой и плоскости, параллельности плоскостей.

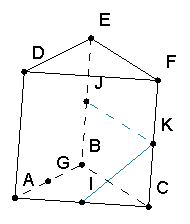
Пример 2. В правильной треугольной призме ABCDEF построить сечение, проходящее через центр грани DEF и параллельное плоскости AEC. («Сечение призмы»)

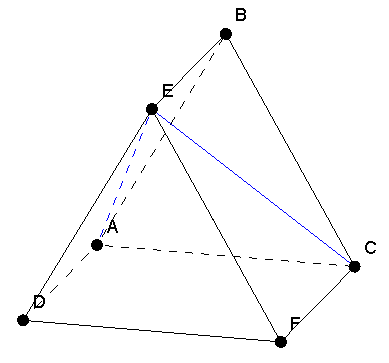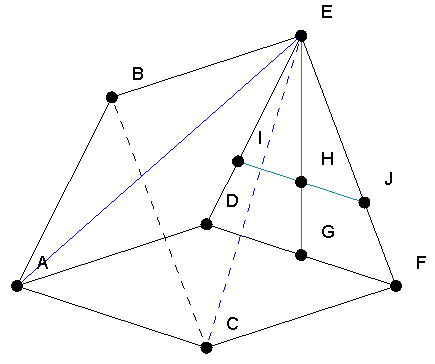Решение. Сначала построим центр грани DEF как точку H, делящую медиану EG в отношении 2:1. Построим прямую, которая проходит через точку H параллельно прямой DF. Отметим, что любая плоскость, проходящая через прямую IJ, по соответствующему признаку будет параллельна прямой AC. Затем через точку I проводим прямую, параллельную прямой AO. Для этого достаточно отметить точку, делящую отрезок AD в отношении 2:1. Аналогично строим прямую в плоскости BEF, параллельную EC. На основании указанного признака параллельности плоскостей плоскость NLI является искомой, так как содержит прямые IL и NL, которые параллельны прямым EA и CA соответственно..

Умения находить точки пересечения прямых и плоскостей, а также производить построения параллельных прямых и плоскостей служат основой для решения практически всех стереометрических задач.

III. Очередной этап изучения стереометрии относится к изучению перпендикулярности прямой и плоскости в пространстве. Для этого нужно освоиться с определением перпендикулярности прямой и плоскости, признаком перпендикулярности и с решением задач следующего вида:

– построить перпендикуляр из данной точки к данной плоскости;

– имея некоторый перпендикуляр к данной плоскости, построить другой перпендикуляр к этой плоскости, проведенный из данной точки.

Пример 3. В кубе ABCDEFGH построить отрезок перпендикуляра, проведенный из точки C к плоскости BDG. («Расстояние от вершины куба до заданной плоскости1»)

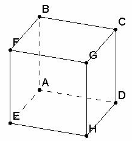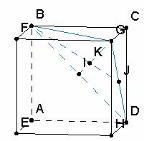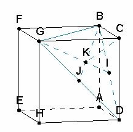Решение. Выделим плоскость BDG, построив отрезки ее пересечения с гранями куба. Затем построим точку K пересечения медиан треугольника BDG. Нетрудно понять, что перпендикуляром из точки C плоскости к плоскости BDG есть отрезок CK. Для обоснования этого итога достаточно осознать, что наклонные CB, СG и CD равны, точка K – центр правильного треугольника BDG.

Задачи на построение сечений многогранников плоскостями, проходящими через три заданные точки, также целесообразно рассматривать на начальном этапе изучения стереометрии. В задачах такого вида сначала желательно обращать внимание на плоскости граней многогранника и смотреть, в какой из них расположено две из указанных точек секущей плоскости. Если такая грань имеется, то можно рассмотреть прямую, проходящую через эти две точки, и точки ее пересечения с другими прямыми в плоскости грани. Если такой грани нет, то задача существенно усложняется.

IV. Очередной этап изучения стереометрии относится к изучению двугранных углов. Умение решать задачи с двугранными углами чаще всего напрямую зависит от умения строить перпендикуляры, так как по своему смыслу величина двугранного угла характеризуется величиной линейного угла, который получается при построении в гранях лучей с общей вершиной на ребре двугранного угла, которые перпендикулярны к ребру. Линейный угол можно получать также как пересечение двугранного угла с плоскостью, которая перпендикулярна ребру двугранного угла.

(«Угол между боковыми гранями пирамиды»).

V. Иногда рассматриваются задачи на вычисление величины угла между прямой и плоскостью. Умение решать задачи с этими углами также зависит от умения строить перпендикуляры, так как угол между наклонной прямой и плоскостью определяется как угол между этой прямой и ее ортогональной проекцией на плоскость («Угол между заданной прямой и гранью призмы»).

VI. Одним из разделов школьного курса стереометрии является изучение тел вращения, в том числе изучение сферы и шара. ЭУМК «Стереометрия» можно приспособить к решению задач, относящихся к сферам, если ограничиваться только построением центров сфер и некоторых радиусов, так как эта часть работы непосредственно зависит от умения строить перпендикуляры к плоскостям и прямым. Действительно, если известно, что сфера касается плоскости, то радиус, проведенный в точку касания, перпендикулярен к этой плоскости; если сфера касается прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Условия для сферы, проходящей через некоторые точки, также удается представить в терминах перпендикулярности. А именно, если сфера проходит через концы отрезка, то центр сферы содержится в плоскости – серединном перпендикуляре к этому отрезку; если сфера проходит через вершины треугольника, то ее центр принадлежит прямой, которая проходит через центр описанной вокруг треугольника окружности и перпендикулярна к плоскости треугольника.

Приведенные примеры наглядно демонстрируют широкие возможности ЭУМК «Стереометрия» по компьютерной поддержке всего школьного курса стереометрии в старших классах общеобразовательной школы. Работа с данной компьютерной программой обеспечивает не только наглядность при изучении данного материала, но и в значительной степени способствует развитию логического мышления, так как процесс работы над задачами предполагает поиск каждого очередного действия на основании анализа той ситуации, которая возникает в результате применения всех предшествующих действий. Оставаясь наедине с компьютером, такие ученики довольно быстро начинают экспериментировать, «нажимать кнопки», и таким образом, получая от компьютера ответную реакцию, постепенно осваиваются, и через какое-то время начинают выполнять успешные действия. Конструктивная направленность программы позволяет обращать внимание на одну из частей решения абсолютного большинства задач по стереометрии.

Наиболее важной чертой программы является генератор задач, который позволяет учителю простыми и наглядными средствами пополнять список задач и добавлять новые разделы. При создании новой задачи при помощи генератора задач можно задавать все вершины и ребра вручную, а можно начать построение с автофигуры (куб, призма, треугольная или четырехугольная пирамида) и вручную добавить лишь дополнительно заданные на этой фигуре точки. Цвета построенных отрезков определяются пользователем. Для того чтобы невидимые линии рисовались пунктиром, надо в редакторе задач все грани фигуры задать прозрачными.

Особый эффект в обучении достигается в сочетании мультимедийных демонстраций с использованием интерактивной доски, которая может применяться и на уроках геометрии. Использование интерактивной доски на уроках геометрии позволяет учителю решать сразу же несколько задач:

• демонстрировать заранее подготовленные чертежи и динамические модели фигур и их комбинаций;

• в короткий промежуток времени проводить дополнительные построения на готовых чертежах к рас­сматриваемым задачам, тем самым максимально эффективно расходовать время урока;

• самостоятельно в интерактивном режиме создавать изображения фигур; сохранять выполненные в ходе урока чертежи.

Графические пакеты и особенно стереоконструкторы позволяют изменить отношение учащегося к геомет­рическому объекту, созданному своим трудом. Он помнит процесс его создания, какие трудности пришлось преодолеть, прежде чем прийти к желаемому результату. Применение стероконструкторов и графических пакетов в обучении:

• развивает навыки самостоятельного мышления;

• повышает самооценку учащегося;

• выявляет заинтересованность и потребность в получении дополнительных знаний;

• пробуждает интерес к научной деятельности;

• формирует положительное и ответственное отношение к учебе, при этом прослеживается тенденция к росту успеваемости.


4. Практикум «Решение задач на построение сечений с помощью ЭУМК «Стереометрия»

Раздел: Сечения многогранников (1 уровень)

1. Сечение треугольной призмы1



2. Сечение четырехугольной пирамиды1



3. Сечение куба по трем точкам на ребрах3